3.7 Carga Ativa em Espelho

3.7.1 Introdução

O principal desafio proposto para realização do amplificador diferencial desde o início desse capítulo foi: ter dois amplificadores simples iguais que formassem uma saída proporcional à diferença entre as entradas de cada um deles, eliminando o ruído (sinal em modo comum) no processo de amplificação. Vimos algumas alternativas que nos ajudassem a melhorar a $CMRR$ e também reduzir as dimensões físicas do circuito¹⁸. O que nos falta agora é arranjar uma forma de manter o circuito equilibrado, transistores amplificadores e de carga iguais entre si, porém fornecendo a saída com apenas uma única conexão.

Essa característica é essencial para que possamos acoplar outros estágios simples, formando o que chamaremos de amplificadores multiestágio. Os amplificadores multiestágio são o assunto do próximo capítulo. O circuito integrado comercial com amplificadores multiestágio mais conhecido é o amplificador operacional. Isto é, para que possamos chegar ao circuito de um amplificador diferencial, precisamos que o amplificador diferencial, circuito de entrada, possa se conectar com amplificadores simples, que têm apenas uma entrada.

A modificação do circuito da seção anterior para que essa característica seja viabilizada pode ser vista nas Figuras 3.8 e 3.9 nas suas versões NMOS e PMOS, respectivamente.

Figura 3.8: Amplificador diferencial NMOS com carga ativa em espelho.

Figura 3.9: Amplificador diferencial PMOS com carga ativa em espelho.

Existe uma diferença entre as tensões disponíveis para ambos os amplificadores: $V_{DD}$ e terra, para a versão NMOS, e $V_{DD}$ e $V_{SS}$ para a versão PMOS. Essa diferença é proposital para mostrar que há possibilidades diversas para a elaboração desse amplificador, tudo dependendo do objetivo de uso desse amplificador e, de forma direta, das tensões disponíveis no sistema em que esse amplificador será inserido.

A grande diferença aqui é que teremos a carga ativa (que nos ajuda com o tamanho físico do dispositivo) conectada em espelho de corrente. A carga ativa em espelho nos ajuda a “transportar a corrente” da entrada 1, ou não-inversora, para a entrada 2, inversora, possibilitando que as duas correntes geradas pelas tensões de entrada possam produzir a tensão de saída na impedância de saída, presente no dreno de $M_{2}$ e $M_{4}$.

Importante observar que o espelho de carga ativa também serve para manter as correntes de polarização o mais próximo da igualdade possível, tornando:

• $I_{{DS}_1}=I_{{DS}_2}$;
• $g_{m_1}=g_{m_2}$ e $g_{m_3}=g_{m_4}$;
• $r_{o_1}=r_{o_2}$ e $r_{o_3}=r_{o_4}$.

Sim, haverá desbalanço entre a corrente $i_{d_1}$ de referência, no dreno de $M_{1}$, e a corrente $i_{d_1}$ espelhada no dreno de $M_{2}$ pois $v_{o}$ poderá flutuar numa tensão diferente de $V_{DD}-|V_{{GS}_3}|$.

Contudo o amplificador diferencial com carga ativa em espelho ainda é uma solução muito adequada para a proposta inicial:

• Formada apenas por trasistores, o que leva a um consumo de área de chip menor que as versões passivas;

• Usa um espelho de corrente como carga ativa, possibilitando a saída estar disponível em apenas 1 (um) nó;

• Usa uma fonte de corrente de polarização que permite uma elevação da $CMRR$, sendo o ganho em modo comum menor que o ganho diferencial.

Os detalhes da operação do circuito concernentes aos modos de operação serão abordados nas próximas seções.

3.7.2 Análise em Modo Diferencial

O modo diferencial, embora esteja explicitado nos circuitos anteriores de forma mais genérica, seja na Figura 3.8 ou na Figura 3.9, será aqui detalhado suficientemente para que compreendamos a sua operação. Podemos dizer que há essa apresentação pelo fato de $i_{d_1}$ e $i_{d_2}$ terem os seus sentidos opostos, tal como foi mostrado na Seção 3.6.1. Com os amplificadores perfeitamente equilibrados, a tensão diferencial se divide igualmente entre $M_{1}$ e $M_{2}$, causando a diferença de sinais das correntes, mantendo o seu módulo igual.

O que precisa ficar explicitado aqui é como essas correntes interagem no nó $v_{o}$ de saída. Para iniciarmos a análise, repetiremos a Figura 1.51, com o modelo de pequenos sinais do MOSFET para baixas frequências.

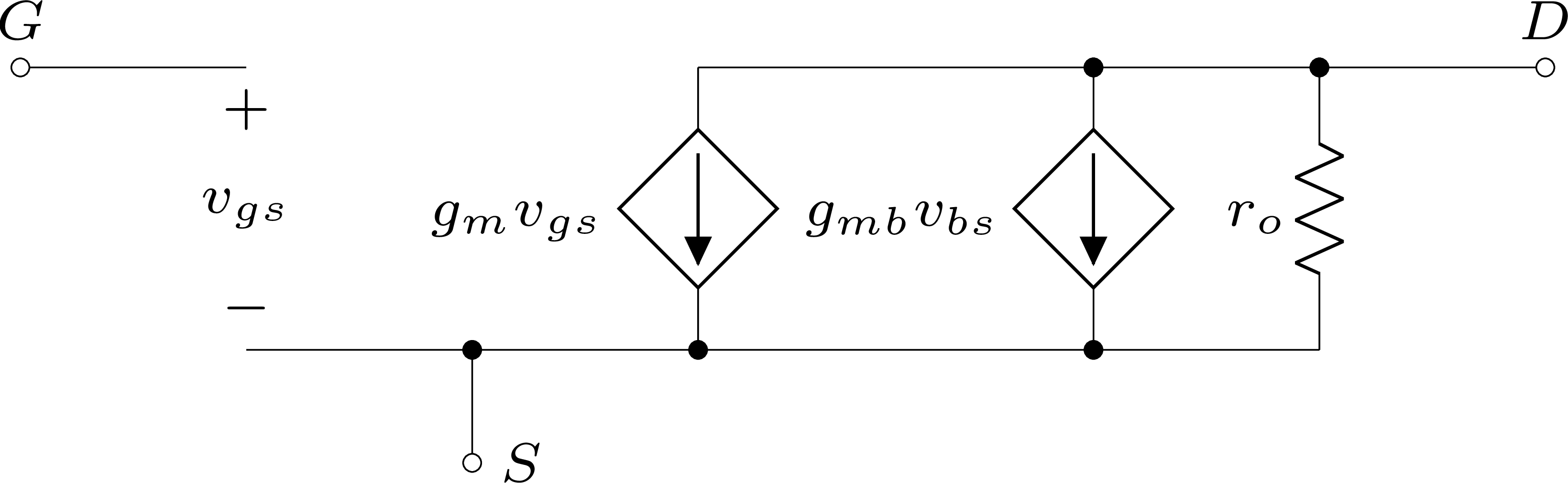
Figura 3.10: Modelo de pequenos sinais de MOSFET para baixas frequências.

Replicando esse modelo para os quatro transistores, podemos chegar ao circuito da Figura 3.11. Para ver a figura em tamanho maior, clique aqui. As conexões entre dreno e fonte de $M_{3}$ e entre as portas de $M_{3}$ e $M_{4}$ estão explicitadas na figura.

Figura 3.11: Modelo de pequenos sinais do Amp. Diferencial com carga ativa em modo diferencial.

Tendo essa última figura como base, faremos algumas mudanças no circuito para simplificar a sua análise. Começaremos pela fonte de corrente de $M_{3}$: a tensão que controla a fonte é a própria tensão nos terminais da fonte, $v_{gs_3}$, o que configura o comportamento de um resistor ôhmico. Logo, podemos substituir essa fonte por um resistor com resistência igual a $\dfrac{1}{g_{m_3}}$. Essa tensão $v_{gs_3}$ que é igual à $v_{bs_4}$ por força das ligações feitas.

E, para facilitar a análise do circuito também substituiremos as correntes das fontes dependentes de $M_{1}$ e $M_{2}$:

• $i_{g_1}\ =\ g_{m_1} v_{{gs}_1}$
• $i_{b_1}\ =\ g_{{mb}_1} v_{{bs}_1}$
• $i_{g_2}\ =\ g_{m_2} v_{{gs}_2}$
• $i_{b_2}\ =\ g_{{mb}_2} v_{{bs}_2}$

Essas mudanças estão expostas na Figura 3.12, a seguir. Para ver a figura em tamanho maior, clique aqui.

Figura 3.12: Modelo de pequenos sinais do Amp. Diferencial com carga ativa em modo diferencial - Simplificado.

No que concerne aos transistores do circuito, no modo diferencial, nenhum deles sofrerá o efeito de corpo. Para $M_{3}$ e $M_{4}$, corpo e fonte estão no mesmo potencial. Sendo a tensão diferencial de entrada dividida igualmente entre $M_{1}$ e $M_{2}$ e também recorrendo às Equações (3.4) e (3.5), podemos dizer que:

• $v_{gs_1}\ =\ \dfrac{v_{id}}{2}$

• $v_{gs_2}\ =\ -\dfrac{v_{id}}{2}$

A fonte de corrente $g_{m_4}v_{gs_3}$ fará o espelhamento de $i_{d_1}$, mantendo o seu sentido em relação ao que está no modelo. A corrente $i_{d_2}$ terá o seu sentido invertido ao do modelo já que $v_{gs_2}< 0$. Esses são os sentidos que estão nas Figuras 3.8 e 3.9. Como já explicado anteriormente, sendo as correntes iguais em módulo, mas com sentidos contrários, então a corrente de sinal em $R_{B}$ será nula.

Fazendo-se a análise por partes, começamos com apenas o sinal $v_{i_1}$ ativo e $vido$, aterrado. Nesse caso, do transistor $M_{2}$ restará apenas $r_{o_2}$ conectada entre $v_{o}$ e o terra de sinal, aparecendo em paralelo com $r_{o_4}$. Se a saída dependesse apenas de $i_{d_1}$, então ela seria:

$$\begin{equation} v_{o_1}\ =\ g_{m_4}v_{gs_3}(r_{o_2}||r_{o_4})\ =\ g_{m_1}v_{gs_1}(r_{o_2}||r_{o_4})\ =\ \dfrac{1}{2}g_{m_1}v_{id}(r_{o_2}||r_{o_4}) \tag{3.20} \end{equation}$$

As igualdades se explicam pelo fato de que $i_{d_1}=g_{m_1}v_{gs_1}=g_{m_4}v_{gs_3}$. Ou seja, Se $M_{2}$ estiver completamente desligado, a tensão de saída é dependente apenas de $v_{i_1}$, cujo efeito se faz presente na saída através do espelho de corrente. Seguiremos com a análise com o caso contrário: $M_{1}$ está desligado e $M_{2}$ está ligado. Nesse caso, a fonte de corrente $g_{m_4}v_{gs_3}$ estará desligada, restando do transistor $M_{4}$ apenas $r_{o_4}$ no circuito, conectado entre $v_{o}$ e o terra. Para o transistor $M_{2}$ temos:

• A fonte $g_{m_2}v_{gs_2}$ estará ativa pela entrada $v_{i_2}$;

• A fonte $g_{{mb}_2}v_{bs_2}$ estará desativada, pois $v_s$ será terra de sinal (ver Seção 3.5);

• A resistência de saída $r_{o_2}$ estará em paralelo com $r_{o_4}$, entre $v_{o}$ e o terra.

Consideradas essas observações, podemos escrever a saída em função da entrada $v_{i_2}$:

$$\begin{equation} v_{o_2}\ =\ g_{m_2}v_{gs_2}(r_{o_2}||r_{o_4})\ =\ \dfrac{1}{2}g_{m_2}v_{id}(r_{o_2}||r_{o_4}) \tag{3.21} \end{equation}$$

Importante notar o sentido da corrente $i_{d_2}$ que leva à saída com sinal positivo em relação a entrada $v_{i_2}$. Pelo teorema da superposição podemos escrever a expressão final para a saída em função de ambas as entradas:

$$\begin{equation} v_{o}\ =\ v_{o_1} + v_{o_2}\ =\ \dfrac{1}{2}g_{m_1}v_{id}(r_{o_2}||r_{o_4}) + \dfrac{1}{2}g_{m_2}v_{id}(r_{o_2}||r_{o_4})\ =\ g_{m_2}v_{id}(r_{o_2}||r_{o_4}) \tag{3.11} \end{equation}$$

Logo o ganho em modo diferencial ou apenas ganho diferencial é:

$$\begin{equation} A_{d}\ =\ g_{m_2}(r_{o_2}||r_{o_4}) \tag{3.22} \end{equation}$$

3.7.3 Análise em Modo Comum

Para a entrada em modo comum, teremos:

• $v_{gs_1}\ =\ v_{gs_2}\ =\ v_{cm}$

Sendo as tensões porta-fonte iguais, em módulo e sinal, então também serão mantidos os sentidos das correntes das fontes dependentes. Também já foi analisado anteriormente: ambas as correntes se somarão em $R_{B}$, levando a $v_s\ \neq 0$. Esse fato muda a condição do efeito de corpo para os transistores de entrada, estando as fontes dependentes ativas no caso do modo comum. Essa situação pode ser acompanhada na Figura 3.13, a seguir.

Figura 3.13: Modelo de pequenos sinais do Amp. Diferencial com carga ativa em modo comum.

O fato de $v_s$ não ser mais o terra de sinal traz alguns desafios na análise do circuito, mas não intransponíveis. Seguiremos com a análise de forma paulatina, quase passo a passo. Primeiramente escreveremos as expressões gerais para $i_{d_1}$, $i_{d_2}$ e $v_s$:

$$\begin{equation} i_{d_1}\ =\ i_{g_1}+ i_{b_1}+ \dfrac{v_{d_3}-v_s}{r_{o_1}} \tag{3.23} \end{equation}$$

$$\begin{equation} i_{d_2}\ =\ i_{g_2}+ i_{b_2}+ \dfrac{v_{o}-v_s}{r_{o_2}} \tag{3.24} \end{equation}$$

$$\begin{equation} v_s\ =\ R_{B}(i_{d_1}+ i_{d_2}) \tag{3.25} \end{equation}$$

A partir de $M_{3}$ podemos escrever:

$$\begin{equation} v_{d_3}\ =\ -i_{d_1}\left(r_{o_3}||\dfrac{1}{g_{m_3}}\right)\ =\ -i_{d_1}R_1\because\ R_1=\ \left(r_{o_3}||\dfrac{1}{g_{m_3}}\right) \tag{3.26} \end{equation}$$

No nó de saída, podemos escrever as duas expressões abaixo:

$$\begin{equation} i_{d_2}\ =\ g_{m_4}v_{d_3}+ i_{4}=\ g_{m_4}i_{d_1}R_1\ + i_{4} \tag{3.27} \end{equation}$$

$$\begin{equation} v_{o}\ =\ r_{o_4}i_{4}=\ g_{m_4}i_{d_1}R_1\ + i_{4}=\ (i_{d_2}- g_{m_4}R_1i_{d_1})r_{o_4} \tag{3.28} \end{equation}$$

Para simplificar as análises, trataremos os amplificadores como sendo iguais, de forma que:

• $g_{m_1}=\ g_{m_2}=\ {g_{m}}$
• $g_{{mb}_1}=\ g_{{mb}_2}=\ g_{{m}_{b}}$
• $r_{o_1}=\ r_{o_2}=\ {r_{o}}$
• $g_{{m}_{T}}=\ {g_{m}}+ g_{{m}_{b}}$

Trabalhando os termos da Equação (3.23):

$$\begin{align} i_{d_1}\ &= i_{g_1}+ i_{b_1}- \dfrac{R_1i_{d_1}}{{r_{o}}} - \dfrac{v_s}{{r_{o}}}\\ &= \dfrac{(i_{g_1}+i_{b_1}){r_{o}}-v_s}{{r_{o}}+R_1}\\ &= \dfrac{{g_{m}}v_{cm}{r_{o}}- {g_{m}}v_s{r_{o}}- g_{{m}_{b}}v_s{r_{o}}- v_s}{{r_{o}}+ R_1}\\ &= \dfrac{{g_{m}}{r_{o}}v_{cm}- (1 + g_{{m}_{T}}{r_{o}})v_s}{{r_{o}}+ R_1} \tag{3.29} \end{align}$$

AVISO!

Estamos em construção!

3.7.4 Impedâncias de Entrada e de Saída

3.7.5 Resposta em Frequência

3.7.6 Resumo da Carga em Espelho

3.7.7 Códigos para análise na frequência

---

18. elementos passivos são muito grandes em circuitos integrados.↩︎