5.1 Conceitos Importantes
Uma forma mais atual de se representar a ideia de Black pode ser vista na figura a seguir.
Figura 5.2: Forma mais moderna do sistema de Black.
O estudo dos amplificadores feito até então envolvia a construção de um sistema de amplificação em malha aberta, isto é, havia apenas um sinal de entrada que passaria pelo sistema de amplificação que forneceria um sinal de saída a uma carga. O sistema de amplificação pode ser formado por um único transistor amplificador quanto por um amplificador multiestágio com vários transistores. Nesse último caso então, a depender de quantos e quais estágios estivessem envolvidos e ainda, da tecnologia de fabricação escolhida, pode-se chegar a ganhos muito elevados: \(\geq\ 100.000\times\). O amplificador operacional mais popular do mundo, o 741, tem um ganho de malha aberta de \(200.000\ V/V\), em corrente contínua, com uma faixa de passagem \(< 4\ Hz\), como pode-se ver na sua folha de dados.
É claro que ao se colocar \(1\ V\) na entrada de um amplificador com ganho tão alto, não se terá \(200.000\ V\) na saída, dado que a limitação de tensão será dada pelo circuito de polarização. As perguntas que se pode fazer são:
qual o objetivo de se ter um ganho tão alto?
para que se ter um amplificador com três ou mais estágios?
para que um ganho tão alto com um faixa de passagem tão baixa?
E todas elas podem ser respondidas ao se conhecer a teoria de Black sobre a realimentação negativa. Quando se pensava que, para que os sinais pudessem alcançar maiores distâncias apenas fazendo-se uma realimentação positiva ou apenas amplificadores com ganho maior, de uma certa forma havia razão para se dedicar a isso. Contudo, a questão da estabilidade do sistema se mostrava como um problema. Amplificadores com ganho muito elevado, formados por vários estágios, não se mostravam tão fáceis de se manter operando por muito tempo. A deriva de parâmetros nas válvulas era muito grande com relação a vários fatores, principalmente temperatura e tensão de alimentação. Essa última não tão estável quanto nas fontes que temos hoje. Black trouxe então a realimentação negativa e a grande quebra de paradigma: diminuir o ganho do amplificador ao se fechar a malha.
Sim, ele provou que, ao se fechar a malha negativamente:
O sistema teria seu ganho diminuído;
A polo dominante se deslocaria para frequências mais altas, aumentando a faixa de passagem do sistema;
Haveria uma melhora das condições de acoplamento tanto na entrada quanto na saída;
O nível de ruído seria diminuído na saída;
Haveria menor distorção harmônica na saída devida ao funcionamento do amplificador;
Logo, ao mesmo tempo em que pregava a redução do ganho em malha fechada, Black permitiu que se conseguisse estabilizar a operação de amplificadores com ganhos elevados formados por vários estágios. Dessa forma, ter um ganho tão elevando quando o do 741 não seria um problema, mas sim uma solução para manter o amplificador operanado numa faixa de frequência maior que a de malha aberta. Manter o amplificador operacional.
A seguir faremos uma análise mais minuciosa de resultados extremamente importantes que podem ser retirados desse sistema tão simples.
5.1.1 A influência de \(A(s)\) em \(A_f(s)\)
:::justa
Assim, uma prmeira observação técnica sobre amplificadores realimentados negativamente é a constatação da diminuição do ganho. Usando um sistema mais à teoria adotada nos dias de hoje:
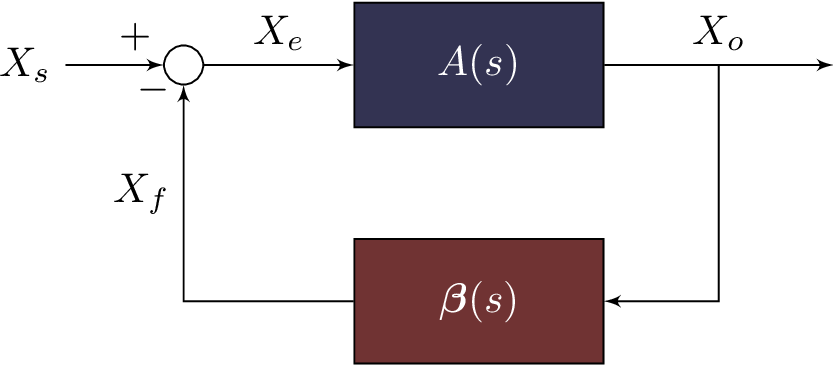
Figura 5.3: Sistema de Black na teoria moderna.
Em que:
- \(X_s\): sinal de entrada;
- \(X_o\): sinal de saída;
- \(X_f\): sinal de realimentação;
- \(X_e\): sinal de erro.
- \(A(s)\): amplificador em malha aberta;
- \(\beta (s)\): malha de realimentação.
Usou-se X como forma genérica, uma vez que pode representar tanto tensão quanto corrente. Para esse sistema, podemos escrever as seguintes equações:
\[\begin{align} X_o &= A(s)X_e \tag{5.1}\\ X_e &= X_s - X_f \tag{5.2}\\ X_o &= A(s)(X_s - X_f) \tag{5.3}\\ X_o &= A(s)[X_s - \beta(s)X_o] \tag{5.4}\\ A(s)X_s &= X_o[1 + \beta(s)A(s)] \tag{5.5} \end{align}\]
Com essas equações podemos escrever a relação de \(X_{o}\) para \(X_{s}\), o que determina o ganho em malha fechada:
\[\begin{equation} A_f(s)\ \equiv\ \dfrac{X_{o}}{X_{s}}\ =\ \dfrac{A(s)}{1 + \beta (s)A(s)} \tag{5.6} \end{equation}\]
Analisando-se a Equação (5.6) a partir da premissa da existência de uma malha aberta necessariamente não-inversora (fase zero), podemos perceber que, a depender da malha de realimentação \(\beta (s)\), poderá haver uma faixa de frequências em que ela será positiva, tornando o denominador maior que o numerador. Nessas condições, o ganho em malha fechada será sempre menor que o ganho de malha aberta.
Resta claro que, sendo a malha de realimentação composta por elementos passivos, alcançar essas condições não é tão complexo assim. No caso específico em que essa malha é composta apenas por resistores, essa condição já é pré-estabelecida. Na presença de capacitores e indutores, a condição já não pode ser estabelecida diretamente e precisará ser analisada para cada malha, já que há dependência da condição com: (i) a quantidade de componentes armazenadores de energia; e (ii) a forma de conexão desses componentes.
Contudo, a segunda observação importante acerca da teoria de Black é que, se o ganho em malha aberta \(A(s)\) for suficientemente grande, pode-se conquistar uma condição muito especial de operação. Avalia-se através do limite do ganho em malha fechada \(A_f(s)\) quando o ganho de malha aberta tende ao infinito:
\[\begin{equation} \lim_{A \to \infty} A_f = \dfrac{1}{\beta} \tag{5.7} \end{equation}\]
Essa é uma das observações mais importantes: com um ganho de malha aberta suficientemente alto, o ganho em malha fechada depende única e exclusivamente da malha de realimentação.
Por simplicidade omitiu-se a dependência com a frequência. Fica implícito que, se numa determinada frequência a condição do ganho de malha aberta não mais se sustentar em valores suficientemente altos, logo, o ganho de malha fechada também dependerá da malha aberta.
É preciso, portanto, definir o que é suficientemente alto. Para tanto, observe as figuras a seguir. Em todos os casos o ganho de realimentação \(\beta\) é unitário, isto é, de acordo com o resultado anterior, para \(A \rightarrow \infty\) o ganho de malha fechada deve tender a \(1/\beta\) que será a unidade. A primeira figura mostra a evolução do ganho de malha fechada com o ganho de malha aberta chegando até \(100\). A segunda, até \(1.000\) e a terceira, até \(10.000\).
Figura 5.4: \(A_f(s)\ \text{vs. }A(s) \rightarrow A_{max}=100\).
Figura 5.5: \(A_f(s)\ \text{vs. }A(s) \rightarrow A_{max}=1.000\).
Figura 5.6: \(A_f(s)\ \text{vs. }A(s) \rightarrow A_{max}=10.000\).
| \(A_{max}\) | \(A_f\) |
|---|---|
| 100 | 0.990099 |
| 1.000 | 0.999001 |
| 10.000 | 0.999900 |
| 200.000 | 0.999995 |
:::
5.1.2 A Dessensibilidade (\(D\))
A segunda observação mais importante que podemos fazer em relação ao sistema anterior é verificarmos a sensibilidade do ganho de malha fechada com o ganho de malha aberta. Isto é, quão sensível torna-se o ganho de malha fechada com as variações do ganho de malha aberta. Para tanto, encontraremos a derivada de \(A_f(s)\) em relação a \(A(s)\):
\[\begin{equation} \dfrac{\partial A_f}{\partial A} = \dfrac{1}{(1+\beta A)^2} \tag{5.8} \end{equation}\]
Usando a definição do ganho de malha fechada, Equação (5.6), podemos reescrever a equação acima de maneira mais apropriada para a análise de sensibilidade:
\[\begin{equation} \dfrac{\partial A_f}{\partial A} = \dfrac{1}{1+\beta A}\times\dfrac{A_f}{A} \Rightarrow \dfrac{\partial A_f}{A_f} = \dfrac{1}{1+\beta A}\dfrac{\partial A}{A} \tag{5.9} \end{equation}\]
Ou ainda na forma final que nos interessa:
\[\begin{equation} \dfrac{\partial A_f}{A_f} = \dfrac{1}{D}\dfrac{\partial A}{A} \tag{5.10} \end{equation}\]
Percebemos que as variações percentuais no ganho de malha fechada tornam-se menos sensíveis às variações do ganho de malha aberta, pela mesma proporção que o primeiro é menor que o segundo. Por isso chamaremos essa quantidade \(D = 1 + \beta A\) de dessensibilidade: o ganho de malha fechada torna-se menos sensível ao ganho de malha aberta quanto maior for a redução do ganho de malha aberta com o fechamento da malha. Ela foi definida a partir do ganho, mas estará presente em todas as análises que faremos de amplificadores realimentados.
Importante destacar uma consequência prática desse resultado:
Num amplificador em malha aberta, variações de temperatura ou das tensões de alimentação introduzem mudanças no ponto de operação que podem afetar significativamente o desempenho do amplificador. Ambos fatores externos estarão presentes em diversos circuitos práticos. Contudo, num amplificador realimentado negativamente, percebemos que as variações no ganho de malha fechada se tornarão muito menores quando comparadas às do ganho de malha aberta, nas memsas condições de perturbação.
O sistema em malha fechada é menos sensível às perturbações externas.
A redução do ganho do amplificador com a malha fechada negativamente, que era um problema, também traz alguns benefícios. Além dos dois que já foram destacados: a independência com o ganho de malha aberta19 e a dessensibilidade do ganho de malha fechada, podemos apontar outros também muito importantes e que, de certa forma já foram apresentados no início da seção, mas não foram formalizados. Isso será feito na próxima seção para o amplificador de tensão e estendido aos demais amplificadores.
5.1.3 Faixa de passagem
Para iniciar e exemplificar o efeito da realimentação negativa na faixa de passagem de um amplificador, tomaremos o caso mais comum dentre os amplificadores operacionais comerciais: um amplificador com apenas 1 polo dominante na faixa de frequência até o ganho unitário. Esse tipo de sistema pode ser aproximado pela função de transferência a seguir:
\[\begin{equation} A(s)\ =\ \dfrac{\omega_{c}A_0}{s + \omega_{c}} \tag{5.11} \end{equation}\]
Esse amplificador, quando numa malha fechada negativamente, leva a um ganho de malha fechada igual a:
\[\begin{align} A_f(s)\ &=\ \dfrac{\dfrac{\omega_{c}A_0}{s + \omega_{c}}}{1 + \beta\dfrac{\omega_{c}A_0}{s + \omega_{c}}}\\ &= \dfrac{{\omega_{c}A_0}}{s + \omega_{c}+ \beta \omega_{c}A_0}\\ &= \dfrac{{\omega_{c}A_0}}{s + \omega_{c}(1 + \beta A_0)} \tag{5.12} \end{align}\]
O que pode ser reescrito como:
\[\begin{equation} A_f(s)\ =\ \dfrac{\omega_{{c}_{f}}A_{f0}}{s + \omega_{{c}_{f}}} \tag{5.13} \end{equation}\]
Em que: \[A_{f0}= \dfrac{A_{0}}{1 + \beta A_{0}}\]
\[\omega_{{c}_{f}}= \omega_{c}(1 + \beta A_{0})\]
Como a relação entre \(\omega_{c}\) e \(f_{c}\) é apenas a constante \(2\pi\), pode-se estender a análise para a frequência linear:
\[\begin{equation} f_{{c}_{f}}\ =\ f_{c}(1 + \beta A_{0}) \tag{5.14} \end{equation}\]
Ou seja, a frequência de corte do sistema aumenta na mesma proporção em que o ganho cai: a dessensibilidade. Voltando à questão da faixa de passagem tão restrita do 741, vemos que ela não é um problema quando a real intenção do projeto de um amplificador operacional é para a operação em malha fechada, com ganhos muito menores que os 200.000 da malha aberta. Isso fará com que o amplificador operacional trabalhe com uma frequência de corte em malha fechada muito mais alta que os \(\hz{4}\).
A Figura 5.7 ilustra essa situação. Claramente há uma simplificação na figura considerando apenas as assíntotas do diagrama de Bode, contudo não deixa de retratar o comportamento real do circuito. Atentar para o fato de que não há como ir além do limite físico do próprio sistema de malha aberta.
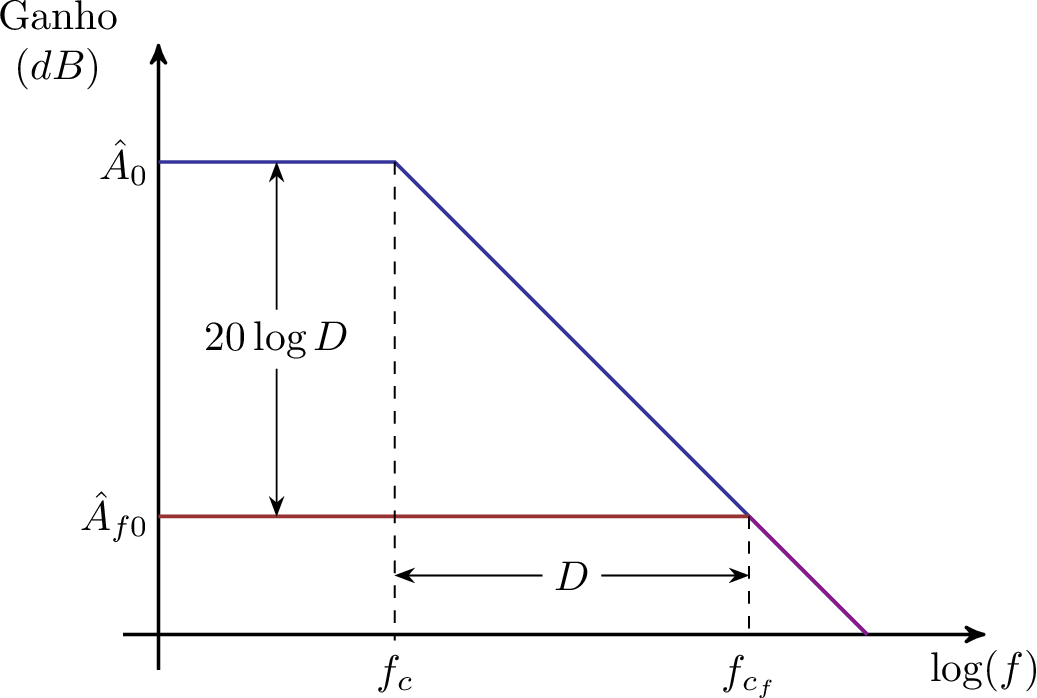
Figura 5.7: Efeito da realimentação negativa na frequência de corte.
Na figura, tem-se que:
\[\hat{A}_0 = 20\log{A_{0}}\] e
\[\hat{A}_{f0} = 20\log{A_{f0}}\]
Para ganhos de malha aberta suficientemente altos.↩︎