2.4 Dreno Comum

Nessa configuração o dreno é o ponto comum (terra de sinal) entre a entrada na porta e a saída na fonte do transistor. Nas Figuras 2.45 e 2.46 pode-se ver as versões com carga resistiva do dreno comum com NMOS e PMOS como amplificador, respectivamente.

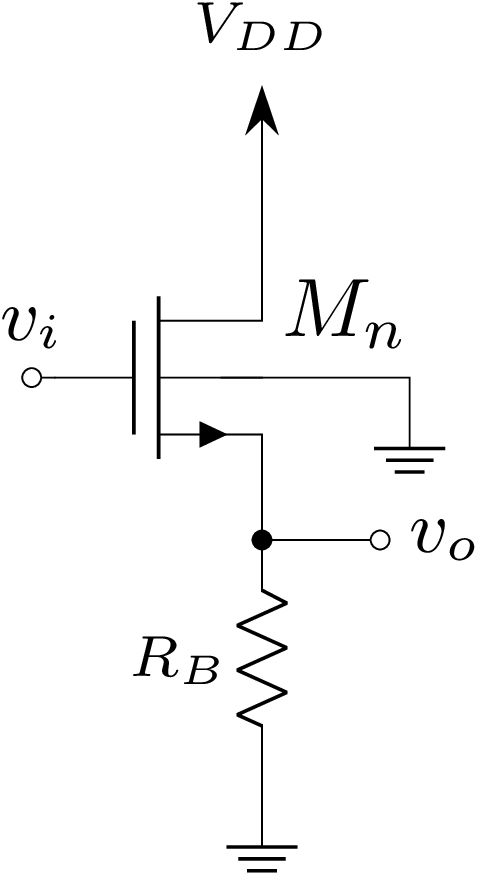
Figura 2.45: Dreno comum NMOS com carga resistiva.

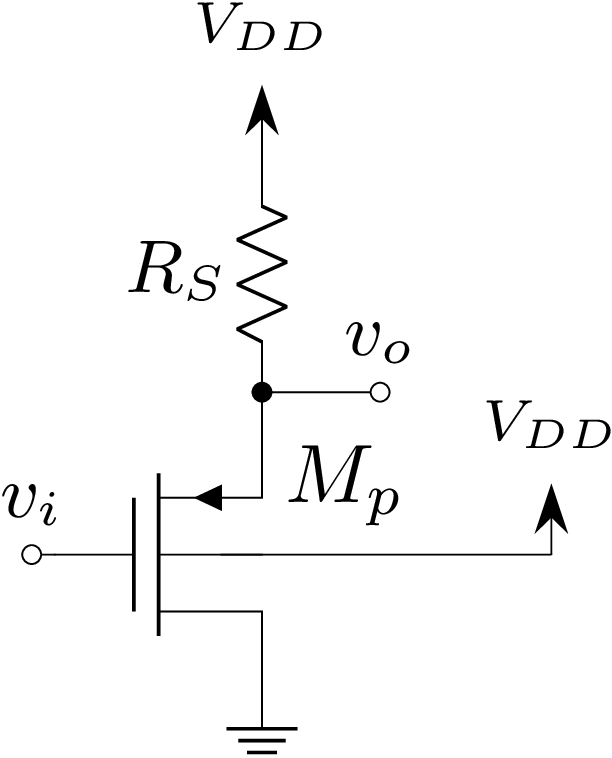
Figura 2.46: Dreno comum PMOS com carga resistiva.

Os motivos para utilização de carga ativa prevalecem para esse amplificador, contudo começaremos com a versão com carga passiva para que se entenda a versão final, com carga ativa provida por espelho de corrente. Para iniciarmos a análise dos circuitos acima vamos montar o circuito de pequenos sinais em baixas frequências para o dreno comum, baseado no modelo geral, que já foi visto na Figura 2.23. Lembre-se que o circuito equivalente serve para ambas as polaridades. Os parâmetros mostrados na figura podem ser relembrados na Seção 1.3. O circuito equivalente desse amplificador pode ser encontrado na Figura 2.47.

Figura 2.47: Modelo de pequenos sinais de um dreno comum para baixas frequências.

Diferentemente do fonte comum, o terminal de corpo tem um papel importante no funcionamento do dreno comum. E, por isso mesmo ele está evidenciado na figura, bem como a tensão \(v_{bs}\). A porta do NMOS estará no terra de circuito enquanto a do PMOS estará em \(V_{DD}\). A fonte de ambos os transistores é a saída do amplificador que flutuará numa tensão contínua certamente diferente de terra ou \(V_{DD}\). Essa condição de operação ativará a fonte de corrente dependente da transcondutância de corpo e a implicação desse fato será explicada adiante.

Do circuito da Figura 2.47 podemos observar as seguintes relações:

• \(v_{gs}=v_{i}- v_{o}\);

• \(v_{bs}=-v_{o}\);

• A fonte de corrente dependente de \(g_{{m}_{b}}\) depende da tensão que está entre os seus terminais e, portanto, comporta-se como um resistor!

A última relação mostrada anteriormente leva ao circuito da Figura 2.48.

Figura 2.48: Modelo de pequenos sinais de um dreno comum para baixas frequências: rearranjo do efeito de corpo.

Também por essa figura nota-se que os três resistores estão em paralelo: conectados entre a saída e o terra de sinal. Podemos então partir para a última simplificação do circuito que é substituir os três resistores por \({R_{o}}=(R_{A}||{r_{o}})||\frac{1}{gmb}\). O circuito final do dreno comum com todas as simplificações listadas pode ser visto na Figura 2.49.

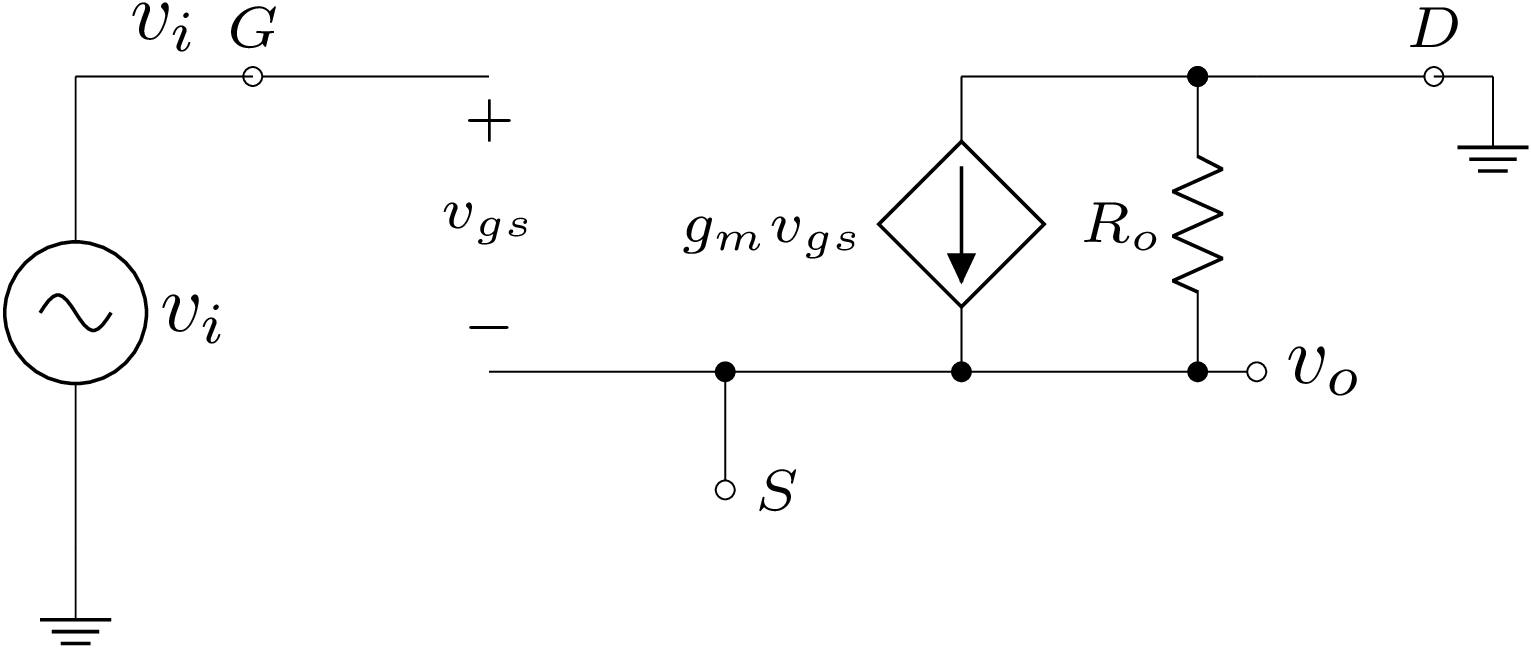
Figura 2.49: Modelo de pequenos sinais de um dreno comum para baixas frequências: circuito final.

A partir da figura podemos calcular o ganho de tensão esperado para dreno comum:

\[\begin{align} v_{o}&= {g_{m}}v_{gs}{R_{o}}\\ v_{o}&= {g_{m}}(v_{i}-v_{o}){R_{o}}\\ v_{o}(1+{g_{m}}{R_{o}}) &= {g_{m}}{R_{o}}v_{i}\\ \dfrac{v_{o}}{v_{i}} &= A_{v}= \dfrac{{g_{m}}{R_{o}}}{1+{g_{m}}{R_{o}}} \\ A_{v}\ &= \dfrac{{g_{m}}\left(R_{A}||{r_{o}}||\dfrac{1}{g_{{m}_{b}}}\right)}{1+{g_{m}}\left(R_{A}||{r_{o}}||\dfrac{1}{g_{{m}_{b}}}\right)} = \dfrac{\left(R_{A}||{r_{o}}||\dfrac{1}{g_{{m}_{b}}}\right)}{\dfrac{1}{{g_{m}}}+\left(R_{A}||{r_{o}}||\dfrac{1}{g_{{m}_{b}}}\right)} \tag{2.21} \end{align}\]

Podemos fazer uma simplificação na expressão acima se considerarmos que tanto \(R_{A}\) quanto \({r_{o}}\) são algumas ordens de grandeza maiores que \(1/gmb\). O que nos permite reescrever o ganho como:

\[\begin{equation} A_{v}\ =\ \dfrac{\dfrac{1}{g_{{m}_{b}}}}{\dfrac{1}{{g_{m}}}+\dfrac{1}{g_{{m}_{b}}}} =\ \dfrac{{g_{m}}}{{g_{m}}+ g_{{m}_{b}}} =\ \dfrac{{g_{m}}}{{g_{m}}+ \chi {g_{m}}}\ =\ \dfrac{1}{1+\chi} \tag{2.22} \end{equation}\]

Em que \(\chi\) é um fator de proporcionalidade entre a transcondutancia de corpo e a transcondutancia de porta. Esse fator de proporcionalidade não é constante e depende de diversos fatores sendo os principais: o ponto de operação e as dimensões do dispositivo. O importante a se ressaltar nesse fator de proporcionalidade é que ele está entre 0 e 1, tipicamente na faixa \(0,\!1 \leq \chi \leq 0,\!3\). Quando analisamos a Equação (2.22), percebemos que, devido ao efeito de corpo, o ganho do dreno comum pode se aproximar da unidade mas nunca chegará lá. Essa é uma diferença grande para os transistores bipolares que não apresentam tal efeito e facilmente chegam a ganhos praticamente unitários¹¹. De maneira prática, com os cuidados com a polarização pode-se obter ganhos acima de \(0,\!8\ V/V\) sem muita dificuldade.

A partir dessas análises iniciais concluímos que o dreno comum não inverte a fase de nenhum sinal e possui ganho entre 0 e 1, o que já o difere muito do fonte comum visto anteriormente.

2.4.1 Carga Ativa

Como já explorado anteriormente para obtermos a versão com carga ativa substituiremos o resistor de carga por um transistor funcionando como corrente. Ao fazer essa substituição podemos chegar aos circuitos das Figuras 2.50 e 2.51.

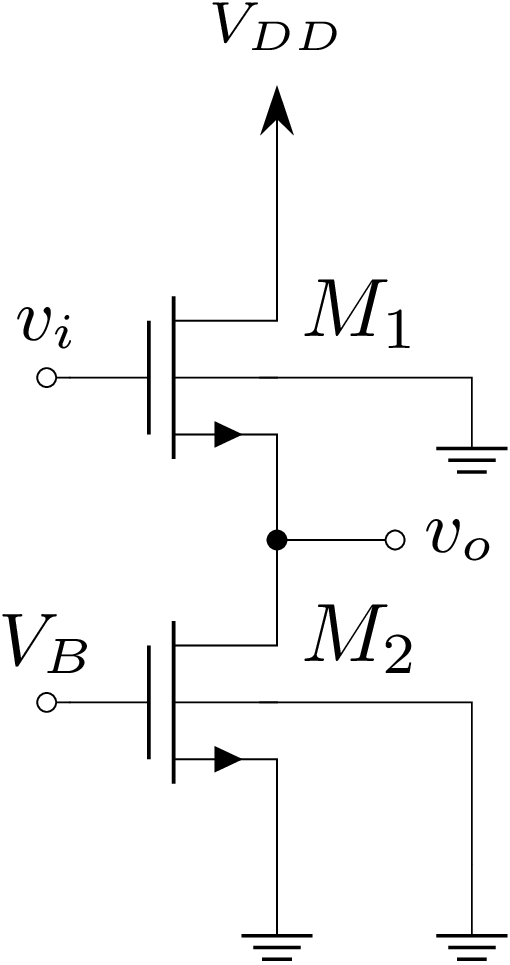
Figura 2.50: Dreno comum NMOS com carga ativa - versão simplificada.

Figura 2.51: Dreno comum PMOS com carga ativa - versão simplificada.

Esses circuitos são equivalentes aos circuitos das Figuras 2.52 e 2.53 logo a seguir.

Figura 2.52: Dreno comum NMOS com carga ativa - versão com fonte de corrente.

Figura 2.53: Dreno comum PMOS com carga ativa - versão com fonte de corrente.

Ao aplicarmos a análise de pequenos sinais nos circuitos das Figuras 2.52 e 2.53, a fonte de corrente será aberta restando no circuito apenas a sua resistência de saída. Ou ainda, de forma análoga ao exposto para o fonte comum, chegaremos à conclusão de que o modelo de pequenos sinais para o transistor de carga ativa se resume apenas à sua resistência de saída. Enfim, tal como foi para o fonte comum também é verdadeiro para o dreno comum que o circuito equivalente de pequenos sinais é único, independentemente se a carga é passiva ou ativa. A conclusão direta de tudo isso é que a expressão de ganho é a mesma em qualquer situação, mudando apenas o valor da resistência de carga.

E, construindo o circuito completo do dreno comum: amplificador junto com a fonte de corente, implementada com um espelho de corrente, chegamos às Figuras 2.54 e 2.55. As ligações do terminal de corpo dos transistores foram omitidas por simplicidade.

Figura 2.54: Dreno comum NMOS com carga ativa - circuito completo.

Figura 2.55: Dreno comum PMOS com carga ativa - circuito completo.

2.4.2 Resistências de Entrada e de Saída

Falta analisarmos as resistências de entrada e saída. Começamos com a mais simples de analisar que é a resistência de entrada, a qual consideraremos como infinita. Mesmo que haja uma corrente de porta não zero, ela é muito pequena e será desprezada, o que faz com que \(R_{in}=\infty\).

Análise de resistência de saída é feita da mesma forma, em todos os casos. Forma que repetiremos aqui, por simplicidade:

• a entrada do circuito deve ser nula para que não interfira na análise e

• aplica-se uma fonte de teste \(V_{X}\) no terminal de saída do amplificador, sendo a resistência de saída a resultante da expressão:

\[\begin{equation} R_{out}\ =\ \dfrac{V_{X}}{I_{X}} \tag{2.23} \end{equation}\]

Para calcularmos a resistência de saída do dreno comum tomaremos por base o circuito da Figura ??.

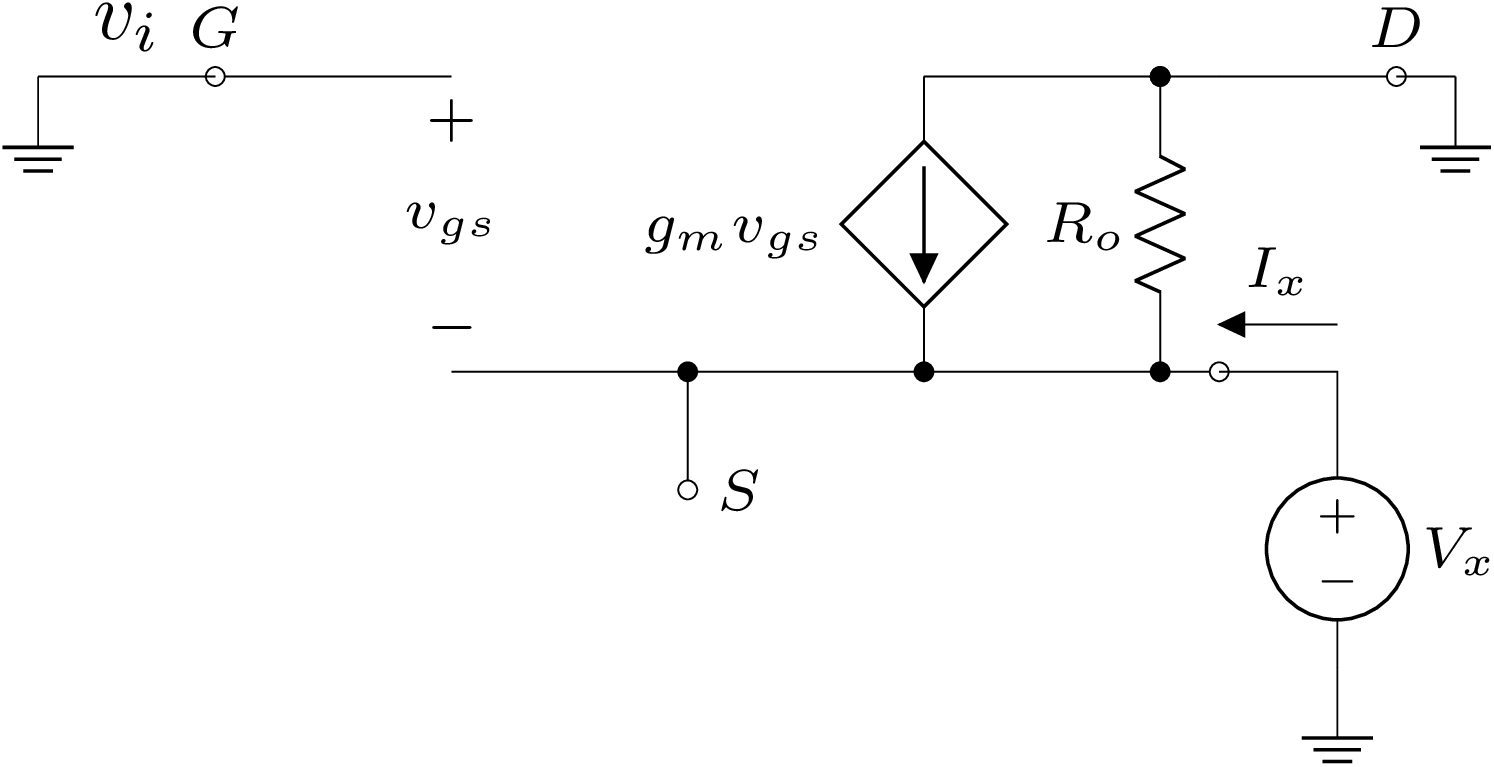
Figura 2.56: Modelo de pequenos sinais de um dreno comum para baixas frequências: análise da resistência de saída.

Pela figura é possível ver que \(v_{gs}=-v_{o}=V_{X}\). E, portanto, a fonte de corrente dependente tem o seu sentido inverso ao que está na figura. Isso nos permite escrever a equação a seguir:

\[\begin{align} I_{X}&= {g_{m}}V_{X}+ \dfrac{V_{X}}{{R_{o}}} \\ {R_{o}}I_{X}&= {g_{m}}{R_{o}}V_{X}+ V_{X}\\ {R_{o}}I_{X}&= V_{X}(1+{g_{m}}{R_{o}})\\ R_{out}&= \dfrac{V_{X}}{I_{X}}\ =\ \dfrac{{R_{o}}}{1+{g_{m}}{R_{o}}} \\ R_{out}&= \dfrac{\left(R_{A}||{r_{o}}||\dfrac{1}{g_{{m}_{b}}}\right)}{1+{g_{m}}\left(R_{A}||{r_{o}}||\dfrac{1}{g_{{m}_{b}}}\right)} \tag{2.24} \end{align}\]

Essa última expressão com as mesmas simplificações usadas para o ganho de tensão pode ser reduzida a:

\[\begin{equation} R_{out}\ =\ \dfrac{\dfrac{1}{g_{{m}_{b}}}}{1+\dfrac{{g_{m}}}{g_{{m}_{b}}}}\ =\ \dfrac{1}{{g_{m}}+g_{{m}_{b}}} \tag{2.25} \end{equation}\]

A Equação (2.25) evidencia que, com os devidos cuidados de polarização, a resistência de saída do dreno comum pode ser muito baixa (\(< 100\ \Omega\)). Outra diferença significativa com relação ao fonte comum. E, tal como foi para o fonte comum, não é coincidência que o ganho de tensão seja:

\[\begin{equation} A_{v}\ =\ {g_{m}}R_{out} \tag{2.26} \end{equation}\]

2.4.3 Modelo para Altas Frequências

A análise em altas frequências¹² para o dreno comum seguirá os mesmos moldes da que foi feita anteriormente para o fonte comum. Primeiramente vamos explicitar as capacitâncias ativas no circuito antes de iniciar a análise em pequenos sinais. As Figuras 2.57 e 2.58 contém as versões NMOS e PMOS do dreno comum com as capacitâncias ativas, respectivamente.

Figura 2.57: Dreno comum NMOS com carga ativa - versão simplificada - altas frequências.

Figura 2.58: Dreno comum PMOS com carga ativa - versão simplificada - altas frequências.

As capacitâncias \(C_{db_1}\), \(C_{gs_2}\) e \(C_{sb_2}\) não estarão ativas pois seus terminais estão ambos em terra de sinal e, portanto, elas não contribuem para a resposta em frequência do circuito. Observando-se essas figuras e adicionando-se as capacitâncias ativas ao circuito de pequenos sinais para baixas frequências (Figura 2.49), podemos chegar ao circuito completo para análise de resposta em frequência para o dreno comum:

Figura 2.59: Modelo de pequenos sinais do dreno comum para altas frequências.

É possível perceber que as capacitâncias ligadas ao nó de saída \(v_{o}\) estão em paralelo e entrarão numa simplificação do circuito com a definição de \(C_{o}=C_{sb_1}||C_{gd_2}||C_{db_2}=C_{sb_1}+C_{gd_2}+C_{db_2}\). Com essa simplificação, obtemos o circuito da Figura 2.60:

Figura 2.60: Modelo final de pequenos sinais do dreno comum para altas frequências.

É possível perceber, devido à ligação do dreno comum, que a sua capacitância de entrada principal é \(C_{gd_1}\) e não estará ativa nessa primeira versão do circuito, tal como foi percebido na análise do fonte comum para a capacitância de entrada \(C_{gs_1}\). Para o circuito da Figura 2.60, podemos escrever a equação para a Lei de Kirchhoff para as correntes do nó \(v_{o}\):

\[\begin{equation} C_{gs_1}s(V_{i}-V_{o}) + {g_{m}}(V_{i}-V_{o}) = \dfrac{V_{o}}{Z_{o}} \tag{2.27} \end{equation}\]

Em que \(Z_{o}={R_{o}}||\dfrac{1}{sC_{o}}=\dfrac{{R_{o}}}{s{R_{o}}C_{o}+ 1}\). Nessa equação e nas próximas em que usamos a variável de Laplace, as tensões e correntes aparecerão em letras miúsculas, indicando que trata-se de uma versão abreviada dessas grandezas no domínio da frequência. Isto é, está implicito que \(V_{i}=V_{i}(s)\) e \(V_{o}=V_{o}(s)\), por exemplo. Desenvolvendo a equação anterior:

\[\begin{align} C_{gs_1}sV_{o}+ \dfrac{V_{o}}{Z_{o}} &= C_{gs_1}sV_{i}+ {g_{m}}(V_{i}-V_{o}) \\ V_{o}\left(C_{gs_1}s + {g_{m}}+ \dfrac{1}{Z_{o}}\right) &= V_{i}\left(C_{gs_1}s + {g_{m}}\right) \\ V_{o}\left(\dfrac{Z_{o}C_{gs_1}s + {g_{m}}Z_{o}+ 1}{Z_{o}}\right) &= V_{i}\left(C_{gs_1}s + {g_{m}}\right) \\ \dfrac{V_{o}}{V_{i}} = A_{v}(s)&= \dfrac{Z_{o}(C_{gs_1}s + {g_{m}})}{Z_{o}C_{gs_1}s + {g_{m}}Z_{o}+ 1} \\ A_{v}(s)&= \dfrac{{R_{o}}(C_{gs_1}s + {g_{m}})}{{R_{o}}C_{gs_1}s + {g_{m}}{R_{o}}+ {R_{o}}C_{o}s + 1}\\ A_{v}(s)&= \dfrac{{R_{o}}(C_{gs_1}s + {g_{m}})}{{R_{o}}(C_{gs_1}+ C_{o})s + {g_{m}}{R_{o}}+ 1} \tag{2.28} \end{align}\]

Tal como esperado, a impedância de entrada \(C_{gd_1}\) não aparece nas equações anteriores. Tal como foi analisado para o fonte comum, o efeito dessa capacitância irá aparecer quando da presença de uma resistência de acoplamento \(R_{sig}\) entre a fonte de sinal \(v_{sig}\) e o amplificador. Da memsa forma que antes, podemos escrever a equação da Lei de Kirchhoff para as correntes no nó de entrada \(v_{i}\):

\[\begin{equation} \dfrac{V_{sig}-V_{i}}{R_{sig}} = C_{gs_1}s(V_{i}-V_{o}) + C_{gd_1}sV_{i} \tag{2.29} \end{equation}\]

Na obtenção da Equação (2.28) tem-se a relação pura entre \(V_{i}\) e \(V_{o}\). Ao substituirmos \(V_{i}\) na Equação (2.29) a partir dessa relação com \(V_{o}\) vinda da Equação (2.28), chegamos à função de transferência do dreno comum, quando há uma resistência de acoplamento entre a fonte de sinal e o amplificador:

\[\begin{equation} A_v \ = \ \dfrac{V_{o}}{V_{sig}}\ =\ \dfrac{{g_{m}}{R_{o}}\left(1+\dfrac{C_{gs_1}}{{g_{m}}}s\right)}{as^2+bs+{g_{m}}{R_{o}}+1} \tag{2.30} \end{equation}\]

Em que:

• \(a = {R_{o}}R_{sig}[C_{gs_1}C_{gd_1}+ C_{o}(C_{gd_1}+C_{gs_1})]\)

• \(b = R_{sig}[C_{gd_1}(1+{g_{m}}{R_{o}})+C_{gs_1}]+{R_{o}}(C_{gs_1}+C_{o})\)

A diferença principal entre o fonte comum e o dreno comum é o terminal de saída. Isso também está contemplado na parte da resposta em frequência relativa ao nó de saída em que \(C_{gd_1}\) e \(C_{gs_1}\) se alternam entre o fonte comum e o dreno comum, respectivamente. Elas são as capacitâncias que fornecem um caminho direto entre entrada e saída para cada amplificador, respectivamente. Funcionam como uma espécie de feedforward próximo da frequência em que sua reatância torna-se pequena o suficiente para que entrada e saída estejam praticamente curto-circuitadas.

Diferentemente do fonte comum, o zero do dreno comum é negativo e tornando-o não susceptível aos problemas de estabilidade em malha fechada tal como o fonte comum. Por fim, tal como observado para o fonte comum, é possível verificar que o ganho em corrente-contínua (baixas frequências ou \(s=0\)) é idêntico ao calculado anteriormente (Equação (2.21)).

2.4.4 Impedâncias de Entrada e de Saída

Agora que já passamos pela análise para altas frequências do amplificador, temos como avançar o modelo completo para aumentarmos a previsibilidade das análises, mesmo que não se tenha uma impedância de acoplamento da fonte de sinal (\(R_{sig}\)) considerável (não desprezível). Para analisarmos as impedâncias de entrada e saída, usaremos as mesmas regras já expostas na Seção 2.4.2. Para as análises das impedâncias usaremos o circuito final da análise em altas frequências exposto na Figura 2.60. Para a impedância de entrada \(Z_{in}\) tomaremos a fonte de teste \(V_{X}\) acoplada diretamente ao nó \(v_{i}\). Na entrada teremos:

\[\begin{equation} I_{X}= C_{gs_1}(V_{X}-V_{o}) s + C_{gd_1}V_{X}s \tag{2.31} \end{equation}\]

E, no nó de saída:

\[\begin{equation} \dfrac{V_{o}}{Z_{o}} = {g_{m}}(V_{X}-V_{o}) + C_{gs_1}(V_{X}-V_{o})s \tag{2.32} \end{equation}\]

No processo de análise, pode-se desevolver a Equação (2.32) para que possamos escrever \(V_{o}\) em função de \(V_{X}\). Ao fazê-lo chegamos a:

\[\begin{equation} V_{o}= \dfrac{Z_{o}(sC_{gs_1}+{g_{m}})}{Z_{o}C_{gs_1}s + {g_{m}}Z_{o}+ 1}V_{X} \tag{2.33} \end{equation}\]

Substituindo-se a Equação (2.33) e a expressão para \(Z_{o}\) na Equação (2.32) e fazendo-se os devidos arranjos, chega-se a:

\[\begin{equation} Z_{in}(s) = \dfrac{{R_{o}}(C_{gs_1}+C_{o})s+{g_{m}}{R_{o}}+1}{{R_{o}}[C_{o}(C_{gs_1}+C_{gd_1})+C_{gs_1}C_{gd_1}]s^2+({g_{m}}{R_{o}}C_{gd_1}+C_{gs_1}+C_{gd_1})s} \tag{2.34} \end{equation}\]

Em termos práticos, para baixas frequências (\(s=0\)) teremos:

\[\begin{equation} \lim_{s \to 0} Z_{in}(s) = \infty \tag{2.35} \end{equation}\]

E, para altas frequências (\(s \to \infty\)) teremos:

\[\begin{equation} \lim_{s \to \infty} Z_{in}(s) = 0 \tag{2.36} \end{equation}\]

Os resultados das Equações (2.35) e (2.36) são compatíveis com o que já se esperava da observação do circuito. Para baixas frequências consideramos a entrada como sendo perfeitamente isolada. E, ao observarmos o circuito para altas frequências (Figura 2.60), em altas frequências a reatância de \(C_{gd_1}\) tenderá a um curto-circuito, de forma que impedância de entrada realmente irá a zero.

Para a impedância de saída, com base no mesmo circuito, lembrando que a entrada deve ser anulada, podemos escrever a equação no nó de saída:

\[\begin{equation} I_{X}= C_{gs_1}V_{X}s + \dfrac{V_{X}}{Z_{o}} - {g_{m}}(0-V_{X}) \tag{2.37} \end{equation}\]

Resolvendo essa equação podemos chegar a:

\[\begin{equation} Z_{out}(s) = \dfrac{{R_{o}}}{{R_{o}}(C_{gs_1}+C_{o})s+{g_{m}}{R_{o}}+1} \tag{2.38} \end{equation}\]

Em termos práticos, para baixas frequências (\(s=0\)) teremos:

\[\begin{equation} \lim_{s \to 0} Z_{out}(s) = \dfrac{{R_{o}}}{1+{g_{m}}{R_{o}}} \tag{2.39} \end{equation}\]

E, para altas frequências (\(s \to \infty\)) teremos:

\[\begin{equation} \lim_{s \to \infty} Z_{out}(s) = 0 \tag{2.40} \end{equation}\]

Esses resultados também estão de acordo com as análises realizadas anteriormente.

2.4.5 Operação em Altas Frequências: Cálculo vs Simulação

Assim como feito para o fonte comum, Seção 2.3.5, faremos também a comparação da análise na frequência do dreno comum com o simulador de circuitos (NGSpice) e um programa de cálculo (Octave). As premissas e parâmetros analisados são os mesmos expostos na referida seção.

A Figura 2.61 contém a saída da simulação do NGSpice para o amplificador sem \(R_{sig}\). O módulo da função de transferência pode ser visto na Figura 2.62 e a fase, na Figura 2.63.

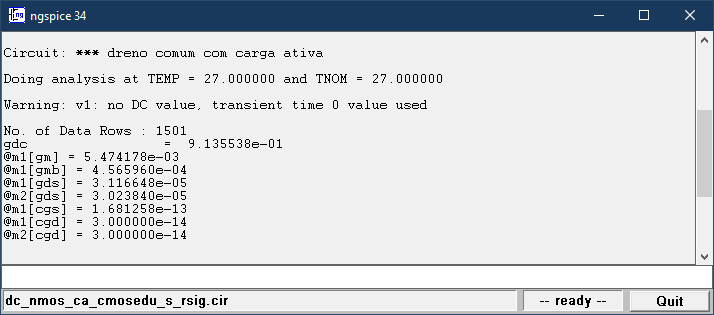
Figura 2.61: Dreno comum: log do NGSpice com resultados da simulação AC. Sem \(R_{sig}\).

Figura 2.62: Dreno comum: módulo da resposta em frequência, resultado da simulação AC. Sem \(R_{sig}\).

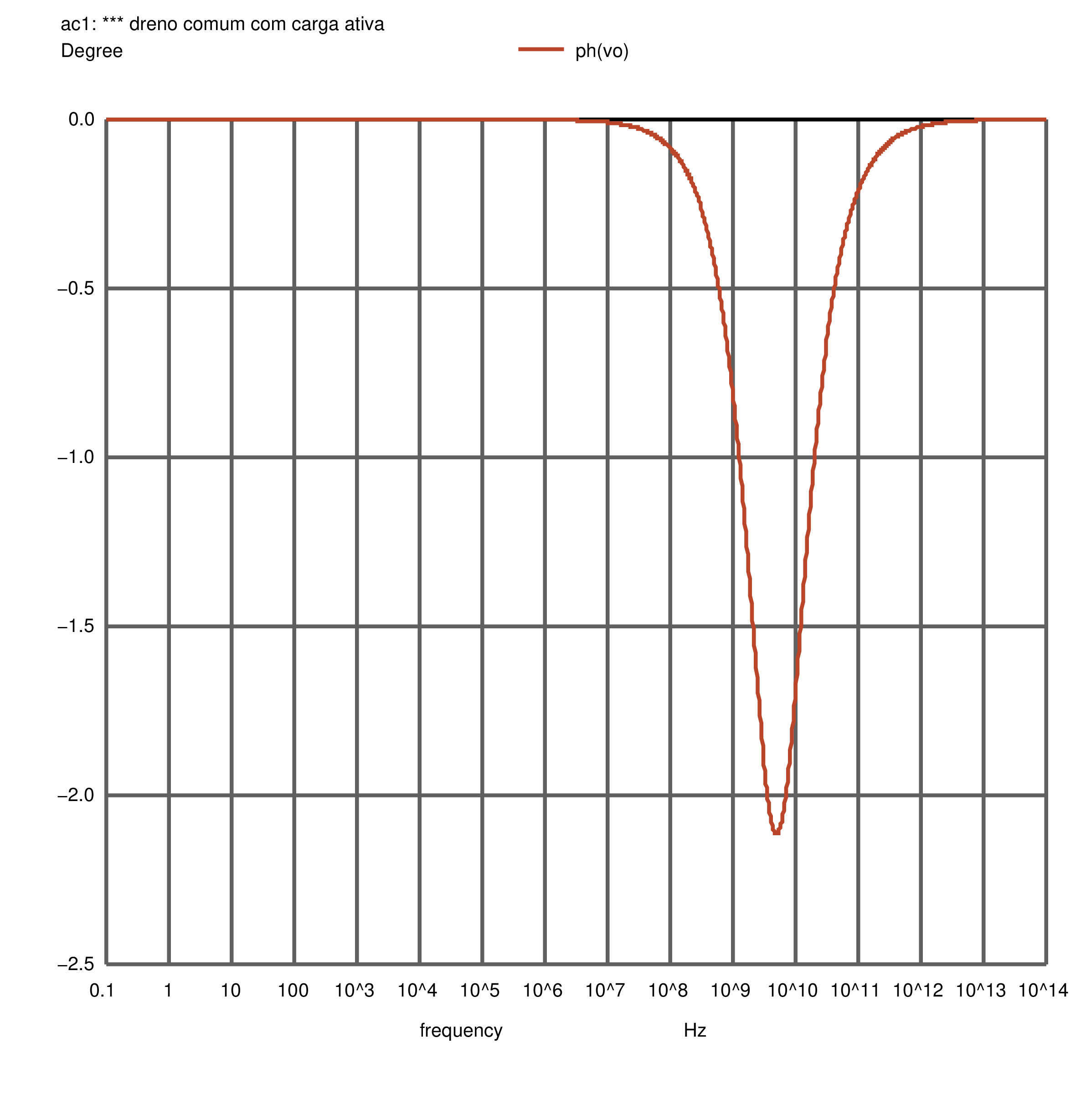
Figura 2.63: Dreno comum: fase da resposta em frequência, resultado da simulação AC. Sem \(R_{sig}\).

Os parâmetros exibidos na Figura 2.61 foram usados para calcular a função de transferência da Equação (2.28) através do Octave e o diagrama de Bode foi traçado, cujo resultado pode ser visto na Figura 2.64.

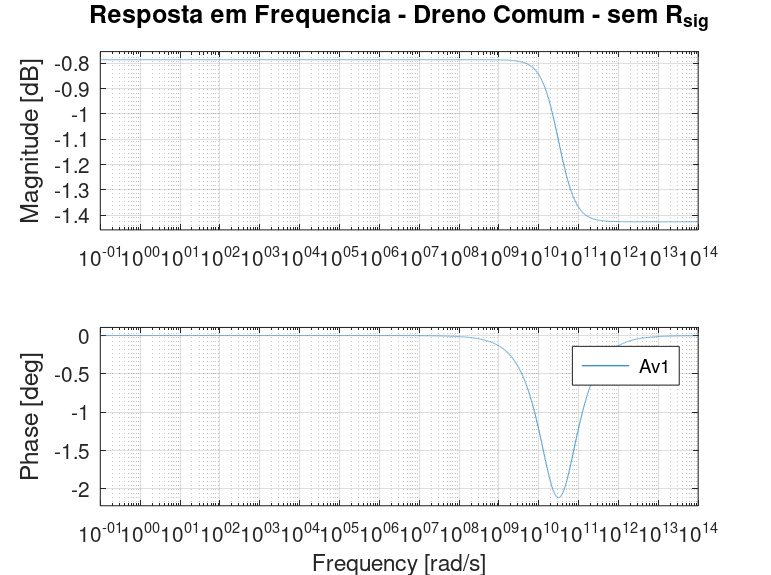
Figura 2.64: Dreno comum: diagrama de Bode calculado no Octave. Sem \(R_{sig}\).

Percebe-se a proximidade das respostas com uma inspeção visual. Proximidade que fica evidente quando usamos os resultados vistos no log do NGSpice e a saída do código do Octave e os colocamos na Tabela 2.4. Importante dizer que não há frequência de corte mensurável para o caso do dreno comum sem \(R_{sig}\), dado que o ganho não diminuirá de \(3\ dB\). Também não haverá frequência de ganho unitário, visto que o ganho inicial já é menor que a unidade.

Tabela 2.4: Dreno Comum - NGSpice vs Octave - Sem \(R_{sig}\).

Parâmetro	NGSpice	Octave	Diferença (%)
Ganho CC	9.135538e-01	9.135538e-01	0e+00
Ganho CC (dB)	-7.853174e-01	-7.853171e-01	4e-05
\(f_{c}\) (Hz)	NA	NA	NA
\(f_u\) (Hz)	NA	NA	NA
Polo 1 (rad/s)	-3.024430e+10	-3.024431e+10	-5e-05
Polo 2 (rad/s)	NA	NA	NA
Zero (rad/s)	-3.256000e+10	-3.256001e+10	-4e-05

Também aqui a referência é dada pelos valores do simulador NGSpice. E, também para o dreno comum, as diferenças entre a simulação e o cálculo manual da função de transferência são desprezíveis, desde que utilizemos os parâmetros de pequenos sinais obtidos a partir da própria simulação. Com esses parâmetros obtidos de outra forma, por aproximação via folha de dados da tecnologia, por exemplo, talvez as diferenças fossem maiores, mas não de forma a dizer que ambos os métodos não se equivalem.

Para o caso da existência da resistência de fonte \(R_{sig}\), que é o caso real de todos os amplificadores, podemos ver a saída da simulação do NGSpice para o amplificador na Figura 2.65. O módulo da função de transferência pode ser visto na Figura 2.66 e a fase, na Figura 2.67.

Figura 2.65: Dreno comum: log do NGSpice com resultados da simulação AC. Com \(R_{sig}\).

Figura 2.66: Dreno comum: módulo da resposta em frequência, resultado da simulação AC. Com \(R_{sig}\).

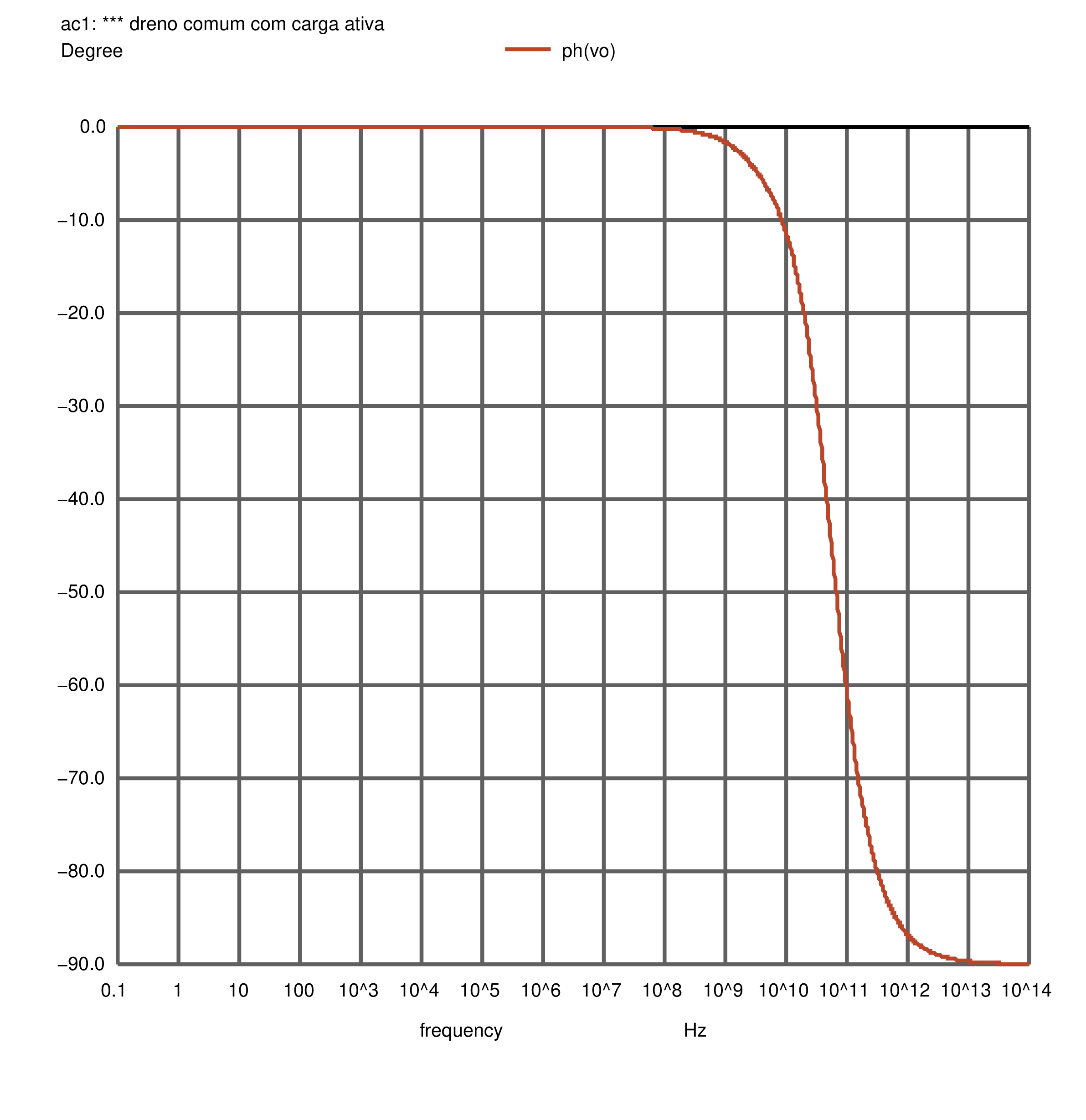
Figura 2.67: Dreno comum: fase da resposta em frequência, resultado da simulação AC. Com \(R_{sig}\).

Os parâmetros exibidos na Figura 2.61 foram usados para calcular a função de transferência da equação (2.30) através do Octave e o diagrama de Bode foi traçado, cujo resultado pode ser visto na Figura 2.68.

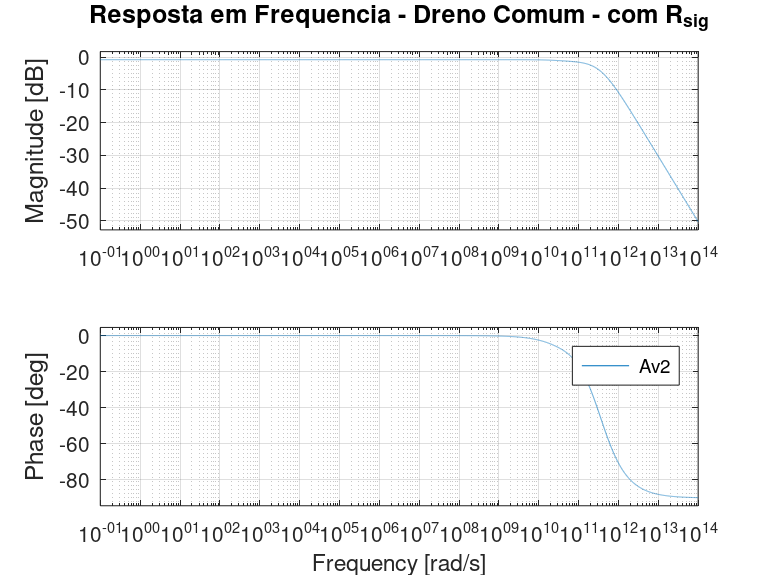
Figura 2.68: Dreno comum: diagrama de Bode calculado no Octave. Com \(R_{sig}\).

Tal como foi para o amplificador sem \(R_{sig}\), visualmente as respostas parecem iguais e, também como antes, uma comparação numérica se faz necessária. A Tabela 2.5 contém o resumo da comparação entre a simulação e o cálculo manual através da função de transferência. Diferentemente do caso sem \(R_{sig}\), há como calcular o equivalente a uma frequência de corte, dado que o ganho cai a ponto de haver uma diferença de \(3\ dB\) em relação ao valor em baixas frequências.

Tabela 2.5: Dreno Comum - NGSpice vs Octave - Com \(R_{sig}\).

Parâmetro	NGSpice	Octave	Diferença (%)
Ganho CC	9.135538e-01	9.135538e-01	0.00000
Ganho CC (dB)	-7.853174e-01	-7.853171e-01	0.00004
\(f_{c}\) (Hz)	5.007604e+10	5.004027e+10	0.07143
\(f_u\) (Hz)	NA	NA	NA
Polo 1 (rad/s)	-3.080070e+10	-3.080062e+10	0.00027
Polo 2 (rad/s)	-3.536120e+11	-3.541234e+11	-0.14461
Zero (rad/s)	-3.256000e+10	-3.256001e+10	-0.00004

2.4.6 Códigos para análise na frequência

Código de simulação (NGSpice) para o dreno comum, sem \(R_{sig}\)

*** Dreno Comum com carga ativa
*** Estudo da resposta em frequencia
*** Sem resistor de fonte
.global gnd vdd vss
.options savecurrents
.options filetype=ascii
.options wnflag=1
.options numdgt=14
.options measdgt=14

*** Circuito completo do Amplificador
** Transistor amplificador: nome dreno porta fonte corpo modelo L= W=
M1 vdd vin vo gnd N_1u L=1u W=150u
** Transistor de carga ativa
M2 vo vb gnd gnd N_1u L=1u W=150u ;L=1.0u W=12u

*** Definicao de parametros e inclusao de arquivos
.include "..\..\..\modelos\cmosedu_models.txt" ; precisa ser modificado para o seu computador
.param offset=4 ; flutuacao continua da senoide de entrada
.param amp=1m ; define a amplitude da senoide de entrada
.param vd=5 ;valor de Vdd
.param vb=1.1 ; polarizacao da carga ativa para ganho maximo

*** Definicao das fontes do circuito
** Fonte CC de alimentacao do circuito
vdd vdd gnd dc {vd}
** Fonte de sinal aplicada a entrada
v1 vin gnd sine ({offset} {amp} 10k) AC 1
** Fonte CC para polarizacao da carga ativa
vb vb gnd dc {vb}
.end

.control
set color0=white ; cor de fundo dos graficos = branco
set color1=black ; cor da grade dos graficos = preto
set units=degrees

*** Analise da resposta em frequencia do circuito
ac dec 100 0.1 100t
** Medicoes de interesse a partir a analise AC
meas ac gdc find vm(vo) at=0.1 ; mede o ganho em corrente continua

*** Impressao dos parametros de pequenos sinais
print @m1[gm] ; mostra a transcondutancia do amplificador
print @m1[gmb] ; mostra a transcondutancia de corpo do amplificador
print @m1[gds] ; mostra a transcondutancia dreno-fonte do amplificador
print @m2[gds] ; mostra a transcondutancia dreno-fonte da carga ativa
print @m1[cgs] ; mostra a capacitancia porta-fonte do amplificador
print @m1[cgd] ; mostra a capacitancia porta-dreno do amplificador
print @m2[cgd] ; mostra a capacitancia porta-dreno da carga ativa

*** Visualizacao dos graficos de magnitude e fase
plot db(vo)
plot ph(vo)

*** Exportar os graficos para arquivo
set hcopypscolor=1 ; ajusta fundo branco para figuras salvas
* Salva em formato EPS os graficos gerados
* observe que apos nome do arquivo a chamada e identica
* a chamada anterior com o comando 'plot'
* O formato pode ser alterado para PostScript (.ps)
hardcopy dc_nmos_ca_resp_freq_s_rsig_mag.eps db(vo)
hardcopy dc_nmos_ca_resp_freq_s_rsig_fase.eps ph(vo)

*** Analise de polos e zeros vistos na transferencia entre
** saida (vo) e entrada (vi)
pz vin 0 vo 0 vol pz
** salva os resultados num arquivo .txt
print all > polos_zeros_s_rsig.txt

.endc

Código de simulação (NGSpice) para o dreno comum, com \(R_{sig}\)

*** Dreno Comum com carga ativa
*** Estudo da resposta em frequencia
*** Com resistor de fonte
.global gnd vdd vss
.options savecurrents
.options filetype=ascii
.options wnflag=1
.options numdgt=14
.options measdgt=14

*** Circuito completo do Amplificador
** Transistor amplificador: nome dreno porta fonte corpo modelo L= W=
M1 vdd vin vo gnd N_1u L=1u W=150u
** Transistor de carga ativa
M2 vo vb gnd gnd N_1u L=1u W=150u ;L=1.0u W=12u

*** Definicao de parametros e inclusao de arquivos
.include "..\..\..\modelos\cmosedu_models.txt" ; precisa ser modificado para o seu computador
.param offset=4 ; flutuacao continua da senoide de entrada
.param amp=1m ; define a amplitude da senoide de entrada
.param vd=5 ;valor de Vdd
.param vb=1.1 ; polarizacao da carga ativa para ganho maximo

*** Definicao das fontes do circuito
** Fonte CC de alimentacao do circuito
vdd vdd gnd dc {vd}
** Fonte de sinal aplicada a entrada com Rsig
v1 vi gnd sine ({offset} {amp} 10k) AC 1
r1 vi vin 50
** Fonte CC para polarizacao da carga ativa
vb vb gnd dc {vb}
.end

.control
set color0=white ; cor de fundo dos graficos = branco
set color1=black ; cor da grade dos graficos = preto
set units=degrees

*** Analise da resposta em frequencia do circuito
ac dec 100 0.1 100t
** Medicoes de interesse a partir a analise AC
meas ac gdc find vm(vo) at=0.1 ; mede o ganho em corrente continua
let gco = gdc/sqrt(2) ; mede o ganho na frequencia de corte: - 3dB
meas ac fcorte when vm(vo)=gco ; mede a frequencia de corte

*** Impressao dos parametros de pequenos sinais
print @m1[gm] ; mostra a transcondutancia do amplificador
print @m1[gmb] ; mostra a transcondutancia de corpo do amplificador
print @m1[gds] ; mostra a transcondutancia dreno-fonte do amplificador
print @m2[gds] ; mostra a transcondutancia dreno-fonte da carga ativa
print @m1[cgs] ; mostra a capacitancia porta-fonte do amplificador
print @m1[cgd] ; mostra a capacitancia porta-dreno do amplificador
print @m2[cgd] ; mostra a capacitancia porta-dreno da carga ativa

*** Visualizacao dos graficos de magnitude e fase
plot db(vo)
plot ph(vo)

*** Exportar os graficos para arquivo
set hcopypscolor=1 ; ajusta fundo branco para figuras salvas
* Salva em formato EPS os graficos gerados
* observe que apos nome do arquivo a chamada e identica
* a chamada anterior com o comando 'plot'.
* O formato pode ser alterado para PostScript (.ps)
hardcopy dc_nmos_ca_resp_freq_c_rsig_mag.eps db(vo)
hardcopy dc_nmos_ca_resp_freq_c_rsig_fase.eps ph(vo)

*** Analise de polos e zeros vistos na transferencia entre
** saida (vo) e entrada (vi)
pz vi 0 vo 0 vol pz
** salva os resultados num arquivo .txt
print all > polos_zeros_c_rsig.txt

.endc

Código de cálculo (Octave) para o dreno comum, sem \(R_{sig}\)

%%% Dreno Comum
%%% Calculo da funcao de transferencia - Sem Rsig
clear all
close all
clc
pkg load control
pkg load signal

%%% Definicao das variaveis vindas da simulacao
% resistencia da fonte de sinal
Rsig=50;
% transcondutancia
gm=5.474178e-3;
% transcondutancia de corpo
gmb=4.565960e-4;
% resistencia de saida M1
ro1=1/3.116648e-05;
% resistencia de saida M2
ro2=1/3.023840e-05;
% resistencia de saida 
Ro1=ro1*ro2/(ro1+ro2);
Ro=1/((1/Ro1)+gmb)
%% Capacitancias dos transistores
Cgs1=1.681258e-13;
Cgd1=3.000000e-14;
Cgd2=3.000000e-14;
Co=Cgd2;

%%% Funcao de transferencia sem Rsig
w = logspace(-1,14,5000);
num1 = [Ro*Cgs1 gm*Ro];
den1 = [Ro*(Cgs1+Co) (gm*Ro+1)];
Av1 = tf(num1,den1);

%%% Calculo, Plotagem e Exportacao de resultados
figure(1);
bode(Av1,w); % calcula o bode do sistema e plota
[m1,f1]=bode(Av1,w); % calcula o bode e armazena os resulados
gcc=m1(1) % ganho em corrente continua
gccdb=20*log10(gcc)
[z,p,k]=tf2zp(num1,den1)
h1=gcf; % armazena info da figura
ax = findall(h1,'type','axes'); % armazena os handles dos eixos 
title(ax(3), 'Resposta em Frequencia - Dreno Comum - sem R_{sig}'); % muda o titulo da figura
title_handle = get(ax(3),'title'); % armazena o handle do titulo do grafico
set(title_handle,'fontsize', 12); % ajusta a fonte do titulo
y1 = get(ax(3),'ylabel'); % armazena o handle do eixo de magnitude
set(y1,'fontsize', 12); % ajusta a fonte do eixo de magnitude
y2 = get(ax(2),'ylabel'); % armazena o handle do eixo de fase
set(y2,'fontsize', 12); % ajusta a fonte do eixo de fase
print -depsc dc_ca_verificacao_resp_freq_s_rsig.eps
print('color','dc_ca_verificacao_resp_freq_s_rsig.png'); % salva um PNG com o bode ajustado

Código de cálculo (Octave) para o dreno comum, com \(R_{sig}\)

%%% Dreno Comum
%%% Calculo da funcao de transferencia - Com Rsig
clear all
close all
clc
pkg load control
pkg load signal

%%% Definicao das variaveis vindas da simulacao
% resistencia da fonte de sinal
Rsig=50;
% transcondutancia
gm=5.474178e-03;
% transcondutancia de corpo
gmb=4.565960e-04;
% resistencia de saida M1
ro1=1/3.116648e-05;
% resistencia de saida M2
ro2=1/3.023840e-05;
% resistencia de saida 
Ro1=ro1*ro2/(ro1+ro2);
Ro=1/((1/Ro1)+gmb)
%% Capacitancias dos transistores
Cgs1=1.681258e-13;
Cgd1=3.000000e-14;
Cgd2=3.000000e-14;
Co=Cgd2;

%%% Funcao de transferencia sem Rsig
w = logspace(-1,14,5000);
a = Ro*Rsig*(Co*(Cgd1+Cgs1)+Cgs1*Cgd1);
b = Rsig*(Cgd1*(1+gm*Ro)+Cgs1)+Ro*(Cgs1+Co);
num2 = [Ro*Cgs1 gm*Ro];
den2 = [a b (gm*Ro+1)];
Av2 = tf(num2,den2);

%%% Calculo, Plotagem e Exportacao de resultados
figure(1);
bode(Av2,w); % calcula o bode do sistema e plota
[m2,f2]=bode(Av2,w); % calcula o bode e armazena os resulados
gcc=m2(1) % ganho em corrente continua
gccdb=20*log10(gcc)
[z,p,k]=tf2zp(num2,den2)
gco=m2(1)/sqrt(2); % ganho na frequencia de corte
i_fc=lookup(m2,gco); % indice da frequencia de corte
wc=w(i_fc) % frequencia de corte, angular
fc=wc/2/pi % frequencia de corte, linear
h1=gcf; % armazena info da figura
ax = findall(h1,'type','axes'); % armazena os handles dos eixos 
title(ax(3), 'Resposta em Frequencia - Dreno Comum - com R_{sig}'); % muda o titulo da figura
title_handle = get(ax(3),'title'); % armazena o handle do titulo do grafico
set(title_handle,'fontsize', 12); % ajusta a fonte do titulo
y1 = get(ax(3),'ylabel'); % armazena o handle do eixo de magnitude
set(y1,'fontsize', 12); % ajusta a fonte do eixo de magnitude
y2 = get(ax(2),'ylabel'); % armazena o handle do eixo de fase
set(y2,'fontsize', 12); % ajusta a fonte do eixo de fase
print -depsc dc_ca_verificacao_resp_freq_c_rsig.eps
print('color','dc_ca_verificacao_resp_freq_c_rsig.png'); % salva um PNG com o bode ajustado

2.4.7 Resumo do Dreno Comum

A Tabela 2.6 contém os principais resultados para o dreno comum que foram analisados ao longo dessa seção. Tal como feito para o fonte comum, as linhas Ganho, \(R_{in}\) ideal e \(R_{out}\) ideal contêm dois valores, cada uma. A de ganho refere-se ao ganho em tensão | corrente. As outras são para entrada e saía em: tensão | corrente, respectivamente. Essas linhas foram colocadas para facilitar a comparação do amplificador em estudo com as características ideais para entrada em tensão ou corrente.

É notório que a impedância de entrada infinita não favorece a utilização do dreno comum como um amplificador com entrada em corrente, já descartando-o para utilização como amplificador de corrente e de transimpedância. Contudo, está adequada para a entrada em tensão, ficando os amplificadores de tensão e de transadmitância favorecidos.

Como sua resistência de saída pode ser muito baixa, isso o torna um excelente amplificador de tensão, mesmo com ganho baixo. Não por acaso é considerado o buffer mais simples possível: ganho unitário, alta impedância de entrada e baixa impedância de saída. Como amplificador de transadmitância, grante-se a entrada, mas a saída fica prejudicada, de forma que essa configuração poderá ser usado para esse fim, apenas não será um excelente amplificador de transadmitância.

Tabela 2.6: Tabela resumo do Dreno Comum.

Parâmetro	Dreno Comum
Ganho	\(\dfrac{{g_{m}}{R_{o}}}{1+{g_{m}}{R_{o}}}\) (\(\approx 1\)) | -
Fase	\(0^o\)
\(R_{in}\) ideal	\(\infty\) | \(0\)
\(R_{{in}}\)	\(\infty\)
\(R_{out}\) ideal	\(0\) | \(\infty\)
\(R_{{out}}\)	\(\dfrac{{R_{o}}}{1+{g_{m}}{R_{o}}}\) (↓)

Em que \({R_{o}}=R_{A}||{r_{o}}||\dfrac{1}{g_{{m}_{b}}}\).

---

11. Diferenças na quinta casa decimal ou menor são possíveis sem muito esforço para os transistores bipolares.↩︎

12. Um detalhamento sobre o que é considerada uma alta frequência foi feito na Seção 2.3.3. Importante ler os dois primeiros parágrafos para melhor compreensão.↩︎