5.2 Modelos e Análise

A análise do sistema simplificado da Figura 5.3 já rendeu dois resultados muito importantes sobre a teoria da realimentação negativa de Black. Para os demais resultados, faremos a transposição dos sistemas mostrados na figura para diagramas de circuito representativos de suas partes. Essa transposição começará com circuitos simplificados sobre os quais os detalhes serão aos poucos acrescentados até que tornem-se abrangentes o suficiente para retratar um sistema real.

Dessa forma, começaremos com circuitos equivalentes aos amplificadores para baixas frequências e com malhas de realimentação ideias. Por malha de realimentação ideal entende-se aquela em que os sinais serão medidos na saída e levados de volta à entrada sem provocar carga em nenhum dos terminais, isto é, não haverá mudanças no sinal de entrada ou de saída pela conexão da malha de realimentação. De maneira prática:

mede-se tensão na saída com uma impedância infinita;
mede-se corrente na saída com um curto-circuito;
realimenta-se tensão na entrada com impedância série (equivalente de Thèvenin) de acompalamento igual a zero;
realimenta-se tensão na entrada com impedância paralela (equivalente de Norton) de acompalamento infinita;

Também por simplificidade, nesse momento não usaremos a impedância de acoplamento da fonte de sinal e nem a impedância de carga alimentada pelo amplificador.

5.2.1 Amplificador de tensão realimentado

As observações anteriores, quando aplicadas a um amplificador de tensão, levam ao seguinte esquema:

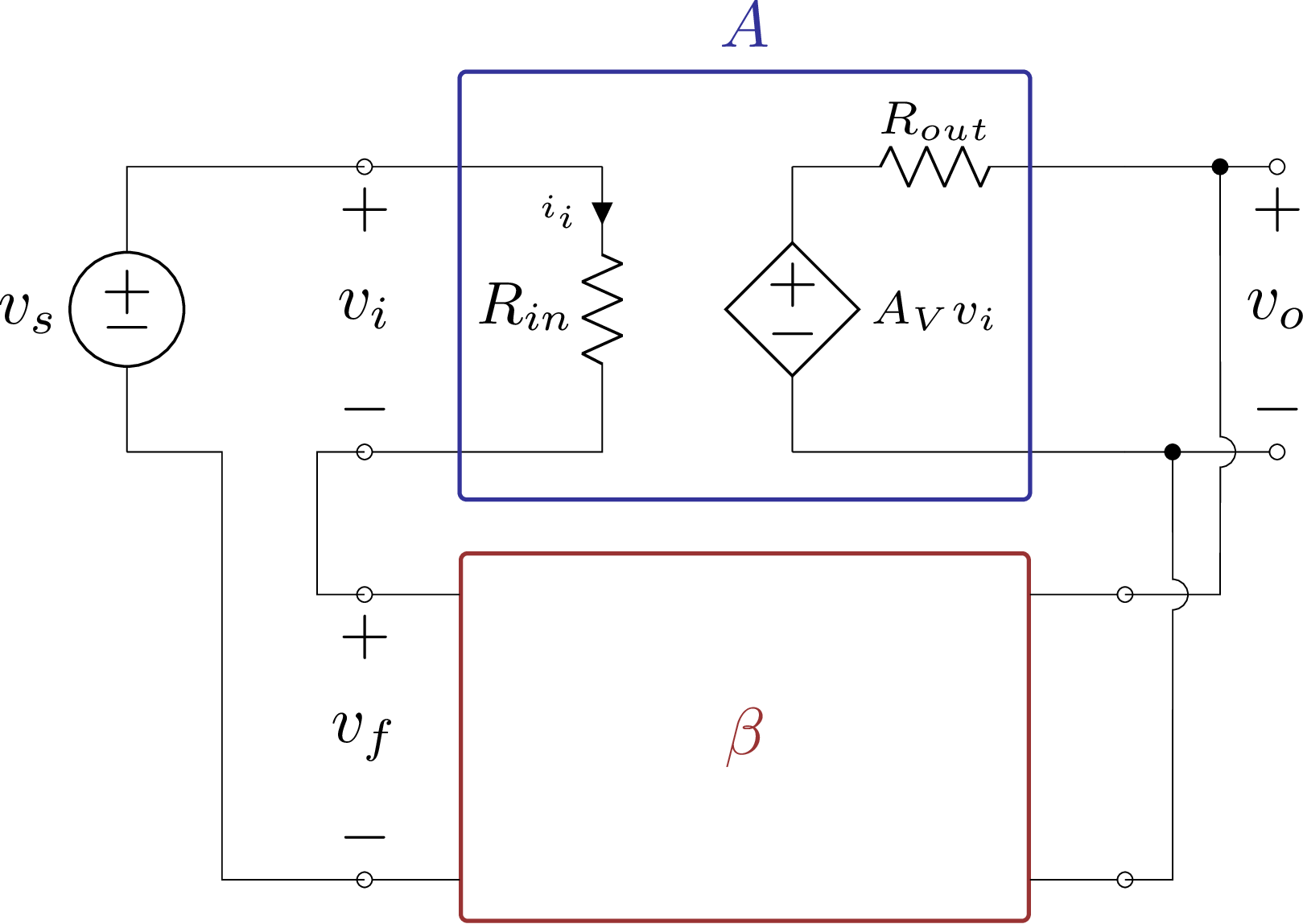
Figura 5.8: Amplificador de tensão realimentado - versão simples.

Em que:

$v_s$: tensão da fonte de sinal;
$v_i$: tensão de entrada do amplificador;
$i_i$: corrente de entrada do amplificador;
$v_o$: tensão de saída do amplificador;
$A_V$: ganho de tensão em malha aberta;
$v_f$: tensão de saída da realimentação;
$R_{in}$: resistência de entrada do amplificador em malha aberta.
$R_{out}$: resistência de saída do amplificador em malha aberta.

Pelo circuito, por analogia ao sistema da Figura 5.3, tem-se que:

$v_s$ é $X_{s}$;
$v_i$ é $X_{e}$;
$v_f$ é $X_{f}$;
$v_o$ é $X_{o}$.

Por mais óbvio que pareça, é importante ressaltarmos os pontos a seguir, pois a complexidade da análise é maior quando tomamos um circuito real ao invés do seu modelo fechado, como dito anteriormente. Logo, nem sempre será fácil separar claramente: a malha de realimentação e os seus sinais de entrada e saída. Eles são:

Uma vez definidos os sinais de entrada e saída, também já estão definidos: o tipo de amplificador (tensão, corrente, transimpedância, transadmitância) e o sinal de realimentação.
Não é possível subtrair tensão de corrente e vice-versa. Logo, num amplificador de transimpedância, é preciso que a malha de realimentação seja de transadmitância e vice-versa.
A subtração de tensão é feita em série e a de corrente em paralelo, logo, cada tipo de sinal terá sua forma de ser realimentado;
A medição de tensão é feita em paralelo e a de corrente em série, logo, cada tipo de sinal terá a sua forma de ser medido para ser realimentado;

Após todas essas observações, podemos começar a análise comparando o ganho em malha fechada desse amplificador com o resultado da equação (5.6):

\[\begin{align} v_o&= A_Vv_i\\ v_o&= A_V(v_s- v_f) \\ v_o&= A_V(v_s- \beta v_o)\\ \dfrac{v_o}{v_s} &= \dfrac{A_V}{1 + \beta A_V} \tag{5.15} \end{align}\]

Para a análise de impedâncias, precisamos lembrar que:

A impedância de entrada de um amplificador com saída em tensão é medida com a saída aberta, isto é, sem carga acoplada;
A impedância de entrada de um amplificador com saída em corrente é medida com a saída aterrada, isto é, em curto-circuito;
A impedância de saída de um amplificador é medida com a entrada de sinal igual a zero:
- Fontes de sinal de corrente serão abertas;
- Fontes de sinal de tensao serão curto-circuitadas.
A impedância de entrada é aquela que a fonte de sinal “enxerga” no circuito;
A impedância de saída é medida através de uma fonte de teste colocada nos terminais de saída do amplificador.

Aplicando-se essas observações ao circuito podemos escrever a impedância de entrada para o amplificador realimentado $R_{{in}_{f}}$:

\[R_{{in}_{f}}\ =\ \dfrac{v_s}{i_i}\] E, pela análise de circuito podemos explicitá-la:

\[\begin{align} v_s&= v_i+ v_f\\ v_s&= R_{in}i_i+ \beta v_o\\ v_s&= R_{in}i_i+ \beta(A_Vv_i) \\ v_s&= R_{in}i_i+ \beta(A_VR_{in}i_i) \\ R_{{in}_{f}}&= R_{in}+ \beta A_VR_{in}\\ R_{{in}_{f}}&= R_{in}(1+\beta A_V)\\ R_{{in}_{f}}&= DR_{in} \tag{5.16} \end{align}\]

Para obtermos a impedância de saída, usaremos a fonte de teste com a fonte de tensão zerada, conforme o circuito abaixo, sabendo que:

\[R_{{out}_{f}}\ =\ \dfrac{v_x}{i_x}\]

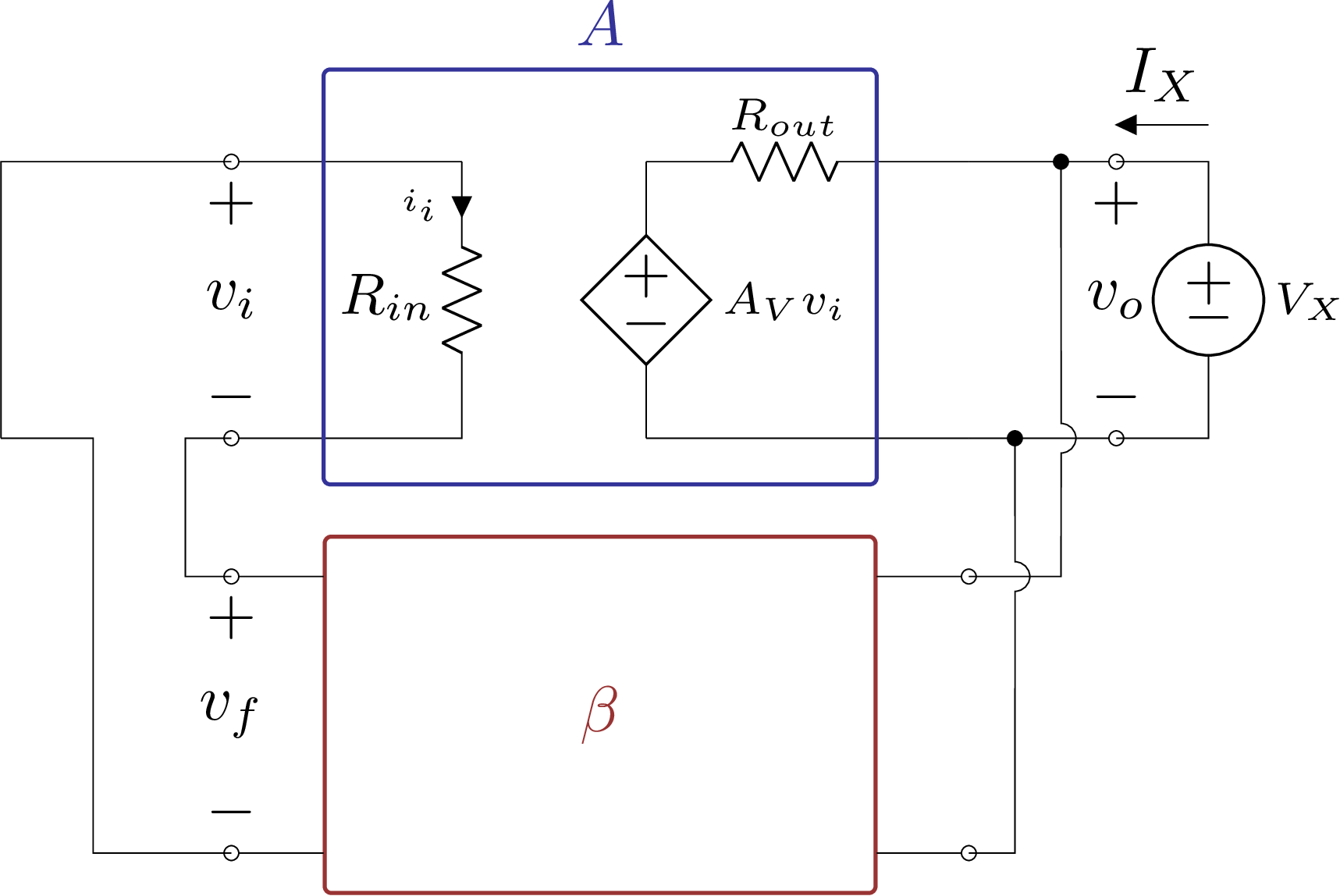
$Cálculo de $R_{{out}_{f}}$ - Amplificador de tensão realimentado.$

Figura 5.9: Cálculo de $R_{{out}_{f}}$ - Amplificador de tensão realimentado.

Pelo circuito:

\[\begin{align} v_x&= A_Vv_i+ R_{out}i_x\\ v_x&= A_V(-v_f) + R_{out}i_x\\ v_x&= A_V(-\beta v_x) + R_{out}i_x\\ v_x&(1 + \beta A_V) = R_{out}i_x\\ R_{{out}_{f}}&= \dfrac{R_{out}}{1 + \beta A_V} \\ R_{{out}_{f}}&= \dfrac{R_{out}}{D} \tag{5.17} \end{align}\]

Pelas análises feitas, constatamos a melhoria de acoplamento introduzida pela realimentação negativa. A impedância ideal de entrada de um amplificador de tensão é infinita, permitindo que não haja efeito de carga na impedância de saída da fonte de sinal. A impedância ideal de saída de um amplificador de tensão é zero, para que a carga possa receber toda a tensão amplificada.

Como a tensão de realimentação é realimentada em série e a tensão de saída é medida em paralelo, diz-se que essa é uma malha de realimentação série-paralelo, na analogia: entrada-saída.

5.2.2 Demais amplificadores

Isso nos permite dizer que a realimentação negativa levou o amplificador de tensão a trabalhar mais próximo do ideal no que se refere às suas impedâncias de entrada e saída. Se fizermos as mesmas análises para os demais amplificadores: corrente, transimpedância e transadmitância, comprovaremos que todos eles terão as suas impedâncias melhoradas com a introdução da realimentação. Esse desenvolvimento não será feito nesse material, contudo, após a tabela resumo a seguir, tem-se os circuitos equivalentes dos demais amplificadores em relação ao sistema básico de realimentação negativo apresentado.

Tabela 5.2: Tabela resumo de sistemas realimentados.
Sinal/Ganho	Amp. Tensão	Amp. Corrente	Amp. Transimpedância	Amp. Transadmitância
$X_s$	Tensão	Corrente	Corrente	Tensão
$X_f$, $X_e$, $X_o$	Tensão	Corrente	Tensão	Corrente
$\beta$	$\dfrac{v_f}{v_o}$	$\dfrac{i_f}{i_o}$	$\dfrac{i_f}{v_o}$	$\dfrac{v_f}{i_o}$
$R_{in}$ ideal	$\infty$	$0$	$0$	$\infty$
$R_{{in}_{f}}$	$R_{in}\times D$ (↑)	$\dfrac{R_{in}}{D}$ (↓)	$\dfrac{R_{in}}{D}$ (↓)	$R_{in}\times D$ (↑)
$R_{out}$ ideal	$0$	$\infty$	$0$	$\infty$
$R_{{out}_{f}}$	$\dfrac{R_{out}}{D}$ (↓)	$R_{out}\times D$ (↑)	$\dfrac{R_{out}}{D}$ (↓)	$R_{out}\times D$ (↑)

Para obter os demais resultados da tabela anterior, pode-se usar os circuitos a seguir.

5.2.2.1 Amplificador de Corrente

Percebe-se que $i_i$ é a diferença entre a fonte de sinal $i_s$ e a corrente de realimentação $i_f$. Logo, se a corrente $i_i$ será menor então a tensão $v_i$ também será e a impedância vista pela fonte $i_s$ será menor.

Sinal de saída em corrente será medido em série idealmente por um curto-circuito. Na saída da malha de realimentação tem-se $i_f$ realimentado em paralelo. Por isso, a malha de realimentação do amplificador de corrente também é chamada de paralelo-série.

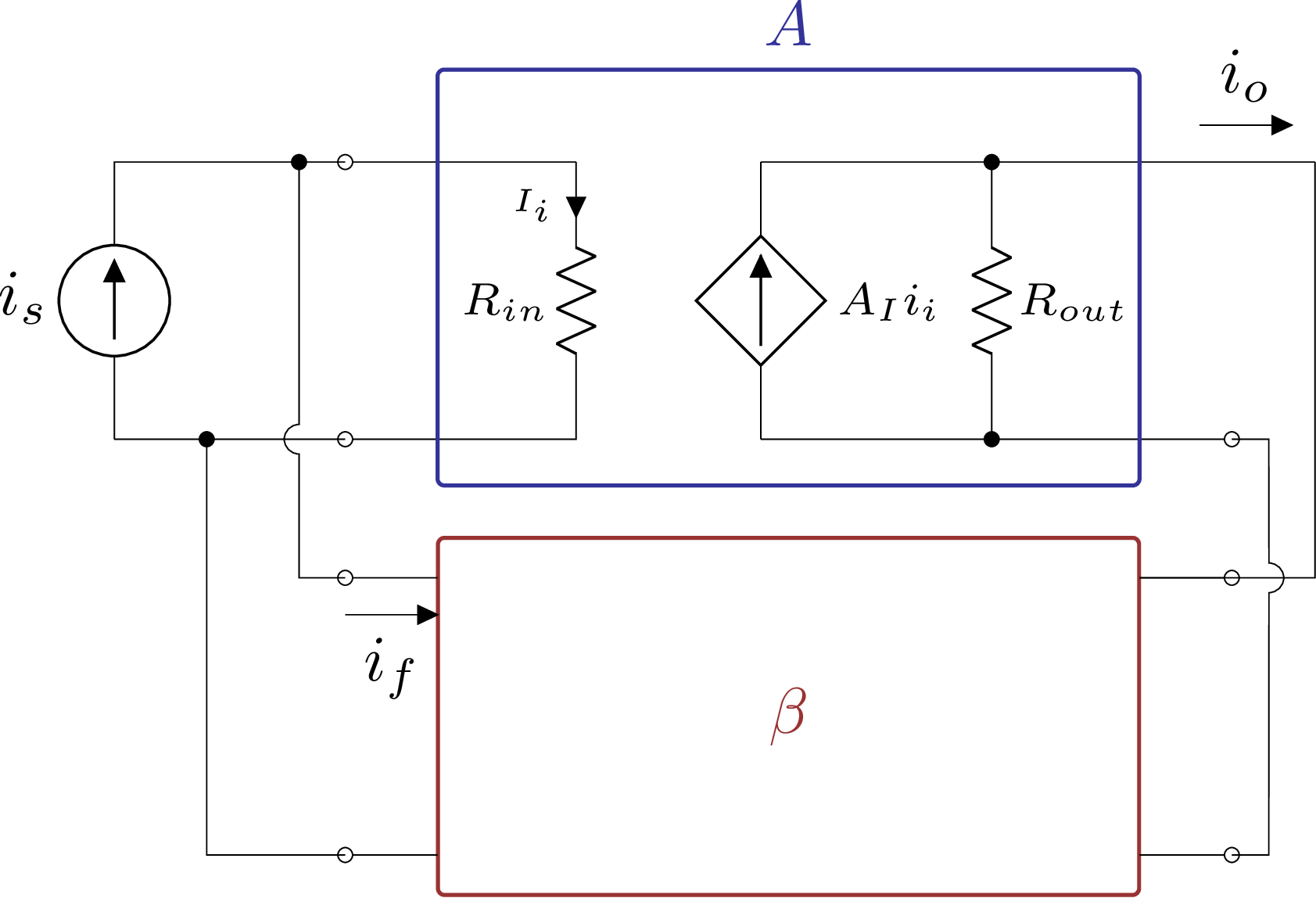
Figura 5.10: Amplificador de corrente realimentado - versão simples.

Para a avaliação da impedância de saída, usa-se a fonte de teste com a fonte de sinal zerada. No caso em questão: aberta. Com isso $i_i=-i_f=-\beta i_o$. Dessa forma a fonte de teste deverá fornecer corrente para $R_{out}$, mas será “ajudada” pela corrente da fonte de amplificação. Dessa forma, dada uma mesma tensão (teste) para uma corrente menor, a impedância vista na saída será maior.

5.2.2.2 Amplificador de Transimpedância

As análises serão muito parecidas com as anteriores para tensão e corrente. A questão é que será feita a medição em paralelo da tensão de saída e realimentação em paralelo da corrente de realimentação.

Seguindo a analogia entrada-saída, aplicada aos demais sistemas, a malha do amplificador de transimpedância realimentado será classificada como paralelo-paralelo.

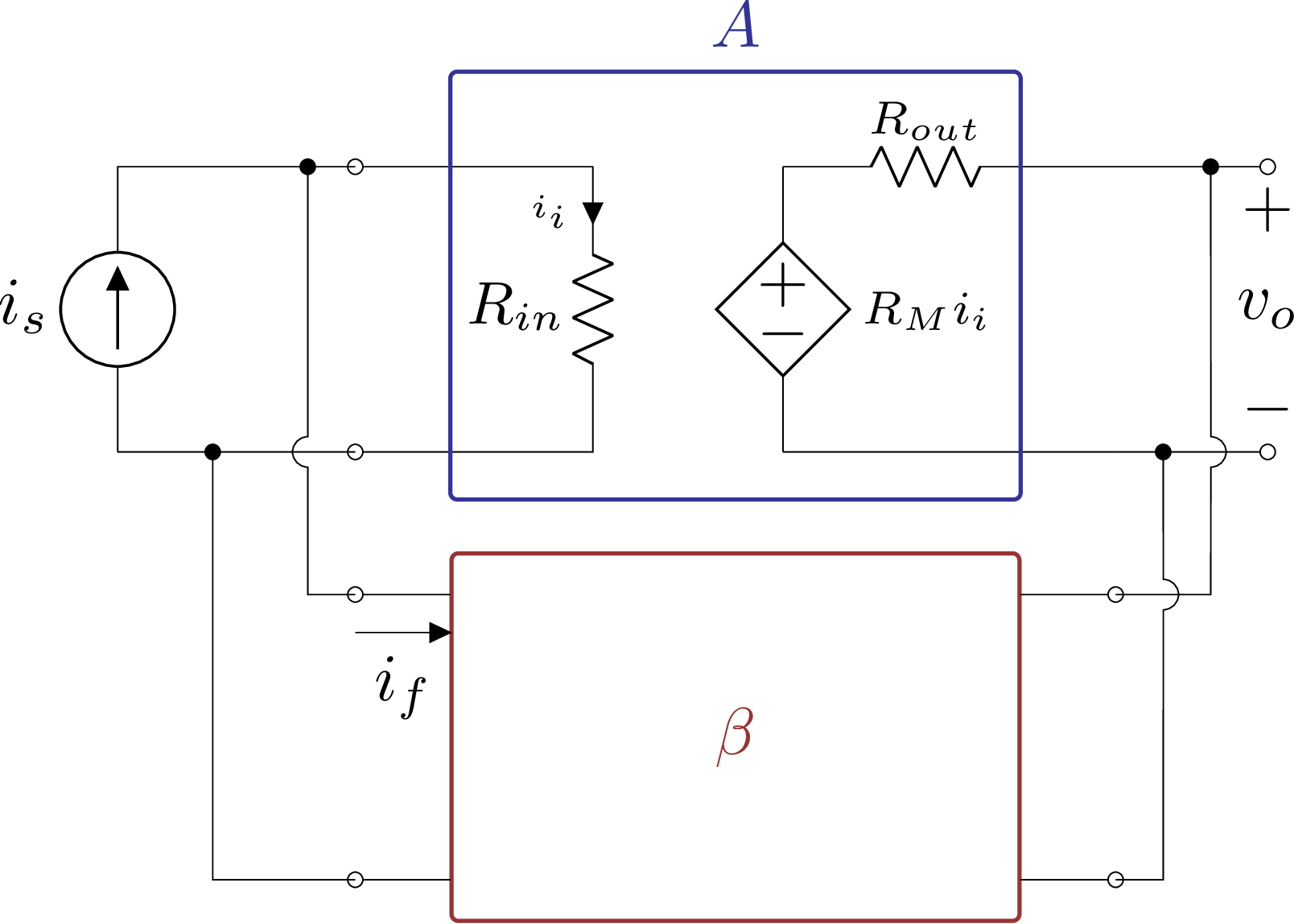
Figura 5.11: Amplificador de transimpedância realimentado - versão simples.

5.2.2.3 Amplificador de Transadmitância

Por fim, o sistema série-série, em que a tensão de realimentação é realimentada em série e a corrente de saída é medida em série.

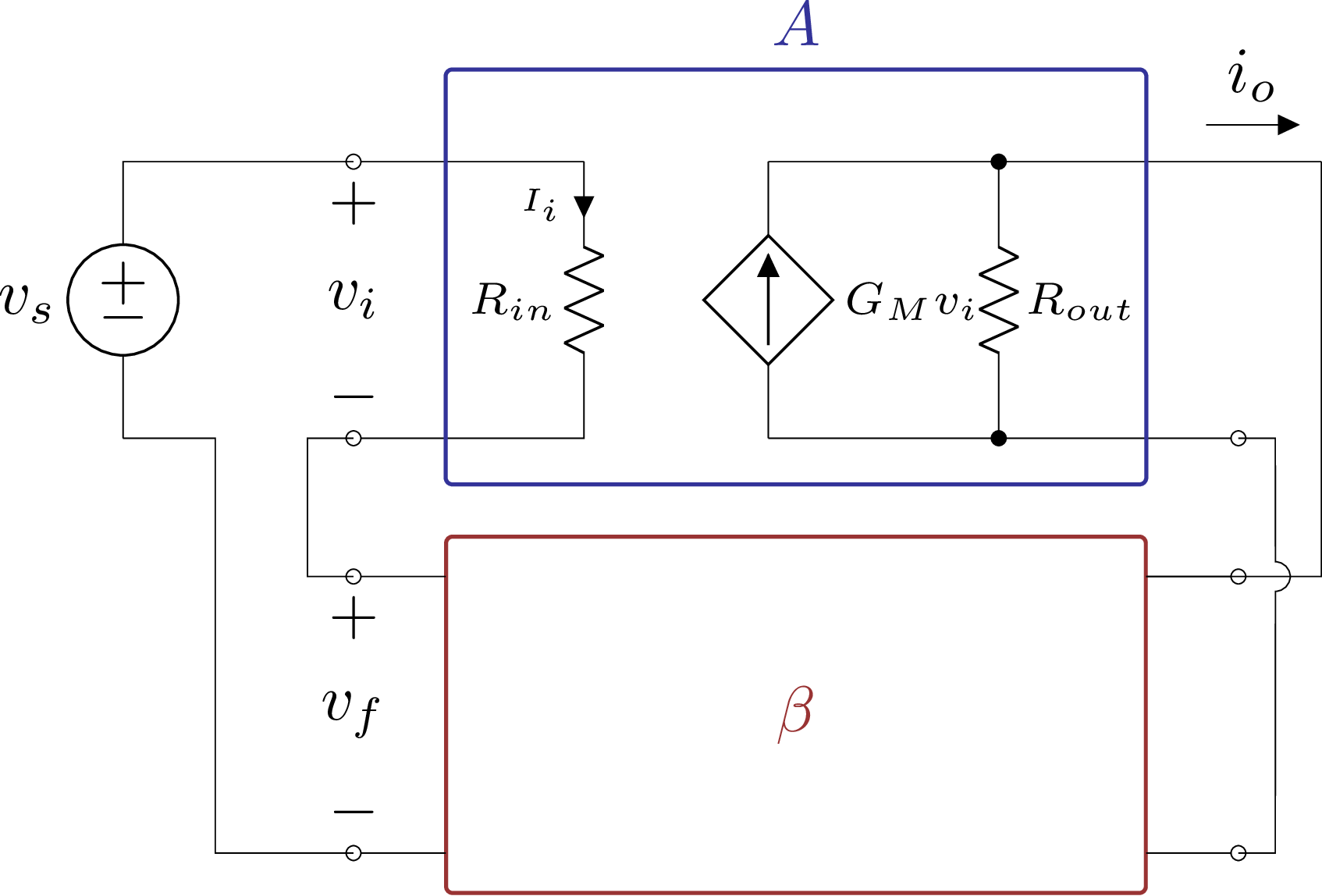
Figura 5.12: Amplificador de transadmitância realimentado - versão simples.

Sinal/Ganho	Amp. Tensão	Amp. Corrente	Amp. Transimpedância	Amp. Transadmitância
\(X_s\)	Tensão	Corrente	Corrente	Tensão
\(X_f\), \(X_e\), \(X_o\)	Tensão	Corrente	Tensão	Corrente
\(\beta\)	\(\dfrac{v_f}{v_o}\)	\(\dfrac{i_f}{i_o}\)	\(\dfrac{i_f}{v_o}\)	\(\dfrac{v_f}{i_o}\)
\(R_{in}\) ideal	\(\infty\)	\(0\)	\(0\)	\(\infty\)
\(R_{{in}_{f}}\)	\(R_{in}\times D\) (↑)	\(\dfrac{R_{in}}{D}\) (↓)	\(\dfrac{R_{in}}{D}\) (↓)	\(R_{in}\times D\) (↑)
\(R_{out}\) ideal	\(0\)	\(\infty\)	\(0\)	\(\infty\)
\(R_{{out}_{f}}\)	\(\dfrac{R_{out}}{D}\) (↓)	\(R_{out}\times D\) (↑)	\(\dfrac{R_{out}}{D}\) (↓)	\(R_{out}\times D\) (↑)