3.5 Fonte Comum com Resistor de Fonte
Uma variação possível do fonte comum é a sua versão com um resistor de fonte. As topologias básicas, NMOS e PMOS, podem ser vistas nas Figuras 3.4 e 3.5, respectivamente. A fonte de corrente \(I_B\) implica na utilização de carga ativa, necessariamente.
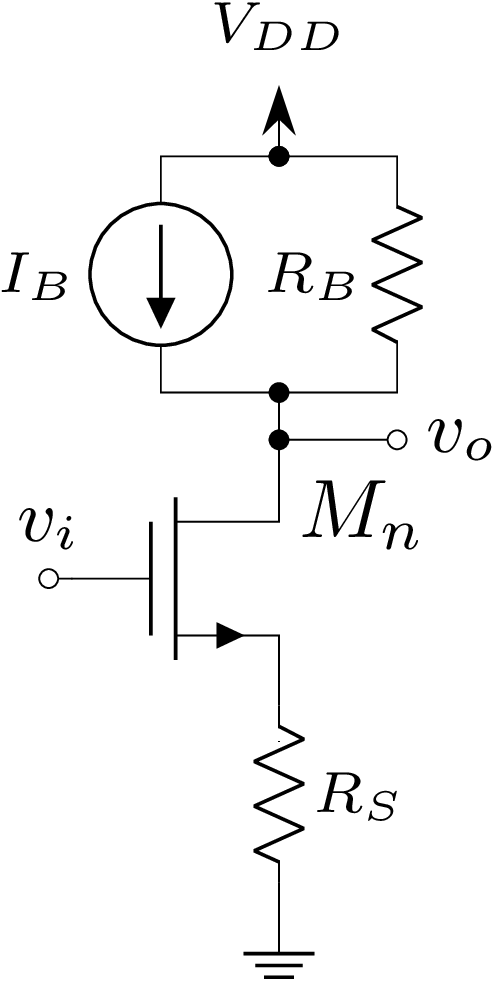
Figura 3.4: Amplificador fonte comum NMOS com resistor de fonte.
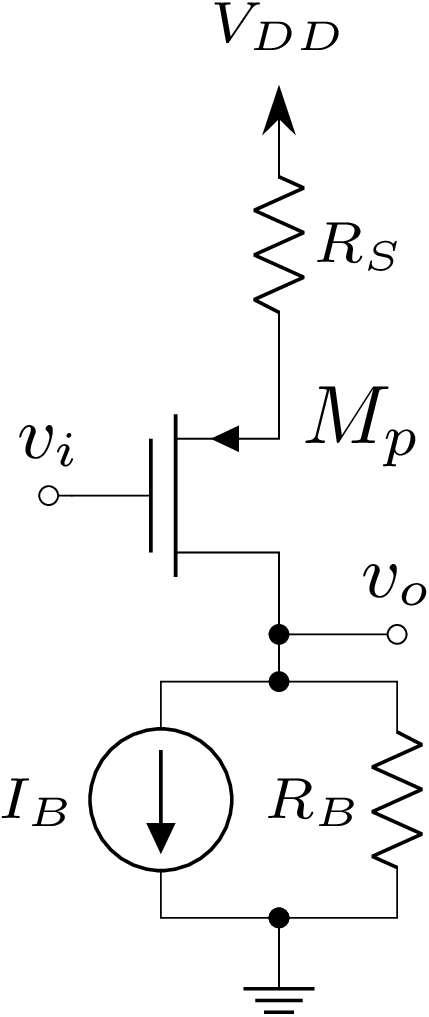
Figura 3.5: Amplificador fonte comum PMOS com resistor de fonte.
A introdução de \(R_S\) no circuito produz uma realimentação negativa para o amplificador. Essa realimentação acontece quando a corrente \(I_{DS}\) produz uma queda de tensão em \(R_S\). A tensão no resistor de fonte faz diminuir a tensão \(V_{GS}\) na porta do transistor, levando a corrente \(I_{DS}\) a diminuir também. Com a diminuição da corrente a tensão em \(R_S\) cai e \(V_{GS}\) volta a subir, aumentando novamente a corrente. Esse ciclo irá forçar uma estabilização do circuito mais rápida, ajudando na sua estabilidade17.
E, como já se espera num sistema com realimentação negativa (baseado em elementos físicos reais), há um redução do ganho do amplificador em malha aberta. Logo, o ganho final está baseado no ganho do fonte comum sem \(R_S\), mas com uma redução baseada no efeito desse mesmo resistor.
A partir dessa alteração é preciso perceber que o efeito de corpo estará ativo, estando a fonte não mais no menor potencial de circuito, assim como no Dreno Comum (ver Seção 2.4) e no Porta Comum (ver Seção 2.5); portanto, fazendo parte da análise de ganho dessa topologia. Análise essa que estará baseada no circuito de pequenos sinais exposto na Figura 3.6, a seguir.

Figura 3.6: Modelo de pequenos sinais de um fonte comum com resistor de fonte para baixas frequências.
Para o nó de dreno podemos escrever duas relações de corrente:
\[\begin{equation} \dfrac{v_{o}}{R_{A}}\ =\ -\dfrac{v_s}{R_S} \to\ v_s\ =\ -\dfrac{R_S}{R_{A}}v_{o} \tag{3.14} \end{equation}\]
\[\begin{equation} \dfrac{v_{o}}{R_{A}}\ =\ {g_{m}}v_{gs}+ g_{{m}_{b}}v_{bs}+ \dfrac{v_{o}- v_s}{{r_{o}}} \tag{3.15} \end{equation}\]
Do circuito, também podemos escrever:
\(v_{gs}=v_{i}- v_s\);
\(v_{bs}=-v_s\);
Substituindo-se a Equação (3.14) na Equação (3.15), juntamente com as relações apresentadas anteriormente, chegamos a:
\[\begin{align} {g_{m}}v_{i}\ &=\ -\left[\dfrac{1}{R_{A}} + \dfrac{{g_{m}}R_S}{R_{A}} + \dfrac{g_{{m}_{b}}R_S}{R_{A}} + \dfrac{1}{{r_{o}}} + \dfrac{R_S}{{r_{o}}R_{A}} \right]v_{o}\\ &=\ -\left[1 + ({g_{m}}+g_{{m}_{b}})R_S+ \dfrac{R_S}{{r_{o}}} + \dfrac{R_{A}}{{r_{o}}} \right]\dfrac{v_{o}}{R_{A}}\\ &=\ -\left[1 + g_{{m}_{T}}R_S+ \dfrac{R_S}{{r_{o}}} + \dfrac{R_{A}}{{r_{o}}} \right]\dfrac{v_{o}}{R_{A}} \tag{3.16} \end{align}\]
Rearranjando os termos podemos escrever uma expressão para o ganho de tensão desse amplificador:
\[\begin{align} {g_{m}}R_{A}v_{i}\ &=\ -\dfrac{\left[1 + ({g_{m}}+ g_{{m}_{b}})R_S\right]{r_{o}}+(R_{A}+ R_S)}{{r_{o}}}v_{o}\\ {g_{m}}{r_{o}}R_{A}v_{i}\ &=\ -\left[(1 + g_{{m}_{T}}R_S){r_{o}}+ (R_{A}+ rs)\right]v_{o}\\ \dfrac{v_{o}}{v_{i}} &=\ A_{v}\ =\ \dfrac{-{g_{m}}{r_{o}}R_{A}}{(1 + g_{{m}_{T}}R_S){r_{o}}+R_{A}} \tag{3.17} \end{align}\]
Percebe-se a redução do ganho do amplificador fonte comum (um dos efeitos da realimentação negativa), com a redução inversamente proporcional à \(R_S\) e às transcondutâncias. O efeito de corpo, além de estar presente, contribui para a redução do ganho. Essa redução no ganho era esperada e será de grande utilidade para a realização da topolgia final do amplificador diferencial pretendida nesse texto. Importante dizer que, se \(R_S=0\), que é o caso do fonte comum original, o ganho se torna:
\[\begin{align} A_{v}\ &=\ \dfrac{-{g_{m}}{r_{o}}R_{A}}{{r_{o}}+R_{A}}\ =\ -{g_{m}}({r_{o}}||R_{A}) \tag{3.18} \end{align}\]
Que é exatamente o ganho do fonte comum sem resistor de fonte.