2.5 PRIMJER 5
- Na osnovu 50 poduzeća procijenjena je logistička regresija. Zavisna je varijabla “kotacija” (ne-\(0\), da-\(1\)) dok je nezavisna varijabla “prihod” (u tisućama kn):
\[log\bigg(\dfrac{p_i}{1-p_i}\bigg)=-1001.011+9.938 x_i\]
Interpretirajte koeficijent uz varijablu “prihod”!
Kolika je vjerojatnost da će poduzeće kotirati na burzi ako ostvaruje prihod od \(100.67\) tisuća kuna?
U koju će se grupu klasificirati to poduzeće ako je razina praga (cutoff) \(0.3\) odnosno \(0.5\)?
Formirajte dvije klasifikacijske matrice.
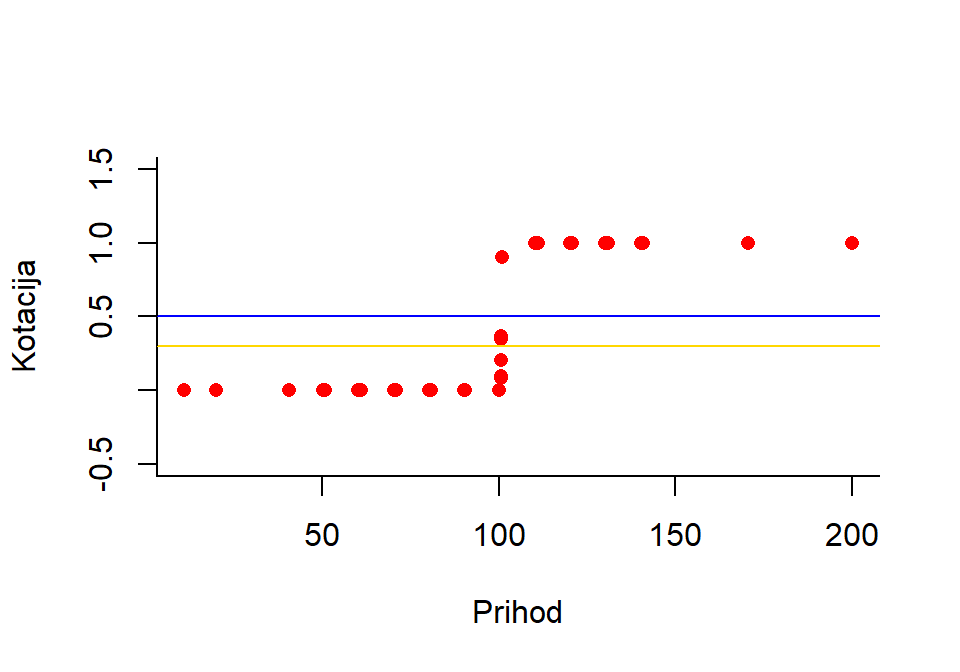
Slika 2.3: Logistička regresija s zavisnom varijablom \(y_i=\{0,~1\}\)
- Interpretacija:
\[exp(\beta_1)=exp(9.938)=20702.3\]
- Ako se prihod poduzeća poveća za \(1\) tisuću kuna tada se povećava vjerojatnost da će poduzeće kotirati na burzi za \(20702.3\) puta (\(20702\) puta je veća šansa da će poduzeće kotirati na burzi nego da neće kotirati ako mu se prihod u prosjeku poveća za \(1\) tisuću kuna).
- Potrebna je inverzna logit transformacija, tj.
\[\begin{align} \hat{p}_i&=\dfrac{1}{1+exp(-(-1001.011+9.9938 \cdot 100.67))} \\ \hat{p}_i&=\dfrac{1}{1+exp(-(-0.55254))} \\ \hat{p}_i&=\dfrac{1}{1+exp(0.55254)} \\ \hat{p}_i&=0.365275 \end{align}\]
Ako je vjerojatnost da će poduzeće kotirati na burzi \(0.365275\) veća od razine praga \(0.3\) tada se ono može svrstati u očekivanu skupinu poduzeća koja kotiraju na burzi (kategorija “da”). Ako je pak vjerojatnost da će poduzeće kotirati na burzi manja od razine praga \(0.5\) tada se ono može svrstati u očekivanu skupinu onih koji ne kotiraju na burzi (kategorija “ne”).
Sva se poduzeća klasificiraju istovremeno prema stvarnoj i očekivanoj pripadnosti
|
|
- Kako procijeniti logističku regresiju u programu R Studio?
mojipodaci$d3=ifelse(mojipodaci$kotacija=="da",1,0)
logisticka=glm(d3~prihod,data=mojipodaci,family=binomial(link="logit"))
summary(logisticka)
mojipodaci$p=predict(logisticka,type="response")
head(mojipodaci)##
## Call:
## glm(formula = d3 ~ prihod, family = binomial(link = "logit"),
## data = mojipodaci)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -0.9555 0.0000 0.0000 0.0000 1.7745
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -1001.011 873.003 -1.147 0.252
## prihod 9.938 8.674 1.146 0.252
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 68.0292 on 49 degrees of freedom
## Residual deviance: 5.4827 on 48 degrees of freedom
## AIC: 9.4827
##
## Number of Fisher Scoring iterations: 15## prihod zaduzenost djelatnost kotacija zaposleni reklama rizik d1 d2 d3
## 1 60.53 0.88859 trgovina ne 16 58.80 5 0 1 0
## 2 50.33 0.06934 proizvodnja ne 13 37.27 1 1 0 0
## 3 130.61 0.21144 usluge da 41 40.00 2 0 0 1
## 4 100.67 0.55482 trgovina ne 33 42.98 3 0 1 0
## 5 130.25 0.14767 trgovina da 41 72.00 1 0 1 1
## 6 130.95 0.14211 trgovina da 41 63.07 1 0 1 1
## p
## 1 0.0000
## 2 0.0000
## 3 1.0000
## 4 0.3665
## 5 1.0000
## 6 1.0000- Za formiranje klasifikacijske matrice potrebno je instalirati i učitati paket
InformationValue. Nakon instalacije i učitavanje paketa upotrijebite naredbuconfusionMatrix()te zatimmisClassError()za izračun postotka točne klasifikacije.
install.packages("InformationValue")
library(InformationValue)
confusionMatrix(mojipodaci$d3,mojipodaci$p,threshold=0.3)
1-misClassError(mojipodaci$d3,mojipodaci$p,threshold=0.3)## 0 1
## 0 27 1
## 1 2 20## [1] 0.94confusionMatrix(mojipodaci$d3,mojipodaci$p,threshold=0.5)
1-misClassError(mojipodaci$d3,mojipodaci$p,threshold=0.5)## 0 1
## 0 29 1
## 1 0 20## [1] 0.98