1.6 R-Studio
Kako riješiti primjer u programu R-Studio?
Otvorite novu \(R\) skriptu: \(\verb|File|\) \(\Rightarrow\) \(\verb|New File|\) \(\Rightarrow\) \(\verb|R Script|\)
Učitajte podatke iz datoteke \(\verb|poduzeca.txt|\) pomoću naredbe
read.table()koristeći URL adresu veze, a objekt nazovitemojipodaci.
mojipodaci=read.table(url("http://www.efzg.hr/userdocsimages/sta/jarneric/poduzeca.txt"),header=TRUE)- Prikažite prvih 6 redaka objekta
mojipodacipomoću naredbehead()
head(mojipodaci)## prihod zaduzenost djelatnost kotacija zaposleni reklama rizik
## 1 60.53 0.88859 trgovina ne 16 58.80 5
## 2 50.33 0.06934 proizvodnja ne 13 37.27 1
## 3 130.61 0.21144 usluge da 41 40.00 2
## 4 100.67 0.55482 trgovina ne 33 42.98 3
## 5 130.25 0.14767 trgovina da 41 72.00 1
## 6 130.95 0.14211 trgovina da 41 63.07 1- Koje je klase objekt
mojipodaci, kojih dimenzija i koje strukture?
class(mojipodaci)
dim(mojipodaci)
str(mojipodaci)## [1] "data.frame"## [1] 50 7## 'data.frame': 50 obs. of 7 variables:
## $ prihod : num 60.5 50.3 130.6 100.7 130.2 ...
## $ zaduzenost: num 0.8886 0.0693 0.2114 0.5548 0.1477 ...
## $ djelatnost: chr "trgovina" "proizvodnja" "usluge" "trgovina" ...
## $ kotacija : chr "ne" "ne" "da" "ne" ...
## $ zaposleni : int 16 13 41 33 41 41 6 23 35 38 ...
## $ reklama : num 58.8 37.3 40 43 72 ...
## $ rizik : int 5 1 2 3 1 1 5 5 3 3 ...- Izračuanjte prosječan prihod za sva poduzeća zajedno pomoću naredbe
mean()
mean(mojipodaci$prihod)## [1] 95.4804- Izračuanjte prosječan prihod poduzeća za svaku djelatnost pojedinačno pomoću naredbe
aggregate()
aggregate(mojipodaci$prihod,list(mojipodaci$djelatnost),mean)## Group.1 x
## 1 proizvodnja 103.27056
## 2 trgovina 89.08762
## 3 usluge 94.93727- Izračuanjte standardnu devijaciju prihoda poduzeća za svaku djelatnost pojedinačno pomoću iste naredbe
aggregate(mojipodaci$prihod,list(mojipodaci$djelatnost),sd)## Group.1 x
## 1 proizvodnja 36.48760
## 2 trgovina 28.87795
## 3 usluge 51.07280- Izračuanjte varijancu prihoda poduzeća za svaku djelatnost pojedinačno pomoću iste naredbe
aggregate(mojipodaci$prihod,list(mojipodaci$djelatnost),var)## Group.1 x
## 1 proizvodnja 1331.3447
## 2 trgovina 833.9359
## 3 usluge 2608.4311- Izračuanjte omjer najveće i najmanje varijance
2608.4311/833.9359## [1] 3.127856- Provedite jednofaktorsku analizu varijance pomoću naredbe
aov()te ju sačuvajte kao objekt pod nazivomtablica1. Potom prikažite rezultate sadržane u objektutablica1pomoću naredbesummary()
tablica1=aov(prihod~djelatnost,data=mojipodaci)
summary(tablica1)## Df Sum Sq Mean Sq F value Pr(>F)
## djelatnost 2 1954 976.9 0.702 0.501
## Residuals 47 65396 1391.4- Kreirajte dummy varijable \(d_1\) i \(d_2\) pomoću naredbe
ifelse()te ponovno provjerite sadržaj objektamojipodaci
mojipodaci$d1=ifelse(mojipodaci$djelatnost=="proizvodnja",1,0)
mojipodaci$d2=ifelse(mojipodaci$djelatnost=="trgovina",1,0)
head(mojipodaci)## prihod zaduzenost djelatnost kotacija zaposleni reklama rizik d1 d2
## 1 60.53 0.88859 trgovina ne 16 58.80 5 0 1
## 2 50.33 0.06934 proizvodnja ne 13 37.27 1 1 0
## 3 130.61 0.21144 usluge da 41 40.00 2 0 0
## 4 100.67 0.55482 trgovina ne 33 42.98 3 0 1
## 5 130.25 0.14767 trgovina da 41 72.00 1 0 1
## 6 130.95 0.14211 trgovina da 41 63.07 1 0 1- Procijenite jednadžbu linearne regresije s dummy varijablama pomoću naredbe
lm()pri čemu je zavisna varijablaprihod. Dobivenu regresiju sačuvajte kao objekt pod nazivomregresijate rezultate iste prikažite pomoću naredbesummary()
regresija=lm(prihod~d1+d2,data=mojipodaci)
summary(regresija)##
## Call:
## lm(formula = prihod ~ d1 + d2, data = mojipodaci)
##
## Residuals:
## Min 1Q Median 3Q Max
## -92.461 -18.815 -0.829 20.209 105.053
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 94.937 11.247 8.441 5.64e-11 ***
## d1 8.333 14.276 0.584 0.562
## d2 -5.850 13.883 -0.421 0.675
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 37.3 on 47 degrees of freedom
## Multiple R-squared: 0.02901, Adjusted R-squared: -0.01231
## F-statistic: 0.7021 on 2 and 47 DF, p-value: 0.5007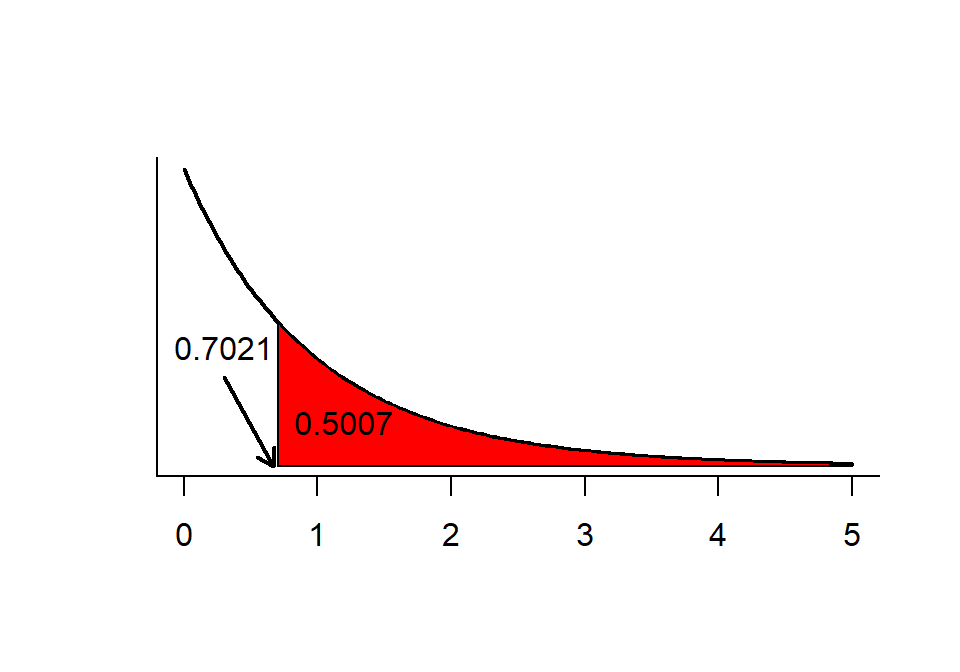
Slika 1.3: F-distribucija i p-vrijendost (kritično područje)
- Izračunajte p-vrijednost F-omjera s 2 stupnja slobode u brojniku i 47 stupnjeva slobode u nazivniku pomoću naredbe
pf()
1-pf(0.7021,2,47)## [1] 0.500666- Zaključujemo da dvije metode
aov()ilm()daju iste rezultate u konkretnom slučaju primjene te se oslanjaju na istim pretpostavkama