1.6 Otras distribuciones discretas
Analizamos diferentes ejemplos en los que estamos interesados en evaluar un sistema que involucra a una o más variables de tipo discreto, y donde únicamente disponemos de información sobre la función de masa de probabilidad o sobre la función de distribución.
1.6.1 Una variable discreta
Supongamos un sistema en el que contamos con información de una única variable discreta de interés que deseamos estudiar. En los casos más sencillos que tratamos aquí, las situaciones planteadas se pueden resolver teóricamente sin mucha dificultad, pero el objetivo es mostrar el uso de la simulación para llegar a resultados aproximados a los que proporcionan los métodos análiticos.
Ejemplo 1.12 Una empresa que fabrica piezas para maquinaria de fabricación de calzado tiene diseñada la cadena de producción de tal forma que las piezas fabricadas se almacenan (y venden) en cajas de dos unidades. El beneficio estimado de una caja sin defectos es de 300 euros. La política de la empresa establece que si al servir una caja a los clientes, esta contiene una pieza defectuosa, debe ser devuelta de forma inmediata para su reemplazo, lo que supone una pérdida de 50 euros por pieza defectuosa (y la devolución de los 300 euros de beneficio por la venta). El problema es que una vez cerradas las cajas en la cadena de producción no se inspeccionan para estimar el número de cajas que se podrían devolver. La única información disponible hace referencia a la tasa de defectos observada en cada caja cuando esta es devuelta, junto con el porcentaje de cajas que son devueltas. En base a esta información, si \(N\) refleja el número de piezas defectuosas observadas, la empresa ha establecido que:
\[\begin{equation} Pr(N = k) = \begin{cases} 0.82 & \text{ para } k = 0\\ 0.15 & \text{ para } k = 1\\ 0.03 & \text{ para } k = 2\\ \end{cases} \tag{1.10} \end{equation}\]La empresa quiere estudiar el beneficio estimado de acuerdo a la politica de producción actual para el próximo mes, sabiendo que se pueden llegar a producir hasta 1500 cajas en ese periodo. Además la empresa está interesada en conocer el beneficio estimado si cambiara su politica de calidad reduciendo su tasa de defectos por caja de acuerdo a las siguientes proporciones:
\[\begin{equation} Pr(N = k) = \begin{cases} 0.85 & \text{ para } k = 0\\ 0.13 & \text{ para } k = 1\\ 0.02 & \text{ para } k = 2\\ \end{cases} \tag{1.11} \end{equation}\]Para resolver las inquietudes de la empresa, vamos a simular el proceso en las dos situaciones planteadas, para el horizonte propuesto de un mes, esto es, simulando las 1500 cajas y estimando el beneficio obtenido de acuerdo a las políticas de calidad dadas en (1.10) y (1.11).
Proponemos el siguiente algoritmo de simulación para obtener la ganancia asociada a cada una de las políticas de calidad, y con dichas ganancias compararlas y concluir cuál es la más beneficiosa.
Algoritmo de simulación Ante una política de calidad:
- Fijar las condiciones de simulación: nº cajas (\(nsim = 1500\)).
- Obtener las función de distribución acumulada vinculada con la politica de calidad de interés y aplicar el algoritmo dado en al definición 1.19 para obtener una muestra de \(N\), \(x_1,...,x_n\), relativas al número de piezas defectuosas en cada caja.
- Calcular el beneficio obtenido para cada caja, vinculado a cada valor \(x_i\), denominado \(b_i\).
- Obtener la ganancia global con todas las cajas simuladas como:
\[G = \sum_{i=1}^n b_i\]
Lancemos el algoritmo para cada situación y obtengamos los beneficios esperados.
# Parámetros de la simulación
set.seed(19)
nsim <- 1500
# datos uniformes
unif <- runif(nsim)
# Valores a devolver (piezas defectuosas por caja)
valores <- c(0, 1, 2)
# Valores a devolver y probabilidad acumulada para la política 1
prob1 <- c(0.82, 0.15, 0.03)
probacum1 <- cumsum(prob1)
# Valores a devolver y probabilidad acumulada para la política 2
prob2 <- c(0.85, 0.13, 0.02)
probacum2 <- cumsum(prob2)
# Inicialización de variables donde almacenamos las simulaciones
xs1 <- c(); benef1 <- c()
xs2 <- c(); benef2 <- c()
# Simulación de la variable de interés
i <- 1
while (i <= nsim)
{
# politica 1
xs1[i] <- valores[min(which(unif[i] <= probacum1))]
benef1[i] <- ifelse(xs1[i]==0, 300, -50*xs1[i]) # beneficios
# politica 2
xs2[i] <- valores[min(which(unif[i] <= probacum2))]
benef2[i] <- ifelse(xs2[i]==0, 300, -50*xs2[i])
# nueva simulación
i <- i+1
}
# Resultados para las nsim simulaciones
simulacion <- data.frame(defec.s1 = xs1, benef.s1 = benef1,
defec.s2 = xs2, benef.s2 = benef2)
cat("Una muestra de las simulaciones realizadas es ...\n")## Una muestra de las simulaciones realizadas es ...head(simulacion)## defec.s1 benef.s1 defec.s2 benef.s2
## 1 0 300 0 300
## 2 0 300 0 300
## 3 0 300 0 300
## 4 0 300 0 300
## 5 0 300 0 300
## 6 0 300 0 300# Rendimientos globales
beneficios=simulacion %>%
summarise(G1 = sum(benef.s1), G2 = sum(benef.s2),
Dif = G2 - G1)
cat("Beneficios S1 (€):",beneficios$G1,
"Beneficios S2 (€):",beneficios$G2,
"Diferencia S2-S1 (€):",beneficios$Dif)## Beneficios S1 (€): 350950 Beneficios S2 (€): 367200 Diferencia S2-S1 (€): 16250En consecuencia, se aprecia cómo una leve mejora de la calidad en la producción (reduciendo la tasa de defectos) proporciona a la empresa una ganancia sustancial, por lo que la política S2 sin duda es la más ventajosa para su negocio.
Ejemplo 1.13 Una empresa de inversiones está considerando tres nuevos planes de inversión. Cada plan requiere una inversión de 25.000 dólares y el retorno será un año después. El plan A retornará de forma fija 27.500 dólares. El plan B retornará 27.000 dólares o 28.000 dólares, con probabilidades 0.4 y 0.6, respectivamente. El plan C retornará 24.000, 27.000 o 33.000 dólares con probabilidades de 0.2, 0.5 y 0.3, respectivamente. Si el objetivo de la empresa es maximizar el rendimiento esperado, ¿qué plan debería elegir?
Hay que tener en cuenta que en este caso no sólo es relevante el rendimiento esperado, sino también la volatilidad esperada para ese beneficio, expresada en términos de variabilidad o incertidumbre. Será pues interesante, calcular el rendimiento o el retorno esperado en cada situación, además de su varianza o desviación típica.
Vamos a plantear un proceso de simulación para estimar los beneficios y volatilidad asociadas a cada plan. Fijaremos el mismo número de simulaciones en cada plan, con el fin de hacer comparables los resultados. El algoritmo se presenta a continuación.
Algoritmo de simulación
- Fijar condiciones de simulación (\(nsim = 1000\))
- Obtener la función de distribución acumulada vinculada con cada uno de los planes de inversión y aplicar el algoritmo dado en la definición 1.19 para obtener una muestra de cada uno de ellos.
- Calcular el beneficio obtenido para cada simulación en cada plan.
- Obtener la ganancia estimada de cada plan como la media de los beneficios obtenidos para cada simulación, y la volatilidad como la desviación típica de los beneficios obtenidos.
Y procedemos con la simulación, calculando el beneficio esperado y la desviación típica en cada plan de inversión. Considerando que el plan A no tiene incertidumbre alguna (Varianza=0) y el beneficio fijo que generará será de $2500, no lo incluimos en la simulación.
# Parámetros de la simulación
set.seed(1970)
nsim <- 1000
# datos uniformes
unif <- runif(nsim)
# Beneficios asociados a cada plan
BpB <- c(2000, 3000) # beneficio variable
BpC <- c(-1000, 2000, 8000) # beneficio variable
# Distribuciones de probabilidiad para los planes B y C
probB <- c(0.4, 0.6)
probacumB <- cumsum(probB) # función de distribución plan B
probC <- c(0.2, 0.5, 0.3)
probacumC <- cumsum(probC) # función de distribución plan
# Inicialización de variables donde almacenamos las beneficios
# individuales para cada simulación
benefB <- c()
benefC <- c()
# Simulación de la variable de interés
i <- 1
while (i <= nsim)
{
# plan B
benefB[i] <- BpB[min(which(unif[i] <= probacumB))]
# plan C
benefC[i] <- BpC[min(which(unif[i] <= probacumC))]
# nueva simulación
i <- i+1
}
# Resultado
simulacion <- data.frame(A=rep(2500,nsim),B = benefB, C = benefC)
cat("Una muestra de las simulaciones realizadas es ...\n")## Una muestra de las simulaciones realizadas es ...head(simulacion)## A B C
## 1 2500 2000 -1000
## 2 2500 3000 8000
## 3 2500 2000 -1000
## 4 2500 2000 -1000
## 5 2500 3000 8000
## 6 2500 3000 8000beneficios=simulacion %>%
summarise(mPB = mean(B), sdPB = sd(B),
mPC = mean(C), sdPC = sd(C))
cat("Beneficios PlanA ($):",2500,
"Volatilidad (sd):",0,
"Beneficios PlanB ($):",beneficios$mPB,
"Volatilidad (sd):",beneficios$sdPB,
"Beneficios PlanC ($):",beneficios$mPC,
"Volatilidad (sd):",beneficios$sdPC)## Beneficios PlanA ($): 2500 Volatilidad (sd): 0 Beneficios PlanB ($): 2604 Volatilidad (sd): 489.3091 Beneficios PlanC ($): 3122 Volatilidad (sd): 3315.435Podemos ver que aunque el plan C es el que proporcioanrá más retorno esperado, también es el que tiene una mayor volatilidad (sd), lo que produce incertidumbre y podría repercutir en una mayor pérdida al final del periodo de inversión. El plan A tiene un beneficio fijo sin volatilidad ninguna, pero es inferior al beneficio del plan B. A efetos estadísticos, ya que la volatilidad (desviación típica) del plan B toma un valor inferior a la media, el coeficiente de variación (\(cv=sd/media\)) resulta inferior a 1, y en consecuencia da una alternativa razonable al plan A. Por contra, no ocurre así en el plan C (\(cv>1\)) lo que lo coloca en una situación de inferioridad frente a los otros planes de inversión.
Con el fin de afinar en nuestra comparación de los tres planes de inversión, no nos vamos a conformar con valores esperados y desviaciones típicas, y vamos a calcular la probabilidad de que beneficio obtenido sea mayor a 2500 dólares con cada plan, cálculo que podemos resolver fácilmente a partir de las simulaciones obtenidas.
# Probabilidad beneficio > 2500
c(prA = sum(simulacion$A>2500)/1000,
prB = sum(simulacion$B>2500)/1000,
prC = sum(simulacion$C>2500)/1000)## prA prB prC
## 0.000 0.604 0.289Con este cálculo, el plan B sale claramente reforzado, con una probabilidad destacable de generar un beneficio superior a $2500 (prob=0.6), frente al plan A (prob=0) y al C (prob=0.29). El plan A no puede superar unos rendimientos superiores a 2500, al ser este valor su fijo.
1.6.2 Mixturas de Discretas
Estas situaciones son muy habituales e involucran la combinación de diferentes variables de tipo discreto en un mismo sistema, en lo que se viene a denominar mixtura de variables aleatorias de tipo discreto o modelos secuenciales. Sobre este tipo de distribuciones resulta bastante sencillo plantear un algoritmo de simulación. Antes de comenzar veamos desde un punto de vista téorico el concepto de mixtura de variables.
Definición 1.20 Sean \(X_1, X_2,...,X_n\) un conjunto de variables aleatorias independientes de tipo discreto y sea \(I\) una variable indicador de tipo discreto, definida en los valores \(\{1,..., n\}\), tal que \[Pr(I=j)=p_j, j=1,..., n, \quad \sum_{j=1}^n p_j = 1.\]
La variable aleatoria \(T\) que se define como:
\[ T = \sum_{j =1}^n p_j X_j\]
se denomina mixtura del conjunto \(X_1,...,X_n\) con índice \(I\), y además cumple que:
\[E(T) = \sum_{j=1}^n p_j E(X_j)\]
\[E(T^2) = \sum_{j=1}^n p_j (V(X_j) + E(X_j)^2).\]
Así, la varianza de \(T\) se puede calcular fácilmente a partir de la expresión:
\[V(T) = E(T^2) - E(T)^2\]
El algoritmo para simular de una mixtura es bastante sencillo y se basa en la aplicación consecutiva en dos pasos del algoritmo de la transformada inversa para variables discretas en la Definición 1.19.
Definición 1.20 Algoritmo simulación mixtura variables discretas
En la situación descrita en la definición 1.20 el algoritmo para generar una muestra de la mixtura debe proporcioanr en cada simulación un vector de dos componentes: variable seleccionada (\(I\)) y valor generado de \(X_I\). En concreto:
- Paso 1. Establecer el tamaño de muestra a simular \(nsim\).
Repetir los pasos 2 y 3 para cada iteración \(i\) de \(1, 2,..., nsim\):
Paso 2. Simular un valor para el indicador \(I_i\) de la variable de mixtura, mediante el algoritmo de la transformada inversa para una variable discreta (Definición 1.19) con probabilidades \(p_1,...,p_n\), y seleccionar la variable \(X_{I_i}\) para dicho indicador.
Paso 3. Simular un valor \(x_{I_i}\) mediante el algoritmo de la transformada inversa para \(X_i\).
Paso 4. Devolver el conjunto de simulaciones \(\{I_i, x_{I_i}\}_{i=1}^{nsim}.\)
Pasamos a estudiar un par de ejemplos de situaciones secuenciales para variables discretas que se pueden modelizar según una mixtura y donde podemos aplicar el algoritmo anterior.
Ejemplo 1.14 Una tienda de electrodomésticos desea analizar las ventas de hornos microondas. Los gerentes de la tienda saben que en muchas ocasiones la gente entra en la tienda simplemente para curiosear, pero de todas las personas con intenciones claras de compra, el 50% acaba comprando uno de los tres modelos disponibles y el otro 50% finalmente no realiza ninguna compra. De los clientes que compran un horno, el 25% adquiere el modelo sencillo, el 50% el modelo estándar y el 25% el modelo de lujo. El modelo sencillo produce una ganancia de 30 dólares; el modelo estándar produce una ganancia de 60 dólares y el modelo de lujo produce una ganancia de 75 dólares.
Los gerentes están interesados en estimar el beneficio medio por cliente de todos aquellos con intención de comprar, y que por tanto utilizan el asesoramiento (y tiempo) de los vendedores.
El enfoque habitual para estimar el beneficio promedio sería mantener registros de todos los clientes que hablan con los vendedores y calcular con esos datos una estimación del beneficio esperado por cliente. Sin embargo, este proceso puede ser simulado sin mucha dificultad a partir de la información proporcionada, para estimar, por ejemplo, el beneficio promedio por cliente para los próximos cien clientes.
Este proceso se puede describir mediante una mixtura con dos variables \(X_0\) y \(X_1\) que expresan cuál es el beneficio que genera un cliente que entra en la tienda, mediante una variable indicador \(I\), que identifica si un cliente está interesado o no en comprar.
Sea \(X_i\) la ganancia generada por cada cliente que entra a la tienda, para cada uno de los tipos de cliente: 0=no compra, 1=sí compra: \[X_i, \quad i=0,1\]
La probabilidad de que un cliente compre o no viene dada por: \[\begin{equation*} Pr(I = i)= \begin{cases} 0.5 & i=1 \text{ (si compra)} \\ 0.5 & i=0 \text{ (si no compra) } \end{cases} \end{equation*}\]
De modo que un cliente que no compra produce beneficios 0 con probabilidad 1, \[Pr(X_0=0)=1,\] y el beneficio de un cliente que no compra tiene como distribución de probabilidad: \[\begin{equation*} Pr(X_1 = k) = \begin{cases} 0.25 & \text{ para } k = 30 \text{ modelo sencillo}\\ 0.50 & \text{ para } k = 60 \text{ modelo estándar}\\ 0.25 & \text{ para } k = 75 \text{ modelo lujo}. \end{cases} \end{equation*}\]
Es fácil simular cualquiera de estas distribuciones discretas mediante el algoritmo de la transformada inversa para variables discretas en la Definición 1.19, para acabar simulando de \(T\) con el algoritmo anterior en la Definición 1.20.
Simulemos pues el proceso de venta para 30 clientes, recopilando, además de la ganancia que genera cada uno, la ganancia acumulada por las compras realizadas. Construimos una función para simular el proceso, en la que introducimos como parámetros la semilla de inicialización de la simulación y el número de clientes, por si deseamos ampliar el espectro de simulación en algún momento.
simula.ventas.micro <- function(clientes, semilla)
{
# Descripción del proceso de compra o no compra
compra <- c("Si", "No")
pcompra <- 0.50
# Descripción del proceso de adquisión del microondas
tipo <- c("Sencillo", "Estándar", "Lujo")
prmicro <- c(0.25, 0.50, 0.25) # fmp X1
prmicroacum <- cumsum(prmicro) # fon. distribución X1
beneficio <- c(30, 60, 75)
# Inicialización de variables para las simulaciones
indicador <- c() # proceso de compra
micro <- c() # tipo microondas adquirido
bind <- rep(0, clientes) # beneficio individual
bacum <- rep(0, clientes) # beneficio acumulado
## Simulación del proceso
##########################
i <- 1
# Generamos uniformes para describir el proceso de compra y
# el tipo de microondas adquirido
set.seed(semilla)
ucompra <- runif(clientes) # uniformes para el indicador
umicro <- runif(clientes) # uniformes para la compra
# Bucle de simulación
while (i <= clientes)
{
# Proceso de compra
indicador[i] <- ifelse(ucompra[i] <= 0.5, compra[1], compra[2])
# Tipo de microndas
if(indicador[i] == compra[1])
{
pos <- min(which(umicro[i] <= prmicroacum))
micro[i] <- tipo[pos]
bind[i] <- beneficio[pos]
}
else
{
micro[i] <- "Sin venta"
bind[i] <- 0
}
bacum[i] <- sum(bind[1:i]) # se acumulan todos los beneficios
# nueva simulación
i <- i+1
}
# Resultado
return(data.frame(Compra = indicador, Tipo = micro,
Bind = bind, Bacum = bacum))
}Generamos el proceso para 30 clientes y analizamos los resultados
simulacion <- simula.ventas.micro(30, 123)
head(simulacion)## Compra Tipo Bind Bacum
## 1 Si Lujo 75 75
## 2 No Sin venta 0 75
## 3 Si Estándar 60 135
## 4 No Sin venta 0 135
## 5 No Sin venta 0 135
## 6 Si Estándar 60 195# el beneficio acumulado tras el paso de 30 clientes
tail(simulacion,n=1)## Compra Tipo Bind Bacum
## 30 Si Estándar 60 600El beneficio acumulado tras el paso de 30 clientes un día cualquiera que hemos simulado es de 600 dólares.
En la Figura 1.11 se han representado los resultados de las simulaciones generadas (30 clientes que pasan a la tienda), así como los beneficios acumulados por las ventas realizadas.
g1=simulacion %>%
group_by(Tipo) %>%
summarise(n=n()) %>%
mutate(prop=n/nrow(simulacion)) %>%
ggplot(aes(x = Tipo, y = prop)) +
geom_col(aes(fill = Tipo), position = "dodge") +
geom_text(aes(label = scales::percent(prop),
y = prop, group = Tipo),
position = position_dodge(width = 0.9),
vjust = 1.5)+
labs(x="Tipo de cliente",y="Proporción")+
theme(legend.position="none")
g2 <- ggplot(simulacion, aes(1:30, Bacum)) +
geom_line() +
labs(x = "Cliente", y = "Beneficio acumulado")
grid.arrange(g1, g2, nrow = 1)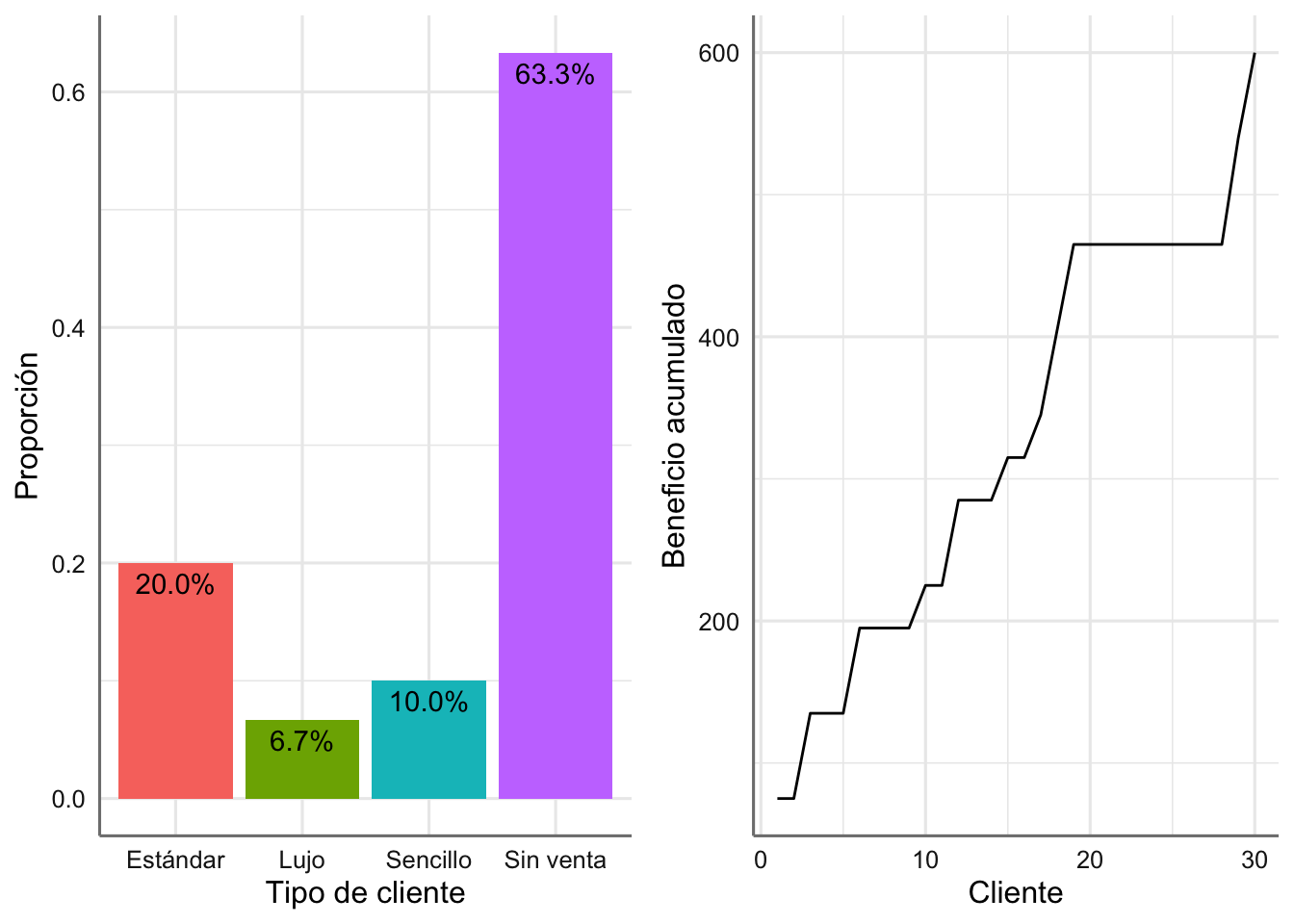
Figura 1.11: Frecuencia relativa de cada tipo de venta (izquierda) y beneficio acumulado para los 30 clientes (derecha).
Podemos también calcular la ganancia promedio que se obtiene con esos 30 clientes a partir de la variable simulaciones$Bind, que resulta de
mean(simulacion$Bind)## [1] 20Si queremos aproximar el beneficio esperado por cliente, bastará simular muchos clientes, y promediar los beneficios que le dan a la tienda, o incluso el beneficio esperado por cliente que compra un microondas.
nsim <- 1000 # número de clientes simulados
simulacion <- simula.ventas.micro(nsim,123)
# aproximación MC del beneficio medio de un cliente cualquiera
mean(simulacion$Bind)## [1] 29.025# beneficio medio de un cliente de compra
mean(simulacion$Bind[simulacion$Compra=="Si"])## [1] 57.24852Así, el beneficio medio por cliente es aproximadamente de 29.03 dólares, mientras que el beneficio esperado por cliente que compra un microondas es de 57.25 dólares. El beneficio esperado por cada 30 clientes que entran en la tienda será de \(20.025 \times 30=870.75\) dólares.
Ejemplo 1.15 Un fabricante de galletas presenta muchos productos nuevos cada año, de los cuales cerca del 60% fracasan, 30% tienen un éxito moderado y un 10% tienen un gran éxito. Para mejorar sus posibilidades, el fabricante somete a una prueba sus nuevos productos, ante un grupo de clientes que actúa como jurado calificador. De los productos que fracasaron, 50% son calificados como malos, 30% como regulares y 20% como buenos. Para los que tuvieron un éxito moderado, la calificación es mala para un 20%, regular para un 40% y buena para otro 40%. Para los que tuvieron un gran éxito, los porcentajes son: malos 10%, regulares 30% y buenos 60%. El fabricante está interesado en conocer:
¿Cuál es la probabilidad conjunta de que un producto tenga un éxito moderado y reciba una mala calificación?
Si un nuevo producto tiene una buena calificación, ¿cuál es la probabilidad de que fracase?
¿Cuál es la probabilidad de que un producto tenga éxito moderado dado que este obtuvo una mala calificación?
Modelicemos el problema como una mixtura de distribuciones discretas según la Definición 1.20.
Sea \(I_i\) la variable indicadora tal que \[\begin{equation*} Pr(I = k) = \begin{cases} 0.25 & \text{ para } k = 1 \text{ fracaso}\\ 0.50 & \text{ para } k = 2 \text{ éxito moderado}\\ 0.25 & \text{ para } k = 3 \text{ gran éxito}. \end{cases} \end{equation*}\]
Luego definimos las variables \(X_i\) que representan la calificación del jurado de un producto cuyo éxito o fracaso funcionó según \(I=i\): \(X_1\) calificación de un producto que fue un fracaso (\(I=1\)), \(X_2\) calificación de un producto con un éxito moderado (\(I=2\)) y \(X_3\) calificación de un producto con una gran éxito (\(I=3\)). Las distribuciones de \(X_1, X_2, X_3\) vienen dadas por: \[\begin{equation*} Pr(X_1 = k) = \begin{cases} 0.5 & \text{ para } k = 1 \text{ malo}\\ 0.3 & \text{ para } k = 2 \text{ regular}\\ 0.2 & \text{ para } k = 3 \text{ bueno}. \end{cases} \end{equation*}\] \[\begin{equation*} Pr(X_2 = k) = \begin{cases} 0.2 & \text{ para } k = 1 \text{ malo}\\ 0.4 & \text{ para } k = 2 \text{ regular}\\ 0.4 & \text{ para } k = 3 \text{ bueno}. \end{cases} \end{equation*}\] \[\begin{equation*} Pr(X_3 = k) = \begin{cases} 0.1 & \text{ para } k = 1 \text{ malo}\\ 0.3 & \text{ para } k = 2 \text{ regular}\\ 0.6 & \text{ para } k = 3 \text{ bueno}. \end{cases} \end{equation*}\]
Veamos el algoritmo de simulación necesario para este problema. Queremos simular productos que pueden haber tenido un gran éxito, un éxito moderado y o haber fracasado. Y para cada uno de ellos, queremos simular su calificación por el jurado que lo evaluó.
Consideramos una variable \(I\) que indica el éxito de un nuevo producto y \(X_I\) que indica la evaluación del producto por un jurado (para cada tipo de producto \(I\)). En esta situación debemos proporcionar las simulaciones correspondientes a \(I\) e \(X_I\). En concreto:
- Paso 1. Establecer tamaño de muestra a simular \(nsim\).
Repetir los pasos 2 y 3 para cada iteración \(i\) de \(1, 2,..., nsim\):
Paso 2. Simular de la variable indicador, \(I_i\), mediante el algoritmo de la transformada inversa para una variable discreta con probabilidades \(0.6, 0.3, 0.1\) (fracaso, éxito moderado, gran éxito), y seleccionar la variable \(X_{I_i}\).
Paso 3. Simular un valor \(x_{I_i}\) mediante el algoritmo de la transformada inversa para \(X_i\) con valores malos, regulares, buenos, y probabilidades dadas por:
- fracasos (0.5, 0.3, 0.2)
- éxito moderado (0.2, 0.4, 0.4)
- gran éxito (0.1, 0.3, 0.6)
Paso 4. Devolver el conjunto de simulaciones \(\{(I_i, x_{I_i})\}_{i=1}^{nsim}.\)
Procedamos pues, a simular el proceso para, con las simulaciones, responder a las preguntas planteadas por la empresa.
# Parámetros iniciales
nsim <- 5000
semilla <- 12
# Descripción variable indicadora
exito <- c("Fracaso", "Moderado", "Éxito")
pexito <- c(0.6, 0.3, 0.1)
pexitoacum <- cumsum(pexito)
# Descripción del proceso de adquisión del microondas
clasifi <- c("Malo", "Regular", "Bueno")
p1 <- c(0.5, 0.3, 0.2)
p2 <- c(0.2, 0.4, 0.4)
p3 <- c(0.1, 0.3, 0.6)
p1acum <- cumsum(p1)
p2acum <- cumsum(p2)
p3acum <- cumsum(p3)
# Inicialización de variables para las simulaciones
producto <- c() # éxito producto
jurado <- c() # clasificación jurado
## Simulación del proceso
##########################
i <- 1
# Generamos uniformes para describir el proceso de indicadores de éxito
# y también el de evaluación o clasificación por el jurado
set.seed(semilla)
uexito <- runif(nsim)
uclasi <- runif(nsim)
# Bucle de simulación
while (i <= nsim)
{
# Éxito del producto
producto[i] <- exito[min(which(uexito[i] <= pexitoacum))]
# Tipo de microndas
if(producto[i] == exito[1])
{
jurado[i] <- clasifi[min(which(uclasi[i] <= p1acum))]
}
else if (producto[i] == exito[2])
{
jurado[i] <- clasifi[min(which(uclasi[i] <= p2acum))]
}
else
{
jurado[i] <- clasifi[min(which(uclasi[i] <= p3acum))]
}
# nueva simulación
i <- i+1
}
# Resultado
simulacion <- data.frame(producto = producto, jurado = jurado)A partir de las simulaciones, obtenemos la tabla conjunta de frecuencias (Tabla 1.1) y las frecuencias relativas (Tabla 1.2), que constituyen una aproximación de las probabilidades de ocurrencia.
distri.conjunta.frec <- table(simulacion)
kbl(distri.conjunta.frec,caption="Frecuencias observadas en las simulaciones.") %>%
kable_styling(bootstrap_options = c("striped", "hover"),full_width = F)| Bueno | Malo | Regular | |
|---|---|---|---|
| Éxito | 327 | 47 | 166 |
| Fracaso | 650 | 1516 | 844 |
| Moderado | 616 | 292 | 542 |
distri.conjunta=as.data.frame(table(simulacion)/nsim)
kbl(distri.conjunta,caption="Frecuencias relativas observadas en las simulaciones. Aproximación de la distribución conjunta.") %>%
kable_styling(bootstrap_options = c("striped", "hover"),full_width = F)| producto | jurado | Freq |
|---|---|---|
| Éxito | Bueno | 0.0654 |
| Fracaso | Bueno | 0.1300 |
| Moderado | Bueno | 0.1232 |
| Éxito | Malo | 0.0094 |
| Fracaso | Malo | 0.3032 |
| Moderado | Malo | 0.0584 |
| Éxito | Regular | 0.0332 |
| Fracaso | Regular | 0.1688 |
| Moderado | Regular | 0.1084 |
Podemos contestar ahora a las preguntas planteadas sin más que mirar la tabla anterior o realizar calculos sencillos con los datos obtenidos:
- ¿Cuál es la probabilidad conjunta de que un producto tenga un éxito moderado y reciba una mala calificación? Estamos interesados en la probabilidad
\[Pr(\text{Éxito = "Moderado" y Evaluación = "Malo"})\] cuyo valor es 0.0584.
- Si un nuevo producto tiene una buena calificación, ¿cuál es la probabilidad de que fracase? Para responder a esta pregunta podemos aplicar el Teorema de Bayes para resolver la probabilidad condicionada siguiente a partir de las frecuencias observadas en la simulación y mostradas en la Tabla 1.1,
\[Pr(\text{E= "Fracaso" | Eval= "Bueno"}) = \frac{Pr(\text{ E="Fracaso" , Eval= "Bueno"})}{Pr(\text{ Eval= "Bueno"})}\]
donde \(E=\)Éxito y \(Eval=\)Evaluación,
distri.conjunta.frec[2,1]/sum(distri.conjunta.frec[,1])## [1] 0.4080352o directamente seleccionar sobre la Tabla 1.2 las simulaciones en las que el producto fue evaluado como “Bueno” por el jurado, y contabilizar en cuántas de ellas el producto finalmente fracasó (a través del ratio correspondiente).
distri.conjunta %>%
filter(jurado == "Bueno") %>%
mutate(pr.bueno = sum(Freq), resultado = round(Freq/pr.bueno,4)) %>%
kbl(caption="Distribución condicionada a que el producto fue evaluado como Bueno por el jurado.")%>%
kable_styling(bootstrap_options =c("striped","hoover"),full_width = F)| producto | jurado | Freq | pr.bueno | resultado |
|---|---|---|---|---|
| Éxito | Bueno | 0.0654 | 0.3186 | 0.2053 |
| Fracaso | Bueno | 0.1300 | 0.3186 | 0.4080 |
| Moderado | Bueno | 0.1232 | 0.3186 | 0.3867 |
La probabilidad de interés resulta 0.4080. De hecho, en la Tabla 1.3 se muestran, en la columna “resultado,” las probabilidades condicionadas a que el jurado emitió una buena calificación del producto. ¿Cómo podemos interpretar esas probabilidades?
- ¿Cuál es la probabilidad de que un producto tenga éxito moderado dado que éste obtuvo una mala calificación? Procedemos como en la pregunta anterior ya que estamos interesados en
\[Pr(\text{E= "Moderado" | Eval = "Malo"}) = \frac{Pr(\text{E= "Moderado" , Eval = "Malo"})}{Pr(\text{ Eval= "Malo"})}\] Y lo resolvemos de nuevo generando la distribución condicionada a que la evaluación por el jurado sea “Mala,” que se muestra en la Tabla 1.4
distri.conjunta %>%
filter(jurado == "Malo") %>%
mutate(pr.malo = sum(Freq), resultado = round(Freq/pr.malo,4)) %>%
kbl(caption="Distribución condicionada a que el producto fue evaluado como Malo por el jurado.") %>%
kable_styling(bootstrap_options =c("striped","hoover"),full_width = F)| producto | jurado | Freq | pr.malo | resultado |
|---|---|---|---|---|
| Éxito | Malo | 0.0094 | 0.371 | 0.0253 |
| Fracaso | Malo | 0.3032 | 0.371 | 0.8173 |
| Moderado | Malo | 0.0584 | 0.371 | 0.1574 |
La probabilidad de interés es 0.1574. ¿Cómo podemos interpretar la Tabla 1.4 de probabilidades obtenida?