4.2 Descripción del proceso

En virtud del teorema 4.1 todas las CMTC con espacios de estado finitos que tienen tiempos de permanencia no nulos en cada estado pueden ser descritos a través de las tasas de permanencia y la matriz de saltos. En este punto detallamos este análisis e introducimos todos los conceptos necesarios para el análisis del proceso.

De forma análoga a las CMTD, una CMTC también puede representarse gráficamente mediante de un grafo dirigido, cuyos nodos (o vértices) indican cada uno d elos estados del proceso, y se establece un arco dirigido del nodo \(i\) al nodo \(j\) si \(p_{ij} > 0\). La tasa de transición de \(i\) a \(j\), \(r_{ij} = r_i p_{ij}\) , se escribe junto a este arco. Obsérvese que no hay bucles propios (arcos de \(i\) a \(i\)). Esta representación gráfica se denomina diagrama de tasas de la CMTC.

Podemos entender la dinámica de la CMMTC visualizando una partícula que se mueve de nodo en nodo en el diagrama de tasas de la siguiente manera: permanece en el nodo \(i\) durante una cantidad de tiempo \(Exp(r_i)/\) y luego elige uno de los arcos de salida del nodo \(i\) con probabilidades proporcionales a las tasas de los arcos y se desplaza al nodo del otro extremo del arco. Este movimiento continúa para siempre. El nodo ocupado por la partícula en el tiempo \(t\) es el estado de la CMTC en el tiempo t .

En esta situación resulta posible obtner los valores de \(r_i\) y \(p_{ij}\) a partir de las tasas \(r_{ij}\) dado que:

\[r_i = \sum_{j=1}^{N} r_{ij}\] \[p_{ij} = \frac{r_{ij}}{r_i} \quad \text{ si } r_i \neq 0\]

Para un mejor manejo de la información resulta conveniente construir la matriz de tasas teniendo en cuenta que \(r_{ii} = 0\) para cualquier valor de \(i\), y por tanto la diagonal de la matriz R es siempre cero. Así tenemos que:

\[R = \begin{pmatrix} 0 & r_{12} & ... & r_{1N}\\ r_{21} & 0 & ... & r_{2N}\\ ... & ... & ... & ...\\ r_{N1} & r_{N2} & ... & 0 \end{pmatrix}\]

A partir de la matriz \(R\) se puede obtener la denominada matriz generadora de la CMTC \(Q\), que se define como:

\[q_{ij} = -r_i \text{ si } i = j, \text{ y } q_{ij} = r_{ij} \text{ si } i \neq j\] de forma que:

\[Q = \begin{pmatrix} -r_1 & r_{12} & ... & r_{1N}\\ r_{21} & -r_2 & ... & r_{2N}\\ ... & ... & ... & ...\\ r_{N1} & r_{N2} & ... & -r_N \end{pmatrix}\]

Ejemplo 4.1 Continuando con el sistema de vida útil del satélite del ejemplo ?? podemos establecer que \(r_0 = 0\) y \(r_1 = \mu\), con \(p_{10} = 1\) y \(p_{01}\) no definida, de forma que:

\[R = \begin{pmatrix} 0 & 0 \\ \mu & 0 \end{pmatrix} \quad \text{ y } \quad Q = \begin{pmatrix} 0 & 0 \\ \mu & -\mu \end{pmatrix}\]

En esta situación el diagrama de tasas viene dado por:

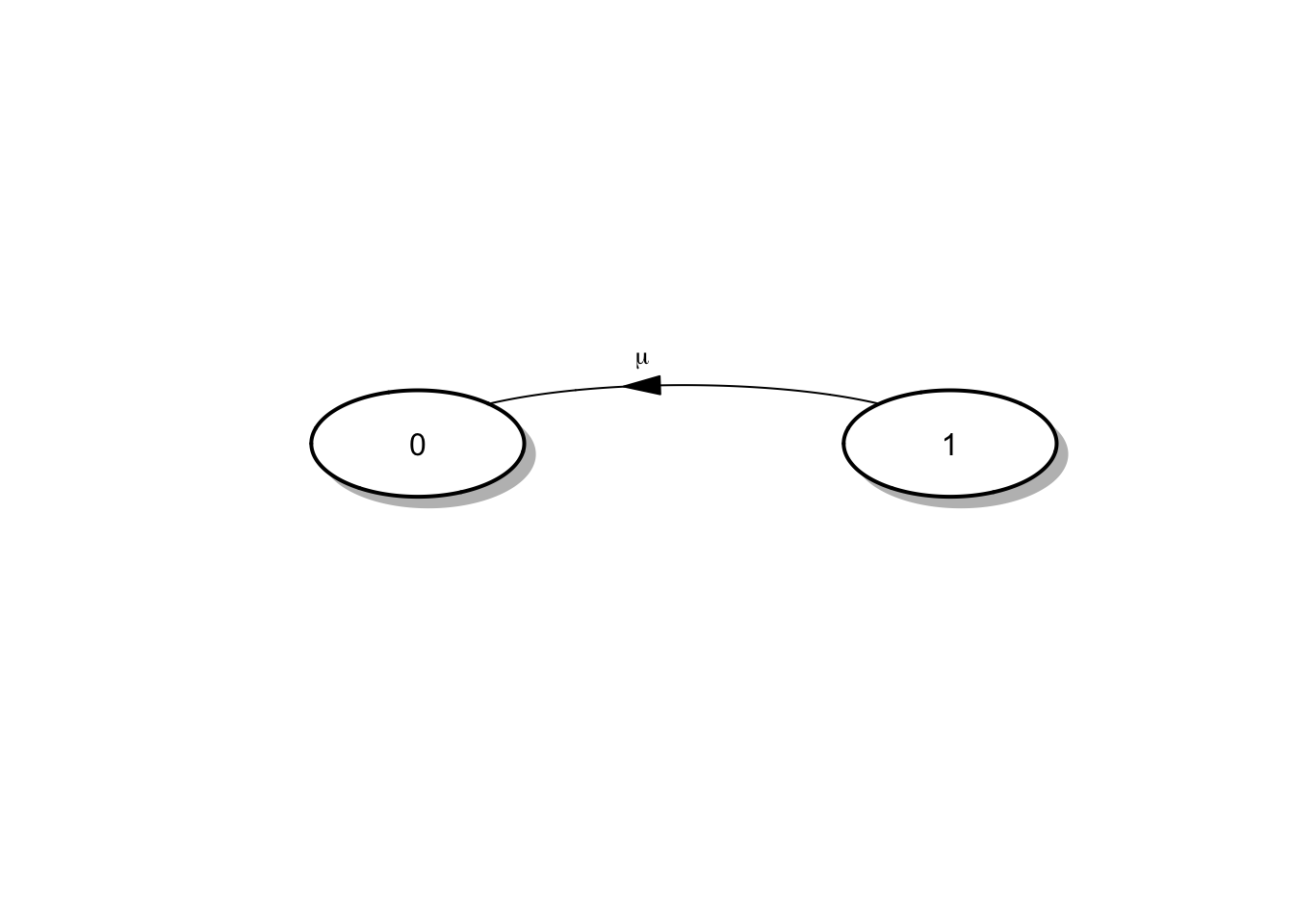
Figura 4.1: Diagrama de tasas para el tiempo de vida del Satélite

Ejemplo 4.2 Continuando con el sistema del viajante descrito en el ejemplo ?? ya que conocemos las tasas medias y las probabilidades de salto podemos obtener la matriz \(R\) de forma inmediata:

estados <- c("0", "1", "2")
nestados <- length(estados)

P <- matrix(nrow = nestados, ncol = nestados, 
            data = c(0, 0.5, 0.5, 0.75, 0, 0.25, 0.75, 0.25, 0), 
            byrow = 3)
r <- matrix(nrow = nestados, ncol = nestados, 
            data = rep(c(0.5, 1, 1.5),3))

R <- P*r
R

##       [,1]  [,2] [,3]
## [1,] 0.000 0.250 0.25
## [2,] 0.750 0.000 0.25
## [3,] 1.125 0.375 0.00

de forma que el diagrama de tasas viene dado por (asignamos el valor de la ciudad a cada uno de los posibles estados del sistema)

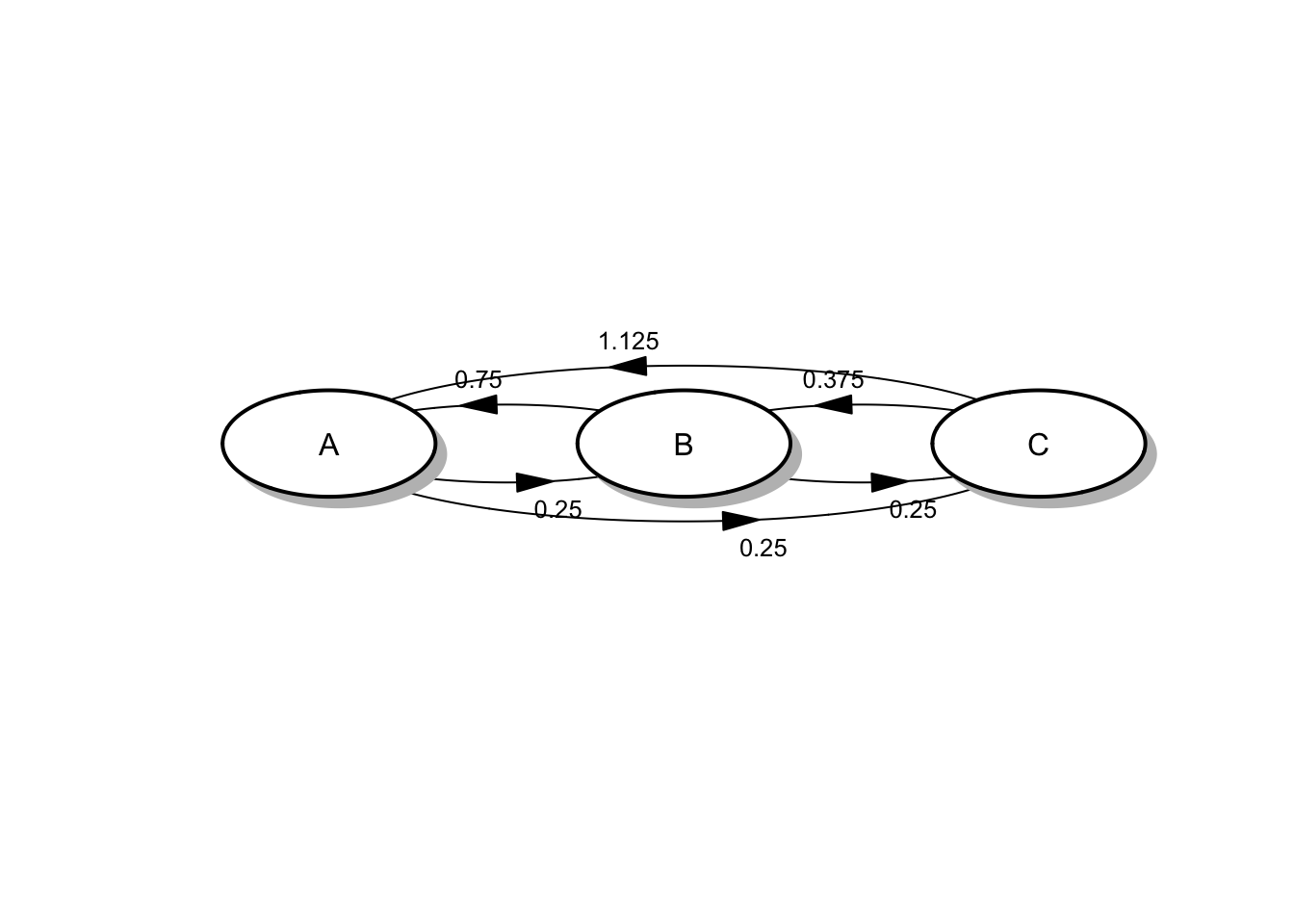
Figura 4.2: Diagrama de tasas para el proceso del vendedor

El diagrama representa el comportamiento de todo el proceso de viajes y estancias del vendedor.

::: {.example #excmtc005 name = “Sistema vida útil de una máquina”}

Consideramos un sistema compuesto por una máquina que funciona durante un cantidad de tiempo que vienee determianda por una variable aleatoria \(Exp(\mu)\) hasta que falla. Una vez se detecta la averia la máquina se repara. El tiempo de reparación es una variable aleatoria \(Exp(\lambda)\) y es independiente del pasado. La máquina está como nueva después de la reparación. Sea \(X(t)\) el estado de la máquina en tiempo \(t\), de forma que toma el valor 1 si está en marcha y 0 si está parada (está siendo reparada).

En esta situación el tiempo de estancia en el estado 0 es el tiempo de reparación, de forma que \(r_0 = \lambda\), mientras que el tiempo en el estado 1 es el tiempo de funcionamiento con \(r_1 = \mu\). Además las probabiliddes de salto de interés son \(p_{01} = 1\) y \(p_{10} = 1\), dado que la máquina siempre es reparada y vuelve a funcionar y porque sabemos que la máquina debe estropearse en algún momento.

El proceso definido de esta forma \(\{X_t; t \geq 0\}\) es una CMTC cuya matriz de tasas y matriz generadora del sietema vienen dadas por: :::

\[R = \begin{pmatrix} 0 & \lambda \\ \mu & 0 \end{pmatrix} \quad \text{ y } \quad Q = \begin{pmatrix} -\lambda & \lambda \\ \mu & -\mu \end{pmatrix}\]

El diagrama del sistema viene dado por:

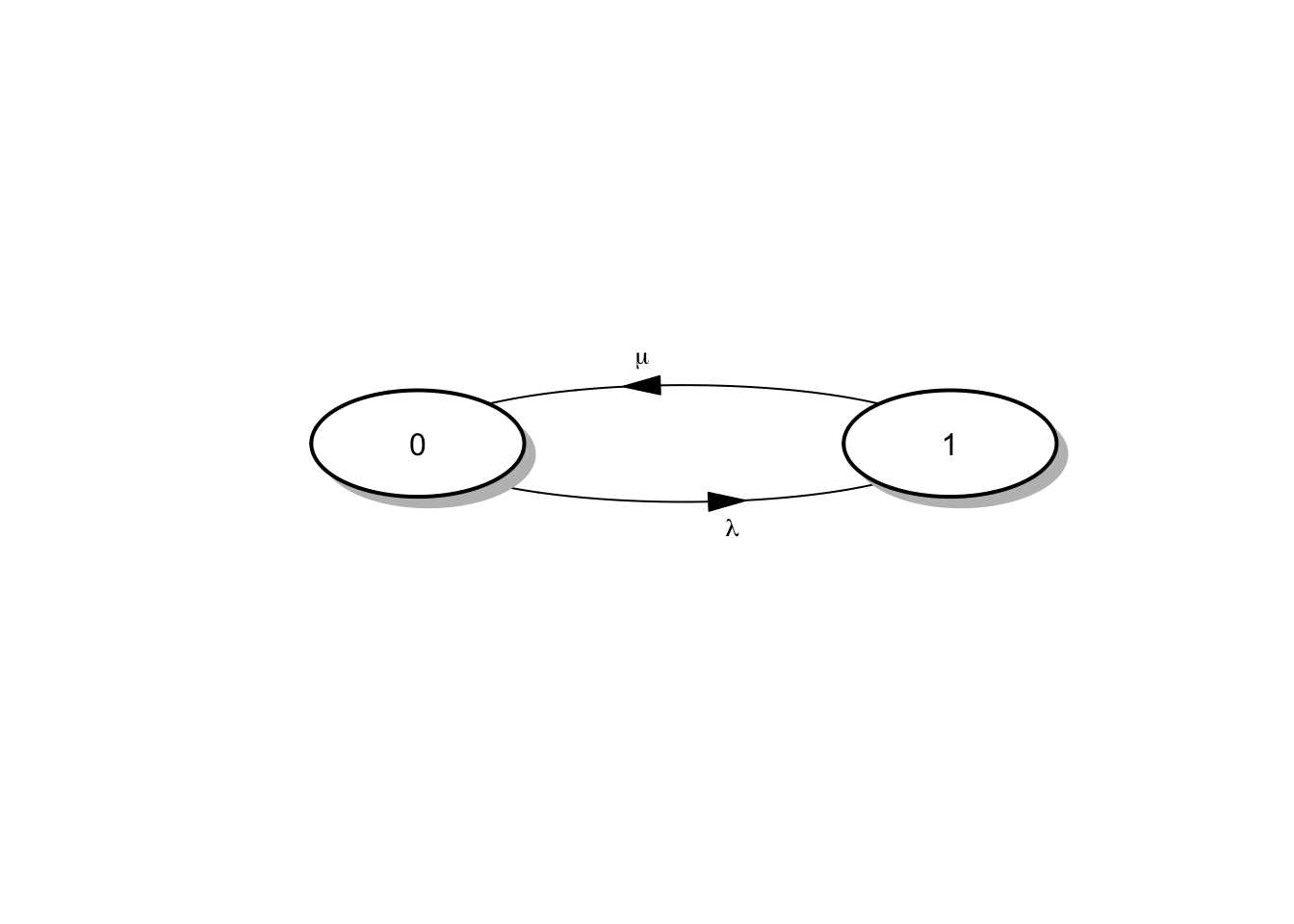
Figura 4.3: Diagrama de tasas para el sistema de una máquina