2.3 Aplicaciones
Las aplicaciones de las CMTD son muy numerosas. A continuación presentamos una colección de ejemplos basados en aplicaciones prácticas de estos procesos, con algunos de los cuales trabajaremos a lo largo de la unidad.
2.3.1 Colas de espera
Supongamos una consulta médica en un centro de salud, en el que los pacientes que llegan se colocan en una única cola de espera, son atendidos consecutivamente y sólo se atiende a un paciente en cada periodo de 5 minutos. Consideramos las variables aleatorias:
- \(Y_n:\) Número de clientes que acuden a la consulta durante el n-ésimo periodo de servicio, con posibles valores \(\{0, 1, 2,...\}\) donde
\[Pr(Y_n = k) = a_k, \quad k=0, 1, 2,...; \quad 0 \leq a_k \leq 1; \quad \sum_{k=0}^{\infty} a_k =1\]
- \(X_n:\) Número de pacientes que hay esperando en la cola en el momento que empieza el n-ésimo periodo de servicio, con posibles valores \(\{0, 1, 2,...\}\), que conforman un proceso estocástico discreto con:
de forma que cada \(X_n\) sólo dependerá de lo que haya ocurrido en el periodo inmediatamente anterior, luego \(\{X_n, n \in \mathbb{N}\}\) es una \(CMTD\), con probabilidades de transición dadas por:
\[\begin{eqnarray*} p_{0j} &=& Pr[X_{n+1} = j | X_{n} = 0] = Pr[Y_n = j] = a_j \\ p_{ij} &=&Pr[X_{n+1} = j | X_{n} = i] = Pr[i - 1 + Y_n = j] = a_{j-i+1}; \quad i\neq 0; \ j \geq i-1 \\ p_{ij} &=& 0; \quad j+1<i\neq0. \end{eqnarray*}\]La matriz de transición viene dada por:
\[P = \begin{pmatrix} a_0 & a_1 & a_2 & a_3 &...& a_j & ...\\ a_0 & a_1 & a_2 & a_3 &...& a_j & ...\\ 0 & a_0 & a_1 & a_2 &...& a_{j-1} & ...\\ 0 & 0 & a_0 & a_1 &...& a_{j-2} & ...\\ ... & ... & ... & ... &...& ... & ... \end{pmatrix}\]
2.3.2 Fiabilidad de máquinas
La empresa Depend-On-Us fabrica una máquina que está encendida o apagada (“On”/“Off”). Si está “On” al principio de un día, entonces está “On” al principio del día siguiente con una probabilidad de 0.98 (independientemente del historial de la máquina), o falla con una probabilidad de 0.02. Una vez que la máquina falla, la empresa envía a una persona para que la repare. Si la máquina está averiada al principio de un día, está “Off” al principio del día siguiente con una probabilidad de 0.03 (independientemente del historial de la máquina), o la reparación se completa y la máquina está “On” con probabilidad de 0.97. Una máquina reparada está como nueva.
Podemos modelar este sistema mediante una \(CMTD\) si consideramos la variable aleatoria \(X_n\) que refleja el estado de la máquina en el día \(n\) definida como:
\[\begin{equation*} X_{n} = \begin{cases} 0 & \text{ Off}\\ 1 & \text{ On} \end{cases} \end{equation*}\]de forma que la matriz de transicción viene dada por: \[P = \begin{pmatrix} 0.03 & 0.97\\ 0.02 & 0.98 \end{pmatrix}\]
Supongamos ahora que la empresa mantiene dos máquinas de este tipo que son idénticas, se comportan de forma independiente y cada una tiene su propio reparador.
Sea \(Y_n\) el número de máquinas en estado “On” al principio del día \(n\), que constituye una CMTD cuyo espacio de estados es \(\{0, 1, 2\}\), puesto que la situación de las máquinas un día cualquiera sólo depende de cómo estaban el día anterior (cumplen la Ecuación (2.1).
Calculemos la probabilidad de transición para un caso concreto: \(Y_n = i = 1\) e \(Y_{n+1} = j = 0\), que identifica una situación en la que una máquina está en funcionamiento y otra en paro el día \(n\), pero al día siguiente ambas están paradas. Así, la máquina que está “Off” el día \(n\) debe permanecer “Off” al día siguiente, y la máquina que está “On” debe cambiar a “Off” el día siguiente. Como las máquinas son independientes, la probabilidad de cambio de estado es:
\[p_{10}=Pr[Y_{n+1} = 0 | Y_n = 1] = 0.03 * 0.02 = 0.0006\] Procediendo de la misma forma obtenemos la matriz completa de transición de un paso del proceso como:
\[P = \begin{pmatrix} 0.0009 & 0.0582 & 0.9409\\ 0.0006 & 0.0488 & 0.9506\\ 0.0004 & 0.0392 & 0.9604 \end{pmatrix}\]
Representamos a continuación este sistema en forma de grafo en la Figura 2.2. Para ello acudimos a la librería markovchain.
# Definimos estados
estados <- c("0", "1", "2")
# Matriz de transición
pmat <- matrix(data = c(0.0009, 0.0582, 0.9409,
0.0006, 0.0488, 0.9506,
0.0004, 0.0392, 0.9604),
byrow = TRUE, nrow = 3,
dimnames = list(estados, estados))
# CMTD
fiabilidad <- new("markovchain", states = estados,
byrow = TRUE, transitionMatrix = pmat,
name = "Fiabilidad")
# Verificamos los datos introducidos
fiabilidad## Fiabilidad
## A 3 - dimensional discrete Markov Chain defined by the following states:
## 0, 1, 2
## The transition matrix (by rows) is defined as follows:
## 0 1 2
## 0 9e-04 0.0582 0.9409
## 1 6e-04 0.0488 0.9506
## 2 4e-04 0.0392 0.9604# Diagrama
plot(fiabilidad, vertex.color="steelblue",
vertex.label.font = 2,
edge.label.size = 0.1,
edge.arrow.size=0.5,
vertex.shape = "rectangle",
vertex.size = 20)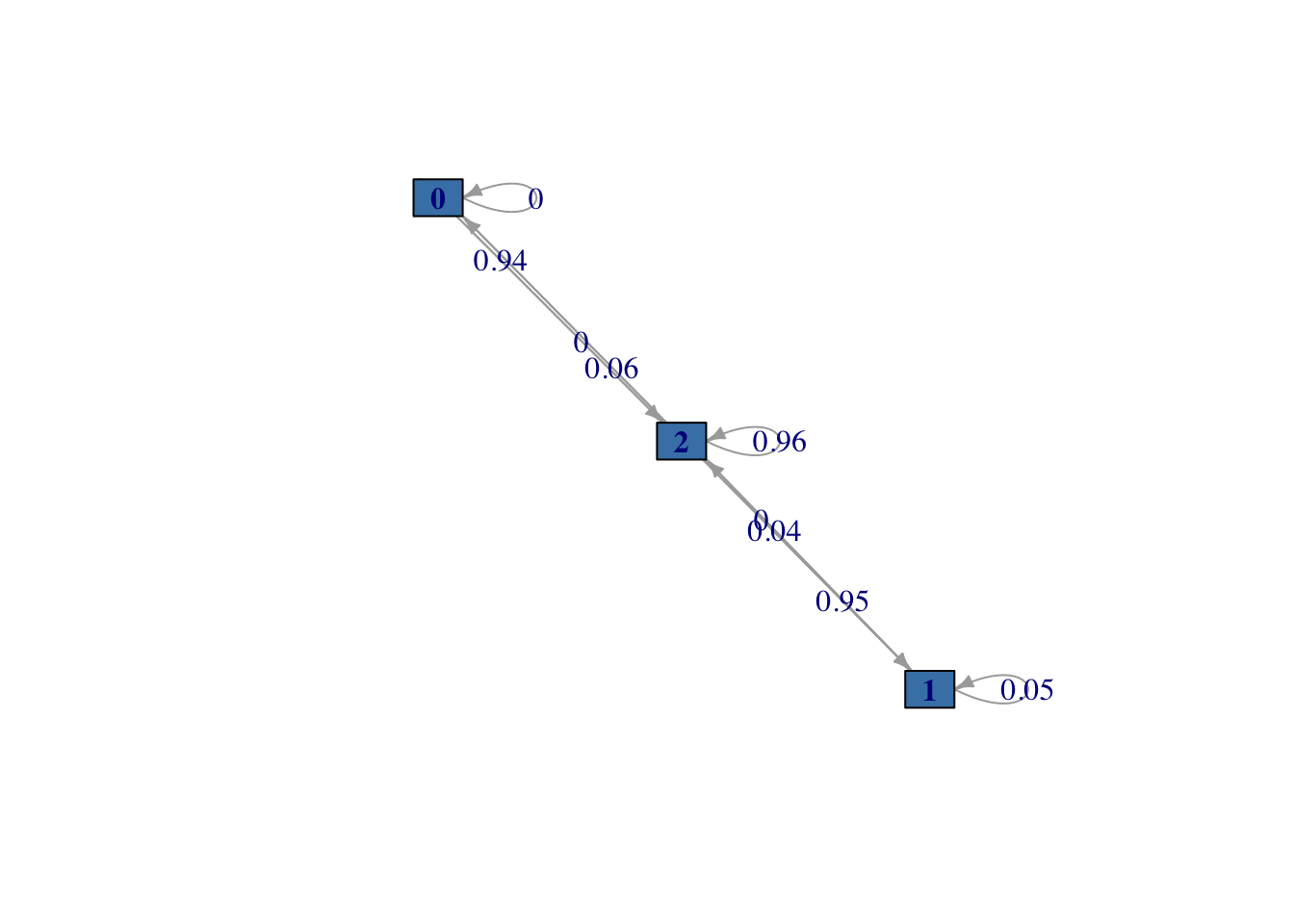
Figura 2.2: Diagrama del sistema de fiabilidad
2.3.3 Meteorología
El tiempo en la ciudad de Heavenly se clasifica como soleado, nublado o lluvioso. Supongamos que el tiempo de mañana depende sólo del tiempo de hoy de la siguiente manera: si hoy hace sol, mañana estará nublado con una probabilidad de 0.3 y lluvioso con probabilidad 0.2; si hoy está nublado, mañana estará soleado con probabilidad 0.5 y lluvioso con probabilidad 0.3; y finalmente, si hoy está lluvioso, mañana estará soleado con probabilidad 0.4 y nublado con probabilidad 0.5.
Consideramos la variable aleatoria \(X_n\) que registra las condiciones meteorológicas del día \(n\) como:
\[\begin{equation*} X_{n} = \begin{cases} 1 & \text{ soleado}\\ 2 & \text{ nublado}\\ 3 & \text{ lluvioso} \end{cases} \end{equation*}\]de forma que el proceso \(\{X_n, n \in \mathbb{N}\}\) con espacio de estados \(S = \{1, 2, 3\}\) se puede considerar como una \(CMTD\), cuya matriz de transición se puede obtener de forma muy rápida como:
\[P = \begin{pmatrix} 0.50 & 0.30 & 0.20\\ 0.50 & 0.20 & 0.30\\ 0.40 & 0.50 & 0.10 \end{pmatrix}\]
Representamos a continuación este sistema en forma de grafo en la Figura 2.3.
# Definimos estados
estados <- c("Soleado", "Nublado", "LLuvioso")
# Matriz de transición
pmat <- matrix(data = c(0.50, 0.30, 0.20,
0.50, 0.20, 0.30,
0.40, 0.50, 0.10),
byrow = TRUE, nrow = 3,
dimnames = list(estados, estados))
# CMTD
meteo <- new("markovchain", states = estados,
byrow = TRUE, transitionMatrix = pmat,
name = "Meteorología")
# Verificamos los datos introducidos
meteo## Meteorología
## A 3 - dimensional discrete Markov Chain defined by the following states:
## Soleado, Nublado, LLuvioso
## The transition matrix (by rows) is defined as follows:
## Soleado Nublado LLuvioso
## Soleado 0.5 0.3 0.2
## Nublado 0.5 0.2 0.3
## LLuvioso 0.4 0.5 0.1# Diagrama
plot(meteo, vertex.color="steelblue",
vertex.label.font = 2,
edge.label.size = 0.1,
edge.arrow.size=0.5,
vertex.shape = "rectangle",
vertex.size = 60)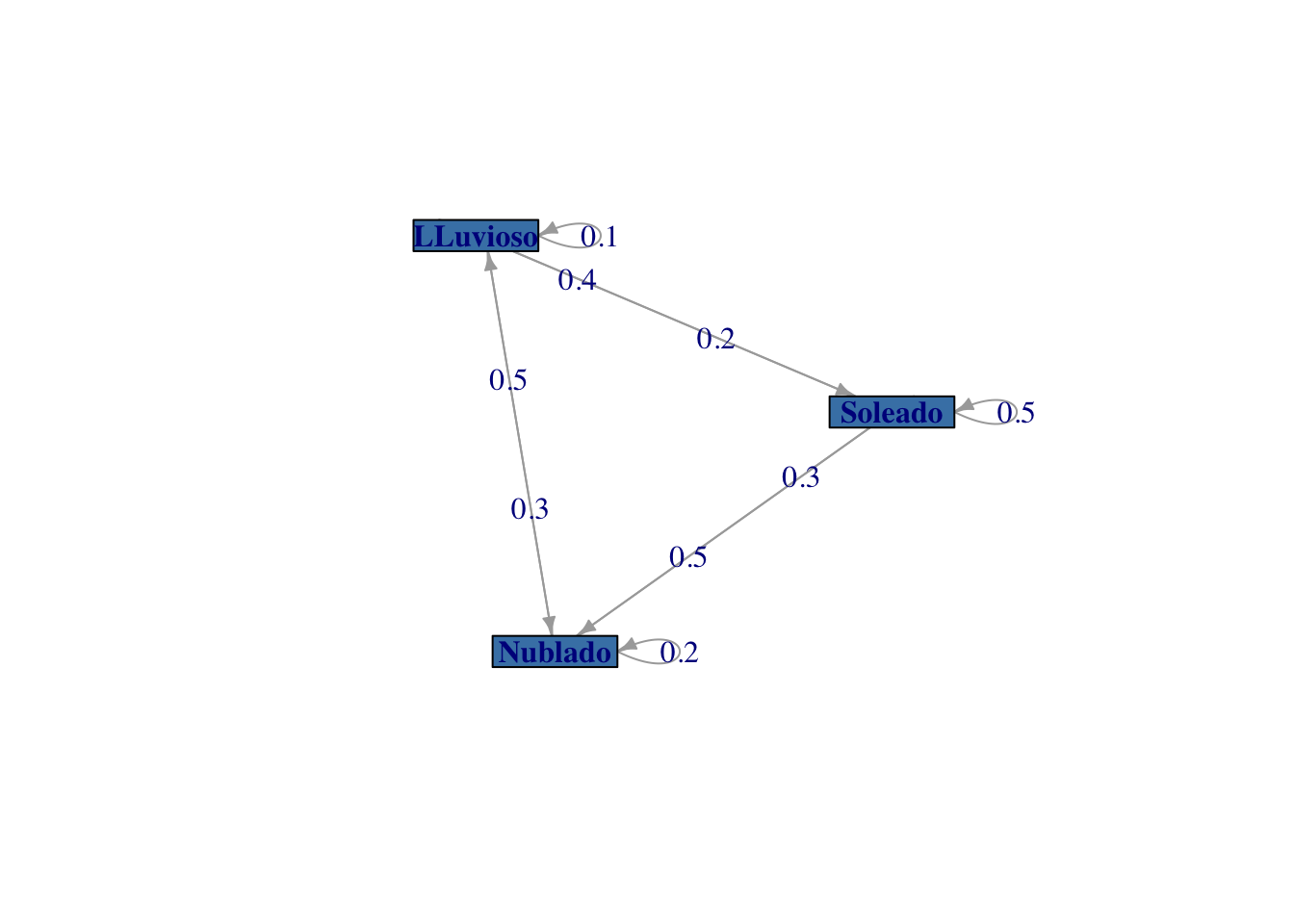
Figura 2.3: Diagrama del sistema de metereología
2.3.4 Problema de inventario
Computers-R-Us almacena una amplia variedad de PCs para la venta al por menor. La tienda abre de lunes a viernes de 8:00 a.m. a 5:00 p.m., y utiliza la siguiente política operativa para controlar el inventario al inicio de semana, en función del número de PCs que quedan en stock el viernes de la semana anterior a las 5:00 p.m:
Si el stock al finalizar una semana es inferior a dos, se piden suficientes ordenadores para disponer de un stock total de cinco al inicio la semana siguiente.
Si el stock al final de la semana es de dos o más, no se realiza ningún pedido.
La demanda de ordenadores durante la semana es una variable aleatoria de Poisson con media 3. Cualquier demanda que no pueda ser satisfecha inmediatamente se pierde.
Se consideran las variables aleatorias:
- \(X_n:\) número de PCs en stock a las 8:00 a.m del lunes de la semana \(n\).
- \(D_n:\) número de PCs demandados durante la semana \(n\).
De esta forma el número de Pcs que hay en la tienda al inicio de la semana \(n+1\) viene dado por los que habían en stock al inicio de la semana anterior menos los que se han vendido, siempre que dicho balance sea al menos de 2 unidades, y será de 5 en otro caso:
\[\begin{equation*} X_{n+1} = \begin{cases} X_n - D_n & \text{ si } X_n - D_n \geq 2\\ 5 & \text{ si } X_n - D_n < 2 \end{cases} \end{equation*}\]Necesariamente entonces, \(X_{n+1} \geq X_n\) dado que \(D_n \geq 0\).
Se trata de una CMTD con espacio de estados \(\{2, 3, 4, 5\}\), puesto que el estado del sistema en la semana \(n+1\) sólo depende de su estado en la semana anterior \(n\). Calculemos las probabilidades de transición.
- Para \(j= 2, 3, 4\)
\[\begin{array}{ll} Pr[X_{n+1} = j | X_n = i] & = Pr[X_n - D_n = j | X_n = i]\\ & = Pr[D_n=X_n-j | X_n = i]\\ & = Pr[D_n = i - j] \\ &=\begin{cases} Pr[D_n = i - j] \quad \text{ si } i\geq j \\ 0 \qquad \qquad \qquad \quad \text{ si } i< j \end{cases} \end{array}\]
- Para \(j=5\) e \(5>i\geq 2\)
\[\begin{array}{ll} Pr[X_{n+1} = 5 | X_n = i] & = Pr[X_n - D_n \leq 1 | X_n = i]\\ &=Pr[D_n \geq X_n-1|X_n=i] \\ & = Pr(D_n \geq i - 1). \end{array}\]
- Para \(j=5\) e \(i=5\), podría ocurrir que durante la semana anterior no se hubiera vendido nada \(D_n=0\) o se hubieran vendido al menos cuatro ordenadores, \(D_n \geq 4\) (para dejar un stock inferior a 2),
\[\begin{array}{ll} Pr[X_{n+1} = 5 | X_n = 5] & = Pr[X_n - D_n =5 | X_n = 5]\\ &=Pr[D_n =0] + Pr(D_n \geq 4). \end{array}\]
Usando el hecho de que la variable \(D_n \sim Po(3)\) podemos obtener la tabla de probabilidades siguientes:
| \(k\) | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| \(Pr[D_n = k]\) | 0.0498 | 0.1494 | 0.2240 | 0.2240 | 0.1680 |
| \(Pr[D_n \geq k]\) | 1.0000 | 0.9502 | 0.8008 | 0.5768 | 0.3528 |
Usando los datos de esta tabla calculamos fácilmente la matriz de transición asociada a la \(CMTD\) como:
\[P = \begin{pmatrix} 0.0498 & 0 & 0 & 0.9502\\ 0.1494 & 0.0498 & 0 & 0.8008\\ 0.2240 & 0.1494 & 0.0498 & 0.5768\\ 0.2240 & 0.2240 & 0.1494 & 0.4026 \end{pmatrix}\]
Representamos a continuación este sistema en forma de grafo en la Figura 2.4.
# Definimos estados
estados <- c("2 PCs", "3 PCs", "4 PCs", "5 PCs")
# Matriz de transición
pmat <- matrix(data = c(0.0498, 0, 0, 0.9502,
0.1494, 0.0498, 0, 0.8008,
0.2240, 0.1494, 0.0498, 0.5768,
0.2240, 0.2240, 0.1494, 0.4026),
byrow = TRUE, nrow = 4,
dimnames = list(estados, estados))
# CMTD
inventario <- new("markovchain", states = estados,
byrow = TRUE, transitionMatrix = pmat,
name = "inventario")
# Verificamos los datos introducidos
inventario## inventario
## A 4 - dimensional discrete Markov Chain defined by the following states:
## 2 PCs, 3 PCs, 4 PCs, 5 PCs
## The transition matrix (by rows) is defined as follows:
## 2 PCs 3 PCs 4 PCs 5 PCs
## 2 PCs 0.0498 0.0000 0.0000 0.9502
## 3 PCs 0.1494 0.0498 0.0000 0.8008
## 4 PCs 0.2240 0.1494 0.0498 0.5768
## 5 PCs 0.2240 0.2240 0.1494 0.4026# Diagrama
plot(inventario, vertex.color="steelblue",
vertex.label.font = 2,
edge.label.size = 0.1,
edge.arrow.size=0.5,
vertex.shape = "rectangle",
vertex.size = 40)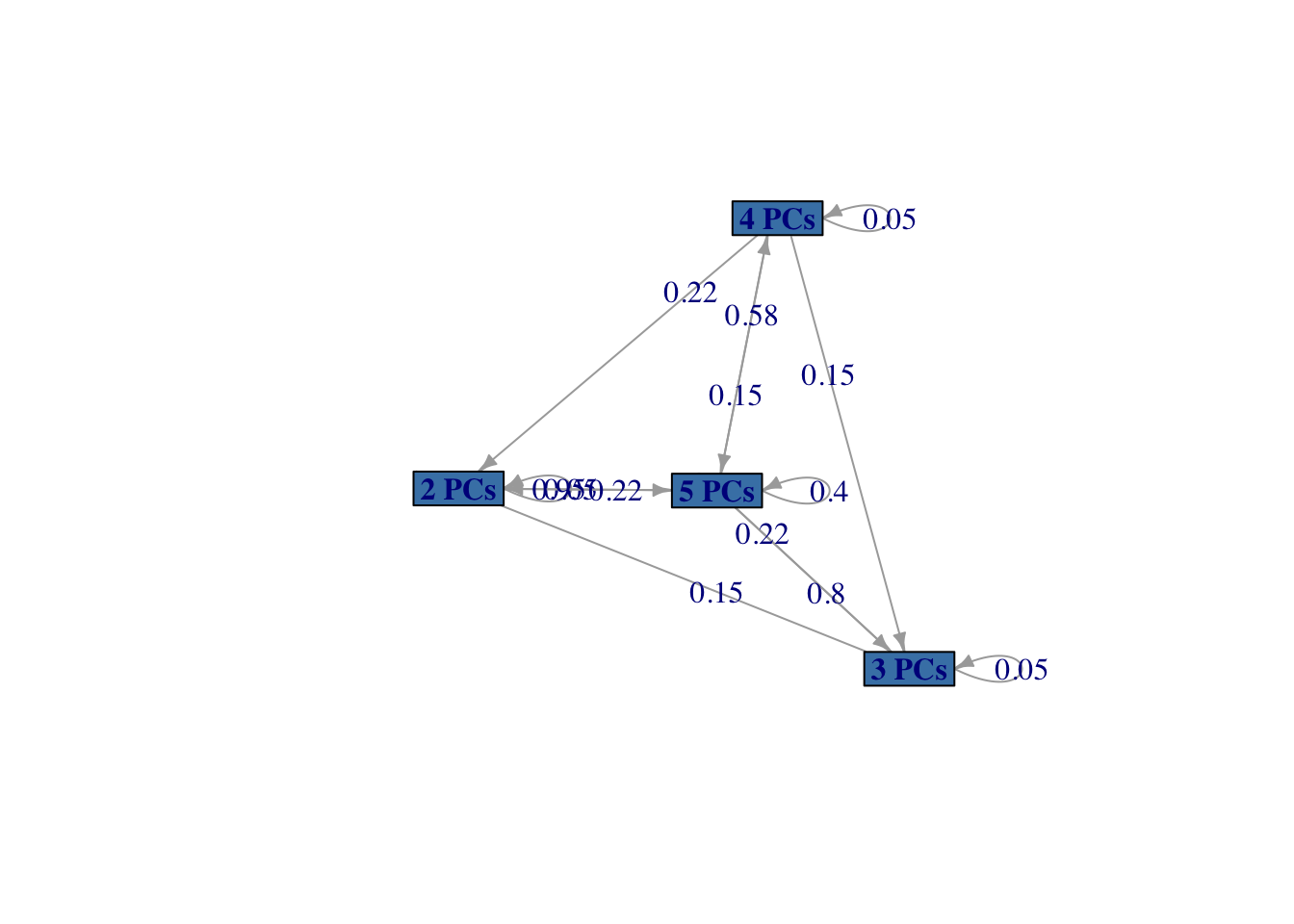
Figura 2.4: Diagrama del sistema de inventario
2.3.5 Planificación de mano de obra
Paper Pushers, Inc. es una empresa de seguros que emplea a 100 trabajadores organizados en cuatro grados, etiquetados como \(1\), \(2\), \(3\) y \(4\). Por razones de simplicidad, supondremos que los trabajadores pueden ser promovidos de un grado a otro, o dejar la empresa, sólo al principio de la semana. Un trabajador en el grado 1 al principio de la semana asciende al grado 2 con probabilidad 0.03, deja la empresa con una probabilidad de 0.02, o continúa en el mismo grado al principio de la semana siguiente. Un trabajador que se encuentra en el grado 2 al principio de la semana asciende al grado 3 con probabilidad 0.01, abandona la empresa con probabilidad 0.008 o continúa en el mismo grado al principio de la semana siguiente. Un trabajador de grado 3 al principio de la semana asciende al grado 4 con una probabilidad de 0.005, abandona la empresa con una probabilidad de 0.02, o continúa en el mismo grado al principio de la semana siguiente. Un trabajador que se encuentra en el grado 4 al principio de la semana deja la empresa con una probabilidad de 0.01 o continúa en el mismo grado al principio de la semana siguiente. Si un trabajador abandona la empresa, es sustituido instantáneamente por otro de grado 1. El movimiento de los trabajadores dentro de la empresa puede modelizarse utilizando una \(CMTD\).
Supondremos que todos los ascensos de los trabajadores se deciden de manera independiente. Esto simplifica considerablemente nuestro modelo. En lugar de hacer un seguimiento de los 100 trabajadores, tenemos en cuenta a un único trabajador, digamos el trabajador \(k\), donde \(k = 1, 2,...,100\). Pensamos en \(k\) como un ID de trabajador, y cuando este trabajador deja la empresa, se le asigna al nuevo sustituto. Sea \(X_n^k\) el grado en el que se encuentra el trabajador \(k\) al principio de la n-ésima semana. Ahora, si suponemos que los ascensos de los trabajadores se determinan independientemente del historial del trabajador (es decir, que el tiempo transcurrido en un grado determinado no afecta a las posibilidades de promoción), vemos que para \(k = 1, 2,...,100\) el conjunto \(\{X_n^k, n \in \mathbb{N}\}\) es una \(CMTD\) con espacio de estados \(S =\{1, 2, 3, 4\}\).
Para obtener la matriz de transiciones procedemos con un ejemplo. Supongamos que \(X_n^k = 3\) entonces:
- Si es promocionado (\(X_{n+1}^k = 4\)), tenemos que \(Pr[X_{n+1}^k = 4 | X_n^k = 3] = 0.005.\)
- Si deja la empresa, es reemplazado por un nuevo empleado de grado 1 (\(X_{n+1}^k = 1\)) de forma que \(Pr[X_{n+1}^k = 1 | X_n^k = 3] = 0.02.\)
- Si se mantiene en el mismo puesto, tenemos que \(Pr[X_{n+1}^k = 3 | X_n^k = 3] = 0.975.\)
Procediendo de forma similar en el resto de situaciones tenemos la matriz de transición para cualquiera de los trabajores como:
\[P = \begin{pmatrix} 0.970 & 0.030 & 0 & 0\\ 0.008 & 0.982 & 0.010 & 0\\ 0.020 & 0 & 0.975 & 0.005\\ 0.010 & 0 & 0 & 0.990 \end{pmatrix}\]
Representamos a continuación este sistema en forma de grafo en la Figura 2.5.
# Definimos estados
estados <- c("1", "2", "3", "4")
# Matriz de transición
pmat <- matrix(data = c(0.9700, 0.0300, 0, 0,
0.0080, 0.9820, 0.0100, 0,
0.0200, 0, 0.9750, 0.0050,
0.0100, 0, 0, 0.9900),
byrow = TRUE, nrow = 4,
dimnames = list(estados, estados))
# CMTD
planificacion <- new("markovchain", states = estados,
byrow = TRUE, transitionMatrix = pmat,
name = "planificacion")
# Verificamos los datos introducidos
planificacion## planificacion
## A 4 - dimensional discrete Markov Chain defined by the following states:
## 1, 2, 3, 4
## The transition matrix (by rows) is defined as follows:
## 1 2 3 4
## 1 0.970 0.030 0.000 0.000
## 2 0.008 0.982 0.010 0.000
## 3 0.020 0.000 0.975 0.005
## 4 0.010 0.000 0.000 0.990# Diagrama
plot(planificacion, vertex.color="steelblue",
vertex.label.font = 2,
vertex.label.color = "white",
edge.label.size = 0.2,
edge.arrow.size=0.5,
vertex.shape = "rectangle",
vertex.size = 20)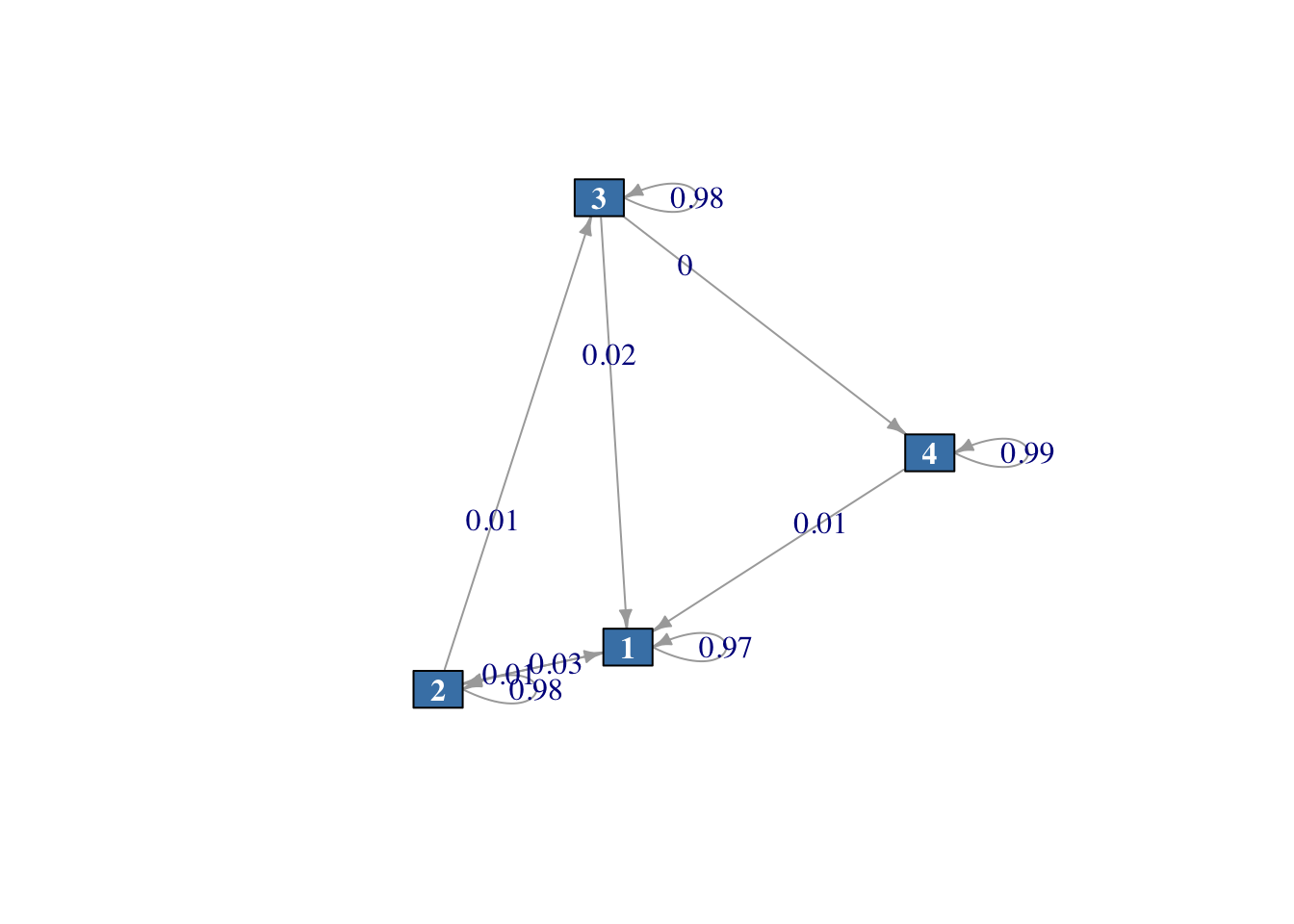
Figura 2.5: Diagrama del sistema de planificación
2.3.6 Mercado de valores
Las acciones ordinarias de la empresa Gadgets-R-Us se cotizan en el mercado de valores. El director financiero de Gadgets-R-Us compra y vende las acciones de su propia empresa para que el precio nunca baje de 2 dólares y nunca supera los 10 dólares. Para simplificar, suponemos que \(X_n\), es el precio de las acciones al final del día \(n\), y sólo toma valores enteros; es decir, el espacio de estados del proceso \(\{X_n, n \in \mathbb{N}\}\) es \(S = 2, 3,...,10\). Si denominamos \(I_{n+1}\) al movimiento potencial del precio de las acciones en el día \(n+1\) en ausencia de cualquier intervención del director financiero, entonces tenemos que:
\[\begin{equation*} X_{n+1} = \begin{cases} 2 & \text{ si } X_n + I_{n+1} \leq 2\\ X_n + I_{n+1} & \text{ si } 2 < X_n + I_{n+1} < 10\\ 10 & \text{ si } X_n + I_{n+1} \geq 10 \end{cases} \end{equation*}\]Un análisis continuado de los datos del pasado sugieren que los movimientos potenciales \(\{I_n, n \geq 1\}\) son una secuencia de variables iid con función de masa de probabilidad dada por:
\[Pr(I_n = k) = 0.2, \quad k = -2, -1, 0, 1, 2.\]
Esto implica que \(\{X_n, n \in \mathbb{N}\}\) es una \(CMTD\) con espacio de estados \(S = \{2, 3,...,10\}\), donde las probabilidadees de transición se pueden obtener de forma sencilla. A modo de ejemplo presentamos los tres casos siguientes:
\[\begin{array}{ll} Pr[X_{n+1} = 2 | X_n = 3] & = Pr[X_n + I_{n+1} \leq 2 | X_n = 3]\\ & = Pr[I_{n+1} \leq -1]\\ & = 0.4 \end{array}\]
\[\begin{array}{ll} Pr[X_{n+1} = 6 | X_n = 5] & = Pr[X_n + I_{n+1} = 6 | X_n = 3]\\ & = Pr[I_{n+1} = 1]\\ & = 0.2 \end{array}\]
\[\begin{array}{ll} Pr[X_{n+1} = 10 | X_n = 10] & = Pr[X_n + I_{n+1} \geq 10 | X_n = 10]\\ & = Pr[I_{n+1} \geq 0]\\ & = 0.6 \end{array}\]
de forma que la matriz de transición del sistema viene dada por:
\[P = \begin{pmatrix} 0.6 & 0.2 & 0.2 & 0 & 0 & 0 & 0 & 0 & 0\\ 0.4 & 0.2 & 0.2 & 0.2 & 0 & 0 & 0 & 0 & 0\\ 0.2 & 0.2 & 0.2 & 0.2 & 0.2 & 0 & 0 & 0 & 0\\ 0 & 0.2 & 0.2 & 0.2 & 0.2 & 0.2 & 0 & 0 & 0\\ 0 & 0 & 0.2 & 0.2 & 0.2 & 0.2 & 0.2 & 0 & 0\\ 0 & 0 & 0 & 0.2 & 0.2 & 0.2 & 0.2 & 0.2 & 0\\ 0 & 0 & 0 & 0 & 0.2 & 0.2 & 0.2 & 0.2 & 0.2\\ 0 & 0 & 0 & 0 & 0 & 0.2 & 0.2 & 0.2 & 0.4\\ 0 & 0 & 0 & 0 & 0 & 0 & 0.2 & 0.2 & 0.6 \end{pmatrix}\]
Representamos a continuación este sistema en forma de grafo en la Figura 2.6.
# Definimos estados
estados <- c("2", "3", "4", "5", "6", "7", "8", "9", "10")
# Matriz de transición
pmat <- matrix(data = c(0.6 , 0.2 , 0.2 , 0 , 0 , 0 , 0 , 0 , 0,
0.4 , 0.2 , 0.2 , 0.2 , 0 , 0 , 0 , 0 , 0,
0.2 , 0.2 , 0.2 , 0.2 , 0.2 , 0 , 0 , 0 , 0,
0 , 0.2 , 0.2 , 0.2 , 0.2 , 0.2 , 0 , 0 , 0,
0 , 0 , 0.2 , 0.2 , 0.2 , 0.2 , 0.2 , 0 , 0,
0 , 0 , 0 , 0.2 , 0.2 , 0.2 , 0.2 , 0.2 , 0,
0 , 0 , 0 , 0 , 0.2 , 0.2 , 0.2 , 0.2 , 0.2,
0 , 0 , 0 , 0 , 0 , 0.2 , 0.2 , 0.2 , 0.4,
0 , 0 , 0 , 0 , 0 , 0 , 0.2 , 0.2 , 0.6),
byrow = TRUE, nrow = 9,
dimnames = list(estados, estados))
# CMTD
mercado.valores <- new("markovchain", states = estados,
byrow = TRUE, transitionMatrix = pmat,
name = "Mercado de valores")
# Verificamos los datos introducidos
mercado.valores## Mercado de valores
## A 9 - dimensional discrete Markov Chain defined by the following states:
## 2, 3, 4, 5, 6, 7, 8, 9, 10
## The transition matrix (by rows) is defined as follows:
## 2 3 4 5 6 7 8 9 10
## 2 0.6 0.2 0.2 0.0 0.0 0.0 0.0 0.0 0.0
## 3 0.4 0.2 0.2 0.2 0.0 0.0 0.0 0.0 0.0
## 4 0.2 0.2 0.2 0.2 0.2 0.0 0.0 0.0 0.0
## 5 0.0 0.2 0.2 0.2 0.2 0.2 0.0 0.0 0.0
## 6 0.0 0.0 0.2 0.2 0.2 0.2 0.2 0.0 0.0
## 7 0.0 0.0 0.0 0.2 0.2 0.2 0.2 0.2 0.0
## 8 0.0 0.0 0.0 0.0 0.2 0.2 0.2 0.2 0.2
## 9 0.0 0.0 0.0 0.0 0.0 0.2 0.2 0.2 0.4
## 10 0.0 0.0 0.0 0.0 0.0 0.0 0.2 0.2 0.6# Diagrama
plot(mercado.valores, vertex.color="steelblue",
vertex.label.font = 2,
vertex.label.color = "white",
edge.label.size = 0.2,
edge.arrow.size=0.5,
vertex.shape = "rectangle",
vertex.size = 20)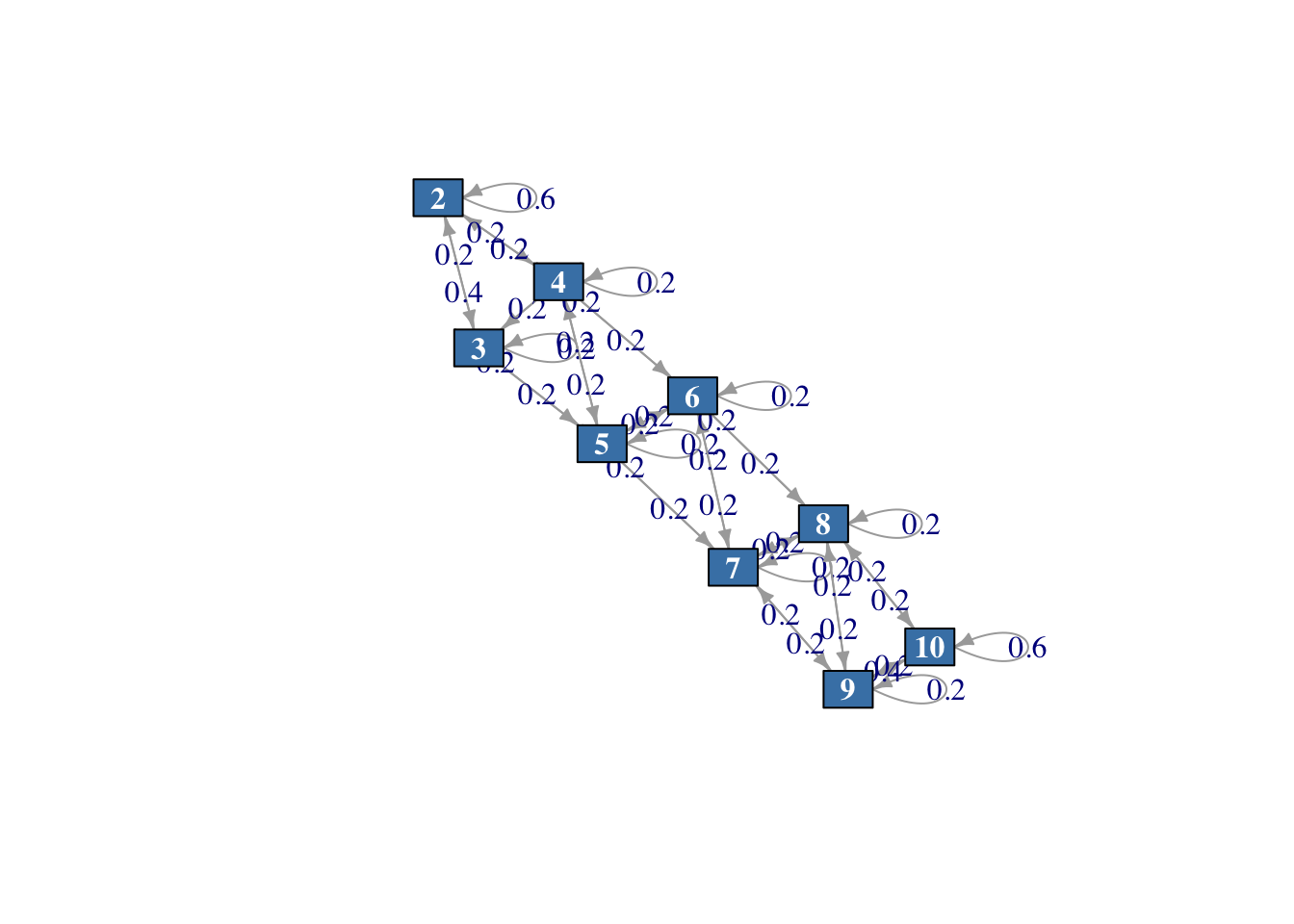
Figura 2.6: Diagrama del sistema del Mercado de valores
2.3.7 Telecomunicaciones
La empresa Tel-All Switch Corporation fabrica equipos de conmutación para redes de comunicación. Las redes de comunicación mueven los datos de un conmutador a otro a la velocidad del rayo en forma de paquetes, es decir, mediante cadenas de ceros y unos (llamadas bits). Los conmutadores Tel-All manejan paquetes de datos de longitud constante, es decir, el mismo número de bits en cada paquete. A nivel conceptual podemos pensar en el conmutador como un dispositivo de almacenamiento donde los paquetes llegan desde la red de usuarios según un proceso aleatorio, se almacenan en un buffer con capacidad para almacenar \(K\) paquetes y se eliminan del buffer uno a uno según un protocolo preestablecido. Uno de los protocolos utilizados considera el tiempo dividido en intervalos de duración fija llamados “ranuras” (por ejemplo, un microsegundo), y consiste en que: si hay algún paquete en el buffer al principio de un intervalo o ranura, se elimina uno instantáneamente; si no hay ningún paquete al principio de un intervalo, no se elimina ningún paquete durante el intervalo, aunque lleguen más paquetes durante el mismo; por último, si un paquete llega durante una ranura y no hay espacio para él, se descarta. Este proceso se puede modelar como una \(CMTD\).
Sean:
- \(A_n\) el número de paquetes que llegan al conmutador durante la enésima ranura (algunos pueden ser descartados)
- \(X_n\) el número de paquetes en el buffer al final de la enésima ranura.
Ahora, si \(X_n = 0\), entonces no hay paquetes disponibles para la transmisión al principio de la ranura \(n+1\). Por lo tanto, todos los paquetes que llegan durante esa ranura, es decir, \(A_{n+1}\), están en el buffer al final de esa ranura mientras tenga capacidad, esto es, \(A_{n+1} \leq K\); si \(A_{n+1}>K\), entonces la memoria intermedia está llena al final de la ranura \(n+1\), \(X_{n+1}=K\). Por lo tanto, en general \(X_{n+1} = min(A_{n+1}, K)\), cuando \(X_n=0\).
Por otro lado, si hay algún paquete al final del instante \(n\), \(X_n > 0\), pasan al conumtador en la siguiente ranura \(n+1\), se elimina un paquete al principio de la misma y se añaden los paquetes que lleguen durante esa ranura, \(A_{n+1}\), con sujeción a las limitaciones de capacidad.
Combinando estos casos, obtenemos:
\[\begin{equation*} X_{n+1} = \begin{cases} min(A_{n+1}, K) & \text{ si } X_n = 0\\ min(X_n + A_{n+1} - 1, K) & \text{ si } 0 < X_n \leq K \end{cases} \end{equation*}\]Asumimos que \(\{A_n, n \geq 1\}\) es una secuencia de variables iid con función de masa de probabilidad dada por:
\[Pr(A_n = k) = a_k, \quad k \geq 0.\]
Bajo esta condición \(\{X_n, n \in \mathbb{N}\}\) es una \(CMTD\) con espacio de estados \(S = \{0, 1, 2,..., K\}\), cuyas probabilidades de transición vienen dadas a continuación:
Para \(0 \leq j < K\):
\[\begin{array}{ll} Pr[X_{n+1} = j | X_n = 0] & = Pr[min(A_{n+1}, K) = j | X_n = 0]\\ & = Pr[A_{n+1} = j]\\ & = a_j \end{array}\]
\[\begin{array}{ll} Pr[X_{n+1} = K | X_n = 0] & = Pr[min(A_{n+1}, K) = K | X_n = 0]\\ & = Pr[A_{n+1} \geq K]\\ & =\sum_{k=K}^{\infty} a_k =1-\sum_{k=0}^{K-1} a_k \end{array}\]
De igual forma, para \(0 \leq i -1 \leq j < K,\)
\[\begin{array}{ll} Pr[X_{n+1} = j | X_n = i] & = Pr[min(X_n + A_{n+1} - 1, K) = j | X_n = i]\\ & = Pr[A_{n+1} = j - i + 1]\\ & = a_{j-i+1} \end{array}\]
y para \(1 \leq i \leq K,\)
\[\begin{array}{ll} Pr[X_{n+1} = K | X_n = i] & = Pr[min(X_n + A_{n+1} - 1, K) = K | X_n = i]\\ & = Pr[A_{n+1} \geq K - i + 1]\\ & = \sum_{k=K-i+1}^{\infty} a_k=1-\sum_{k=0}^{K-i} a_k \end{array}\]
Si consideramos:
\[b_j = \sum_{k=j}^{\infty} a_k\] la matriz de transiciones de un paso la podemos escribir como:
\[P = \begin{pmatrix} a_0 & a_1 & ... & a_{K-1} & b_K\\ 0 & a_0 & ... & a_{K-2} & b_{K-1}\\ ...&...&...&...&...\\ 0 & 0 & ... & a_0 & b_1 \end{pmatrix}\]
2.3.8 Inventario con desabastecimiento
El gestor de un almacén desea analizar el comportamiento de uno de sus productos en función de la demanda del producto y de la capacidad del almacén.
Consideramos como \(Y_n\) a la variable aleatoria que describe la demanda del producto durante el n-ésimo periodo de tiempo, de forma que:
\[Pr[Y_n = k] = a_k, \quad k=0, 1, 2,... \text{ con } \sum_{k=0}^{\infty} a_k =1\]
Denotamos por \(X_n\) a la variable aleatoria que registra la cantidad de producto almacenado al finalizar el n-ésimo periodo de tiempo, \(A\) el nivel mínimo de almacenaje del producto, y \(B\) el nivel máximo. La política de reposición es la siguiente:
- Si al finalizar un periodo el almacén tiene una cantidad de producto \(X_n\) menor o igual que \(A\), entonces se reabastece hasta \(B\).
- Si al finalizar un periodo el almacén tiene una cantidad de producto mayor que \(A\) y menor o igual a \(B\), entonces no se reabastece y espera hasta el instante de tiempo siguiente.
En esta situación el proceso \(\{X_n, n \in \mathbb{N}\}\) es un proceso estocástico de tiempo discreto
\[\begin{array}{ll} \text{ si } X_n \leq A & \rightarrow X_{n+1} = B - Y_{n+1} \\ \text{ si } A < X_n \leq B & \rightarrow X_{n+1} = X_n - Y_{n+1} \end{array}\] con espacio de estados \(S = \{B, B-1,..., 1, 0, -1, -2,...\}\), donde los valores negativos indican que la demanda supera a la cantidad almacenada y será servida en instantes posteriores (demanda insatisfecha).
Las probabilidades de transición vienen dadas por:
- si \(i \leq A\)
\[\begin{array}{ll} Pr[X_{n+1} = j | X_{n} =i]&= Pr[B - Y_{n+1} = j] \\ &=Pr[Y_{n+1} = B-j] \\ & = \begin{cases} a_{B-j}, \quad \text{si } B \geq j\\ 0, \qquad \text{ si } B < j \end{cases} \end{array}\]
- si \(A < i \leq B\)
\[\begin{array}{ll} Pr[X_{n+1} = j | X_{n}=i] & = Pr[i - Y_{n+1} = j] \\ &=Pr[Y_{n+1} = i-j] \\ & = \begin{cases} a_{i-j}, \quad \text{ si } i \geq j\\ 0, \qquad \text{ si } i < j \end{cases} \end{array}\]
A modo de ejemplo consideramos \(A = 0\), \(B = 2\), con probabilidades para \(Y_n\) dadas por:
\[Pr[Y_n = 0] = 0.5; \quad Pr[Y_n = 1] = 0.4; \quad Pr[Y_n = 2] = 0.1,\] entonces la matriz de transición, para el espacio de estados \(S = \{-1, 0, 1, 2\}\), viene dada por:
\[P = \begin{pmatrix} 0 & 0.1 & 0.4 & 0.5\\ 0 & 0.1 & 0.4 & 0.5\\ 0.1 & 0.4 & 0.5 & 0\\ 0 & 0.1 & 0.4 & 0.5 \end{pmatrix}\]
Representamos a continuación este sistema en forma de grafo en la Figura 2.7.
# Definimos estados
estados <- c("-1", "0", "1", "2")
# Matriz de transición
pmat <- matrix(data = c(0 , 0.1 , 0.4 , 0.5,
0 , 0.1 , 0.4 , 0.5,
0.1 , 0.4 , 0.5 , 0,
0 , 0.1 , 0.4 , 0.5),
byrow = TRUE, nrow = 4,
dimnames = list(estados, estados))
# CMTD
inventario2 <- new("markovchain", states = estados,
byrow = TRUE, transitionMatrix = pmat,
name = "Inventario 2")
# Verificamos los datos introducidos
inventario2## Inventario 2
## A 4 - dimensional discrete Markov Chain defined by the following states:
## -1, 0, 1, 2
## The transition matrix (by rows) is defined as follows:
## -1 0 1 2
## -1 0.0 0.1 0.4 0.5
## 0 0.0 0.1 0.4 0.5
## 1 0.1 0.4 0.5 0.0
## 2 0.0 0.1 0.4 0.5# Diagrama
plot(inventario2, vertex.color="steelblue",
vertex.label.font = 2,
vertex.label.color = "white",
edge.label.size = 0.2,
edge.arrow.size=0.5,
vertex.shape = "rectangle",
vertex.size = 20)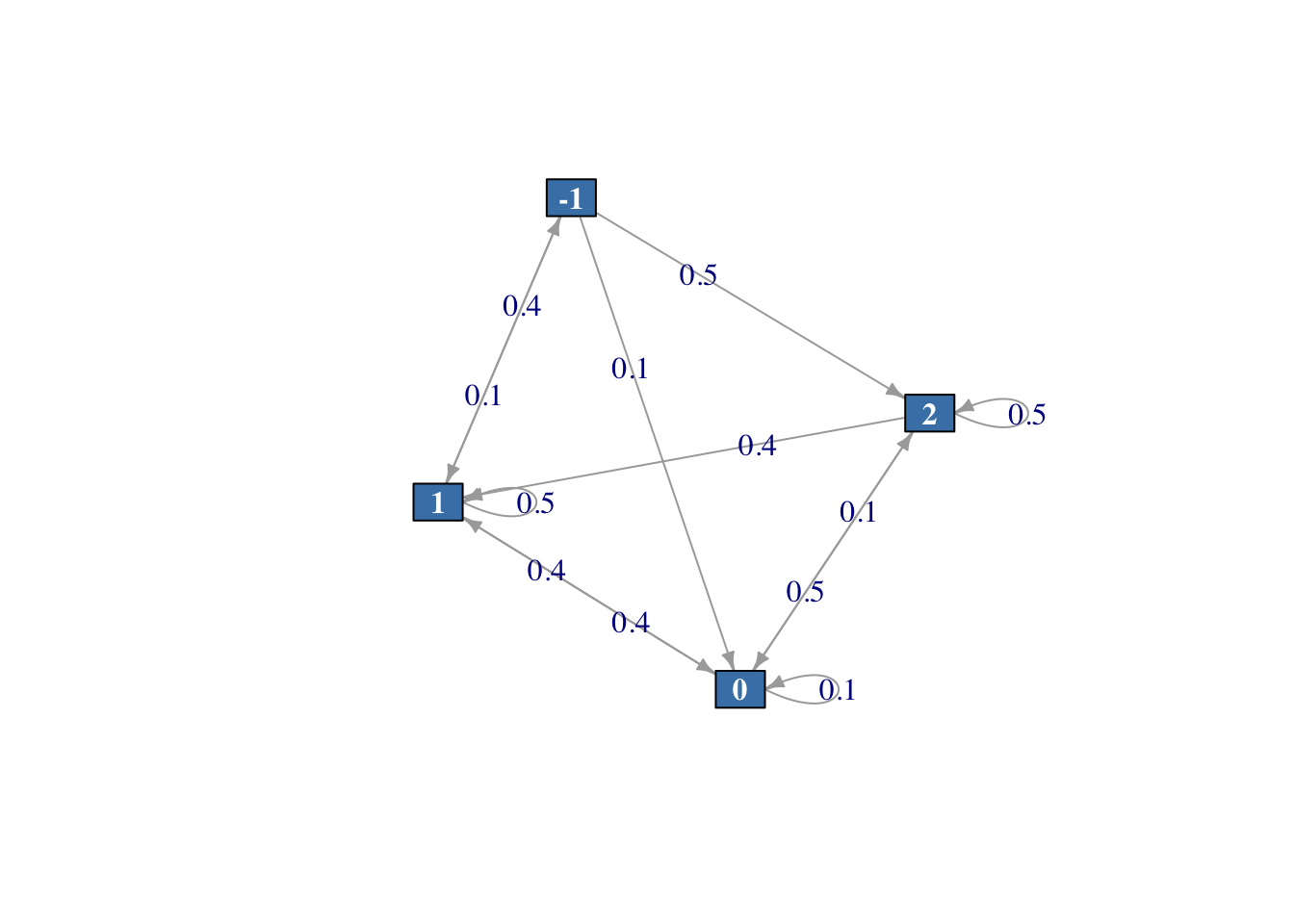
Figura 2.7: Diagrama del sistema del problema de inventario.