1.7 Otras distribuciones continuas

En el caso de variables de tipo continuo de las que no disponemos de un generador de valores aleatorios pero sí disponemos de su función de densidad o distribución, podemos utilizar el algoritmo de la transformada inversa, dado en la definición 1.18, para obtener una muestra aleatoria de tamaño \(n\) de su distribución.

En primer lugar estudiamos situaciones con una variable y posteriormente vemos ejemplos de sistemas de variables continuas o mixturas de discretas y continuas.

1.7.1 Una variable continua

Estudiamos aquí, a través de ejemplos, la simulación de variables aleatorias de tipo continua para las que conocemos la función de densidad o distribución, y se quiere revolver algún problema inferencial.

Ejemplo 1.16 Sea \(X\) una variable aleatoria de tipo continuo cuya función de densidad viene dada por: \[\begin{equation*} f(x) = 2e^{-2x} \text{ para } x \geq 0 \end{equation*}\]

Estamos interesados en conocer:

¿Cuál es la probabilidad de que la variable de interés tome valores en el intervalo [1, 2]?
¿Cuál es la probabilidad de que la variable de interés tome valores mayores o iguales a 1.5?
¿Cuál es el valor esperado de la variable? ¿y la desviación típica?

Para poder responder a las preguntas planteadas debemos obtener en primer lugar la función de distribución asociada a \(X\), que viene dada por:

\[\begin{equation} F(x) = \int_0^x 2e^{-2s} ds=1 - e^{-2x} \text{ para } x \geq 0 \tag{1.12} \end{equation}\]

Podemos aplicar ahora el método de la transformada inversa para obtener una muestra de \(X\).

El algoritmo de simulación basado en la transformada inversa, en la Definición 1.18 viene dado por:

Si \(F(X)\) es la función de distribución para \(X\) dada en la Ecuación (1.12)

Paso 1. Establecer el tamaño de muestra a simular \(nsim\).

Repetir los pasos 2 y 3 para cada iteración \(i\) de \(1, 2,..., nsim\):

Paso 2. Generar \(u_i\) a partir de una \(U(0,1)\).
Paso 3. Aplicar el método de la transformada inversa para obtener \(x_i = F^{-1}(u_i)\) con \(F^{1}(u_i) = -log(1-u_i)/2.\)
Paso 4. Devolver el conjunto de simulaciones \(\{x_i\}_{i=1}^{nsim}\).

Apliquemos pues el algoritmo anterior, y generemos una muestra de tamaño \(nsim=5000\) para \(X\). Aprovechamos el calculo vectorial de R para no tener que hacer un bucle.

# Parámetros iniciales
nsim <- 5000
set.seed(12)
# Generamos uniformes 
uniforme <- runif(nsim)
# Calculamos x con F^-1
xs <- -log(1-uniforme)/2

Y con las simulaciones obtenidas, respondamos a cada una de las preguntas planteadas:

# Pr(1 <= X <= 2)
cat("Pr(1 <= X <= 2)=",round(mean(xs >= 1 & xs <= 2), 4))

## Pr(1 <= X <= 2)= 0.121

# Pr(X >= 1.5)
cat("Pr(X >= 1.5)=",round(mean(xs >= 1.5), 4))

## Pr(X >= 1.5)= 0.053

# Valor esperado y varianza
cat("E(X)=",round(mean(xs), 4))

## E(X)= 0.5046

cat("V(X)=",round(sd(xs), 4))

## V(X)= 0.5078

1.7.2 Transformaciones y Método de Composición

En ocasiones, se nos plantea el problema de inferir, a través de simulación, sobre una variable aleatoria \(Y\) que se obtiene como una transformación continua de otra variable \(X\) cuya distribución conocemos, esto es, \[Y=h(X), \quad \text{ con } X \sim F(x).\]

En particular, \[E(Y)=\int_S h(x) f(x)dx.\]

Se propone un algoritmo sencillo para simular muestras aleatorias de la variable \(Y\), denominado método de composición y que se presenta a continuación.

Definición 1.21 Método de composición

Si \(X\) es una variable aleatoria continua con función de distribución \(F(X)\), e \(Y\) otra variable aleatoria que se obtiene como \(Y = h(X)\), donde \(h()\) es una función continua, podemos obtener una muestra de \(Y\) a partir del siguiente proceso:

Paso 1. Fijar el número de simulaciones (\(nsim\)).

Repetir los pasos 2 y 3 hasta alcanzar el número de simulaciones del paso 1.

Paso 2. Generar un valor de la variable \(X\), \(\{x_i \sim F(x)\}\).
Paso 3. Calcular el valor de la variable \(Y\) para esa simulación mediante \(y_i = h(x_i)\).
Paso 4. Devolver el conjunto de valores simulados \(\{y_i\}_{i=1}^{nsim}.\)

Ejemplo 1.17 Sea \(X\) una variable aleatoria de tipo continuo cuya función de densidad viene dada por:

\[\begin{equation*} f(x) = 3x^2 \text{ para } 0 < x < 1 \end{equation*}\]

y consideramos la variable aleatoria \(Y = 1 - X^2\). Estamos interesados en conocer:

¿Cuál es el valor esperado de la variable \(Y\)? ¿Y su desviación típica?
\(Pr(Y \in [0,1])\)
\(Pr(Y \geq 0.5)\)

Puesto que la distribución de \(X\) no es de las estándar, para simular de ella hemos de utilizar el método de la transformada inversa (Definición 1.18), para lo que hemos de obtener necesariamente su función de distribución, que viene dada por:

\[\begin{equation} F(x) = \begin{cases} 0 & \text{ para } x <= 0\\ x^3 & \text{ para } 0 < x < 1\\ 1 & \text{ para } x \geq 1 \end{cases} \tag{1.13} \end{equation}\]

La función de distribución inversa es pues: \[F^{-1}(u)=u^{1/3}\]

El algoritmo para obtener una muestra de \(Y\) viene dado por:

Si \(F(X)\) es la función de distribución para \(X\) dada en (1.13)

Paso 1. Establecer tamaño de muestra a simular \(nsim\).

Repetir los pasos 2 a 4 para cada iteración \(i\) de \(1, 2,..., nsim\):

Paso 2. Generar \(u_i\) a partir de una \(U(0,1)\).
Paso 3. Aplicar el método de la transformada inversa para obtener \(x_i = F^{-1}(u_i)=u^{1/3}\).
Paso 4. Actuar por composición y calcular \(y_i = 1 - x_i^2\).
Paso 5. Devolver el conjunto \(\{y_i\}_{i=1}^{nsim}.\)

Procedemos con el algoritmo de simulación.

# Parámetros iniciales
nsim <- 5000
set.seed(12)
# Generamos uniformes 
uniforme <- runif(nsim)
# Calculamos x con F^-1
xs <- uniforme^(1/3)
# Calculamos y = h(x)
ys <- 1 - xs
# Devolvemos los valores de x e y
simulacion <- data.frame(sim = 1:nsim, x = xs, y = ys)

Podemos calcular ahora las cantidades de interés:

# Valor esperado y desviación típica de Y 
datos <- simulacion$y
cat("E(Y)=", round(mean(datos), 4))

## E(Y)= 0.2478

cat("sd(Y)=", round(sd(datos), 4))

## sd(Y)= 0.1915

# Pr(0 <= Y <= 1) 
cat("Pr(0 <= Y <= 1)=", round(sum(datos >= 0 & datos <= 1)/nsim, 4))

## Pr(0 <= Y <= 1)= 1

# Pr(Y >= 1) 
cat("Pr(Y >= 0.5)=", round(sum(datos >= 0.5)/nsim, 4))

## Pr(Y >= 0.5)= 0.121

Representamos gráficamente las simulaciones obtenidas tanto para la variable \(X\) como la \(Y\).

g1 <- ggplot(simulacion, aes(x, ..density..)) + 
  geom_histogram(fill = "steelblue") +
  geom_density()+
  labs(x = "X", y = "Densidad")
g2 <- ggplot(simulacion, aes(y, ..density..)) + 
  geom_histogram(fill = "steelblue") +
  geom_density()+
  labs(x = "Y", y = "Densidad")
grid.arrange(g1, g2, nrow = 1)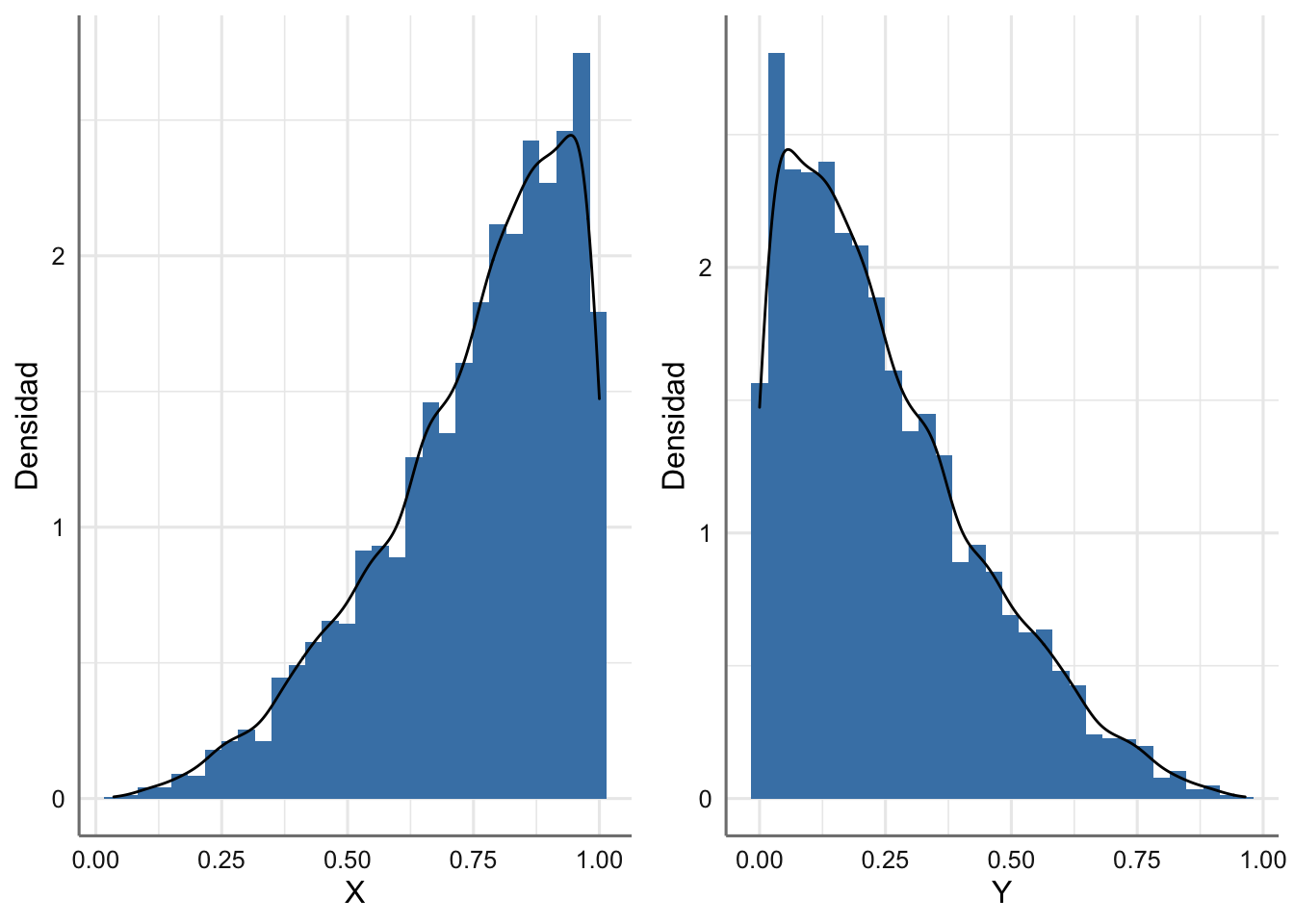

Figura 1.12: Función de densidad empírica e histogramas para X e Y.

1.7.3 Combinaciones de variables

Continuamos este bloque con un tipo de problema que nos encontraremos en muchas ocasiones en el análisis de sistemas, como es la definición de nuevas variables al operar (combinar aritméticamente) otras cuya distribución es conocida. Un ejemplo típico es la suma o resta de variables aleatorias. Imaginemos que tenemos dos variables \(X_1\) y \(X_2\) con funciones de densidad \(f_1(x_1)\) y \(f_2(x_2)\) respectivamente, y estamos interesados en estudiar las variables:

\[Y = X_1 + X_2 \quad\text{ y } \quad Z = X_1 - X_2\] Para el estudio de \(Y\) y \(Z\) podemos proceder teóricamente mediante los correspondientes cambios de variable, pero en situaciones má complejas o con más variables ese procedimiento es poco práctico. En dichas situaciones, podemos utilizar el método de composición para obtener una muestra de las nuevas variables.

Definición 1.22 Método de composición para combinaciones de variables

Si \(X_1,..., X_n\) es un conjunto de variables aleatorias continuas con funciones de distribución \(F_1,..., F_n\) y se define la variable aleatoria \(Y\) mediante una transformación \(h(X_1,...,X_n)\), donde \(h()\) es una función continua, podemos obtener una muestra de \(Y\) mediante el siguiente procedimiento:

Paso 1. Fijar el número de simulaciones (\(nsim\)).

Repetir pasos 2 y 3 hasta alcanzar el número de simulaciones fijado en el paso 1

Paso 2. Generar un valor de cada variable \(X_i\), \(x_{ji} \sim F(x_j), \quad j=1,\ldots,n\).
Paso 3. Calcular el valor de la variable \(Y\) mediante \(y_i = h(x_{1i},...,x_{ni})\).
Paso 4. Devolver el conjunto de valores simulados \(\{y_i\}_{i=1}^{nsim}.\)

Estudiamos a continuación algunos ejemplos donde se aplica el algoritmo expuesto.

Ejemplo 1.18 Supongamos que tenemos un conjunto de 10 variables \(X_1,...,X_{10}\), tales que cada una de ellas se distribuye de forma independiente como: \[X_i \sim U(0,1), \quad i=1,...,10\] y consideramos además las variables aleatorias \[\begin{eqnarray*} Y_{min} &=& min\{X_1,...,X_{10}\},\\ Y_{max} &=& max\{X_1,...,X_{10}\}. \end{eqnarray*}\]

Estamos interesados en conocer:

¿Cuál es el valor de \(Pr[(Y_{min} \leq 0.1) \cap (Y_{max} \geq 0.8)]\).
¿Cuál es el valor esperado del rango, definido como \(R = Y_{max} - Y_{min}\)?
¿Cuál es el valor de \(Pr(R \geq 0.5)\)?

Auque el problema teórico se puede resolver fácilmente, vamos a plantear un algoritmo de simulación para responder a las cuestiones de interés.

Algoritmo para obtener una muestra de \(Y_{min}, Y_{max}\) y \(R\).

Paso 1. Fijar el número de simulaciones (\(nsim\)).

Repetir los pasos 2 a 4 hasta alcanzar el número de simulaciones fijado en el paso 1.

Paso 2. Generar valores \(x_{1,i},...,x_{10,i} \sim U(0,1)\).
Paso 3. Aplicando composición calcular \(y_{min,i} = min\{x_{1,i},...,x_{10,i}\}\) e \(y_{max,i} = max\{x_{1,i},...,x_{10,i}\}\).
Paso 4. Aplicando composición calcular \(r_{i} = y_{max,i} - y_{min,i}.\)
Paso 5. Devolver el conjunto de valores simulados \(\{y_{min,i}, y_{max,i}, r_{i}\}_{i=1}^{nsim}.\)

Procedemos con el algoritmo de simulación. Aprovechamos las ventajas de R para el cálculo vectorial y evitar los bucles.

# Parámetros iniciales
nsim <- 5000
nvar <- 10  # número de variables
set.seed(12)
# Generamos matriz de datos uniformes de dimensiones nsim*nvar 
uniforme <- matrix(runif(nsim*nvar), nrow = nsim)
# Calculamos y_min e y_max
ymin <- apply(uniforme, 1, min)
ymax <- apply(uniforme, 1, max)
# Calculamos rango
rango <- ymax - ymin
# Devolvemos los valores 
simulacion <- data.frame(sim = 1:nsim, 
                         ymin = ymin, ymax = ymax, 
                         rango = rango)

Podemos evaluar ahora las cuestiones de interés a partir de la muestra obtenida para las tres variables.

#  Pr(Y_{min} <= 0.1, Y_{max} >= 0.8)$
p1 = mean((simulacion$ymin <= 0.1) & (simulacion$ymax >= 0.8))
cat("Pr(Y_{min} <= 0.1, Y_{max} >= 0.8)=", round(p1, 4))

## Pr(Y_{min} <= 0.1, Y_{max} >= 0.8)= 0.5732

# Valor esperado del rango 
cat("E(R)=",round(mean(simulacion$rango), 4))

## E(R)= 0.8183

# Pr(R >= 0.5)
cat("Pr(R >= 0.5)=",round(mean(simulacion$rango >= 0.5), 4))

## Pr(R >= 0.5)= 0.9874

Representamos en la Figura 1.13 la distribución obtenida a partir de las simulaciones para las tres variables consideradas.

orden <- c("ymin", "ymax", "rango")
# Construimos matriz de datos para el gráfico
datos <- pivot_longer(simulacion, cols = 2:4, 
                      names_to = "Medida", values_to = "Valor")
# gráfico
ggplot(datos, aes(Valor,fill = Medida))+
  geom_histogram(aes(y = ..density..), position = "identity", alpha = 0.3, bins = 50)+
  labs(y = "Densidad",x = "",fill = "Variables")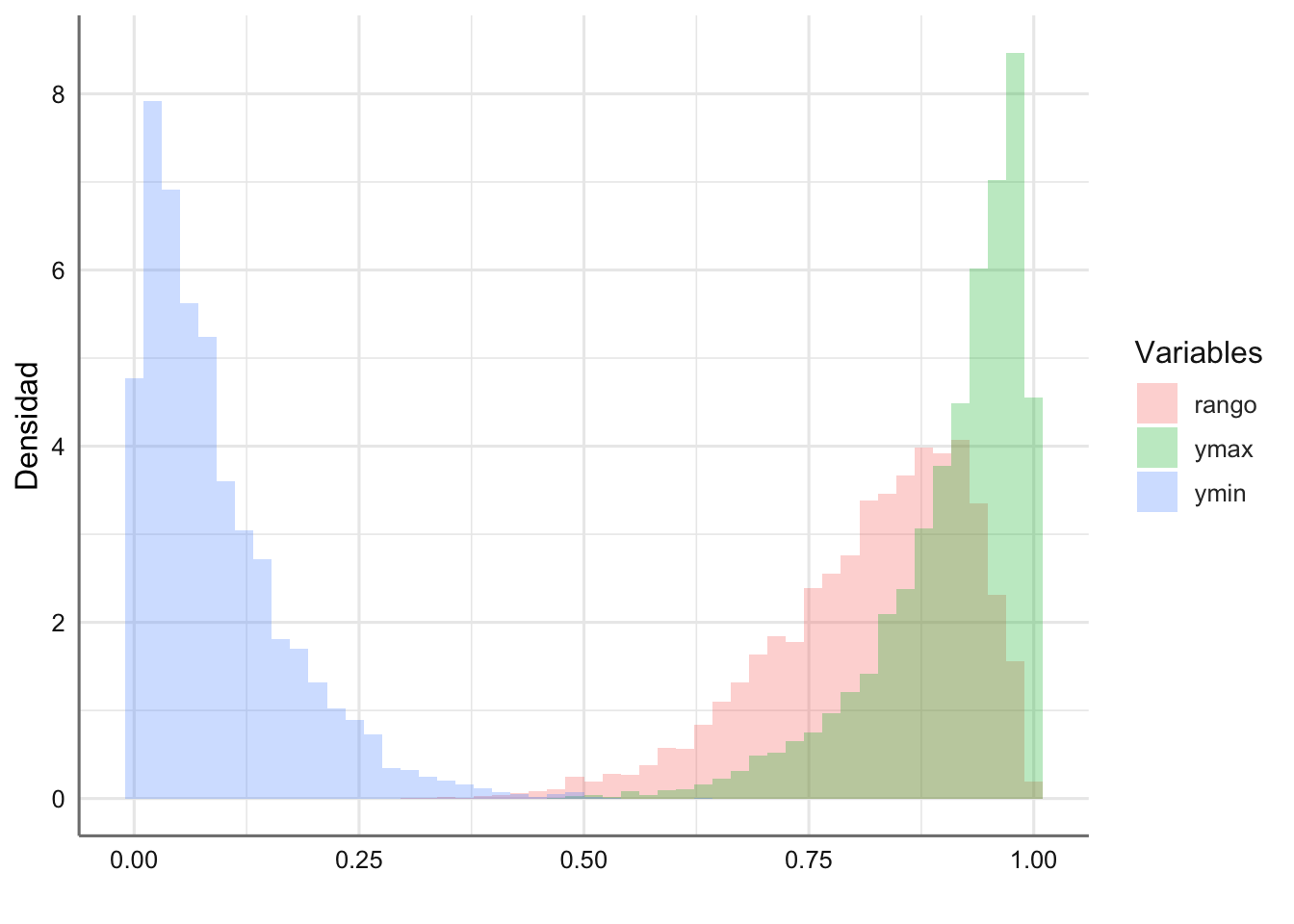

Figura 1.13: Simulaciones del mímimo, máximo y rango de X1,…,X10 v.a. U(9,1).

Ejemplo 1.19 En un estudio de calidad se está analizando el ajuste entre las pernos y las tuercas de cierto proceso de fabricación. Los pernos y las tuercas se fabrican de forma independiente y se colocan en dos cajas. Posteriormente se elige un perno y una tuerca y se prueba si encajan entre sí. Un perno y una tuerca ajustarán si el diámetro del agujero de la tuerca es mayor que el diámetro del perno y la diferencia entre estos diámetros no es mayor que 0.06 centímetros. Cuando no se cumplen estas especificaciones, tanto la tuerca como el perno se desechan. Las especificaciones de fabricación de los pernos indican que su diámetro se puede considerar que es una variable Normal con media 2 centimetros y desviación típica de 0.01 centímetros, mientras que el diámetro de las tuercas es una variable Normal con media 2.03 centímetros y desviación típica de 0.02 centímetros.

¿Cuál es la probabilidad de que encajen un perno y una tuerca elegidos al azar en una caja cualquiera?
Si se fabrican 10000 pernos y tuercas en un día, ¿cuántas desecharemos?
Si el porcentaje de desechos es inferior al 15% en un día no se modificarán las especificaciones de fabricación ¿Consideras que deberían modificarse las especificaciones de fabricación?

Partimos pues, para resolver el problema, de las variables \(T\sim N(2.03, 0.02)\), que representa el diámetro de una tuerca, y \(P \sim N(2, 0.01)\) que representa el diámetro de un perno. Las especificaciones de calidad exigen que \(T>P\) y que \(Dif=T-P\leq 0.6\), o lo que es lo mismo, \(0<Dif\leq 0.6\).

Veamos cómo podríamos simular para responder a las preguntas planteadas.

Algoritmo para obtener la diferencia entre los diámetros de las tuercas y los pernos.

Paso 1. Fijar el número de simulaciones (\(nsim\)).

Repetir los pasos 2 a 4 hasta alacanzar el número de simulaciones fijado en el paso 1.

Paso 2. Generar valores \(t_i\sim F(T)\) y \(p_i \sim F(P)\) de sus respectivas distribuciones.
Paso 3. Aplicando composición, calcular \(dif_i = t_i - p_i.\)
Paso 4. Verificar el requisito de calidad: \(0 < dif_i \leq 0.06\) y asignar \(valid_i = 1\) si se cumple con el criterio y \(valid_i = 0\) en otro caso.
Paso 5. Devolver el conjunto de valores simulados \(\{t_i, p_i, dif_i, valid_i\}_{i=1}^{nsim}.\)

Pongamos en práctica el algoritmo diseñado.

# Parámetros iniciales
nsim <- 5000
set.seed(12)
# Generamos diámetros para tuercas y pernos
tuercas <- rnorm(nsim, 2.03, 0.02)
pernos <- rnorm(nsim, 2.00, 0.01)
# Calculamos la diferencia y creamos filtro de calidad
diferencia <- tuercas - pernos
valid<- 1*(diferencia >0 & diferencia <= 0.06)
# Devolvemos los valores 
simulacion <- data.frame(sim = 1:nsim, 
                         tuercas = tuercas, 
                         pernos = pernos, 
                         diferencia= diferencia, 
                         valid = valid)

Representamos los datos simulados en la Figura 1.14, con la que podemos ya responder la primera pregunta:

¿Cuál es la probabilidad de que encajen un perno y una tuerca elegidos al azar en una caja cualquiera? Como vemos en la gráfica superior izquierda, la respuesta es 0.82, a la vista de que el 82% de las cajas inspeccionadas son válidas.

# Calidad del proceso
g1 <- simulacion %>%
  count(valid)%>%
  mutate(prop = prop.table(n)) %>%
  ggplot(aes(x = as.factor(valid), y = prop, label = scales::percent(prop))) + 
  geom_col(fill = "steelblue", position = "dodge") +
  scale_x_discrete(labels = c("No", "Sí")) +
  scale_y_continuous(labels = scales::percent)+
  geom_text(position = position_dodge(width = 0.9), vjust = 1.5,size = 3)+
  labs(x = "Resultado del proceso: validez", y = "Porcentaje")
# Diferencia
g2 <- ggplot(simulacion, aes(diferencia)) + 
  geom_histogram(fill = "steelblue",color="grey") +
  geom_vline(xintercept = c(0, 0.06), col = "red") +
  labs(x = "Diferencia Tuerca-Perno", y = "Frecuencia")
# Diámetros
orden <- c("tuercas", "pernos")
datos <- pivot_longer(simulacion, cols = 2:3, names_to = "Medida", values_to = "Valor")
# gráfico
g3 <- ggplot(datos, aes(Medida, Valor)) + 
  geom_boxplot(fill = "steelblue") +
  scale_x_discrete(limits = orden, labels = orden) +
  labs(x = "", y = "Diámetro")
# Combinación
grid.arrange(g1, g2, g3, nrow = 2)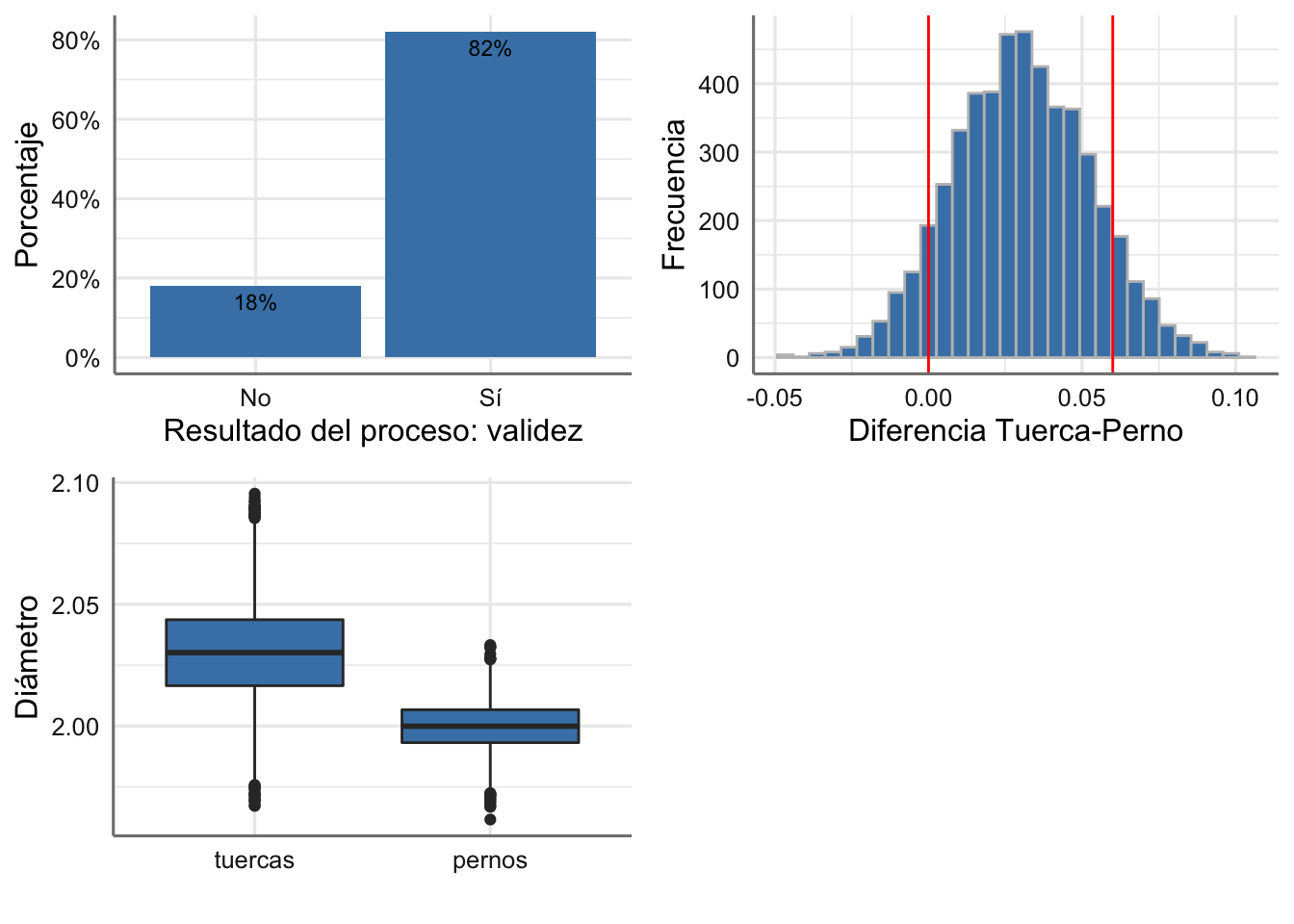

Figura 1.14: Simulaciones del proceso de calidad para tuercas y pernos.

Respondemos las siguientes preguntas:

Si se fabrican 10000 pernos y tuercas en un día, ¿cuántas desecharemos? Si nuestra producción es de 10000 parejas, el número de parejas desechadas será igual a:

10000*(1 - mean(simulacion$valid == 1))

## [1] 1794

Si el porcentaje de desechos es inferior al 15% en un día no se modificarán las especificaciones de fabricación ¿Consideras que deberían modificarse las especificaciones de fabricación? Realmente el porcentaje de piezas desechadas es del 18% (gráfico superior izquierdo en la Figura 1.14), por lo que la recomendación sería abordar un proceso de mejora en la fabricación para reducir los defectos.

Ejemplo 1.20 Una empresa de fabricación de componentes para aviones tiene entre sus productos una barra que se coloca como sujeción en las alas, y que se construye mediante la unión consecutiva de tres secciones A, B, y C. Las especificaciones de fabricación establecen que la longitud (en pulgadas) de cada barra es una distribución Normal. Más concretamente la sección A tiene una media de 20 pulgadas y una varianza de 0.04. la longitud de la sección B tiene una media de 14 y varianza de 0.01, mientras que la sección C tiene una media de 26 y varianza 0.04. Las tres piezas se unen consecutivamente (A con B y B con C) de forma que se encajan superponiendo 2 pulgadas en cada unión. La barra sólo puede ser utilizada si su longitud total está entre 55.5 y 56.5 pulgadas.

¿Cuál es la probabilidad de que la barra sea utilizable?
Si en un mes se fabrican 25000 barras ¿cuál es el número de barras desechadas?
Por cada barra dentro de especificaciones se obtiene un beneficio de 300 euros, pero si se desecha, se genera una pérdida de 100 euros. ¿Cuál será el beneficio estimado en un mes?

Si denominamos \(LA\), \(LB\), y \(LC\) a las variables aleatorias correspondientes a las longitudes de las secciones A, B, y C respectivamente, las distribuciones asociadas vienen dadas por:

\[LA \sim N(20, \sqrt{0.04}); \quad LB \sim N(14, \sqrt{0.01}); \quad LC \sim N(26, \sqrt{0.04})\] La otra variable involucrada es la suma de barra al unir las piezas, que se obtiene como \(L=LA+LB+LC-4\), dado que en cada junta se pierden 2 pulgadas. Las especificaciones de calidad sobre ella son \(55.5 \leq L \leq y 56.5\).

Proponemos pues, un algoritmo de simulación que nos permita simular la longitud total de la barra a partir de cada una de las secciones, y verificar si está dentro de las especificaciones de calidad establecidas.

Paso 1. Fijar el número de simulaciones (\(nsim\)).

Repetir los pasos 2 a 4 hasta alcanzar el número de simulaciones fijado en el paso 1.

Paso 2. Generar valores \(LA_i\), \(LB_i\), y \(LC_i\) a partir de sus distribuciones correspondientes.
Paso 3. Aplicando composición, calcular \(L_i = LA_i + LB_i + LC_i - 4.\)
Paso 4. Verificar el requisito de calidad: \(55.5 \leq L_i \leq 56.5\) y asignar \(valid_i = 1\) si lo cumple, y \(valid_i = 0\) si no lo cumple.
Paso 5. Devolver el conjunto de valores simulados \(\{LA_i, LB_i, LC_i, L_i, valid_i\}_{i=1}^{nsim}.\)

Programemos el algoritmo.

# Parámetros iniciales
nsim <- 5000
set.seed(12)
# Generamos longitudes de las secciones
LA <- rnorm(nsim, 20, sqrt(0.04))
LB <- rnorm(nsim, 14, sqrt(0.01))
LC <- rnorm(nsim, 26, sqrt(0.04))
# Calculamos longitud total y verificamos requisitos
L <- LA + LB + LC - 4
valid <- 1*(L >= 55.5 & L <= 56.5)
# Devolvemos los valores 
simulacion <- data.frame(sim = 1:nsim, LA = LA, LB = LB, 
                         LC = LC, L = L,valid=valid)

Respondamos a las preguntas a partir de las simulaciones obtenidas.

¿Cuál es la probabilidad de que la barra sea utilizable? La respuesta viene aproximada por la proporción de piezas válidas. Calculamos también un intervalo de confianza utilizando la ecuación (1.1).

#  Pr proceso cumpla criterios calidad
p = mean(simulacion$valid == 1)
error = sqrt((sum(simulacion$valid-p)^2)/(nsim^2))
alpha = 0.05 # 1-alpha=nivel de confianza para el IC
ic.low = p - qnorm(1-alpha/2)*error
ic.up = p + qnorm(1-alpha/2)*error
cat("Pr(barra utilizable)=", p)

## Pr(barra utilizable)= 0.9016

cat("Error de la aproximación=", error)

## Error de la aproximación= 4.298784e-17

cat("IC(", 1-alpha,"%)= [", ic.low,",", ic.up,"]")

## IC( 0.95 %)= [ 0.9016 , 0.9016 ]

Dado el error tan pequeño que genera el proceso de simulación, la estimación proporcionada es claramente precisa.

Si en un mes se fabrican 25000 barras ¿cuál es el número de barras desechadas?

desechos=25000*(1-p)
cat("Barras desechadas en un mes:", desechos)

## Barras desechadas en un mes: 2460

Por cada barra dentro de especificaciones se obtiene un beneficio de 300 euros, pero si se desecha, se genera una pérdida de 100 euros. ¿Cuál será el beneficio estimado en un mes?

benef=(25000-desechos)*300-desechos*100
cat("Beneficio obtenido en un mes:", benef, "€")

## Beneficio obtenido en un mes: 6516000 €

1.7.4 Modelos secuenciales

En la última sección para variables de tipo continuo presentamos los primeros modelos de simulación para variables aleatorias que actúan de forma consecutiva a lo largo del tiempo. Será pues, una introducción a los modelos estocásticos que estudiaremos en el resto de unidades. En estas situaciones todas las variables involucradas en el sistema hacen referencia al tiempo de ocurrencia de los eventos de interés. Trabajemos con ejemplos, para entender los conceptos y problemas involucrados.

Ejemplo 1.21 El equipo de mantenimiento de una empresa debe programar las visitas a cierta instalación para establecer una calendario eficiente de revisiones. El sistema que debe analizar está compuesto por tres procesos (A, B, y C) que funcionan de forma independiente, pero que están conectados en serie, de forma que todo el sistema se detiene si un proceso falla. El tiempo de vida o tiempo hasta un fallo o avería, medido en horas, para cada uno de los procesos se puede considerar aleatorio y responde a distribuciones exponenciales con medias 1000, 333, y 167 respectivamente.

El proceso de fabricación completo, que involucra a los tres procesos A, B y C, funciona 24 horas al día y completa un ciclo cada siete días, tras el cual realiza un parón para tareas de mantenimiento. En ese ciclo, los procesos A, B y C operan consecutivamente durante un día: \(A\) trabaja durante 15.6 horas, luego entra en funcionamiento el proceso \(B\) durante 5.52 horas, y finalmente el \(C\) durante 2.88 horas.

En la actualidad el equipo de manteniento está interesado en reajustar el ciclo para realizar las labores de mantenimiento, si fuera necesario, y reducir el tiempo muerto en que el sistema está parado, pues en estos momentos se dedican 24 horas tras cada ciclo, para las tareas de mantenimiento.

¿Cuál es la probabilidad de que el sistema falle antes de finalizar un ciclo de trabajo?
¿Cuál de los procesos está generando más parones en el ciclo debidos a una avería?
¿Cuál es el tiempo medio de funcionamiento del sistema sin ningún fallo? Interesa además, un rango o intervalo de confianza para dicha estimación. ¿Cuál sería el tiempo óptimo del ciclo para abordar las tareas de mantenimiento?

En primer lugar modelicemos el sistema en base a la información proporcionada. Definamos las variables aleatorias \(TA\), \(TB\), y \(TC\) que representan, respectivamente, el tiempo de funcionamiento -o tiempo a fallo- (en horas) de cada proceso A, B y C. Sus distribuciones son: \[TA \sim Exp(1/1000); \quad TB \sim Exp(1/333); \quad TC \sim Exp(1/167).\] También son importantes las siguientes cantidades: - El tiempo de funcionamiento requerido cada día para cada uno de los procesos \(ta=15.6, tb=5.52, tc=2.88\) y el número de días que conforma cada ciclo, \(nciclo=7\).

El tiempo de vida potencial del sistema completo, esto es, el tiempo \(T\) que funciona el sistema de fabricación hasta un fallo, y que se calcula a partir del mínimo número de días que funciona cada proceso, \(min \{TA/ta,TB/tb,TC/tb\}\).

Propongamos pues, un algoritmo de simulación que reproduzca el proceso de fabricación para un número \(nsim\) de ciclos simulados, cuyas simulaciones permitan responder a las preguntas planteadas.

Algoritmo para el estudio de fallo del sistema

Paso 1. Fijar el número de simulaciones o ciclos a simular (\(nsim\)).

Repetir los pasos 2 a 4 tantas veces como simulaciones a generar (nsim).

Paso 2. Generar valores \(TA_i\), \(TB_i\), y \(TC_i\) de los tiempos a fallo de cada proceso según su distribución.
Paso 3. Calcular el número de días que dura sin fallos cada proceso, con los ratios \(rt_i=\{TA_i/ta, TB_i/tb, TC_i/tc\}\). Identificar cuál falla primero (\(min(rt_i)\)).
Paso 4. Verificar si el primero en fallar lo hace antes de terminar el ciclo, \(min(rt_i)<=7\). Si es que sí, guardar cuál es el proceso responsable del fallo y calcular la duración del ciclo mediante \(24*rt_i\) horas. Si es que no, indicarlo y especificar como duración del ciclo \(24*7\) horas.
Paso 5. Devolver los valores de las simulaciones de los tiempos a fallo de cada proceso, de la duración del ciclo, el indicador de fallo y el proceso responsable en cada ciclo (simulación).

# Función para simular el proceso de fabricación con tres subprocesos ABC encadenados.
simula.proceso=function(nsim, nciclo, alpha, beta, delta, ta, tb, tc){
# semilla=Semilla aleatoria y nsim=nº simulaciones o ciclos a simular
#nciclo es el número de días del ciclo
# alpha, beta y delta son los parámetros de las exponenciales TA,TB,TC
# ta,tb y tc son los tiempos de funcionamiento diarios para los procesos A, B y C.
Tciclo=Dciclo = rep(0, nsim)   # tiempo de ciclo (en horas T y días D)
Tpotencial = rep(0, nsim)      # tiempo(en horas) que funcionaría sin fallos
fallo = c()                   # qué proceso ha fallado en cada ciclo
procesos = c("A", "B", "C")

# simulamos las duraciones para todos los ciclos
TA = rexp(nsim, alpha)  
TB = rexp(nsim, beta)
TC = rexp(nsim, delta)
t = c(ta, tb, tc) # funcionamiento diario de cada proceso

for(j in 1:nsim){
  T = c(TA[j], TB[j], TC[j])      # tiempos de vida para el ciclo j
  nfallo = T/t                  # número días que funcionará cada proceso
  falla = which.min(nfallo)     # qué proceso falla primero
  if(nfallo[falla] <= nciclo){  # si falla antes de cerrar el ciclo
   fallo[j] = procesos[falla]   #identificamos el proceso que falla
   Dciclo[j] = T[falla]/t[falla]   # y lo pasamos a días
   Tciclo[j] = Tpotencial[j]=24*Dciclo[j]   # duración del ciclo (en horas)
  }
  else{                       #si no falla ninguno antes de cerrar el ciclo
    Tciclo[j] = 24*7            #cerramos el ciclo sin fallos
    Dciclo[j] = 7
    fallo[j] = "No"
    Tpotencial[j] = T[falla]/t[falla]*24    # y guardamos la duración potencial 
  }
} # fin del for (j)
resultado = data.frame(ciclo = 1:nsim, fallo,
                     Tciclo = round(Tciclo, 2),Dciclo = round(Dciclo, 2),
                     Tpotencial = round(Tpotencial, 2),
                     DA = round(TA/ta, 2), DB = round(TB/tb, 2), DC = round(TC/tc, 2))

return(resultado)
}

Lanzamos el proceso para los valores del ejemplo, y visualizamos los resultados en la Tabla 1.5

nciclo = 7; alpha = 1/1000; beta = 1/333; delta = 1/167
ta = 15.6;tb = 5.52; tc = 2.88
semilla = 12

set.seed(semilla)
nsim=5000                  
simulacion=simula.proceso(nsim,nciclo,alpha,beta,delta,ta,tb,tc)
kbl(head(simulacion),caption="Simulaciones para el proceso de fabricación con tres subprocesos encadenados A, B y C. Tipo de fallo, tiempos de funcionamiento del sistema (Tciclo en horas, Dciclo en días) y tiempo de funcionamiento potencial (Tpotencial en horas). Días de vida DA, DB, DC de los procesos.") %>%
 kable_styling(bootstrap_options = "striped", full_width = F, position = "left")

Tabla 1.5: Simulaciones para el proceso de fabricación con tres subprocesos encadenados A, B y C. Tipo de fallo, tiempos de funcionamiento del sistema (Tciclo en horas, Dciclo en días) y tiempo de funcionamiento potencial (Tpotencial en horas). Días de vida DA, DB, DC de los procesos.
ciclo	fallo	Tciclo	Dciclo	Tpotencial	DA	DB	DC
1	No	168.00	7.00	219.46	140.33	9.14	59.78
2	No	168.00	7.00	171.59	40.74	7.15	18.27
3	C	96.63	4.03	96.63	7.52	32.32	4.03
4	B	34.45	1.44	34.45	183.16	1.44	259.42
5	No	168.00	7.00	617.69	116.45	87.16	25.74
6	No	168.00	7.00	435.89	18.16	83.25	112.44

¿Cuál es la probabilidad de que el sistema falle antes de finalizar un ciclo de trabajo?

m = mean(simulacion$fallo != "No")
error = sqrt(sum(((simulacion$fallo != "No")*1-m)^2) / (nsim^2))
ic.low = m - qnorm(0.975)*error
ic.up = m + qnorm(0.975)*error
cat("Pr(fallo antes del ciclo=",m)

## Pr(fallo antes del ciclo= 0.2876

cat("IC(Probabilidad)=[",round(ic.low, 4),",",round(ic.up, 4),"]")

## IC(Probabilidad)=[ 0.2751 , 0.3001 ]

¿Cuál de los procesos está generando más parones en el ciclo debidos a una avería?

En la Figura 1.15 representamos (a la izquierda) el porcentaje que se detiene el proceso de fabricación antes de finalizar el ciclo, para cada uno de los tipos de fallo posible (debido a un parón en A, B o C), y difieren muy poco entre sí. El más frecuente, dentro de la similaridad es el fallo en el proceso C, con una probabilidad de 0.0986. A la derecha de la gráfica vemos cómo los tres tipos de fallo están dando tiempos de fabricación muy similares en media y variabilidad.

#  Representación gráfica del ciclo de vida: tabla de probabilidades
g1 = simulacion %>%
  group_by(fallo) %>%
  summarise(n = n(), prop = n/nrow(simulacion)) %>%
  ggplot(aes(x = fallo, y = prop)) +
    geom_col(aes(fill = fallo), position = "dodge") +
    geom_text(aes(label = scales::percent(prop), 
                  y = prop, group = fallo),
              position = position_dodge(width = 0.9),
              vjust = 1.5)+
  labs(x = "Tipo de fallo",y = "Proporción")+
  theme(legend.position = "none")


# Tiempo de vida en función del ciclo
g2 <- ggplot(simulacion, aes(fallo, Tciclo)) + 
  geom_boxplot(fill = "steelblue") +
  labs(x = "Tipo de fallo", y = "Tiempo de funcionamiento (horas)")
grid.arrange(g1, g2, nrow = 1)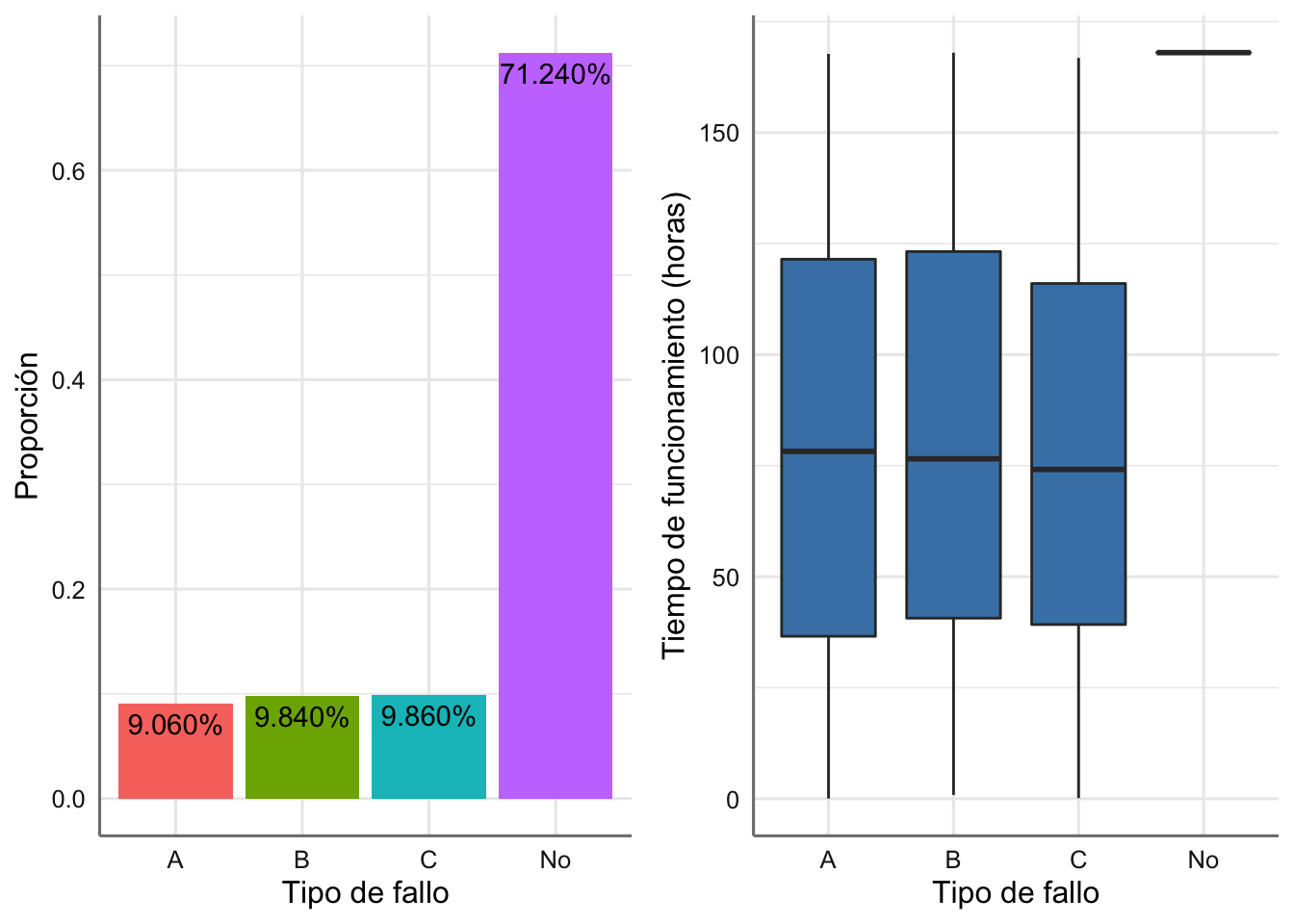

Figura 1.15: Gráfico del ciclo de vida y de la probabilidad del tiempo de fabricación sin fallos.

¿Cuál es el tiempo medio de funcionamiento del sistema sin ningún fallo? Interesa además, un rango o intervalo de confianza para dicha estimación. ¿Cuál sería el tiempo óptimo del ciclo para abordar las tareas de mantenimiento?

Respondemos esta pregunta utilizando no el tiempo de ciclo impuesto como cota superior, sino el tiempo de funcionamiento que el sistema es capaz de aguantar sin fallos, recogido en la variable Tpotencial(en horas). Damos una estimación y construimos un intervalo de confianza al 95% para responder la pregunta.

m = mean(simulacion$Tpotencial)
error = sqrt(sum((simulacion$Tpotencial-m)^2) / (nsim^2))
ic.low = m - qnorm(0.975)*error
ic.up = m + qnorm(0.975)*error
cat("E(Tpotencial)=",round(m/24, 2))

## E(Tpotencial)= 20.54

cat("IC(estimación)=[",round(ic.low/24, 2),",",round(ic.up/24, 2),"]")

## IC(estimación)=[ 19.98 , 21.11 ]

Resulta pues, que el sistema de fabricación tiene capacidad para funcionar sin fallos una media de 20.5 días, y el intervalo de confianza da un límite inferior de 19.98, lo que da justificaría, con unas garantías del 97.5%, reajustar el ciclo y darle un tamaño de 20 días, reduciendo así considerablemente los parones de un día completo de mantenimiento cada 7 en funcionamiento.

Ejemplo 1.22 El gerente de una empresa que se dedica a la extracción y venta de piedra natural está preocupado porque piensa que hay un problema con la máquina que se dedica a cortar, en bloques más manejables, los bloques de piedra que vienen desde la cantera. La máquina trabaja durante 24 horas al día los 365 días del año, y las especificaciones de calidad establecen que la media y varianza del tiempo hasta que la máquina se detiene por un fallo, \(TF\), han de ser de 80 y 50 horas respectivamente.

En el histórico de mantenimiento de la empresa se han detectado tres tipos de fallos que se han catalogado como leves, moderados y graves. Además, la información del equipo de mantenimiento indica que el tipo de fallo que se produce está muy relacionado con el tiempo de funcionamiento de la máquina, de forma que la probabilidad de que se produzca un fallo u otro varía de acuerdo a la tabla siguiente:

TF vs Fallo	Leve	Moderado	Grave
\(TF \leq 1500\)	0.85	0.10	0.05
\(1500 < TF \leq 3000\)	0.75	0.15	0.10
\(TF > 3000\)	0.65	0.20	0.15

Los tiempos de reparación (medidos en minutos), \(TR\), tienen medias y varianzas dadas por:

Fallo	Media	Varianza
Leve	30	15
Moderado	60	30
Grave	120	45

Además se sabe que si el fallo es leve, no es necesario detener la producción por completo, ya que esta se puede reducir al 60% y seguir trabajando mientras se realiza la reparación. En los otros dos casos la máquina debe detenerse por completo.

El gerente está interesado en conocer el funcionamiento de la máquina en los próximos seis meses asumiendo que las variables de tiempo de funcionamiento y tiempo de reparación son de tipo Weibull. En concreto desea saber qué porcentaje del tiempo la máquina estará trabajando a pleno rendimiento, a rendimiento reducido y parada.

Antes de plantear un algoritmo de simulación, tratemos de entender y modelizar bien la secuenciación de variables involucradas, según las especificaciones dadas. Las variables descritas son:

\(TF\): Tiempo de funcionamiento de la máquina hasta fallo.
\(averia\): Tipo de avería cuando el sistema falla: leve, moderado, grave. Su distribución depende de \(tf\).
\(TR.xx\): Tiempo de reparación para una avería “xx={leve, moderado, grave},” que depende del tipo de avería.

El tiempo de funcionamiento a pleno rendimiento vendrá dado por el tiempo acumulado en el que el sistema funciona sin ningún fallo, obtenido de todos los \(TF\) simulados. El funcionamiento a rendimiento reducido se dará mientras se está reparando alguna avería de tipo leve. El tiempo de parada del sistema corresponde a los periodos en los que se está reparando alguna avería de tipo moderada o grave. Puesto que el funcionamiento del sistema depende del tipo de avería, nos interesará guardar información sobre el tipo de avería que se está reparando, información que recopilaremos en la variable \(averia\). El tiempo dedicado a reparaciones lo guardaremos en una variable global denominada \(TREPARA\), que nos permitirá calcular cuándo el sistema no funciona a pleno rendimiento.

\(TREPARA\): Tiempo total dedicado a reparaciones.

En cada simulación nos interesará contabilizar el tiempo transcurrido, en una variable

\(ciclo\): Tiempo de funcionamiento hasta fallo + tiempo de reparación.

Interesa simular el funcionamiento del sistema en los próximos seis meses, de modo que dicho periodo expresado en minutos es de 2.592^{5}, y la simulación parará cuando \(ttotal<259200\) minutos, siendo

\(ttotal\): tiempo total acumulado de funcionamiento y reparaciones.

Puesto que nos piden modelizar con distribuciones Weibull y sólo nos han dado su media y su varianza, hemos de calcular los parámetros a utilizar, para lo que acudimos a la función que ya propusimos en la Ecuación (??).

# Parámetros tiempo funcionamiento (en minutos)
tf.params <- estima.weibull(80*60, 50*60); tf.params

## [1]    1.64 5365.22

# Tiempo de reparación para avería leve
tr.leve <- estima.weibull(30, 15); tr.leve

## [1]  2.10 33.87

# Tiempo de reparación para avería moderada
tr.moderado <- estima.weibull(60, 30); tr.moderado

## [1]  2.10 67.74

# Tiempo de reparación para avería moderada
tr.grave <- estima.weibull(120, 45); tr.grave

## [1]   2.90 134.58

Así, tendremos las siguientes distribuciones para el tiempo de funcionamiento \(tf\) y los tiempos de reparación \(tr\): \[\begin{eqnarray*} TF &\sim& Weib(1.64,5365.22) \\ TR.leve &\sim& Weib(2.10, 33.87) \\ TR.moderado &\sim& Weib(2.10, 67.74) \\ TR.grave &\sim& Weib(2.90, 134.58). \end{eqnarray*}\]

Veamos ahora el algoritmo de simulación para este problema.

Algoritmo secuencial para el estudio de fallo de la máquina

Paso 1. Inicializar todos las variables temporales a 0.

Repetir los pasos 2 a 5 hasta que \(tiempo > 6*30*24*60 = 259200\) minutos.

Paso 2. Generar \(tf\).
Paso 3. Generar el tipo de averia \(averia\) en función de \(tf\).
Paso 4. Generar el tiempo de reparación \(trepara\) en función del tipo de avería.
Paso 5. Actualizar el tiempo total acumulado \(ttotal\) con el tiempo de funcionamiento y reparación.
Paso 6. Devolver el conjunto de valores simulados.

# Fijamos semilla y límite de tiempo para la simulación
semilla <- 12
set.seed(semilla)
Tsim <- 259200
# Incicializamos variables
tf <- c()
trepara <- c()
averia <- c()
ttotal <- 0
ciclo <- c(0)
# Creamos variables necesarias para la simulación del tipo de avería:
# probabilidades de avería leve, moderada y grave
eti <- c("leve", "moderada", "grave")
pr1 <- c(0.85, 0.10, 0.05)  # si tf<=1500
pr1acu <- cumsum(pr1)
pr2 <- c(0.75, 0.15, 0.10)  # si 1500<tf<=3000
pr2acu <- cumsum(pr2)
pr3 <- c(0.65, 0.20, 0.15)  # si tf>3000
pr3acu <- cumsum(pr3)

#############################
## Simulación del proceso
#############################
i <- 1
while (ttotal<= Tsim)
{
  # Tiempo de funcionamiento
  tf[i] <- rweibull(1, tf.params[1], tf.params[2])
  # Tipo Averia
  if(tf[i] <= 1500)
      averia[i] <-eti[min(which(runif(1) <= pr1acu))]
  else if(tf[i] > 1500 & tf[i] <= 3000)
      averia[i] <-eti[min(which(runif(1) <= pr2acu))] 
  else if(tf[i] > 3000)
       averia[i] <-eti[min(which(runif(1) <= pr3acu))]
 # tiempo de reparación
  if(averia[i] == "leve")
      trepara[i] <- rweibull(1, tr.leve[1], tr.leve[2])
  else if(averia[i] == "moderada" )
      trepara[i] <- rweibull(1, tr.moderado[1], tr.moderado[2])
  else if(averia[i] == "grave")
      trepara[i] <- rweibull(1, tr.grave[1], tr.grave[2]) 
  # actualizamos tiempo total
  ciclo[i]=tf[i]+trepara[i]
  ttotal=ttotal+ciclo[i]
  i <- i + 1
}
simulacion <- data.frame(tf, averia = as.factor(averia), 
                         trepara,tiempo = cumsum(ciclo))

Mostramos en la Tabla 1.6 las simulaciones obtenidas y damos a continuación una breve descripción.

kbl(head(simulacion),caption = "Simulaciones para el sistema de corte de piedra.") %>%
  kable_classic_2(full_width = F)

Tabla 1.6: Simulaciones para el sistema de corte de piedra.
tf	averia	trepara	tiempo
9761.123	moderada	17.61378	9778.737
6330.278	leve	60.52762	16169.542
7472.127	leve	63.77925	23705.449
13942.609	leve	15.95977	37664.017
5291.304	leve	38.77331	42994.094
4762.548	leve	26.86817	47783.511

# Descriptivo del sistema
summary(simulacion)

##        tf               averia      trepara            tiempo      
##  Min.   :  532.4   grave   : 5   Min.   :  5.171   Min.   :  9779  
##  1st Qu.: 2460.9   leve    :41   1st Qu.: 21.329   1st Qu.: 84710  
##  Median : 3878.1   moderada: 9   Median : 33.343   Median :146116  
##  Mean   : 4687.1                 Mean   : 43.292   Mean   :142494  
##  3rd Qu.: 6600.7                 3rd Qu.: 59.206   3rd Qu.:204825  
##  Max.   :13942.6                 Max.   :159.389   Max.   :260174

Respondamos ya a diversas preguntas de interés.

¿Cuál es tiempo total de funcionamiento del sistema, incluidas reparaciones?
¿Qué porcentaje del tiempo total el sistema ha estado a pleno rendimiento, reducido y en parada?

# Tiempo total de funcionamiento del sistema (con reparaciones)
ttotal <- last(simulacion$tiempo)
# Tiempo a pleno rendimiento
tpleno <- sum(simulacion$tf)
# Tiempo a rendimiento reducido
tparcial <-sum((simulacion$averia == "leve")*trepara*0.6)
# Tiempo parado (reparaciones moderadas y graves)
tdetenido <- sum((simulacion$averia != "leve")*trepara)
# Juntamos los tiempos y calculamos porcentajes sobre el tiempo de funcionamiento total
kbl(round(100*cbind(ttotal, tpleno, tparcial, tdetenido)/ttotal,2),
    col.names=c("%Tiempo total","%Pleno rendimiento","%Rendimiento reducido","%Parado")) %>%
  kable_classic_2(full_width = F)

%Tiempo total	%Pleno rendimiento	%Rendimiento reducido	%Parado
100	99.08	0.3	0.42

Se concluye que el 99.08% del tiempo durante los seis meses simulados, el sistema ha estado a pleno rendimiento, operando sin averías.