1.4 Distribuciones continuas

En este punto estudiamos las principales variables de tipo continuo. La especificación de estas variables se hace a partir de la función de densidad.

1.4.1 Uniforme

La distribución uniforme es la distribución de probabilidad continua más sencilla y se refiere a eventos infinitos que tienen la misma probabilidad de ocurrir en una intervalo dado. Si $a$ y $b$ son dos números reales con $a < b$ entonces la función de distribución asociada a la probabilidad acumulada a la izquierda de cualquier valor $x \in [a, b]$ viene dada por: \[\begin{equation} F(x) = \begin{cases} 0 & \text{ si } x < a \\ \frac{x-a}{b-a} & \text{ si } a \leq x \leq b\\ 1 & \text{ si } a \leq x \leq b. \end{cases} (\#eq:var-uniforme2) \end{equation}\]

Definición 1.13 Una variable aleatoria $X$ tiene una distribución uniforme en el intervalo $[a, b]$, con $a,b R,

\[X \sim U(a,b)\]

si su función de densidad viene dada por la expresión \[\begin{equation} f(x) = \begin{cases} \frac{1}{b-a} & \text{ si } a \leq x \leq b\\ 0 & \text{ en otro caso } \end{cases} (\#eq:var-uniforme) \end{equation}\] de forma que $E(X) = (a+b)/2$ y $V(X) = (b-a)^2/12.$

La variable uniforme más famosa es la $U(0,1)$ ya que se utiliza habitualmente para modelizar la incertidumbre sobre una probabilidad desconocida, y es la base para muchos de los algoritmos de simulación de variables y procesos que estudiaremos en el futuro.

La función runif(n, a, b) permite generar $n$ valores de una variable uniforme en el intervalo $[a, b]$; runif(n) da una muestra para una distribución uniforme en [0, 1].
dunif(x,a,b) da la fdp en $x$.
punif(x,a,b) da la probabilidad acumulada para cualquier punto $x \in [a,b]$.

1.4.2 Exponencial

La distribución exponencial es una distribución muy común en la modelización probabilística. Esta distribución describe procesos que describen el tiempo entre sucesos consecutivos, con la peculiaridad de que sus probabilidades no dependen del instante en que se produzcan los eventos. Es decir:

\[Pr(X > t+s | X > t) = Pr(X > s)\] Esta propiedad es característica de la distribución exponencial y se denomina “propiedad de la pérdida de memoria.”

Ejemplos de este tipo de distribución son:

El tiempo que tarda una partícula radiactiva en desintegrarse. El conocimiento de la ley que sigue este evento se utiliza en ciencias para, por ejemplo, la datación de fósiles o cualquier materia orgánica mediante la técnica del carbono 14.
El tiempo que puede transcurrir en un servicio de urgencias, entre llegadas de pacientes, o en una fábrica entre roturas de una máquina.

Esta distribución está muy relacionada con unos procesos que estudiaremos más adelante, denominados Procesos de Poisson.

La distribución exponencial viene completamente especificada, a través del parámetro $\lambda >0$ que mide el número esperado de veces que ocurre el evento de interés por cada unidad de tiempo, y cuya función de distribución viene dada por:

\[\begin{equation} F(x) = \begin{cases} 0 & \text{ si } x < 0 \\ 1 - e^{\lambda x} & \text{ si } x \geq 0. \end{cases} \tag{1.6} \end{equation}\]

Definición 1.14 Una variable aleatoria $X$ tiene una distribución exponencial de parámetro $\lambda$, que se denota por

\[X \sim Exp(\lambda)\]

si su función de densidad viene dada por \[\begin{equation} f(x)=\lambda e^{-\lambda x}, \quad x \geq 0, \end{equation}\] de forma que $E(X) = 1/\lambda$ y $V(X) = 1/\lambda^2.$

Las funciones relacionadas con la distribución exponencial en R son:

La función dexp(x, lambda) nos permite evaluar la función de densidad para una variable poisson de parámetro $\lambda$.
pexp(x, lambda) nos permite evaluar la función de distribución.
rexp(n, lambda) permite generar $n$ valores de una variable Exponencial de parámetro $\lambda$.

A continuación estudiamos dos ejemplos de uso de la distribución exponencial. Como siempre presentamos los resultados téoricos y procedemos mediante simulación para ver la aproximación conseguida.

Ejemplo 1.10 Se ha comprobado que el tiempo de vida de cierto tipo de marcapasos sigue una distribución exponencial con media 16 años. (1) ¿Cuál es la probabilidad de que a una persona a la que se le ha implantado este marcapasos se le deba reimplantar otro antes de 20 años? (2) Si el marcapasos lleva funcionando correctamente 5 años en un paciente, ¿cuál es la probabilidad de que haya que cambiarlo antes de 25 años desde que se implantó?

Si $T$ es la variable aleatoria que indica el tiempo de vida del marcapasos tenemos que:

\[T \sim Exp(\lambda = 1/16)\]
Se puede reponder fácilmente a las preguntas planteadas sin más que hacer uso de la función pexp(). Sin embargo, también simularemos para aproximarlas. Hemos de calcular

(1). Si es preciso implantar antes de 20 años, es porque el tiempo de vida no va a ser superior a 20. Hemos de calcular pues, $Pr(T \leq 20)$. (2). Nos piden $Pr(T \leq 25|T>5)=Pr(T\leq 20)$, por la propiedad de la pérdida de memoria. Es decir, respondiendo a (1) tendremos respondidas las dos preguntas formuladas.

lambda <- 1/16
# Data frame para la representación gráfica
sec <- seq(0, 80, by = 0.01)
datos<- data.frame(sec = sec, densidad = dexp(sec,lambda))
# Gráfico función de densidad
ggplot(datos, aes(sec, densidad)) + 
  geom_line() +
  scale_x_continuous(breaks = seq(0,80,5), labels = seq(0,80,5)) +
  scale_y_continuous(breaks = scales::breaks_extended(10)) +
  geom_vline(xintercept = 20, col = "red") +
  labs(x ="Tiempo de vida del marcapasos (en años)", 
       y = "Función de densidad")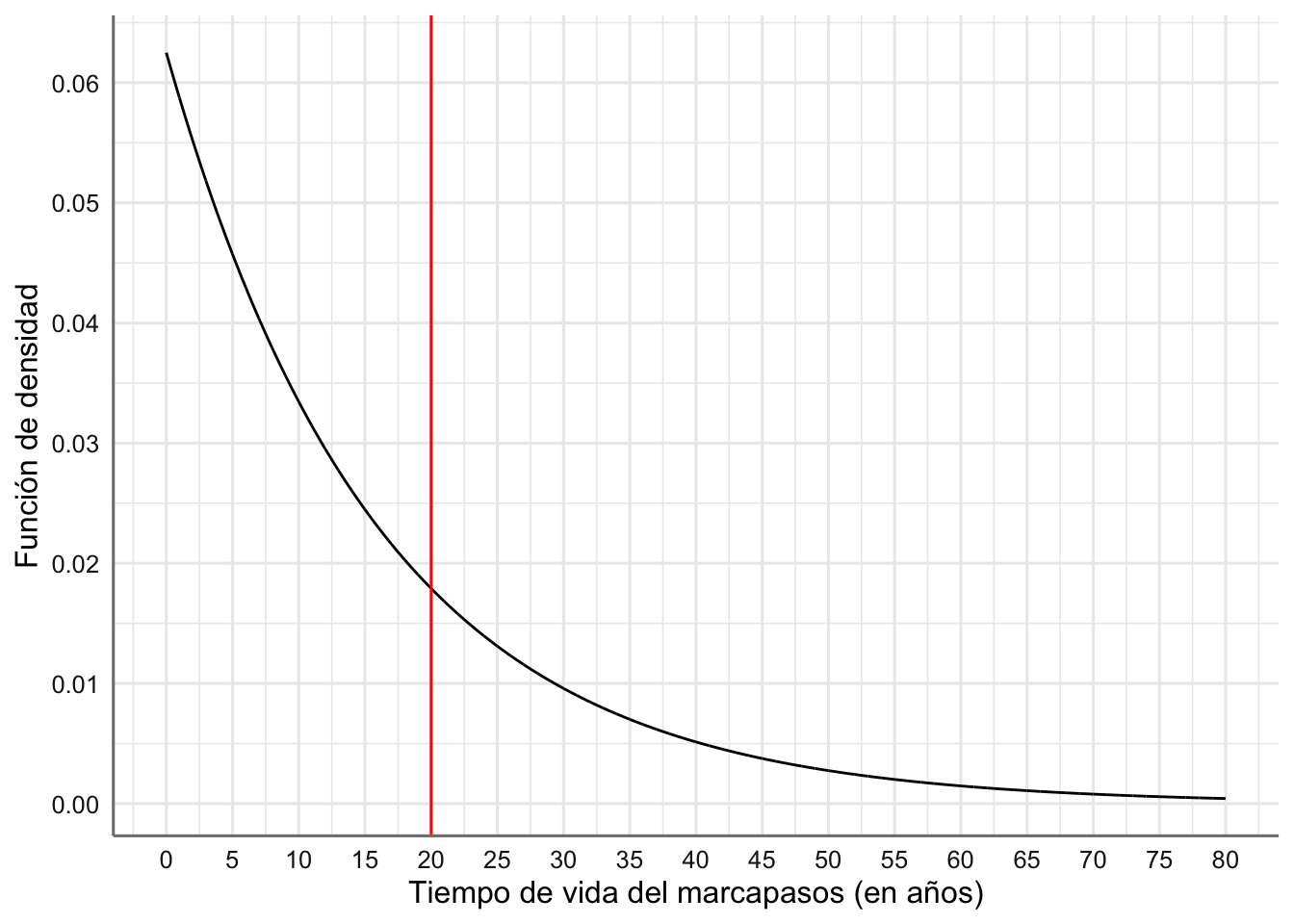

Figura 1.5: Función de densidad del tiempo de vida del marcapasos (en años)

Obtenemos la probabilidad deseada:

# Probabilidad real
lambda=1/16
p=pexp(20,lambda)
cat("Pr(T<=20)=",round(p,3))

## Pr(T<=20)= 0.713

# Parámetros de la simulación
set.seed(123)
nsim <- 5000
# Simulaciones
datos <- rexp(nsim, lambda)
# Probabilidad de interés
pMC=mean(datos <= 20)
cat("Aprox.MC[Pr(T<=20)]=",round(pMC,3))

## Aprox.MC[Pr(T<=20)]= 0.711

La probabilidad de que el marcapasos dure más de 20 años y haya que reemplazarlo es de 0.289, por lo que efectivamente, es muy recomendable reemplazarlo antes. Sin embargo, al paciente en la pregunta (2) se le daría la misma recomendación, cuando la probabilidad de que el marcapasos dure más de 25 años desde su implante, que sería el tiempo que lo llevaría, es considerablemente inferior, 0.21. No es pues recomendable, utilizar esta distribución para modelizar el tiempo de vida de un implante.

Ejemplo 1.11 Un motor eléctrico tiene una vida media de 6 años y se modeliza con una distribución exponencial. ¿Cuál debe ser el tiempo de garantía que debe tener el motor si se desea que a lo sumo el 15 % de los motores fallen antes de que expire su garantía?

Si $T$ es la variable aleatoria que indica el tiempo de vida del producto tenemos que: \[T \sim Exp(\lambda = 1/6).\]
En este caso estamos interesados en encontrar el tiempo para que podamos garantizar que el 85% de los motores siguen funcionando, es decir, buscamos el cuantil 0.15 de la distribución de $T$. Planteamos un análisis de simulación para estimar dicho valor.

# Calculamos el valor real para el periodo de garantía
lambda <- 1/6
q=qexp(0.15,lambda)
cat("Periodo de garantía recomendado=",round(q,2))

## Periodo de garantía recomendado= 0.98

# Parámetros de la simulación
set.seed(123)
nsim <- 5000
# simulaciones
datos <- rexp(nsim, lambda)
# cuantil de interés
qMC=quantile(datos, 0.15)
cat("Periodo de garantía aproximado=",round(qMC,2))

## Periodo de garantía aproximado= 1.02

Para que tan sólo el 15% de los motores necesiten reparación durante el periodo de garantía, debemos establecer una garantía de aproximadamente 1 año.

En la Figura 1.6 se representan, para los datos simulados, los cuantiles aproximados versus su probabilidad asociada. Con el gráfico se puede atisbar también el periodo de garantía recomendado.

# cuantil de interés
probs <- seq(0.05, 0.95, by = 0.05)
cuantiles <- quantile(datos, probs)
datoscuan <- data.frame(probs, cuantiles)
# Gráfico
ggplot(datoscuan, aes(probs,cuantiles)) + 
  geom_line() +
  scale_x_continuous(breaks = probs, labels = probs) +
  scale_y_continuous(breaks = scales::breaks_extended(10)) +
  geom_vline(xintercept = 0.15, col = "red") +
  labs(x ="Probabilidad", y = "Tiempo a la reparación (en años)")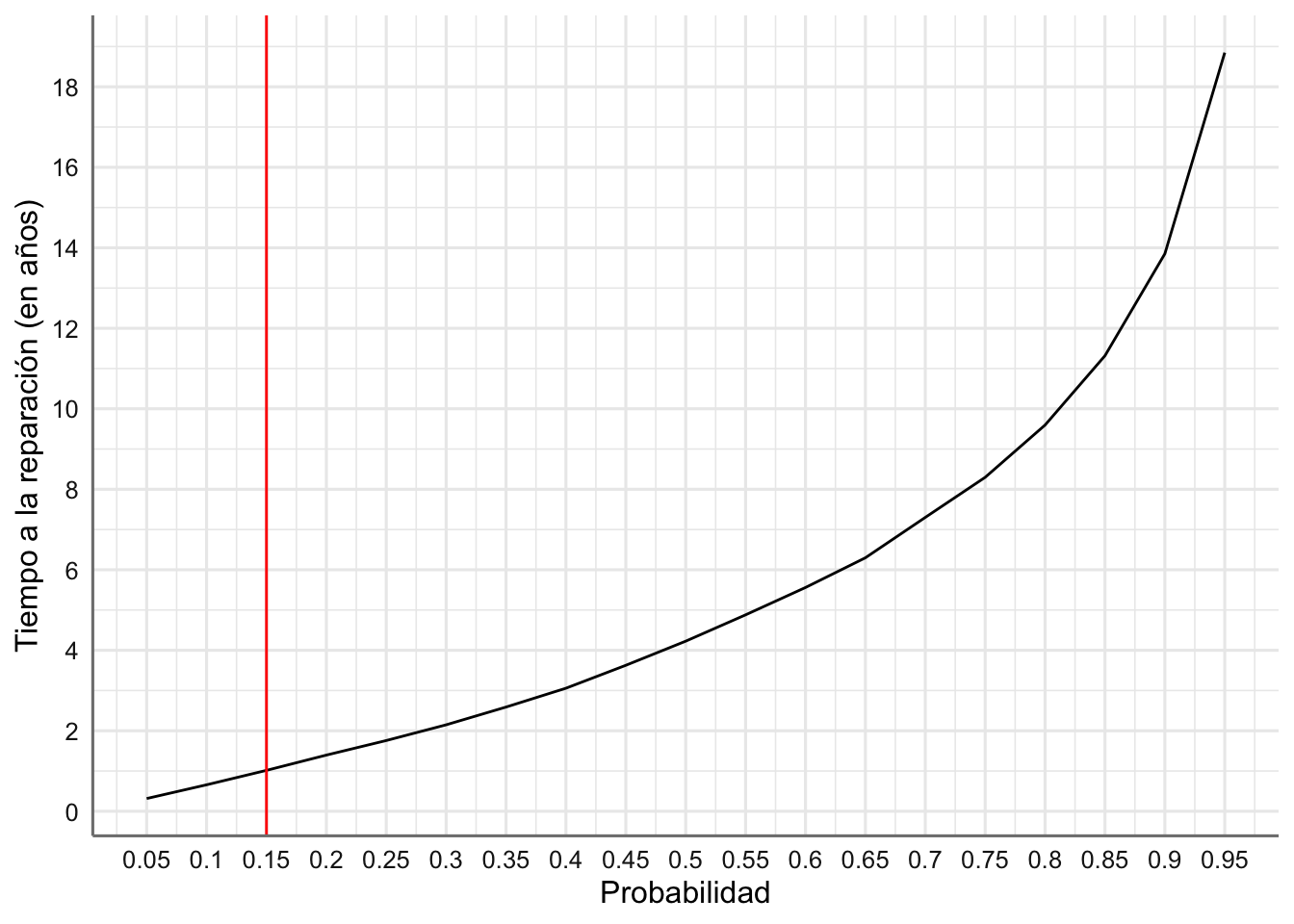

Figura 1.6: Tiempo de garantía recomendado en función de la probabilidad de que los motores necesiten reparación.

Con esta gráfica podemos establecer el tiempo de garantía en función de las especificaciones de la empresa, es decir, fijando el porcentaje de motores que necesitarán reparación.

1.4.3 Gamma

La distribución Gamma, al igual que ocurre con la exponencial, se utiliza habitualmente para modelizar variables aleatorias positivas y asimétricas, y sobre todo para describir procesos de eventos que ocurren en el tiempo. La función de densidad de una variable aleatoria Gamma se caracteriza por dos parámetros: $\alpha$ o parámetro de forma, y $\beta$ o parámetro de escala. El parámetro de forma se denomina así porque al variar su valor se obtienen diferentes formas para la fdp. La variación del parámetro de escala no cambia la forma de la distribución, pero tiende a “estirar” o “comprimir” el rango de valores sobre el que se define la probabilidad.

Definición 1.15 Una variable aleatoria $X$, con $x \geq 0$, tiene una distribución Gamma de parámetros $\alpha > 0$ y $\beta > 0$, denotada por

\[X \sim Ga(\alpha, \beta)\]

si su función de densidad viene dada por la expresión

\[\begin{equation} f(x) = \frac{x^{\alpha -1} e^{-x/\beta}}{\beta^{\alpha} \Gamma(\alpha)}; \quad \text{ para } x \geq 0, \tag{1.7} \end{equation}\]

con $\Gamma()$ la función gamma, de forma que $E(X) = \alpha\beta$ y $V(X) = \alpha\beta^2.$

Un caso especial de la distribución Gamma es la distribución Erlang, que se denota por $X \sim Erlang(k, \beta)$, y que se utiliza habitualmente en la modelización de sistemas de colas de espera. Su función de densidad viene dada por :

\[\begin{equation} f(x) = \frac{k(kx)^{\alpha -1} e^{-xk/\beta}}{\beta^{k} (k-1)!}; \quad \text{ para } x \geq 0, \tag{1.8} \end{equation}\]

con $E(x) = \beta$ y $V(X) = \beta^2/k$. La utilidad de una variable aleatoria Erlang con parámetros $k$ y $\beta$ es que es el resultado de sumar $k$ variables aleatorias exponenciales (independientes) cada una con media $\beta/k$. En la modelización de los tiempos relacionados con un proceso industrial, la distribución exponencial suele ser inadecuada porque la desviación estándar no es tan grande como la media. Los ingenieros suelen tratar de diseñar sistemas que produzcan una desviación estándar de los tiempos del proceso que resulte significativamente menor que su media. La distribución Erlang tiene esta propiedad: su desviación estándar disminuye a medida que aumenta $k$, de modo que los tiempos de proceso con una desviación estándar pequeña a menudo suelen ser aproximados por una variable aleatoria Erlang.

La función dgamma(x, shape, scale) nos permite evaluar la función de densidad para una variable Gamma.
pgamma(x, shape, scale) calcula la función de distribución.
rgamma(n, shape, scale) permite generar $n$ valores de una variable Gamma.

Para simular un dato de una distribución $y \sim (Erlang(k, \beta)$) generamos $k$ datos exponenciales de $x_i \sim Exp(\beta/k), i=1,\ldots,k,$ y calculamos la suma de todos esos valores,$y=\sum_i x_i$. Repetir este proceso tantas veces como indique el tamaño de la muestra simulada que deseamos para la distribución Erlang.

Si disponemos de la media y varianza de los datos resulta muy fácil ajustar los parámetros de la distribución Gamma o Erlang sin más que resolver las ecuaciones que nos dan el valor esperado y la varianza. Si $\bar{x}$ y $s^2$ son respectivamente la media y varianza, podemos ajustar los parámetros de la Gamma con:

\[ \beta = s^2/\bar{x}; \quad \alpha = \bar{x}/\beta\] mientras que para la Erlang tenemos:

\[ \beta = \bar{x}; \quad k = \bar{x}^2/s^2.\]

A continuación se presenta la función para generar datos Erlang a patir de datos exponenciales:

# Función para generar "nsim" simulaciones de una Erlang 
# con parámetros k (entero) y beta>0
rerlang <- function(nsim, k, beta)
{
  # verificamos que k es entero
  if(k%%1 == 0)
  {
    # parámetro de la exponencial
    lambda <- beta/k
    # Generamos y almacenamos datos exponenciales
    datosexp <- matrix(rexp(nsim*k, lambda), nrow = nsim)
    # Obtenemos la muestra de la Erlang
    datoserl <- apply(datosexp, 1, sum)
    return(datoserl)
  }
  else{
    cat("k debe ser entero")
  }
}

1.4.4 Weibull

La distribución Weibull se utiliza para describir la resistencia a la rotura de diversos materiales o para describir los tiempos de fallo de muchos tipos de sistemas diferentes. La distribución Weibull tiene dos parámetros: un parámetro de escala, $\beta$ , y un parámetro de forma $\alpha$, ambos positivos. La funcion de distribución asociada viene dada por:

\[\begin{equation} F(x) = \begin{cases} 0 & \text{ si } x < 0 \\ 1 - e^{-(x/\beta)^{\alpha}} & \text{ si } x \geq 0 \end{cases} \tag{1.9} \end{equation}\]

Como en el caso de la distribución Gamma el parámetro de forma determina la forma general de la fdp y el parámetro de escala expande o contrae la fdp.

Definición 1.16 Una variable aleatoria $X$ tiene una distribución Weibull de parámetros $\alpha>0$ y $\beta>0$, que se denota por

\[X \sim Weib(\alpha, \beta)\]

si su función de densidad viene dada por la expresión \[\begin{equation} f(x)=\frac{\alpha}{\beta}\frac{x}{\beta}^{\alpha-1}e^{-(x/\beta)^{\alpha}}, \quad x \geq 0. (\#eq:var-weibull) \end{equation}\]

El valor esperado y la varianza vienen dados por:

\[E(X) = \beta \Gamma(1 + 1/\alpha); \quad V(X) = \beta^2 (\Gamma(1 + 2/\alpha) - (\Gamma(1 + 1/\alpha))^2).\]

En R tenemos las siguientes funciones relacionadas con la distribución Weibull.

La función dweibull(x, shape, scale) nos permite evaluar la función de densidad para una variable Weibull
pweibull(x, shape, scale) calcula la función de distribución.
rweibull(n, shape, scale) permite generar $n$ valores de una variable Weibull.

A partir de la media ($\bar{x}$) y varianza ($S^2$) de un conjunto de datos, es posible obtener los parámetros de la distribución Weibull sin más que resolver las ecuaciones: \[\begin{eqnarray} \beta &=& \frac{\bar{x}}{\Gamma(1 + 1/ \alpha)} \\ \frac{s^2}{\bar{x}^2} - \frac{\Gamma(1+ 2/\alpha)}{(\Gamma(1 + 1/ \alpha))^2} + 1 &=& 0. (\#eq:estimaweibuleq) \end{eqnarray}\]

A continuación se propone una función que permite obtener los parámetros a partir de la media y varianza de los datos, junto con un pequeño ejemplo para verificar su funcionalidad.

estima.weibull <- function(m, s)
{
  #m=media, s=desviación típica
  library(rootSolve)
  # Función para optimizar alpha
  fun.alpha <- function(a, m, s)
              {
                res<- 1 + (s/m)^2 - gamma(1+2/a)/(gamma(1+1/a))^2
                return(res)
              }
  # Obtención de alpha
    alpha <- round(uniroot(fun.alpha, c(0.1, 10000),m=m,s=s)$root,2)
  # Obtención de beta
  beta <- round(m/gamma(1+1/alpha), 2)
  # Devolvemos alpha y beta
  return(c(alpha, beta))
}

# Datos de ejemplo
m <- 80     # media
s <- sqrt(50)  # desviación típica
# Estimación
res=estima.weibull(m,s)
cat("Weibull alpha=",res[1],", Weibull beta=",res[2])

## Weibull alpha= 13.83 , Weibull beta= 83.06

1.4.5 Normal

La distribución normal es la distribución más común, reconocida por la mayoría de personas por su curva en forma de “campana,” y también llamada “campana de Gauss.” Aunque la distribución normal no se utiliza mucho en la modelización de procesos y sitemas, es sin duda, la más relevante de las distribuciones aleatorias, ya que representa el supuesto básico distribucional para resolver muchos de los problemas de inferencia estadística habituales, como veremos en la sección final de esta unidad.

Definición 1.17 Una variable aleatoria $X$ tiene una distribución Normal de parámetros $\mu$ y $\sigma$ con $\sigma >0$, denotada por \[ X \sim N(\mu, \sigma^2),\]
si su función de densidad viene dada por \[\begin{equation} f(x) = \frac{1}{\sigma\sqrt{2\pi}} exp\left(\frac{-(x-\mu)^2}{2\sigma^2}\right), \quad x \in R \end{equation}\]

con $E(X) = \mu$ y $V(X) = \sigma^2$, y que se denota:

El parámetro $\mu$ identifica la media, y por lo tanto el centro de la distribución al ser simétrica, y el parámetro $\sigma$ la desviación típica.

El caso más destacado es la denominada distribución Normal estándar, para la que $\mu = 0$ y $\sigma = 1$, por su utilización en problemas inferenciales sencillos donde la variabilidad es conocida.

A partir de cualquier distribución Normal podemos transformar a una distribución Normal estándar. Si $X \sim N(\mu, \sigma^2)$ entonces la variable aleatoria $Z$ definida como

\[Z = \frac{X - \mu}{\sigma} \sim N(0,1).\]

Vinculadas a la distribución Normal surgen las distribuciones $t$ de Student, Chi-chadrado y $F$ de Snedecor (también llamada de Fisher-Snedecor), que son ampliamente utilizadas en inferencia estadística. En el último apartado de esta unidad veremos cómo utilizar estas distrbuciones para resolver mediante simulación problemas de intervalos de confianza o contrastes de hipótesis.

Si $\bar{X_n}=\sum_i X_i/n$ representa la media muestral de $n$ v.a. $N(\mu,\sigma)$ y $S^2=\sum_i(X_i-\bar{X_n})^2/(n-1)$ su varianza muestral, entonces la variable $Y$ \[ Y= \frac{\bar{X_n}-\mu}{S/\sqrt{n}}\sim St(n-1)\] sigue una distribución t de Student con $n-1$ grados de libertad, y se denota por $Y\sim St(n-1)$.

Si tenemos un conjunto de variables normales estándar independientes, $X_i\sim N(0,1), i=1,\ldots,n$, entonces su suma al cuadrado sigue una distribución chi-cuadrado con $n$ grados de libertad. \[Z=\sum_{i=1}^n X_i^2 \sim \chi^2_{n}\] Por último, a partir de dos distribuciones chi-cuadrado independientes, $U\sim \chi^2_n$ y $V\sim \chi^2_m$, tenemos que su cociente, corregido por sus grados de libertad, sigue una distribución F de Snedecor con $n$ y $m$ grados de libertad, \[ W=\frac{U/n}{V/m} \sim F_{(n,m)}.\]

Para la distribución Normal,

La función dnorm(x, mean, sd) nos permite evaluar la función de densidad para una variable Normal.
pnorm(x, mean, sd) calcula la función de distribución.
rnorm(n, mean, sd) permite generar $n$ valores de una variable Normal.

Para la distribución t de Student con $df1$ grados de libertad, las funciones correspondientes son dt(x, df1), pt(x, df1) y rt(n,df1).

Para la distribución chi-cuadrado con $df1$ grados de libertad, contamos con las funciones dchisq(x,df1), pchisq(x,df1) y rchisq(n,df1) respectivamente.

Para la distribución F de Snedecor con $df1$ y $df2$ grados de libertad, tenemos las correspondencias df(x, df1, df2), pf(x, df1, df2) y rf(n,df1,df2).

En la Figura 1.7 aparecen representadas varias distribuciones normales con distinta media y varianza.

x=seq(-10,10,0.1)
y1=dnorm(x)
y2=dnorm(x,0,3)
y3=dnorm(x,2,1)
y4=dnorm(x,2,3)
datos=as.tibble(cbind(x,y1,y2,y3,y4))
levels=c("N(0,1)"="y1","N(0,3)"="y2","N(2,1)"="y3","N(2,3)"="y4")
datos=datos %>%
  pivot_longer(cols=2:5,names_to="tipo",values_to="valor") 
datos$tipo=fct_recode(datos$tipo,!!!levels)

ggplot(datos,aes(x=x,y=valor,color=tipo))+
  geom_line()+
  labs(color="Distribuciones",y="Función de densidad")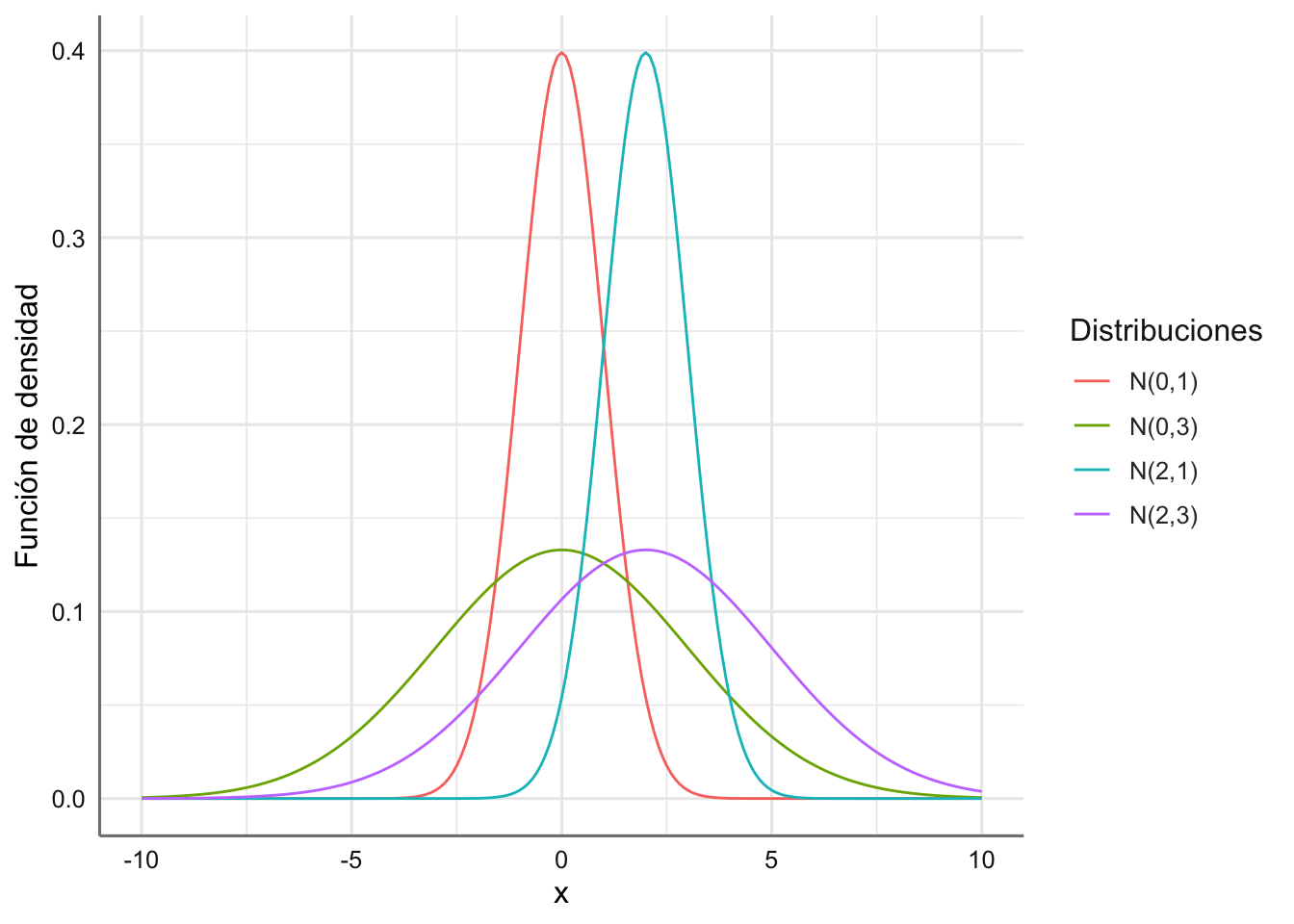

Figura 1.7: Funciones de densidad para varias distribuciones normales.

En la Figura 1.8 aparecen representadas varias distribuciones t de Student con distintos grados de libertad.

x=seq(-5,5,0.1)
y1=dt(x,2)
y2=dt(x,5)
y3=dt(x,10)
y4=dnorm(x)
datos=as.tibble(cbind(x,y1,y2,y3,y4))
levels=c("St(2)"="y1","St(5)"="y2","St(10)"="y3","N(0,1)"="y4")
datos=datos %>%
  pivot_longer(cols=2:5,names_to="tipo",values_to="valor") 
datos$tipo=fct_recode(datos$tipo,!!!levels)

ggplot(datos,aes(x=x,y=valor,color=tipo))+
  geom_line()+
  labs(color="Distribuciones",y="Función de densidad")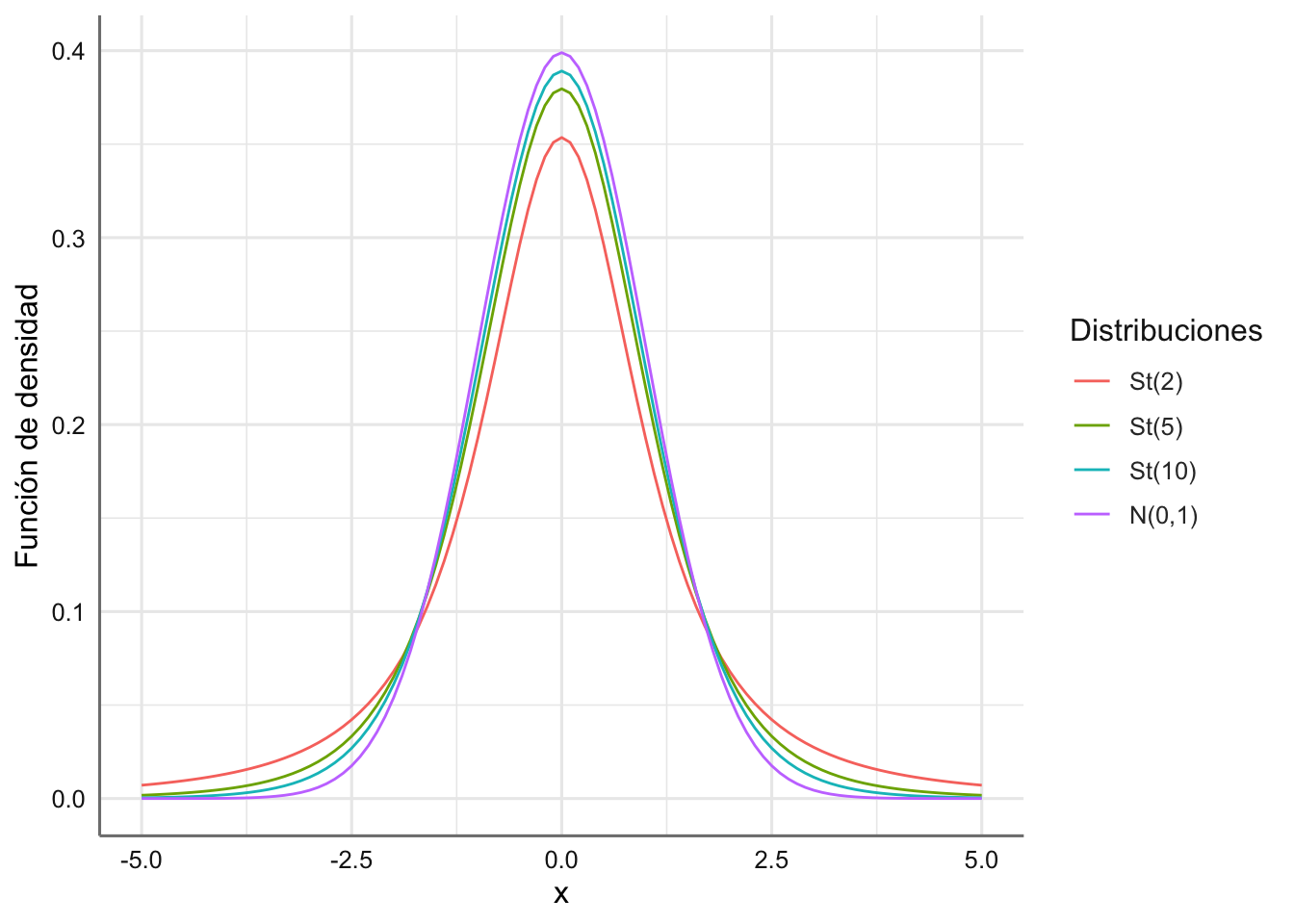

Figura 1.8: Funciones de densidad para varias distribuciones T de Student.

En la Figura 1.9 aparecen representadas varias distribuciones chi-cuadrado con distintos grados de libertad.

x=seq(0,200,0.1)
y1=dchisq(x,5)
y2=dchisq(x,10)
y3=dchisq(x,50)
y4=dchisq(x,100)
datos=as.tibble(cbind(x,y1,y2,y3,y4))
levels=c("Chi2(5)"="y1","Chi2(10)"="y2","Chi2(50)"="y3","Chi2(100)"="y4")
datos=datos %>%
  pivot_longer(cols=2:5,names_to="tipo",values_to="valor") 
datos$tipo=fct_recode(datos$tipo,!!!levels)

ggplot(datos,aes(x=x,y=valor,color=tipo))+
  geom_line()+
  labs(color="Distribuciones",y="Función de densidad")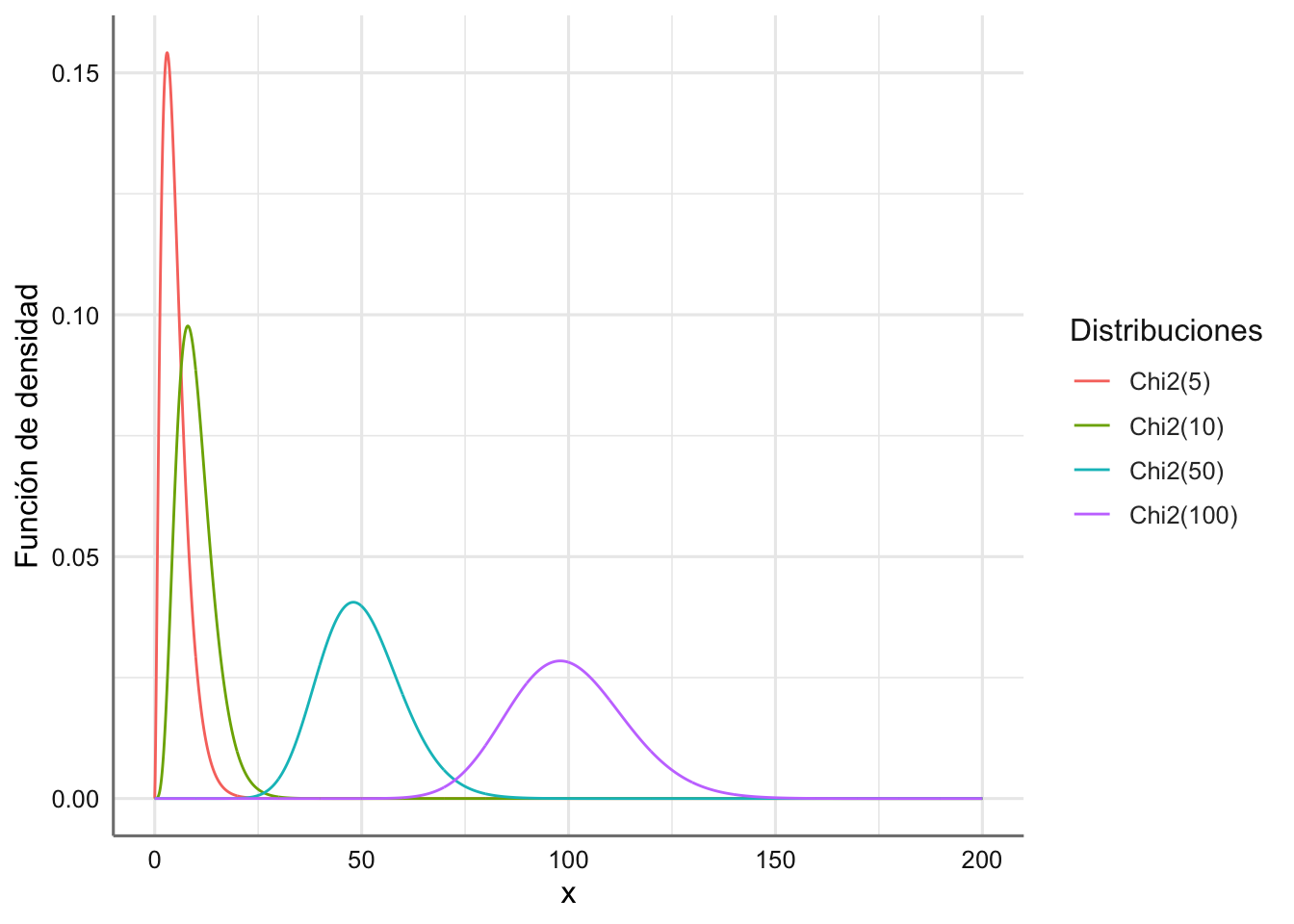

Figura 1.9: Funciones de densidad para varias distribuciones Chi-cuadrado.

En la Figura 1.10 aparecen representadas varias distribuciones F de Snedecor con distintos grados de libertad.

x=seq(0,5,0.01)
y1=df(x,5,5)
y2=df(x,1,5)
y3=df(x,50,10)
y4=df(x,100,200)
datos=as.tibble(cbind(x,y1,y2,y3,y4))
levels=c("F(5,5)"="y1","F(1,5)"="y2","F(50,10)"="y3","F(100,200)"="y4")
datos=datos %>%
  pivot_longer(cols=2:5,names_to="tipo",values_to="valor") 
datos$tipo=fct_recode(datos$tipo,!!!levels)

ggplot(datos,aes(x=x,y=valor,color=tipo))+
  geom_line()+
  labs(color="Distribuciones",y="Función de densidad")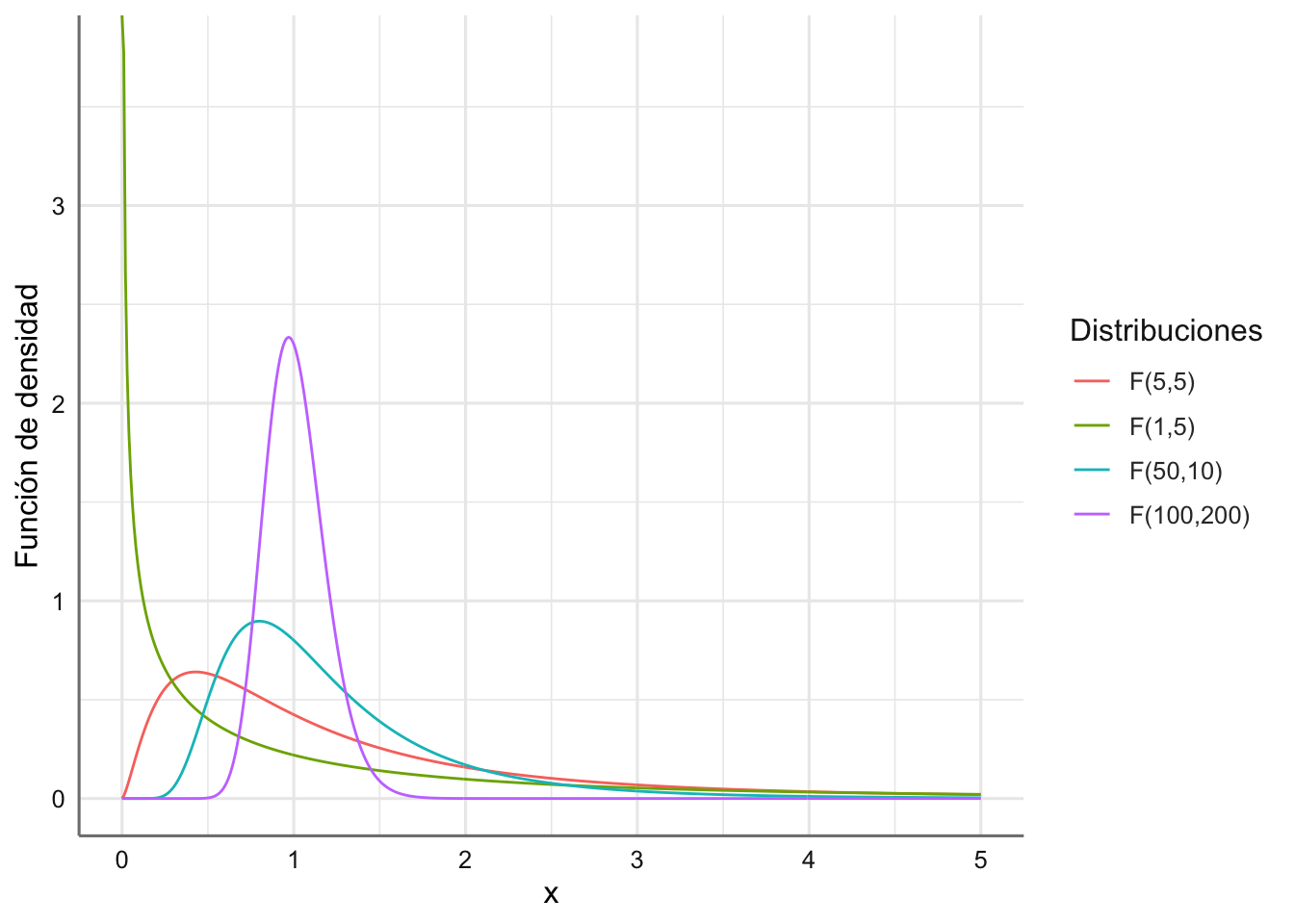

Figura 1.10: Funciones de densidad para varias distribuciones F-Snedecor.