1.3 Distribuciones discretas

Destacamos como principales variables de tipo discreto las siguientes: Bernouilli, Binomial, Geométrica y Poisson.

1.3.1 Bernouilli

Imaginemos una situación experimental donde el resultado de cierta variable que observamos únicamente puede tomar dos valores posibles, denominados “éxito” (codificado con el valor 1) y “fracaso” (codificado con el valor 0). Así pues, la variable aleatoria asociada \(X\) verifica que:

\[\begin{equation} Pr(X = x) = \begin{cases} \theta & \text{ si } x = 1 (\text{ éxito})\\ 1- \theta & \text{ si } x = 0 (\text{ fracaso.}) \end{cases} \tag{1.2} \end{equation}\]

Definición 1.9 Una variable aleatoria \(X\) cuya fmp viene dada por (1.2) se denomina variable Bernouilli, con probabilidad de éxito \(\theta\), y se denota por:

\[X \sim Ber(\theta)\]

de forma que \(E(X) = \theta\) y \(V(X) = \theta(1-\theta).\)

Un ejemplo típico de una variable Bernouilli es el lanzamiento de una moneda que sólo tiene dos posibles resultados: cara o cruz. Si la moneda esta equilibrada tenemos que \(\theta = 0.5\) (idéntica probabilidad para cualquiera de los dos resultados), de forma que si definimos por ejemplo el éxito por conseguir cara, tendremos:

\[X = \text{ Obtener cara } \sim Ber(0.5)\]

Una distribución \(Ber(p)\) es equivalente a una distribución binomial con parámetros 1 y p, \(Bin(1,p)\), de modo que para simular y realizar cálculos de probabilidad con ella utilizaremos las funciones correspondientes a la distribución binomial que vemos a continuación.

  • La función dbinom(x,1,prob) nos permite evaluar la \(Pr(X=x)\) para una variable Bernoilli con probabilidad de éxito prob.
  • La función pbinom(x,1,prob) nos permite evaluar la \(Pr(X \leq x), x=0,1\).
  • La función rbinom(n,1,prob) permite simular \(n\) valores Bernouilli.

1.3.2 Binomial

Consideramos un experimento Bernouilli que repetimos en \(n\) ocasiones, obteniendo en cada repetición sólo dos resultados posibles, “éxito” o “fracaso,” con cierta probabilidad \(\theta\) para el éxito, y contabilizamos el número de éxitos \(N\). Los posibles resultados de este experimento son \(\{0, 1, 2,...,n\}\) éxitos conseguidos en un total de \(n\) pruebas. La probabilidad de observar \(x\) éxitos en \(n\) pruebas viene dada por la función:

\[\begin{equation} Pr(N = x) = \frac{n!}{x!(n-x)!} \theta^{x} (1-\theta)^{n-x} \text{ para } x = 0, 1,\ldots,n, \tag{1.3} \end{equation}\] con \(n\) el número de repeticiones o pruebas Bernouilli realizadas, \(x\) el número de éxitos obtenidos, y \(\theta\) la probabilidad de éxito.

Definición 1.10 La variable aleatoria \(N\) que se obtiene como la suma de \(n\) variables Bernouilli independientes con la misma probabilidad de éxito \(\theta\), y cuya función de masa de probabilidad viene dada en (1.3), se denomina variable Binomial de tamaño \(n\) y probabilidad de éxito \(\theta\), y se denota por:

\[N \sim Bi(n,\theta)\]

con \(E(N) = n\theta\) y \(V(N) = n\theta(1-\theta).\)

A continuación se presentan algunos ejemplos de aplicación de la variable Binomial donde representamos tanto la fmp como la función de distribución asociada al problema de interés. Antes mencionamos las funciones de R relacionadas con esta distribución.

  • La función dbinom(x,size,prob) nos permite evaluar la \(Pr(N=x)\) para una variable Binomial con tamaño size y probabilidad de éxito prob.
  • pbinom(x,size,prob) permite evaluar la \(Pr(N \leq x)\).
  • rbinom(n,size,prob) permite simular \(n\) valores de una variable Binomial de tamaño size y probabilidad de éxito \(prob\).

Ejemplo 1.5 Estamos revisando en una empresa el comportamiento de las bajas laborales. En base al histórico, se tiene que cada día aproximadamente el 3% de los trabajadores faltan al trabajo alegando una baja laboral. Si el número de trabajadores de la empresa es de 150, queremos saber qué porcentaje de días vamos a tener al menos 3 trabajadores de baja.

Denotemos por \(N\) a la variable aleatoria que indica el número de trabajadores de baja en un día cualquiera, e identifiquemos el “éxito” por el hecho de “estar de baja.” Así, podemos asumir que la distribución de \(N\) es binomial, con tamaño 50 y probabilidad 0.03.

\[N \sim Bi(50,0.03).\]

En consecuencia, el valor esperado del número de trabajadores de baja cada día es \(E(N) = 50 \cdot 0.03=1.5\).

A continuación, en la Figura 1.1 representamos la fmp y la función de distribución asociadas.

# los valores posibles de la variable Bin(1000,0.03) son
xs <- 0:50
n=50
p=0.03
# Data frame
datos <- data.frame(xs = xs, probs = dbinom(xs, n,p), 
                    probsacum = pbinom(xs, n,p))
# función de masa de probabilidad
g1 <- ggplot(datos, aes(x=xs, y=probs)) + 
  geom_bar(stat = "identity", fill = "steelblue") +
  ylim(0,0.5) +
  labs(x ="x", y = "Probabilidad puntual. Pr(N=x)")
# función de distribución
g2 <- ggplot(datos, aes(xs, probsacum)) + 
  geom_bar(stat = "identity", fill = "steelblue") +
  scale_y_continuous(breaks = scales::breaks_extended(10)) +
  labs(x ="x", y ="Probabilidad acumulada. Pr(N<=x)")
grid.arrange(g1, g2, nrow = 1)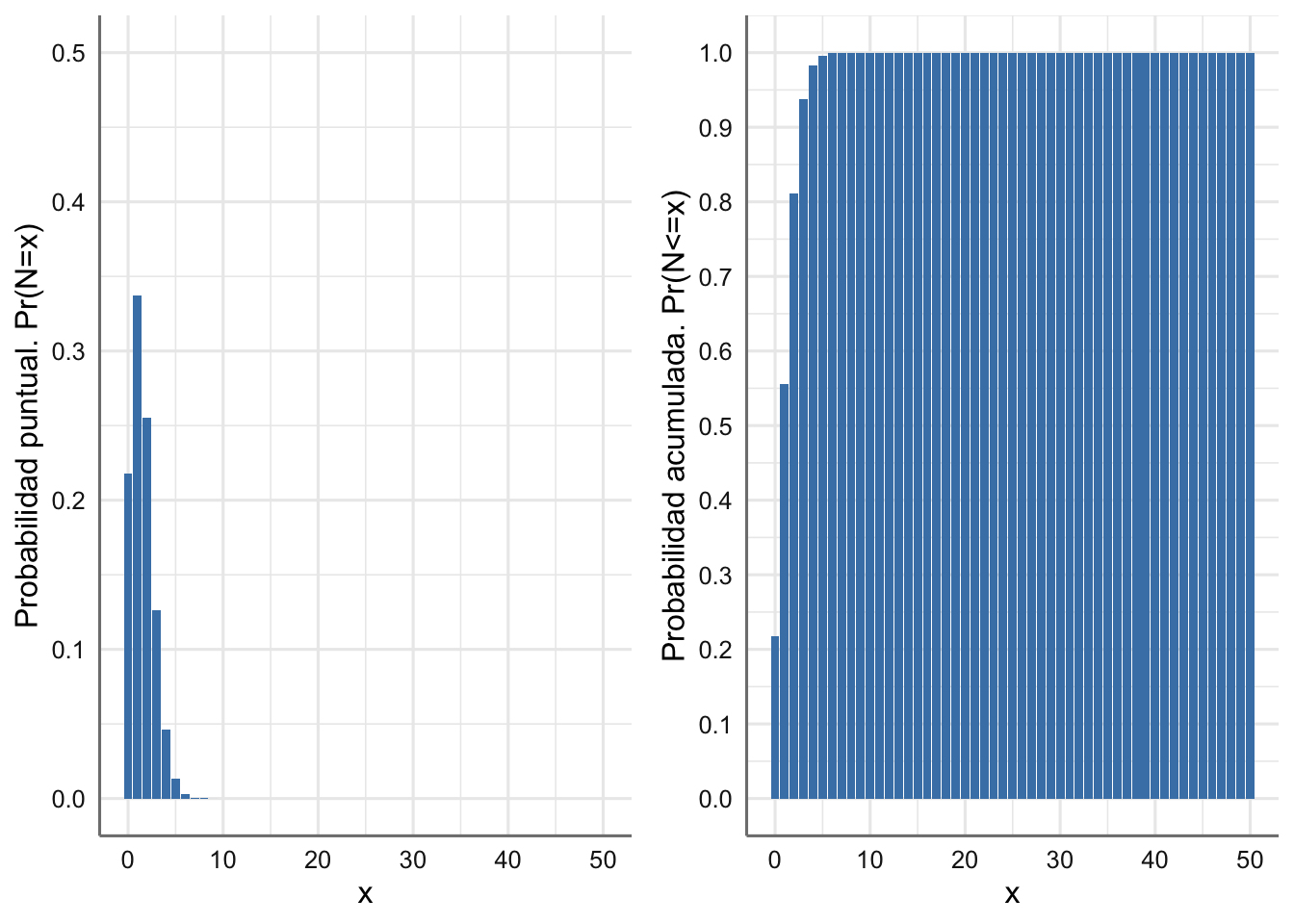
Función de masa de probabilidad y Función de distribución para el número de trabajadores de baja un día cualquiera.

Figura 1.1: Función de masa de probabilidad y Función de distribución para el número de trabajadores de baja un día cualquiera.

En la fmp (Figura 1.1-izquierda) podemos ver que en este caso la probabilidad se concentra en muy pocos valores, en concreto por debajo de 10, de modo que antes de llegar a \(x=10\) la probabilidad acumulada llega al valor 1, como se aprecia en la Figura 1.1-derecha.

La probabilidad que nos reclaman en el enunciado es \[Pr(N\geq 3)=1-Pr(N \leq 2),\] que calculamos y podemos aproximar por MC a partir, por ejemplo, de 1000 simulaciones.

nsim=1000
n=50
p=0.03
# valor real de la probabilidad
prob=1-pbinom(2,n,p)
cat("Pr(N>=3)=",round(prob,3))
## Pr(N>=3)= 0.189
set.seed(1234)
# simulaciones
I.a=(rbinom(nsim,n,p)>=3)*1  # función indicatriz para la probabilidad requerida
prob=mean(I.a)
cat("AproxMC=",prob)
## AproxMC= 0.193

El error estimado de esta aproximación, que calculamos con la raíz cuadrada de (??) es

error=sqrt(sum((I.a-prob)^2)/(nsim^2))
cat("Error.AproxMC=",round(error,3))
## Error.AproxMC= 0.012

de donde podríamos calcular un intervalo de confianza para la aproximación MC de \(Pr(N \geq 3)\) al 95% utilizando la distribución (??) y la fórmula (1.1):

# límites del IC redondeados a 3 cifras decimales
ic.low=round(prob-qnorm(0.975)*error,3)
ic.up=round(prob+qnorm(0.975)*error,3)
cat("IC(95%)[AproxMC]=[",ic.low,",",ic.up,"]")
## IC(95%)[AproxMC]=[ 0.169 , 0.217 ]

Ejemplo 1.6 Una empresa de fabricación produce piezas, de las cuales el 97% están dentro de las especificaciones y el 3% son defectuosas (fuera de las especificaciones). Aparentemente no hay ningún patrón en la producción de piezas defectuosas. La cadena de producción empaqueta las piezas en cajas de 20 piezas cada una, y produce 1000 cajas al día. Al gerente de la empresa le gustaría estimar el número de cajas con al menos dos piezas defectuosas, de entre todas las que se producen al día durante un día cualquiera.

Si \(N\) es la variable aleatoria que recoge el número de piezas defectuosas en una caja, tenemos que: \[N \sim Bi(20, 0.03)\] La probabilidad de que una caja tenga al menos dos piezas defectuosas se calcula con \(p_N=Pr(N \geq 2)=1-Pr(N\leq 1)\).

n=20
p=0.03
prob=(1 - pbinom(1, n,p))
cat("Probabilidad de que una caja tenga al menos dos defectos=",prob)
## Probabilidad de que una caja tenga al menos dos defectos= 0.119838

Sin embargo, lo que nos piden es, de un total de 1000 cajas, cuál es el número esperado de cajas con al meos dos piezas defectuosas. Para ello, surge la variable \(D_N\) que representa el número de cajas, de un total de 1000, con al menos 2 piezas defectuosas, que es binomial de tamaño 1000 y probabilidad \(p_N\), \[D_N \sim Bin(1000,p_N),\] y lo que nos están pidiendo es \(E(D_N)=1000 p_N\).

Si simulamos con la distribución de \(N\) lo acontecido un día, esto es, con 1000 cajas o simulaciones, y contamos el número de cajas con 2 o más piezas defectuosas, obtenemos una aproximación a la cantidad que nos piden.

n=20
p=0.03
sum(rbinom(1000,n,p)>=2)
## [1] 99

El problema es que no todos los días son iguales. De hecho si repites los siguientes cálculos varias veces, verás como el resultado varía. La aproximación Monte Carlo habría de considerar simulaciones de la variable \(D_n\) , esto es, nsim días, para con ellos poder sacar una conclusión “promedio” de lo que puede ocurrir un día cualquiera.

nsim=5000 # número de días simulados
n=1000
p=prob
# valor real del valor esperado
media=n*p
cat("E(D_N)=",round(media,3))
## E(D_N)= 119.838
# simulaciones
xi=rbinom(nsim,n,p)
m=mean(rbinom(nsim,n,p))
cat("AproxMC=",m)
## AproxMC= 119.7926
# Error MC
error=sqrt(sum((xi-m)^2)/(nsim^2))
# límites del IC redondeados a 3 cifras decimales
ic.low=round(m-qnorm(0.975)*error,3)
ic.up=round(m+qnorm(0.975)*error,3)
cat("IC(95%)[AproxMC]=[",ic.low,",",ic.up,"]")
## IC(95%)[AproxMC]=[ 119.51 , 120.076 ]

1.3.3 Geométrica

Imaginemos una situación experimental donde se repite un experimento hasta que sucede un “éxito.” En otras palabras, se piensa en \(\theta\) como la probabilidad de éxito para un solo ensayo, y realizamos sucesivamente los ensayos hasta que se produce un éxito. La variable aleatoria \(N\) se define entonces como el número de ensayos Bernouilli realizados hasta conseguir un éxito. Nótese que aunque la variable aleatoria geométrica es discreta, su rango es infinito, y su fmp viene dada por:

\[\begin{equation} Pr(N = x) = \theta (1-\theta)^{x} \text{ para } x = \text{1, 2,...} \tag{1.4} \end{equation}\] con \(x\) el número de repeticiones hasta alcanzar un éxito, y \(\theta\) la probabilidad de éxito.

Definición 1.11 La variable aleatoria \(N\) cuya función de masa de probabilidad viene dada en (1.4) se denomina variable Geométrica de parámetro \(\theta\), y se denota por:

\[N \sim Ge(\theta)\]

con \(E(N) = \frac{1 - \theta}{\theta}\) y \(V(N) = \frac{1-\theta}{\theta^2}.\)

Las funciones de R relacionadas con esta distribución se presentan a continuación, y tras ello un ejemplo de aplicación de la variable Geométrica.

  • La función dgeom(x, prob) nos permite evaluar la \(Pr(N=x)\) para una variable Geométrica con probabilidad de éxito prob.
  • pgeom(x, prob) calcula la función de distribución.
  • rgeom(n, prob) permite generar \(n\) valores de una variable Geométrica con probabilidad de éxito \(prob\). Los resultados que proporciona son el número de repeticiones realizadas hasta alcanzar el primer éxito.

Ejemplo 1.7 Una vendedora de coches ha hecho un análisis estadístico de su historial de ventas anterior y ha determinado que cada día tiene un 10% de probabilidad de vender un coche de lujo. Tras un cuidadoso análisis posterior, también está claro que la venta de un coche de lujo en un día es independiente de la ventas realizadas cualquier otro día. El día de Año Nuevo (un día festivo en el que el concesionario estaba cerrado) la vendedora está intentando predecir cuándo venderá su primer coche de lujo del año.

Si consideramos \(N\) como la variable aleatoria que indica el día de la primera venta de coches de lujo (N = 1 implica que la venta se realizaría el día 2 de enero), entonces: \[N \sim Ge(0.1)\]

En este caso el valor esperado del número de días transcurridos hasta la venta del primer coche de lujo es \(E(N) = 0.9/0.1 = 9\) días, con una desviación típica de 9.5 días. Así pues, es posible que el día 10 de enero tenga su primera venta. En la Figura 1.2 se muestran la fmp y la función de distribución asociadas.

# Valores de N
xs <- seq(0, 60, 1)
# Data frame
datos <- data.frame(xs = xs, probs = dgeom(xs, 0.1), 
                    probsacum = pgeom(xs, 0.1))
# función de masa de probabilidad
g1 <- ggplot(datos, aes(xs, probs)) + 
  geom_bar(stat = "identity", fill = "steelblue") +
  ylim(0,0.12) +
  labs(x ="x", y = "Probabilidad puntual. Pr(N=x)")
# función de distribución
g2 <- ggplot(datos, aes(xs, probsacum)) + 
  geom_bar(stat = "identity", fill = "steelblue") +
  scale_y_continuous(breaks = scales::breaks_extended(10)) +
  labs(x ="x", y = "Probabilidad acumulada Pr(N<=x)")
grid.arrange(g1, g2, nrow = 1)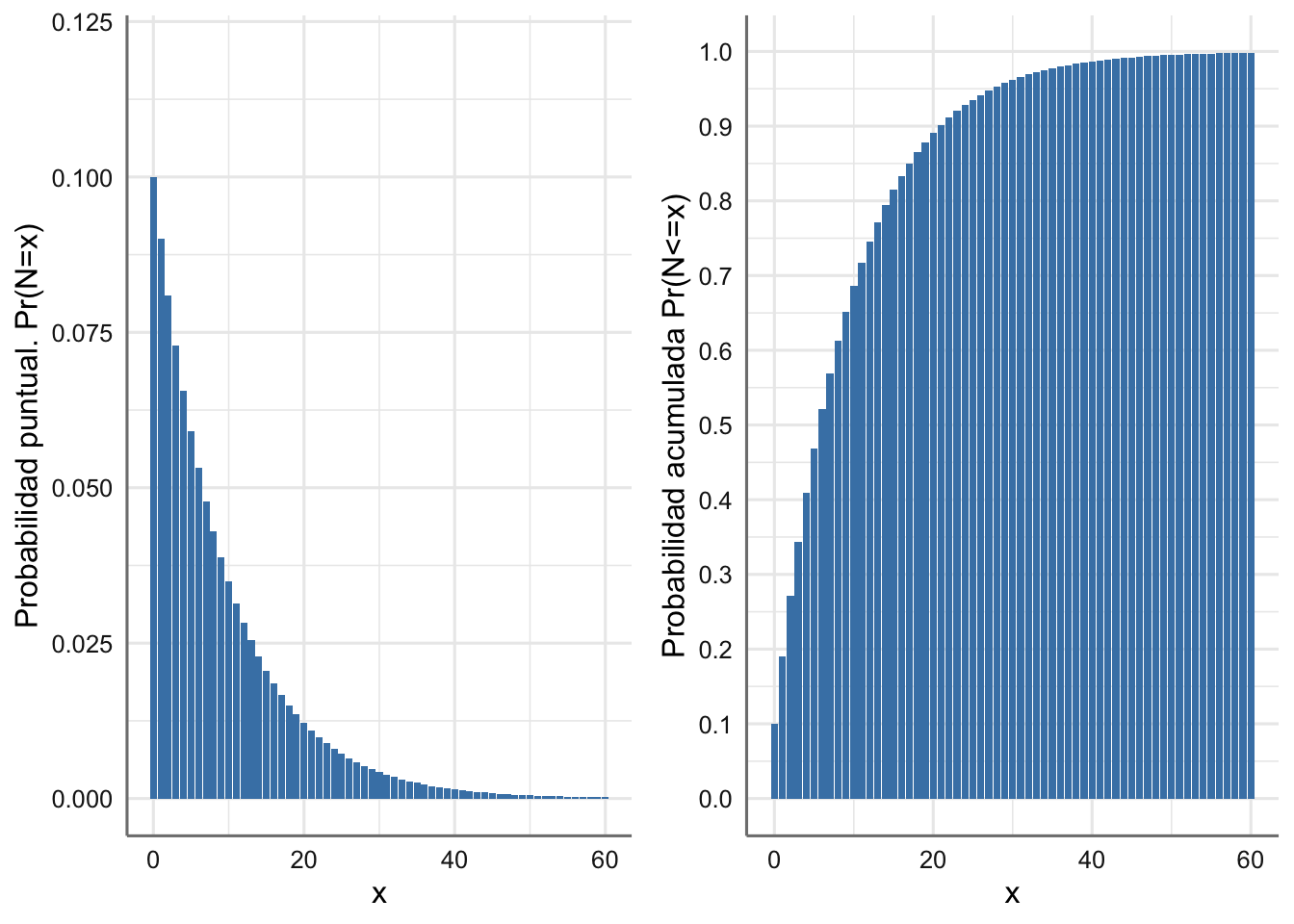
Función de masa de probabilidad y Función de distribución para el día en que venderá el primer coche de lujo.

Figura 1.2: Función de masa de probabilidad y Función de distribución para el día en que venderá el primer coche de lujo.

Hacemos a continuación un análisis de simulación para aproximar los datos teóricos dados en la definición 1.11. Simulamos 1000 valores de una \(Ge(0.1)\), con los que calculamos una aproximación al valor esperado de los días que deben transcurrir para vender un coche de lujo, y construimos un intervalo de confianza para la aproximación MC según (1.1).

# Parámetros de la simulación

set.seed(1970)
nsim <- 10000
prob <- 0.1
media<-(1-prob)/prob
cat("E(N)=",media)
## E(N)= 9
# Valores simulados
datos <- rgeom(nsim, prob)
# Aproximación MC del valor esperado
m=round(mean(datos),0)
cat("AproxMC=",m)
## AproxMC= 9
# Error MC
error=sqrt(sum((datos-m)^2)/(nsim^2))
# límites del IC redondeados a 3 cifras decimales
ic.low=round(m-qnorm(0.975)*error,3)
ic.up=round(m+qnorm(0.975)*error,3)
cat("IC(95%)[AproxMC]=[",ic.low,",",ic.up,"]")
## IC(95%)[AproxMC]=[ 8.811 , 9.189 ]

1.3.4 Poisson

La distribución de Poisson se emplea como un modelo para variables aleatorias de tipo discreto cuando se quieren obtener las probabilidades de ocurrencia de un evento que se distribuye al azar en el espacio o el tiempo. Algunos ejemplos de esta distribución se presentan a continuación.

  • En el estudio de cierto organismo acuático, se toman un gran número de muestras de un lago y se cuenta el número de dichos organismos que aparecen en cada muestra. Podríamos plantear como objetivo el conocer cuál es la probabilidad de encontrar dicho organismo en una próxima muestra si la media observada en el conjunto de muestras es de 2 organismos.

  • En un estudio sobre la efectividad de un insecticida sobre cierto tipo de insecto, se fumiga una gran región. Posteriormente se crea una cuadrícula sobre el terreno, se selecciona de forma aleatoria un conjunto de ellas, y se cuenta el número de insectos vivos dentro de cada una. Planteamos como objetivo conocer cuál es la probabilidad de que no encontremos ningún insecto vivo en una próxima cuadrícula si se sabe que la media de insectos vivos en las cuadrículas analizadas es de 0.5.

  • Un grupo de investigadores observó la ocurrencia de hemangioma capilar retiniano (RCH) en pacientes con la enfermedad de von Hippel-Lindau (VHL). RCH es un tumor vascular benigno de la retina. Usando una revisión retrospectiva de series de casos consecutivos, los investigadores encontraron que el número de medio de tumores RCH por ojo para pacientes con VHL era de 4. Están interesados en conocer cuál es la probabilidad de que se detecten más de cuatro tumores por ojo.

La variable aleatoria \(N\) se define entonces como el número de eventos que ocurren en un espacio o un tiempo determinados, y viene caracterizada por la denominada tasa de eventos o número medio de eventos que ocurren en el tiempo o espacio, y que se denota habitualmente por \(\lambda\). El rango de esta variable es infinito y su fmp viene dada por:

\[\begin{equation} Pr(N = x) = \frac{e^{-\lambda}\lambda^x}{x!} \text{ para } x = \text{1, 2,...} \tag{1.5} \end{equation}\] con \(\lambda\) es la tasa y \(x\) es el número de eventos que han ocurrido.

Definición 1.12 La variable aleatoria \(X\) cuya función de masa de probabilidad viene dada en (1.5) se denomina variable poisson de parámetro \(\lambda > 0\), y se denota por:

\[N \sim Po(\lambda)\]

con \(E(N) = \lambda\) y \(V(N) = \lambda.\)

A continuación vemos diferentes ejemplos de uso de la distribución de Poisson, tras presentar las funciones de R relacionadas.

  • La función dpois(x, lambda) nos permite evaluar la \(Pr(X=x)\) para una variable poisson de media \(\lambda\).
  • ppois(x, lambda) calcula la función de distribución.
  • rpois(n, lambda) permite generar \(n\) valores de una variable Poisson con media \(\lambda\). Los resultados que proporciona son el número de eventos que ocurren en el tiempo o espacio determinado.

Ejemplo 1.8 Una empresa de asesoramiento está realizando el análisis del funcionamiento de una panadería y ha estimado que el número medio de barras de pan que se venden en un periodo de media hora es de 12. La empresa está interesada en saber cuál es la capacidad de venta en cada franja de diez minutos (pues es prácticamente el tiempo de horneado), y también cuál es la probabilidad de que el número de barras que se venden en diez minutos sea exactamente de tres.

Como nuestro interés radica en un periodo de diez minutos y el número de intervalos de diez minutos en un periodo de 30 minutos es tres, tenemos que el número medio de barras puestas a la venta en ese periodo viene dado por: \[\lambda = 12/3 = 4.\]
La variable aleatoria que reproduce el número de barras que se venden en una franja de cinco minutos es:

\[N \sim Po(4)\]

En este caso el valor esperado del número de barras que se venden es 4 y la desviación típica es igual a 2(\(=\sqrt{4}\)). En la Figura 1.3 se muestran la fmp y la función de distribución asociadas.

# Valores de N
lambda=4
xs <- seq(0, 10, 1)
# Data frame
datos <- data.frame(xs = xs, probs = dpois(xs, lambda), 
                    probsacum = ppois(xs, lambda))
# función de masa de probabilidad
g1 <- ggplot(datos, aes(xs, probs)) + 
  geom_bar(stat = "identity", fill = "steelblue") +
  scale_x_continuous(breaks = 0:10, labels = 0:10) +
  ylim(0,0.3) +
  labs(x ="x", y = "Probabilidad puntual. Pr(N=x)")
# función de distribución
g2 <- ggplot(datos, aes(xs, probsacum)) + 
  geom_bar(stat = "identity", fill = "steelblue") +
  scale_x_continuous(breaks = 0:10, labels = 0:10) +
  scale_y_continuous(breaks = scales::breaks_extended(10)) +
  labs(x ="x", y = "Probabilidad acumulada Pr(N<=x)")
grid.arrange(g1, g2, nrow = 1)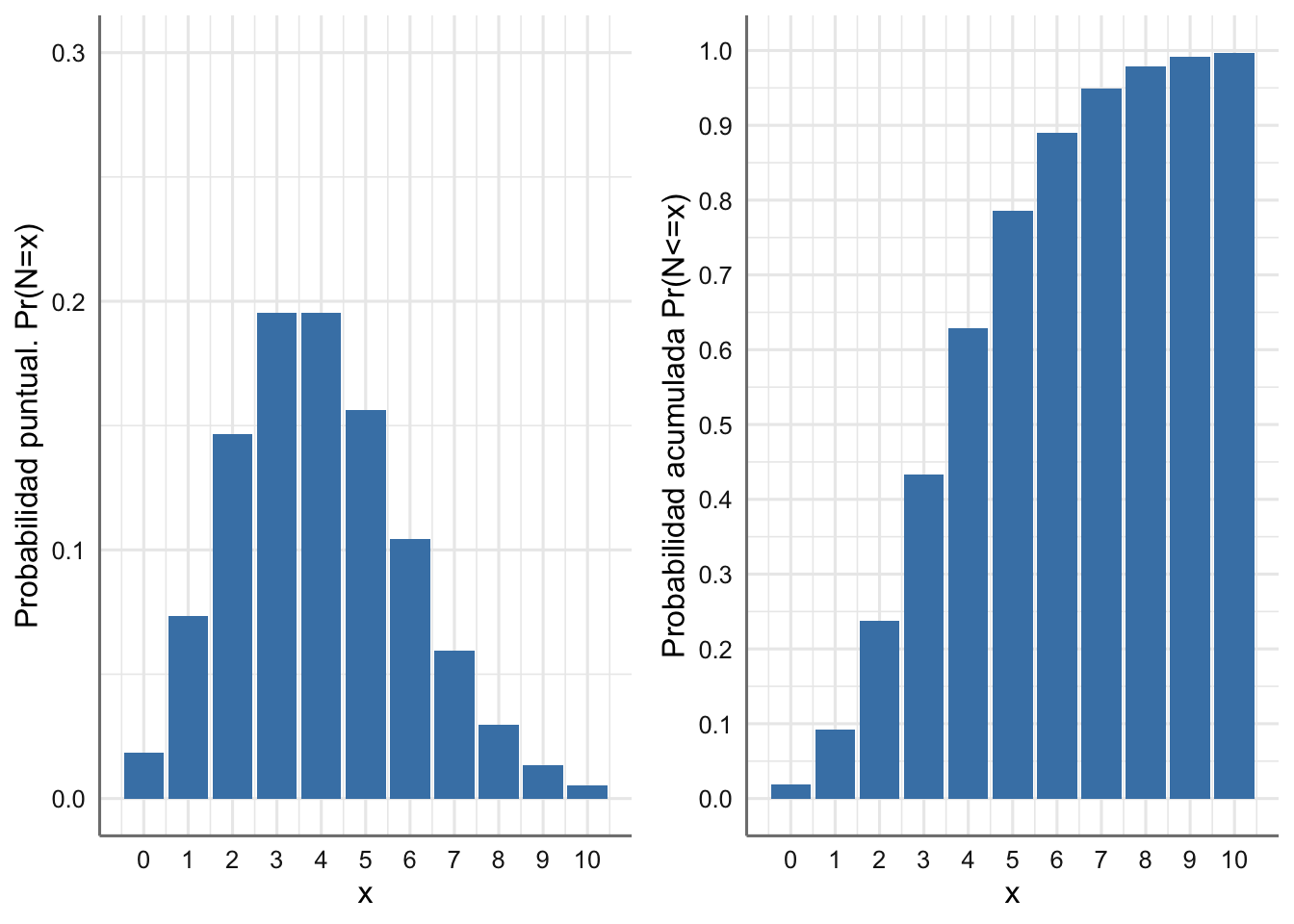
Función de masa de probabilidad y Función de distribución para el número de barras de pan que se venden cada cinco minutos.

Figura 1.3: Función de masa de probabilidad y Función de distribución para el número de barras de pan que se venden cada cinco minutos.

Podemos reconoder en la Figura 1.3-izquierda los valores más probables con las barras más altas (3 y 4(. De hecho, en la Figura 1.3-derecha, la probabilidad de que a lo sumo se vendan menos de 5 barras es algo superior a 0.6.

Para calcular la probabilidad pretendida, esto es, \(Pr(N=3)\) utilizamos la función fmp correspondiente en R y la aproximamos por MC con 1000 simulaciones, dando también una banda de confianza.

lambda=4
# Probabilidad buscada P(N=3) para la poisson con media 2
media=dpois(3,lambda)
cat("Pr(N=4)=",round(media,3))
## Pr(N=4)= 0.195
nsim <- 10000
# Simulamos de la poisson y evaluamos la función indicatriz para la prob de interés
set.seed(1970)
I.a <- (rpois(nsim, lambda)==3)*1
# Realizamos la aproximación MC
m=mean(I.a)
cat("AproxMC=",m)
## AproxMC= 0.1934
# Error MC
error=sqrt(sum((I.a-m)^2)/(nsim^2))
# límites del IC redondeados a 3 cifras decimales
ic.low=round(m-qnorm(0.975)*error,3)
ic.up=round(m+qnorm(0.975)*error,3)
cat("IC(95%)[AproxMC]=[",ic.low,",",ic.up,"]")
## IC(95%)[AproxMC]=[ 0.186 , 0.201 ]

Si la aproximación la hacemos con 10 veces más simulaciones, el intervalo de estimación resultará más preciso:

lambda=4
# Probabilidad buscada P(N=3) para la poisson con media 2
media=dpois(3,lambda)
cat("Pr(N=4)=",round(media,3))
## Pr(N=4)= 0.195
nsim <- 10000*10
# Simulamos de la poisson y evaluamos la función indicatriz para la prob de interés
set.seed(1970)
I.a <- (rpois(nsim, lambda)==3)*1
# Realizamos la aproximación MC
m=mean(I.a)
cat("AproxMC=",m)
## AproxMC= 0.19375
# Error MC
error=sqrt(sum((I.a-m)^2)/(nsim^2))
# límites del IC redondeados a 3 cifras decimales
ic.low=round(m-qnorm(0.975)*error,3)
ic.up=round(m+qnorm(0.975)*error,3)
cat("IC(95%)[AproxMC]=[",ic.low,",",ic.up,"]")
## IC(95%)[AproxMC]=[ 0.191 , 0.196 ]

Ejemplo 1.9 Una empresa de fabricación de galletas de chocolate está analizando la calidad en su empresa para responder del mejor modo posible a sus clientes. Para ello ha fijado que con probabilidad 0.8 las galletas deben contener al menos tres trozos de chocolate para satisfacer las exigencias de los clientes. Se trata pues de fijar el valor medio de trozos de chocolate que debe ir suministrando en la cadena de producción para cumplir con el nivel de exigencia establecido.

Si \(N\) es la variable aleatoria que indica el número de trozos de chocolate en una galleta, tenemos que: \[N \sim Po(\lambda)\]
donde en este caso el valor de \(\lambda\) es desconocido y representa el número medio de trozos de chocolate en cada galleta. Planteamos un estudio de simulación para aproximar dicho valor.

Algoritmo para aproximar el valor de \(\lambda\).

  1. Considerar una secuencia de valores de \(\lambda_i\), \(i=1,...,K\)
  2. Obtener una muestra de tamaño \(nsim\) para cada distribución \(Po(\lambda_i)\), \(M_i=\{x_{i_1},\ldots,x_{i_{nsim}}\}\).
  3. Con cada muestra \(M_i\) aproximar la probabilidad de que el número de trozos sea mayor o igual a 3, \(p_i\approx Pr(N_{\lambda_i}\geq3)\).
  4. Obtener el valor mínimo de \(\lambda\), de entre \(\{\lambda_1,\ldots,\lambda_K\}\) que verifica \(p_i \geq 0.8\).

En la Figura 1.4 se muestra el proceso de simulación realizado a continuación y el resultado obtenido para el valor de \(\lambda\) para cumplir los requisitos de la empresa.

# Paso 1
set.seed(1970)
nsim <- 5000
lams <- seq(0.1, 5, 0.01) # valores de lambda
nlams <- length(lams)     # número de lambdas para evaluar
prob <- c()  # vector de probabilidades

# Pasos 2 y 3
for(i in 1:nlams){
  datos <- rpois(nsim, lams[i])    
  prob[i] <- mean(datos >= 3)   
}

# Paso 4. Resultado del problema
lambda=lams[min(which(prob >= 0.8))];lambda
## [1] 4.25
# Pintamos los resultados de la simulación realizada
dat=data.frame(lams=lams,prob=prob)
ggplot(dat,aes(x=lams,y=prob))+
  geom_point()+
  geom_hline(yintercept=0.8)+
  geom_vline(xintercept=lambda)+
  labs(x="lambda",y="Pr(N>=3)")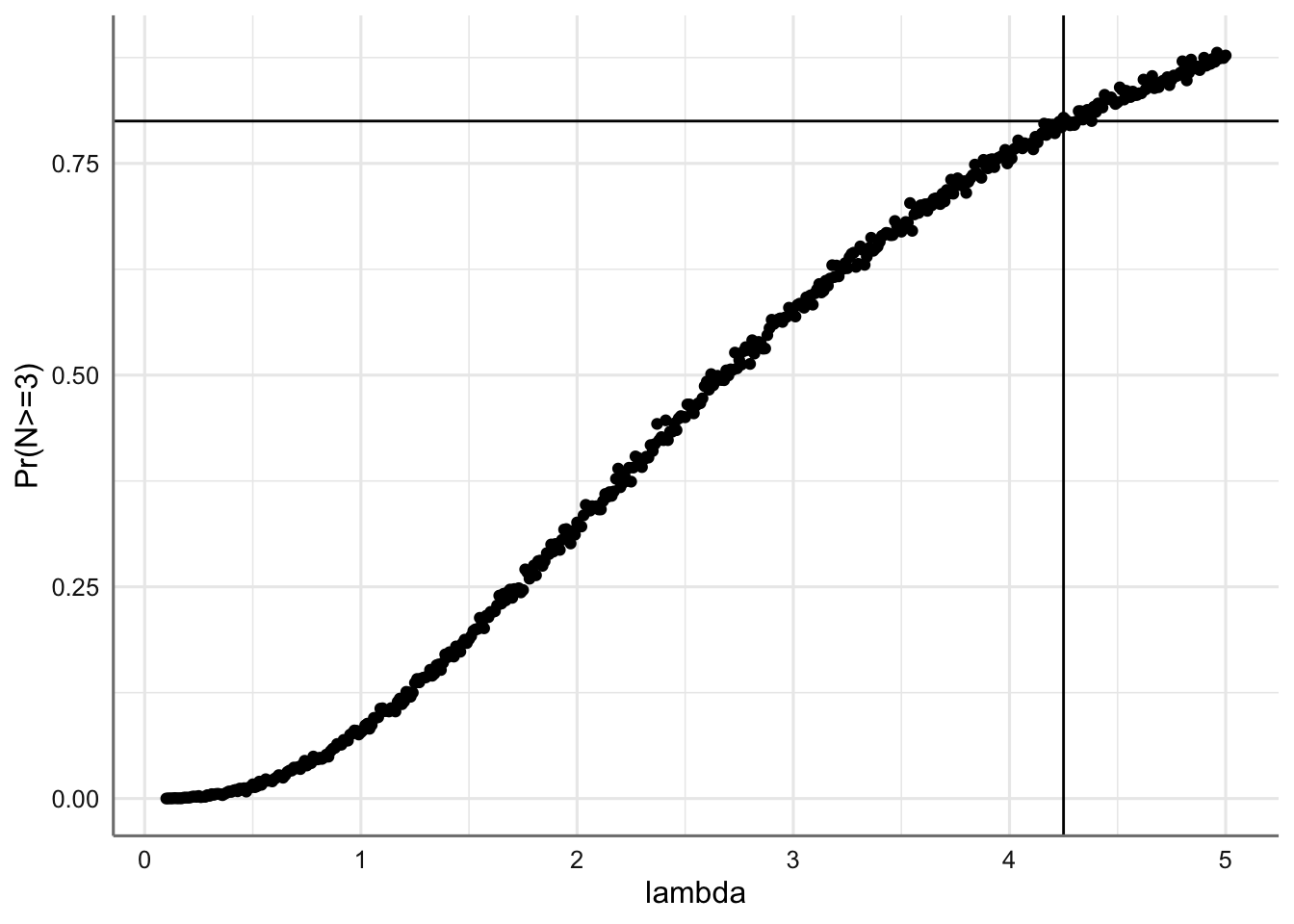
Probabilidad estimada de conseguir al menos 3 trozos de chocolate en cada galleta, en función de lambda.

Figura 1.4: Probabilidad estimada de conseguir al menos 3 trozos de chocolate en cada galleta, en función de lambda.

Así pues, el número medio de trozos de chocolate que ha de suministrarse a cada galleta ha de ser al menos de 4.25.