4.3 Análisis preliminar del proceso
Aunque más adelante estudiaremos los aspectos teóricos para el análisis completo de una CMTC, en este punto utilizamos la simulación del sistema para analizar su comportamiento. Nos centramos en las herramientas de simulación estudiadas hasta este punto para más adelante presentar con detalle la libreria simmer que nos permite simular procesos y sistemas complejos.
Nos centraremos en los ejemplos ?? y ?? dado que le sitema descrito en el ejemplo ?? se puede analizar sin más que describir la tasa corrrespondiente al tiempo de vida del satélite. Comenzamos con el algoritmo correspondiente al ejemplo ??.
Algoritmo para el sistema de vidad útil de una máquina:
- Fijar tasas de funcionamiento \(\mu\) y reparación \(\lambda\), así como el tiempo en que el sistema estará funcionando (\(tfin\)).
- Fijar el tiempo de funcionamiento \(tfun = 0\), tiempo de reparación \(trep = 0\), y tiempo de funcionamiento del sistema \(tsis = tfun + trep\).
- Fijamos el número de vistas al estado de funcionamiento \(nfun = 0\) y al estado de reparación \(nrep =0\).
Repetir los pasos siguientes hasta que abandonemos el sistema:
- Generar \(tfun \sim Exp(\mu)\) actualizando \(tsis\) y \(nfun\).
- Si \(tsis > tfin\) abandonar el sistema.
- Generar \(trep \sim Exp(\lambda)\) actualizando \(tsis\) y \(nrep\).
- Si \(tsis > tfin\) abandonar el sistema.
Los valores \(tfun\), \(trep\), así como las veces que vistamos los estados de funcionamiento y reparación nos permiten describir el funcionamiento del sistema para un tiempo prefijado.
Para facilitar el análisis establecemos que todos los tiempos del sistema están en días y que deseamos estudiar el sistema durante un año. Creamos una función que nos permite modificar los valores de la tasa del tiempo de funcionamiento (recíproco de la media de tiempo en funcionamiento ), tasa de reparación /recíproco de la media del tiempo de reparación y el tiempo total de funcionamiento del sistema. Almacenamos los resultados de cada paso por el sistema para poder realziar los análisis correspondientes.
TSIM_one_machine <- function(tasafun, tasarep, tfin)
{
# Parámetros de la función
# =========================
# tasafun: tasa de funcionamiento
# tasarep: tasa de reparación
# tfin: tiempo de funcionamiento del sistema
# inicialización de parámetros del sistema
tfun = trep = nfun = nrep = tsis = vector()
# estado inicial del sistema
i <- 1
tfun[i] = trep [i] = nfun[i] = nrep[i] = 0
tsis[i] <- tfun[i] + trep[i]
# Fijamos semilla
set.seed(123)
# Bucle de simulación
while(tsis[i] <= tfin)
{
i<- i + 1
# Máquina en funcionamiento
nfun[i] = nfun[i-1] + 1
tfun[i] = rexp(1, tasafun)
tsis[i] = tsis[i-1] + tfun[i]
trep[i] = 0 #Actualizamos estos dos parámetros ya que no hemos entrado en reparación
nrep[i] = nrep[i-1]
if(tsis[i] > tfin) {
# adaptamos valores para quedarnos en los 365 días
tfun[i] <- tfin - tsis[i-1]
tsis[i] <- tsis[i-1] + tfun[i]
break
}
# Máquina en reparación
nrep[i] = nrep[i-1] + 1
trep[i] = rexp(1, tasarep)
tsis[i] = tsis[i] + trep[i]
if(tsis[i] > tfin) {
# adaptamos valores para quedarnos en los 365 días
trep[i] <- tfin - tsis[i-1]
tsis[i] = tsis[i] + trep[i]
break
}
}
res <- tibble(tfun, nfun, trep, nrep, tsis)
# Devolvemos resultados del sistema quitando la fila de inicialización
return(res[-1,])
}Supongamos que a través de los registros históricos de funcionamiento y reparación de la máquina se sabe que el tiempo medio de funcionamiento es de 60 días (\(\mu = 1/60\)) y el tiempo medio de reparación es de cuatro días (\(\lambda = 1/4\)). Además se esta interesado en estudiar el funcionamiento del sistema para el próximo año (365 días). Estamos interesados:
- Proporción del tiempo que la máquina está funcionando y en reparación.
- Número de ocasiones en que la máquina debe ser reparada.
- Si el beneficio neto es de 100 euros por cada día que la máquina está funcionando y una pérdida de 1500 euros por cada día que está en reparación ¿cuál es el beneficio esperado para el próximo año?
Obtenemos la simulación del sistema:
mu <- 1/60
lambda <- 1/4
simulacion <- TSIM_one_machine(mu, lambda, 365)
simulacion## # A tibble: 6 × 5
## tfun nfun trep nrep tsis
## <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 50.6 1 2.31 1 52.9
## 2 79.7 2 0.126 2 133.
## 3 3.37 3 1.27 3 137.
## 4 18.9 4 0.581 4 157.
## 5 164. 5 0.117 5 321.
## 6 44.5 6 0 5 365Podemos ver que el número de ciclos en que la máquina esta en fucionamiento es 6 mientras que el número de veces que ha necesitado reparación son 5.
Calculamos ahora los tiempos totales de funcionamiento y reparación:
tiempos <- apply(simulacion[c(1,3)], 2, sum)
tiempos## tfun trep
## 360.603564 4.396436Por tanto, la proporción de tiempo que la máquina está en funcionamiento es 0.99, y el beneficio estimado para el próximo año viene dado por:
beneficio <- 100 * tiempos["tfun"] - 1500 * tiempos["trep"]
beneficio## tfun
## 29465.7A continuación analizamos el sistema del viajante correspondiente al ejemplo ??. En primer lugar establecemos el algoritmo de simulación del sistema. Para facilitar todas las posibilidades del algoritmo asumimos que el vendedor comienza el recorrido en la ciudad en la que reside.
Algoritmo para el análisis del sistema del viajante:
- Fijar tasas de permanencia en cada ciudad \(\mu_A\), \(\mu_B\), y \(\mu_C\), así como las probabilidades de salto dadas en la matriz \(P\), y una varibale que indica la ciudad en la que nos encontramos (\(ciudad\)).
- Fijar el tiempo de funcionamiento del sistema \(tsis = 0\), tiempo de permanencia en cada ciudad \(tiempo = 0\), y el tiempo de estudio \(tfin\).
- Generar \(tiempo \sim Exp(\mu_a)\) y actualizar \(tsis\), de forma que si \(tsis > tfin\) abandonamos el sistema.
- Generamos un salto de la ciudad \(A\) de acuerdo a las probabilidades de \(P\) correspondientes a la ciudad \(A\).
Repetir los pasos siguientes hasta que el tiempo en el sistema supere el tiempo fijado:
- Actualizamos \(ciudad\), generamos \(tiempo \sim Exp(\mu_{ciudad})\) y actualizamos \(tsis\), de forma que si \(tsis > tfin\) abandonamos el sistema.
- Generamos un salto de la ciudad del paso anterior de acuerdo a las probabilidades de \(P\) correspondientes a dicha ciudad.
Los valores \(tiempo\), y \(ciudad\) nos permiten describir el funcionamiento del sistema para un tiempo prefijado.
A continuación tenemos la función necesaria para simular el sistema descrito:
TSIM_viajante <- function(tasaA, tasaB, tasaC, tfin)
{
# Parámetros de la función
# =========================
# tasaA: tasa de permanencia en A
# tasaB: tasa de permanencia en B
# tasaC: tasa de permanencia en C
# tfin: tiempo de funcionamiento del sistema
# inicialización de parámetros del sistema
tiempo = tsis = ciudad = vector()
# Probabilidades de salto. Fijamos la primera ya que la otra es complementaria
pA <- 0.5 # de A a B. De A a C es 1-pA
pB <- 0.75 # de B a A. De B a C es 1-pB
pC <- 0.75 # de C a A. De C a B es 1-pC
# estado inicial del sistema
i <- 1
ciudad[i] <- "A"
# Fijamos semilla
set.seed(123)
# Primer tiempo de estancia
tiempo[i] = rexp(1, tasaA)
tsis[i] <- tiempo[i]
# Saltamos de la ciudad A
uniforme <- runif(1)
ifelse(uniforme <= pA, ciudad[i+1] <- "B", ciudad[i+1] <- "C")
# Bucle de simulación
while(tsis[i] <= tfin)
{
i<- i + 1
uniforme <- runif(1)
if(ciudad[i] == "A")
{
# Calculamos tiempo de permanencia
tiempo[i] <- rexp(1, tasaA)
# Actualizamos y valoramos si hemos alcanzado el tiempo límite
tsis[i] = tsis[i-1] + tiempo[i]
if(tsis[i] > tfin){
tiempo[i] <- tfin - tsis[i-1]
tsis[i] = tsis[i-1] + tiempo[i]
break
}
# Si no hemos alcanzado el límite realizamos un nuevo salto
ifelse(uniforme <= pA, ciudad[i+1] <- "B", ciudad[i+1] <- "C")
}
if(ciudad[i] == "B")
{
# Calculamos tiempo de permanencia
tiempo[i] <- rexp(1, tasaB)
# Actualizamos y valoramos si hemos alcanzado el tiempo límite
tsis[i] = tsis[i-1] + tiempo[i]
if(tsis[i] > tfin){
tiempo[i] <- tfin - tsis[i-1]
tsis[i] = tsis[i-1] + tiempo[i]
break
}
# Si no hemos alcanzado el límite realizamos un nuevo salto
ifelse(uniforme <= pB, ciudad[i+1] <- "A", ciudad[i+1] <- "C")
}
if(ciudad[i] == "C")
{
# Calculamos tiempo de permanencia
tiempo[i] <- rexp(1, tasaC)
# Actualizamos y valoramos si hemos alcanzado el tiempo límite
tsis[i] = tsis[i-1] + tiempo[i]
if(tsis[i] > tfin){
tiempo[i] <- tfin - tsis[i-1]
tsis[i] = tsis[i-1] + tiempo[i]
break
}
# Si no hemos alcanzado el límite realizamos un nuevo salto
ifelse(uniforme <= pC, ciudad[i+1] <- "A", ciudad[i+1] <- "C")
}
}
# Devolvemos resultados del sistema
ciudad <- factor(ciudad)
res <- tibble(tiempo, ciudad, tsis)
return(res)
}Supongamos que estamos interesados en aproximar el comportamiento del vendedor durante el próximo año (52 semanas) para poder contestar a las preguntas siguientes:
- Proporción de tiempo que el vendedor pasa en cada ciudad.
- Número de ocasiones en que visita cada ciudad.
Obtenemos la simulación del sistema y contestamos a las preguntas planteadas:
tasaA <- 1/2
tasaB <- 1/1
tasaC <- 2/3
tfin <- 52
simulacion <- TSIM_viajante(tasaA, tasaB, tasaC, tfin)
# Análsis del sistema
simulacion %>%
group_by(ciudad) %>%
summarise(visita = n(), estancia = sum(tiempo)) %>%
mutate(proporcion = estancia/52)## # A tibble: 3 × 4
## ciudad visita estancia proporcion
## <fct> <int> <dbl> <dbl>
## 1 A 16 30.3 0.583
## 2 B 8 10.7 0.206
## 3 C 11 11.0 0.211Aunque más adelante estudiaremos la librería simmer presentamos aqui el algoritmo necesario para simular los procesos anteriores con el objeto de ver la simplicidad de programación en estos sistemas más sencillos.
La libreria simmer permite simular de sistemas tanto continuos como discretos bajos dos premisas fundamentales:
- Proceso de llegadas (“arrivals”): proceso por el que el sujeto o bien accede al sistema.
- Proceso de servicio (“server”): tareas (denominadas trayectorias) a la que es sometido la persona o bien dentro del sistema a las que les asigna uno o más recursos (“resources”).
Para el sistema descrito en ejemplo ?? el proceso de llegadas correspondería al momento en que despueés de estar funcionando un timepo la máquina debe ser reparada, mientras que el proceso de servicio es el tiempo dedicado a la reparación de la máquina. En este caso el recurso es el reparador encargado de poner en marcha la máquina de nuevo.
El primer paso del algoritmo de simulación es cargar las librerías y deifnir la semilla de simulación:
library(simmer)
library(simmer.plot)
library(simmer.bricks)
set.seed(1234)Definimos ahora el entorno de simulación del sistema:
# Tasas de permanencia del sistema
##################################
lambda <- 1/4 # reparación
mu <- 1/60 # funcionamiento
# Sistema
#################################################
sistema.1m <- function(t, lambda, mu)
{
# tarea dentro de sistema
reparar <- trajectory() %>%
# Máquina estropeada
seize("Off", amount = 1) %>%
# Tiempo de reparación
timeout(function() rexp(1, lambda)) %>%
# Máquina reparada
release("Off", amount = 1)
# Configuración del sistema
#################################################
simmer() %>%
# Activación del estado de reparación
add_resource("Off", capacity = 1, queue_size = 0) %>%
# Tiempo de funcionamiento antes de reparar
add_generator("reparando", reparar, function() rexp(1, mu)) %>%
# Tiempo funcionamiento del sistema
run(until = t)
}
### Simulación del sistema
operar <- sistema.1m(365, 1/4, 1/60)Analizamos ahora los resultados que proporciona el sistema simulado. Podemos acceder a las información de dos formas diferentes mediante las funciones get_mon_arrivals() y get_mon_resources().
reparacion = get_mon_arrivals(operar)
reparacion## name start_time end_time activity_time finished replication
## 1 reparando0 150.1055 150.1318 0.02632783 TRUE 1
## 2 reparando1 164.9110 166.4598 1.54873033 TRUE 1
## 3 reparando2 269.4758 272.7721 3.29632606 TRUE 1
## 4 reparando3 274.8728 278.2250 3.35216128 TRUE 1
## 5 reparando4 287.0299 294.5502 7.52030671 TRUE 1
## 6 reparando5 332.6557 339.2903 6.63464954 TRUE 1El objeto resultante tiene las columnas siguientes:
name: estado del sistema de acuerdo a las tareas que se deben realziar.star_time: instante en el que comienza la tarea definida.end_time: instante en el que finaliza la tarea definida.activity_time: tiempo dedicado a la tarea.finished: si la tarea ha finalizado dentro del periodo de tiempo de simualción establecido.replication: número de replicas del sistema.
Con la función get_mon_resources() tenemos una descripción continua del proceso con las columnas:
resource: recursotime: instante de tiempo donde el sistema registra actividadserver: variable dicotómica con valor 1 cuando el sistema está en srvicio y 0 cuando no lo esta.queue: sujetos en la colacapacity: capacidad del sistema.queue_size: tamaño de la cola.system: elementos en el sistemalimit: capacidad límite del sistemareplication: número de replicas del sistema.
recursos = get_mon_resources(operar)
recursos## resource time server queue capacity queue_size system limit replication
## 1 Off 150.1055 1 0 1 0 1 1 1
## 2 Off 150.1318 0 0 1 0 0 1 1
## 3 Off 164.9110 1 0 1 0 1 1 1
## 4 Off 166.4598 0 0 1 0 0 1 1
## 5 Off 269.4758 1 0 1 0 1 1 1
## 6 Off 272.7721 0 0 1 0 0 1 1
## 7 Off 274.8728 1 0 1 0 1 1 1
## 8 Off 278.2250 0 0 1 0 0 1 1
## 9 Off 287.0299 1 0 1 0 1 1 1
## 10 Off 294.5502 0 0 1 0 0 1 1
## 11 Off 332.6557 1 0 1 0 1 1 1
## 12 Off 339.2903 0 0 1 0 0 1 1A partir de los resultados podemos responder a las mismas preguntas que ya planteamos antes:
- Proporción del tiempo que la máquina está funcionando y en reparación.
- Número de ocasiones en que la máquina debe ser reparada.
- Si el beneficio neto es de 100 euros por cada día que la máquina está funcionando y una pérdida de 1500 euros por cada día que está en reparación ¿cuál es el beneficio esperado para el próximo año?
Para responder al primer pregunta basta con sumar los tiempos de actividad y calcualr su proporción sobre los 365 días de simulación:
tiempo_reparacion <- sum(reparacion$activity_time)
propor <- round(100*(1-(tiempo_reparacion/365)), 2)
propor## [1] 93.87La proporción de tiempo en que la máquina está funcionando es del 93.87% y el tiempo que está en repación es del 6.13%.
El número de ocasiones en que la máquina está en reparación corresponde al número de veces que accedemos a la tarea de repación que en este caso es de 6.
Para calcular el beneficio utilizamos el tiempo de reparación obtenido:
(365-tiempo_reparacion)*100 - tiempo_reparacion*1500## [1] 694.3972Como se puede ver los resultados no son muy similares a los obtenidos con el algoritmo anterior, ya que los tiempos de reparación son superiores. Para conseguir resultados más estables deberiamos realizar diferentes replicaciones del sistema y promediar los beneficios obtenidos mediante un estimador Monte-Carlo. Sin embargo, podemos replicar el sistema añadiendo dos líneas de código a la definición del sistema. En este caso establecemos un parámetro para indicar el número de replicas del sistema.
replicas <- 500
envs <- lapply(1:replicas, function(i){
operar <- sistema.1m(365, 1/4, 1/60)
})Ahora almacenamos todas las simulaciones, calculamos el resumen de las simulaciones obtenidas (tiempo total de reparación y número de repraciones dentro de cada simulación), y obtnemmos las medidas descriptivas correspondientes (estimadores Monte-Carlo).
simulaciones<-as_tibble(get_mon_arrivals(envs))
salida<-simulaciones %>%
group_by(replication) %>%
# Resumen de las simualciones
summarise(nreparaciones = n(),
tiempoparada = sum(activity_time)) %>%
summarise(mmedia_nrepara = mean(nreparaciones),
min_nrepara = min(nreparaciones),
max_nrepara = max(nreparaciones),
media_taveria = mean(tiempoparada),
q25_taveria = quantile(tiempoparada, 0.25),
q50_taveria = quantile(tiempoparada, 0.50),
q75_taveria = quantile(tiempoparada, 0.75),
sd_taveria = sd(tiempoparada)
)
salida## # A tibble: 1 × 8
## mmedia_nrepara min_nrepara max_nrepara media_taveria q25_taveria q50_taveria
## <dbl> <int> <int> <dbl> <dbl> <dbl>
## 1 5.81 1 17 20.8 11.8 18.8
## # … with 2 more variables: q75_taveria <dbl>, sd_taveria <dbl>Tenemos una media de 21.3 días de máquina en reparación lo que proporciona un beneficio de:
(365-salida$media_taveria)*100 - salida$media_taveria*1500## [1] 3299.58En la peor situación (mayor número de días con la máquina en reparación = escenario pesismista) podríamos utilizar el cuantil 75 de los tiempos de reparación, mientras que en la mejor situación utilizaríamos el cuantil 25 (escenario optmista), de forma que el beneficio estimado vendrá dado por:
(365-salida$q75_taveria)*100 - salida$q75_taveria*1500## 75%
## -7261.455(365-salida$q25_taveria)*100 - salida$q25_taveria*1500## 25%
## 17559.92¿ qué conclusiones podemos extraer de este análisis?
Pra finalizar este apartado presentamos un nuevo ejemplo donde el espacio de estados está compuesto por una pareja de valores y no por un único valor como en los ejemplso que hemos prsentado hasra ahora.
::: {.example #excmtc006 name = “Mantenimiento aeronaves”}
Una empresa de manteniento de aeronaves está interesado en el proceso de avería-repación de cierto tipo de aviones. El tipo de avión de interés es Un avión comercial a reacción con cuatro motores, dos en cada ala. Cuando un motor se enciende el tiempo que se puede mantener en funcionamiento hasta que falla es una variable aleatoria exponencial con parámetro \(\lambda\). Si el fallo se produce en vuelo, no puede haber reparación, pero el avión necesita al menos un motor en cada ala para funcionar correctamente y poder volar con seguridad. En concreto, la empresa está interesada en poder predecir la probabilidad de un vuelo sin problemas.
Si denotamos por \(X_L(t)\) y \(X_R(t)\) el número de motores funcionando en el instante \(t\) en el ala izquierada y el ala derecha respectivamente, podemos considerar el estado del sistema en el instante \(t\) como \(X(t) = (X_L(t), X_R(t))\). Si asumimos que los fallos en los motores son independientes entre si podemos ver que el proceo \(\{X(t), t \geq 0\}\) es una CMTC con espacio de estados:
\[S = \{ (0, 0), (0, 1), (0, 2), (1, 0), (1, 1), (1, 2), (2, 0), (2, 1), (2,2) \}\]
En esta situación el avión sigue funcionando en el subconjunto de estados \[S = \{ (1, 1), (1, 2), (2, 1), (2,2) \}\] :::
Vamos a asumir (aunque no es real) que el sistema sigue funcionando, incluso cuando hay posibilidad de un accidente, hasta que llegamos al estado \((0, 0)\). Dado que no hay reparación posible la matriz de tasas entre estados del sistema viene dada por
\[R = \begin{pmatrix} 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \lambda & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 2\lambda & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \lambda & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & \lambda & 0 & \lambda & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & \lambda & 0 & 2\lambda & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 2\lambda & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 2\lambda & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 2\lambda & 0 & 2\lambda & 0 \end{pmatrix} \]
y el diagrama viene dado por:
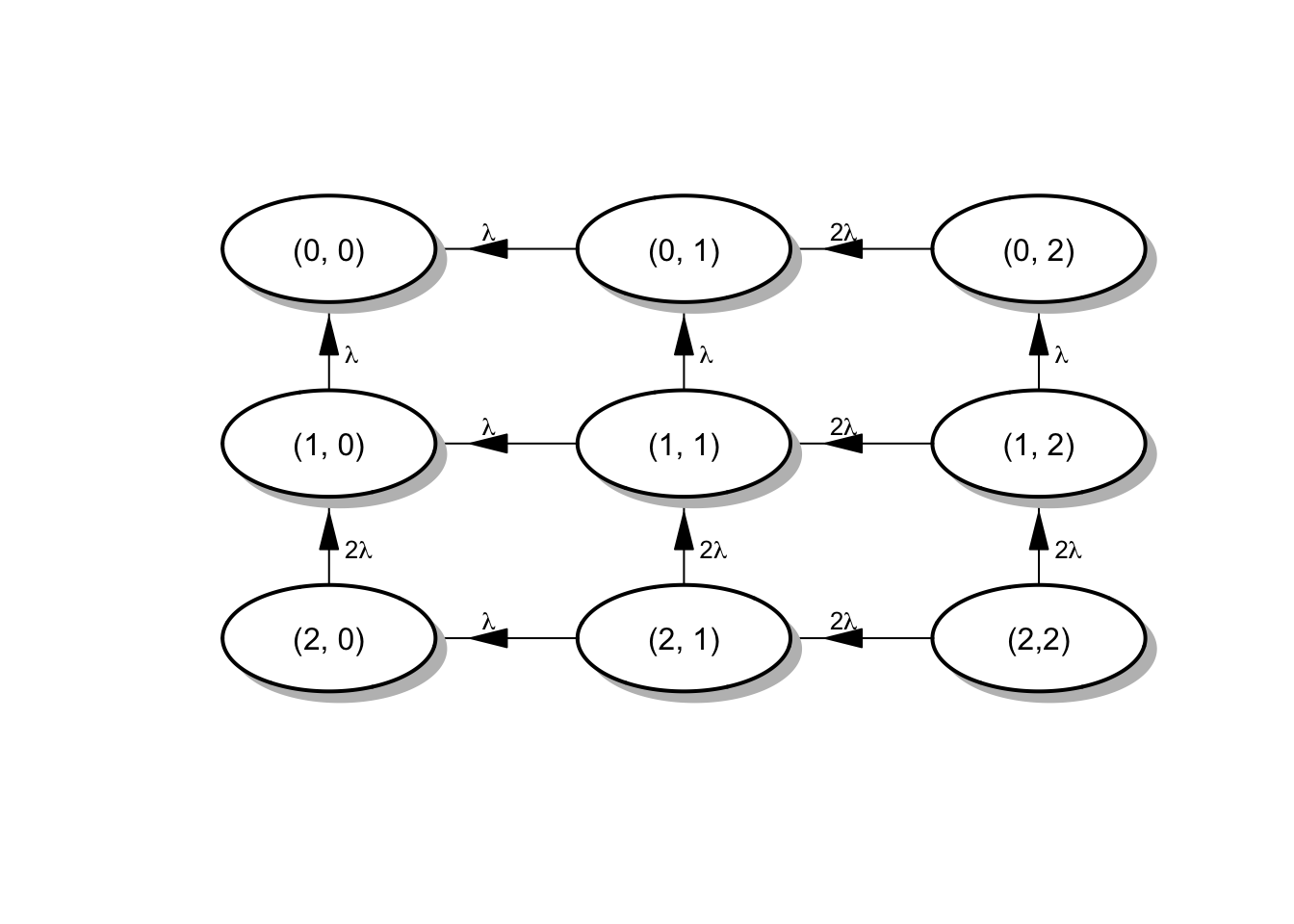
Figura 4.4: Diagrama de tasas para el sistema motores de aviones
Para facilitar el algoritmo de simulación en esta situación vamos a asignar un código a cada uno de los posibles estados del sistema:
\[S = \{ 1 = (0, 0), 2 = (0, 1), 3 = (0, 2), 4 = (1, 0), 5 = (1, 1), 6 = (1, 2), 7 = (2, 0), 8 = (2, 1), 9 = (2,2) \}\] y asumimos que la media del tiempo hasta que un motor falla cuando esta encendido es de 20 horas, es decir, \(\lambda = 1/20\). A continuación tenemos la función necesaria para simular el sistema descrito:
TSIM_aviones <- function(tasa)
{
# Parámetros de la función
# =========================
# tasa: tasa de fallo de un motor
# Valores fijos del sistema
# codigos de motores funcionando obviando el estado inicial
codigo <- 1:8
# motores con fallo de acuerdo al código
motoresOFF <- c(4, 3, 2, 3, 2, 1, 2, 1)
# inicialización de parámetros del sistema
tiempo = estado = fallos = vector()
i<-1
# Primer fallo
# Posibles estados de salto
saltos = c(codigo[6], codigo[8])
# tiempos asociados a cada fallo
simula = rexp(2, 2*tasa)
# Seleccionamos el salto
posicion = which.min(simula)
if(posicion == 1)
{
estado[i] <- saltos[posicion]
tiempo[i] <- simula[posicion]
fallos[i] <- motoresOFF[saltos[posicion]]
# nuevo salto
i <- i + 1
saltos = c(codigo[3], codigo[5])
simula = c(rexp(1, tasa), rexp(1, 2*tasa))
posicion = which.min(simula)
if(posicion == 1)
{
estado[i] <- saltos[posicion]
tiempo[i] <- simula[posicion]
fallos[i] <- motoresOFF[saltos[posicion]]
# dos últimos saltos
estado[i+1] <- 2; estado[i+2] <- 1
tiempo[i+1] <- rexp(1, 2*tasa); tiempo[i+2] <- rexp(1, tasa)
fallos[i+1] <- motoresOFF[estado[i+1]]; fallos[i+2] <- motoresOFF[estado[i+2]]
}
else
{
estado[i] <- saltos[posicion]
tiempo[i] <- simula[posicion]
fallos[i] <- motoresOFF[saltos[posicion]]
# dos últimos saltos
estado[i+1] <- 2; estado[i+2] <- 1
tiempo[i+1] <- rexp(1, tasa); tiempo[i+2] <- rexp(1, tasa)
fallos[i+1] <- motoresOFF[estado[i+1]]; fallos[i+2] <- motoresOFF[estado[i+2]]
}
}
else
{
estado[i] <- saltos[posicion]
tiempo[i] <- simula[posicion]
fallos[i] <- motoresOFF[saltos[posicion]]
# nuevo salto
i <- i + 1
saltos = c(codigo[7], codigo[5])
simula = c(rexp(1, tasa), rexp(1, 2*tasa))
posicion = which.min(simula)
if(posicion == 1)
{
estado[i] <- saltos[posicion]
tiempo[i] <- simula[posicion]
fallos[i] <- motoresOFF[saltos[posicion]]
# dos últimos saltos
estado[i+1] <- 2; estado[i+2] <- 1
tiempo[i+1] <- rexp(1, 2*tasa); tiempo[i+2] <- rexp(1, tasa)
fallos[i+1] <- motoresOFF[estado[i+1]]; fallos[i+2] <- motoresOFF[estado[i+2]]
}
else
{
estado[i] <- saltos[posicion]
tiempo[i] <- simula[posicion]
fallos[i] <- motoresOFF[saltos[posicion]]
# dos últimos saltos
estado[i+1] <- 2; estado[i+2] <- 1
tiempo[i+1] <- rexp(1, tasa); tiempo[i+2] <- rexp(1, tasa)
fallos[i+1] <- motoresOFF[estado[i+1]]; fallos[i+2] <- motoresOFF[estado[i+2]]
}
}
# Devolvemos resultados del sistema
res <- tibble(estado, tiempo, fallos)
return(res)
}Veamos una simulación del sistema:
set.seed(12)
tasa <- 1/20
sistema <- TSIM_aviones(tasa)
sistema## # A tibble: 4 × 3
## estado tiempo fallos
## <dbl> <dbl> <dbl>
## 1 8 6.36 1
## 2 7 2.35 2
## 3 2 18.2 3
## 4 1 5.67 4El resultado obtenido es el estado en cada paso del algoritmo hasta llegar a la parada total, los tiempos para alcanzar cada estado, y el número de motores con fallo. Podemos operar los tiempos para saber cuando alcanzaremos más de dos motores con fallo (últimas dos filas de la simulación). Si el vuelo que acabamos de empezar es de x horas ¿cómo podemos estimar la probabilidad de no poder terminar el vuelo de forma segura? En este caso podemos calcular la proporción de tiempo que corresponde con un fallo leve (1 o 2 motores con fallo) con respecto a las x horas de duración del vuelo.
Calculamos el tiempo de fallo del sistema y evaluamos la probabildiad para diferentes tiempos de duración de vuelo
# Tiempo de fallo
Tfallo <- round(sum(sistema$tiempo[sistema$fallos <= 2]), 2)
# Duración del vuelo
td <- seq(0.1, 12, by = 0.1)
prob <- vector()
# Probabilidad viaje seguro
for(i in 1:length(td))
{
prob[i] <- ifelse(Tfallo >= td[i], 1, round(Tfallo/td[i], 3))
}
# Obtenemos el valor mínimo de tiempo para asegurar un viaje seguro
limite <- min(td[which(prob != 1)])
limite## [1] 8.8Cualquier viaje inferior a 8.8 horas será un viaje seguro, mientras que si el tiempo es susperior la probabilidad de no tener un viaje seguro va aumentando.
Para estudiar la estabildiad de dichas probabilidades realizamos 1000 simulaciones del sistema y estimamos dichas probabilidades mediante estimadores Monte-Carlo de los tiempos de fallo.
nsim <- 1000
Tfallo <- vector()
# Repetición del sistema y calculo de tiempo
for(i in 1:nsim)
{
sistema <- TSIM_aviones(tasa)
Tfallo[i] <- round(sum(sistema$tiempo[sistema$fallos <= 2]), 2)
}
# Estimador Monte-Carlo
estimMC<- mean(Tfallo)
# Duración del vuelo
td <- seq(0.1, 20, by = 0.1)
prob <- vector()
# Probabilidad viaje seguro
for(i in 1:length(td))
{
prob[i] <- ifelse(estimMC >= td[i], 1, round(estimMC/td[i], 3))
}
# Obtenemos el valor mínimo de tiempo para asegurar un viaje seguro
limite <- min(td[which(prob != 1)])
limite## [1] 11.9Cualquier viaje inferior a 11.9 horas será un viaje seguro, mientras que si el tiempo es susperior la probabilidad de no tener un viaje seguro va aumentando. Podemos representar el gráfico de probabilidad de un viaje seguro:
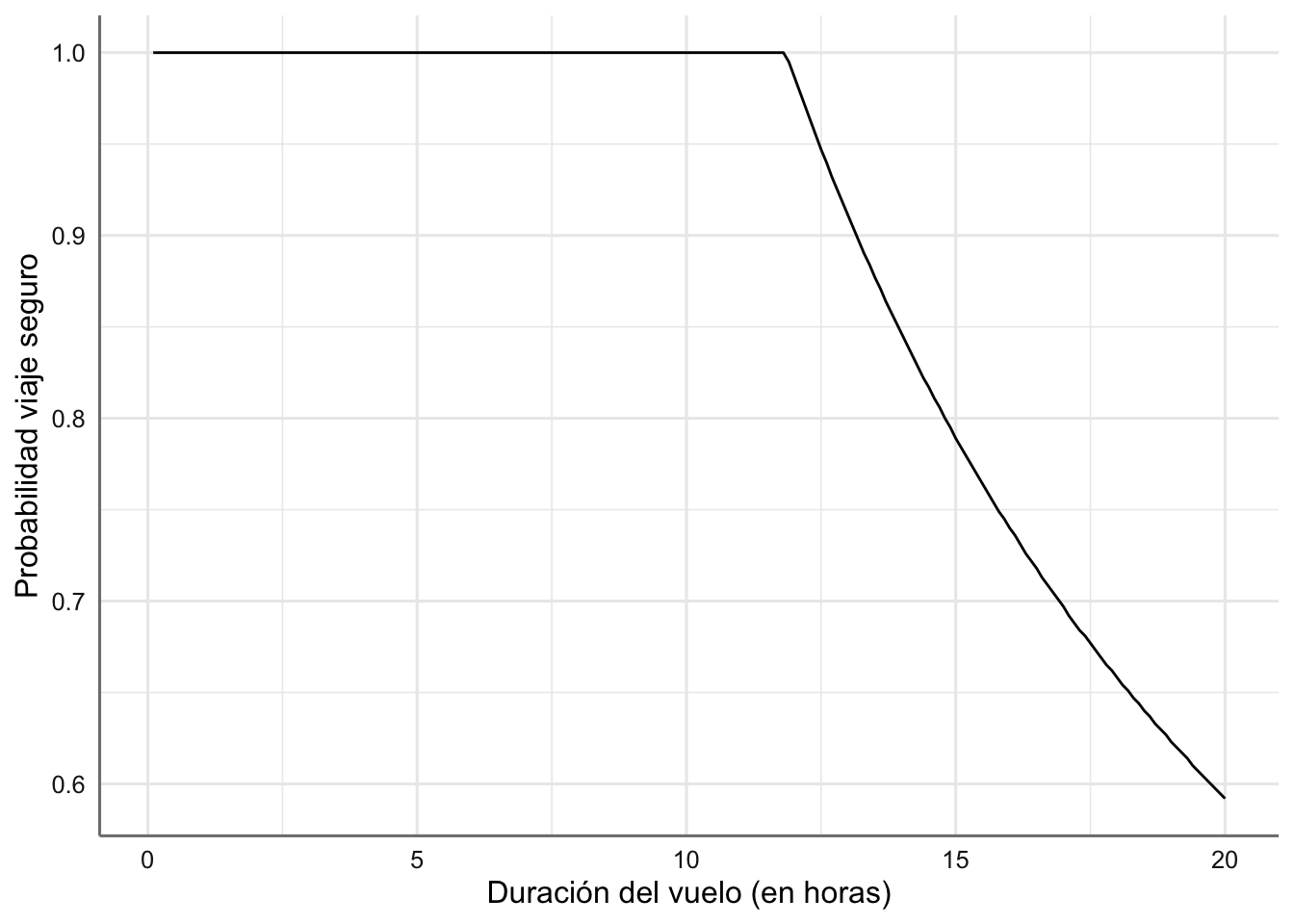
Figura 4.5: Probabilidad de un viaje seguro