2.2 Librería markovchain

Para trabajar con procesos \(CMTD\) con R es útil la librería markovchain (Spedicato et al. 2021). Trabajamos a continuación sobre un problema sencillo, para crear la matriz y el diagrama de transición de la cadena de Markov.

Ejemplo 2.1 Tenemos una \(CMTD\) \(\{X(t), t \in \mathbb{N}\}\) con espacio de estados \(S = \{a, b, c\}\) y distribución inicial de la cadena dada por \(p_a(0)=0.4, p_b(0)=0.2\) y \(p_c(0)=0.4\). La matriz de transición de un paso viene dada por:

\[P = \begin{pmatrix} 0.20 & 0.30 & 0.50\\ 0.10 & 0.00 & 0.90\\ 0.55 & 0.00 & 0.45 \end{pmatrix}\]

Planteamos resolver las cuestiones siguientes:

(1). Queremos representar el proceso a través de un grafo.

Para representar el proceso con markovchain, hemos de crear un vector con los estados y la matriz de transición con las probabilidades de transición. Definimos entonces el proceso con la función genérica new() para generar un objeto del tipo markovchain: \[new("markovchain",states,byrow=TRUE,transitionMatrix)\]

introduciendo el vector de estados en states, la matriz de transición en transitionMatrix, y especificando si dicha matriz se ha de leer por filas.

A continuación lo pintamos con la función plot().

Procedemos con el ejemplo que nos atañe. El grafo en la Figura 2.1 muestra los tres estados como nodos y las probabilidades de transición para pasar de un estado a otro en un único paso.

require(markovchain)
# Definimos estados
estados <- c("a", "b", "c")
# Creamos la matriz de transición 
pmat <- matrix(data = c(0.20, 0.30, 0.50, 0.10, 0.00, 0.90,0.55, 0.00, 0.45), 
               byrow = TRUE, nrow = 3, 
               dimnames = list(estados, estados))
# Creamos la CMTD
proceso <- new("markovchain", states = estados, 
               byrow = TRUE, transitionMatrix = pmat)
# Verificamos los datos introducidos
proceso

## Unnamed Markov chain 
##  A  3 - dimensional discrete Markov Chain defined by the following states: 
##  a, b, c 
##  The transition matrix  (by rows)  is defined as follows: 
##      a   b    c
## a 0.20 0.3 0.50
## b 0.10 0.0 0.90
## c 0.55 0.0 0.45

# y obtenemos el diagrama del proceso
plot(proceso)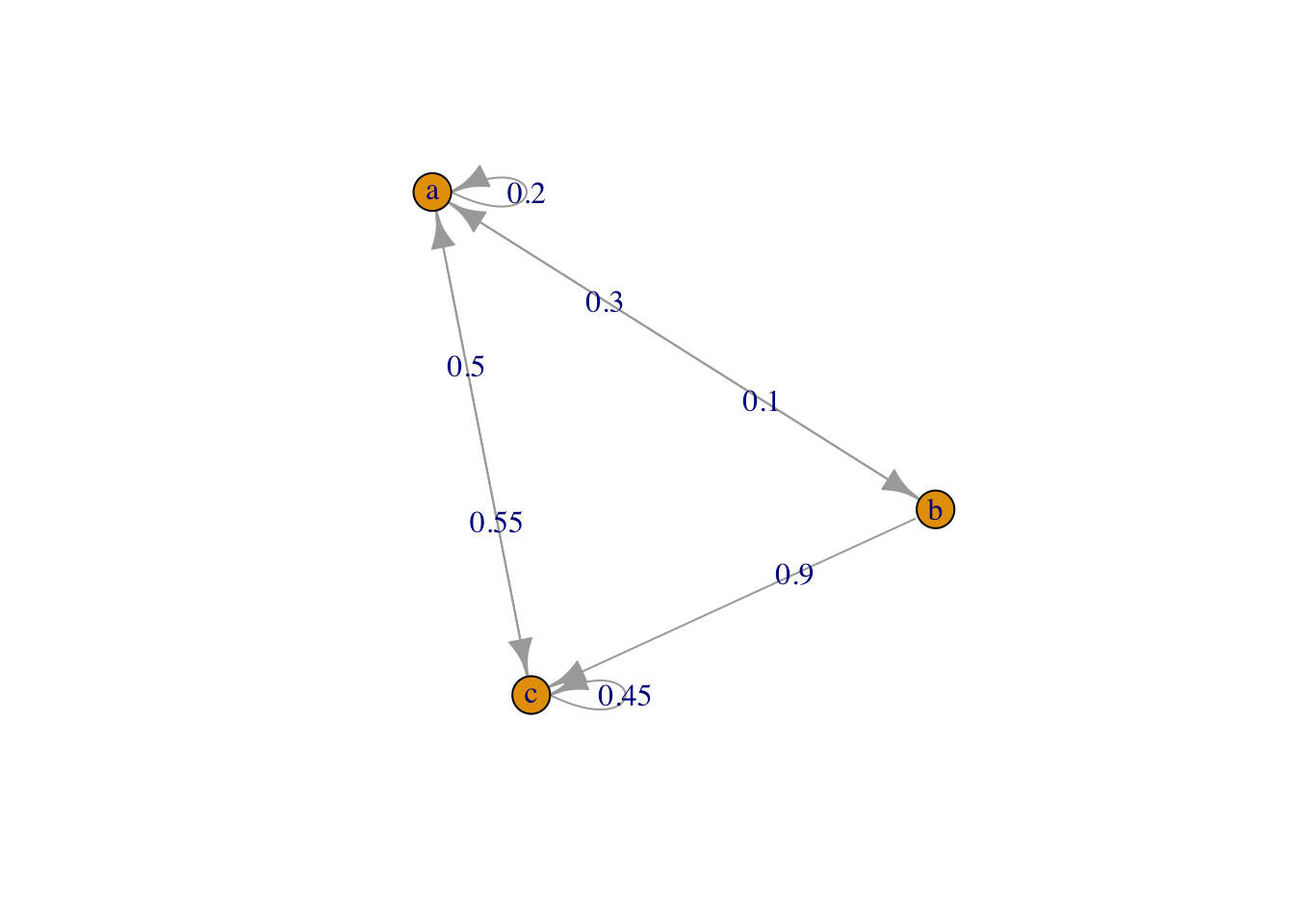

Figura 2.1: Grafo del proceso.

(2). Si la \(CMTD\) está en el estado \(c\) en el momento 17, ¿cuál es la probabilidad de que esté en el estado \(a\) en el momento 18?

RESPUESTA: Nos preguntan por la probabilidad de transición para pasar, en un solo paso, del estado \(c\) (3) al estado \(a\) (1), por lo que viene dada por la componente \(p_{31}\) de la matriz de transición, es decir, 0.55.

Para resolver el cálculo con el ordenador basta utilizar la función transitionProbability(), con los argumentos: object (la cadena de markov), t0 (el estado en el instante inicial), t1 (el estado en el instante final).

Así la pregunta (2) se responde con:

transitionProbability(object = proceso, t0 = "c", t1 = "a")

## [1] 0.55

(3). Si la \(CMTD\) está en el estado \(c\) en un momento dado, ¿cuál es la probabilidad de que esté en el estado \(a\) transcurridos tres unidades de tiempo? ¿y después de 10?

RESPUESTA: Para resolver esta cuestión definimos el estado inicial y lo multiplicamos por la matriz de transición que corresponda, que en este caso, aplicando la Ecuación (2.5), será \(P^n\), para \(n=3\) y \(n=10\). Obtendremos así la distribución de probabilidad en \(n\) transiciones, con la probabilidad de llegar a cada uno de los eventos posibles, \(\{a,b,c\}\) en \(n\), partiendo de un estado inicial dado.

# Estado inicial en c
sini <- c(0, 0, 1)
# matriz de transición de 3 pasos
mt3 <- proceso^3
# Situación del proceso dentro de 3 instantes
sini*mt3

##             a       b        c
## [1,] 0.350625 0.10725 0.542125

# matriz de transición de 10 pasos
mt10 <- proceso^10
# Situación del proceso dentro de 10 instantes
sini*mt10

##              a         b         c
## [1,] 0.3703899 0.1110948 0.5185153

(4). ¿Cuál es la distribución de probabilidad del proceso transcurridos \(10\) instantes de tiempo desde el momento inicial del proceso, sea cual sea su estado?

RESPUESTA: Si conocemos la distribución de probabilidad en el estado inicial, \(p(0)\), podemos obtener la distribución de probabilidad en \(n\) transiciones con la Ecuación :

### Distribución de probabilidad del proceso dentro de 10 instantes
# Distribución de  probabilidad inicial
dini <- c(0.4, 0.2, 0.4)
# matriz de transición de 10 pasos
mt10 <- proceso^10
# distribución de probabilidad en 10 pasos
dini*mt10

##             a         b         c
## [1,] 0.370364 0.1111134 0.5185226

En base a la distribución del proceso tras \(n=10\) pasos, apreciamos que lo más probable es que el sistema se ecuentre en el estado “c” (prob=0.52), y lo menos probable es que se encuentre en el estado “b” (prob=0.11).

(5). Corroborar los resultados analíticos obtenidos en (4) con simulaciones.

RESPUESTA: Para ver el comportamiento de un proceso después de que transcurran \(n\) pasos habrá que simularlo durante \(n\) instantes de tiempo. Puesto que buscamos una estimación de lo que va a ocurrir en ese momento, simularemos \(nsim=100\) veces el proceso hasta el instante \(n=10\), nos quedaremos con el estado en que se encuentra el proceso en ese instante \(n\) y evaluaremos las probabilidades obtenidas para los tres estados \(\{a,b,c\}\). Los resultados serán más próximos a la solución analítica, cuanto mayor sea el número de simulaciones (prueba a modificar \(nsim\)).

Para simular una CMTD hasta una transición \(n\) con la librería markovchain basta utilizar la función rmarkovchain(n, proceso), donde proceso ha sido definido previamente con la función new().

### Simulación del proceso para n=10 instantes 
res=vector()
nsim=100
n=10
for(i in 1:nsim){
  res[i]=rmarkovchain(n, proceso)[n]}
prop.table(table(res))

## res
##    a    b    c 
## 0.44 0.04 0.52

References

Spedicato, Giorgio Alfredo, Tae Seung Kang, Sai Bhargav Yalamanchi, Deepak Yadav, and Ignacio Cordón. 2021. Markovchain: Easy Handling Discrete Time Markov Chains. https://github.com/spedygiorgio/markovchain/.