4.4 Procesos de nacimiento y muerte
Los procesos de nacimiento y muerte que estudiamos en este apartado juegan un pael muy importante dentro de las CMTC ya que son de uso habitual en muchas aplicaciones prácticas que veremos de ahora en adelante.
Definición 4.2 Una CMTC \(\{X_t; t \geq 0\}\) con espacio de estados \(S = \{0, 1, 2,...,K\}\) y matriz de tasas dad por:
\[R = \begin{pmatrix} 0 & \lambda_0 & 0 & 0 & \ldots & 0 & 0 \\ \mu_1 & 0 & \lambda_1 & 0 & \ldots & 0 & 0 \\ 0 & \mu_2 & 0 & \lambda_2 & \ldots & 0 & 0 \\ \vdots & \vdots & \vdots & \vdots & \ldots & \vdots & \vdots \\ 0 & 0 & 0 & 0 & \ldots & 0 & \lambda_{k-1} \\ 0 & 0 & 0 & 0 & \ldots &\mu_k & 0 \end{pmatrix} \]
se denomina proceso finito de nacimiento y muerte donde los \(\lambda_i\) se denominan parámetros de nacimiento (transición del estado \(i\) al \(i+1\)) y los \(\mu_i\) se denominan parámetros de muerte (transición del estado \(i\) al \(i-1)\), donde ppr conveniencia se asume que \(\lambda_k = 0\) y \(\mu_0 = 0\) indicando que no hya nacimientos en el estado \(K\) y que no hay muertes en el estado \(0\).
En esta situación el proceso permanece una cantidad de tiempo \(exp(\lambda_i + \mu_i)\) en el estado \(i\) y entonces salta al estado \(i+1\) con probabilidad \(\lambda_i/(\lambda_i + \mu_i)\), o al estado \(i-1\) con probabilidad \(\mu_i/(\lambda_i + \mu_i)\). Además, la matriz generadora del proceso viene dada por:
\[R = \begin{pmatrix} - \lambda_0& \lambda_0 & 0 & 0 & \ldots & 0 & 0 \\ \mu_1 & -(\mu_1 + \lambda_1) & \lambda_1 & 0 & \ldots & 0 & 0 \\ 0 & \mu_2 & -(\mu_2 + \lambda_2) & \lambda_2 & \ldots & 0 & 0 \\ \vdots & \vdots & \vdots & \vdots & \ldots & \vdots & \vdots \\ 0 & 0 & 0 & 0 & \ldots & -(\mu_{k-1} + \lambda_{k-1}) & \lambda_{k-1} \\ 0 & 0 & 0 & 0 & \ldots & \mu_k & -\mu_k \end{pmatrix} \]
A continuación presentamos diferentes ejemplos de aplicación de los procesos de nacimiento y muerte.
4.4.1 Colas de espera de capacidad finita con un servidor
Aunque en la unidad siguiente estudiaremos con mucho más detalle los diferentes sistemas de colas de espera, vamos a presentar aquí el mmodelo más sencillo para ver que se puede modelar como un procedimiento de nacimiento y muerte.
Imaginemos que tenemos un cajero bancario al que los clientes acuden de acuerdo a Proceso de Poisson de parámetro \(\lambda\), es decir que las llegadas son aleatorias y se distribuyen según una \(Exp(\lambda)\). Si hay \(K-1\) clientes haciendo cola para ser atendidos, un cliente nuevo tomará la opción de buscar otro cajero, es decir, el sisetma tiene capacidad \(K\) (1 cliente atendido y \(K-1\) en la cola de espera). Además, el tiempo de servicio del cajero es una nueva variable aleatoria \(Exp(\mu)\).
En esta situación la variable \(X(t)\) que indica el número de sujetos en el sistema en el instante \(t\) es una CMTC denominada cola \(M/M/1/K\), donde \(M\) hace referencia a los tiempos de llegada y servicio exponenciales, el \(1\) hace referencia a la capacidad del servicio, \(K\) el tamaño del sistema, y con espacio de estados \(S = \{0, 1, 2,...K \}\). Este tipo de sistemas son procesos de nacimiento y muerte con:
\[\lambda_i = \lambda, \quad 0 \leq i \leq K-1,\]
\[\mu_i = \mu, \quad 0 \leq i \leq K,\]
donde el “nacimiento” y la “muerte” hacen referencia a la llegada al cajero y la salida del cajero respectivamente.
Veamos la descripción del sistema:
En el estado 0, el sistema está vacío y el único evento que puede ocurrir es una llegada, que se produce después de un tiempo \(Exp(\lambda)\) provocando una transición al estado 1. En este caso \(r_{01} = \lambda\).
En el estado \(i\) (\(1 \leq i \leq K-1\)), tenemos dos posibilidades en el sitema: una llegada o una salida. En el primer caso tenemos \(r_{i i+1} = \lambda\), mientras que en el segundo tenemos \(r_{i i-1} = \mu\).
En el estado \(K\) sólo se puede producir una salida de forma que \(r_{K K-1} = \mu\).
Por tanto, la matriz de tasas correspondiente a este proceso viene dada por:
\[R = \begin{pmatrix} 0 & \lambda & 0 & 0 & \ldots & 0 & 0 \\ \mu & 0 & \lambda & 0 & \ldots & 0 & 0 \\ 0 & \mu & 0 & \lambda & \ldots & 0 & 0 \\ \vdots & \vdots & \vdots & \vdots & \ldots & \vdots & \vdots \\ 0 & 0 & 0 & 0 & \ldots & 0 & \lambda \\ 0 & 0 & 0 & 0 & \ldots &\mu & 0 \end{pmatrix} \]
El diagrama de tasas para una cola \(M/M/1/4\), es decir con una capacidad de 4 usuarios en el sistema (1 atendido y tres en espera) es:
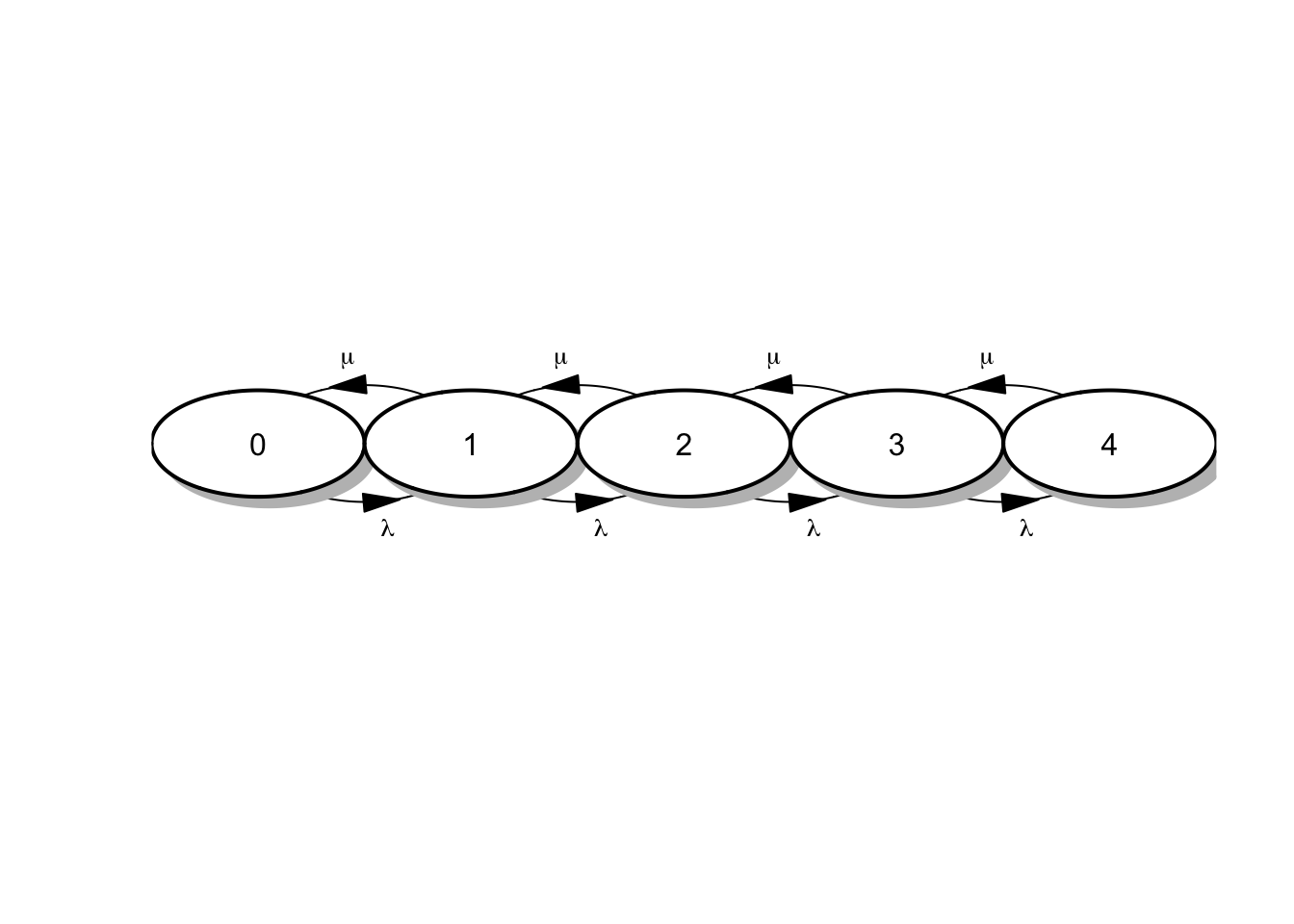
Figura 4.6: Diagrama de tasas para cola M/M/1/4.
Este sistema puede implementarse fácilmente en simmer si entendemos como “resource” al servicio del cajero y como “generator” la llegada al cajero. Escribimos el algoritmo de forma general para cualquier valor de \(K\).
# Sistema
#################################################
cola.MM1K <- function(t, lambda, mu, servidores, usuarios)
{
# lambda: tasa de llegadas
# mu: tasa de servicio
# servidores: número de servidores
# usuarios: capacidad total del sistema
cola <- usuarios - servidores
servicio <- trajectory() %>%
seize("atendiendo", amount = 1) %>%
timeout(function() rexp(1, mu)) %>%
release("atendiendo", amount = 1)
# Configuración del sistema
#################################################
simmer() %>%
add_resource("atendiendo", capacity = servidores, queue_size = cola) %>%
add_generator("llegada", servicio, function() rexp(1, lambda)) %>%
run(until = t)
}Imaginemos que por la mañanas (de 8 a 15) las llegadas de clientes se producen con una tasa de 15 clientes/hora, mientras que el tiempo medio que el cliente permanece en el cajero es de 6 minutos. Expresando en minutos tendríamos una tasa de llegadas \(\lambda = 15/60\), y una tasa de servicio \(\mu = 1/6\). Se ha observado además que cuando la cola de espera es de tres clientes nadie más espera para hacer cola (\(K = 4\)). Analizamos el sistema de forma básica para una mañana cualquiera, es decir para un periodo de 7 horas (420 minutos).
set.seed(12)
### Simulación del sistema
cajero <- cola.MM1K(420, 15/60, 1/6, 1, 4)
### Salidas del sistema
cajero.df.res <- get_mon_resources(cajero)
cajero.df.arr <- get_mon_arrivals(cajero)Veamos con un poco de detalle las salidas que porporciona el sistema. Comenzamos con el proceso de llegadas al sistema viendo las primeras 10 llegadas al sistema:
head(cajero.df.arr, n = 10)## name start_time end_time activity_time finished replication
## 1 llegada0 8.756865 9.461164 0.704299 TRUE 1
## 2 llegada1 11.299066 22.198513 10.899446 TRUE 1
## 3 llegada2 22.728061 46.307530 23.579469 TRUE 1
## 4 llegada7 53.191599 53.191599 0.000000 FALSE 1
## 5 llegada3 23.861384 53.496376 7.188846 TRUE 1
## 6 llegada9 57.528321 57.528321 0.000000 FALSE 1
## 7 llegada4 40.759227 59.558394 6.062018 TRUE 1
## 8 llegada11 68.130173 68.130173 0.000000 FALSE 1
## 9 llegada12 74.418248 74.418248 0.000000 FALSE 1
## 10 llegada5 45.814971 75.428935 15.870541 TRUE 1En la columna name tenemos el identificador de la llegada a sistema, en las columnas star_time y end_time tenemos el instante de tiempo de acceso al cajero y el tiempo en que salimos del sistema (abandonamos el cajero). En la columna activity_time tenemos el tiempo de servicio, donde le valor 0 son los clientes que han llegado al cajero pero no ha sido atendidos porque se ha sobrepasado la capacidad del sistema. Estos coinciden con los valores FALSE de la columna finished, que indica los clientes que no han podido ser atendidos por el sistema. Con estas salida resulta muy fácil calcular el tiempo de servicio del sistema así como el porcentaje de clientes rechazados, y el tiempo esperando en la cola.
# llegadas al sistema
nsis <- nrow(cajero.df.arr)
# tiempo total de servicio
tserver <- sum(cajero.df.arr$activity_time)
# propoción de tiempo que el sistema está ocupado (atendiendo o en espera)
round(100*tserver/420,2)## [1] 97.14# porcentaje de clientes rechazados
rechazados <- nrow(cajero.df.arr[cajero.df.arr$finished == FALSE,])
round(100*rechazados/nsis,2)## [1] 48.15# Tiempo medio de espera
tespera <- mean(cajero.df.arr$end_time - cajero.df.arr$start_time - cajero.df.arr$activity_time)
tespera## [1] 8.280251Para ser más sofisticados podríamos calcular el tiempo medio en espera en función de los clientes en la cola, o lo que sería más fácil estudiar dichas cantidades mediante un gráfico, pero para ello necesitamos trabajar con el comportamiento de la cola. Veamos dicho comportamiento:
head(cajero.df.res, n = 10)## resource time server queue capacity queue_size system limit
## 1 atendiendo 8.756865 1 0 1 3 1 4
## 2 atendiendo 9.461164 0 0 1 3 0 4
## 3 atendiendo 11.299066 1 0 1 3 1 4
## 4 atendiendo 22.198513 0 0 1 3 0 4
## 5 atendiendo 22.728061 1 0 1 3 1 4
## 6 atendiendo 23.861384 1 1 1 3 2 4
## 7 atendiendo 40.759227 1 2 1 3 3 4
## 8 atendiendo 45.814971 1 3 1 3 4 4
## 9 atendiendo 46.307530 1 2 1 3 3 4
## 10 atendiendo 48.326016 1 3 1 3 4 4
## replication
## 1 1
## 2 1
## 3 1
## 4 1
## 5 1
## 6 1
## 7 1
## 8 1
## 9 1
## 10 1En este caso las variables nos indican el tiempo en el que se produce alguna actividad en el sistema (columna time), si el usuario está en el sistema (valores 0-1 indicando si esta fuera o dentro) en la variable server, el número de clientes en la cola de espera (columna queue), la capacidad de servicio del sistema (columna capacity), el tamaño máximo de la cola (columna queue_size), el número de clientes en el sistema (columna system), la capacidad total de sistema (columna limit), y un indicador de la replicación del sistema.
Con estas salidas podemos describir fácilmente el comportamiento de la cola del sistema ya que podemos estudiar el número de clientes en cola a lo largo del tiempo.
# Evolución del tamaño de la cola
ggplot(cajero.df.res, aes(time, queue)) +
geom_step() +
scale_x_continuous(breaks = seq(0, 420, 60)) +
labs(x = "Tiempo (en minutos)", y = "Tamaño de la cola")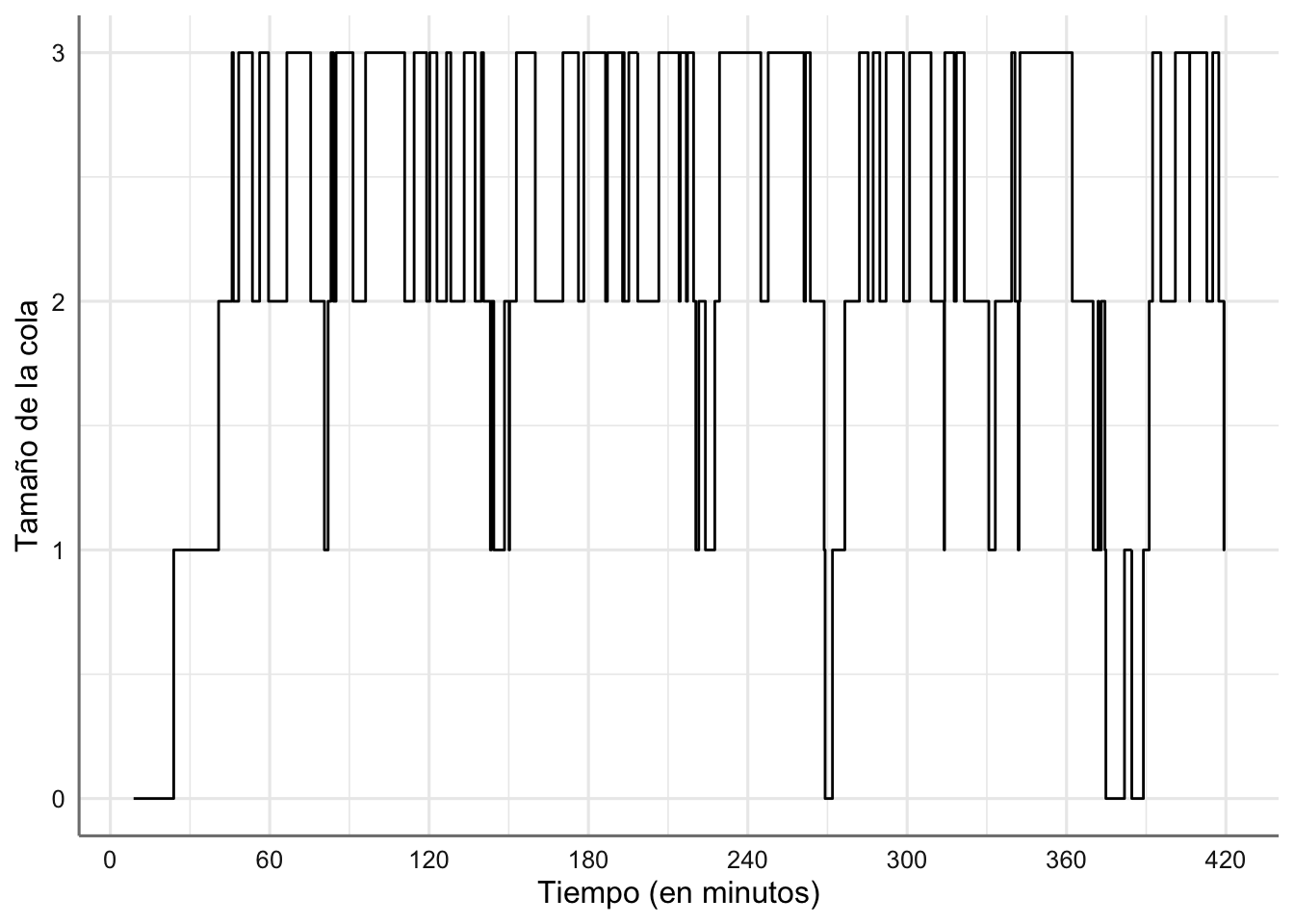
# Porcentaje de clientes en cola
ggplot(cajero.df.res, aes(x = queue)) +
geom_bar(aes(y = ..prop.. , group = 1)) +
scale_y_continuous(labels = scales::percent) +
labs(x = "Clientes en la cola", y = "Porcentaje")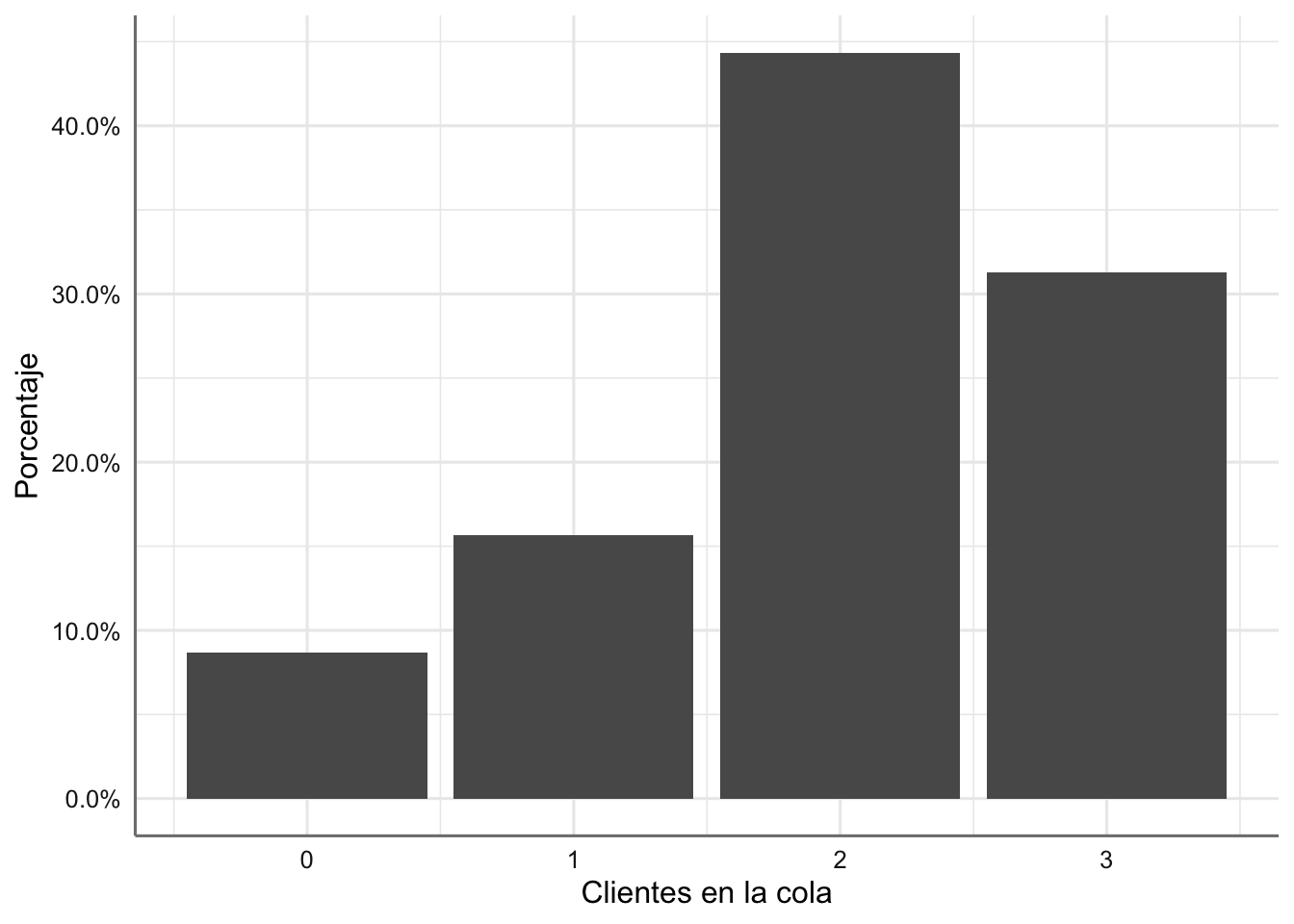
Simulamos ahora el sistema en 500 ocasiones para estudiar la estabildiad de los descriptivos obtenidos.
# Réplicas del sistema
replicas <- 500
envs <- lapply(1:replicas, function(i){
repcajero <- cola.MM1K(420, 15/60, 1/6, 1, 5)
})
# almacenamos análisis de llegadas del sistema
simarrivals<-as_tibble(get_mon_arrivals(envs))
salida<-simarrivals %>%
group_by(replication) %>%
# Resumen de las simualciones
summarise(clientes = n(),
tiemposervicio = sum(activity_time),
proptiemposervicio = round(tiemposervicio/420, 2),
rechazados = clientes - sum(finished),
proprechazados = round(rechazados/clientes,2)) %>%
summarise(media_clientes = mean(clientes),
media_tserver = mean(tiemposervicio),
media_ptserver = 100*mean(proptiemposervicio),
media_rechazados = mean(rechazados),
media_prechazados = 100*mean(proprechazados)
)
salida## # A tibble: 1 × 5
## media_clientes media_tserver media_ptserver media_rechazados media_prechazados
## <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 102. 387. 92.2 36.0 34.9¿Qué conclusiones extraemos del análsis realizado? ¿cómo valorarías la ocupación del sistema? ¿qué ocuriría si añadimos un nuevo cajero y ampliamos la capacidad del sistema a 8 clientes?
4.4.2 Mantenimiento de máquinas
El problema de mantenimiento de máquinas es muy habitual dentro de las CMTC. Supongamos que disponemos de \(N\) máquinas que funcionana durante 24 horas seguidas y \(M\) personas que pueden reparalas (\(M \leq N\)). Las máquinas son idénticas, y los tiempos de vida de las máquinas (necesitan reparación o mantenimiento) son variables aleatorias independientes \(Exp(\mu)\). Cuando las máquinas fallan, son reparadas en el orden de fallo por los \(M\) reparadores. Cada máquina averiada necesita una y sólo una persona de reparación, y los tiempos de reparación son variables aleatorias independientes \(Exp(\lambda)\), de forma que Una máquina reparada se comporta como una máquina nueva. Si \(X(t)\) el número de máquinas que funcionan en el momento \(t\), el proceso \(\{X(t), t \geq 0\}\) es un proceso de nacimiento y muerte con parámetros:
\[\lambda_i = min(N-i, M)\lambda, \quad 0 \leq i \leq N,\]
\[\mu_i = i\mu, \quad 0 \leq i \leq N,\]
donde el “nacimiento” y la “muerte” hacen referencia a la reparación y al funcionamiento de cada máquina respectivamente.
Imaginemos un problema sencillo, que se puede generalizar fácilmente, donde tenemos 4 máquinas y 2 reparador, de forma que el espacio de estados (número de máquinas en funcionamiento) viene dado por \(S = \{0, 1, 2, 3, 4\}\). En este ejemplo vamos a ver como los parámetros de nacimiento y muerte corresponden con los definidos en el ejemplo ??. Descripción del sistema:
En el estado 0, todas las máquinas están estropeadas, dos se encuentran en reparación y dos esperando a ser reparadas, Los tiempos de reparación son iid \(Exp(\lambda)\) y un vez se complete cualquiera de las dos repaciones el sistema cambiará al estado 1. De esta forma, \(r_{01} = \lambda_0 = \lambda + \lambda = 2\lambda\).
En el estado 1, una máquina está en funcionamiento, hay dos en reparación y otra está en espera. Cuando una de las dos máquinas es reparada pasamos al estado 2. De esta forma, \(r_{12} = \lambda_1 = 2\lambda\). Además, en este estado la máquina que está funcionando puede fallar después de mantenerse en funcionamiento un tiempo \(Exp(\mu)\) volviendo al estado 0, de forma que, \(r_{10} = \mu_1 = \mu\).
En el estado 2, con razonamientos similares tendremos que \(r_{23} = \lambda_2 = 2\lambda\) y \(r_{21} = \mu_2 = 2\mu\).
Para el resto de estados tendremos que \(r_{34} = \lambda_3 = \lambda\), \(r_{32} = mu_3 = 3\mu\), y \(r_{43} = \mu_4 = 4\mu\).
En esta situación el diagrama del proceso vieen dado por:
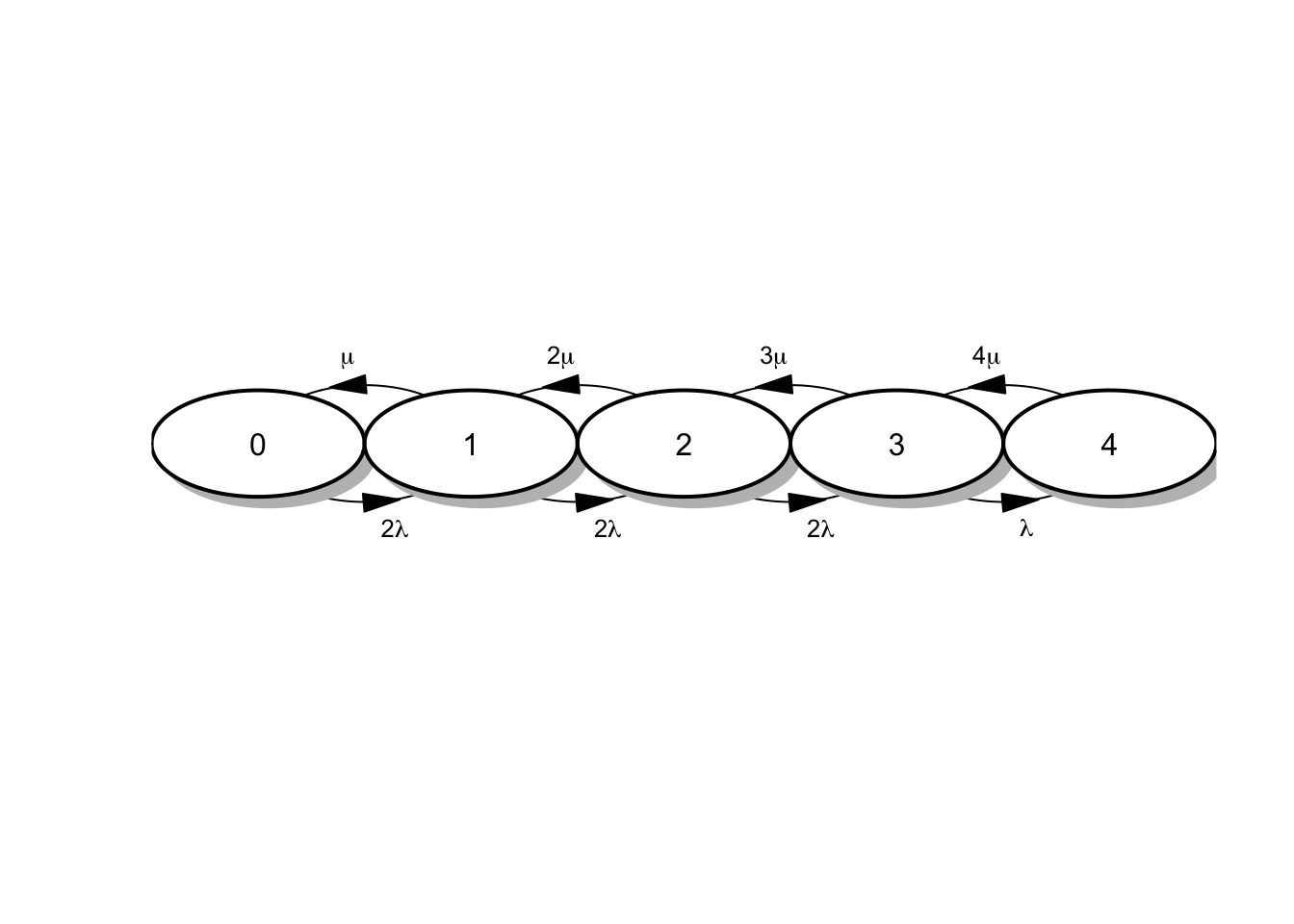
Figura 4.7: Diagrama de tasas para el mantenimiento de máquinas
Este sistema se puede modelizar fácilmente en simmer sin nada más que fijar las tasas correspondientes, el número de máquinas disponibles, y el número de operarios. Supongamos que los tiempos de vida de las máquinas son variables aleatorias exponenciales con media de 3 días, mientras que los tiempos de reparación son variables aleatorias exponenciales con media de 2 horas. Expresando en horas tendríamos una tasa de reparación de \(\lambda = 1/2\), y una tasa de funcionamiento \(\mu = 1/72\).
De nuevo planteamos una función que nos permita cambiar fácilmente los parámetros del sistema si fuera necesario. La empresa está interesada en:
- ¿Cuántas máquinas estarán en funcionamiento después de 3 días?
- ¿cuál es el porcentaje de tiempo en esos tres días que las cuatro máquinas están funcionando?
# Sistema
#################################################
mantenimiento <- function(t, lambda, mu, capacidad)
{
# lambda: tasa de reparación
# mu: tasa de vida de la máquina
# capacidad: reparadores
# K: máquinas
# Distribuciones de tiempos
vida <- function() rexp(1, mu)
reparacion <- function() rexp(1, lambda)
# Trayectoria
maquina <- trajectory() %>%
seize("funcionando") %>%
timeout(vida) %>%
release("funcionando") %>%
seize("reparando") %>%
timeout(reparacion) %>%
release("reparando") %>%
rollback(6)
# Configuración del sistema
simmer() %>%
add_resource("funcionando", capacity = Inf) %>%
add_resource("reparando", capacity = capacidad, queue_size = Inf) %>%
add_generator("sistema", maquina, at(0, 0, 0, 0)) %>%
run(until = t)
}Simulamos el sistema y analizamos un poco la salida. Dado que en este sistema no hay llegadas solo podemos estudiar los recursos.
### Simulación del sistema
maquinas <- mantenimiento(72, 1/2, 1/72, 2)
### Salidas del sistema
maquinas.df.res <- get_mon_resources(maquinas)
head(maquinas.df.res, 10)## resource time server queue capacity queue_size system limit
## 1 funcionando 0.00000 1 0 Inf Inf 1 Inf
## 2 funcionando 0.00000 2 0 Inf Inf 2 Inf
## 3 funcionando 0.00000 3 0 Inf Inf 3 Inf
## 4 funcionando 0.00000 4 0 Inf Inf 4 Inf
## 5 funcionando 15.01074 3 0 Inf Inf 3 Inf
## 6 reparando 15.01074 1 0 2 Inf 1 Inf
## 7 reparando 15.19804 0 0 2 Inf 0 Inf
## 8 funcionando 15.19804 4 0 Inf Inf 4 Inf
## 9 funcionando 16.85568 3 0 Inf Inf 3 Inf
## 10 reparando 16.85568 1 0 2 Inf 1 Inf
## replication
## 1 1
## 2 1
## 3 1
## 4 1
## 5 1
## 6 1
## 7 1
## 8 1
## 9 1
## 10 1Respondemos en primer lugar al número de máquinas en funcionamiento a los tres días
# última iteración del sistema
tail(maquinas.df.res, 1)## resource time server queue capacity queue_size system limit
## 20 funcionando 25.30087 4 0 Inf Inf 4 Inf
## replication
## 20 1A las 72 horas el número de máquinas funcionando se corresponde con el valor de server. Para conocer el tiempo que las cuatro máquinas han estado funcionando debemos manipular los resultados obtenidos en el proceso de simulación.
### Seleccionamos todos los recursos cuando las máquinas están funcionando
maquinas.df.sel <- maquinas.df.res %>%
subset(resource == "funcionando")
### Calculamos los tiempos de funcionamiento
deltas_4 <- diff(maquinas.df.sel$time)
### Seleccionamos cuando las 4 máquinas están activas
both_working_4 <- which(maquinas.df.sel$system == 4)
t_both_working_4 <- deltas_4[both_working_4]
### Caculamos la proporción de tiempo
res<-sum(t_both_working_4, na.rm=TRUE) / max(maquinas.df.sel$time)La proporción de tiempo en que las cuatro máquinas están funcionando simultáneamente es 74. Estudiamos la estabilidad del sistema realizando 500 simulaciones del sistema y estimando las cantidades de interés para la empresa.
# Réplicas del sistema
replicas <- 500
envs <- lapply(1:replicas, function(i){
maquinas <- mantenimiento(72, 1/2, 1/72, 2)
})
# almacenamos análisis de llegadas del sistema
simresources<-as_tibble(get_mon_resources(envs))
## funciones para calcular cantidades de interés
maquinasON <- vector()
propTimeON <- vector()
for (i in 1:500)
{
datos <- simresources[simresources$replication == i,]
# máquinas en funcionamiento
maquinasON[i] <- tail(datos, 1)$server
# Proporción de tiempo
maquinas.df.sel <- datos %>%
subset(resource == "funcionando")
### Calculamos los tiempos de funcionamiento
deltas_4 <- diff(maquinas.df.sel$time)
### Seleccionamos cuando las 4 máquinas están activas
both_working_4 <- which(maquinas.df.sel$system == 4)
t_both_working_4 <- deltas_4[both_working_4]
### Caculamos la proporción de tiempo
propTimeON[i]<-round(100*sum(t_both_working_4, na.rm=TRUE) / max(maquinas.df.sel$time), 2)
}Tenemos entonces que el número de máquinas en funcionamiento es 3.736 y el tiempo de funcionamiento de las cuatro máquinas estimado es 87.38 para un periodo de 72 horas cuando al inicio todas las máquinas están paradas.
4.4.3 Central telefónica
Una centralita telefónica puede atender \(K\) llamadas a la vez en un momento dado. Las llamadas llegan según un proceso de Poisson con tasa \(\lambda\). Si la centralita ya está atendiendo \(K\) llamadas cuando llega una nueva llamada, ésta se pierde. Si una llamada es aceptada, dura un tiempo \(Exp(\mu)\) y luego termina. Todas las llamadas son independientes entre sí. Sea \(X(t)\) el número de llamadas que la centralita gestiona en el momento \(t\).
El proceso \(\{X(t); t \geq 0\}\) es una CMTC con espacio de estados \(S = \{0, 1, 2,...,K\}\) de forma que:
En el estado \(i\), con \(0 \leq i \leq K-1\) la llegada de una llamada desencadena una transición al estado \(i+1\) con tasa \(\lambda\) (\(r_{i i+1} = \lambda\)), mientras que en el estado \(K\) no se pueden recibir llamadas.
En el estado \(i\), con \(1 \leq i \leq K\) cualquiera de las llamadas \(i\) puede completarse y desancedar una transición al estado \(i-1\). La tasa de transición es \(r_{i i-1} = i\mu\). En el estado 0 no hay salidas.
El sistema \(\{X(t); t \geq 0\}\) es un proceso de nacimiento y muerte con:
\[\lambda_i = \lambda, \quad 0 \leq i \leq K-1\] \[\mu_i = i\mu, \quad 0 \leq i \leq K\] que como veremos más adelante se denomina cola \(M/M/K/K\), es decir, llegadas y servicios exponenciales con \(K\) servidores y de capacidad \(K\).
La función de simmer para estudiar este sistema viene dada por:
# Sistema
#################################################
cola.MMKK <- function(t, lambda, mu, servidores, usuarios)
{
# lambda: tasa de llegadas
# mu: tasa de servicio
# servidores: número de servidores
# usuarios: capacidad total del sistema
cola <- usuarios - servidores
servicio <- trajectory() %>%
seize("atendiendo", amount = 1) %>%
timeout(function() rexp(1, mu)) %>%
release("atendiendo", amount = 1)
# Configuración del sistema
#################################################
simmer() %>%
add_resource("atendiendo", capacity = servidores, queue_size = cola) %>%
add_generator("llegada", servicio, function() rexp(1, lambda)) %>%
run(until = t)
}4.4.4 Call Center
El sistema de reservas telefónicas de una aerolínea es un “call center” formado por \(s\) empleados de reservas llamados agentes. Una llamada entrante para una reserva es atendida por un agente si hay uno disponible; de lo contrario, la persona que llama es puesta en espera. El sistema puede poner en espera a un máximo de \(H\) personas. Cuando un agente está disponible, las llamadas en espera se atienden por orden de llegada. Cuando todos los agentes están ocupados y hay \(H\) llamadas en espera, cualquier llamada adicional recibe una señal de ocupado y se pierden permanentemente. Sea \(X(t)\) la varaible aleatoria que registra el número de llamadas en el sistema, las atendidas por los agentes más las que están en espera, en el momento \(t\) . Si las llamadas recibidas se comportan como un \(PP(\lambda)\) y los tiempos de procesamiento de las llamadas son variables aleatorias iid \(Exp(\mu)\), el sistema \(\{X(t); t \geq 0\}\) es una CMTC, con espacio de estados \(S = \{0, 1, 2,...,K\}\) donde \(K = s + H\).
Se puede demostrar fácilmente que este sistema es un proceso de nacimiento y muerte con tasas:
\[\lambda_i = \lambda, \quad 0 \leq i \leq K-1\] \[\mu_i = min(i, s)\mu, \quad 0 \leq i \leq K\] que en la terminologia habitual se denomina cola \(M/M/s/K\). Para simular este proceso podemos utilizar la función del ejemplo anterior.