5.3 Colas con un único servidor
En este apartado presentamos los aspectos más relvantes referidos a los sistemas de colas con un único servidor. empezando por el más sencillo que considera tiempos de llegadas y servicio exponenciales, y con un único servidor.
5.3.1 M/M/1
Comenzamos con le sistema más sencillo donde se consideran tiempos de llegadas y servicio exponenciales, un único servidor, capacidad del sistema infinita y prioridad FIFO. De esta forma, tanto las tasas de llegadas como las tasas de servicio vienen dadas por:
\[ \begin{matrix} \lambda_n = \lambda & n = 0, 1,...\\ \mu_n = \mu & n = 1, 2,... \end{matrix}\]
de forma que la matriz de tasas vieen dada por:
\[ R = \begin{pmatrix} 0 & \lambda & 0 & 0 & ...\\ \mu & 0 & \lambda & 0 & ...\\ 0 & \mu & 0 & \lambda & ...\\ \vdots & \vdots & \vdots & \vdots & \vdots \end{pmatrix}\]
donde a partir de las ecuaciones de equilibrio podemos obtener la relación entre tasas de llegadas y servicio:
\[c_n = \frac{\lambda_{n-1}\lambda_{n-2}...\lambda_0}{\mu_{n}\mu_{n-1}...\mu_1} = \frac{\lambda^n}{\mu^n} = \rho^n, \quad n = 1, 2,...\]
Utilizando propiedades de series geométricas, dado que \(\rho >0\), el modelo será estacionario si \(\rho < 1\). Otra forma de expresarlo es \(\lambda < \mu\), que tiene la interpretación adicional de que el número medio de clientes que entran en el sistema por unidad de tiempo sea menor que el número medio de clientes que podrían ser atendidos por el servidor por unidad de tiempo, en caso de que éste estuviese absolutamente todo el tiempo atendiendo a clientes (cosa que no ocurre siempre).
En lo que sigue supondremos que el sistema de la cola es estacionario (es decir \(\rho < 1\)). Lo primero que debemos calcular es la suma de la serie de las \(c_n\):
\[\sum_{n = 1}^{\infty} c_n = \sum_{n = 1}^{\infty} \rho^n = \frac{\rho}{1-\rho}.\] \[ \begin{matrix} p_0 = 1 - \rho\\ p_n = c_np_0 = (1 - \rho)\rho^n \end{matrix}\]
De esta forma, la distribución de probabilidad de la variable aleatoria del “número de clientes en el sistema” es:
\[P(N = n) = p_n = (1-\rho)\rho^n, \quad n = 0, 1,...\]
que corresponde con una distribuión geométrica de parámetro \((1 - \rho)\). Por tanto, el valor de \(L\) viene dado por:
\[L = E(N) = \sum_{n = 0}^{\infty} np_n = (1 - \rho)\rho \sum_{n = 1}^{\infty} n \rho^{n-1} = (1 - \rho)\rho\frac{1}{(1 - \rho^2)} = \frac{\rho}{1 - \rho} = \frac{\lambda}{\mu - \lambda}.\]
A partir de ella podemos obtener:
\[L_q = L - (1 - p_0)\]
que es válido para cualquier sistema de cola, y que en nuestro caso es:
\[L_q = \frac{\lambda^2}{\mu(\mu-\lambda)}\]
Aplicando las fórmulas de Little tenemos:
\[ \begin{matrix} W = \frac{L}{\lambda} = \frac{1}{\mu - \lambda},\\ W_q = \frac{L_q}{\lambda} = \frac{\lambda}{\mu(\mu - \lambda),} \end{matrix}\]
de donde podemos deducir:
\[W = W_q + \frac{1}{\mu}\]
Si se desea tener más información sobre la espera de clientes en la cola o en el sistema, debe calcularse la distribución de rpoabbildiad de las variables \(T\) y \(T_q\). Estas distribuciones permitirán calcular la probabilidad de cualquier suceso relativo al tiempo de estancia en la cola o en el sistema. Si denotamos por \(W(t)\) y \(W_q(t)\) a las coorespondientes funciones de distribución de \(T\) y \(T_q\) tendremos:
\[W(t) = 1 - exp[-(\mu - \lambda)t]\]
\[ W_q(t) = \begin{cases} 1 - \frac{\lambda}{\mu}exp[-(\mu - \lambda)t] & \text{ si } t \geq 0\\ 0 & \text{ si } t < 0 \end{cases} \]
::: {.example #colas001 name = “Operador de elevador”}
Un operador de un pequeño elevador de grano tiene un único muelle de descarga. Las llegadas de camiones durante la temporada alta forman un proceso de Poisson con una tasa de llegada media de cuatro por hora. Debido a la variación de las cargas (y al deseo de los conductores de hablar) el tiempo que cada camión pasa frente al muelle de descarga se aproxima por una variable aleatoria exponencial con una media de 14 minutos. Suponiendo que que las plazas de aparcamiento son ilimitadas, el sistema de colas \(M/M/1\) puede describir el comportamiento del proceso con tasas de llegadas \(\lambda = 4 hora\) y tasa de servicio \(\mu = 60/14 hora\).
- ¿cuál es la probabilidad de que el muelle de descarga esté inactivo?
- ¿cuál es la probabilidad de que haya exactamente tres camiones esperando?
- ¿cuál es la probabilidad de que haya cuatro o más camiones en el sistema?
:::
Resolvemos el ejemplo de dos formas diferentes: 1) teóricamente con las fórmulas anteriores, 2) con la libreria queueing. Al final de la unidad presentamos la solución de simmer para simular de una cola \(M/M/1\). En este último caso deberemos aproximar las cantidades de interés mediante los correspondientes estimadores Monte-Carlo, si repetimos las imualacion del sistema un número adecuado de veces.
Para responder a la primera pregunta tenemos en cuenta que \(\rho = 0.9333\) y que la probabilidad buscada es la que corresponde al estado \(0\) de la distribución estacionaria, es decir,
\[p_0 = 1 - \rho = 0.0667\] En cuanto a la segunda pregunta debemos tener en cuenta que:
\[P(N_q = 3) = P(N = 4) = p_4 = 0.0667*0.9333^4 = 0.0506.\]
Para resolver la última pregunta tenemos que:
\[P(N \geq 4) = 1 - P(N \leq 3) = 1 - \sum_{n = 0}^{3} p_n = \rho^4 = 0.759.\]
Utilizamos ahora la librería queueing para resolver las mismas preguntas. En primer lugar tenemos que definir el sistema y sus características (tasas de llegada, tasas de servicio, y número de elementos de la distribución estacionaria que debemos calcular). Para ello utilizamos la función NewInput() con \(n = 4\) elemntos de la distribución estacionaria, ya que las probabildiades buscadas hacen referencia a esos cuatro primeros valores.
# Deficición del entorno
env.MM1 <- NewInput.MM1(lambda = 4, mu = 60/14, n = 4)
# Características del sistema
s.MM1 <- QueueingModel(env.MM1)Los valores y funciones del sistema que proporciona la función son:
- \(RO\) = valor de intensidad de tráfico \(\rho\).
- \(Lq\) = número medio de clientes en la cola.
- \(VNq\) = varianza del número de clientes e la cola.
- \(Wq\) = tiempo medio de espera en la cola.
- \(VTq\) = varianza del tiempo de espera en la cola.
- \(L\) = número medio de clientes en el sistema.
- \(VN\) = varianza del número de clientes en el sistema.
- \(W\) = tiempo medio que un cliente está en el sistema.
- \(VT\) = varianza del tiempo que un cliente está en el sistema.
- \(Wqq\) = tiempo medio que un cliente permanece en la cola cuando está existe.
- \(Lqq\) = número medio de clientes en la cola cuando está existe.
- \(Pn\) = Distribición estacionaria de sistema.
- \(Qn\) = Probabilidad de que un cliente encuentre \(n\) clientes.
- \(FW\) = Función de distribución de \(W\) para un conjunto de valores de \(t\).
- \(FWq\) = Función de distribución de \(W_q\) para un conjunto de valores de \(t\).
Veamos la salida completa:
# Medidas del sistema
s.MM1## $Inputs
## $lambda
## [1] 4
##
## $mu
## [1] 4.285714
##
## $n
## [1] 4
##
## attr(,"class")
## [1] "i_MM1"
##
## $RO
## [1] 0.9333333
##
## $Lq
## [1] 13.06667
##
## $VNq
## [1] 208.1956
##
## $Wq
## [1] 3.266667
##
## $VTq
## [1] 12.19556
##
## $Throughput
## [1] 4
##
## $L
## [1] 14
##
## $VN
## [1] 210
##
## $W
## [1] 3.5
##
## $VT
## [1] 12.25
##
## $Wqq
## [1] 3.5
##
## $Lqq
## [1] 15
##
## $Pn
## [1] 0.06666667 0.06222222 0.05807407 0.05420247 0.05058897
##
## $Qn
## [1] 0.06666667 0.06222222 0.05807407 0.05420247 0.05058897
##
## $FW
## function (t)
## {
## 1 - exp(-t/W)
## }
## <bytecode: 0x7fa55f619f90>
## <environment: 0x7fa55f616f60>
##
## $FWq
## function (t)
## {
## 1 - (RO * exp(-t/W))
## }
## <bytecode: 0x7fa55f6199a8>
## <environment: 0x7fa55f616f60>
##
## attr(,"class")
## [1] "o_MM1"Podemos respondera ahora a las cuestiones de interés sin más que buscar en los elemntos que proporciona la función.
# ¿cuál es la probabilidad de que el muelle de descarga esté inactivo?
s.MM1$Pn[1]## [1] 0.06666667# ¿cuál es la probabilidad de que haya exactamente tres camiones esperando?
# se corresponde con el elmento 4 + 1 de pn
s.MM1$Pn[5]## [1] 0.05058897# ¿cuál es la probabilidad de que haya cuatro o más camiones en el sistema?
1- sum(s.MM1$Pn[1:4])## [1] 0.7588346::: {.example #colas002 name = “Estación de trabajo”}
En una estación de trabajo con un único procesador se ejecutan programas (que se supone prácticamente su única carga de trabajo) con tiempo de CPU de distribución exponencial de media 3 minutos. Los programas se atienden según una disciplina FIFO. Sabiendo que las llegadas de programas a la estación se producen según un proceso de Poisson con una intensidad de 15 programas cada hora, por término medio, se pide:
- ¿Cuál es la probabilidad de que haya más de dos programas en espera de ejecución (además del que se está ejecutando)?
- Calcular el tiempo medio que transcurre desde que se envía un programa al servidor hasta que se termina su ejecución. ¿Cuál es la relación entre este tiempo y el tiempo medio de CPU?
- Calcular la probabilidad de que el programa esté en el servidor (esperando o ejecutándose) más de 10 minutos.
- ¿Cuál es el número medio de programas que están a la espera de comenzar a ejecutarse?
- Obtener las respuestas a los apartados anteriores suponiendo que ahora se ha incrementado la llegada de programas hasta 18 a la hora, por término medio.
En este caso utilizaremos la librería queueing para los cálculos numéricos. Si tomamos como unidad de tiempo las horas tendremos que \(\lambda = 15\) y \(1/\mu = 3 /60\), con lo cual \(\mu = 20.\)
:::
# Deficición del entorno
env.MM1 <- NewInput.MM1(lambda = 15, mu = 20, n = 10)
# Características del sistema
s.MM1 <- QueueingModel(env.MM1)Para responder a la cuestión 1 debemos calcular:
\[P(N_q \geq 3) = P(N \geq 4) = 1 - P(N \leq 3)\]
1- sum(s.MM1$Pn[1:4])## [1] 0.3164062Para el primer apartado de la segunda cuestión sólo necesitamos el valor de \(W\), que corresponde con el tiempo medio en el sistema:
s.MM1$W## [1] 0.2El tiempo medio es de 0.2 horas o 12 minutos. Para responder a la segunda pregunta hay que tener en cuenta que el tiempo de CPU corresponde con el tiempo de servicio, es decir, la relción buscada es:
\[\frac{W}{1/\mu}\]
s.MM1$W/(1/20)## [1] 4Cada proceso está en la estación un tiempo equivalente a cuatro veces su tiempo de CPU.
Para respondear al tercer apartado debemos calcular (expresado en las unidades de tiempo utilizadas:
\[P(T > 10/60)\] Dicha probabilidad se obtiene a partir de la función de distribuvión de los tiempos que el cliente está en el sistema:
1 - s.MM1$FW(10/60)## [1] 0.4345982La cuarta cuestión se corresponde con el valor de \(L_q\):
s.MM1$Lq## [1] 2.25de forma que el número de procesos en espera es de 2.25.
Para responder al quinto apartado debemos cambiar el valor de la tasa de llegadas y volver a hacer los cálculos:
# Deficición del entorno
env.MM1 <- NewInput.MM1(lambda = 18, mu = 20, n = 10)
# Características del sistema
s.MM1 <- QueueingModel(env.MM1)
# Cuestión 1
1- sum(s.MM1$Pn[1:4])## [1] 0.6561# Cuestión 2.1
s.MM1$W## [1] 0.5# Cuestión 2.2
s.MM1$W/(1/20)## [1] 10# Cuestión 3
1 - s.MM1$FW(10/60)## [1] 0.7165313# Cuestión 4
s.MM1$Lq## [1] 8.1Como puede verse numéricamente el sistema está bastante más congestionado ahora. Podemos representar gráficamente ambas soluciones.
# Primer sistema
env.MM1 <- NewInput.MM1(lambda = 15, mu = 20, n = 10)
s.MM1.1 <- QueueingModel(env.MM1)
# Segundo sistema
env.MM2 <- NewInput.MM1(lambda = 18, mu = 20, n = 10)
s.MM1.2 <- QueueingModel(env.MM2)
# Establecemos secuencia de tiempos pra el análisis
tiempos <- seq(0, 4, 0.01)
# Almaceamos los resultados
sistema <- data.frame(tiempos = tiempos,
FW1 = s.MM1.1$FW(tiempos),
FWq1 = s.MM1.1$FWq(tiempos),
FW2 = s.MM1.2$FW(tiempos),
FWq2 = s.MM1.2$FWq(tiempos))
# gráficos
g1 <- ggplot(sistema, aes(tiempos, FW1)) +
geom_line(linetype = 1) +
geom_line(aes(tiempos, FW2), linetype = 2) +
labs(x = "Tiempo (en horas)", y = "Probabilidad", title = "W(t)")
g2 <- ggplot(sistema, aes(tiempos, FWq1)) +
geom_line(linetype = 1) +
geom_line(aes(tiempos, FWq2), linetype = 2) +
labs(x = "Tiempo (en horas)", y = "Probabilidad", title = "Wq(t)")
grid.arrange(g1, g2, ncol = 2)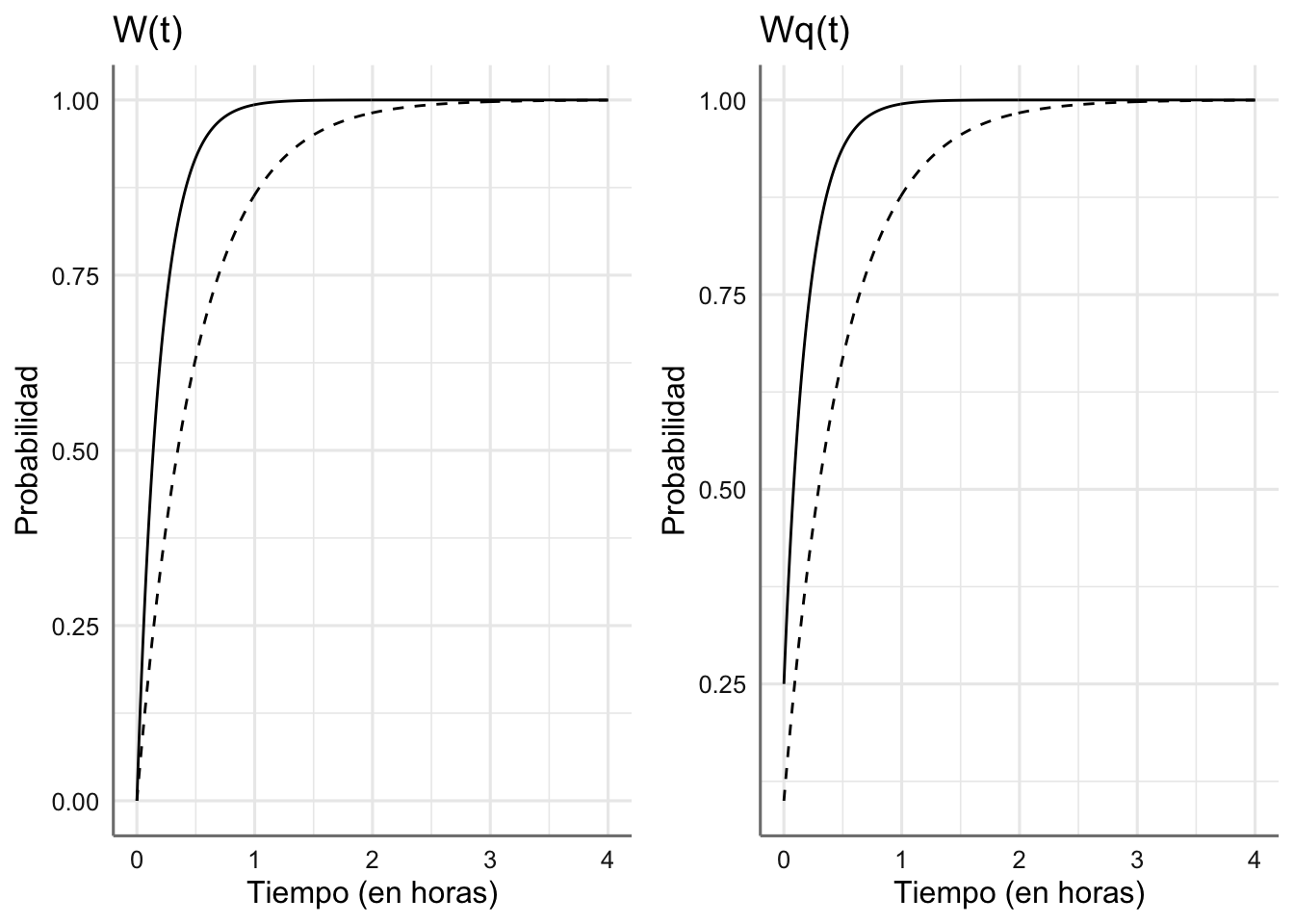
Figura 5.1: Funciones de distribución de W y Wq para ambos sistemas (sistema 1 = línea continua, sistema 2 = línea discontinua.
Como se puede ver los tiempos medios de espera de los clientes en el sistema y en la cola para la segunda opción tienen probabildides más bajas a lo largo del tiempo, lo que indica que el sistema está más congestionado porque los tiempos de atención son superiores (valores donde se alcanza la probabilidad 1).
5.3.2 M/M/1/K
Se trata de un modelo como el \(M/M/1\), ya estudiado, pero con límitación \(K\) para el tamaño de la cola. Es decir, la distribución del tiempo entre dos intentos de llegadas al sistema de clientes consecutivos es un PP de tasa \(\lambda\), mietras que la distribución del tiempo de servicio es exponencial de media \(1/\mu\) y sólo hay un servidor. Además el número de clientes que pueden estar en la cola es como mucho \(K\), la población potencial es infinita y la disciplina es FIFO. Obviamente, en este modelo se puede dar el caso de que un cliente que intente entrar en el sistema no lo consiga, por estar la cola llena.
En esta situación tenemos que las tasas de llegadas viene dadas por:
\[ \lambda_n = \begin{cases} \lambda & \text{ si } n = 0, 1,...,K\\ 0 & \text{ si } n = K+1, K+2,... \end{cases} \] mientras que las tasas de servicio se corresponden con la cola \(M/M/1\)
\[ \mu_n = \mu, \quad n = 1, 2,... \] donde a partir de las ecuaciones de equilibrio podemos obtener la relación entre tasas de llegadas y servicio:
\[ c_n = \begin{cases} \rho^n & \text{ si } n = 0, 1,...,K, K+1\\ 0 & \text{ si } n = K+2, K+3,... \end{cases} \] En este caso, por muy frecuente que sea la llegada de clientes al sistema en relación con la capacidad del servidor para dar servicio, la propia limitación en el tamaño de la cola fuerza a la estacionariedad, pues lo peor que podríamos imaginar es que prácticamente todo el tiempo estuviese el sistema saturado (es decir \(P(N = K + 1) = 1\)). Para analizar el comportamiento de la serie distinguiremos que \(\rho \neq 1\) y \(\rho = 1\).
Caso \(\rho \neq 1\)
De esta forma, la distribución de probabilidad de la variable aleatoria del “número de clientes en el sistema” es:
\[ P(N = n) = p_n = \begin{cases} \frac{\rho - 1}{\rho^{K+2} - 1} \rho^n & \text{ si } n = 0, 1,..., K+1\\ 0 & \text{ si } n = K+2, K+3,... \end{cases} \]
El número medio de clientes en el sistema es:
\[L = \frac{\rho}{1 - \rho} - \frac{(K + 2)\rho^{K+2}}{1 - \rho^{K+2}}\]
Dado que las tasas de llegada no son contantes, necesitamos obtener el valor de \(\bar{\lambda}\) para aplicar la fórmula de Little al resto de cantidades de interés. En este caso:
\[\bar{\lambda} = \frac{\lambda(\rho^{K+1} - 1)}{\rho^{K+1} - 1}\]
A partir de esta expresión podemos obtener el tiempo medio de espera de los clientes en la cola como:
\[W = \frac{1}{\mu - \lambda} - \frac{(K+1)\rho^{K+2}}{\lambda(1-\rho^{K+1})}\]
De la relación entre \(W\) y \(W_q\) podemos obtener:
\[W_q = \frac{\lambda}{\mu(\mu - \lambda)} - \frac{(K+1)\rho^{K+2}}{\lambda(1-\rho^{K+1})}\] Por último:
\[L_q = \frac{\rho^2}{1 - \rho} - \frac{(K + 1 + \rho)\rho^{K+2}}{1 - \rho^{K+2}}\]
Caso \(\rho = 1\)
En este caso las fórmulas anteriroes se simplifican a:
\[p_n = \frac{1}{K+2}, \text{ para } n = 0, 1,...,K + 1\] \[L = \frac{K + 1}{2}\] \[\bar{\lambda} = \frac{\lambda(K + 1)}{K + 2}\]
\[W = \frac{K + 2}{2\lambda}\] \[W_q = \frac{K}{2\lambda}\] \[L_q = \frac{K(K + 1)}{2(K+2)}\]
En este modelo (y en otros posteriores) el significado de \(\rho\) como intensidad de tráfico se desvirtúa. Aquí \(\rho\) no puede interpretarse como el cociente entre número medio de llegadas de clientes al sistema por unidad de tiempo y el número medio de clientes a los que el servidor tendría capacidad de dar servicio por unidad de tiempo, sinó más bien como un cociente semejante, pero donde el númerador representa el número medio de intentos de llegada, más que de llegadas efectivas al sistema. De hecho, por este motivo \(\rho\) puede ser mayor o igual que 1, aún siendo el sistema estacionario. El valor de \(\bar{\lambda}\) sí representa el número medio de entradas efectivas de clientes en el sistema por unidad de tiempo y, así, la verdadera intensidad de tráfico podría medirse a través de:
\[ \bar{\rho} = \frac{\bar{\lambda}}{\mu} = \begin{cases} \frac{K+1}{K+2} & \text{ si } \rho = 1 \\ \frac{\rho^{K+2}-\rho}{\rho^{K+2}-1} & \text{ si } \rho \neq 1 \end{cases} \] que efectivamente sí es siempre menor que 1.
::: {.example name = “Taller Mecánico”}
En un taller mecánico llegan vehículos para una puesta a punto antes de pasar la ITV, las llegadas siguen un proceso de Poisson de promedio 18 vehículos/hora. Las dimensiones del taller sólo permiten que haya 4 vehículos, y las ordenanzas municipales no permiten esperar en la vía pública. El taller despacha un promedio de 6 vehículos/hora de acuerdo con una distribución exponencial. Se pide:
- ¿Cuál es la probabilidad de que no haya ningún vehículo en el taller?
- ¿Cuál es el promedio de vehículos en el taller?
- ¿Cuánto tiempo pasa por término medio un vehículo en el taller?
- ¿Cuánto tiempo esperan por término medio los vehículos en la cola?
- ¿Cuál es la longitud media de la cola?
:::
Se trata de un sistema \(M/M/1/K\) con \(K = 4\), y utilizaremos la librería queueing para los cálculos numéricos. Si tomamos como unidad de tiempo las horas tendremos que \(\lambda = 18\) y \(\mu = 6\). Geenramos el sistema de cola definido y procedemos con los cálculos solicitados.
# Deficición del entorno
env.MM1K <- NewInput.MM1K(lambda = 18, mu = 6, k = 4)
# Características del sistema
s.MM1K <- QueueingModel(env.MM1K)Las medidas proporcionadas por la función son las mismas que con el modelo \(M/M/1\). Comenzamos a responder las preguntas:
- Apartado 1. La probabilidad de que no haya ningún vehículo en el taller es \(p_0\):
s.MM1K$Pn[1]## [1] 0.008264463- Apartado 2. Obtenemos el número medio de vehículos en el sistema \(L\):
s.MM1K$L## [1] 3.520661- Apartado 3. En este caso estamos interesados en el tiempo medio de estancia en el sistema (\(W\)):
s.MM1K$W## [1] 0.5916667- Apartado 4. En este caso estamos interesados en el tiempo medio de estancia en la cola (\(W_q\)):
s.MM1K$Wq## [1] 0.425- Apartado 5. En este caso estamos interesados en el número medio de clientes en la cola (\(L_q\)):
s.MM1K$Lq## [1] 2.528926Para el resto de sistemas de colas que vamos a presentar no desarrollaremos de forma completa todas las fórmulas teóricas, y nos centraremos en los resultados numéricos que proporciona la libreria queueing para la resolución de aplicaciones.