34 Tests for means of two independent groups

You have learnt to ask a RQ, design a study, classify and summarise the data, construct confidence intervals, and perform some hypothesis tests. In this chapter, you will learn to:

identify situations where conducting a test for comparing two means is appropriate.
conduct hypothesis tests for comparing two means.
determine whether the conditions for using these methods apply in a given situation.

34.1 Introduction: garter snakes

Some Mexican garter snakes (Thamnophis melanogaster) live in habitats with no crayfish, while some live in habitats with crayfish and hence use crayfish as a food source. Manjarrez, Macias Garcia, and Drummond (2017) were interested in whether the snakes in these two regions were different:

For female Mexican garter snakes, is the mean snout--vent length (SVL) different for those in regions with crayfish and without crayfish?

Two different groups of snakes are studied (a between-individuals comparison), and the data are shown below.

A numerical summary must summarise the difference between the means, as the RQ is about this difference. Both groups should be summarised too. The information can be found using software (Fig. 34.1), and compiled into a table (Table 34.1). The appropriate summary for graphically summarising the data is (for example) a boxplot (Fig. 34.2, left panel). An error bar chart Sect. 27.4), which compares the sample means, should also be produced (Fig. 34.2, right panel).

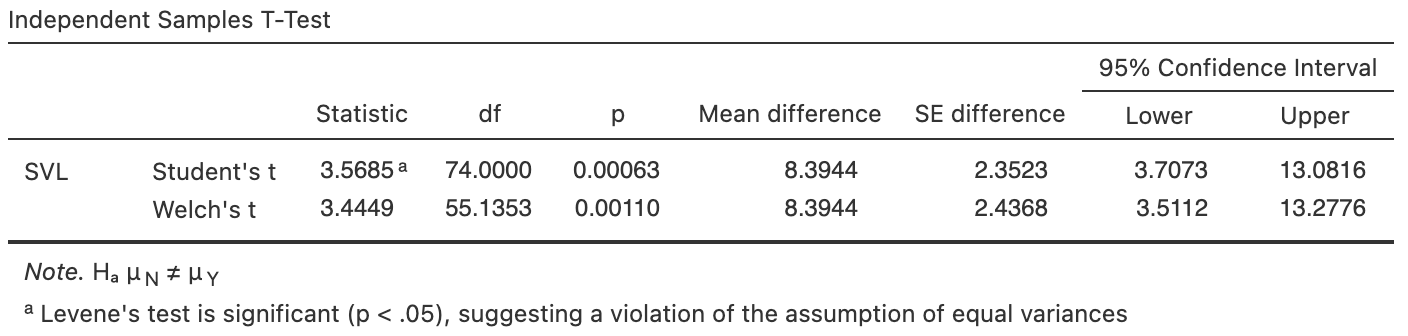
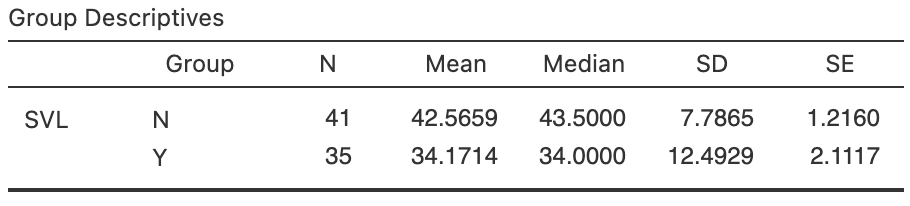
FIGURE 34.1: Software output for the garter-snakes data.

TABLE 34.1: Numerical summaries of SVL (in cm) for female snakes in two regions.
	Mean	Sample size	Standard deviation	Standard error
Crayfish region	$34.17$	$12.49$	$35$	$2.112$
Not-crayfish region	$42.57$	$\phantom{0}7.79$	$41$	$1.216$
Difference	$\phantom{0}8.39$			$2.437$

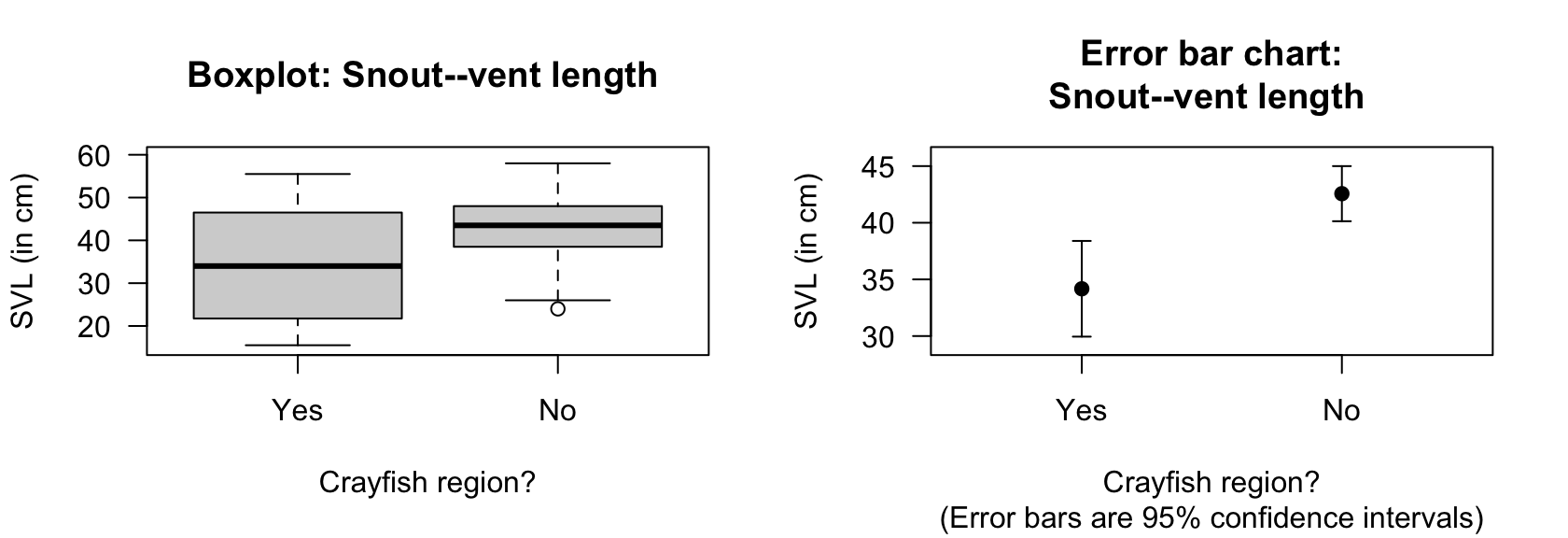
FIGURE 34.2: Boxplot (left) and error bar chart (right) of SVL for female snakes in two regions.

Since two groups are being compared, subscripts are used to distinguish between the statistics for the two groups; say, Groups $A$ and $B$ in general (Table 34.2). Using this notation, the parameter in the RQ is the difference between population means: $\mu_A - \mu_B$. As usual, the population values are unknown, so this is estimated using the statistic $\bar{x}_A - \bar{x}_B$.

TABLE 34.2: Notation used to distinguish between the two independent groups.
	Group A	Group B	Comparing groups
Sample sizes:	$n_A$	$n_B$
Population means:	$\mu_A$	$\mu_B$	$\mu_A - \mu_B$
Sample means:	$\bar{x}_A$	$\bar{x}_B$	$\bar{x}_A - \bar{x}_B$
Standard deviations:	$s_A$	$s_B$
Standard errors:	$\displaystyle\text{s.e.}(\bar{x}_A) = \frac{s_A}{\sqrt{n_A}}$	$\displaystyle\text{s.e.}(\bar{x}_B) = \frac{s_B}{\sqrt{n_B}}$	$\displaystyle\text{s.e.}(\bar{x}_A - \bar{x}_B)$

For the garter-snake data, define the differences as the mean for females snakes living in non-crayfish regions ($N$), minus the mean for female snakes in crayfish regions ($C$): $\mu_N - \mu_C$. This is the parameter. By this definition, the differences refer to how much larger (on average) the SVL is for snakes living in non-crayfish regions.

Here the difference is computed as the mean SVL for snakes living in non-crayfish regions, minus the mean SVL for snakes living in crayfish regions. Computing the difference as the mean SVL for snakes in crayfish regions, minus non-crayfish regions is also correct.

You need to be clear about how the difference is computed, and be consistent throughout. The meaning of the conclusions will be the same whichever direction is used.

34.2 Tests for comparing two means: $t$-test

As always, the null hypothesis is the default 'no difference, no change, no relationship' position; any difference between the parameter and statistic is due to sampling variation (Sect. 32.2). Hence, the null hypothesis is 'no difference' between the population mean SVL of the two groups:

$H_0$: $\mu_N - \mu_C = 0$ (equivalent to $\mu_N = \mu_C$).

From the RQ, the alternative hypothesis is two-tailed:

$H_1$: $\mu_N - \mu_C\ne 0$ (equivalent to $\mu_N \ne \mu_C$).

The alternative hypothesis proposes that any difference between the sample means is because a difference really exists between the population means.

The sample mean difference between the SVL in the two groups depends on which one of the many possible samples is randomly obtained, even if the difference between the means in the population is zero. The difference between the sample means is $8.394$, but this difference will vary from sample to sample; that is, sampling variation exists.

Definition 34.1 (Sampling distribution for the difference between two sample means) The sampling distribution of the difference between two sample means $\bar{x}_A$ and $\bar{x}_B$ is (when the appropriate conditions are met; Sect. 34.3), described by:

an approximate normal distribution,
centred around the sampling mean whose value is ${\mu_{A}} - {\mu_{B}} = 0$, the difference between the population means (from $H_0$),
with a standard deviation of $\displaystyle\text{s.e.}(\bar{x}_A - \bar{x}_B)$.

The value of the standard error for the difference between the means is \[ \text{s.e.}(\bar{x}_A - \bar{x}_B) = \sqrt{ \text{s.e.}(\bar{x}_A)^2 + \text{s.e.}(\bar{x}_B)^2}, \] though this value will often be given (e.g., on computer output).

For the SVL data, the sampling variation of $\bar{x}_N - \bar{x}_C$ can be described as having:

an approximate normal distribution,
centred around the sampling mean whose value is ${\mu_{N}} - {\mu_{C}} = 0$, the difference between the means (from $H_0$),
with a standard deviation, called the standard error of the difference between the means, of \[ \text{s.e.}(\bar{x}_N - \bar{x}_C) = \sqrt{1.2160^2 + 2.1117^2 } = 2.4368. \] The calculation uses the standard errors from Table 34.1. The answer agrees with the second row of the software output (Fig. 34.1).

Most software gives two confidence intervals: one assuming the standard deviations in the two groups are the same, and another not assuming the standard deviations in the two groups are the same.

We will use the information that does not assume the standard deviations in the two groups are the same. In the software output in Fig. 34.1, this is the second row of the bottom table (labelled 'Welch's $t$'). (The information in both rows are often similar anyway.)

The observed difference between sample means, relative to what was expected, is found by computing the test statistic; in this case, a $t$-score. The software output (Fig. 34.1) gives the $t$-score, but the $t$-score can also be computed using the information in Table 34.1: \[\begin{align*} t &= \frac{\text{sample statistic} - \text{mean of sampling distribution (from $H_0$)}} {\text{standard deviation of sampling distribution}}\\[6pt] &= \frac{ (\bar{x}_P - \bar{x}_C) - (\mu_P - \mu_C)} {\text{s.e.}(\bar{x}_P - \bar{x}_C)} = \frac{8.39 - 0}{2.4368} = 3.44, \end{align*}\] as in the software output.

A $P$-value determines if the sample statistic is consistent with the assumption (i.e., $H_0$). Since the $t$-score is large, the $P$-value will be small using the $68$--$95$--$99.7$ rule (and less than $0.003$). This is confirmed by the software (Fig. 34.1): the two-tailed $P$-value is $0.0011$.

A small $P$-value suggests the observations are inconsistent with the assumption of no difference (Table 32.1), and the difference between the sample means could not be reasonably explained by sampling variation, if $\mu_N - \mu_C = 0$.

Click on the pins in the following image, and describe what the software output tells us.

In conclusion, write:

Strong evidence exists in the sample (two independent samples $t = 3.445$; two-tailed $P = 0.0011$) that the population mean SVL is different for female snakes living in crayfish regions (mean: $34.17$ cm; $n = 35$) and non-crayfish regions (mean: $42.57$; $n = 41$; $95$% CI for the difference: $3.51$ to $13.28$longer for those in non-crayfish regions).

The conclusion contains an answer to the RQ, the evidence leading to this conclusion ($t = 3.44$; two-tailed $P = 0.0011$), and sample summary statistics, including a CI (using the ideas in Chap. 27).

34.3 Statistical validity conditions

As usual, these results apply under certain conditions, which are the same as those for forming a CI for the difference between two means. Statistical validity can be assessed using these criteria:

When both samples have $n \ge 25$, the test is statistically valid. (If the distribution of a sample is highly skewed, the sample size for that sample may need to be larger.)
When one or both groups have $25$ or fewer observations, the test is statistically valid only if the populations corresponding to both comparison groups have an approximate normal distribution.

The sample size of $25$ is a rough figure; some books give other values (such as $30$).

This condition ensures that the distribution of the difference between sample means has an approximate normal distribution (so that, for example, the $68$--$95$--$99.7$ rule can be used). The histograms of the sample data can be used to determine if normality of the populations seems reasonable.

The units of analysis are also assumed to be independent (e.g., from a simple random sample).

If the statistical validity conditions are not met, other similar options include using a Mann-Whitney test (Conover 2003) or using resampling methods (Efron and Hastie 2021).

Example 34.1 (Statistical validity) For the garter-snake data, the samples sizes exceed $25$ ($41$ and $35$), so the test is statistically valid. The data in each group do not need be normally distributed, since both sample sizes are larger than $25$, and the data are not severely skewed (Fig. 34.2, left panel).

34.4 Tests for comparing more than two means: ANOVA

Often, more than two means need to be compared. This requires a different method, called analysis of variance (or ANOVA). The details are are beyond the scope of this book. In this section, a very brief overview of using a one-way ANOVA is given, using an example. Importantly, this example shows that the basic principles of hypothesis testing from Chap. 32 still apply.

Example 34.2 (ANOVA) [Dataset: BMI] E. Johnson, Millar, and Shiely (2021) collected data from hospital outpatients at an Irish hospital (Table 34.3). One research question involves comparing the mean number of days per week that patients exercise for more than $30$(say, $\mu$) according to their smoking status: daily ($D$), occasionally ($O$) or not at all ($N$). An error bar chart can be used to display the three groups (Fig. 34.3).

As per Sect. 32.2, the null hypothesis is 'no difference' between the population means: \[ \text{$H_0$:}\ \mu_D = \mu_O = \mu_N. \] The alternative hypothesis is that the three means are not all equal. This hypothesis encompasses many possibilities: for example, that the three means are all different from each other, or that the first is different than the other two (which are the same). Because the alternative hypothesis encompasses many possibilities, it is difficult to write using symbols, so we write: \[ \text{$H_1$:}\ \text{Not all means are equal.} \]

For comparing more than two mean, the alternative hypothesis is always two-tailed.

Performing an ANOVA using software (Fig. 34.4) gives $P = 0.00007$. (The test statistic here is an $F$-score; we don't discuss these further.) The $P$-value in this context means the same as usual (Sect. 32.6): there is very strong evidence to support the alternative hypothesis (that the three means are not all equal).

While we know the means are not all the same, we do not know which group means are different from which other group means. One option might be to compare all possible combinations of two groups (i.e., the means of groups $D$ and $O$; the means of groups $D$ and $N$; the means of groups $O$ and $N$) using three separate two-sample $t$-tests. However, this approach increases the probability of declaring a false positive (i.e., or making a Type I error; Sect. 32.7): incorrectly declaring a difference between two sets of means. The correct approach requires methods beyond this book.

TABLE 34.3: Number of days per week where patients do more than $30$ mins of exercise.
Smokes daily	$1.27$	$0.79$	$0.237$	$11$
Smokes occasionally	$2.77$	$1.64$	$0.455$	$13$
Does not smoke	$3.15$	$1.93$	$0.285$	$46$

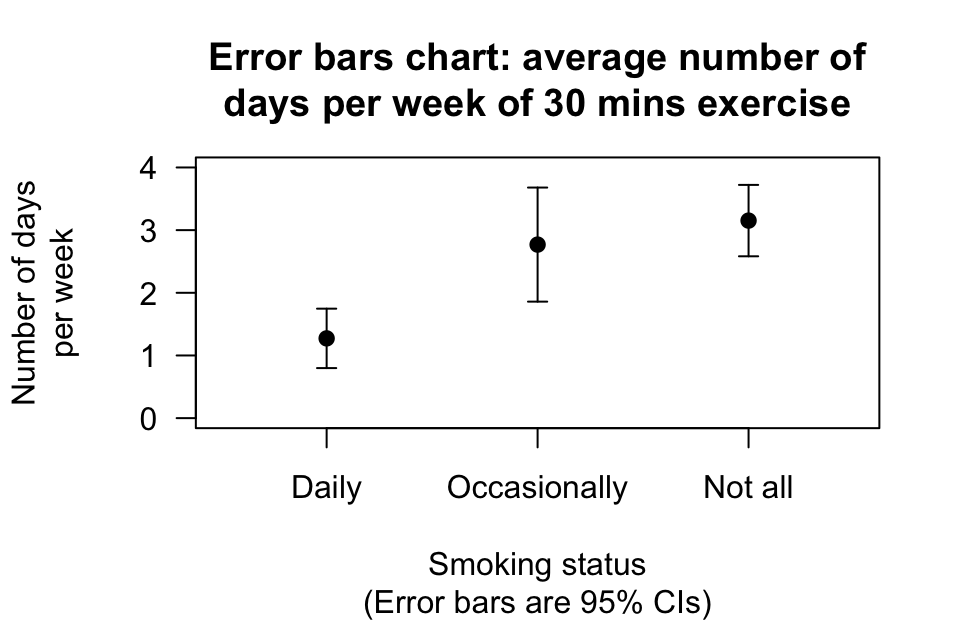
$The error bar chart for comparing the number of days per week on which people do more than $30$\mins of exercise, for different smoking groups.$

FIGURE 34.3: The error bar chart for comparing the number of days per week on which people do more than $30$of exercise, for different smoking groups.

ANOVA is a general tool that can be extended beyond just comparing more than two means, and used in many and varied context for the analysis of data.

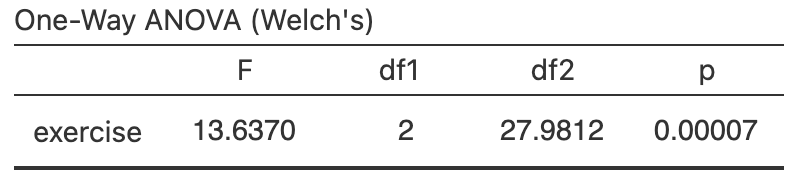
FIGURE 34.4: Software output for the BMI data.

34.5 Example: speed signage

(This study was seen in Sect. 27.7.) To reduce vehicle speeds on freeway exit ramps, Ma et al. (2019) studied adding additional signage. At one site (Ningxuan Freeway), speeds were recorded for $38$ vehicles before the extra signage was added (denoted $B$), and then for $41$ different vehicles after the extra signage was added (denoted $A$); the data are shown in Sect. 27.7. The researchers are hoping the addition of extra signage will reduce the mean speed of the vehicles. The RQ is:

At this freeway exit, does the mean vehicle speed reduce after extra signage is added?

The data are summarised in Table 34.4, where \[ \text{s.e.}(\bar{x}_B - \bar{x}_A) = \sqrt{ \text{s.e.}(\bar{x}_B)^2 + \text{s.e.}(\bar{x}_A)^2} = \sqrt{ 2.140^2 + 2.051^2} = 2.964, \] as in the table. A boxplot of the data is shown in Fig. 27.5 (left panel), and an error bar chart in Fig. 27.5 (right panel).

TABLE 34.4: The signage data summary (in km.h$^{-1}$), before and after extra signage added.
	Mean	Standard deviation	Standard error	Sample size
Before	$\phantom{0}98.02$	$13.19$	$2.140$	$38$
After	$\phantom{0}92.34$	$13.13$	$2.051$	$41$
Speed reduction	$\phantom{0}\phantom{0}5.68$		$2.964$

Define $\mu$ as the mean speed (in km.h^$-1$) on the exit ramp. Then, the parameter is $\mu_B - \mu_A$, the reduction in the population mean speed after signage is added. The hypotheses are:

$H_0$: $\mu_B - \mu_A = 0$: there is no change in the population mean speeds.
$H_1$: $\mu_B - \mu_A > 0$: the population mean speed has reduced.

The best estimate of the difference in population means is the difference between the sample means: $(\bar{x}_B - \bar{x}_A) = 5.68$. Table 34.4 gives the standard error for estimating this difference as $\text{s.e.}(\bar{x}_B - \bar{x}_A) = 2.964$. Using the summary information in Table 34.4, the $t$-score (using Eq. (31.2)) is \[ t = \frac{(\bar{x}_B - \bar{x}_A) - (\mu_B - \mu_A)}{\text{s.e.}(\bar{x}_B - \bar{x}_{A})} = \frac{5.68 - 0}{2.964} = 1.92. \] (Recall that we initially assume that $\mu_B - \mu_A = 0$ from the null hypothesis.)

Remembering that the alternative hypothesis is one-tailed, the $P$-value (using the $68$--$95$--$99.7$ rule) is larger than $0.025$, but smaller than $0.32$, so making a clear decision is difficult without using software. However, since the $t$-score is just less than 2, we suspect that the $P$-value is likely to be closer to $0.025$ than $0.32$.

From software, $P = 0.0297$ (you cannot be this precise just using the $68$--$95$--$99.7$ rule). Using Table 32.1, this $P$-value provides moderate evidence of a reduction in mean speeds. We conclude:

Moderate evidence exists in the sample ($t = 1.92$; one-tailed $P = 0.030$) that mean speeds have reduced after the addition of extra signage (before: mean speed: $98.02$.h^$-1$; $n = 38$; standard deviation: $13.19$.h^$-1$; after: mean speed: $92.34$.h^$-1$; $n = 41$; standard deviation: $13.13$.h^$-1$; 95% CI for the difference: $-0.24$ to $11.6$.h^$-1$).

Whether the mean speed reduction of $5.68$.h^$-1$ has practical importance is a different issue. Using the validity conditions, the CI is statistically valid.

Remember: the conclusion must make clear which mean is larger!

34.6 Example: chamomile tea

(This study was seen in Sects. 26.7, 27.8 and 33.7.) Rafraf, Zemestani, and Asghari-Jafarabadi (2015) studied patients with Type 2 diabetes mellitus (T2DM). They randomly allocated $32$ patients into a control group (who drank hot water), and $32$ to receive chamomile tea (Rafraf, Zemestani, and Asghari-Jafarabadi (2015)).

The total glucose (TG) was measured for each individual, in both groups, both before the intervention and after eight weeks on the intervention. Summary data are given in Table 26.3. Evidence suggests that the chamomile tea group shows a mean reduction in TG (Sect. 33.7), while the hot-water group shows no evidence of a reduction. That is, there appears to be a difference between the two groups regarding the change in TG. However, the differences between the chamomile-tea and the hot-water groups may be due to the samples selected (i.e., sampling variation), so comparing the changes between the two groups is helpful.

The following relational RQ can be asked:

For patients with T2DM, is the mean reduction in TG greater for the chamomile tea group compared to the hot water group?

Notice the RQ is one-tailed; the aim of the study is to determine if the chamomile-tea drinking group performs better (i.e., reduces the mean TG) than the control group.

This RQ is comparing two separate groups; specifically, comparing the differences between the two groups. This study contains both within-individuals comparisons (see Sect. 33.7) and a between-individuals comparison (this section); see Fig. 34.5. This is equivalent to treating the differences for both groups like two separate sets of data in the two-sample test.

FIGURE 34.5: The chamomile-tea study has two within-individuals comparisons, and a between-individuals comparison.

The corresponding hypotheses are: \[ \text{$H_0$: $\mu_T - \mu_W = 0$ \qquad and\qquad $H_1$: $\mu_T - \mu_W > 0$} \] where $\mu$ refers to the mean reduction in TG, $T$ refers to the tea-drinking group, and $W$ to the hot-water drinking group.

The parameter $\mu_T - \mu_W$ is estimated by the statistic $\bar{x}_T - \bar{x}_W = 45.74$.dl^$-1$. The standard error for the statistic was found (in Sect. 27.8) as $\text{s.e.}(\bar{x}_T - \bar{x}_W) = 8.42$. Hence, the test statistic is: \[ t = \frac{(\mu_T - \mu_W) - (\bar{x}_T - \bar{x}_W)}{\text{s.e.}(\bar{x}_T - \bar{x}_W)} = \frac{45.75 - 0}{8.42} = 5.43, \] which is very large, so the $P$ value will be very small (using the $68$--$95$--$99.7$ rule), and certainly smaller than $0.001$.

We write:

There is very strong evidence ($t = 5.43$; one-tailed $P < 0.001$) that the mean reduction in TG for the chamomile-tea drinking group (mean reduction: $36.62$.dl^$-1$) is greater than the mean reduction in TG for the hot-water drinking group (mean reduction: $-7.12$.dl^$-1$; difference between means: $45.74$.dl^$-1$; approx. $95$% CI: $28.64$ to $62.84$.dl^$-1$).

Again, the sample sizes are larger than $25$, so the results are statistically valid.

34.7 Chapter summary

To test a hypothesis about a difference between two population means $\mu_A - \mu_B$:

Write the null hypothesis ($H_0$) and the alternative hypothesis ($H_1$).
Initially assume the value of $(\mu_A - \mu_B)$ in the null hypothesis to be true.
Then, describe the sampling distribution, which describes what to expect from the difference between the sample means based on this assumption: under certain statistical validity conditions, the difference between the sample means vary with:
- an approximate normal distribution,
- with sampling mean whose value is the value of $(\mu_A - \mu_B)$ (from $H_0$), and
- having a standard deviation of $\displaystyle \text{s.e.}(\bar{x}_A - \bar{x}_B)$.
Compute the value of the test statistic: \[ t = \frac{ (\bar{x}_A - \bar{x}_B) - (\mu_A - \mu_B)}{\text{s.e.}(\bar{x}_A - \bar{x}_B)}, \] where $\mu_A - \mu_B$ is the hypothesised difference given in the null hypothesis.
The $t$-value is like a $z$-score, and so an approximate $P$-value can be estimated using the $68$--$95$--$99.7$ rule, or found using software.
Make a decision, and write a conclusion.
Check the statistical validity conditions.

ANOVA is used to compare means for more than two groups.

The following short video may help explain some of these concepts:

34.8 Quick review questions

Y.-M. Lee et al. (2016) studied iron levels in Koreans with Type II diabetes, comparing people on a vegan ($n = 46$) and a conventional ($n = 47$) diet for $12$ weeks. A summary of the data for iron levels are shown in Table 34.5.

TABLE 34.5: Comparing the iron levels (mg) for subjects using a vegan or conventional diet for $12$ weeks.
	Mean	Standard deviation	$n$
Vegan diet	$13.9$	$2.3$	$46$
Conventional diet	$15.0$	$2.7$	$47$
Difference	$\phantom{0}1.1$

The sample size is missing from the Difference row. What should the sample size in this row be?

46 + 47 = 9346 - 47 = -147 - 46 = 1A sample size makes no senseThere is not enough information
What is the standard deviation for the difference?
Compute the standard error for the difference.
The two-tailed $P$-value for the comparison is given as $P = 0.046$. What does this mean?

There is no evidence that the sample means are differentThere is some evidence that the sample means are differentThere is no evidence that the population means are differentThere is some evidence that the population means are differentThere is not enough information

34.9 Exercises

Answers to odd-numbered exercises are available in App. E.

Exercise 34.1 Suppose researchers are comparing the cell diameter of lymphocytes (a type of white blood cell) and tumour cells. Define the mean diameter of lymphocytes as $\mu_L$, and the mean diameter of tumour cells as $\mu_T$.

If the difference between the means were defined as $\mu_L - \mu_T$, what does this mean?

Exercise 34.2 Suppose researchers are comparing the braking distance of cars using two different types of brake pads (Type A and Type B). Define the mean breaking distance for cars with Type A brake pads as $\mu_A$, and mean breaking distance for cars with Type B brake pads as $\mu_B$.

If the difference between the means were defined as $\mu_B - \mu_A$, what does this mean?

Exercise 34.3 (This study was also seen in Exercise 27.1.) Agbayani, Fortune, and Trites (2020) measured (among other things) the length of gray whales (Eschrichtius robustus) at birth. Are female gray whales longer than males, on average, in the population at birth? Summary information is shown in Table 34.6.

TABLE 34.6: Numerical summary of length of whales at birth (in m).
	Mean	Standard deviation	Sample size
Female	$4.66$	$0.38$	$26$
Male	$4.60$	$0.30$	$30$

What is the parameter? Carefully describe what it means.
Write the hypotheses to answer the RQ.
Compute the standard error of the difference.
Compute the $t$-score, and approximate the $P$-value using the $68$--$95$--$99.7$ rule.
Write a conclusion.
Is the test statistically valid?

Exercise 34.4 [Dataset: NHANES] (This study was also seen in Exercise 27.2.) Earlier, the NHANES study (Exercise 15.7) was used to answer this RQ:

Among Americans, is the mean direct HDL cholesterol different for current smokers and non-smokers?

Use the software output in Fig. 34.6 to answer these questions.

What is the parameter? Carefully describe what it means.
Write the hypotheses to answer the RQ.
Write down the standard error of the difference.
Write down the $t$-score and the $P$-value.
Write a conclusion.
Is the test statistically valid?

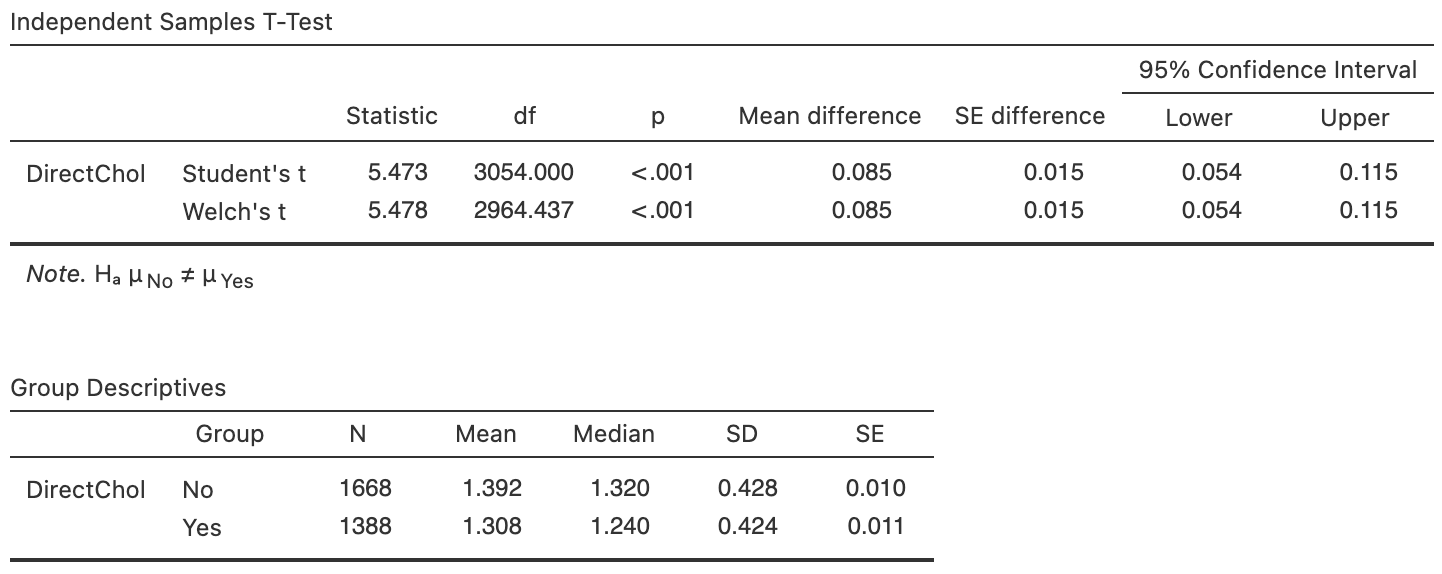
FIGURE 34.6: Software output for the NHANES data.

Exercise 34.5 (This study was also seen in Exercise 27.3.) Barrett et al. (2010) studied the effectiveness of echinacea to treat the common cold, and compared the mean duration of the cold for participants treated with echinacea or a placebo. Participants were blinded to the treatment, and allocated to the groups randomly. A summary of the data is given in Table 27.5.

What is the parameter? Carefully describe what it means.
Write the hypotheses to answer the RQ.
Compute the standard error of the difference.
Compute the $t$-score, and approximate the $P$-value using the $68$--$95$--$99.7$ rule.
Write a conclusion.
Is the test statistically valid?

Exercise 34.6 (This study was also seen in Exercise 27.4.) Carpal tunnel syndrome (CTS) is pain experienced in the wrists. Schmid et al. (2012) compared two different treatments: night splinting, or gliding exercises.

Participants were randomly allocated to one of the two groups. Pain intensity (measured using a quantitative visual analog scale; larger values mean greater pain) were recorded after one week of treatment. The data are summarised in Table 27.6.

What is the parameter? Carefully describe what it means.
Write the hypotheses to answer the RQ.
Compute the $t$-score, and approximate the $P$-value using the $68$--$95$--$99.7$ rule.
Write a conclusion.
Is the test statistically valid?

Exercise 34.7 [Dataset: Dental] (These data were also seen in Exercise 27.7.) Woodward and Walker (1994) recorded the sugar consumption in industrialised (mean: $41.8$ kg/person/year) and non-industrialised (mean: $24.6$ kg/person/year) countries. The software output is shown in Fig. 34.7.

What is the parameter? Carefully describe what it means.
Write the hypotheses.
Write down and interpret the CI.
Write a conclusion for the hypothesis test.
Is the test statistically valid?

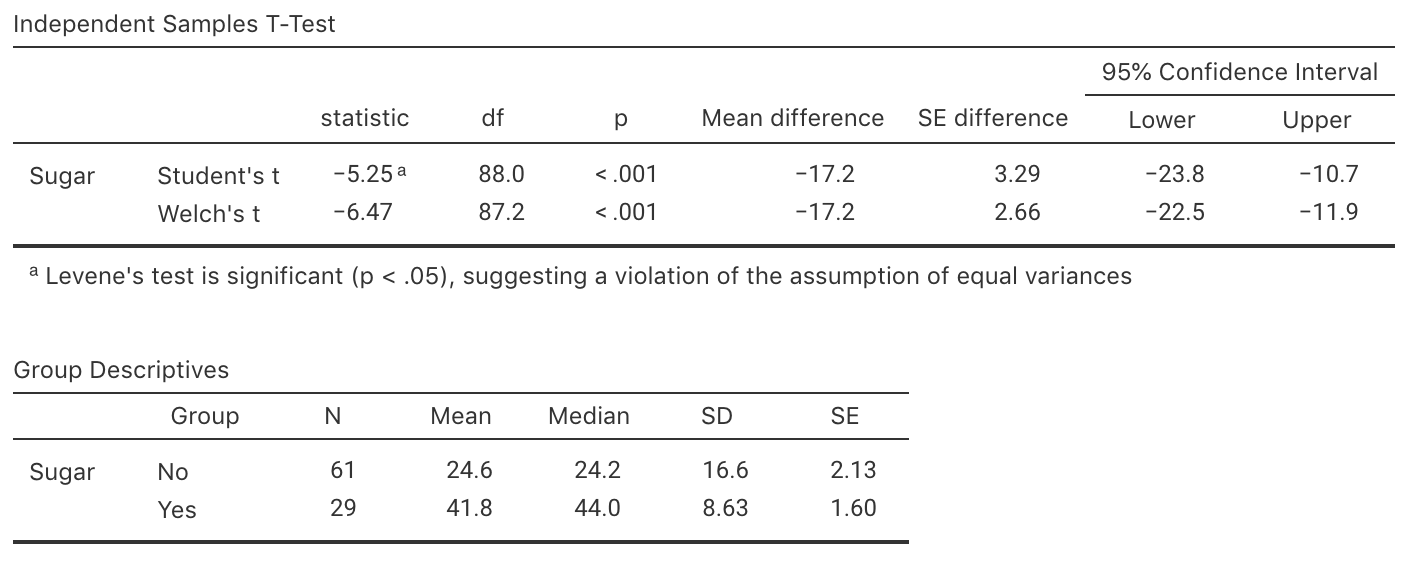
FIGURE 34.7: Software output for the sugar-consumption data.

Exercise 34.8 [Dataset: Deceleration] (These data were also seen in Exercise 27.8.) To reduce vehicle speeds on freeway exit ramps, Ma et al. (2019) studied using additional signage. At one site studied (Ningxuan Freeway), speeds were recorded at various points on the freeway exit for vehicles before the extra signage was added, and then for different vehicles after the extra signage was added.

From this data, the deceleration of each vehicle was determined (Exercise 15.10) as the vehicle left the $120$ km.h^$-1$ speed zone and approached the $80$.h^$-1$ speed zone. Use the data, and the summary in Table 34.7, to test the RQ:

At this freeway exit, is the mean vehicle deceleration the same before extra signage is added and after extra signage is added?

TABLE 34.7: The signage deceleration data summary (in m.s$^{-1}$).
	Mean	Standard deviation	Standard error	Sample size
Before	$\phantom{-}0.0745$	$0.0494$	$0.00802$	$38$
After	$\phantom{-}0.0765$	$0.0521$	$0.00814$	$41$
Change	$-0.0020$		$0.01143$

Exercise 34.9 [Dataset: ForwardFall] (This study was seen in Exercise 27.9.) A study (Wojcik et al. 1999) compared the lean-forward angle in younger and older women (Table 15.6). An elaborate set-up was constructed to measure this lean-forward angle, using harnesses. Consider this RQ:

Among healthy women, is the mean lean-forward angle greater for younger women compared to older women?

Use the software output (Fig. 34.8) to answer these questions:

What is the parameter? Carefully describe what it means.
Is the test one- or two-tailed?
Write the statistical hypothesis.
Use the software output to conduct the hypothesis test.
Write a conclusion.
Is the test statistically valid?

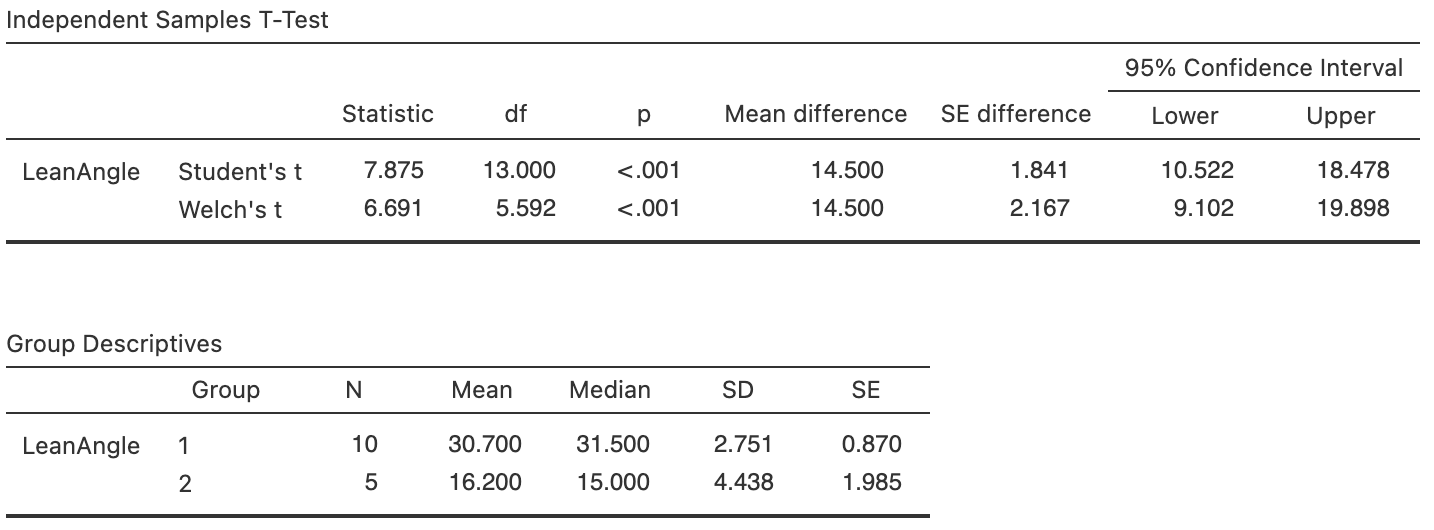
FIGURE 34.8: Software output for the face-plant data.

Exercise 34.10 (This study was seen in Exercise 27.10.) Becker, Stuifbergen, and Sands (1991) compared the access to health promotion (HP) services for people with and without a disability in southwestern of the USA. 'Access' was measured using the quantitative Barriers to Health Promoting Activities for Disabled Persons (BHADP) scale. Higher scores mean greater barriers to health promotion services. The RQ is:

What is the difference between the mean BHADP scores, for people with and without a disability, in southwestern USA?

What is the parameter? Carefully describe what it means.
Write down the hypotheses.
Compute the $t$-score.
Determine the $P$-value.
Write a conclusion.
Is the test statistically valid?

Exercise 34.11 [Dataset: BodyTemp] (This study was seen in Exercise 27.11.) Consider again the body temperature data from Sect. 31.1. The researchers also recorded the gender of the patients, as they also wanted to compare the mean internal body temperatures for females and males.

Use the software output in Fig. 34.9 to perform this test and make a conclusion. Also comment on the practical significance of your results.

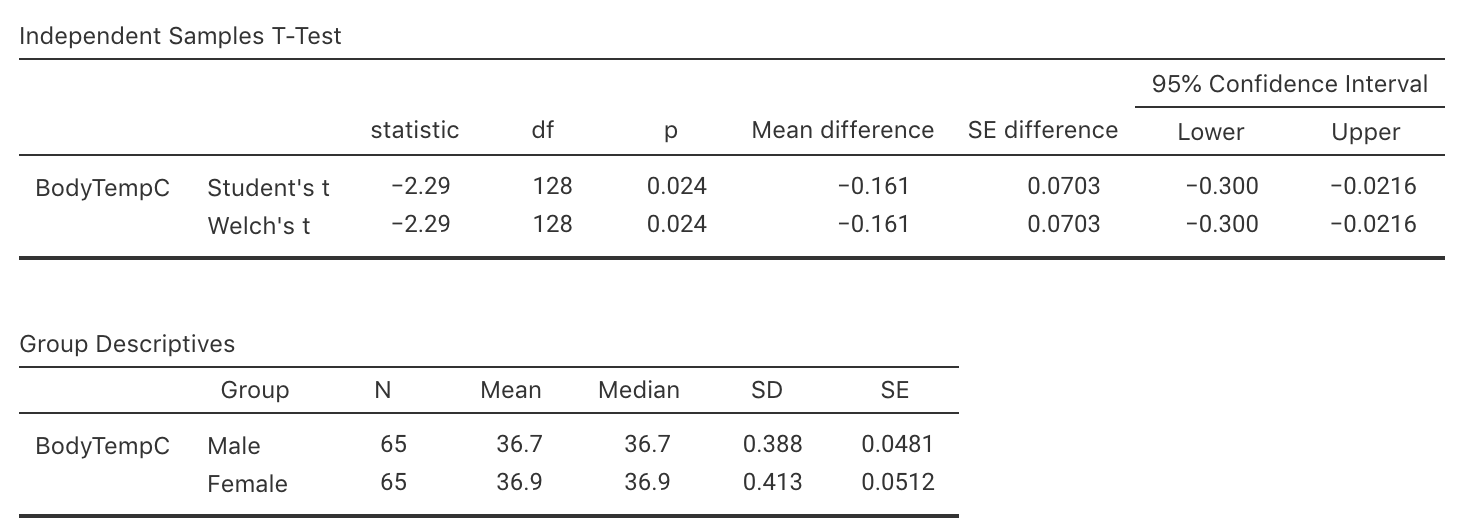
FIGURE 34.9: Software output for the body-temperature data.

Exercise 34.12 (This study was seen in Exercise 27.12.) D. Chapman et al. (2007) compared 'conventional' male paramedics in Western Australia with male 'special-operations' paramedics. Some information comparing their physical profiles is shown in Table 34.8.

Consider comparing the mean grip strength for the two groups of paramedics.
1. Carefully write down the hypotheses.
2. Compute the $t$-score for testing if a difference exists between the two types of paramedics.
3. Approximate the $P$-value using the $68$--$95$--$99.7$ rule.
4. Discuss the conditions required for statistical validity in this context.
5. Make a conclusion.
Consider comparing the mean number of push-ups completed in one minute. The standard error for the difference between the means is $4.0689$.
1. Carefully write down the hypotheses.
2. Compute the $t$-score for testing if a difference exists between the two types of paramedics.
3. Approximate the $P$-value using the $68$--$95$--$99.7$ rule.
4. Discuss the conditions required for statistical validity in this context.
5. Make a conclusion.

TABLE 34.8: The physical profile of conventional ($n=18$) and special operation ($n = 11$) paramedics in Western Australia.
	Conventional	Special Operations
Grip strength (in kg)
Mean	$51$	$56$
Standard deviation	$\phantom{0}8$	$\phantom{0}9$
Standard error
Push-ups (per minutes)
Mean	$36$	$47$
Standard deviation	$10$	$11$
Standard error

33 Tests for the mean difference (paired data)

35 Tests comparing two odds or proportions

	Mean	Sample size	Standard deviation	Standard error
Crayfish region	\(34.17\)	\(12.49\)	\(35\)	\(2.112\)
Not-crayfish region	\(42.57\)	\(\phantom{0}7.79\)	\(41\)	\(1.216\)
Difference	\(\phantom{0}8.39\)			\(2.437\)

	Group A	Group B	Comparing groups
Sample sizes:	\(n_A\)	\(n_B\)
Population means:	\(\mu_A\)	\(\mu_B\)	\(\mu_A - \mu_B\)
Sample means:	\(\bar{x}_A\)	\(\bar{x}_B\)	\(\bar{x}_A - \bar{x}_B\)
Standard deviations:	\(s_A\)	\(s_B\)
Standard errors:	\(\displaystyle\text{s.e.}(\bar{x}_A) = \frac{s_A}{\sqrt{n_A}}\)	\(\displaystyle\text{s.e.}(\bar{x}_B) = \frac{s_B}{\sqrt{n_B}}\)	\(\displaystyle\text{s.e.}(\bar{x}_A - \bar{x}_B)\)

Smokes daily	\(1.27\)	\(0.79\)	\(0.237\)	\(11\)
Smokes occasionally	\(2.77\)	\(1.64\)	\(0.455\)	\(13\)
Does not smoke	\(3.15\)	\(1.93\)	\(0.285\)	\(46\)

	Mean	Standard deviation	Standard error	Sample size
Before	\(\phantom{0}98.02\)	\(13.19\)	\(2.140\)	\(38\)
After	\(\phantom{0}92.34\)	\(13.13\)	\(2.051\)	\(41\)
Speed reduction	\(\phantom{0}\phantom{0}5.68\)		\(2.964\)

	Mean	Standard deviation	\(n\)
Vegan diet	\(13.9\)	\(2.3\)	\(46\)
Conventional diet	\(15.0\)	\(2.7\)	\(47\)
Difference	\(\phantom{0}1.1\)

Scientific Research and Methodology: An introduction to quantitative research and statistics

34 Tests for means of two independent groups

34.1 Introduction: garter snakes

34.2 Tests for comparing two means: \(t\)-test

34.3 Statistical validity conditions

34.4 Tests for comparing more than two means: ANOVA

34.5 Example: speed signage

34.6 Example: chamomile tea

34.7 Chapter summary

34.8 Quick review questions

34.9 Exercises

	Mean	Standard deviation	Standard error	Sample size
Before	\(\phantom{-}0.0745\)	\(0.0494\)	\(0.00802\)	\(38\)
After	\(\phantom{-}0.0765\)	\(0.0521\)	\(0.00814\)	\(41\)
Change	\(-0.0020\)		\(0.01143\)

	Conventional	Special Operations
Grip strength (in kg)
Mean	\(51\)	\(56\)
Standard deviation	\(\phantom{0}8\)	\(\phantom{0}9\)
Standard error
Push-ups (per minutes)
Mean	\(36\)	\(47\)
Standard deviation	\(10\)	\(11\)
Standard error