13 Comparing qualitative data between individuals
So far, you have learnt to ask a RQ, design a study, collect the data, describe the data and summarise the data. In this chapter, you will learn to:
- compare qualitative data between groups of individuals using the appropriate graphs.
- compare qualitative data between groups of individuals using the difference in proportions, odds ratios and summary tables.
13.1 Introduction
Relational RQs compare groups. This chapter considers how to compare qualitative variables in different groups. Tables and graphs are useful this purpose.
13.2 Two-way tables
When more than one qualitative variable is recorded for each individual, the data can be collated into table. When two qualitative variables are cross-tabulated, the resulting table is called a two-way table. As always, the categories for each variable should be exhaustive (cover all levels) and mutually exclusive (observations belong to one and only one level).
Example 13.1 (Two-way tables) Charig et al. (1986) compared two treatments for kidney stones to determine which had a higher success rate. Data were collected from \(700\) UK patients, on two qualitative variables:
- the treatment method ('A' or 'B'): the explanatory variable.
- the result (procedure 'success' or 'failure'): the response variable.
Both variables are qualitative with two levels, and each treatment was used on \(350\) patients. Treatment A was used from 1972--1980, and Treatment B from 1980--1985; that is, treatments were not randomly allocated, and so confounding may be present. For this reason, the researchers also recorded the size of the kidney stone ('small' or 'large') as one possible confounding variable. Firstly, consider just the small stones (Julious and Mullee 1994), displayed in the two-way table in Table 13.1.
| Success | Failure | Total | |
|---|---|---|---|
| Method A | \(\phantom{0}81\) | \(\phantom{0}6\) | \(\phantom{0}87\) |
| Method B | \(234\) | \(36\) | \(270\) |
| Total | \(315\) | \(42\) | \(357\) |
13.3 Summary tables by rows and columns
Each variable in a two-way table can be analysed separately, using percentages or proportions (Sect. 12.4) or odds (Sect. 12.5). For example, the two variables in Table 13.1 (Method; Result) can be analysed separately. For instance:
- the percentage of procedures that were successful is \(315/357\times 100 = 88.2\)%.
- the odds that a procedure was successful is \(315/42 = 7.5\); that is, there were \(7.5\) times as many successful procedures as unsuccessful procedures.
However, to compare Methods A and B, these odds and percentages (or proportions) can be computed for each row (or column) separately.
Example 13.2 (Large kidney stones) The data in Table 13.1 can be summarised by computing proportions or percentages by row. The rows refer to the different Methods, so this will compare success percentages for the two methods.
For the small kidney stones (Table 13.1), the row percentages (Table 13.2 give the proportion of successes for each Method, since the rows represent the counts for Methods A and B. Row proportions allow the proportions within the rows (i.e., for each Method) to be compared:
- Method A: \(81 \div 87 = 0.931\) (or \(93.1\)%) of operations in the sample were successful.
- Method B: \(234\div 270 = 0.867\) (or \(86.7\)%) of operations in the sample were successful.
For small kidney stones, Method A is slightly more successful (\(93.1\)%) than Method B (\(86.7\)%) in the sample. These percentages are collated in Table 13.2.
Odds can also be computed:
- Method A: The odds of success is \(81/6 = 13.5\): there are \(13.5\) more successful procedures than failures for Method A.
- Method B: The odds of success is \(234/36 = 6.5\): there are \(6.5\) more successful procedures than failures for Method B.
The odds of a success is far greater for Method A than Method B in the sample.
| Success | Failure | Total | |
|---|---|---|---|
| Method A | \(93.1\) | \(6.9\) | \(100\) |
| Method B | \(86.7\) | \(13.3\) | \(100\) |
| Success | Failure | |
|---|---|---|
| Method A | \(25.7\) | \(14.3\) |
| Method B | \(74.3\) | \(85.7\) |
| Total | \(100.0\) | \(100.0\) |
Rather than comparing methods (in the rows), the procedure results can be compared (i.e., the columns).
Example 13.3 (Comparing by column) For the small kidney stones (Table 13.1), the column proportions (Table 13.3 give the proportion of successes within each column (i.e., for successes and for failures), since the columns contain the procedure results. Column proportions allow the proportions (or percentages) within columns to be compared:
- Successful procedures: \(81 \div 315 = 0.257\) (or \(25.7\)%) in the sample were with Method A.
- Unsuccessful procedures: \(234\div 315 = 0.143\) (or \(14.3\)%) in the sample were with Method A.
Odds can also be computed:
- Successes: the odds of a success coming from Method A is \(81/234 = 0.346\): there are \(0.346\) more Method A procedures than Method B procedures among the successes.
- Failures: the odds of failure coming from Method A is \(6/36 = 0.167\): there are \(0.167\) more Method A procedures than Method B procedures among the failures.
The odds of a success being a Method A procedure is quite different than the odds of a success being a Method B procedure.
Comparing rows (i.e., using row percentages and row odds) seem more intuitive than column percentages here: they compare the success percentage for each method.
13.4 Graphs
When a qualitative variable is compared across different groups (i.e., comparing between individuals), options for plotting include:
- Stacked bar charts (Sect. 13.4.1);
- Side-by-side bar charts (Sect. 13.4.2); or
- Dot charts (Sect. 13.4.3).
13.4.1 Stacked bar charts
The data can be graphed by using a bar for each level of one variable, and stacking the bars for the levels of the second variable. Bars indicate the counts (or percentages) in each category. The levels can be on the horizontal or vertical axis, but placing the level names on the vertical axis often makes for easier reading, and room for long labels.
The axis displaying the counts (or percentages) should start from zero, since the height of the bars visually implies the frequency of those observations (see Example 17.3).
Example 13.4 (Stacked bar charts) For the kidney-stone data in Example 13.1, a stacked bar chart can be created by producing a bar for each method, and stacking the successes and failures for each method (Fig. 13.1, top left panel).
Rather than using numbers, the percentages separately within each group can be used too (Fig. 13.1, bottom left panel).
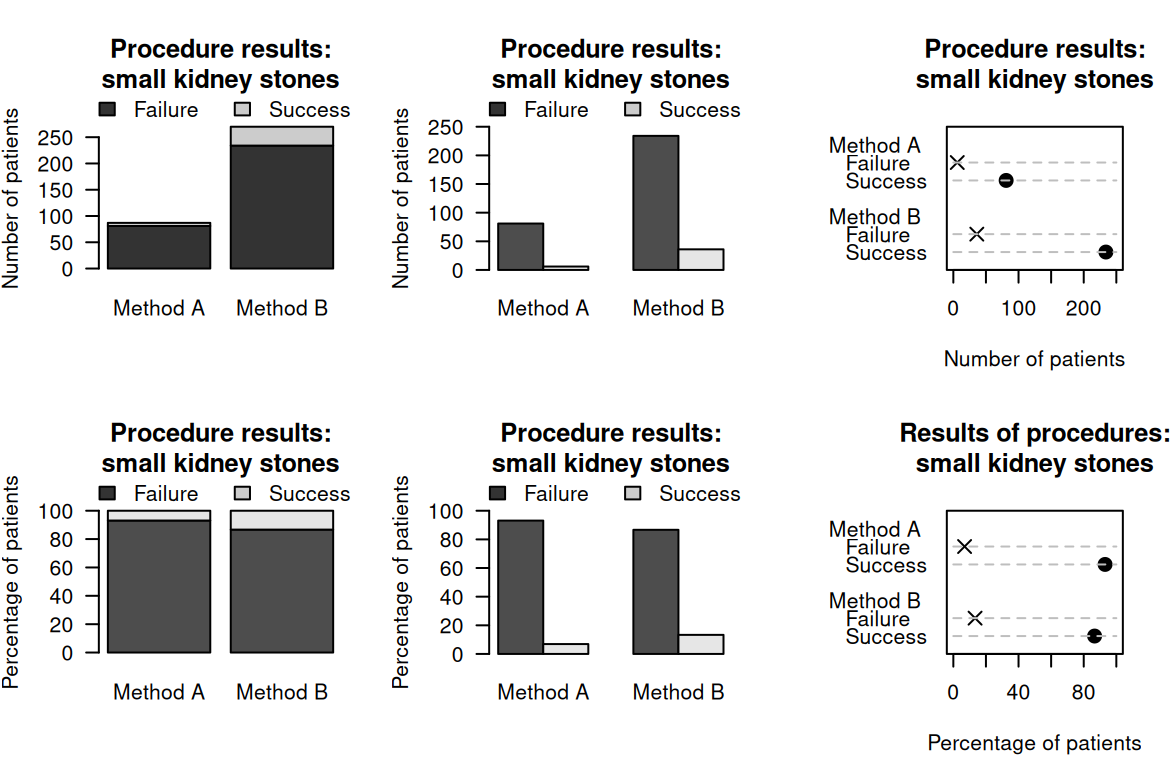
FIGURE 13.1: Six plots for the small kidney-stone data. Top plots: displaying the numbers on the vertical axis. Bottom plots: displaying the percentages for each Method on the vertical axis. Left: stacked bar chart. Centre: side-by-side bar charts. Right: dot charts.
13.4.2 Side-by-side bar charts
Instead of stacking the success and failures bars on top of each other, these bars can be placed side-by-side for each method. Bars indicate the counts (or percentages) in each category. The levels can be on the horizontal or vertical axis, but placing the level names on the vertical axis often makes for easier reading, and room for long labels.
The axis displaying the counts (or percentages) should start from zero, since the height of the bars visually implies the frequency of those observations (see Example 17.3).
Example 13.5 (Side-by-side bar charts) For the kidney-stone data in Example 13.1, a side-by-side bar chart can be created by producing two bars for each method (one for failures; one for successes), and placing these side-by-side (Fig. 13.1, centre panels). Again, numbers or percentages within each method can be graphed.
13.4.3 Dot charts
Instead of bars, dots (or other symbols) can be used in place of the bars in a side-by-side bar chart.
The axis displaying the counts (or percentages) should start from zero, since the distance of the dots from the axis visually implies the frequency of those observations (see Example 17.3).
13.4.4 Other variations
Many variations of these charts are possible, by making certain choices:
- use a stacked bar chart, side-by-side bar chart, or dot chart.
- use percentages or counts on one of the axis. (The percentages can be percentages of the total, or within the total for each level of the variable, as in the centre plots in Fig. 13.1.)
- use the counts (or percentage) on either the horizontal or vertical axis.
- decide which variable can be used as the first division of the data.
The guiding principle remains: the purpose of a graph is to display the information in the clearest, simplest possible way, to facilitate understanding the message(s) in the data.
Using a computer to create graphs is recommended, and using a computer makes it easy to try different variations to find the graph that best displays the message in the data.
13.5 Summarising the comparison: difference between proportions
The small kidney stone data (Table 13.1) can be summarised using proportions (or percentages):
- Method A: the proportion of successful procedures is \(0.931\) (or, the percentages of successful procedures is \(93.1\)%).
- Method B: the proportion of successful procedures is \(0.867\) (or, the percentages of successful procedures is \(86.7\)%).
The difference between these proportions (or percentages) is \(0.064\) (or \(6.4\) percentage points). The difference between the proportions is a statistic, and the (unknown) difference between the population proportiobs is a parameter.
13.6 Summarising the comparison: odds ratios
The small kidney stone data (Table 13.1) can be summarised using odds:
- Method A: the odds of success are \(13.5\) (\(13.5\) times as many successes as failures).
- Method B: the odds of success are \(6.5\) (\(6.5\) times as many successes as failures).
The odds of success for Method A and Method B are very different. In the sample, the odds of success for Method A is many times greater than for Method B. In fact, in the sample, the odds of success for Method A is \(13.5\div 6.5 = 2.08\) times the odds of a success for Method B. This value is the odds ratio (OR). The sample odds ratio is a statistic, and the (unknown) population odds ratio is a parameter.
Definition 13.1 (Odds Ratio (OR)) The odds ratio (often written OR) is the ratio of the odds of an result of interest in one group, compared to the odds of the same result in a different group: \[ \text{Odds ratio} = \frac{\text{Odds of a result in Group A}} {\text{Odds of the same result in Group B}}. \]
Example 13.7 (Odds ratios) For the small kidney stone data, the odds of a success for Method A is \(81\div6 = 13.5\). The odds of a success for Method B is \(234\div36 = 6.5\). The odds ratio is then computed as \(13.5\div 6.5 = 2.08\). The odds have been computed with the rows.
This means that the odds of a success for Method A is about \(2.08\) times the odds of a success for Method B.
Most software computes the odds ratio from a two-way table by using the values in the first row and first column on the top of the fractions when computing the odds and the odds ratio. In Example 13.7, for instance, the odds for both methods were computed with the Column 1 values on the top of the fraction (\(81\) and \(234\)), and the odds ratio comparing the rows was computed with the Row 1 odds (\(13.5\)) on top of the fraction.
However, the odds ratio could also be computed using the odds within the columns (i.e., comparing the columns), rather than within the rows (as in Example 13.8).
Example 13.8 (Odds ratios) For the small kidney stone data, the odds of a success coming from Method A (i.e., Column 1) is \(81/234 = 0.3462\). Likewise, the odds of a failure (i.e., Column 2) coming from Method A is \(6\div36 = 0.1667\). The odds ratio is \(0.3462\div 0.1667 = 2.08\), as in Example 13.7. This means that the odds of Method A producing a success is about \(2.08\) times the odds of Method A producing a failure.
The two odds ratio calculations produce the same value. The odds ratio can be interpreted in either way: as in this example or as in Example 13.7. Both interpretations are correct.
The odds ratio can be interpreted in either of these ways (i.e., both are correct):
- The odds compare Row 1 counts to Row 2 counts, for both columns. The odds ratio then compares the Column 1 odds to the Column 2 odds.
- The odds compare Column 1 counts to Column 2 counts. The odds ratio then compares the Row 1 odds to the Row 2 odds.
Odds and odds ratios are computed with the first row and first column values on the top of the fraction. While both are correct, one way usually makes more sense.
The OR compares the odds of the same result (e.g., success) in two different groups (e.g., Method A and Method B). This means that a \(2\times 2\) table can be summarised using one number: the odds ratio (OR).
When interpreting odds ratios (or ORs):
- odds ratios greater than \(1\) mean the odds of the result is larger for the group on top of the division compared to the group in the bottom.
- odds ratios equal to \(1\) mean the odds of the result is the same for both groups (on the top and the bottom of the division).
- odds ratios is less than \(1\) mean the odds of the result is smaller for the group on the top of the division compared to the group in the bottom.
The following short video may help explain some of these concepts:
The numerical summary information for comparing qualitative variables can be collated in a table. The data should be summarised by one of the qualitative variables, producing percentages and odds for the other.
Example 13.9 (Numerical summary table) For the small kidney-stone data, the summary of the data can be tabulated as in Table 13.4, using percentages and odds.
| Percentage success | Odds of success | Sample size | |
|---|---|---|---|
| Method A | \(93.1\) | \(13.500\) | \(\phantom{0}87\) |
| Method B | \(86.7\) | \(\phantom{-}6.500\) | \(270\) |
| \(6.4\) | \(2.08\) |
13.7 Example: large kidney stones
The data in Table 13.1 are for small kidney stones. Data were also recorded for the large kidney stones (Table 13.5). As for small kidney stones, the success percentages can be computed for both methods:
- Method A: Success proportion for large kidney stones: \(192/263 = 0.730\), or \(73.0\)%.
- Method B: Success proportion for large kidney stones: \(55/80 = 0688\), or \(68.8\)%.
For large kidney stones, then, Method A has a higher success proportion than Method B, just as with the small kidney stones.
| Success | Failure | Total | |
|---|---|---|---|
| Method A | \(192\) | \(71\) | \(263\) |
| Method B | \(\phantom{0}55\) | \(25\) | \(\phantom{0}80\) |
So, could the data for small (Table 13.1) and large kidney stones (Table 13.5) be combined, to produce a single two-way table of just Method and Result (Table 13.6), without separating by size?
| Success | Failure | Total | |
|---|---|---|---|
| Method A | \(273\) | \(77\) | \(350\) |
| Method B | \(289\) | \(61\) | \(350\) |
To summarise:
- Method A is more successful for small stones (\(93.1\)% vs \(86.7\)%);
- Method A is more successful for large stones (\(73.0\)% vs \(68.8\)%); but
- Method B is more successful for all stones combined (\(78.0\)% vs \(82.6\)%).
That seems strange: Method A performs better for small and large kidney stones, but Method B performs better when ignoring size.
The size of the stone is a confounding variable (Fig. 13.2). Size is associated with the method (small stones are treated more often with Method B) and with the result (small stones have a higher success proportion for both methods).
This confounding could have been avoided by randomly allocating a treatment method to patients. However, random allocation was not possible in this study, so the researchers used a different method to manage confounding: recording the size of the kidney stones (see Sect. 7.2).
In this example, incorporating information about a potential confounder (the size of the kidney stone) is important, otherwise the wrong (opposite) conclusion is reached: Method B would be incorrectly considered better if the size of the stones was ignored, when the better method really is Method A.
This is called Simpson's paradox. If the size of the kidney stone had not been recorded, size would be a lurking variable, and the incorrect conclusion would have been reached.
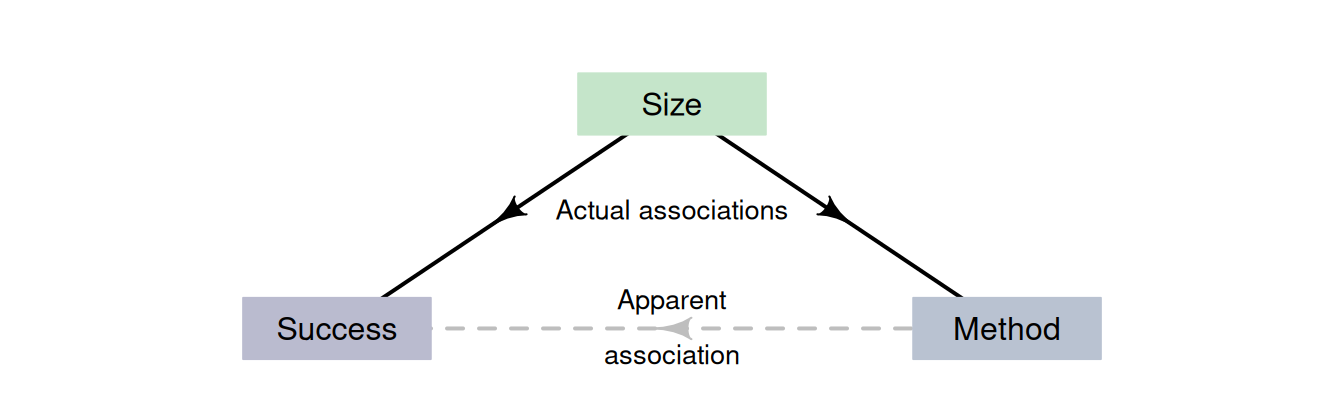
FIGURE 13.2: The size of the stones is associated with both the success percentage and the method.
13.8 Example: water access
López-Serrano et al. (2022) recorded data about access to water for three rural communities in Cameroon (see Sects. 11.10 and 12.7). The study could be used to determine contributors to the incidence of diarrhoea in young children (\(85\) households had children under \(5\)). A cross-tabulation (Table 13.7) shows the relationship with keeping livestock; the numerical summary table (Table 13.8) may suggest a difference due to keeping livestock. The comparison in Fig. 13.3 includes some categories with small sample sizes, so the percentages shown may not be precise estimates of the population values.
As usual, the data come from one of countless possible samples, but the RQ is about the population, so making a definitive decision is difficult.
| No diarrhoea | Diarrhoea | |
|---|---|---|
| Does not have livestock | \(17\) | \(\phantom{0}3\) |
| Has livestock | \(42\) | \(23\) |
| Percentage | Odds | Sample size | |
|---|---|---|---|
| Household does not have livestock | \(\phantom{-}15.0\) | \(0.176\) | \(20\) |
| Household has livestock | \(\phantom{-}35.4\) | \(0.548\) | \(65\) |
| \(-20.4\) | \(0.322\) |
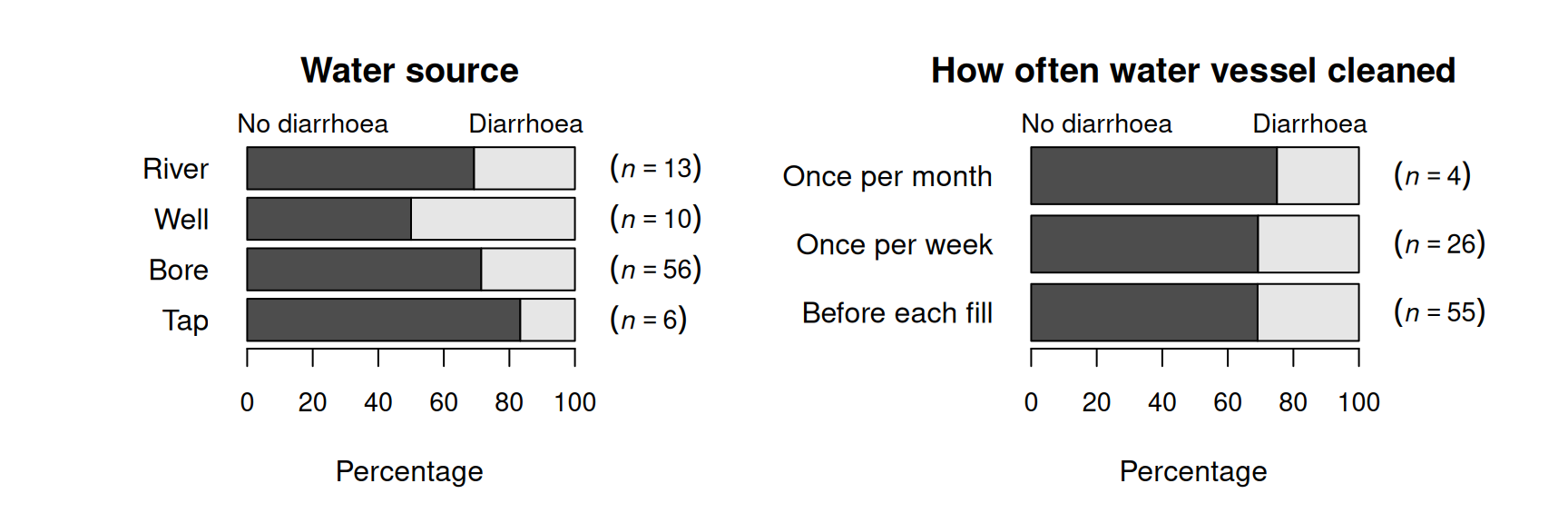
FIGURE 13.3: Percentage of children with and without diarrhoea in the last two weeks, by water source (left) and how often the water vessel was cleaned (right).
13.9 Chapter summary
Qualitative data can be compared between different groups (between individuals comparisons) using a stacked bar chart, side-by-side bar chart or a dot chart. The data can be displayed in a two-way table, then summarised numerically by comparing proportions, percentages and odds. The odds ratio (OR) and the difference between the proportions can be used to compare the two different groups.
13.10 Quick revision questions
A study (Alley et al. 2017) examined social media use (Table 13.9), using a representative sample of Queenslanders at least \(18\) years of age (from the \(2013\) Queensland Social Survey).
- Compute the sample proportion of urban residents who use social media.
- Compute the sample proportion of rural residents who use social media.
- Compute the sample odds of urban residents who use social media.
- Compute the sample odds of rural residents who use social media.
- Compute the sample odds ratio of using social media, comparing urban to rural residents.
- Compute the sample difference between the proportions using social media, comparing urban to rural residents.
| Doesn't use SM | Uses SM | Total | |
|---|---|---|---|
| Rural residents | \(\phantom{0}78\) | \(\phantom{0}89\) | \(167\) |
| Urban residents | \(416\) | \(568\) | \(984\) |
13.11 Exercises
Answers to odd-numbered exercises are available in App. E.
Exercise 13.1 Köchling et al. (2019) studied hangovers and recorded, among other information, when people vomited after consuming alcohol. Table 13.10 shows how many people vomited after consuming beer followed by wine, and how many people vomited after consuming only wine.
- Compute the row proportions. What do these mean?
- Compute the column percentages. What do these mean?
- Compute the overall percentage of drinkers who vomited.
- Compute the sample odds that a wine-only drinker vomited.
- Compute the sample odds that a beer-then-wine drinker vomited.
- Compute the sample odds ratio, comparing the odds of vomiting for wine-only drinkers to beer-then-wine drinkers.
- Compute the sample odds ratio, comparing the odds of vomiting for beer-then-wine drinkers to wine-only drinkers.
- Compute the difference between the sample proportions of people vomiting, comparing beer-then-wine drinkers to wine-only drinkers.
- What do the data suggest about the relationship?
| Beer then wine | Wine only | |
|---|---|---|
| Vomited | \(\phantom{0}6\) | \(\phantom{0}6\) |
| Didn't vomit | \(62\) | \(22\) |
Exercise 13.2 Stirrat (2008) recorded the sex of adult and young wallabies at the East Point Reserve, Darwin. In December 1993, \(91\) males and \(188\) female adult wallabies were recorded, and \(13\) male and \(22\) female young wallabies were recorded.
- Create the two-way table of counts.
- For adult wallabies, what proportion of adult wallabies were males?
- For adult wallabies, what are the odds that a female was observed?
- For young wallabies, what percentage of wallabies were males?
- For young wallabies, what are the odds that a female was observed?
- What is the odds ratio of observing an adult wallaby, comparing females to males?
- What is the difference between the sample proportions of females wallabies, comparing adults to young?
- Create a summary table.
- Sketch a graph to display the data.
- What do the data suggest about the relationship?
Exercise 13.3 [Dataset: EmeraldAug]
The Southern Oscillation Index (SOI) is a standardised measure of the air pressure difference between Tahiti and Darwin, shown to be related to rainfall in some parts of the world (Stone, Hammer, and Marcussen 1996), and especially Queensland, Australia (Stone and Auliciems 1992; P. K. Dunn 2001).
The rainfall at Emerald (Queensland) was recorded for Augusts between 1889 to 2002 inclusive (P. K. Dunn and Smyth 2018), for months when the monthly average SOI was positive and non-positive (zero or negative); see Table 13.11.
- Compute the percentage of Augusts with no rainfall.
- Compute the percentage of Augusts with no rainfall, in Augusts with a non-positive SOI.
- Compute the percentage of Augusts with no rainfall, in Augusts with a positive SOI.
- Compute the odds of no August rainfall.
- Compute the odds of no August rainfall, in Augusts with a non-positive SOI.
- Compute the odds of no August rainfall, in Augusts with a positive SOI.
- Compute the odds ratio of no August rainfall, comparing Augusts with non-positive SOI to Augusts with a positive SOI.
- Interpret this OR.
- Create a summary table.
- Sketch a graph to display the data.
| Non-positive SOI | Positive SOI | |
|---|---|---|
| No rainfall recorded | \(14\) | \(\phantom{0}7\) |
| Rainfall recorded | \(40\) | \(53\) |
Exercise 13.4 Haselgrove et al. (2008) asked boys and girls in Western Australia about back pain from carrying school bags (Table 13.12).
- Compute the percentage of boys reporting back pain from carrying school bags.
- Compute the percentage of girls reporting back pain from carrying school bags.
- Compute the odds of boys reporting back pain from carrying school bags.
- Compute the odds of girls reporting back pain from carrying school bags.
- Compute the odds of a child reporting back pain.
- Compute the odds ratio of reporting back pain, comparing boys to girls.
- Interpret this OR.
- Create a summary table.
- Sketch a graph to display the data.
| Males | Females | |
|---|---|---|
| No back pain | \(330\) | \(226\) |
| Back pain | \(280\) | \(359\) |
Exercise 13.5 Using the information in Table 12.2, create a stacked bar chart to compare the responses to the three questions.
Exercise 13.6 T. C. Russell, Herbert, and Kohen (2009) studied road-kill possums (Table 13.13).
- Identify the two variables, and classify them as nominal or ordinal.
- Sketch some graphs to display the data.
- What is the main message in the data? What graph shows this best?
| Unknown sex | Male | Female | |
|---|---|---|---|
| Autumn | \(75\) | \(25\) | \(21\) |
| Winter | \(74\) | \(27\) | \(22\) |
| Spring | \(71\) | \(10\) | \(18\) |
| Summer | \(58\) | \(10\) | \(12\) |
Exercise 13.7 The data in Table 13.14 come from a study of Iranian children aged \(6\)--\(18\) years old (Kelishadi et al. 2017).
- Compute the proportion of females who skipped breakfast.
- Compute the proportion of males who skipped breakfast.
- Compute the odds of a female skipping breakfast.
- Compute the odds of a male skipping breakfast.
- Compute the odds ratio comparing the odds of skipping breakfast, comparing females to males.
- Interpret this OR.
- Construct a summary table.
| Skips breakfast | Doesn't skip breakfast | Total | |
|---|---|---|---|
| Females | \(2383\) | \(4257\) | \(6640\) |
| Males | \(1944\) | \(4902\) | \(6846\) |
Exercise 13.8 Yonekura et al. (2020) studied Japanese women and their coffee drinking habits (Table 13.15).
- Compute the proportion of coffee drinkers who are also smokers.
- Compute the proportion of non-coffee drinkers who are also smokers.
- Compute the odds of a coffee drinker being a smoker.
- Compute the odds of a non-coffee drinker being a smoker.
- Compute the odds ratio comparing the odds of being a smoker, comparing coffee drinkers to non-coffee drinkers.
- Interpret this OR.
- Construct a summary table.
| Smokers | Non-smokers | |
|---|---|---|
| Coffee drinkers | \(10\) | \(66\) |
| Non-coffee drinkers | \(\phantom{0}2\) | \(84\) |
Exercise 13.9 In a study of how well emergency dispatchers recognised signs of stroke (Oostema, Chassee, and Reeves 2018), the data shown below were collected.
| Sex of patients | Dispatcher suspected stroke | Dispatcher missed stroke |
|---|---|---|
| Male | 67 | 43 |
| Female | 97 | 39 |
- Sketch a side-by-side or stacked bar chart to display the data.
- Of the male patients, what percentage had their stroke symptoms missed by the dispatcher?
- Of the female patients, what percentage had their stroke symptoms missed by the dispatcher?
- For the male patients, what are the odds that they had their stroke symptoms missed by the dispatcher?
- For the female patients, what are the odds that they had their stroke symptoms missed by the dispatcher?
- What is the odds ratio that a patients had their stroke symptoms missed by the dispatcher, comparing males to females?
- Construct a numerical summary table.
Exercise 13.10 Soccer is a unique in that one aspect is 'the purposeful use of the unprotected head for controlling and advancing the ball' (Kirkendall, Jordan, and Garrett 2001). Some researchers suspect that repeatedly 'heading' the ball may impair brain function. A study (Kirkendall, Jordan, and Garrett 2001) was conducted to determine (p. 157)
...whether long-term or chronic neuropsychological dysfunction (i.e., concussion) was present in collegiate soccer players
Data were collected from \(240\) college students for two variables:
- The student type: One of 'soccer player' (\(63\) students), 'non-soccer athlete' (\(96\) students), or 'non-athlete' (\(81\) students).
- The number of head concussions: Each student was asked about the number of head concussions they had experienced; 'zero' (\(158\) students), 'one' (\(45\) students), or 'two or more' (\(37\) students) concussions.
Use the study data (Table 13.16) to answer the following questions.
| 0 | 1 | 2 or more | Total | |
|---|---|---|---|---|
| Soccer players | 45 | 5 | 13 | 63 |
| Non-soccer athletes | 68 | 25 | 3 | 96 |
| Non-athletes | 45 | 15 | 21 | 81 |
| Total | 158 | 45 | 37 | 240 |
- Classify the two variables.
- Compute the percentage of college students in the sample overall that have received exactly one concussion.
- Among the non-athletes, compute the odds of receiving two or more concussions. Interpret what this means.
- Among the soccer players, compute the odds of receiving two or more concussions. Interpret what this means.
- Compute the odds ratio comparing the odds of a non-athlete player receiving two or more concussions to the odds of a soccer player receiving two or more concussions.
- Create a table of column percentages. What do these tell you?
- Create a table of row percentages. What do these tell you?
- Which one of these tables is probably more sensible, and why?