13 Day 13 (June 21)
13.2 Understanding confidence intervals using synthetic data
What should we expect from a confidence interval?
- What is the statistic?
- Which quantities are random and which are fixed?
- How often should a 95% CI covers the true value of \(\beta\)?
How do we know if a CI performs as advertised?
- Derive the CI theoretically
- Evaluate the interval estimator using Monte Carlo simulation
Monte Carlo simulation to evaluate a CI
library(latex2exp) library(plotrix) beta.truth <- c(3,1) # True value of beta sigma2.truth <- 1000 # True value of sigma2 n <- 50 # Sample size for each simulated data set x <- seq(1,100,length.out = n) # Covariate X <- model.matrix (~x) # Design matrix q.sims <- 10^2 # How many data sets should I simulate? sim.results <- matrix(,nrow=q.sims,ncol=3) colnames(sim.results) <- c("beta_1","lower.limit","upper.limit") set.seed(9409) for(i in 1:q.sims){ y <- X%*%beta.truth + rnorm(n,0,sqrt(sigma2.truth)) # Generate data m1 <- lm(y~x) sim.results[i,1:3] <- c(coef(m1)[2],confint(m1)[2,]) } # Mean of beta1 mean(sim.results[,1])## [1] 1.013225# Plot confidence interval library(plotrix) plotCI(c(1:q.sims),sim.results[,1],li=sim.results[,2],ui=sim.results[,3], sfrac=0.005,pch=20,xlab="Simulation data set",ylab=expression(beta[1])) abline(a=beta.truth[2],b=0,col="gold",lwd=3)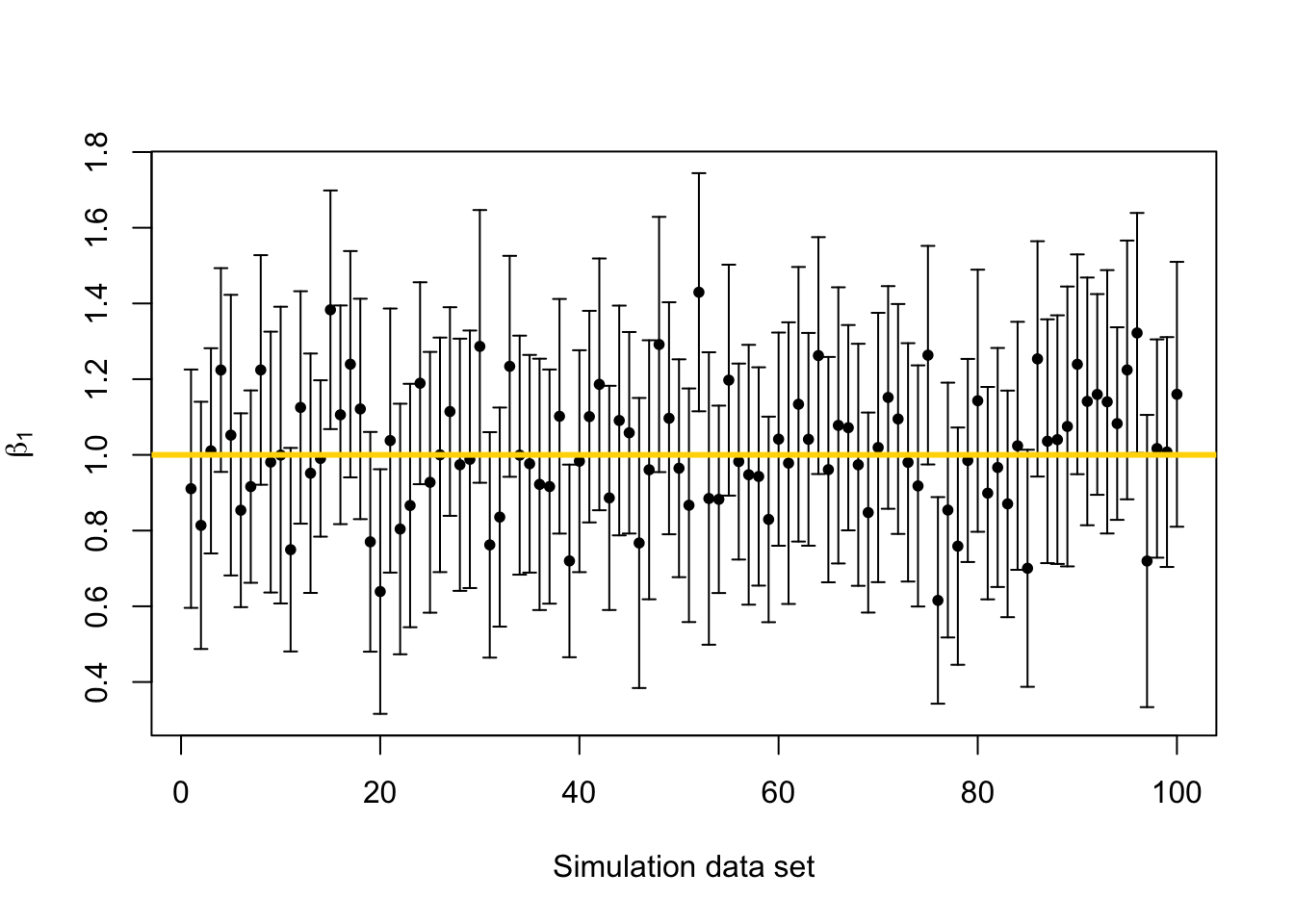
# Calculate the coverage probability covered <- ifelse(sim.results[,2] < beta.truth[2] & sim.results[,3] > beta.truth[2],1,0) mean(covered)## [1] 0.94