Chapter 3 Point estimation
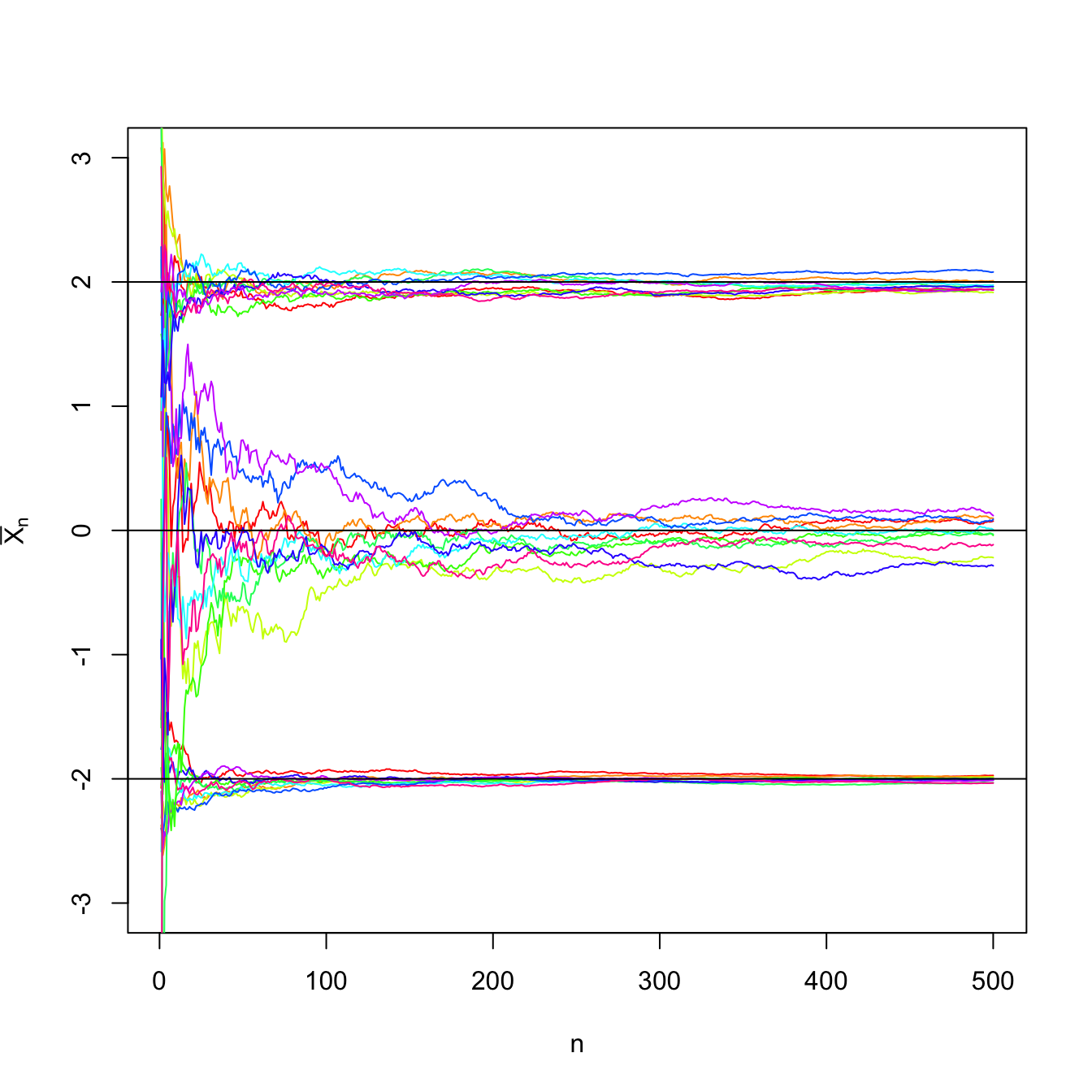
Figure 3.1: Convergence of the sample mean \(\bar{X}_n\) to \(\mu\) in probability as \(n\to\infty\) in a \(\mathcal{N}(\mu,\sigma^2)\) population with \((\mu,\sigma^2)\in\{(-2,0.5),(0,3),(2,1)\}.\) For each set of parameters, \(N=10\) srs’s of sizes increasing until \(n=500\) were simulated. The black horizontal lines represent the values of \(\mu.\) The convergence towards \(\mu\) happens due to the law of large numbers irrespective of the value of \(\sigma^2,\) yet the convergence is faster for smaller variances.
This chapter analyses the most relevant characteristics of an estimator: bias and mean square error, invariance, consistency, sufficiency, efficiency, robustness, etc.
We begin introducing the basic terminology.
Definition 3.1 (Estimation, estimator, and estimate) Estimation is the process of inferring or attempting to guess the value of one or several population parameters from a sample. Therefore, an estimator \(\hat{\theta}\equiv\hat{\theta}(X_1,\ldots,X_n)\) of a parameter \(\theta\in\Theta\) is a statistic of the sample \((X_1,\ldots,X_n)\) with range in the parameter space \(\Theta.\) The observed value or realization of an estimator is referred to as estimate.
Example 3.1 The following table shows the usual estimators for well-known parameters.
| Parameter | Estimator |
|---|---|
| Proportion \(p\) | Sample proportion \(\bar{X}\) |
| Mean \(\mu\) | Sample mean \(\bar{X}\) |
| Variance \(\sigma^2\) | Sample variance \(S^2\) and quasivariance \(S'^2\) |
| Standard deviation \(\sigma\) | Sample standard deviation \(S\) and quasistandard deviation \(S'\) |