Chapter 5 Confidence intervals
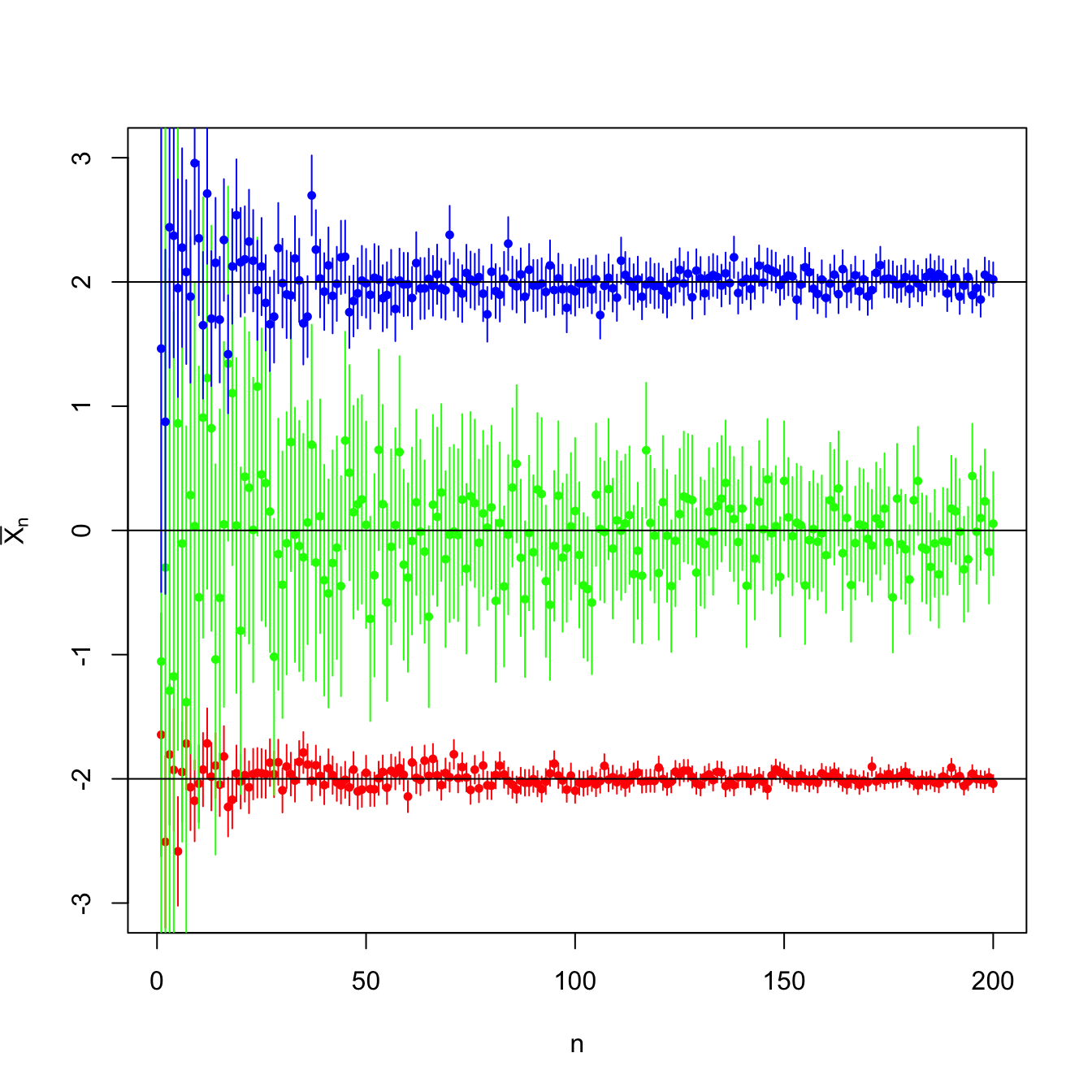
Figure 5.1: Evolution of \(95\%\)-confidence intervals (vertical segments) for the mean \(\mu\) constructed from the sample mean \(\bar{X}_n\) in a \(\mathcal{N}(\mu,\sigma^2)\) population with \((\mu,\sigma^2)\in\{(-2,0.5),(0,3),(2,1)\}.\) For each set of parameters, \(N=10\) srs’s of sizes increasing until \(n=200\) were simulated. As \(n\) grows, the confidence intervals shorten, irrespective of the value of \(\sigma^2.\) The confidence intervals contain most of the time the parameter \(\mu\) (black horizontal lines). A new sample is generated for each \(n\).
Confidence intervals are the main tools in statistical inference for quantifying and summarizing the uncertainty behind an estimation. In this chapter we introduce the principles of confidence intervals, elaborate their specifics for the suite of normal populations, and see their applicability in more general settings through the use of asymptotic approximations.