13 GAMs en regresión
Una forma de extnder el modelo de regresión lineal,
\[ y_i = \beta_0+\beta_1x_{i1}+\ldots+\beta_px_{ip}+\epsilon_i \]
para permitir relaciones no lineales entre cara caracerística y la respuesta es reemplazar cada componente lineal \(\beta_jx_{ij}\) con una función no lineal \(f_j(x_{ij})\) (suave). Podemos escribir el modelo como:
\[ y_i= \beta_0 + \sum_{j=1}^{p}f_j(x_{ij})+\epsilon_i \]
\[ = \beta_0 + f_1(x_{i1})+ f_2(x_{i2})+\cdots+f_p(x_{ip})\epsilon_i \]
Notemos que es aditivo porque podemos calcular funciones separadas para cada variable y luego agregar todas las contribuciones.
Lo que hemos revisado de polinomios locales puede usarse sin problema para especificar cada función.
13.1 Ejemplo
Ajustemos el modelo:
\[ wage = \beta_0 + f_1(year) + f_2(age) + f_3(education) + \epsilon \]
Cargamos y revisamos los datos:
library(ISLR)
data("Wage")
str(Wage)## 'data.frame': 3000 obs. of 11 variables:
## $ year : int 2006 2004 2003 2003 2005 2008 2009 2008 2006 2004 ...
## $ age : int 18 24 45 43 50 54 44 30 41 52 ...
## $ maritl : Factor w/ 5 levels "1. Never Married",..: 1 1 2 2 4 2 2 1 1 2 ...
## $ race : Factor w/ 4 levels "1. White","2. Black",..: 1 1 1 3 1 1 4 3 2 1 ...
## $ education : Factor w/ 5 levels "1. < HS Grad",..: 1 4 3 4 2 4 3 3 3 2 ...
## $ region : Factor w/ 9 levels "1. New England",..: 2 2 2 2 2 2 2 2 2 2 ...
## $ jobclass : Factor w/ 2 levels "1. Industrial",..: 1 2 1 2 2 2 1 2 2 2 ...
## $ health : Factor w/ 2 levels "1. <=Good","2. >=Very Good": 1 2 1 2 1 2 2 1 2 2 ...
## $ health_ins: Factor w/ 2 levels "1. Yes","2. No": 2 2 1 1 1 1 1 1 1 1 ...
## $ logwage : num 4.32 4.26 4.88 5.04 4.32 ...
## $ wage : num 75 70.5 131 154.7 75 ...Ajustamos el modelo con splines naturales (cúbicos) para las dos primeras funciones y una constante para cada nivel de la tercera usando variables dicotómicas:
library(gam)
gam1 <- lm(wage ~ ns(year, 4) + ns(age, 5) + education, data = Wage)
summary(gam1)##
## Call:
## lm(formula = wage ~ ns(year, 4) + ns(age, 5) + education, data = Wage)
##
## Residuals:
## Min 1Q Median 3Q Max
## -120.513 -19.608 -3.583 14.112 214.535
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 46.949 4.704 9.980 < 2e-16 ***
## ns(year, 4)1 8.625 3.466 2.488 0.01289 *
## ns(year, 4)2 3.762 2.959 1.271 0.20369
## ns(year, 4)3 8.127 4.211 1.930 0.05375 .
## ns(year, 4)4 6.806 2.397 2.840 0.00455 **
## ns(age, 5)1 45.170 4.193 10.771 < 2e-16 ***
## ns(age, 5)2 38.450 5.076 7.575 4.78e-14 ***
## ns(age, 5)3 34.239 4.383 7.813 7.69e-15 ***
## ns(age, 5)4 48.678 10.572 4.605 4.31e-06 ***
## ns(age, 5)5 6.557 8.367 0.784 0.43328
## education2. HS Grad 10.983 2.430 4.520 6.43e-06 ***
## education3. Some College 23.473 2.562 9.163 < 2e-16 ***
## education4. College Grad 38.314 2.547 15.042 < 2e-16 ***
## education5. Advanced Degree 62.554 2.761 22.654 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 35.16 on 2986 degrees of freedom
## Multiple R-squared: 0.293, Adjusted R-squared: 0.2899
## F-statistic: 95.2 on 13 and 2986 DF, p-value: < 2.2e-16Vemos que el modelo es significativo. Veamos puntos de influencia:
par(mfrow = c(2,2))
plot(gam1)
par(mfrow = c(1,1))Ahora las relaciones entre las variables
par(mfrow = c(1,3))
plot.Gam(gam1, se = TRUE, col = "red",all.terms = TRUE)## Warning in plot.window(...): "all.terms" is not a graphical parameter## Warning in plot.xy(xy, type, ...): "all.terms" is not a graphical parameter## Warning in axis(side = side, at = at, labels = labels, ...): "all.terms" is not
## a graphical parameter
## Warning in axis(side = side, at = at, labels = labels, ...): "all.terms" is not
## a graphical parameter## Warning in box(...): "all.terms" is not a graphical parameter## Warning in title(...): "all.terms" is not a graphical parameter## Warning in plot.window(...): "all.terms" is not a graphical parameter## Warning in plot.xy(xy, type, ...): "all.terms" is not a graphical parameter## Warning in axis(side = side, at = at, labels = labels, ...): "all.terms" is not
## a graphical parameter
## Warning in axis(side = side, at = at, labels = labels, ...): "all.terms" is not
## a graphical parameter## Warning in box(...): "all.terms" is not a graphical parameter## Warning in title(...): "all.terms" is not a graphical parameter## Warning in plot.window(...): "all.terms" is not a graphical parameter## Warning in plot.xy(xy, type, ...): "all.terms" is not a graphical parameter## Warning in axis(side = side, at = at, labels = labels, ...): "all.terms" is not
## a graphical parameter
## Warning in axis(side = side, at = at, labels = labels, ...): "all.terms" is not
## a graphical parameter## Warning in box(...): "all.terms" is not a graphical parameter## Warning in title(...): "all.terms" is not a graphical parameter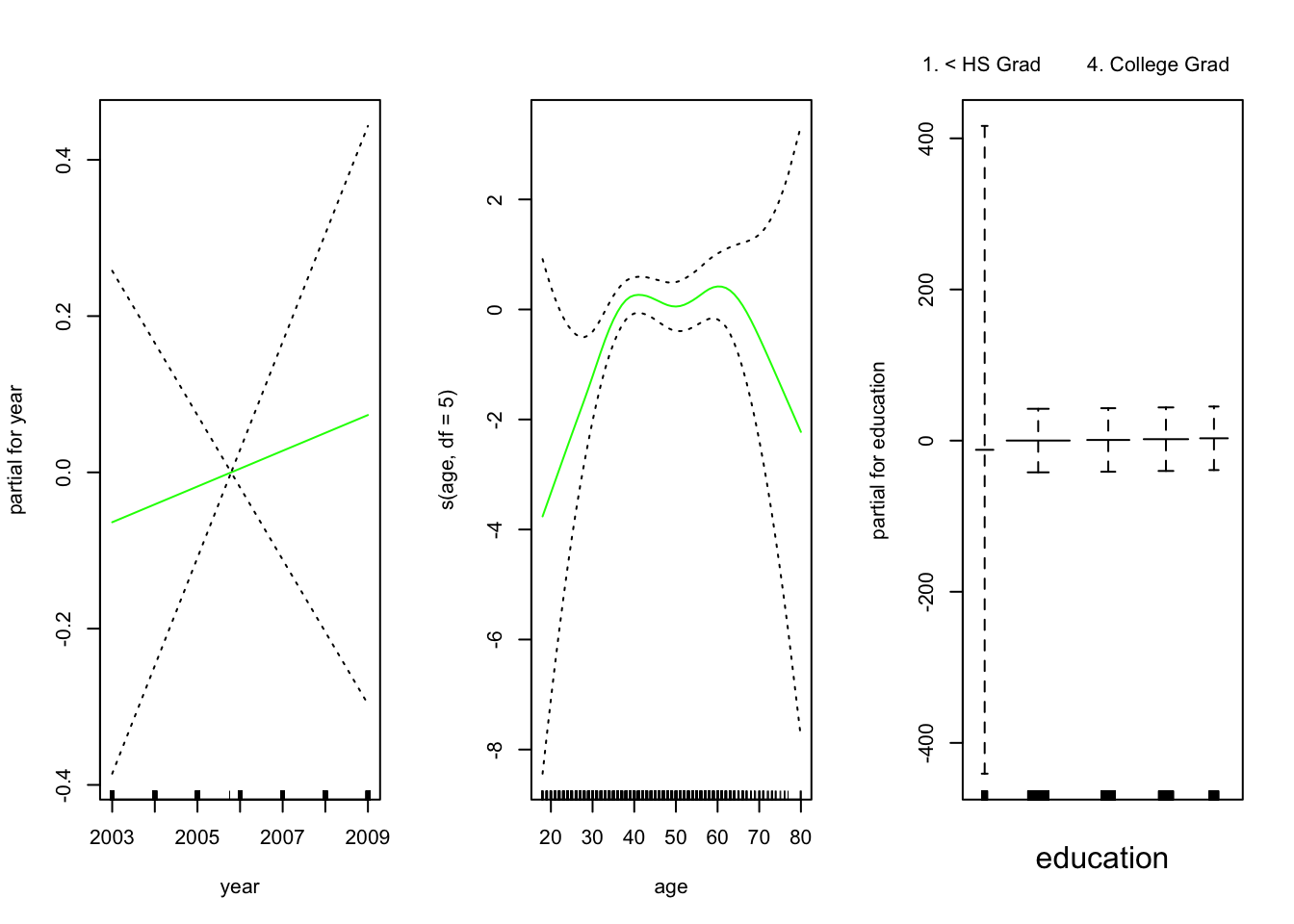
par(mfrow = c(1,1))El panel de la izquierda indica que manteniendo la edad y la educación fijas, el salario tiende a aumentar ligeramente con el año; esto puede ser debido a la inflación.
El panel central indica que la educación y el año se mantienen fijos, el salario tiende a ser más alto para los valores intermedios de la edad, y más bajo para los muy jóvenes y muy viejos.
El panel de la derecha indica que el año y la edad se mantienen fijos, el salario tiende a aumentar con la educación: Cuanto más educada es una persona, mayor es su salario, en promedio. Todos estos hallazgos son intuitivos.
Backfitting: Este método se ajusta a un modelo que involucra múltiples predictores mediante la actualización repetida del ajuste para cada predictor de uno en uno, manteniendo los otros fijos. La belleza de este enfoque es que cada vez que actualizamos una función, simplemente aplicamos el método de ajuste para esa variable a un residuo parcial (\(r_i = y_i-f_1(x_{i1})-f_2(x_{i2})\)).