2 Regresión Lineal

2.1 Una idea general

Abordemos las primeras ideas de regresión lineal a través de un ejemplo práctico:

• Abrir la tabla 2.1
• Creamos dos variables, Ingreso y Consumo Esperado

ingresos <- seq(80,260,20)
consumoEsperado <- c(65,77,89,101,113,125,137,149,161,173)

Ahora:

• Generar un gráfico tipo línea entre ingresos y consumo esperado
• Superponer un gráfico tipo puntos de $X$ e $Y$ (tabla 2.1) sobre el gráfico anterior
• Generar un gráfico tipo puntos $X$ e $Y$ en azul
• Superponer un gráfico tipo lineas de Ingresos y consumo esperado sobre el gráfico anterior en azul

uu <- "https://raw.githubusercontent.com/vmoprojs/DataLectures/master/GA/Tabla2_1.csv"
familia <- read.csv(file=url(uu),sep=";",dec=".",header=T)
names(familia)

## [1] "X" "Y"

cbind(ingresos,consumoEsperado) 

##       ingresos consumoEsperado
##  [1,]       80              65
##  [2,]      100              77
##  [3,]      120              89
##  [4,]      140             101
##  [5,]      160             113
##  [6,]      180             125
##  [7,]      200             137
##  [8,]      220             149
##  [9,]      240             161
## [10,]      260             173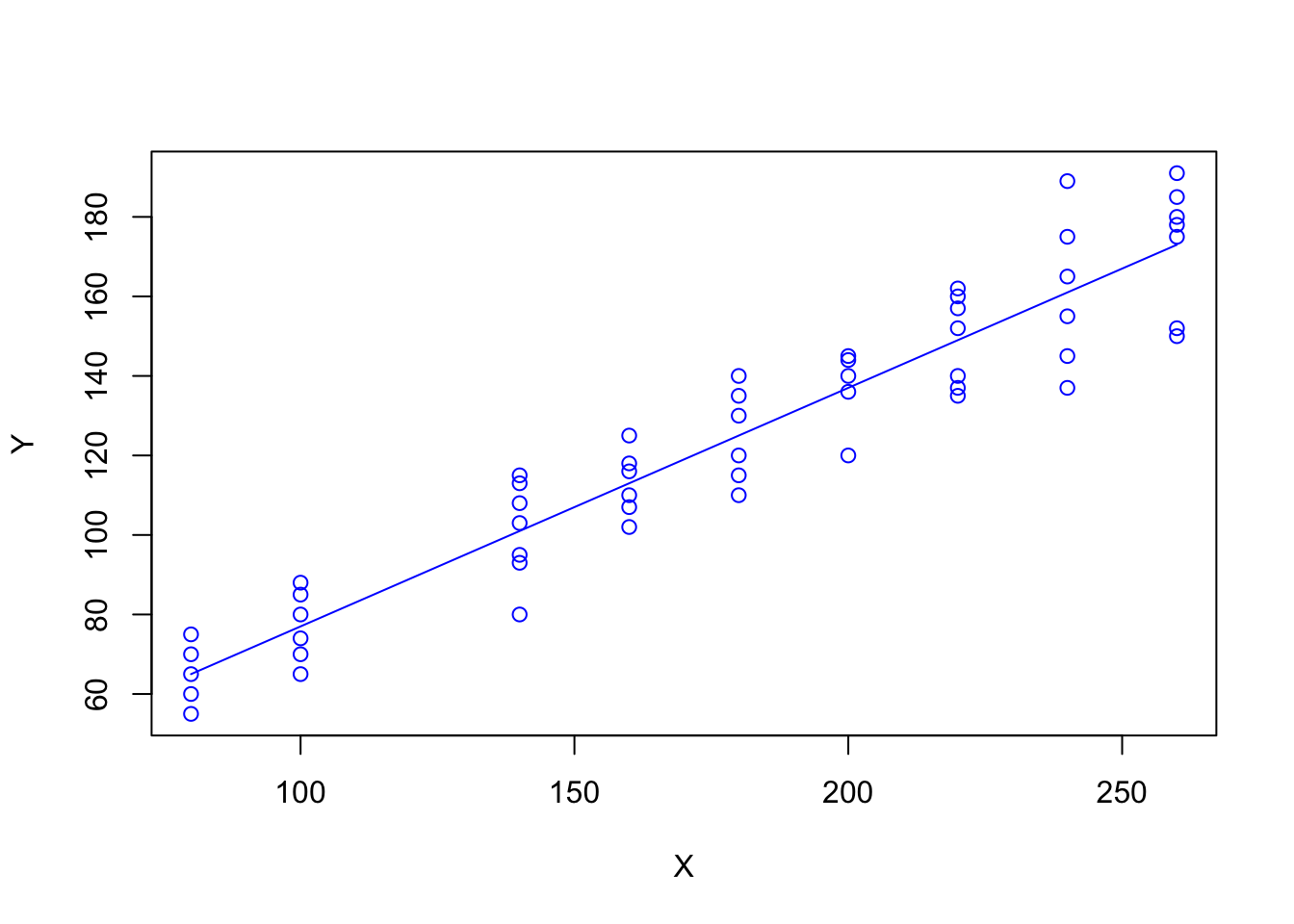

with(familia,plot(X,Y,col="blue"))
lines(ingresos,consumoEsperado,col="blue")

• ¿Qué hemos hecho?

$$E(Y|X_i) = f(X_i)$$

$$E(Y|X_i) = \beta_1+\beta_2X_i$$

$$u_i = Y_i - E(Y|X_i)$$

$$Y_i = E(Y|X_i) + u_i$$

• ¿Qué significa que sea lineal?

El término regresión lineal siempre significará una regresión lineal en los parámetros; los $\beta$ (es decir, los parámetros) se elevan sólo a la primera potencia. Puede o no ser lineal en las variables explicativas $X$

Para evidenciar la factibilidad del uso de RL en este caso, vamos a obtener una muestra de la población:

• Creamos una variable indicadora para obtener una muestra indice=seq(1,55,1)
• Usamos sample para obtener una muestra sin reemplazo del tamaño indicado: muestra <- sample(indice,size=20)
• Obtenemos el valor de la variable $X$ en la posición de muestra + ingreso.muestra <- X[muestra] + consumo.muestra <- Y[muestra]

indice <- seq(1,55,1)  
muestra <- sample( familia$X ,size=20)
muestra <- sample(indice,size=20)
ingreso.muestra <- familia$X[muestra]
consumo.muestra <- familia$Y[muestra]

• Graficamos ingreso.muestra vs consumo.muestra
• Realizar una regresión lineal de las variables muestra: + plot(ingreso.muestra,consumo.muestra) + ajuste.1=(lm(consumo.muestra\sim ingreso.muestra)) + abline(coef(ajuste.1))
• Generar una segunda muestra (muestra.2 por ejemplo) y comparar los coeficientes
• ¿Qué conclusiones puede sacar?

plot(ingreso.muestra,consumo.muestra)
ajuste.1 <- (lm(consumo.muestra~ingreso.muestra))
ajuste.1

## 
## Call:
## lm(formula = consumo.muestra ~ ingreso.muestra)
## 
## Coefficients:
##     (Intercept)  ingreso.muestra  
##         13.4825           0.6019

coef(ajuste.1)

##     (Intercept) ingreso.muestra 
##      13.4824798       0.6018568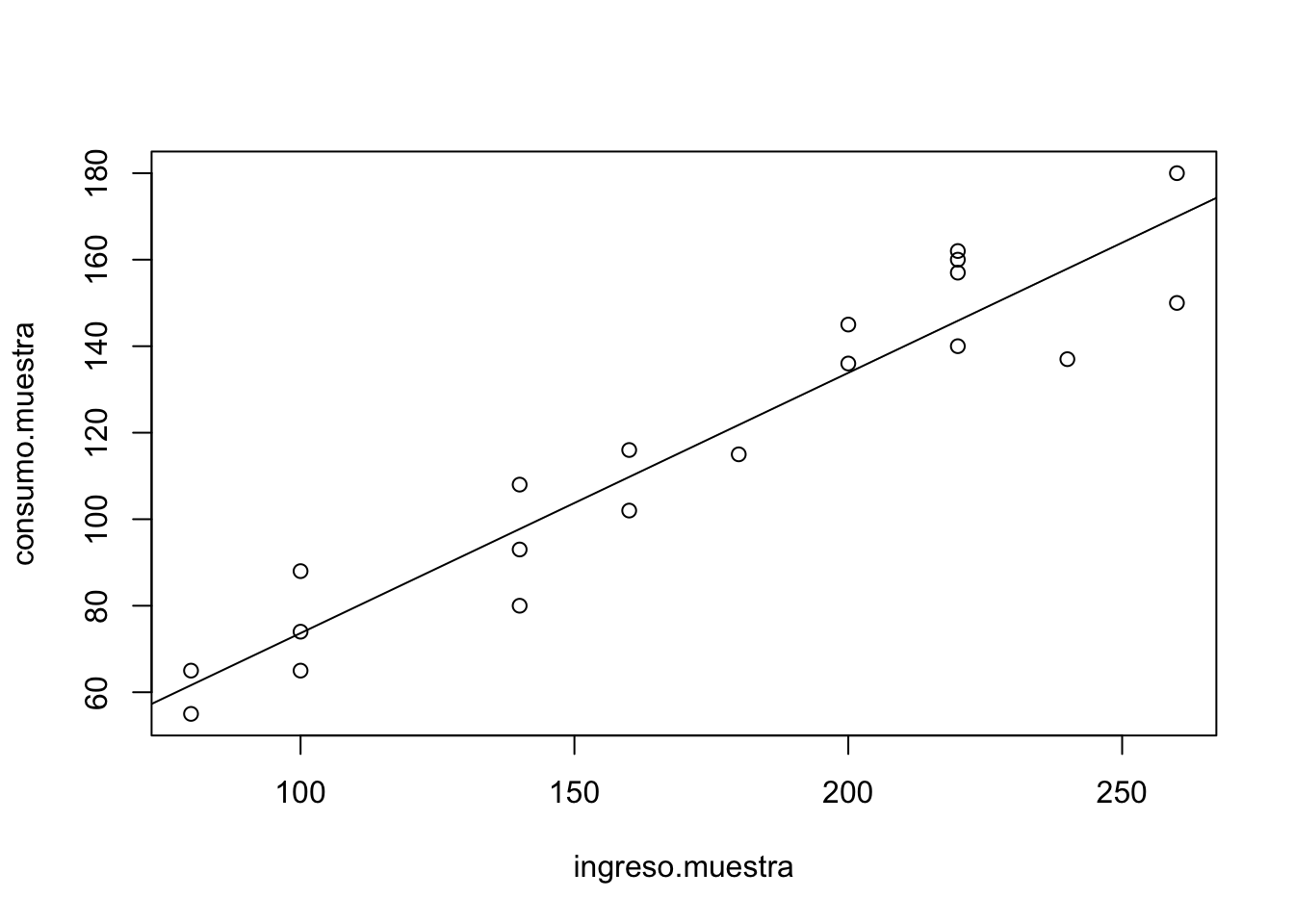

abline(coef(ajuste.1))

2.1.1 Regresión: Paso a paso

La función poblacional sería:

$$Y_i = \beta_1 + \beta_2X_i+u_i$$

Como no es observable, se usa la muestral

$$Y_i=\hat{\beta}_1+\hat{\beta}_2X_i+\hat{u}_i$$

$$Y_i=\hat{Y}_i+\hat{u}_i$$

$$\hat{u}_i = Y_i-\hat{Y}_i$$

$$\hat{u}_i = Y_i- \hat{\beta}_1-\hat{\beta}_2X_i$$

Es por esto que los residuos se obtienen a través de los betas:

$$\label{eq1} \sum\hat{u}_i^2 =\sum (Y_i- \hat{\beta}_1-\hat{\beta}_2X_i)^2$$

$$\sum\hat{u}_i^2 =f(\hat{\beta}_1,\hat{\beta}_2)$$

Diferenciando ([$\eqref{eq1}$]) se obtiene:

$$\hat{\beta}_2 = \frac{S_{xy}}{S_{xx}}$$

$$\hat\beta_1 = \bar{Y} - \hat\beta_2\bar{X}$$ donde

$$S_{xx} = \sum_{i=1}^{n}x_i^2-n\bar{x}^2$$

$$S_{xy} = \sum_{i=1}^{n}x_i y_i-n\bar{x}\bar{y}$$

Abrimos la tabla3.2, vamos a obtener:

• salario promedio por hora (Y) y
• los años de escolaridad (X).

uu <- "https://raw.githubusercontent.com/vmoprojs/DataLectures/master/GA/Tabla3_2.csv"

consumo <- read.csv(url(uu),sep=";",dec=".",header=TRUE)

media_x <- mean(consumo$X, na.rm=T)
media_y <- mean(consumo$Y, na.rm=T)

n <- length(consumo$X)*1

sumcuad_x <- sum(consumo$X*consumo$X)
sum_xy <- sum(consumo$X*consumo$Y)

beta_som <- (sum_xy-n*media_x*media_y)/
    (sumcuad_x-n*(media_x^2))
alpha_som  <- media_y-beta_som*media_x

• Verificamos lo anterior mediante:

reg.1 <- (lm(consumo$Y~consumo$X))
coef(reg.1)

## (Intercept)   consumo$X 
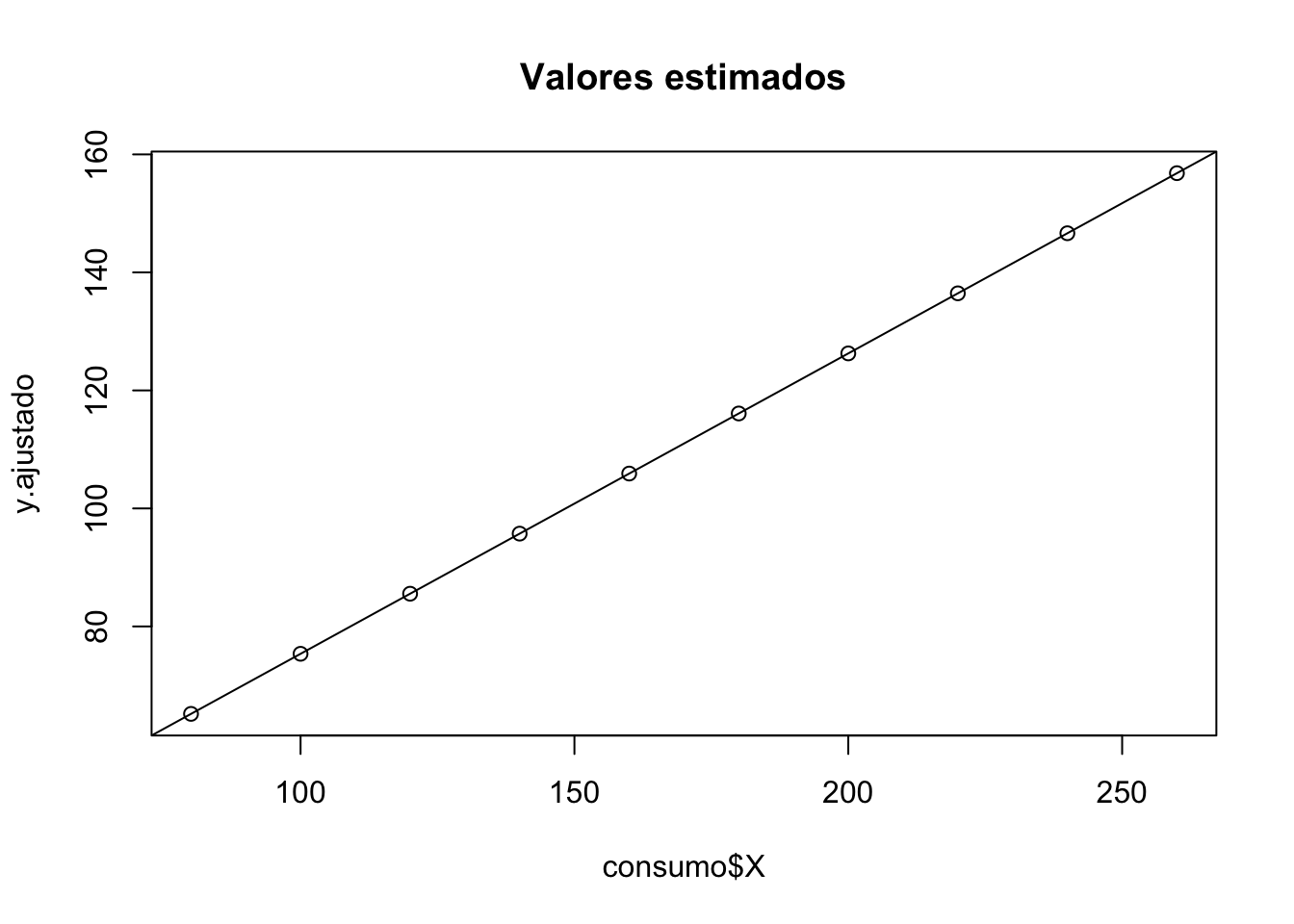
##  24.4545455   0.5090909

• Veamos cómo queda nuestra estimación:

y.ajustado <- alpha_som+beta_som*consumo$X
head(cbind(consumo$X,y.ajustado))

##          y.ajustado
## [1,]  80   65.18182
## [2,] 100   75.36364
## [3,] 120   85.54545
## [4,] 140   95.72727
## [5,] 160  105.90909
## [6,] 180  116.09091

• Gráficamente:

plot(consumo$X,y.ajustado,main="Valores estimados")
abline(a=alpha_som,b=beta_som)

• Encontremos los residuos:

y.ajustado <- alpha_som+beta_som*consumo$X
e <- consumo$Y-y.ajustado

• Comparemos los resultados

head(cbind(consumo$X,consumo$Y,y.ajustado,e))

##              y.ajustado           e
## [1,]  80  70   65.18182   4.8181818
## [2,] 100  65   75.36364 -10.3636364
## [3,] 120  90   85.54545   4.4545455
## [4,] 140  95   95.72727  -0.7272727
## [5,] 160 110  105.90909   4.0909091
## [6,] 180 115  116.09091  -1.0909091

• Veamos la media y la correlación

mean(e) 

## [1] -1.421085e-15

cor(e,consumo$X) 

## [1] 1.150102e-15

• Hallemos el coeficiente de determinación o bondad de ajuste.

• Para ello necesitamos la suma de cuadrados total y la suma de cuadramos explicada

SCT <- sum((consumo$Y-media_y)^2)
SCE <- sum((y.ajustado-media_y)^2)
SCR <- sum(e^2)
R_2 <- SCE/SCT

summary(reg.1)

## 
## Call:
## lm(formula = consumo$Y ~ consumo$X)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -10.364  -4.977   1.409   4.364   8.364 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 24.45455    6.41382   3.813  0.00514 ** 
## consumo$X    0.50909    0.03574  14.243 5.75e-07 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 6.493 on 8 degrees of freedom
## Multiple R-squared:  0.9621, Adjusted R-squared:  0.9573 
## F-statistic: 202.9 on 1 and 8 DF,  p-value: 5.753e-07

Pruebas de hipótesis:

$$H_0:\beta_2=0$$ $$H_1:\beta_2\neq 0$$

• Abrir la tabla 2.8

uu <- "https://raw.githubusercontent.com/vmoprojs/DataLectures/master/GA/table2_8.csv"
datos  <- read.csv(url(uu),sep=";",dec=".",header=TRUE)

• Regresar el gasto total en el gasto en alimentos
• ¿Son los coeficientes diferentes de cero?

t1 <- (0.43681-0)/0.07832
(1-pt(t1,53))*2

## [1] 8.445209e-07

• ¿Son los coeficientes diferentes de $0.5$?

# H0: beta1 = 0.5
t2 <- (0.43681-0.5)/0.07832
(1-pt(abs(t2),53))*2

## [1] 0.4233771

Interpretación de los coeficientes

• El coeficiente de la variable dependiente mide la tasa de cambio (derivada=pendiente) del modelo
• La interpretación suele ser En promedio, el aumento de una unidad en la variable independiente produce un aumento/disminución de $\beta_{i}$ cantidad en la variable dependiente
• Interprete la regresión anterior.

2.1.1.1 Práctica: Paridad del poder de compra

Abrir la tabla 5.9, las variables son:

uu <- "https://raw.githubusercontent.com/vmoprojs/DataLectures/master/GA/Tabla5_9.csv"
datos <- read.csv(url(uu),sep=";",dec=".",header=TRUE)
names(datos) 

## [1] "COUNTRY" "BMACLC"  "BMAC."   "EXCH"    "PPP"     "LOCALC"

• BMACLC: Big Mac Prices in Local Currency
• BMAC$: Big Mac Prices in $
• EXCH: Actual $ Exchange Rate 4/17/2001
• PPP: Implied Purchasing-Power Parity of the Dollar: Local Price Divided by Price in United States
• LOCALC: Local Currency Under (-)/Over (+) Valuation Against $, Percent

Empezamos con el buen summary. ¿Notan algo raro?

• Debemos limpiar los datos

datos$EXCH[which(  datos$EXCH  == -99999)] <- NA
datos$PPP[which(  datos$PPP == -99999)] <- NA
datos$LOCALC[which(  datos$LOCALC   ==-99999)] <- NA

Regresamos la paridad del poder de compra en la tasa de cambio

reg1 <- lm(datos$EXCH~datos$PPP)
summary(reg1)

## 
## Call:
## lm(formula = datos$EXCH ~ datos$PPP)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -816.86   54.64   60.72   61.85  411.42 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -61.38890   44.98703  -1.365    0.183    
## datos$PPP     1.81527    0.03994  45.450   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 235.9 on 28 degrees of freedom
##   (1 observation deleted due to missingness)
## Multiple R-squared:  0.9866, Adjusted R-squared:  0.9861 
## F-statistic:  2066 on 1 and 28 DF,  p-value: < 2.2e-16

La PPA sostiene que con una unidad de moneda debe ser posible comprar la misma canasta de bienes en todos los países.

2.1.1.2 Práctica: Sueño

De la carpeta Datos, abrir sleep.xls

uu <- "https://raw.githubusercontent.com/vmoprojs/DataLectures/master/WO/sleep75.csv"
datos <- read.csv(url(uu), header = FALSE) 

agregamos los nombres:

names (datos) <- c("age","black","case","clerical","construc","educ","earns74","gdhlth","inlf", "leis1", "leis2", "leis3", "smsa", "lhrwage", "lothinc", "male", "marr", "prot", "rlxall", "selfe", "sleep", "slpnaps", "south", "spsepay", "spwrk75", "totwrk" , "union" , "worknrm" , "workscnd", "exper" , "yngkid","yrsmarr", "hrwage", "agesq")    

Veamos los datos gráficamente y corramos la regresión:

#totwrk minutos trabajados por semana
#sleep minutos dormidos por semana
plot(datos$totwrk,datos$sleep)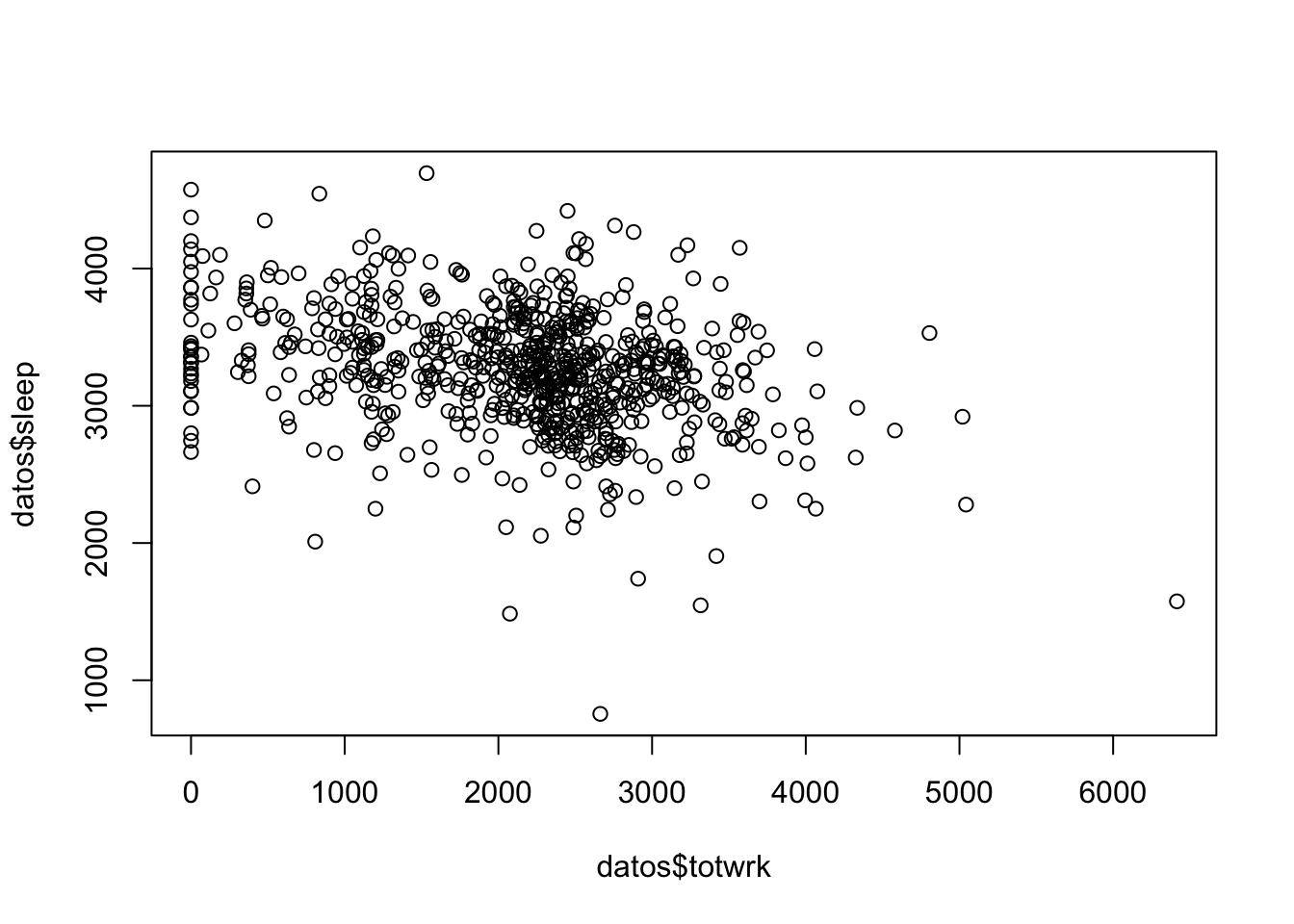

dormir <- lm(sleep~totwrk,data = datos)
summary(dormir)

## 
## Call:
## lm(formula = sleep ~ totwrk, data = datos)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -2429.94  -240.25     4.91   250.53  1339.72 
## 
## Coefficients:
##               Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 3586.37695   38.91243  92.165   <2e-16 ***
## totwrk        -0.15075    0.01674  -9.005   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 421.1 on 704 degrees of freedom
## Multiple R-squared:  0.1033, Adjusted R-squared:  0.102 
## F-statistic: 81.09 on 1 and 704 DF,  p-value: < 2.2e-16

• ¿Existe una relación entre estas variables?
• Interprete el modelo

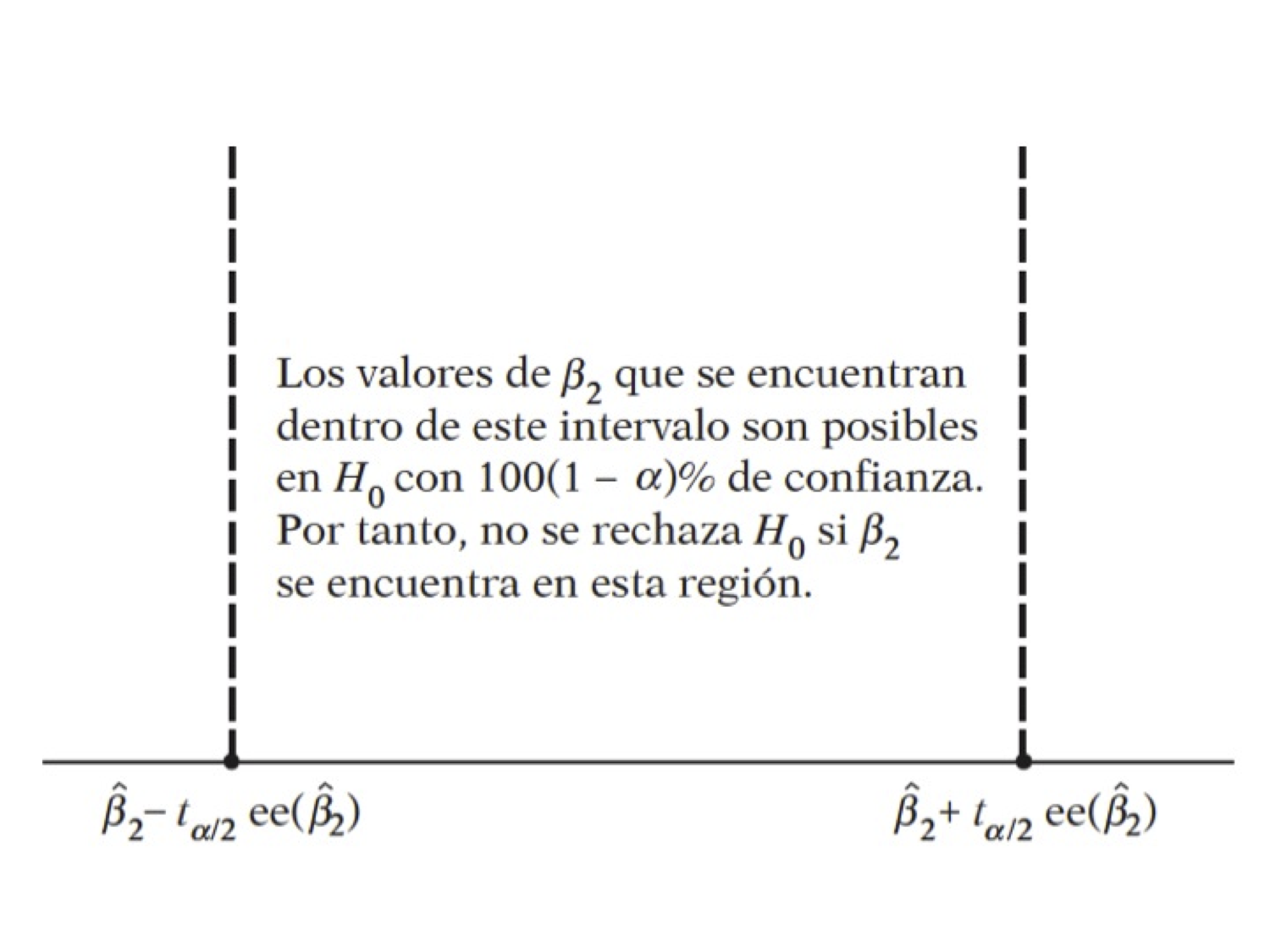
Intervalo de confianza para $\beta_2$ y veamos los residuos

-0.15084-2*c(-0.01677,0.01677)

## [1] -0.11730 -0.18438

hist(resid(dormir),freq=F)
lines(density(resid(dormir)))

Derivaciones del modelo

2.2 Transformaciones Lineales

Abrir la tabla 31.3, regresar el ingreso per cápita en el número de celulares por cada 100 personas:

uu <- "https://raw.githubusercontent.com/vmoprojs/DataLectures/master/GA/Table%2031_3.csv"
datos <- read.csv(url(uu),sep=";",dec=".",header=TRUE)

reg.1 <- lm(Cellphone ~ Pcapincome,data = datos)
summary(reg.1)

## 
## Call:
## lm(formula = Cellphone ~ Pcapincome, data = datos)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -45.226 -10.829  -2.674   8.950  47.893 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 1.248e+01  6.109e+00   2.043   0.0494 *  
## Pcapincome  2.313e-03  3.158e-04   7.326  2.5e-08 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 19.92 on 32 degrees of freedom
## Multiple R-squared:  0.6265, Adjusted R-squared:  0.6148 
## F-statistic: 53.67 on 1 and 32 DF,  p-value: 2.498e-08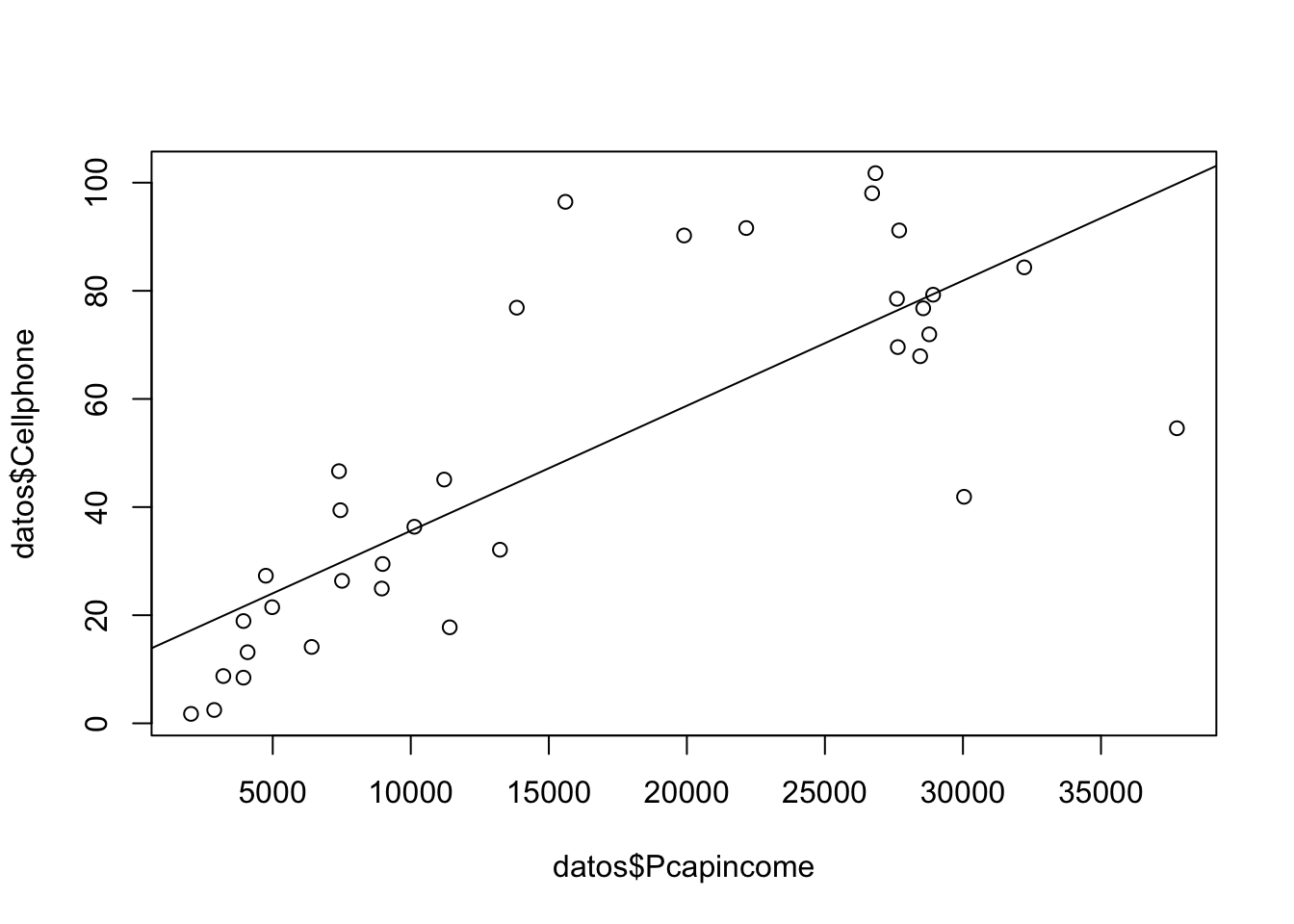

plot(datos$Pcapincome,datos$Cellphone)
abline(coef(reg.1))

2.2.1 Modelo recíproco

Abrir la tabla 6.4, regresar el Producto Nacional Bruto (PGNP) en la tasa de mortalidad (CM).

uu <- "https://raw.githubusercontent.com/vmoprojs/DataLectures/master/GA/tabla_6_4.csv"
datos <- read.csv(url(uu),sep=";",dec=".",header=TRUE)
names(datos)

## [1] "CM"   "FLR"  "PGNP" "TFR"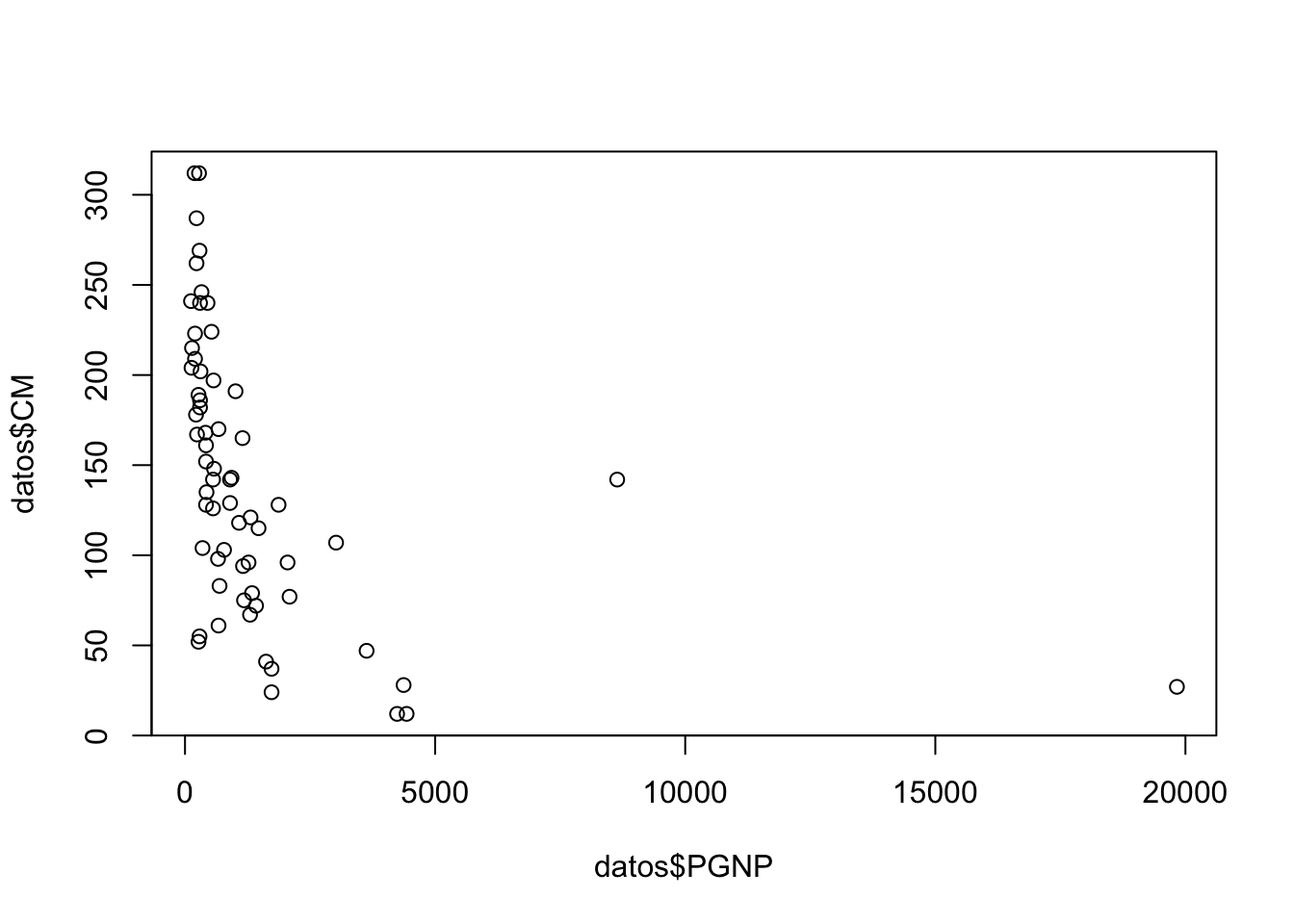

plot(datos$CM~ datos$PGNP)

reg1 <- lm(CM ~ PGNP,data = datos)
summary(reg1)

## 
## Call:
## lm(formula = CM ~ PGNP, data = datos)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -113.764  -53.111   -6.685   48.064  157.758 
## 
## Coefficients:
##               Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 157.424441   9.845583  15.989  < 2e-16 ***
## PGNP         -0.011364   0.003233  -3.516 0.000826 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 69.93 on 62 degrees of freedom
## Multiple R-squared:  0.1662, Adjusted R-squared:  0.1528 
## F-statistic: 12.36 on 1 and 62 DF,  p-value: 0.0008262

reg2 <- lm(CM~I(1/PGNP),data = datos)
summary(reg2)

## 
## Call:
## lm(formula = CM ~ I(1/PGNP), data = datos)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -130.806  -36.410    2.871   31.686  132.801 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)    81.79      10.83   7.551 2.38e-10 ***
## I(1/PGNP)   27273.17    3760.00   7.254 7.82e-10 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 56.33 on 62 degrees of freedom
## Multiple R-squared:  0.4591, Adjusted R-squared:  0.4503 
## F-statistic: 52.61 on 1 and 62 DF,  p-value: 7.821e-10

2.2.2 Modelo log-lineal

Abrir los datos ceosal2.xls,

uu <- "https://raw.githubusercontent.com/vmoprojs/DataLectures/master/WO/ceosal2.csv"
datos <- read.csv(url(uu), header = FALSE) 
names(datos) = c("salary", "age", "college", "grad", "comten", "ceoten", "sales", "profits","mktval", "lsalary", "lsales", "lmktval", "comtensq", "ceotensq", "profmarg")

Regresar la antigüedad del CEO en el logaritmo del salario.

summary(lm(lsalary~ceoten,data = datos))

## 
## Call:
## lm(formula = lsalary ~ ceoten, data = datos)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -2.15314 -0.38319 -0.02251  0.44439  1.94337 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 6.505498   0.067991  95.682   <2e-16 ***
## ceoten      0.009724   0.006364   1.528    0.128    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.6038 on 175 degrees of freedom
## Multiple R-squared:  0.01316,    Adjusted R-squared:  0.007523 
## F-statistic: 2.334 on 1 and 175 DF,  p-value: 0.1284

• Hay una probabilidad de equivocarnos del 12.84% si rechazamos la hipótesis nula
• No hay evidencia de la antiguedad tenga relación con el salario
• Los CEO con 0 años de antiguedad entran ganando exp(6.505)=668.4757 miles de USD exp(6.505)
• En promedio, por cada unidad que aumenta la antigüedad del CEO, su salario aumenta $0.9\%$

2.3 Regresión Lineal Múltiple

Abrir los datos hprice1.xls. Correr los siguientes modelos e interpretarlos:

uu <- "https://raw.githubusercontent.com/vmoprojs/DataLectures/master/WO/hprice1.csv"
precios <- read.csv(url(uu), header = FALSE) 

names(precios)=c("price"   ,  "assess"  , 
                 "bdrms"  ,   "lotsize"  ,
                 "sqrft"   ,  "colonial",
                 "lprice"  ,  "lassess" ,
                 "llotsize" , "lsqrft")

modelo1 <- lm(lprice ~ lassess + llotsize + lsqrft + bdrms,data = precios)
summary(modelo1)

## 
## Call:
## lm(formula = lprice ~ lassess + llotsize + lsqrft + bdrms, data = precios)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -0.53337 -0.06333  0.00686  0.07836  0.60825 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  0.263745   0.569665   0.463    0.645    
## lassess      1.043065   0.151446   6.887 1.01e-09 ***
## llotsize     0.007438   0.038561   0.193    0.848    
## lsqrft      -0.103239   0.138431  -0.746    0.458    
## bdrms        0.033839   0.022098   1.531    0.129    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.1481 on 83 degrees of freedom
## Multiple R-squared:  0.7728, Adjusted R-squared:  0.7619 
## F-statistic: 70.58 on 4 and 83 DF,  p-value: < 2.2e-16

modelo2 <- lm(lprice ~ llotsize + lsqrft + bdrms,data = precios)
summary(modelo2)

## 
## Call:
## lm(formula = lprice ~ llotsize + lsqrft + bdrms, data = precios)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -0.68422 -0.09178 -0.01584  0.11213  0.66899 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -1.29704    0.65128  -1.992   0.0497 *  
## llotsize     0.16797    0.03828   4.388 3.31e-05 ***
## lsqrft       0.70023    0.09287   7.540 5.01e-11 ***
## bdrms        0.03696    0.02753   1.342   0.1831    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.1846 on 84 degrees of freedom
## Multiple R-squared:  0.643,  Adjusted R-squared:  0.6302 
## F-statistic: 50.42 on 3 and 84 DF,  p-value: < 2.2e-16

modelo3 <- lm(lprice ~  bdrms,data = precios)
summary(modelo3)

## 
## Call:
## lm(formula = lprice ~ bdrms, data = precios)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -0.99586 -0.17202 -0.00319  0.14974  0.71355 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  5.03649    0.12635  39.862  < 2e-16 ***
## bdrms        0.16723    0.03447   4.851 5.43e-06 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.2706 on 86 degrees of freedom
## Multiple R-squared:  0.2148, Adjusted R-squared:  0.2057 
## F-statistic: 23.53 on 1 and 86 DF,  p-value: 5.426e-06

2.3.0.1 Predicción

with(precios,pairs(cbind(lprice,llotsize , lsqrft , bdrms), col=rainbow(5)))

• Forma 1 de predicción:

tamano_casa <- 8000
cuartos <- 4
tamano_lote <- 2100

coef(modelo2)

## (Intercept)    llotsize      lsqrft       bdrms 
## -1.29704057  0.16796682  0.70023213  0.03695833

valores <- c(1,log(tamano_lote),log(tamano_casa),cuartos)
valores

## [1] 1.000000 7.649693 8.987197 4.000000

sum(valores*coef(modelo2))

## [1] 6.428811

exp(sum(valores*coef(modelo2)))

## [1] 619.4372

• Forma 2 de predicción:

datos.nuevos <- data.frame(llotsize=log(2100),lsqrft=log(8000),bdrms=4)
predict.lm(modelo2,newdata=datos.nuevos,se.fit=T)

## $fit
##        1 
## 6.428811 
## 
## $se.fit
## [1] 0.1479752
## 
## $df
## [1] 84
## 
## $residual.scale
## [1] 0.1846026

2.3.1 RLM: Cobb-Douglas

El modelo:

$$Y_i = \beta_1X_{2i}^{\beta_2}X_{3i}^{\beta_3}e^{u_i}$$

donde

• $Y$: producción
• $X_2$: insumo trabajo
• $X_3$: insumo capital
• $u$: término de perturbación
• $e$: base del logaritmo

Notemos que el modelo es multiplicativo, si tomamos la derivada obetenemos un modelo más famliar respecto a la regresión lineal múltiple:

$$lnY_i = ln\beta_1 + \beta_2ln(X_{2i})+ \beta_3ln(X_{3i}) + u_i$$

La interpretación de los coeficientes es (Gujarati and Porter 2010):

1. $\beta_2$ es la elasticidad (parcial) de la producción respecto del insumo trabajo, es decir, mide el cambio porcentual en la producción debido a una variación de 1% en el insumo trabajo, con el insumo capital constante.

2. De igual forma, $\beta_3$ es la elasticidad (parcial) de la producción respecto del insumo capital, con el insumo trabajo constante.

3. La suma ($\beta_2+\beta_3$) da información sobre los rendimientos a escala, es decir, la respuesta de la producción a un cambio proporcional en los insumos. Si esta suma es 1, existen rendimientos constantes a escala, es decir, la duplicación de los insumos duplica la producción, la triplicación de los insumos la triplica, y así sucesivamente. Si la suma es menor que 1, existen rendimientos decrecientes a escala: al duplicar los insumos, la producción crece en menos del doble. Por último, si la suma es mayor que 1, hay rendimientos crecientes a escala; la duplicación de los insumos aumenta la producción en más del doble.

Abrir la tabla 7.3. Regresar las horas de trabajo ($X_2$) e Inversión de Capital ($X_3$) en el Valor Agregado ($Y$)

uu <- "https://raw.githubusercontent.com/vmoprojs/DataLectures/master/GA/tabla7_3.csv"
# datos <- read.csv(file="tabla7_3.csv",sep=";",dec=".",header=TRUE)
datos <- read.csv(url(uu),sep=";",dec=".",header=TRUE)

W <- log(datos$X2)

K <- log(datos$X3)

LY <- log(datos$Y)

reg.1 <- lm(LY~W+K,data = datos)
summary(reg.1)

## 
## Call:
## lm(formula = LY ~ W + K, data = datos)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -0.15919 -0.02917  0.01179  0.04087  0.09640 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  -3.3387     2.4491  -1.363 0.197845    
## W             1.4987     0.5397   2.777 0.016750 *  
## K             0.4899     0.1020   4.801 0.000432 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.0748 on 12 degrees of freedom
## Multiple R-squared:  0.8891, Adjusted R-squared:  0.8706 
## F-statistic: 48.08 on 2 and 12 DF,  p-value: 1.864e-06

aov(reg.1)

## Call:
##    aov(formula = reg.1)
## 
## Terms:
##                         W         K Residuals
## Sum of Squares  0.4090674 0.1289876 0.0671410
## Deg. of Freedom         1         1        12
## 
## Residual standard error: 0.07480028
## Estimated effects may be unbalanced

• Las elasticidades de la producción respecto del trabajo y el capital fueron 1.49 y 0.48.

Ahora, si existen rendimientos constantes a escala (un cambio equi proporcional en la producción ante un cambio equiproporcional en los insumos), la teoría económica sugeriría que:

$$\beta_2 +\beta_3 = 1$$

LY_K <- log(datos$Y/datos$X3)
W_K <- log(datos$X2/datos$X3)


reg.2 <- lm(LY_K~W_K)
summary(reg.2)

## 
## Call:
## lm(formula = LY_K ~ W_K)
## 
## Residuals:
##       Min        1Q    Median        3Q       Max 
## -0.164785 -0.041608 -0.008268  0.076112  0.098587 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)   
## (Intercept)   1.7083     0.4159   4.108  0.00124 **
## W_K           0.3870     0.0933   4.147  0.00115 **
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.08388 on 13 degrees of freedom
## Multiple R-squared:  0.5695, Adjusted R-squared:  0.5364 
## F-statistic:  17.2 on 1 and 13 DF,  p-value: 0.001147

aov(reg.2)

## Call:
##    aov(formula = reg.2)
## 
## Terms:
##                        W_K  Residuals
## Sum of Squares  0.12100534 0.09145854
## Deg. of Freedom          1         13
## 
## Residual standard error: 0.08387653
## Estimated effects may be unbalanced

¿Se cumple la hipótesis nula? ¿Existen rendimientos constantes de escala?

Una forma de responder a la pregunta es mediante la prueba $t$, para $Ho: \beta_2 +\beta_3 = 1$, tenemos

$$t = \frac{(\hat{\beta}_2+\hat{\beta}_3)-(\beta_2+\beta_3)}{ee(\hat{\beta}_2+\hat{\beta}_3)}$$ $$t = \frac{(\hat{\beta}_2+\hat{\beta}_3)-1}{\sqrt{var(\hat{\beta}_2)+var(\hat{\beta}_3)+2cov(\hat{\beta}_2,\hat{\beta}_3})}$$ donde la información nececesaria para obtener $cov(\hat{\beta}_2,\hat{\beta}_3)$ en R es vcov(fit.model) y fit.model es el ajuste del modelo.

Otra forma de hacer la prueba es mediante el estadístico $F$:

$$F = \frac{(SCE_{R}-SCE_{NR})/m}{SCR_{NR}/(n-k)}$$

donde $m$ es el número de restricciones lineales y $k$ es el número de parámetros de la regresión no restringida.

SCRNR <- 0.0671410  
SCRRes <- 0.09145854 
numero_rest <- 1
grad <- 12

est_F <- ((SCRRes-SCRNR)/numero_rest)/(SCRNR/grad)
est_F

## [1] 4.346234

valor.p <- 1-pf(est_F,1,12)
valor.p

## [1] 0.05912184

No se tiene suficiente evidencia para rechazar la hipótesis nula de que sea una economía de escala.

Notemos que existe una relación directa entre el coeficiente de determinación o bondad de ajuste $R^2$ y $F$. En primero lugar, recordemos la descomposición de los errores:

$$SCT = SCE + SCR$$

$$\sum_{i=1}^{n}(Y-\bar{Y})^2 = \sum_{i=1}^{n}(\hat{Y}-\bar{Y})^2 + \sum_{i=1}^{n}(\hat{u})^2$$

De cuyos elementos podemos obtener tanto $R^2$ como $F$:

$$R^2 = \frac{SCE}{SCT}$$

$$F = \frac{SCE/(k-1)}{SCT/(n-k)}$$

donde $k$ es el número de variables (incluido el intercepto) y sigue una distribución $F$ con $k-1$ y $n-k$ grados de libertad.

2.3.2 RLM: Dicotómicas

Abrir los datos wage1.xls. Correr los modelos. Se desea saber si el género tiene relación con el salario y en qué medida.

uu <- "https://raw.githubusercontent.com/vmoprojs/DataLectures/master/WO/wage1.csv"
salarios <- read.csv(url(uu), header = FALSE) 

names(salarios) <- c("wage", "educ", "exper", "tenure", "nonwhite", "female", "married",
                     "numdep", "smsa", "northcen", "south", "west", "construc", "ndurman",
                     "trcommpu", "trade", "services",  "profserv", "profocc", "clerocc",
                     "servocc", "lwage", "expersq", "tenursq")

reg3 <- lm(wage~female,data = salarios)
summary(reg3)

## 
## Call:
## lm(formula = wage ~ female, data = salarios)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -5.5995 -1.8495 -0.9877  1.4260 17.8805 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   7.0995     0.2100  33.806  < 2e-16 ***
## female       -2.5118     0.3034  -8.279 1.04e-15 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 3.476 on 524 degrees of freedom
## Multiple R-squared:  0.1157, Adjusted R-squared:  0.114 
## F-statistic: 68.54 on 1 and 524 DF,  p-value: 1.042e-15

reg4 <- lm(wage~female + educ+ exper + tenure,data = salarios)
summary(reg4)

## 
## Call:
## lm(formula = wage ~ female + educ + exper + tenure, data = salarios)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -7.7675 -1.8080 -0.4229  1.0467 14.0075 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -1.56794    0.72455  -2.164   0.0309 *  
## female      -1.81085    0.26483  -6.838 2.26e-11 ***
## educ         0.57150    0.04934  11.584  < 2e-16 ***
## exper        0.02540    0.01157   2.195   0.0286 *  
## tenure       0.14101    0.02116   6.663 6.83e-11 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 2.958 on 521 degrees of freedom
## Multiple R-squared:  0.3635, Adjusted R-squared:  0.3587 
## F-statistic:  74.4 on 4 and 521 DF,  p-value: < 2.2e-16

• La hipotesis es que saber si el coeficiente de female es menor a cero
• Se nota que es menor,
• Tomando en cuenta, educacion experiencia y edad, en promedio a la mujer le pagan 1.81 menos

2.3.3 RLM: Educación con insumos

Abrir los datos gpa1.xls. Correr los modelos.

• ¿Afecta el promedio el tener o no una computadora?

uu <- "https://raw.githubusercontent.com/vmoprojs/DataLectures/master/WO/gpa1.csv"
datosgpa <- read.csv(url(uu), header = FALSE) 

names(datosgpa) <- c("age",  "soph",  "junior",    "senior",    "senior5",  "male", "campus",   "business", "engineer", "colGPA",   "hsGPA",    "ACT",  "job19",    "job20",    "drive",    "bike", "walk", "voluntr",  "PC",   "greek",    "car",  "siblings", "bgfriend", "clubs",    "skipped",  "alcohol",  "gradMI",   "fathcoll", "mothcoll")

Realizamos la regresión lineal:

reg4 <- lm(colGPA ~ PC ,data = datosgpa)
summary(reg4)

## 
## Call:
## lm(formula = colGPA ~ PC, data = datosgpa)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -0.95893 -0.25893  0.01059  0.31059  0.84107 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  2.98941    0.03950  75.678   <2e-16 ***
## PC           0.16952    0.06268   2.704   0.0077 ** 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.3642 on 139 degrees of freedom
## Multiple R-squared:  0.04999,    Adjusted R-squared:  0.04315 
## F-statistic: 7.314 on 1 and 139 DF,  p-value: 0.007697

reg5 <- lm(colGPA~ PC + hsGPA + ACT,data = datosgpa)
summary(reg5)

## 
## Call:
## lm(formula = colGPA ~ PC + hsGPA + ACT, data = datosgpa)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -0.7901 -0.2622 -0.0107  0.2334  0.7570 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 1.263520   0.333126   3.793 0.000223 ***
## PC          0.157309   0.057287   2.746 0.006844 ** 
## hsGPA       0.447242   0.093647   4.776 4.54e-06 ***
## ACT         0.008659   0.010534   0.822 0.412513    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.3325 on 137 degrees of freedom
## Multiple R-squared:  0.2194, Adjusted R-squared:  0.2023 
## F-statistic: 12.83 on 3 and 137 DF,  p-value: 1.932e-07