14 K-medias
El algoritmo k-means es quizás el método de agrupación más utilizado. Después de haber sido estudiado durante varias décadas, sirve como base para muchas técnicas de agrupación más sofisticadas.
El objetivo es minimizar las diferencias dentro de cada grupo y maximizar las diferencias entre los clústeres.
14.1 Algoritmo
Asignar aleatoriamente un número, del \(1\) a \(K\), a cada observación. Estos funcionan como asignaciones iniciales para las observaciones.
Iterar hasta que las asignaciones dejen de cambiar:
2.1. Para cada uno de los \(K\) conglomerados, calcular el centroide del conglomerado. El \(k\)-ésimo centroide del grupo es el vector de las \(p\) medias de características para las observaciones en el \(k\)-ésimo grupo.
2.2. Asignar cada observación al conglomerado cuyo centroide es el más cercano (donde más cercano se define utilizando la distancia euclidiana).
14.2 Ejemplo
14.2.1 Paso 1: recopilación de datos
Tenemos información de tasas (por cada 100 personas) de tipos de crímenes por cada estado de USA.
www <- "https://raw.githubusercontent.com/vmoprojs/DataLectures/master/crime2.csv"
crime <- read.csv(www,sep=",")
str(crime)## 'data.frame': 50 obs. of 7 variables:
## $ murder : num 14.2 10.8 9.5 8.8 11.5 6.3 4.2 6 10.2 11.7 ...
## $ rape : num 25.2 51.6 34.2 27.6 49.4 42 16.8 24.9 39.6 31.1 ...
## $ robbery : num 96.8 96.8 138.2 83.2 287 ...
## $ assault : num 278 284 312 203 358 ...
## $ burglary : num 1136 1332 2346 973 2139 ...
## $ larceny : num 1882 3370 4467 1862 3500 ...
## $ auto.theft: num 281 753 440 183 664 ...14.2.2 Paso 2: Explorar y preparar los datos
¿Qué estados superan 15 en su tasa de homicidios?
## murder rape robbery assault burglary larceny auto.theft
## 18 15.5 30.9 142.9 335.5 1165.5 2469.9 337.7
## 28 15.8 49.1 323.1 355.0 2453.1 4212.6 559.2## murder rape robbery assault burglary larceny
## 14.9519 115.7696 7805.4693 10050.6739 187017.9416 526943.4505
## auto.theft
## 37401.4007rge <- sapply(crime, function(x) diff(range(x))) # obtendo el rango
crime_s <- sweep(crime, 2, rge, FUN = "/") # divido para el rango
sapply(crime_s, mean)## murder rape robbery assault burglary larceny auto.theft
## 0.4995973 0.6040845 0.2701764 0.4785957 0.6436991 0.8276648 0.379156414.2.3 Paso 3: entrenar un modelo en los datos
Agrupamos
## murder rape robbery assault burglary larceny auto.theft
## 1 5.625926 198.2633 315.7508 336.510766 21.70054 311.7775 953.3310
## 2 27.384826 356.0658 1299.5668 9.590907 368.06088 1947.3517 475.4522¿Qué pasa al multiplicar por rge?
14.2.4 Paso 4: evaluar el rendimiento del modelo
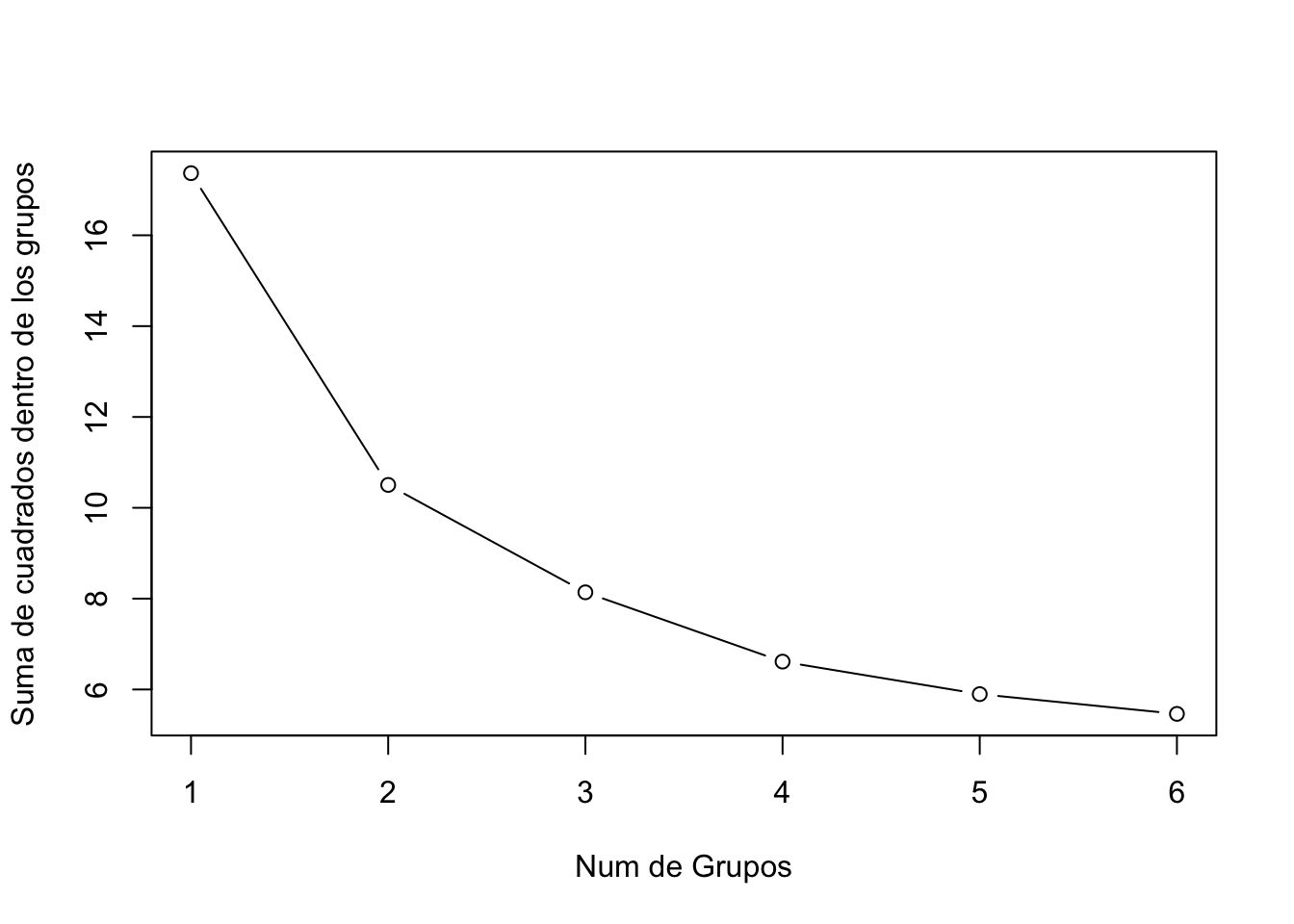
Gráfico de codo
n <- nrow(crime_s)
wss <- rep(0, 6)
wss[1] <- (n - 1) * sum(sapply(crime_s, var))
for (i in 2:6)
wss[i] <- sum(kmeans(crime_s, centers = i)$withinss)
plot(1:6, wss, type = "b", xlab = "Num de Grupos",
ylab = "Suma de cuadrados dentro de los grupos")