8 Polinomios Locales
Paquetes de esta sección
8.1 Introducción
LOWESS (suavizado de dispersión de ponderación local), a veces llamado LOESS (suavizado de ponderación local), es una herramienta popular que se utiliza en el análisis de regresión que crea una línea suave a través de una gráfica de distribución o de dispersión de tiempo para ayudar a ver la relación entre variables y prever tendencias.
8.2 ¿Para qué sirve?
LOWESS se usa típicamente para:
Ajustar una línea a un gráfico de dispersión o gráfico de tiempo donde los valores de datos con ruido, los puntos de datos dispersos o las interrelaciones débiles interfieren con su capacidad para ver una línea de mejor ajuste.
La regresión lineal donde los ajustes de mínimos cuadrados no crea una línea de buen ajuste o es demasiado laboriosa para usar.
Exploración y análisis de datos en las ciencias sociales, particularmente en elecciones y comportamiento electoral.
8.3 Ejemplos
Sintaxis simple
8.3.1 Ejemplo 1: Temperatura de castores
Las dos variables que nos interesan son el tiempo (medido en minutos) y la temperatura corporal de los castores. Extraigamos estos datos de la matriz de datos:
Ahora, podemos calcular los valores de regresión lowess con la función R lowess:
Eso es todo, los valores calculados de \(X\) e \(Y\) de la regresión de lowess se almacenan en el nuevo objeto de datos lowess_values.
Normalmente, los valores lowess se utilizan para la visualización. ¡Hagámoslo!
Primero creamos un gráfico simple de dispersión.
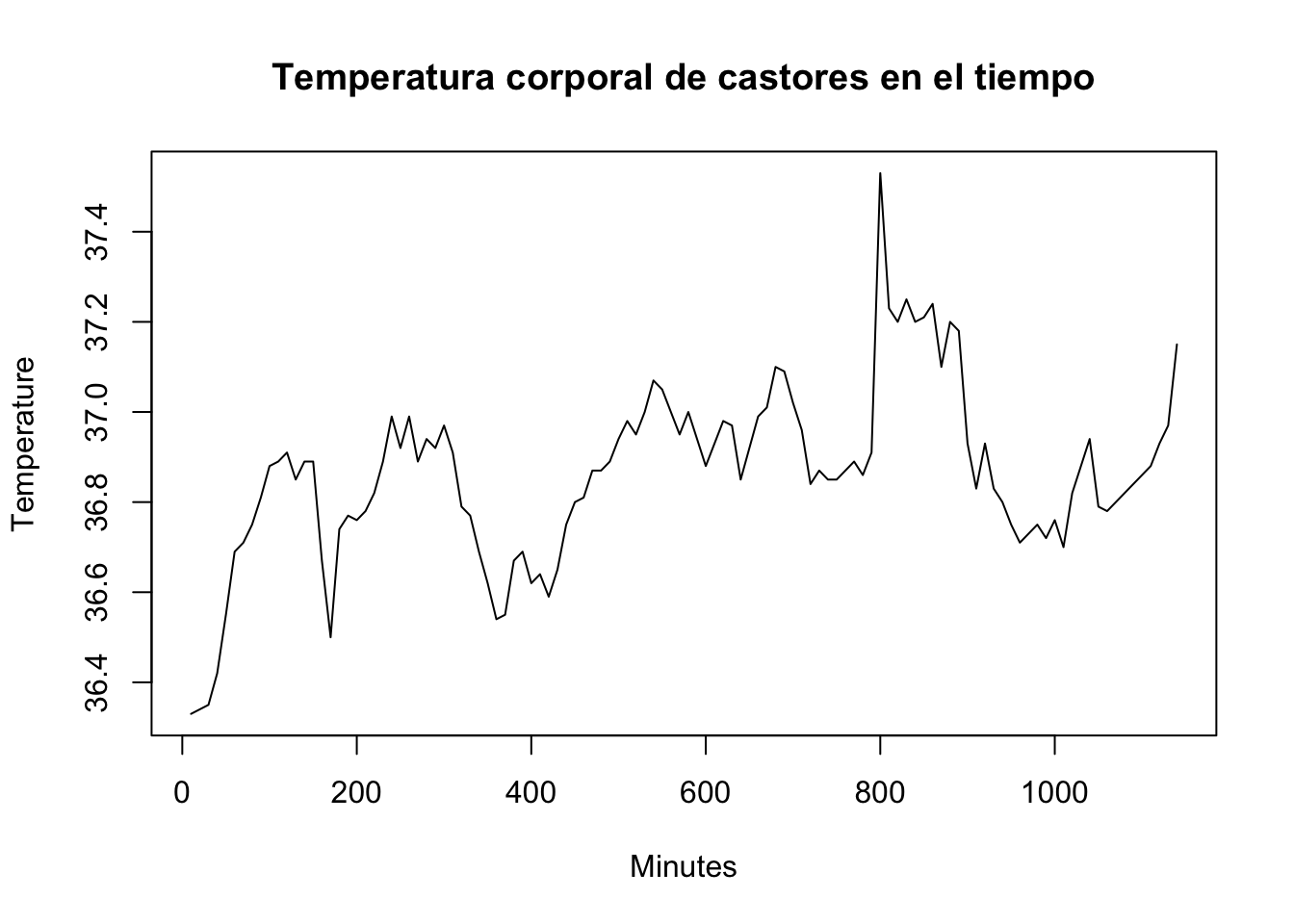
Podemos superponer este diagrama de dispersión con los valores de lowess de la siguiente manera:
plot(Minutes, Temperature, type = "l",
main = "Temperatura corporal de castores en el tiempo")
lines(lowess_values, col = "red") 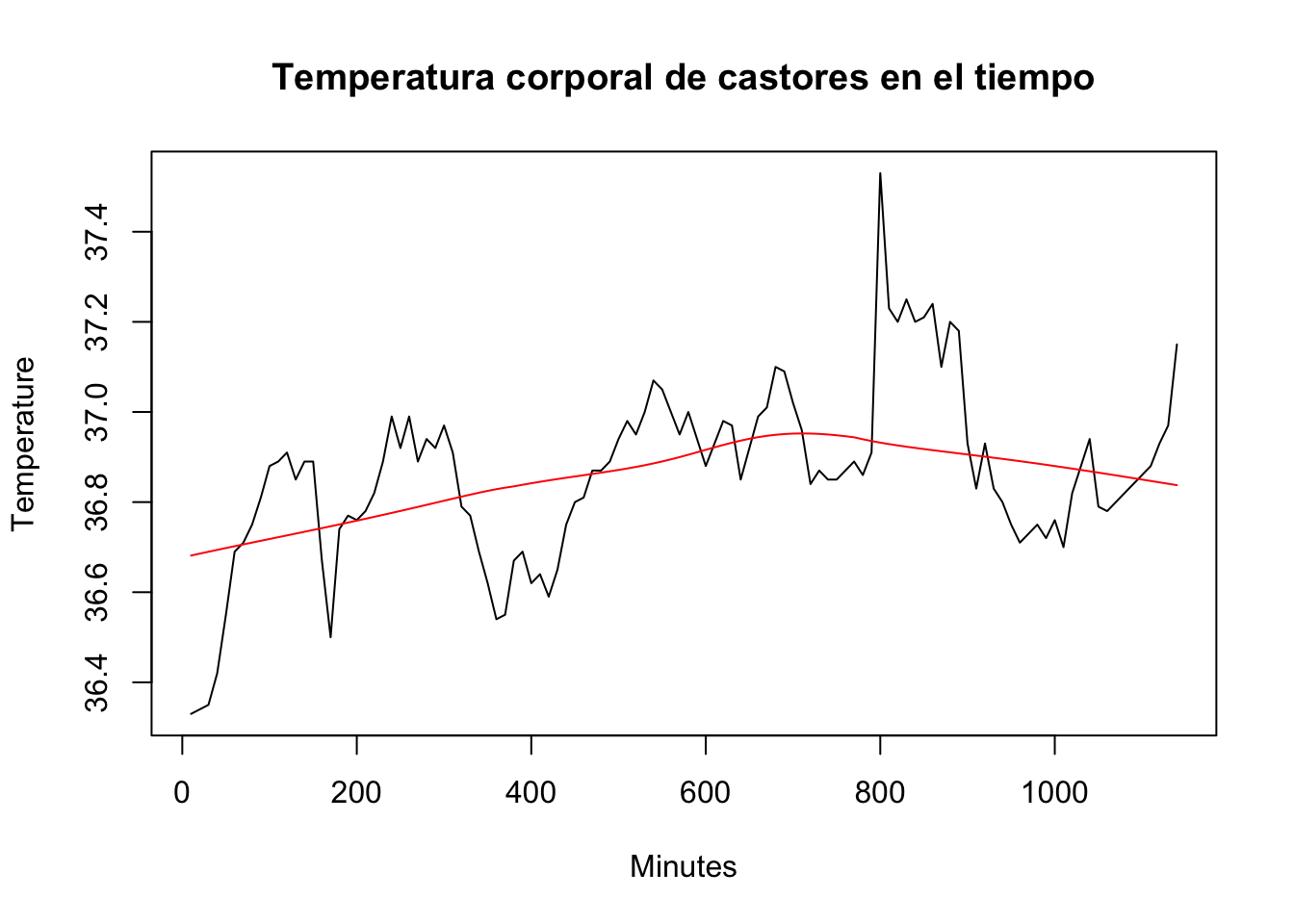
8.3.2 Ejemplo 2: El parámetro de suavizamiento
Una opción importante de la función lowess es el parámetro de suavizamiento. Este determina el número de puntos de datos que influyen en la suavidad en cada valor. Cuanto mayor sea el parámetro, más grande será el suavizado.
Veamos cómo funciona eso en la práctica. Usamos los datos del ejemplo 1.
plot(Minutes, Temperature, type = "l",
main = "Temperatura corporal de castores en el tiempo")
lines(lowess(Minutes, Temperature, f = 0.1), col = "green") # Agregamos los valores lowess con diferentes normalizaciones
lines(lowess(Minutes, Temperature, f = 5), col = "cornflowerblue")
legend("topleft",
col = c("red", "green", "cornflowerblue"),
lty = 1,
lwd = 2,
c("Suavizamiento por defecto", "Par de Suav. = 0.1", "Par de Suav. = 5"))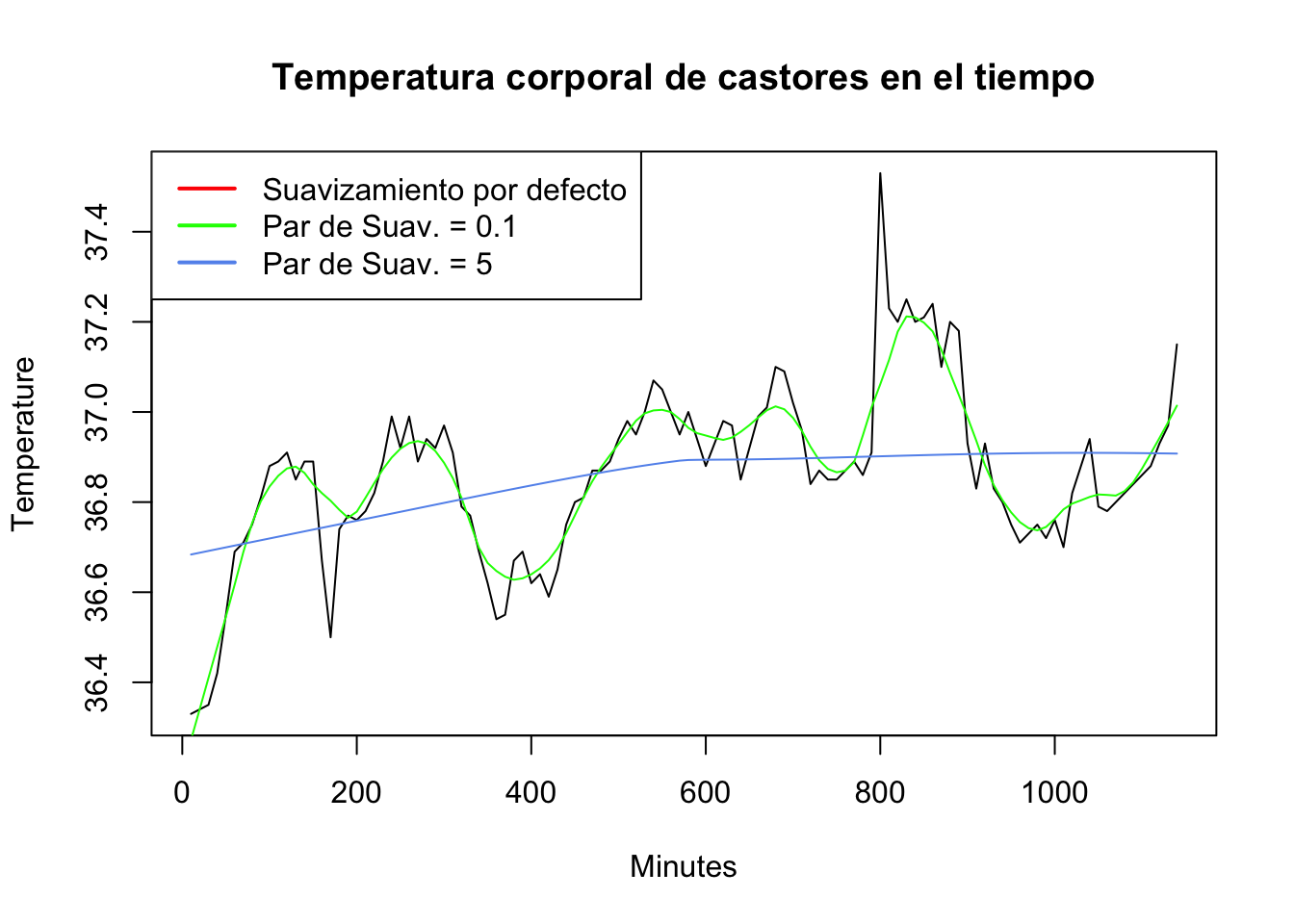
Dibujamos dos líneas de regresión más a nuestra gráfica. Una vez, con un suavizado de \(0.1\) (línea verde) y una vez con un suavizado de \(5\) (línea azul). Como puede ver, el parámetro más pequeño conduce a una aproximación mucho más cercana de los valores observados que el parámetro mayor.
8.3.3 Ejemplo 3: duración del desempleo
Para este ejemplo, intentaremos regresar localmente y suavizar la duración media del desempleo en función del conjunto de datos económicos del paquete ggplot2. Consideramos solo las primeras 80 filas para este análisis, por lo que es más fácil observar el grado de suavizado en los gráficos a continuación.
data(economics, package="ggplot2")
economics$index <- 1:nrow(economics)
economics <- economics[1:80, ] # con 80 filas para mejor visualizacion
loessMod10 <- loess(uempmed ~ index, data=economics, span=0.10) # 10% smoothing span
loessMod25 <- loess(uempmed ~ index, data=economics, span=0.25) # 25% smoothing span
loessMod50 <- loess(uempmed ~ index, data=economics, span=0.50) # 50% smoothing spanHacemos la predicción
smoothed10 <- predict(loessMod10)
smoothed25 <- predict(loessMod25)
smoothed50 <- predict(loessMod50) Graficamos
plot(economics$uempmed, x=economics$date, type="l", main="Loess Smoothing and Prediction", xlab="Date", ylab="Unemployment (Median)")
lines(smoothed10, x=economics$date, col="red")
lines(smoothed25, x=economics$date, col="green")
lines(smoothed50, x=economics$date, col="blue")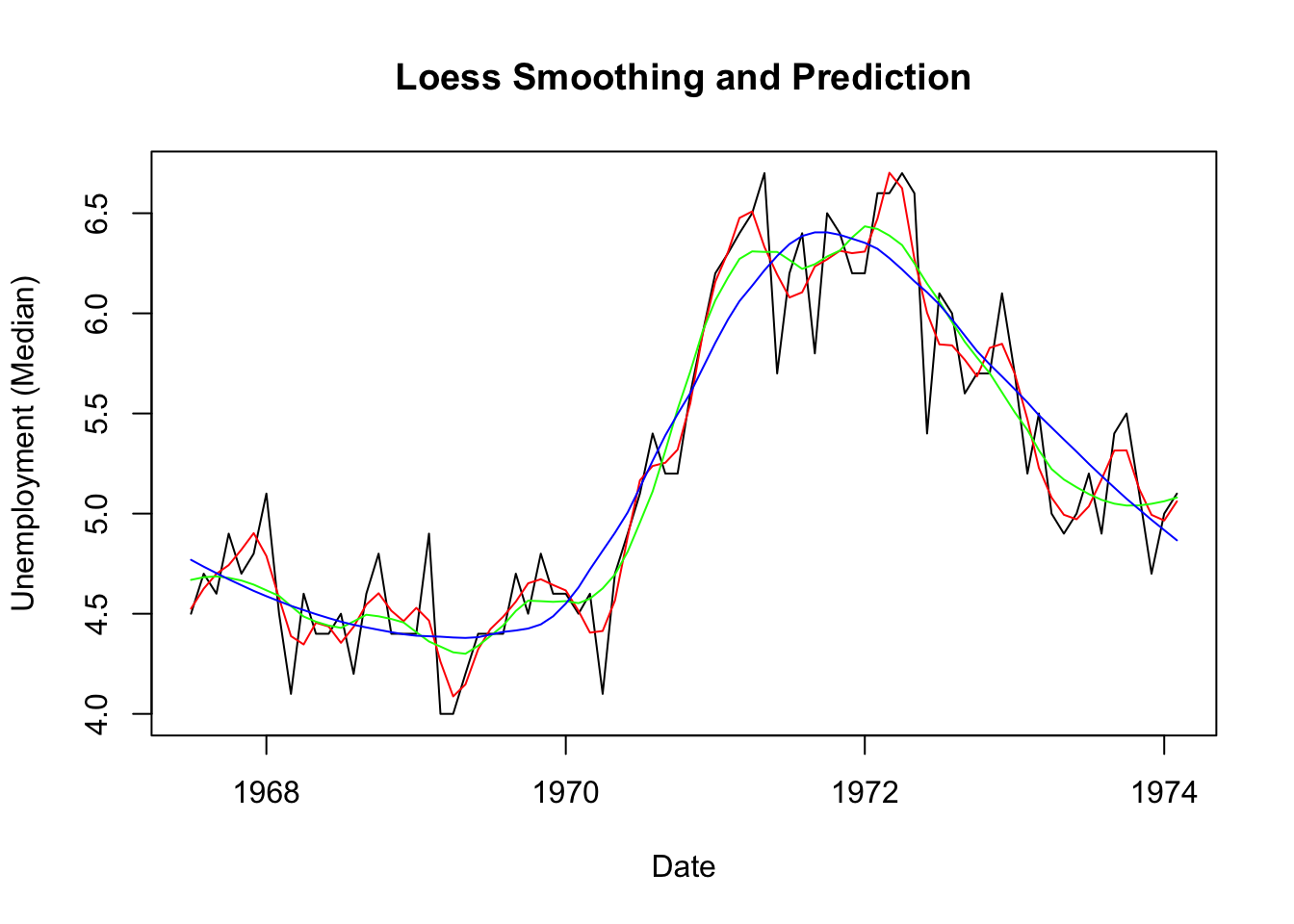
Desde la gráfica, nota que a medida que aumenta el tramo, también se incrementa el suavizado de la curva.
8.4 ¿Cómo encontrar el parámetro de suavizamiento óptimo?
A medida que cambia el intervalo de suavizado, también cambia la precisión de la curva ajustada. Si su intención es minimizar el error, optim() se puede usar para encontrar ese valor de intervalo, que minimiza la suma de errores cuadrados (SSE). Para este caso, es gráficamente intuitivo que un SSE más bajo se logrará con valores de intervalo más bajos, pero para casos más desafiantes, la optimización del intervalo podría ayudar.
Para implementar optim(), definimos la función que calcula el SSE. Se necesita un mecanismo de manejo de errores para abordar valores muy bajos de intervalo y casos donde se producen los no numéricos.
El método simulated annealing (SANN, por sus siglas en inglés) se implementa aquí para encontrar el intervalo que proporciona un SSE mínimo. El argumento par especifica el primer valor del intervalo en el que optim() comenzará la búsqueda.
# definimos la funcion de SSE
calcSSE <- function(x){
loessMod <- try(loess(uempmed ~ index, data=economics, span=x), silent=T)
res <- try(loessMod$residuals, silent=T)
if(class(res)!="try-error"){
if((sum(res, na.rm=T) > 0)){
sse <- sum(res^2)
} else{sse <- 99999}
}else{
sse <- 99999
}
return(sse)
}Ejecutamos optim para encontrar el parámetro que encuentra el minimo SSE, valor inicial en \(0.5\).
## $par
## [1] 0.05902064
##
## $value
## [1] 6.147199e-28
##
## $counts
## function gradient
## 10000 NA
##
## $convergence
## [1] 0
##
## $message
## NULL## $par
## [1] 0.5
##
## $value
## [1] 99999
##
## $counts
## function gradient
## 1 1
##
## $convergence
## [1] 0
##
## $message
## NULLNota: SANN pertenece a la clase de métodos de optimización global estocásticos. Utiliza solo valores de la función pero es relativamente lento. También funcionará para funciones no diferenciables.