19 Compensación entre sesgo & varianza
Tomado de: https://www.cs.cornell.edu/courses/cs4780/2018fa/
Espero que este sea el punto que transforme la forma en la ven a la analítica de datos.
Entender la compensación que existe entre sesgo & varianza es lo que diferencia a las personas que solo juegan con algoritmos de las que saben lo que hacen.
19.1 Setup
Objetivo: obtener un clasificador cuya generalización sea la mejor posible.
\[ D = \{(\mathbf{x}_1, y_1), \dots, (\mathbf{x}_n,y_n)\}, \quad y \in \mathbb{R} \]
se asume que los puntos \((x_i,y_i)\) provienen de una distribución \(P(X,Y)\), donde \(P(X,Y) = P(Y|X)P(X)\).
Consideremos que para cualquier entrada \(\mathbf{x}\) dada puede que no exista una etiqueta única \(y\). Por ejemplo, si su vector \(\mathbf{x}\) describe las características de la casa (por ejemplo, habitaciones, pies cuadrados, …) y la etiqueta es el precio, podría imaginar dos casas con una descripción idéntica vendiéndose a precios diferentes. Entonces, para cualquier vector de características dado \(\mathbf{x}\), hay una distribución sobre posibles etiquetas.
Para un \(\mathbf{x} \in \mathbb{R}^d\) dado, lo que queremos predecir es la esperanza de \(Y\) (la etiqueta esperada):
Etiqueta esperada:
\[ \bar{y}(\mathbf{x}) = E_{y \vert \mathbf{x}} \left[Y\right] = \int\limits_y y \, \Pr(y \vert \mathbf{x}) \partial y. \]
Muy bien, obtenemos nuestro conjunto de entrenamiento \(D\), que consta de \(n\) entradas (inputs), i.i.d. de la distribución \(P\).
Como segundo paso, normalmente aplicamos a algún algoritmo de aprendizaje automático \(A\) en este conjunto de datos para aprender una hipótesis (también conocido como clasificador). Formalmente, denotamos este proceso como \(h_D = \mathcal{A}(D)\).
Para un \(h_D\) dado, aprendido en el conjunto de datos \(D\) con el algoritmo \(A\), podemos calcular el error de generalización (medido en pérdida al cuadrado) de la siguiente manera:
Error esperado sobre los datos test (dado \(h_D\))
\[ E_{(\mathbf{x},y) \sim P} \left[ \left(h_D (\mathbf{x}) - y \right)^2 \right] = \int\limits_x \! \! \int\limits_y \left( h_D(\mathbf{x}) - y\right)^2 \Pr(\mathbf{x},y) \partial y \partial \mathbf{x}. \]
Ten en cuenta que se pueden utilizar otras funciones de pérdida. Usamos la pérdida al cuadrado porque tiene buenas propiedades matemáticas y también es la función de pérdida más común.
La afirmación anterior es cierta para un conjunto de entrenamiento dado \(D\). Sin embargo, recuerda que \(D\) en sí se extrae de \(P^n\) y, por lo tanto, es una variable aleatoria.
Además, \(h_D\) es una función de \(D\) y, por lo tanto, también es una variable aleatoria. Y, por supuesto, podemos calcular su expectativa:
Clasificador esperado (dado \(\mathcal{A}\))
\[ \bar{h} = E_{D \sim P^n} \left[ h_D \right] = \int\limits_D h_D \Pr(D) \partial D \] donde \(\Pr(D)\) es la probabilidad de extraer \(D\) de \(P^n\). Aquí, \(\bar{h}\) es un promedio ponderado de funciones.
También podemos usar el hecho de que \(h_D\) es una variable aleatoria para calcular el error esperado en el conjunto test solo dado \(\mathcal{A}\), tomando la esperanza también sobre \(D\).
Error esperado sobre los datos test (dado \(\mathcal{A}\))
\[ \begin{equation*} E_{\substack{(\mathbf{x},y) \sim P\\ D \sim P^n}} \left[\left(h_{D}(\mathbf{x}) - y\right)^{2}\right] = \int_{D} \int_{\mathbf{x}} \int_{y} \left( h_{D}(\mathbf{x}) - y\right)^{2} \mathrm{P}(\mathbf{x},y) \mathrm{P}(D) \partial \mathbf{x} \partial y \partial D \end{equation*} \] Para ser claros, \(D\) son nuestros puntos de entrenamiento y los pares \((x, y)\) son los puntos de prueba.
Estamos interesados exactamente en esta expresión, porque evalúa la calidad de un algoritmo de aprendizaje automático \(\mathcal{A}\) con respecto a una distribución de datos \(P (X, Y)\). A continuación, mostraremos que esta expresión se descompone en tres términos significativos.
19.2 Descomposición del error esperado en el conjunto de prueba
\[ \begin{align} E_{\mathbf{x},y,D}\left[\left[h_{D}(\mathbf{x}) - y\right]^{2}\right] &= E_{\mathbf{x},y,D}\left[\left[\left(h_{D}(\mathbf{x}) - \bar{h}(\mathbf{x})\right) + \left(\bar{h}(\mathbf{x}) - y\right)\right]^{2}\right] \nonumber \\ &= E_{\mathbf{x}, D}\left[(\bar{h}_{D}(\mathbf{x}) - \bar{h}(\mathbf{x}))^{2}\right] + 2 \mathrm{\;} E_{\mathbf{x}, y, D} \left[\left(h_{D}(\mathbf{x}) - \bar{h}(\mathbf{x})\right)\left(\bar{h}(\mathbf{x}) - y\right)\right] + E_{\mathbf{x}, y} \left[\left(\bar{h}(\mathbf{x}) - y\right)^{2}\right] \label{eq:eq1} \end{align} \]
El término medio de la ecuación anterior es \(0\), como mostramos a continuación.
\[ \begin{align*} E_{\mathbf{x}, y, D} \left[\left(h_{D}(\mathbf{x}) - \bar{h}(\mathbf{x})\right) \left(\bar{h}(\mathbf{x}) - y\right)\right] &= E_{\mathbf{x}, y} \left[E_{D} \left[ h_{D}(\mathbf{x}) - \bar{h}(\mathbf{x})\right] \left(\bar{h}(\mathbf{x}) - y\right) \right] \\ &= E_{\mathbf{x}, y} \left[ \left( E_{D} \left[ h_{D}(\mathbf{x}) \right] - \bar{h}(\mathbf{x}) \right) \left(\bar{h}(\mathbf{x}) - y \right)\right] \\ &= E_{\mathbf{x}, y} \left[ \left(\bar{h}(\mathbf{x}) - \bar{h}(\mathbf{x}) \right) \left(\bar{h}(\mathbf{x}) - y \right)\right] \\ &= E_{\mathbf{x}, y} \left[ 0 \right] \\ &= 0 \end{align*} \] Volviendo a la expresión anterior, nos quedamos con la varianza y otro término
\[ \begin{equation} E_{\mathbf{x}, y, D} \left[ \left( h_{D}(\mathbf{x}) - y \right)^{2} \right] = \underbrace{E_{\mathbf{x}, D} \left[ \left(h_{D}(\mathbf{x}) - \bar{h}(\mathbf{x}) \right)^{2} \right]}_\mathrm{Variance} + E_{\mathbf{x}, y}\left[ \left( \bar{h}(\mathbf{x}) - y \right)^{2} \right] \end{equation} \]
Podemos descomponer el segundo término en la ecuación anterior de la siguiente manera:
\[ \begin{align} E_{\mathbf{x}, y} \left[ \left(\bar{h}(\mathbf{x}) - y \right)^{2}\right] &= E_{\mathbf{x}, y} \left[ \left(\bar{h}(\mathbf{x}) -\bar y(\mathbf{x}) )+(\bar y(\mathbf{x}) - y \right)^{2}\right] \\ &=\underbrace{E_{\mathbf{x}, y} \left[\left(\bar{y}(\mathbf{x}) - y\right)^{2}\right]}_\mathrm{Noise} + \underbrace{E_{\mathbf{x}} \left[\left(\bar{h}(\mathbf{x}) - \bar{y}(\mathbf{x})\right)^{2}\right]}_\mathrm{Bias^2} + 2 \mathrm{\;} E_{\mathbf{x}, y} \left[ \left(\bar{h}(\mathbf{x}) - \bar{y}(\mathbf{x})\right)\left(\bar{y}(\mathbf{x}) - y\right)\right] \end{align} \]
El tercer término en la ecuación anterior es \(0\), como mostramos a continuación.
\[ \begin{align*} E_{\mathbf{x}, y} \left[\left(\bar{h}(\mathbf{x}) - \bar{y}(\mathbf{x})\right)\left(\bar{y}(\mathbf{x}) - y\right)\right] &= E_{\mathbf{x}}\left[E_{y \mid \mathbf{x}} \left[\bar{y}(\mathbf{x}) - y \right] \left(\bar{h}(\mathbf{x}) - \bar{y}(\mathbf{x}) \right) \right] \\ &= E_{\mathbf{x}} \left[ E_{y \mid \mathbf{x}} \left[ \bar{y}(\mathbf{x}) - y\right] \left(\bar{h}(\mathbf{x}) - \bar{y}(\mathbf{x})\right)\right] \\ &= E_{\mathbf{x}} \left[ \left( \bar{y}(\mathbf{x}) - E_{y \mid \mathbf{x}} \left [ y \right]\right) \left(\bar{h}(\mathbf{x}) - \bar{y}(\mathbf{x})\right)\right] \\ &= E_{\mathbf{x}} \left[ \left( \bar{y}(\mathbf{x}) - \bar{y}(\mathbf{x}) \right) \left(\bar{h}(\mathbf{x}) - \bar{y}(\mathbf{x})\right)\right] \\ &= E_{\mathbf{x}} \left[ 0 \right] \\ &= 0 \end{align*} \] Esto nos da la descomposición del error de prueba esperado de la siguiente manera
\[ \begin{equation*} \underbrace{E_{\mathbf{x}, y, D} \left[\left(h_{D}(\mathbf{x}) - y\right)^{2}\right]}_\mathrm{Expected\;Test\;Error} = \underbrace{E_{\mathbf{x}, D}\left[\left(h_{D}(\mathbf{x}) - \bar{h}(\mathbf{x})\right)^{2}\right]}_\mathrm{Variance} + \underbrace{E_{\mathbf{x}, y}\left[\left(\bar{y}(\mathbf{x}) - y\right)^{2}\right]}_\mathrm{Noise} + \underbrace{E_{\mathbf{x}}\left[\left(\bar{h}(\mathbf{x}) - \bar{y}(\mathbf{x})\right)^{2}\right]}_\mathrm{Bias^2} \end{equation*} \]
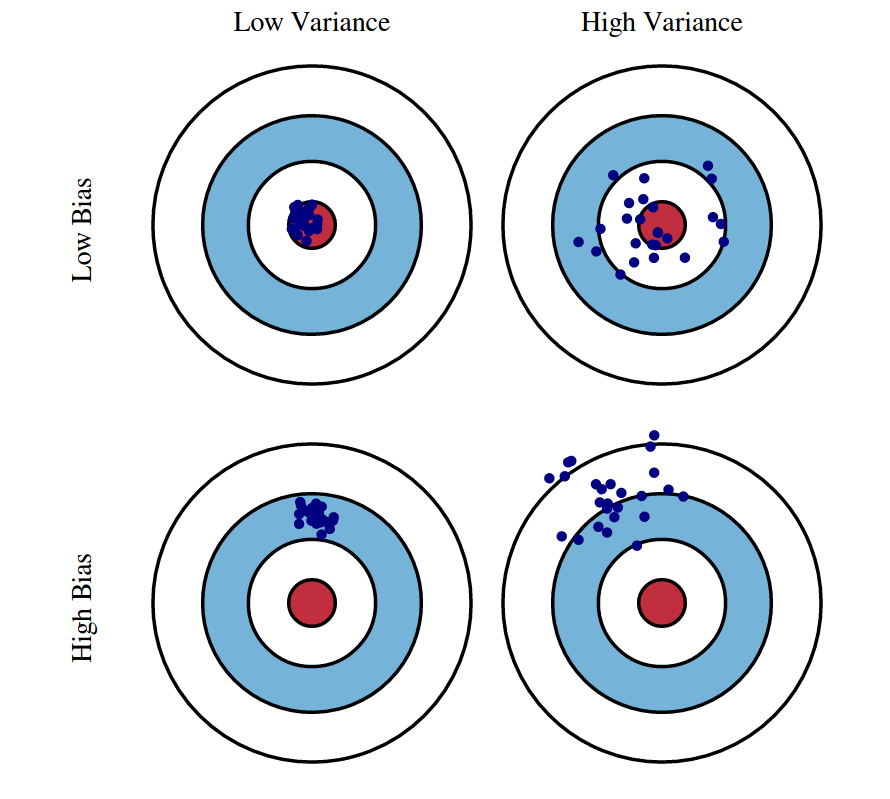
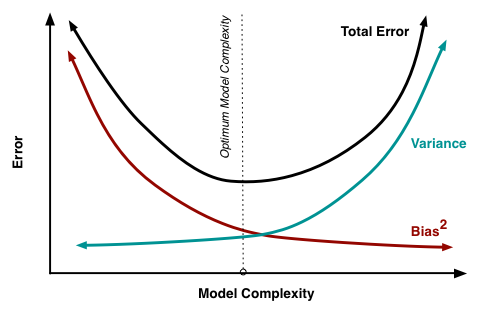
Varianza: captura cuánto cambia su clasificador si entrena en un conjunto de entrenamiento diferente. ¿Qué tan demasiado especializado es su clasificador para un conjunto de entrenamiento en particular (sobreajuste)? Si tenemos el mejor modelo posible para nuestros datos de entrenamiento, ¿qué tan lejos estamos del clasificador promedio?
Sesgo: ¿Cuál es el error inherente que obtiene de su clasificador incluso con datos de entrenamiento infinitos? Esto se debe a que su clasificador está sesgado a un tipo particular de solución (por ejemplo, clasificador lineal). En otras palabras, el sesgo es inherente a su modelo.
Ruido: ¿Qué tan grande es el ruido intrínseco a los datos? Este error mide la ambigüedad debido a su distribución de datos y representación de características. Nunca se puede superar esto, es un aspecto de los datos.
19.3 Detección de alto sesgo y alta varianza
Si un clasificador tiene un rendimiento deficiente (por ejemplo, si el error de prueba o entrenamiento es demasiado alto), hay varias formas de mejorar el rendimiento. Para saber cuál de estas muchas técnicas es la adecuada para la situación, el primer paso es determinar la raíz del problema.
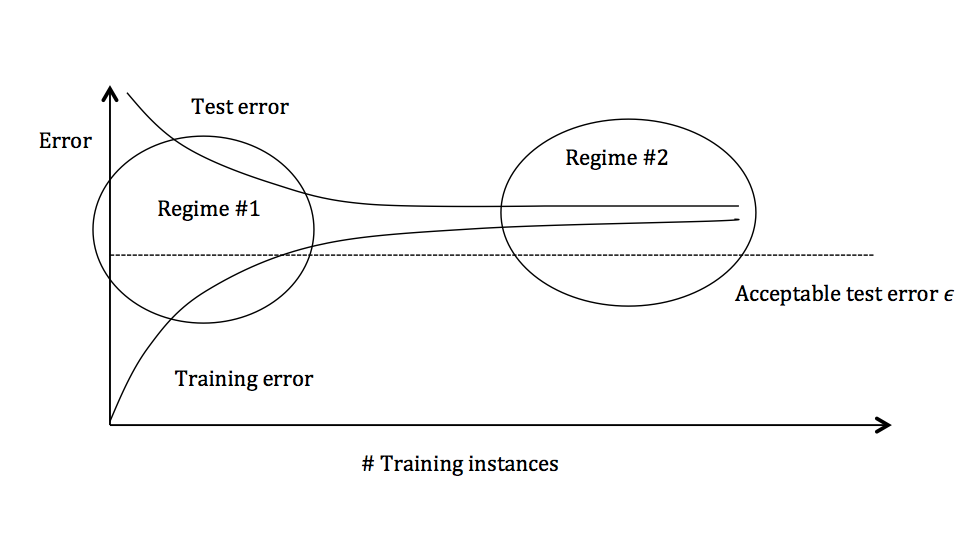
El gráfico anterior muestra el error de entrenamiento y el error de prueba y se puede dividir en dos regímenes generales.
En el primer régimen (en el lado izquierdo del gráfico), el error de entrenamiento está por debajo del umbral de error deseado (indicado por \(\epsilon\)), pero el error de prueba es significativamente mayor.
En el segundo régimen (en el lado derecho del gráfico), el error de prueba está notablemente cerca del error de entrenamiento, pero ambos están por encima de la tolerancia deseada de \(\epsilon\).
19.3.1 Régimen 1 (alta varianza)
En el primer régimen, la causa del bajo rendimiento es una gran varianza
Síntomas:
El error de entrenamiento es mucho menor que el error de prueba
El error de entrenamiento es menor que \(\epsilon\)
El error de prueba está por encima de \(\epsilon\)
Remedios:
Agrega más datos de entrenamiento
Reducir la complejidad del modelo: los modelos complejos son propensos a una gran varianza
Bagging
19.3.2 Régimen 2 (alto sesgo)
A diferencia del primer régimen, el segundo régimen indica un alto sesgo: el modelo que se utiliza no es lo suficientemente robusto para producir una predicción precisa.
Síntomas:
- El error de entrenamiento es mayor que \(\epsilon\)
Remedios:
Utilice un modelo más complejo (por ejemplo, kernelizar, utilizar modelos no lineales)
Agrega características (variables)
Boosting
19.3.3 Simulación
Esta sección es obtenida de: https://daviddalpiaz.github.io/r4sl/biasvariance-tradeoff.html
Ilustraremos estas descomposiciones, lo más importante, la compensación sesgo-varianza, a través de la simulación. Suponga que nos gustaría entrenar un modelo para aprender verdadera función de regresión \(h_D(x) = x^2\):
Generemos datos:
get_sim_data = function(f, sample_size = 100) {
x = runif(n = sample_size, min = 0, max = 1)
eps = rnorm(n = sample_size, mean = 0, sd = 0.75)
y = f(x) + eps
data.frame(x, y)
}Para especificar completamente el proceso de generación de datos, hemos hecho más supuestos del modelo que simplemente \(\mathbb{E}[Y \mid X = x] = x^2\) y \(\mathbb{V}[Y \mid X = x] = \sigma ^ 2\). En particular,
- \(x_i\) in \(\mathcal{D}\) se obtienen de una distribución uniforme \([0, 1]\).
- \(x_i\) and \(\epsilon\) son independentes.
- \(y_i\) in \(\mathcal{D}\) se obtienen de una distribución normal condicionada:
\[ Y \mid X \sim N(f(x), \sigma^2). \] Con este proceso de generación de datos, generamos conjuntos de datos, \(D\) con tamaño muestral \(n = 100\) y ajustamos los modelos
\[ \begin{aligned} \texttt{predict(fit0, x)} &= \hat{f}_0(x) = \hat{\beta}_0\\ \texttt{predict(fit1, x)} &= \hat{f}_1(x) = \hat{\beta}_0 + \hat{\beta}_1 x \\ \texttt{predict(fit2, x)} &= \hat{f}_2(x) = \hat{\beta}_0 + \hat{\beta}_1 x + \hat{\beta}_2 x^2 \\ \texttt{predict(fit9, x)} &= \hat{f}_9(x) = \hat{\beta}_0 + \hat{\beta}_1 x + \hat{\beta}_2 x^2 + \ldots + \hat{\beta}_9 x^9 \end{aligned} \]
Para tener una idea de los datos y estos cuatro modelos, generamos un conjunto de datos simulado y ajustamos los cuatro modelos.
fit_0 = lm(y ~ 1, data = sim_data)
fit_1 = lm(y ~ poly(x, degree = 1), data = sim_data)
fit_2 = lm(y ~ poly(x, degree = 2), data = sim_data)
fit_9 = lm(y ~ poly(x, degree = 9), data = sim_data)Al graficar estos cuatro modelos entrenados, vemos que el modelo de predictor cero funciona muy mal. El modelo de primer grado es razonable, pero podemos ver que el modelo de segundo grado se ajusta mucho mejor.
set.seed(42)
plot(y ~ x, data = sim_data, col = "grey", pch = 20,
main = "Cuatro modelos polinomiales para ajustar un conjunto de datos simulado")
grid()
grid = seq(from = 0, to = 2, by = 0.01)
lines(grid, f(grid), col = "black", lwd = 3)
lines(grid, predict(fit_0, newdata = data.frame(x = grid)), col = "dodgerblue", lwd = 2, lty = 2)
lines(grid, predict(fit_1, newdata = data.frame(x = grid)), col = "firebrick", lwd = 2, lty = 3)
lines(grid, predict(fit_2, newdata = data.frame(x = grid)), col = "springgreen", lwd = 2, lty = 4)
lines(grid, predict(fit_9, newdata = data.frame(x = grid)), col = "darkorange", lwd = 2, lty = 5)
legend("topleft",
c("y ~ 1", "y ~ poly(x, 1)", "y ~ poly(x, 2)", "y ~ poly(x, 9)", "verdadero"),
col = c("dodgerblue", "firebrick", "springgreen", "darkorange", "black"), lty = c(2, 3, 4, 5, 1), lwd = 2)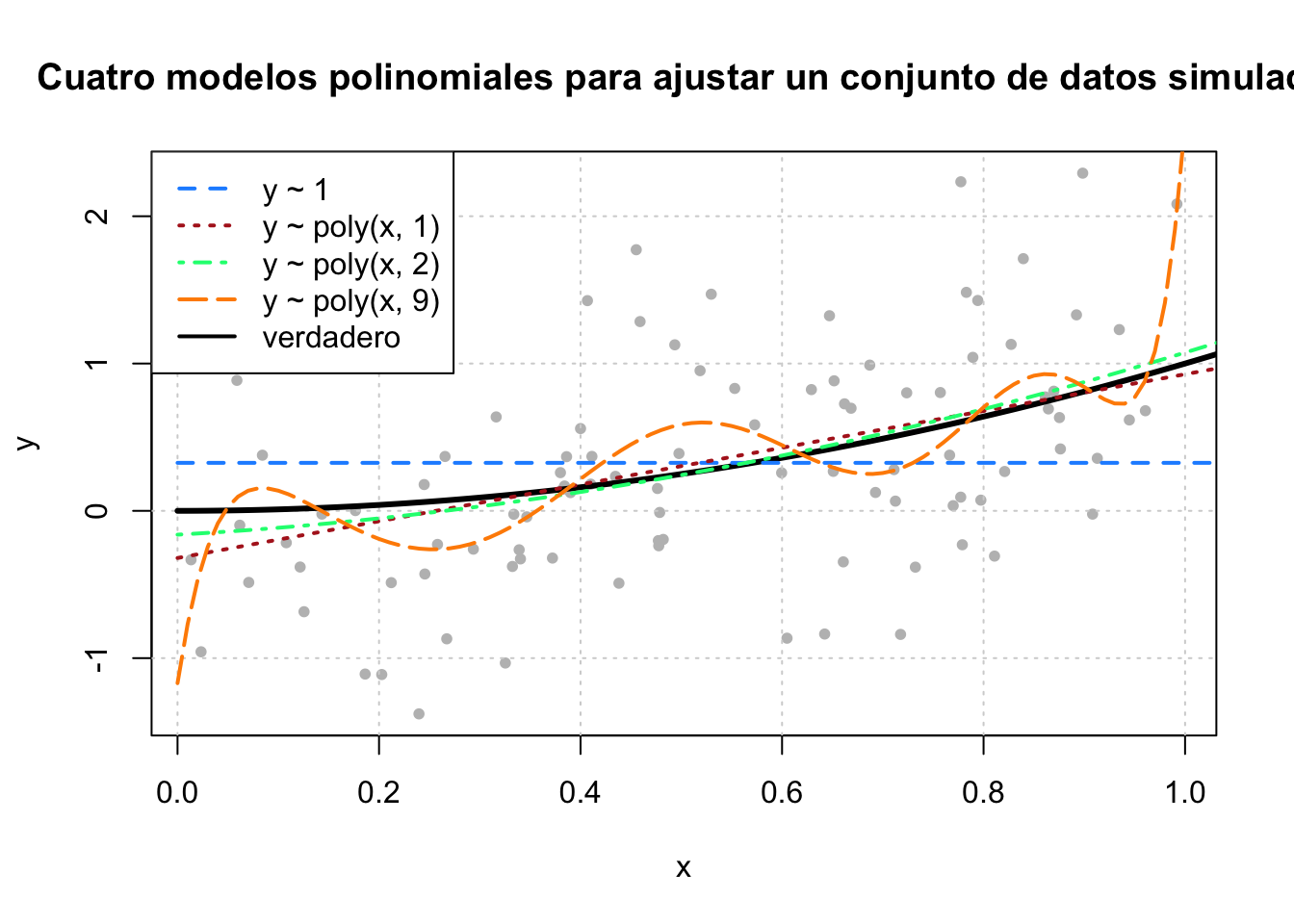
Ahora completaremos el estudio de simulación para comprender la relación entre el sesgo, la varianza y el error cuadrático medio para las estimaciones de \(h_D (x)\) dadas por estos cuatro modelos en el punto \(x = 0.90\). Usamos simulación para completar esta tarea, ya que realizar los cálculos analíticos resultaría bastante tedioso y difícil.
set.seed(1)
n_sims = 250
n_models = 4
x = data.frame(x = 0.90) # punto dijo al que hacemos predicción
predictions = matrix(0, nrow = n_sims, ncol = n_models)for (sim in 1:n_sims) {
# simulamos datos nuevos, aleatorios de entrenamiento
# esta es la única parte aleatria del cálculo del sesgo, varianza y mse
# esto nos permite calcula la esperanza sobre D
sim_data = get_sim_data(f)
# Ajuste de modelos
fit_0 = lm(y ~ 1, data = sim_data)
fit_1 = lm(y ~ poly(x, degree = 1), data = sim_data)
fit_2 = lm(y ~ poly(x, degree = 2), data = sim_data)
fit_9 = lm(y ~ poly(x, degree = 9), data = sim_data)
# Obtenemos las predicciones
predictions[sim, 1] = predict(fit_0, x)
predictions[sim, 2] = predict(fit_1, x)
predictions[sim, 3] = predict(fit_2, x)
predictions[sim, 4] = predict(fit_9, x)
}
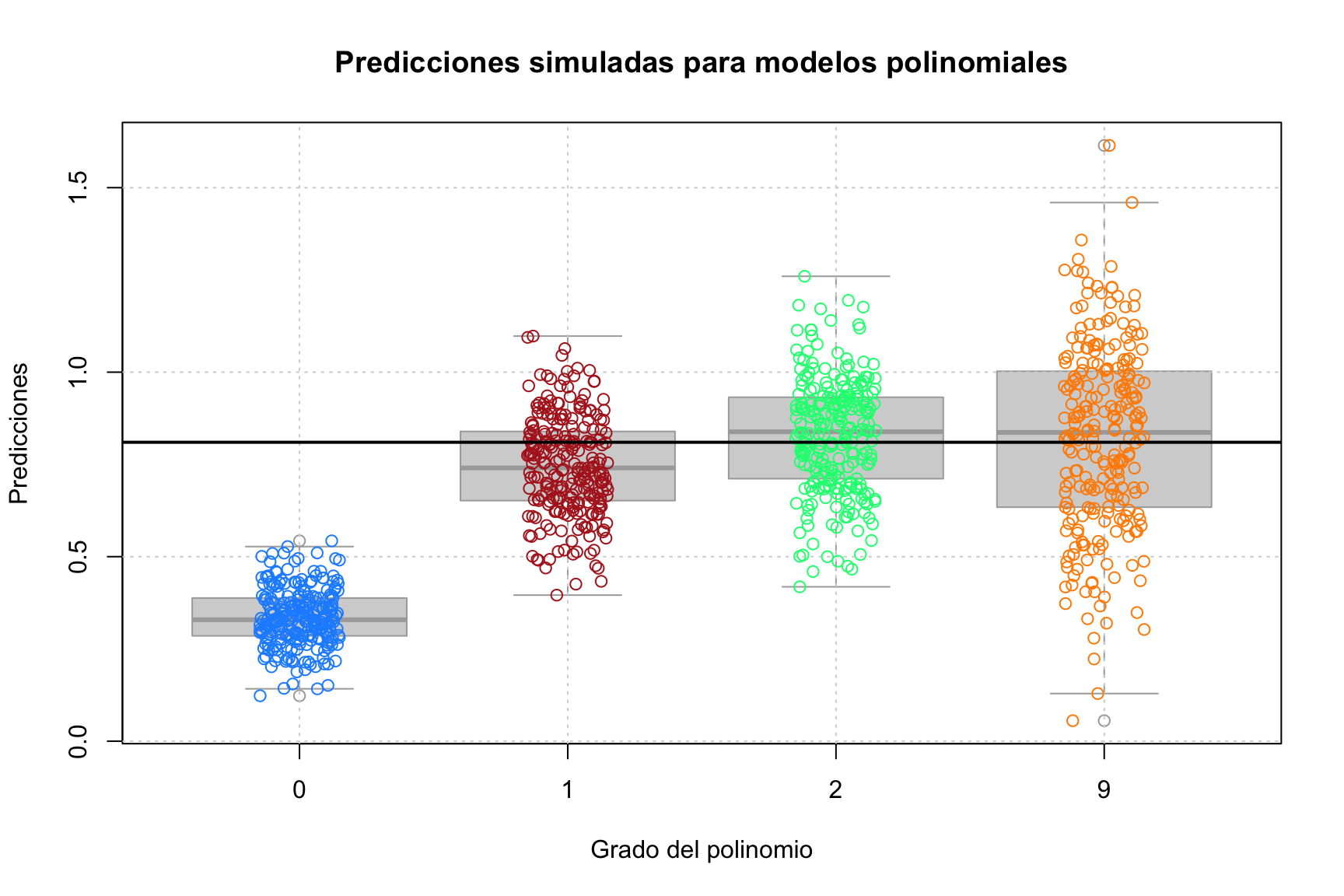El gráfico anterior muestra las predicciones para cada una de las \(250\) simulaciones de cada uno de los cuatro modelos de diferentes grados polinomiales. La verdadera, \(h_D (x = 0.90) = (0.9)^2 = 0.81\), está dada por la línea horizontal negra sólida.
Dos cosas quedan claras de inmediato:
A medida que aumenta la complejidad, el sesgo disminuye. (La media de las predicciones de un modelo está más cerca de la verdad).
A medida que aumenta la complejidad, aumenta la varianza. (La varianza sobre la media de las predicciones de un modelo aumenta).
El objetivo de este estudio de simulación es mostrar que lo siguiente es válido para cada uno de los cuatro modelos.
\[ \text{MSE}\left(h(0.90), \hat{h}_k(0.90)\right) = \underbrace{\left(\mathbb{E} \left[ \hat{h}_k(0.90) \right] - h(0.90) \right)^2}_{\text{bias}^2 \left(\hat{h}_k(0.90) \right)} + \underbrace{\mathbb{E} \left[ \left( \hat{h}_k(0.90) - \mathbb{E} \left[ \hat{h}_k(0.90) \right] \right)^2 \right]}_{\text{var} \left(\hat{h}_k(0.90) \right)} \] Para estimar el error cuadrático medio de nuestras predicciones, usaremos
\[ \widehat{\text{MSE}}\left(h(0.90), \hat{h}_k(0.90)\right) = \frac{1}{n_{\texttt{sims}}}\sum_{i = 1}^{n_{\texttt{sims}}} \left(h(0.90) - \hat{h}_k(0.90) \right)^2 \]
Del mismo modo, para el sesgo de nuestras predicciones utilizamos
\[ \widehat{\text{bias}} \left(\hat{h}(0.90) \right) = \frac{1}{n_{\texttt{sims}}}\sum_{i = 1}^{n_{\texttt{sims}}} \left(\hat{h}_k(0.90) \right) - h(0.90) \]
Por último, para la variación de nuestras predicciones tenemos
\[ \widehat{\text{var}} \left(\hat{h}(0.90) \right) = \frac{1}{n_{\texttt{sims}}}\sum_{i = 1}^{n_{\texttt{sims}}} \left(\hat{h}_k(0.90) - \frac{1}{n_{\texttt{sims}}}\sum_{i = 1}^{n_{\texttt{sims}}}\hat{h}_k(0.90) \right)^2 \]
Obtenemos los resultados:
bias = apply(predictions, 2, get_bias, truth = f(x = 0.90))
variance = apply(predictions, 2, get_var)
mse = apply(predictions, 2, get_mse, truth = f(x = 0.90))Resumimos los resultados en la siguiente tabla
| Grado | MSE (Mean Squared Error) | Sesgo (Bias) | Varianza |
|---|---|---|---|
| 0 | 0.23094 | 0.22492 | 0.00601 |
| 1 | 0.02249 | 0.00411 | 0.01838 |
| 2 | 0.02418 | 0.00033 | 0.02384 |
| 9 | 0.06371 | 0.00013 | 0.06358 |
Varias cosas a tener en cuenta aquí:
Usamos el sesgo al cuadrado en esta tabla. Dado que el sesgo puede ser positivo o negativo, el sesgo al cuadrado es más útil para observar la tendencia a medida que aumenta la complejidad.
El sesgo al cuadrado que vemos aquí está disminuyendo a medida que aumenta la complejidad, lo que esperamos ver en general.
Exactamente lo contrario ocurre con la varianza. A medida que aumenta la complejidad del modelo, aumenta la varianza.
El error cuadrático medio, que es una función del sesgo y la varianza, disminuye y luego aumenta. Este es el resultado de la compensación sesgo-varianza.
Podemos disminuir el sesgo aumentando la varianza. O podemos disminuir la varianza aumentando el sesgo. ¡Al encontrar el equilibrio correcto, podemos encontrar un buen error cuadrático medio!
plot(results[,1],results[,3],t = "l",xlab = "Complejidad del modelo",ylab = "Error", col = "red") # sesgo
lines(results[,1],results[,4], col ="lightblue") # varianza
lines(results[,1],results[,2]) #mse
legend("topright",legend = c("Sesgo","Varianza","MSE"),col=c("red","lightblue","black"),lty = 1)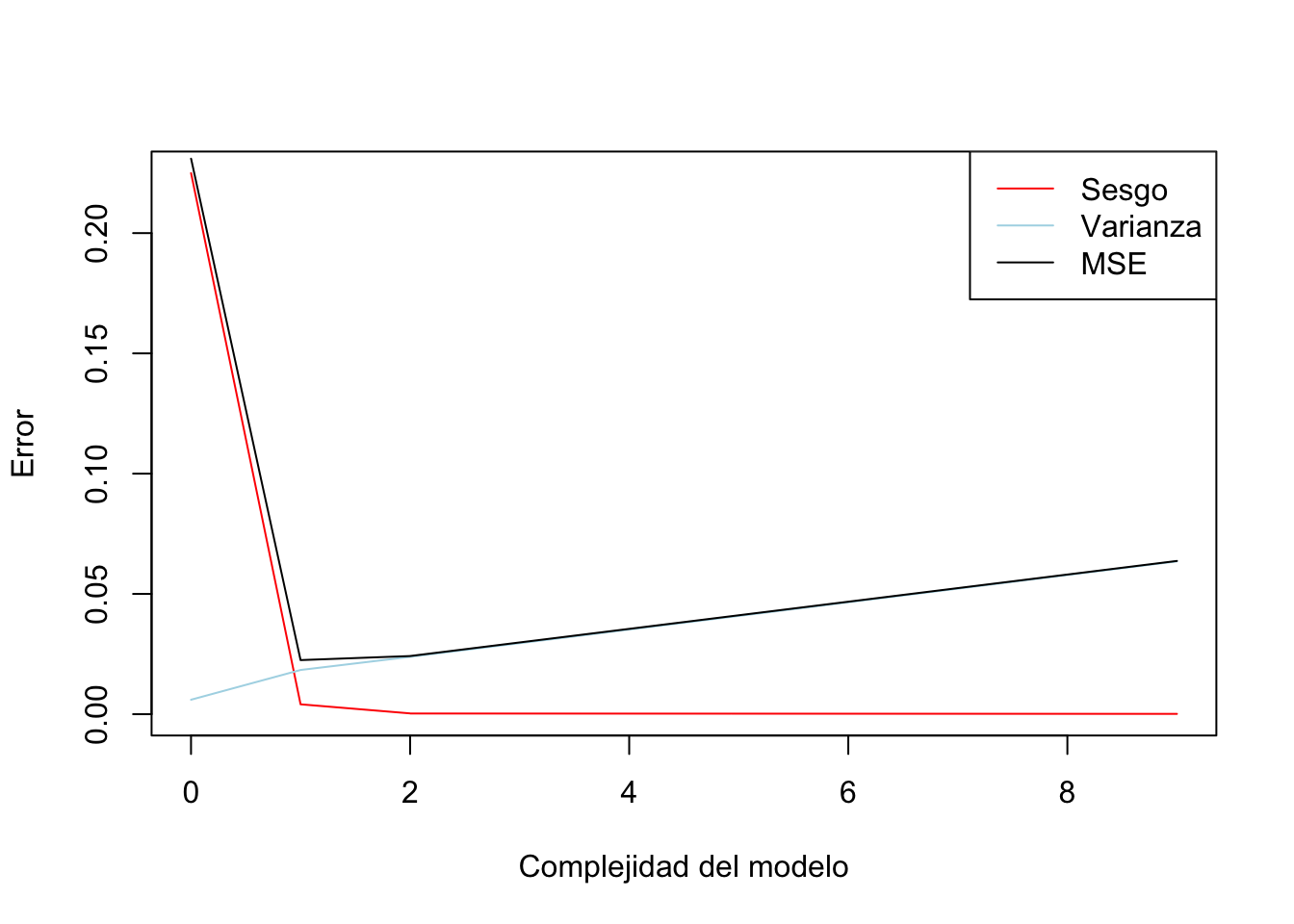
19.4 Selección de variables y remuestreo
19.4.1 Selección de variables
Dentro del análisis supervisado, hemos recorrido varios métodos que nos permiten hacer selección de variables. Entre ellos:
- Análisis de componentes principales: Una técnica de selección de variables que suele utilizarse para seleccionar variables es el análisis de componentes principales.
Leemos los datos:
# rm( list ( ls()))
# **** Importo datos: VAB no petrolero
uu <- "https://raw.githubusercontent.com/vmoprojs/DataLectures/master/SpatialData/VABNoPetroleroCantones2007-2019.csv"
datos <- read.csv(uu,sep = ",")
datos$COD_CANT[nchar(datos$COD_CANT)==3] = paste("0",datos$COD_CANT[nchar(datos$COD_CANT)==3],sep = "")
datos <- subset(datos,datos$YEAR == 2019)
# **** Importo datos: Población por cantones
uu <- "https://raw.githubusercontent.com/vmoprojs/DataLectures/master/SpatialData/proyeccion_cantonal_total_2010-2020.csv"
poblacion <- read.csv(uu,sep = ";")
names(poblacion)[1] <- "CODIGO"
poblacion$CODIGO[nchar(poblacion$CODIGO)==3] = paste("0",poblacion$CODIGO[nchar(poblacion$CODIGO)==3],sep = "")
# **** Importo datos: NBI
uu <- "https://raw.githubusercontent.com/vmoprojs/DataLectures/master/SpatialData/NBI_PER_CANT.csv"
NBI <- read.csv(uu, sep = ";")
names(NBI)[1] <- "CODIGO"
NBI$CODIGO[nchar(NBI$CODIGO)==3] = paste("0",NBI$CODIGO[nchar(NBI$CODIGO)==3],sep = "")
datos <- merge(datos,poblacion[,c("CODIGO","A_2020","SuperficieKM2")],by.x = "COD_CANT",by.y = "CODIGO",all.x = TRUE)
datos <- merge(datos,NBI[,c("CODIGO","POBRES_P")],by.x = "COD_CANT",by.y = "CODIGO",all.x = TRUE)
datos$VAB_PC <- datos$VAB/datos$A_2020 #miles de USD / pob
datos$PRODUCCION_PC <- datos$PRODUCCION/datos$A_2020 #miles de USD / pob
datos$CONSUMO_INTERMEDIO_PC <- datos$CONSUMO_INTERMEDIO/datos$A_2020 #miles de USD / pob
datos$DensPob <- datos$A_2020/datos$SuperficieKM2
# **** Importo datos: NBICOVID (https://www.covid19ecuador.org/cantones)
uu <- "https://raw.githubusercontent.com/andrab/ecuacovid/master/datos_crudos/positivas/por_fecha/cantones_por_dia_acumuladas.inec.csv"
uu <- "https://raw.githubusercontent.com/vmoprojs/DataLectures/master/cantones_por_dia_acumuladas_inec.csv"
c19 <- read.csv(uu, sep = ",")
c19 <- c19[,c("inec_canton_id","X29.06.2021")]
c19$inec_canton_id[nchar(c19$inec_canton_id)==3] = paste("0",c19$inec_canton_id[nchar(c19$inec_canton_id)==3],sep = "")
names(c19) <- c("COD_CANT","C19")
# names(datos)
datos <- merge(datos,c19, by.x = "COD_CANT",all.x = TRUE)
datos$C19_pc <- (datos$C19/datos$A_2020)*1000
datos <- na.omit(datos)depvar <- "POBRES_P"
y <- datos[,depvar]
X <- datos[,c(10,13,14,16,18)]
denormalize <- function(x_norm,x_orig)
{
#x_norm: normalized dats
#x_orig: original data
mmin <- min(x_orig);mmax <- max(x_orig)
denorm_val <- x_norm*(mmax-mmin)+mmin
return(denorm_val)
}
normalize <- function(x) {
return((x - min(x)) / (max(x) - min(x)))
}
X_c <- normalize(X)
y_c <- normalize(y)
set.seed(851)
index <- caret::createDataPartition(y_c, p=0.75, list=FALSE)
X_train <- X_c[ index, ]
X_test <- X_c[-index, ]
y_train <- y_c[index]
y_test <- y_c[-index]pca <- prcomp(X_train,scale = TRUE)
summary(pca)
round((pca$sdev/sum(pca$sdev))*100)
varImp_pca <- rownames(pca$rotation)[order(pca$rotation[,1])]m1 <- lm(y_train~.,data = X_train)
ff <- paste("y_train~",paste(varImp_pca[1:3],collapse = "+"))
m2 <- lm(ff,data = X_train)
caret::R2(predict(m1,newdata = X_test),y_test)
caret::R2(predict(m2,newdata = X_test),y_test)Notemos que usando las 3 primeras variables del ACP logramos un \(R^2\) no muy lejano del estimado con todas las variables en los datos test.
- Árboles de decisión: el algoritmo de árboles de decisión devuelve una jerarquía de las variables analizadas:
library(rpart)
m_ar1 <- rpart(y_train~.,data = X_train)
varImp_ar <- m_ar1$variable.importance
ff <- paste("y_train~",paste(names(varImp_ar)[1:3],collapse = "+"))
ar1 <- lm(ff,data = X_train)
caret::R2(predict(m1,newdata = X_test),y_test) # RLM
caret::R2(predict(m2,newdata = X_test),y_test) # RLM_ACP
caret::R2(predict(m_ar1,newdata = X_test),y_test) # Tree
caret::R2(predict(ar1,newdata = X_test),y_test) # RLM_ar- Algoritmo step: hace una selección de variables hacia adelante aumentado variables o hacia atrás eliminando variables del modelo
19.4.2 Ejercicio 1
El siguiente ejercicio aplica una técnica donde se crean variables usando un árbol de decisión, a esta técnica se le conoce como modelo de vectores.
Estudie el código y comente cada línea.
uu <- "https://raw.githubusercontent.com/vmoprojs/DataLectures/master/Bank_churn_modelling.csv"
datos <- read.csv(uu,sep = ",")
datos <- datos[,3:ncol(datos)]
numvar <- sapply(datos,class)!="character"
datos <- datos[,numvar]
depvar <- "Exited"
y <- factor(datos[,depvar],ordered = TRUE)
X <- datos[,!names(datos) %in%depvar]set.seed(851)
index <- caret::createDataPartition(y, p=0.75, list=FALSE)
X_train <- X[ index, ]
X_test <- X[-index, ]
y_train <- y[index]
y_test <- y[-index]ff <- paste("y_train","~",paste(names(X_train),collapse = "+"))
m1 <- rpart(ff, data = X_train)
# formas de extraer las reglas:
library(rpart.plot)
# rpart.rules(m1)
library(partykit)
reglas <- partykit:::.list.rules.party(as.party(m1,data = TRUE))aux_train <- X_train
aux_test <- X_test
for(i in 1:length(reglas))
{
# i = 1
fil <- with(X_train,eval(parse(text = reglas[i])))
fil1 <- with(X_test,eval(parse(text = reglas[i])))
aux_train <- cbind(aux_train,fil)
names(aux_train)[ncol(aux_train)] <- paste("fil_",i,sep = "")
aux_test <- cbind(aux_test,fil1)
names(aux_test)[ncol(aux_test)] <- paste("fil_",i,sep = "")
}
# ff <- paste("y_train","~","(",paste(names(aux_train)[9:16],collapse = "+"),")^2")
ff <- paste("y_train","~",paste(names(aux_train),collapse = "+"))
m_logit_reglas <- glm(ff,data = aux_train,family = binomial(link = "logit"))
m_logit_reglas <- step(m_logit_reglas,trace = 0)
ff <- paste("y_train","~",paste(names(X_train),collapse = "+"))
m_logit_normal <- glm(ff,data = X_train,family = binomial(link = "logit"))
m_logit_normal <- step(m_logit_normal,trace = 0)library(pROC)
pp <- roc(y_test,predict(m_logit_normal,newdata = X_test,type = "response"))
corte <- as.numeric(coords(pp, "best")[1])
y_pred_lnorm <- factor((predict(m_logit_normal,newdata = X_test,type = "response")>corte)*1)
levels(y_pred_lnorm) <- c("0","1")
pp <- roc(y_test,predict(m_logit_reglas,newdata = aux_test,type = "response"))
corte <- as.numeric(coords(pp, "best")[1])
y_pred_reglas <- factor((predict(m_logit_normal,newdata = X_test,type = "response")>corte)*1)
levels(y_pred_reglas) <- c("0","1")
caret::confusionMatrix(predict(m1,type = "class",newdata = X_test),y_test)
caret::confusionMatrix(y_pred_lnorm,y_test)
caret::confusionMatrix(y_pred_reglas,y_test)19.5 Cross-validación
La cross validación es parte de lo que se conoce como métodos de remuestreo. Estos implican extraer repetidamente muestras de un conjunto de entrenamiento y reajustar un modelo de interés en cada muestra para obtener información adicional sobre el modelo ajustado.
Los enfoques de remuestreo pueden ser costosos desde el punto de vista computacional, porque implican ajustar el mismo método estadístico varias veces utilizando diferentes subconjuntos de los datos de entrenamiento.
El proceso de evaluación del desempeño de un modelo se conoce como evaluación del modelo, mientras que el proceso de seleccionar el nivel adecuado de flexibilidad de un modelo, se conoce como selección del modelo.
El error de prueba se puede calcular fácilmente si se dispone de una prueba estadística (por ejemplo, normalidad). Desafortunadamente, este no suele ser el caso.
19.5.1 Ejemplo 1
Tenemos datos del impacto de tres medios publicitarios (youtube, facebook y periódico) en las ventas. Los datos son el presupuesto publicitario en miles de dólares junto con las ventas. El experimento publicitario se ha repetido 200 veces.
# usaremos `caret` para realizar la validación cruzada
library(caret)
# el conjunto de datos se encuentra en el paquete `datarium`
# install.packages("datarium")
data("marketing", package = "datarium")
head(marketing)## youtube facebook newspaper sales
## 1 276.12 45.36 83.04 26.52
## 2 53.40 47.16 54.12 12.48
## 3 20.64 55.08 83.16 11.16
## 4 181.80 49.56 70.20 22.20
## 5 216.96 12.96 70.08 15.48
## 6 10.44 58.68 90.00 8.64Los parámetros de la función trainControl:
method: se define el método de remuestreo. En este caso es la validación cruzada repetida.number: define el número de grupos en el que se particiona el conjunto de datos.repeats: define el número de veces que se repite el proceso de validación cruzada.
Se entrena el modelo asignando las ventas como variable dependiente y las demás variables como independientes.
# Se genera la semilla para reproducir los resultados
set.seed(125)
train_control <- trainControl(method = "repeatedcv",
number = 10, repeats = 3)
model <- caret::train(sales ~., data = marketing,
method = "lm",
trControl = train_control)
# se imprimen los resultados:
print(model)## Linear Regression
##
## 200 samples
## 3 predictor
##
## No pre-processing
## Resampling: Cross-Validated (10 fold, repeated 3 times)
## Summary of sample sizes: 181, 180, 180, 179, 180, 180, ...
## Resampling results:
##
## RMSE Rsquared MAE
## 2.020061 0.9038559 1.541517
##
## Tuning parameter 'intercept' was held constant at a value of TRUENos devuelve el número de datos usados, 3 predictor está relacionado al parámetro repeats. Se indica que los datos no fueron pre procesados.
Otra forma de estimar el error ante diferentes tamaños de la muestra de entrenamiento es usando la función learning_curve_dat.
set.seed(29510)
lda_data <- learning_curve_dat(dat = marketing,
outcome = "sales",
proportion = (1:10)/10,
test_prop = 1/4,
## `train` arguments:
method = "lm",
metric = "RMSE")## Training for 10% (n = 15)
## Training for 20% (n = 30)
## Training for 30% (n = 45)
## Training for 40% (n = 60)
## Training for 50% (n = 75)
## Training for 60% (n = 90)
## Training for 70% (n = 105)
## Training for 80% (n = 120)
## Training for 90% (n = 135)
## Training for 100% (n = 151)ggplot(lda_data, aes(x = Training_Size, y = RMSE, color = Data)) +
geom_smooth(formula = y ~ x,method = loess, span = .8)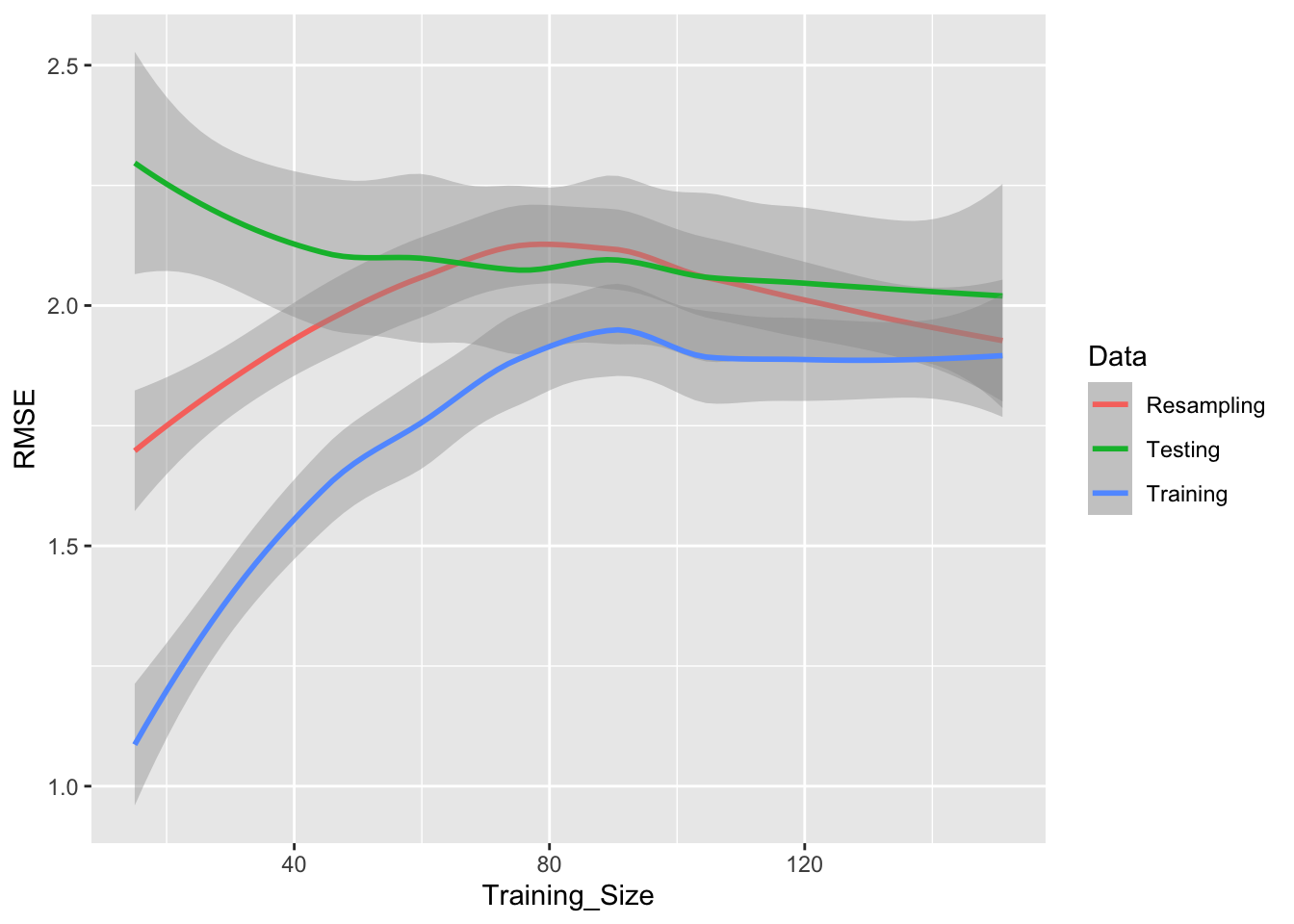
Notemos que el modelo se entrena incrementalmente en proporciones (parámetro proportion = (1:10)/10) de los datos de entrenamiento.
El entrenamiendo llega a \(n\sim 150\) porque se ha separado un 25% para los datos test (usando el parámetro test_prop = 1/4).
19.6 Estimación de hiperparámetros
Recuerda que los modelos disponibles para ser usados con caret están en: (http://topepo.github.io/caret/available-models.html).
Para la estimación de hiperparámetros, usamos el parámetro tuneGrid. Nota que los parámetros deben tener el mismo nombre que se usa en el modelo (lambda y alpha en nuestro ejemplo) y se usa la función expand.grid.
Estos valores de los hiperparámetros son puestos aprueba mediante validación cruzada descritos en la función trainControl.
En el siguiente ejemplo se postulan diferentes especificaciones para el modelo de regularización elastic net,
\[ \sum_{i = 1}^n\left(y_i-\beta_0-\sum_{j=1}^p \beta_jx_{ij}\right)^2/2n+\lambda\sum_{j = 1}^{p} \beta_j^2 = \text{RSS/2n}+\lambda\left(\left(\frac{1-\alpha}{2}\right)\sum_{j = 1}^{p} \beta_j^2+\alpha\sum_{j = 1}^{p} |\beta_j|\right), \]
Es decir, el parámetro \(\alpha\) (elasticnet mixing parameter) es un parámetro establece un punto intermedio entre lasso (\(\alpha=1\)) y ridge (\(\alpha=0\)).
set.seed(125)
tGrid <- expand.grid(lambda = seq(0,1,0.1),alpha = seq(0,1,0.1))
train_control <- trainControl(method = "repeatedcv",
number = 10, repeats = 3)
model <- caret::train(sales ~., data = marketing,
method = "glmnet",
trControl = train_control,
tuneGrid =tGrid,
metric = "RMSE")
model$bestTune## alpha lambda
## 112 1 0.1La estimación anterior usa validación cruzada para determinar los mejores valores de \(\alpha\) y \(\lambda\). Una vez que tenemos estos valores, podemos fijarlos para así ver su error de entrenamiento y prueba:
lda_data <- learning_curve_dat(dat = marketing,
outcome = "sales",
test_prop = 1/4,
## `train` arguments:
method = "glmnet",
metric = "RMSE",
tuneGrid =expand.grid(alpha = 1, lambda = 0.1))## Training for 10% (n = 15)
## Training for 20% (n = 30)
## Training for 30% (n = 45)
## Training for 40% (n = 60)
## Training for 50% (n = 75)
## Training for 60% (n = 90)
## Training for 70% (n = 105)
## Training for 80% (n = 120)
## Training for 90% (n = 135)
## Training for 100% (n = 151)ggplot(lda_data, aes(x = Training_Size, y = RMSE, color = Data)) +
geom_smooth(method = loess, span = .8)## `geom_smooth()` using formula = 'y ~ x'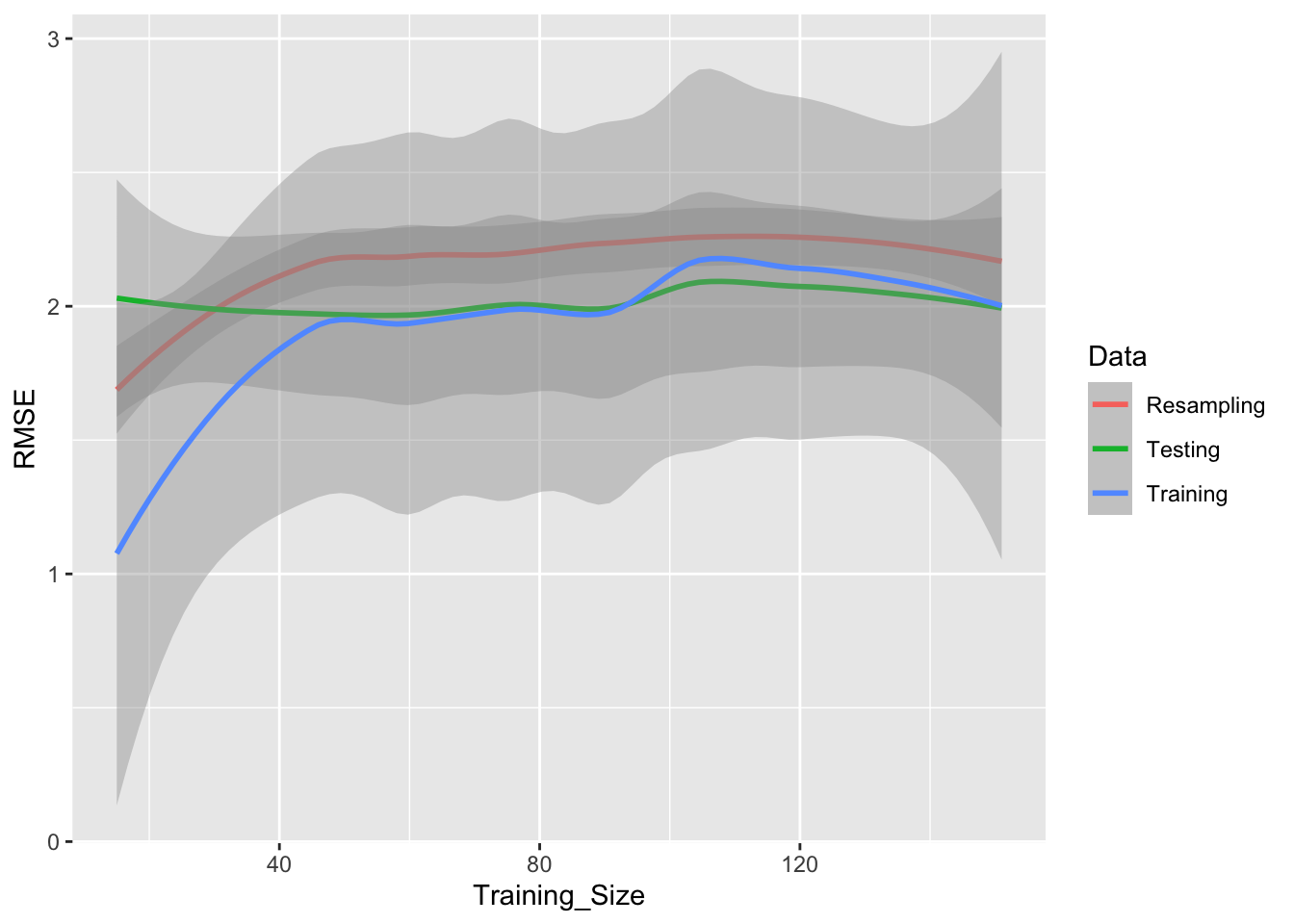
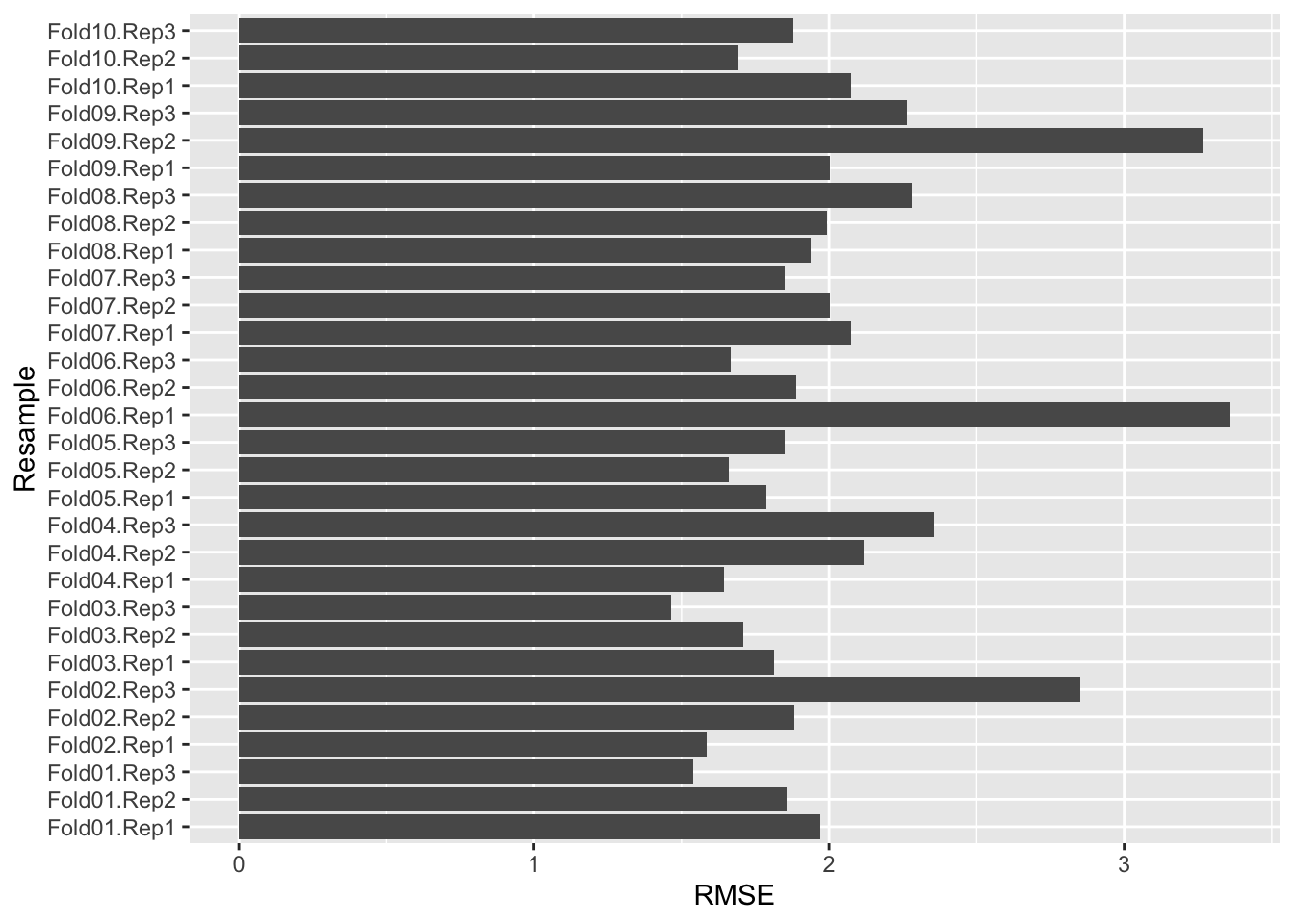
19.6.1 Ejemplo 2
Usar las variables numéricas para aplicar el algoritmo de vecinos más cercanos knn. La descripción de los datos se encuentra en https://github.com/vmoprojs/DataLectures/blob/master/Bank_churn_modelling.txt. La variable dependiente es Exited que indica si el cliente ha desertado.
uu <- "https://raw.githubusercontent.com/vmoprojs/DataLectures/master/Bank_churn_modelling.csv"
datos <- read.csv(uu,sep = ",")
datos <- datos[,3:ncol(datos)]
numvar <- sapply(datos,class)!="character"
datos <- datos[,numvar]
depvar <- "Exited"Creamos la partición de los datos:
X <- datos[,!(names(datos) %in% depvar)]
y <- datos[,depvar]
X_c <- normalize(X)
y_c <- normalize(y)
set.seed(851)
index <- caret::createDataPartition(y_c, p=0.75, list=FALSE)
X_train <- X_c[ index, ]
X_test <- X_c[-index, ]
y_train <- y_c[index]
y_test <- y_c[-index]Entrenamos el modelo con k = 2 vecinos más cercanos y evaluamos los resultados sobre los datos test:
library(class)
sol <- knn(X_train,X_test,cl = y_train,k = 2)
confusionMatrix(table(y_test,sol),positive = "1")Ahora lo estimamos usando caret. Usamos validación cruzada en 10 particiones repetida 3 veces, indicamos la función twoClassSummary (calcula la sensibilidad, la especificidad y el área bajo la curva ROC) y classProbs es un valor lógico que determina si las probabilidades deben calcularse para muestras retenidas durante el remuestreo.
Se plantea valores de k entre 5 y 25 como hiperparámetros:
set.seed(400)
ctrl <- trainControl(method="repeatedcv",repeats = 1,summaryFunction = twoClassSummary,classProbs = TRUE,number = 10)
y_train <- factor(y_train)
levels(y_train) <- c("No","Yes")
knnFit <- caret::train(x = X_train,
y = factor(y_train),
method = "knn",
trControl = ctrl,
tuneGrid = expand.grid(k = 5:20),
metric = "ROC")
knnFit$bestTuneVeamos la matriz de confusión del modelo estimado:
y_test <- factor(y_test)
levels(y_test) <- c("No","Yes")
p_knn <- predict(knnFit,newdata = X_test)
confusionMatrix(table(y_test,p_knn),positive = "Yes")Una vez que tenemos estos valores, podemos fijarlos para así ver su error de entrenamiento y prueba:
y_train_aux <- factor(y_train)
levels(y_train_aux) <- c("No","Yes")
dd <- data.frame(X_train,Exited =factor(y_train_aux))
ctrl <- trainControl(summaryFunction = twoClassSummary,classProbs = TRUE)
lda_data <- learning_curve_dat(dat = dd,
trControl = ctrl,
outcome = "Exited",
test_prop = 1/4,
## `train` arguments:
method = "knn",
metric = "ROC",
tuneGrid =expand.grid(k = 18))
head(lda_data)
ggplot(lda_data, aes(x = Training_Size, y = ROC, color = Data)) +
geom_smooth(formula = y ~ x,method = loess, span = .8)