7 Mínimos cuadrados no lineales
Paquetes de esta sección
Todos los modelos que hemos analizado hasta ahora han sido lineales en los parámetros (es decir, lineales en los beta). El modelo de regresión final fue solo una combinación lineal de predictores de orden superior.
Ahora estamos interesados en estudiar el modelo de regresión no lineal:
\[ Y=f(\textbf{X},\beta)+\epsilon \]
donde \(\textbf{X}\) es un vector de \(p\) predictores, \(\beta\) es un vector de \(k\) parámetros, \(f(\cdot)\) es una función de regresión conocida y \(\epsilon\) es un término de error cuya distribución puede o no ser normal.
Observe que ya no necesariamente tenemos la dimensión del vector de parámetros simplemente uno mayor que el número de predictores. Algunos ejemplos de modelos de regresión no lineal son:
\[ y_{i}=\frac{e^{\beta_{0}+\beta_{1}x_{i}}}{1+e^{\beta_{0}+\beta_{1}x_{i}}}+\epsilon_{i} \]
\[ y_{i}=\frac{\beta_{0}+\beta_{1}x_{i}}{1+\beta_{2}e^{\beta_{3}x_{i}}}+\epsilon_{i} \]
\[ y_{i}=\beta_{0}+(0.4-\beta_{0})e^{-\beta_{1}(x_{i}-5)}+\epsilon_{i} \]
Sin embargo, hay algunos modelos no lineales que en realidad se llaman intrínsecamente lineales porque se pueden hacer lineales en los parámetros mediante una simple transformación. Por ejemplo:
\[ Y=\frac{\beta_{0}X}{\beta_{1}+X} \]
puede ser re escrito como:
\[ \frac{1}{Y}=\frac{1}{\beta_{0}}+\frac{\beta_{1}}{\beta_{0}}\frac{1}{X} \]
\[ \frac{1}{Y}=\theta_{0}+\theta_{1}\frac{1}{X} \]
Lo cual es lineal en los parámetros transformados \(\theta\) y \(\theta\). En tales casos, la transformación de un modelo a su forma lineal a menudo proporciona mejores procedimientos de inferencia e intervalos de confianza, pero uno debe ser consciente de los efectos que la transformación tiene en la distribución de los errores.
7.1 Mínimos cuadrados no lineales
Volviendo a los casos en los que no es posible transformar el modelo a una forma lineal, considere la configuración
\[ Y_{i}=f(\textbf{X}_{i},\beta)+\epsilon_{i}, \]
donde \(\epsilon\) es iid normal con media \(0\) y varianza constante. Para esta configuración, podemos confiar en parte de la teoría de los mínimos cuadrados. Para otros términos de error no normales, se deben emplear diferentes técnicas.
Primero, sea
\[ Q=\sum_{i=1}^{n}(y_{i}-f(\textbf{X}_{i},\beta))^{2}. \]
Para hallar:
\[ \hat{\beta}=\arg\min_{\beta}Q, \]
Primero encontramos cada una de las derivadas parciales de \(Q\) con respecto a \(\beta_j\). Luego, establecemos cada una de las derivadas parciales igual a \(0\) y los parámetros \(\beta_k\) son reemplazados por \(\hat{\beta}_k\) Las funciones a resolver no son lineales en los parámetros \(\hat{\beta}_k\) estimados y, a menudo, son difíciles de resolver, incluso en los casos más simples. Por lo tanto, a menudo se emplean métodos numéricos iterativos. ¡Aún más dificultades surgen en que pueden ser posibles múltiples soluciones!
Los algoritmos para la estimación de mínimos cuadrados no lineales incluyen:
El método de Newton, un método clásico basado en un enfoque de gradiente pero que puede ser computacionalmente desafiante y muy dependiente de buenos valores iniciales.
El algoritmo de Gauss-Newton, una modificación del método de Newton que proporciona una buena aproximación de la solución a la que debería haber llegado el método de Newton pero que no está garantizado que converja.
El método de Levenberg-Marquardt, que puede resolver las dificultades de cálculo que surgen con los otros métodos, pero puede requerir una tediosa búsqueda del valor óptimo de un parámetro de ajuste.
7.2 La función nls
Sirve para encontrar parámetros en funciones no lineales. Veamos.
Ajuste de una curva
Se desea ajustar:
\[ y(\theta) = x^{\theta}+\epsilon_i \]
donde \(\epsilon_i\) sigue una distribución uniforme.
len <- 24
x = runif(len)
y = x^3 + runif(len, min = -0.1, max = 0.1)
plot(x, y)
s <- seq(from = 0, to = 1, length = 50)
lines(s, s^3, lty = 2)
df <- data.frame(x, y)
m <- nls(y ~ I(x^power), data = df, start = list(power = 1), trace = T)## 1.985263 (2.18e+00): par = (1)
## 0.3913990 (1.66e+00): par = (1.915544)
## 0.1008292 (5.39e-01): par = (2.736064)
## 0.07699343 (7.71e-02): par = (3.106307)
## 0.07651022 (5.79e-03): par = (3.168432)
## 0.07650750 (3.68e-04): par = (3.173222)
## 0.07650748 (2.31e-05): par = (3.173527)
## 0.07650748 (1.45e-06): par = (3.173546)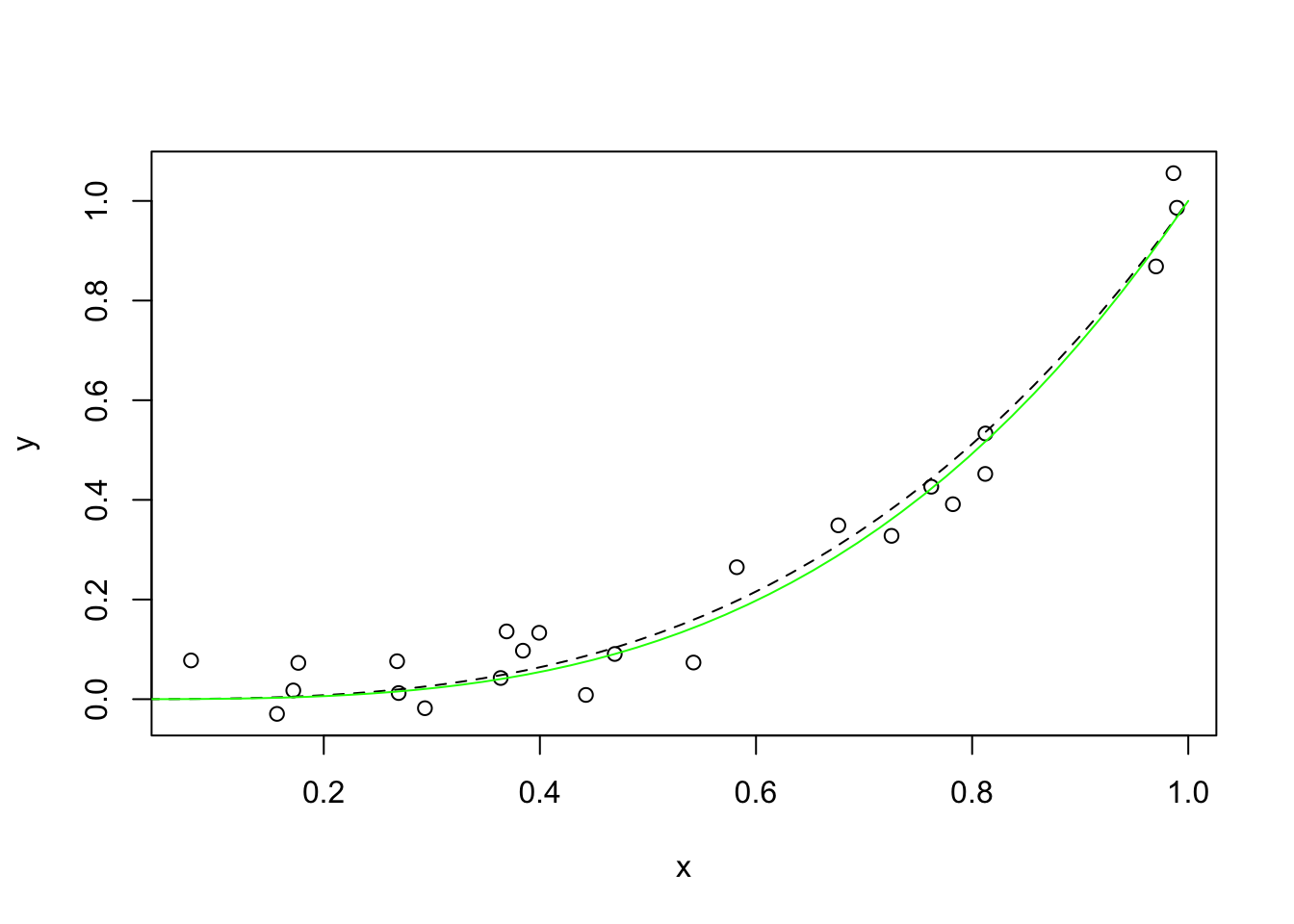
Veamos los resultados:
##
## Formula: y ~ I(x^power)
##
## Parameters:
## Estimate Std. Error t value Pr(>|t|)
## power 3.1735 0.1728 18.37 3.07e-15 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.05768 on 23 degrees of freedom
##
## Number of iterations to convergence: 7
## Achieved convergence tolerance: 1.447e-06Calculando el R cuadrado
## [1] 0.07650748## [1] 2.313283## [1] 0.9669269Ajuste a una función exponencial
Redefinamos el modelo \(m\) de modo que sea exponencial y volvamos a calcular los resultados:
## 4.839969 (3.92e+00): par = (0.5 0.5)
## 1.148557 (2.53e+00): par = (0.1625616 1.178678)
## 0.7921056 (2.69e+00): par = (0.09819158 1.759985)
## 0.5804294 (2.65e+00): par = (0.06190553 2.307225)
## 0.4274265 (2.35e+00): par = (0.042332 2.780717)
## 0.3564876 (2.12e+00): par = (0.02149037 3.530102)
## 0.06891666 (2.27e-01): par = (0.01407509 4.305956)
## 0.06649095 (1.17e-01): par = (0.01670066 4.126178)
## 0.06559653 (9.77e-04): par = (0.01676064 4.138797)
## 0.06559647 (1.36e-05): par = (0.01676678 4.138279)
## 0.06559647 (4.03e-07): par = (0.01676656 4.138293)plot(x, y)
lines(s, s^3, lty = 2)
lines(s, predict(m, list(x = s)), col = "green")
lines(s, predict(m.exp, list(x = s)), col = "red")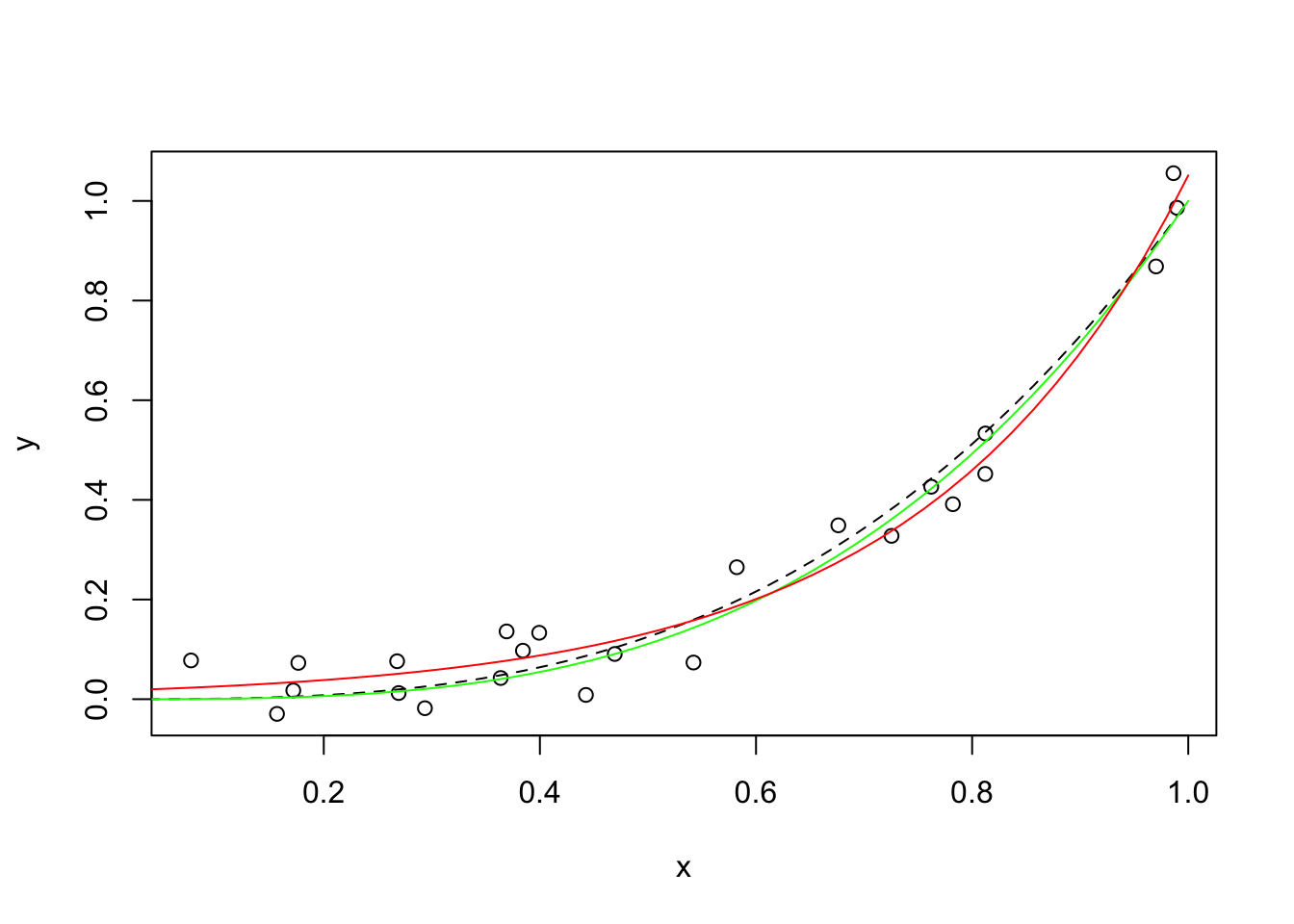
De lo anterior, podemos ver que una función exponencial, con la forma \(y = \alpha e^ {\beta x}\) también se ajusta bien a los datos, aunque la curva parece demasiado pronunciada hacia el lado derecho de la gráfica .
Para probar si este modelo se ajusta mejor a los datos, podemos volver a ejecutar el R cuadrado:
## [1] 0.06559647## [1] 2.313283## [1] 0.9716436Está claro que la curva exponencial se ajusta menos a los datos.
Ajustando datos a una función predefinida
Podemos usar la función nls para alterar de manera iterativa cualquier número de coeficientes en cualquier función que nos interese usar.
Asumamos brevemente que la relación \(y\) y \(x\) no es en realidad cúbica sino exponencial, con la siguiente forma: \(y = e^{a + b sin(x)}\). La función se puede definir utilizando el método genérico.
exp.eq <- function(x, a, b) {
exp(1)^(a + b * sin(x^4))
}
exp.eq(2, 1, 3) # Hacemos una prueba de la ecuación## [1] 1.146014Ahora que se ha definido esta forma funcional, nls se puede usar para encontrar los coeficientes que mejor reflejan los datos:
## 258.7550 (4.65e+01): par = (1 1)
## 30.70190 (1.51e+01): par = (0.0294069 1.171411)
## 3.108184 (4.21e+00): par = (-0.8868435 1.546754)
## 0.3700107 (9.27e-01): par = (-1.647089 2.136109)
## 0.2089358 (8.72e-02): par = (-2.054863 2.574945)
## 0.2074475 (6.25e-03): par = (-2.107065 2.629595)
## 0.2074405 (8.62e-04): par = (-2.103087 2.623503)
## 0.2074404 (1.19e-04): par = (-2.103669 2.624349)
## 0.2074404 (1.64e-05): par = (-2.103589 2.624233)
## 0.2074404 (2.25e-06): par = (-2.1036 2.624249)plot(x, y)
lines(s, s^3, lty = 2)
lines(s, predict(m, list(x = s)), col = "green")
lines(s, predict(m.exp, list(x = s)), col = "red")
lines(s, predict(m.sinexp, list(x = s)), col = "blue")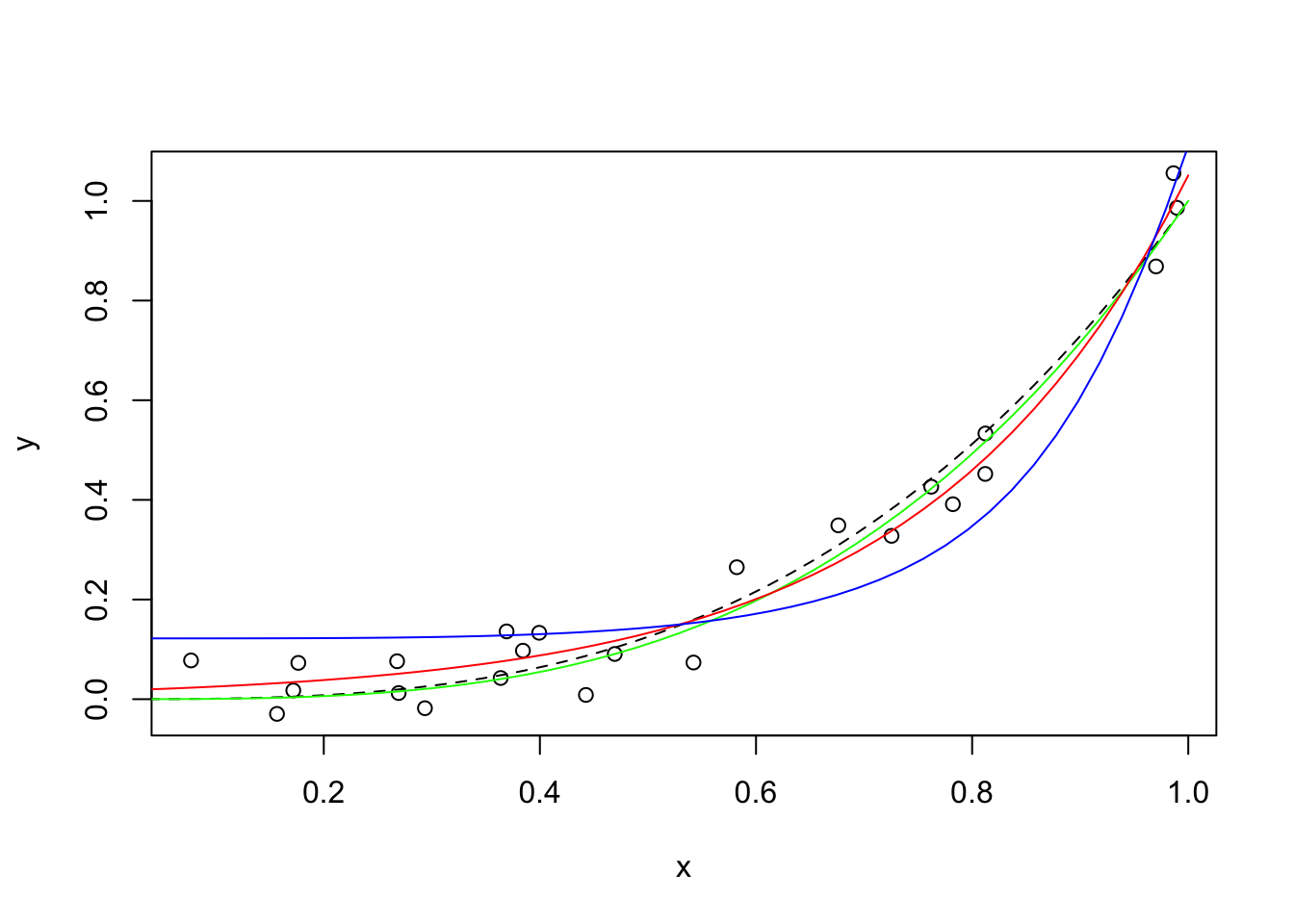
Claramente, la función exponencial final era tonta y no se ajustaba bien a los datos. Sin embargo, nos mostró cómo podemos usar la función nls para ajustar nuestras funciones predefinidas a los datos existentes.
El Problema de los valores iniciales
Encontrar buenos valores iniciales es muy importante en la regresión no lineal para permitir que el algoritmo del modelo converja. Si se establece valores de parámetros iniciales completamente fuera del rango de los valores de los parámetros potenciales, el algoritmo fallará o devolverá parámetros no sensitivos como, por ejemplo, devolver una tasa de crecimiento de \(1000\) cuando el valor real es \(1.04\).
La mejor manera de encontrar el valor inicial correcto es hacer una inspección gráfica de los datos, representándolos y basándose en el entendimiento que tiene de la ecuación para encontrar valores de inicio aproximados para los parámetros.
7.2.1 Ejemplo: crecimiento poblacional
Es muy común que diferentes campos científicos utilicen diferentes parametrizaciones (es decir, diferentes ecuaciones) para el mismo modelo, un ejemplo es el modelo de crecimiento logístico de la población, en ecología se usa la siguiente forma:
\[ N_{t} = \frac{K*N_{0}*e^{r*t}}{K + N_{0} * (e^{r*t} – 1)} \]
Siendo \(N_{t}\) el número de individuos en el momento \(t\), \(r\) siendo la tasa de crecimiento de la población y \(K\) la capacidad de carga. Podemos reescribir esto como una ecuación diferencial:
\[ dN/dt = R*N*(1-N/K) \]
library(deSolve)
#simulamos el crecimiento exponencial con la ecuacion logistica y estimamos los parametros usando nls
log_growth <- function(Time, State, Pars) {
with(as.list(c(State, Pars)), {
dN <- R*N*(1-N/K)
return(list(c(dN)))
})
}
#los parametros para la ecuacion logistica
pars <- c(R=0.2,K=1000)
# los parametros iniciales
N_ini <- c(N=1)
#los pasos de tiempo para evaluar la funcion ode
times <- seq(0, 50, by = 1)
#la ecuaciones diferenciales ordinarias (ODE)
out <- ode(N_ini, times, log_growth, pars)
# agregamos variaciones aleatorias
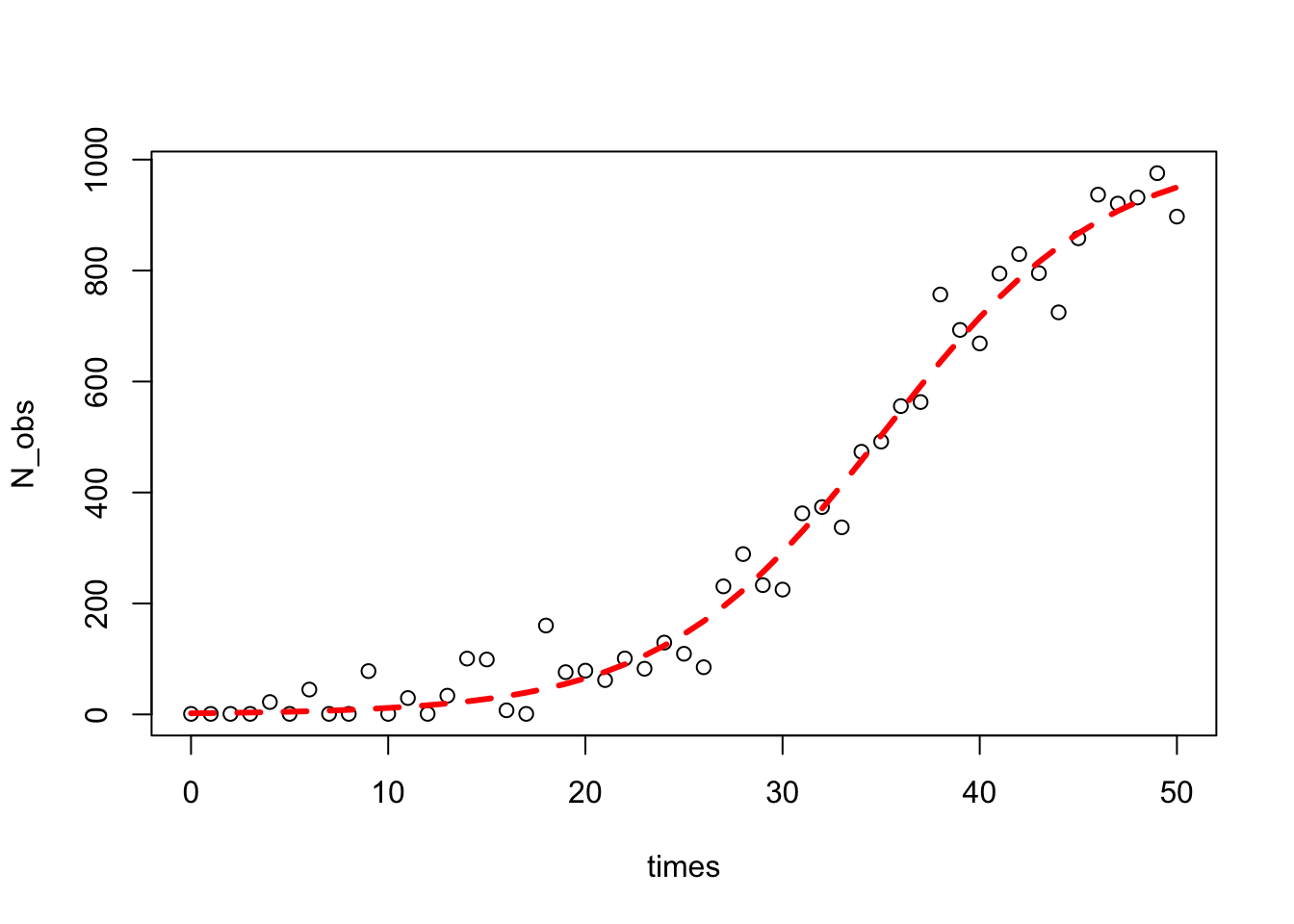
N_obs<-out[,2]+rnorm(51,0,50)
# quitamos los valores mayores que 1
N_obs<-ifelse(N_obs<1,1,N_obs)
#plot
plot(times,N_obs)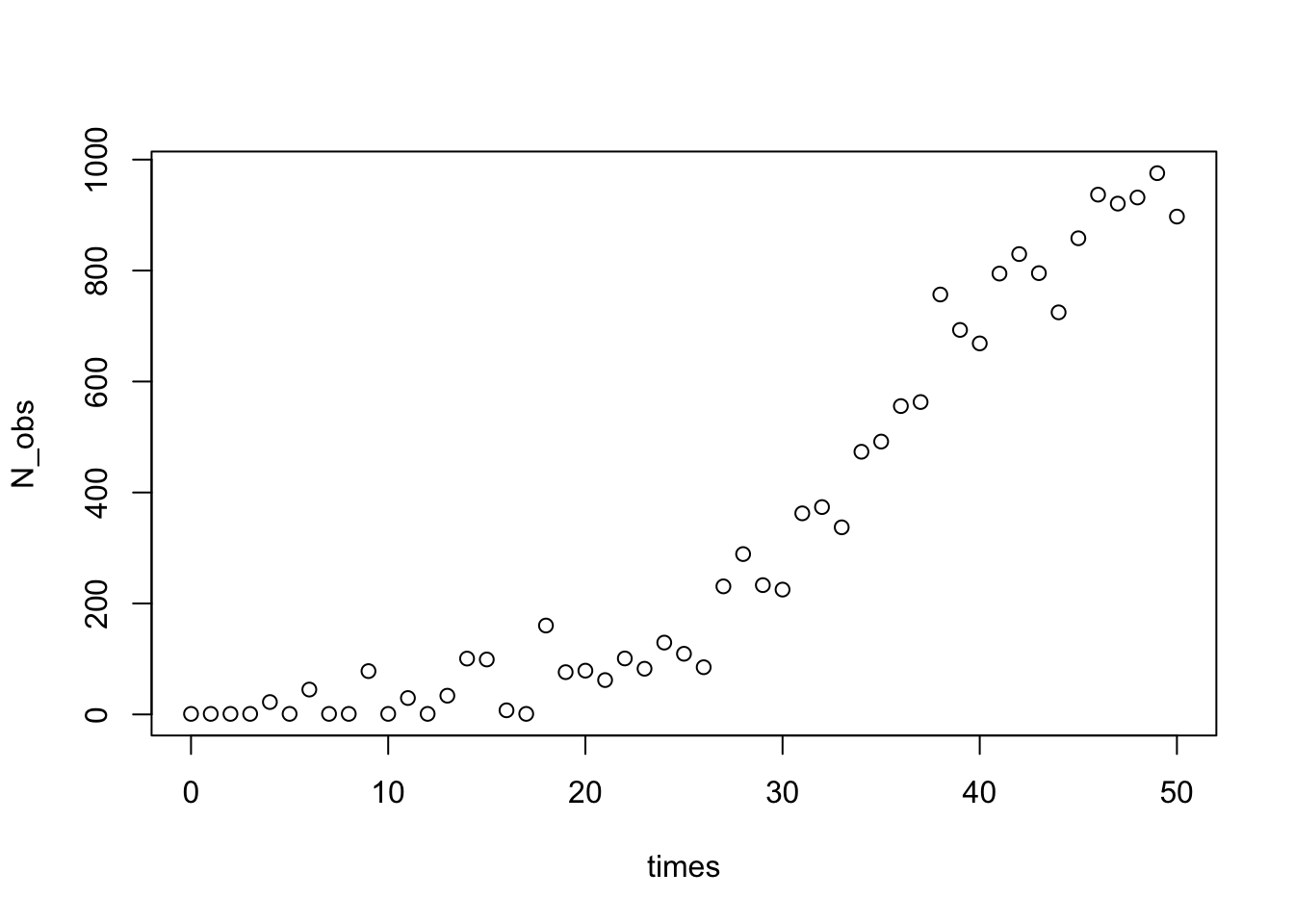
Esta parte fue solo para simular algunos datos con un error aleatorio, ahora viene la parte difícil para estimar los valores iniciales.
Ahora R tiene una función incorporada para estimar los valores iniciales para el parámetro de una ecuación logística (SSlogis) pero usa la siguiente ecuación:
\[ N_{t} = \frac{\alpha}{1+e^{\frac{xmid-t}{scale}}} \]
#encontramos los parametros de la ecuacion
SS<-getInitial(N_obs~SSlogis(times,alpha,xmid,scale),data=data.frame(N_obs=N_obs,times=times))Usamos la función getInitial que proporciona algunas conjeturas iniciales sobre los valores de los parámetros en función de los datos. Pasamos a esta función un modelo de inicio automático (SSlogis) que toma como argumento un vector de entrada (los valores de \(t\) donde se evaluará la función), y los nombres de los tres parámetros para la ecuación logística.
Sin embargo, como los SSlogis utilizan una parametrización diferente, necesitamos usar un poco de álgebra para pasar de los valores estimados de inicio automático devueltos desde SSlogis a los que están en la ecuación que queremos usar.
#usamos una parametrizacion diferente
K_start<-SS["alpha"]
R_start<-1/SS["scale"]
N0_start<-SS["alpha"]/(exp(SS["xmid"]/SS["scale"])+1)
#la formula del modelo
log_formula<-formula(N_obs~K*N0*exp(R*times)/(K+N0*(exp(R*times)-1)))
#ajustamos el modelo
m<-nls(log_formula,start=list(K=K_start,R=R_start,N0=N0_start))
#parametros estimados
summary(m)##
## Formula: N_obs ~ K * N0 * exp(R * times)/(K + N0 * (exp(R * times) - 1))
##
## Parameters:
## Estimate Std. Error t value Pr(>|t|)
## K.alpha 1.018e+03 4.019e+01 25.341 <2e-16 ***
## R.scale 1.772e-01 1.297e-02 13.664 <2e-16 ***
## N0.alpha 2.006e+00 8.108e-01 2.474 0.017 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 46.59 on 48 degrees of freedom
##
## Number of iterations to convergence: 0
## Achieved convergence tolerance: 2.696e-06## [1] 0.9910699Graficamos
7.2.2 Ejemplo: Cobb-Douglas
El modelo:
\[ Y_i = \beta_1X_{2i}^{\beta_2}X_{3i}^{\beta_3}e^{u_i} \]
donde
- \(Y\): producción
- \(X_2\): insumo trabajo
- \(X_3\): insumo capital
- \(u\): término de perturbación
- \(e\): base del logaritmo
Notemos que el modelo es multiplicativo, si tomamos la derivada obetenemos un modelo más familiar respecto a la regresión lineal múltiple:
\[ lnY_i = ln\beta_1 + \beta_2ln(X_{2i})+ \beta_3ln(X_{3i}) + u_i \]
uu <- "https://raw.githubusercontent.com/vmoprojs/DataLectures/master/GA/tabla7_3.csv"
# datos <- read.csv(file="tabla7_3.csv",sep=";",dec=".",header=TRUE)
datos <- read.csv(url(uu),sep=";",dec=".",header=TRUE)##
## Call:
## lm(formula = LY ~ W + K)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.15919 -0.02917 0.01179 0.04087 0.09640
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -3.3387 2.4491 -1.363 0.197845
## W 1.4987 0.5397 2.777 0.016750 *
## K 0.4899 0.1020 4.801 0.000432 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.0748 on 12 degrees of freedom
## Multiple R-squared: 0.8891, Adjusted R-squared: 0.8706
## F-statistic: 48.08 on 2 and 12 DF, p-value: 1.864e-06Si se desea evaluar la hipótesis \(\beta_2 +\beta_3 = 1\), se usa (vcov(fit.model)):
\[ t = \frac{(\hat{\beta}_2+\hat{\beta}_3)-1}{\sqrt{var(\hat{\beta}_2)+var(\hat{\beta}_3)+2cov(\hat{\beta}_2,\hat{\beta}_3})} \]
Si se desea estimar el modelo de forma no lineal, tenemos
produccion <- function(a,b1,b2,X2,X3)
{
y <- a * (X2^(b1)) * (X3^(b2))
y
}
# nls(produccion(a,b1,b2,X2,X3), data=datos, start =
# c(a=exp(-3.6529493),b1=1.0376775,b2 = 0.7187662), trace = TRUE)
cd.nls <- nls(Y~a * (X2^(b1)) * (X3^(b2)), data=datos, start =
c(a=exp(-3.3),b1=1.1,b2 = 0.4), trace = TRUE)## 8.708133e+09 (1.74e+01): par = (0.03688317 1.1 0.4)
## 8.675850e+09 (1.74e+01): par = (0.02100187 1.189688 0.4092905)
## 8.587365e+09 (1.73e+01): par = (0.01442634 1.26103 0.4165611)
## 8.419671e+09 (1.71e+01): par = (0.008348108 1.368361 0.427335)
## 7.881004e+09 (1.65e+01): par = (0.005458489 1.494727 0.4396179)
## 6.583036e+09 (1.51e+01): par = (0.005979914 1.576162 0.4469403)
## 4.808542e+09 (1.29e+01): par = (0.008585679 1.604185 0.4490754)
## 2.619388e+09 (9.50e+00): par = (0.0133584 1.613127 0.449614)
## 6.633558e+08 (4.70e+00): par = (0.02053829 1.61482 0.4496652)
## 2.867702e+07 (2.09e-03): par = (0.02771585 1.614763 0.4496533)
## 2.867690e+07 (3.72e-07): par = (0.02771594 1.614776 0.4496567)##
## Formula: Y ~ a * (X2^(b1)) * (X3^(b2))
##
## Parameters:
## Estimate Std. Error t value Pr(>|t|)
## a 0.02772 0.05775 0.480 0.63990
## b1 1.61478 0.42800 3.773 0.00266 **
## b2 0.44966 0.07430 6.052 5.74e-05 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1546 on 12 degrees of freedom
##
## Number of iterations to convergence: 10
## Achieved convergence tolerance: 3.724e-077.2.3 Taller
Recuerde que el error en los mínimos cuadrados ordinarios es aditivo. Si no cuenta con esa estructura, busque la forma función que lo sea.
Considere la siguiente ecuación:
\[ Y = \frac{\epsilon}{1+e^{\beta_1X_1+\beta_2X_2}} \]
\[ log(Y) = -log(1+e^{\beta_1X_1+\beta_2X_2})+log(\epsilon) \]
La segunda ecuación es la versión transformada que usaremos para la estimación.
- Usando como semilla =1, simule 100 valores de \(X_1\) y \(X_2\) con distribución uniforme entre 0 y 1.
- Usando el modelo propuesto, simule valores de \(Y\) donde \(a = 0.8\) y \(b = 0.5\).
- El ruido tiene distribución normal con media cero y varianza 1.
Debe obtener los siguientes resultados:
##
## Formula: log(Y) ~ -log(1 + exp(a * X1 + b * X2))
##
## Parameters:
## Estimate Std. Error t value Pr(>|t|)
## a 0.8470 0.2697 3.141 0.00223 **
## b 0.5962 0.2718 2.193 0.03065 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.6517 on 98 degrees of freedom
##
## Number of iterations to convergence: 3
## Achieved convergence tolerance: 2.313e-06