4 Árboles de decisión
Librerías usadas en esta sección
rpartrepmisvisNetworksparklinegmodels
Para ilustrar el proceso de construcción del árbol, consideremos un ejemplo simple. Imagine que está trabajando para un estudio de cine de Hollywood, y su escritorio está repleto de guiones. En lugar de leer cada uno de principio a fin, usted decide desarrollar un algoritmo de árbol de decisión para predecir si una película potencial podría clasificarse en una de tres categorías:
- impacto mainstream,
- amado por la crítica (critic’s choice) o
- fracaso de taquilla (box office bust).
Después de revisar los datos de 30 guiones de películas diferentes, surge un patrón. Parece haber una relación entre el presupuesto de rodaje propuesto por la película, el número de celebridades A para los papeles protagónicos y las categorías de éxito.
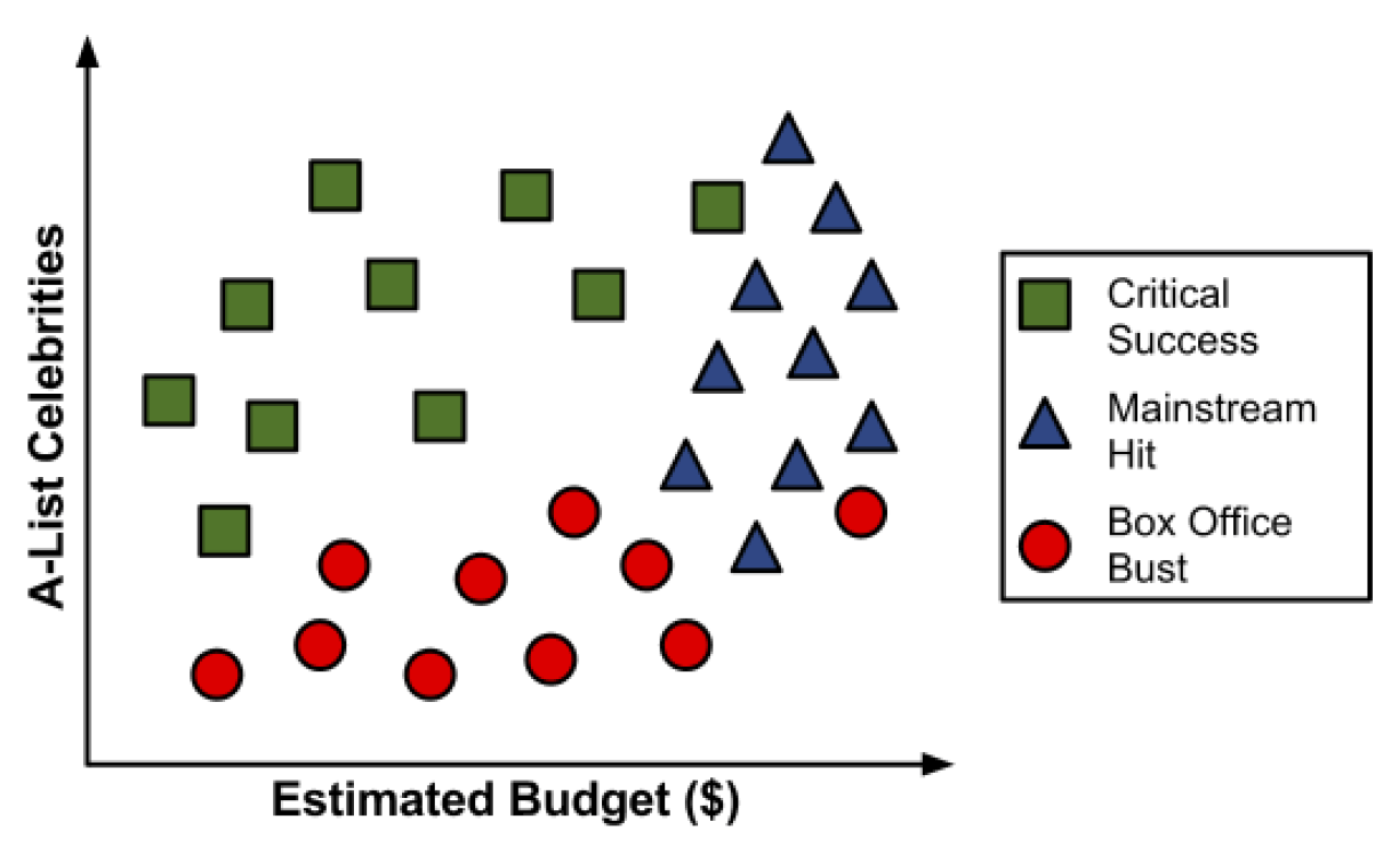
Para construir un árbol de decisión simple usando esta información, podemos aplicar una estrategia de dividir y vencer.
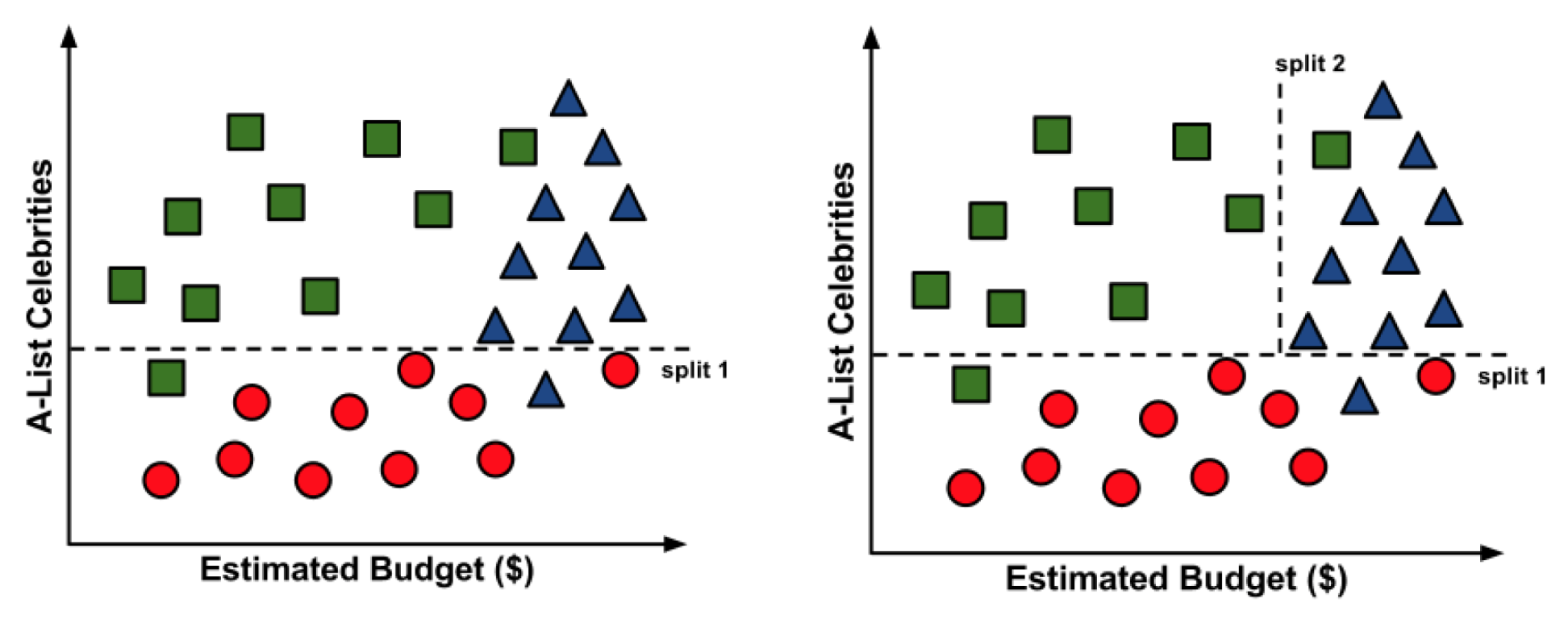
Resultado:
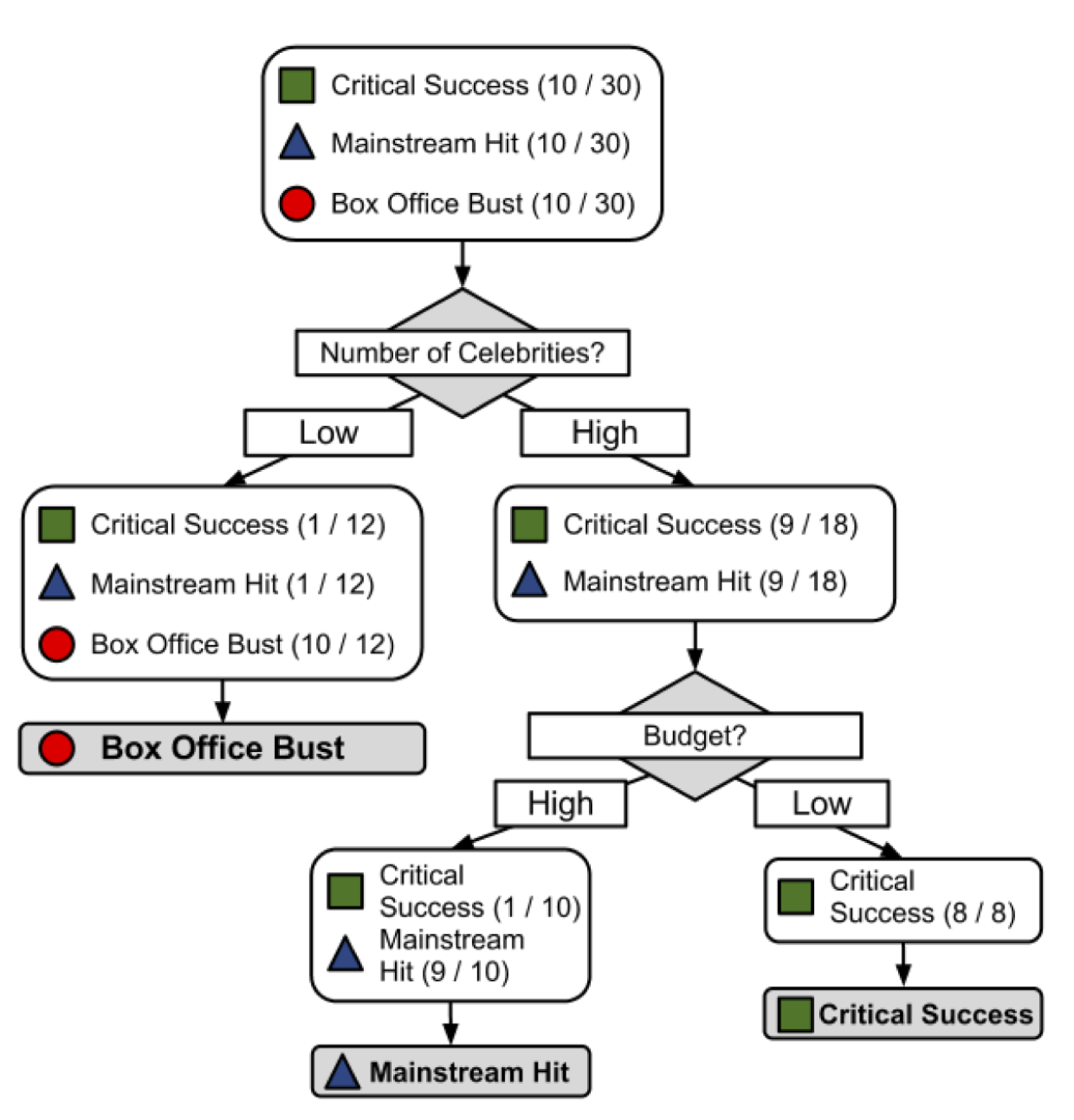
Es posible que hayas notado que las líneas diagonales podrían haber dividido los datos aún más limpiamente. Esta es una limitación de del árbol de decisiones, que utiliza divisiones paralelas a los ejes. El hecho de que cada división considere una característica a la vez evita que el árbol de decisiones forme decisiones más complejas, como “si el número de celebridades es mayor que el presupuesto estimado, entonces será un éxito crítico”.
Entonces, ¿qué es un árbol de decisión?
- El modelo en sí mismo comprende una serie de decisiones lógicas, similares a un diagrama de flujo, con nodos de decisión que indican una decisión sobre un atributo. Estos se dividen en ramas que indican las elecciones de la decisión. El árbol termina con nodos de hoja o leaf nodes (también conocidos como nodos terminales) que denotan el resultado de seguir una combinación de decisiones.
| Fortalezas | Debilidades |
|---|---|
| Un clasificador multiuso que funciona bien en la mayoría de los problemas | Los modelos de árbol de decisión a menudo están sesgados hacia divisiones en características que tienen una gran cantidad de niveles |
| El proceso de aprendizaje altamente automático puede manejar características numéricas o nominales, datos faltantes | Es fácil sobreajustar o ajustar el modelo |
| Utiliza solo las características más importantes | Puede tener problemas para modelar algunas relaciones debido a la dependencia de divisiones paralelas al eje |
| Se puede usar en datos con relativamente pocos ejemplos de entrenamiento o un número muy grande | Pequeños cambios en los datos de entrenamiento pueden generar grandes cambios en la lógica de decisión |
| Resultados en un modelo que puede interpretarse sin un fondo matemático (para árboles relativamente pequeños) | Los árboles grandes pueden ser difíciles de interpretar y las decisiones que toman pueden parecer contradictorias |
| Más eficiente que otros modelos complejos |
4.1 Elegir la mejor partición
Entropía
La entropía de una muestra de datos indica qué tan mezclados están los valores de clase; el valor mínimo de 0 indica que la muestra es completamente homogénea, mientras que 1 indica la cantidad máxima de desorden.
\[ Entropy(S) = \sum_{i=1}^{c}-p_ilog_2(p_i) \]
En la fórmula de entropía, para un segmento dado de datos \((S)\), el término \(c\) se refiere al número de diferentes niveles de clase, y \(p_i\) se refiere a la proporción de valores que caen en el nivel de clase \(i\). Por ejemplo, supongamos que tenemos una partición de datos con dos clases: rojo (\(60\) por ciento) y blanco (\(40\) por ciento). Podemos calcular la entropía como:
## [1] 0.9709506Podemos examinar la entropía para todos los posibles arreglos de dos clases. Si sabemos que la proporción de ejemplos en una clase es \(x\), entonces la proporción en la otra clase es \(1 - x\). Usando la función curve(), podemos trazar la entropía para todos los valores posibles de \(x\):
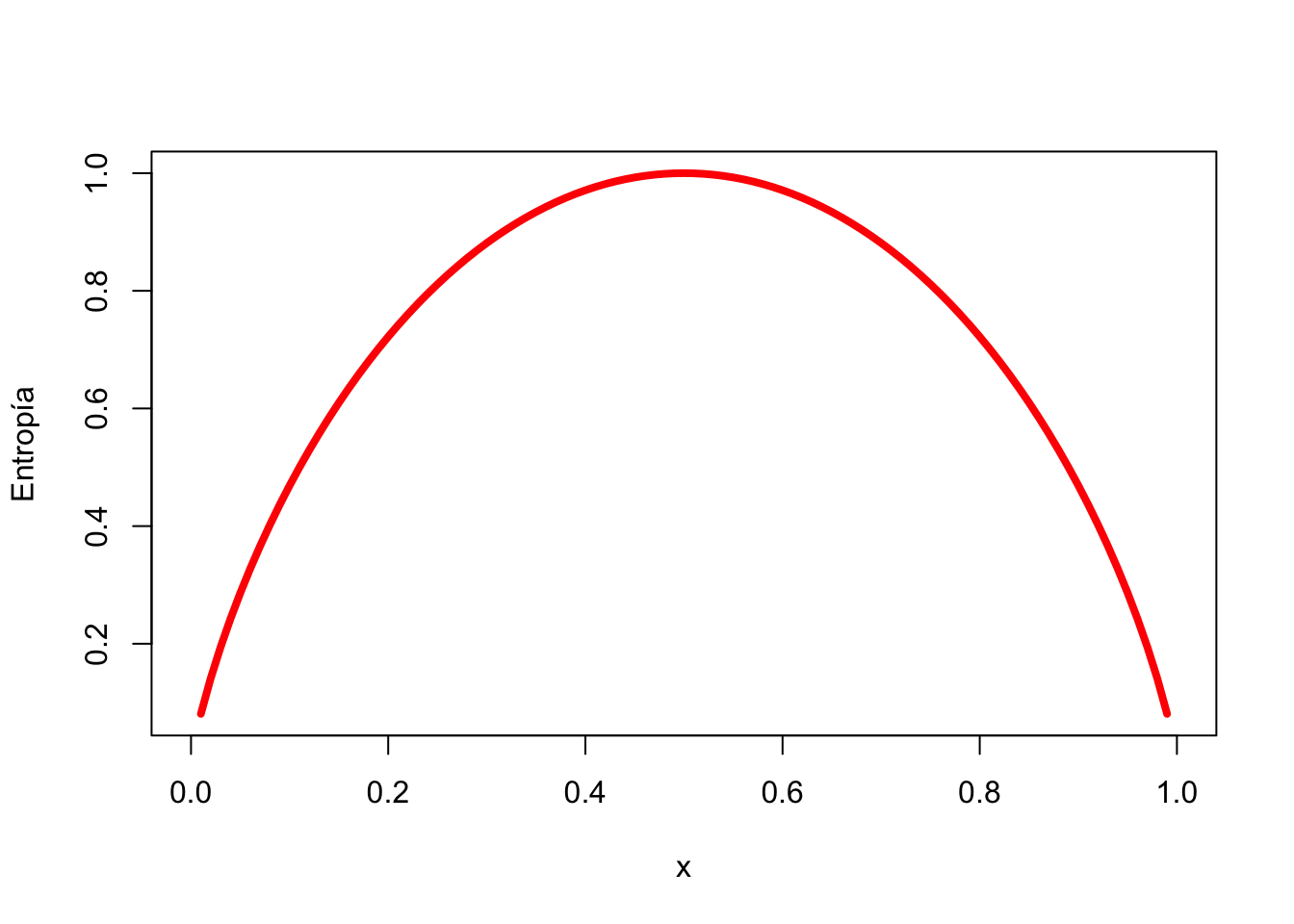
Como se ilustra por el pico en entropía en \(x = 0.50\), una división \(50-50\) da como resultado la entropía máxima. A medida que una clase domina cada vez más a la otra, la entropía se reduce a cero.
Dada esta medida de pureza (como la entropía), el algoritmo aún debe decidir qué característica dividir. Para esto, el algoritmo usa la entropía para calcular el cambio en la homogeneidad resultante de una división en cada característica posible. El cálculo se conoce como ganancia de información. La ganancia de información para una característica \(F\) se calcula como la diferencia entre la entropía en el segmento antes de la división \((S_1)\) y las particiones resultantes de la división \((S_2)\)
\[ InfoGain (F) = Entropy(S_1)-Entropy(S_2) \]
Cuanto mayor sea la ganancia de información, mejor será una función para crear grupos homogéneos después de una división en esa función.
Aunque es utilizado por C5.0, la ganancia de información no es el único criterio de división que se puede usar para construir árboles de decisión. Otros criterios comúnmente utilizados son el índice de Gini, la estadística Chi-cuadrado y la relación de ganancia. Para profundizar en estos criterios revisa: Mingers (1989)
4.2 Ejemplo: Identificando el riesgo de un préstamo
4.2.1 Paso 1: recopilación de datos
Los datos representan los préstamos obtenidos de una agencia de crédito en Alemania.
uu <- "https://github.com/vmoprojs/DataLectures/blob/master/credit.RData?raw=true"
library(repmis)
source_data(uu)## [1] "credit"## 'data.frame': 1000 obs. of 17 variables:
## $ checking_balance : Factor w/ 4 levels "< 0 DM","> 200 DM",..: 1 3 4 1 1 4 4 3 4 3 ...
## $ months_loan_duration: int 6 48 12 42 24 36 24 36 12 30 ...
## $ credit_history : Factor w/ 5 levels "critical","good",..: 1 2 1 2 4 2 2 2 2 1 ...
## $ purpose : Factor w/ 6 levels "business","car",..: 5 5 4 5 2 4 5 2 5 2 ...
## $ amount : int 1169 5951 2096 7882 4870 9055 2835 6948 3059 5234 ...
## $ savings_balance : Factor w/ 5 levels "< 100 DM","> 1000 DM",..: 5 1 1 1 1 5 4 1 2 1 ...
## $ employment_duration : Factor w/ 5 levels "< 1 year","> 7 years",..: 2 3 4 4 3 3 2 3 4 5 ...
## $ percent_of_income : int 4 2 2 2 3 2 3 2 2 4 ...
## $ years_at_residence : int 4 2 3 4 4 4 4 2 4 2 ...
## $ age : int 67 22 49 45 53 35 53 35 61 28 ...
## $ other_credit : Factor w/ 3 levels "bank","none",..: 2 2 2 2 2 2 2 2 2 2 ...
## $ housing : Factor w/ 3 levels "other","own",..: 2 2 2 1 1 1 2 3 2 2 ...
## $ existing_loans_count: int 2 1 1 1 2 1 1 1 1 2 ...
## $ job : Factor w/ 4 levels "management","skilled",..: 2 2 4 2 2 4 2 1 4 1 ...
## $ dependents : int 1 1 2 2 2 2 1 1 1 1 ...
## $ phone : Factor w/ 2 levels "no","yes": 2 1 1 1 1 2 1 2 1 1 ...
## $ default : Factor w/ 2 levels "no","yes": 1 2 1 1 2 1 1 1 1 2 ...El conjunto de datos crediticios incluye \(1000\) ejemplos de préstamos, más una combinación de características numéricas y nominales que indican las características del préstamo y del solicitante del préstamo.
Una variable indica si el préstamo entró en default. Veamos si podemos determinar un patrón que prediga este resultado.
4.2.2 Paso 2: Explorar y preparar los datos
Veamos algunos de los resultados de table() para un par de características de préstamos que parecen predecir un incumplimiento. Las características checking_balance y savings_balance indican el saldo de la cuenta de cheques y de ahorros del solicitante, y se registran como variables categóricas:
##
## < 0 DM > 200 DM 1 - 200 DM unknown
## 274 63 269 394##
## < 100 DM > 1000 DM 100 - 500 DM 500 - 1000 DM unknown
## 603 48 103 63 183Dado que los datos del préstamo se obtuvieron de Alemania, la moneda se registra en Deutsche Marks (DM). Parece una suposición válida que los saldos de cuentas corrientes y de ahorro más grandes deberían estar relacionados con una menor posibilidad de impago del préstamo.
Algunas de las funciones del préstamo son numéricas, como su plazo (months_loan_duration) y el monto de crédito solicitado (amount).
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 4.0 12.0 18.0 20.9 24.0 72.0## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 250 1366 2320 3271 3972 18424Los montos de los préstamos oscilaron entre 250 DM y 18420 DM a plazos de 4 a 72 meses, con una duración media de 18 meses y un monto de 2320 DM.
La variable default indica si el solicitante del préstamo no pudo cumplir con los términos de pago acordados y entró en incumplimiento. Un total del 30 por ciento de los préstamos entraron en mora:
##
## no yes
## 700 300Una alta tasa de incumplimiento no es deseable para un banco porque significa que es poco probable que el banco recupere completamente su inversión. Si tenemos éxito, nuestro modelo identificará a los solicitantes que es probable que presenten un incumplimiento, tal que este número se pueda reducir.
Creamos el conjunto de entrenamiento y de prueba
- ordenar al azar su data de crédito antes de dividir.
Confirmemos que los datos no han cambiado
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 250 1366 2320 3271 3972 18424## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 250 1366 2320 3271 3972 18424- Ahora, podemos dividir los datos en entrenamiento (90 por ciento o 900 registros) y datos de prueba (10 por ciento o 100 registros)
Si todo salió bien, deberíamos tener alrededor del 30 por ciento de los préstamos impagos en cada uno de los conjuntos de datos.
##
## no yes
## 0.7022222 0.2977778##
## no yes
## 0.68 0.324.2.3 Paso 3: entrenar un modelo en los datos
La columna 17 en credit_train es la variable default, por lo que debemos excluirla del marco de datos de entrenamiento como una variable independiente, pero suministrarla como dependiente para la clasificación:
library(rpart)
credit_model <- rpart(default~checking_balance+months_loan_duration+credit_history+purpose+amount+savings_balance+employment_duration+percent_of_income+years_at_residence+age+other_credit+housing+existing_loans_count+job+dependents+phone,data = credit_train)Para mirar las decisiones, usamos summary
## n= 900
##
## node), split, n, loss, yval, (yprob)
## * denotes terminal node
##
## 1) root 900 268 no (0.70222222 0.29777778)
## 2) checking_balance=> 200 DM,unknown 414 57 no (0.86231884 0.13768116) *
## 3) checking_balance=< 0 DM,1 - 200 DM 486 211 no (0.56584362 0.43415638)
## 6) months_loan_duration< 22.5 274 94 no (0.65693431 0.34306569)
## 12) credit_history=critical,good,poor 249 76 no (0.69477912 0.30522088) *
## 13) credit_history=perfect,very good 25 7 yes (0.28000000 0.72000000) *
## 7) months_loan_duration>=22.5 212 95 yes (0.44811321 0.55188679)
## 14) savings_balance=> 1000 DM,unknown 36 9 no (0.75000000 0.25000000) *
## 15) savings_balance=< 100 DM,100 - 500 DM,500 - 1000 DM 176 68 yes (0.38636364 0.61363636)
## 30) months_loan_duration< 47.5 145 65 yes (0.44827586 0.55172414)
## 60) amount>=2249 114 56 no (0.50877193 0.49122807)
## 120) amount< 8015.5 93 41 no (0.55913978 0.44086022)
## 240) percent_of_income< 2.5 37 10 no (0.72972973 0.27027027) *
## 241) percent_of_income>=2.5 56 25 yes (0.44642857 0.55357143)
## 482) job=management,unemployed 10 2 no (0.80000000 0.20000000) *
## 483) job=skilled,unskilled 46 17 yes (0.36956522 0.63043478)
## 966) amount< 3080.5 21 9 no (0.57142857 0.42857143) *
## 967) amount>=3080.5 25 5 yes (0.20000000 0.80000000) *
## 121) amount>=8015.5 21 6 yes (0.28571429 0.71428571) *
## 61) amount< 2249 31 7 yes (0.22580645 0.77419355) *
## 31) months_loan_duration>=47.5 31 3 yes (0.09677419 0.90322581) *Después de la salida del árbol, el resumen (credit_model) muestra una matriz de confusión, que es una tabulación cruzada que indica los registros incorrectamente clasificados del modelo en los datos de capacitación.
Los árboles de decisión son conocidos por tener una tendencia a sobreajustar el modelo a los datos de entrenamiento. Por esta razón, la tasa de error informada en los datos de entrenamiento puede ser demasiado optimista, y es especialmente importante evaluar los árboles de decisión en un conjunto de datos de prueba.
4.2.4 Paso 4: evaluar el rendimiento del modelo
Revisemos el ajuste
library(gmodels)
CrossTable(credit_test$default, credit_pred,
prop.chisq = FALSE, prop.c = FALSE, prop.r = FALSE,
dnn = c('actual default', 'predicted default'))##
##
## Cell Contents
## |-------------------------|
## | N |
## | N / Table Total |
## |-------------------------|
##
##
## Total Observations in Table: 100
##
##
## | predicted default
## actual default | no | yes | Row Total |
## ---------------|-----------|-----------|-----------|
## no | 64 | 4 | 68 |
## | 0.640 | 0.040 | |
## ---------------|-----------|-----------|-----------|
## yes | 20 | 12 | 32 |
## | 0.200 | 0.120 | |
## ---------------|-----------|-----------|-----------|
## Column Total | 84 | 16 | 100 |
## ---------------|-----------|-----------|-----------|
##
## De los 100 registros de solicitud de préstamo de prueba, nuestro modelo predijo correctamente que 64 no incumplieron y 12 incumplieron, lo que arrojó una precisión del \(76\%\) y una tasa de error del \(24\%\). Esto es algo peor que su rendimiento en los datos de entrenamiento, pero no es inesperado, dado que el rendimiento de un modelo es a menudo peor en datos no vistos.
También ten en cuenta que el modelo solo predijo correctamente el \(37.5%\) por ciento de los 32 valores predeterminados de préstamo en los datos de prueba (12/32). Desafortunadamente, este tipo de error es un error potencialmente muy costoso. Veamos si podemos mejorar el resultado con un poco más de esfuerzo.
4.2.5 Paso 5: mejorando el ajuste (pruning)
##
## Classification tree:
## rpart(formula = default ~ checking_balance + months_loan_duration +
## credit_history + purpose + amount + savings_balance + employment_duration +
## percent_of_income + years_at_residence + age + other_credit +
## housing + existing_loans_count + job + dependents + phone,
## data = credit_train)
##
## Variables actually used in tree construction:
## [1] amount checking_balance credit_history
## [4] job months_loan_duration percent_of_income
## [7] savings_balance
##
## Root node error: 268/900 = 0.29778
##
## n= 900
##
## CP nsplit rel error xerror xstd
## 1 0.041045 0 1.00000 1.00000 0.051188
## 2 0.013682 4 0.80970 0.90672 0.049697
## 3 0.011194 9 0.72388 0.90299 0.049632
## 4 0.010000 10 0.71269 0.91045 0.049761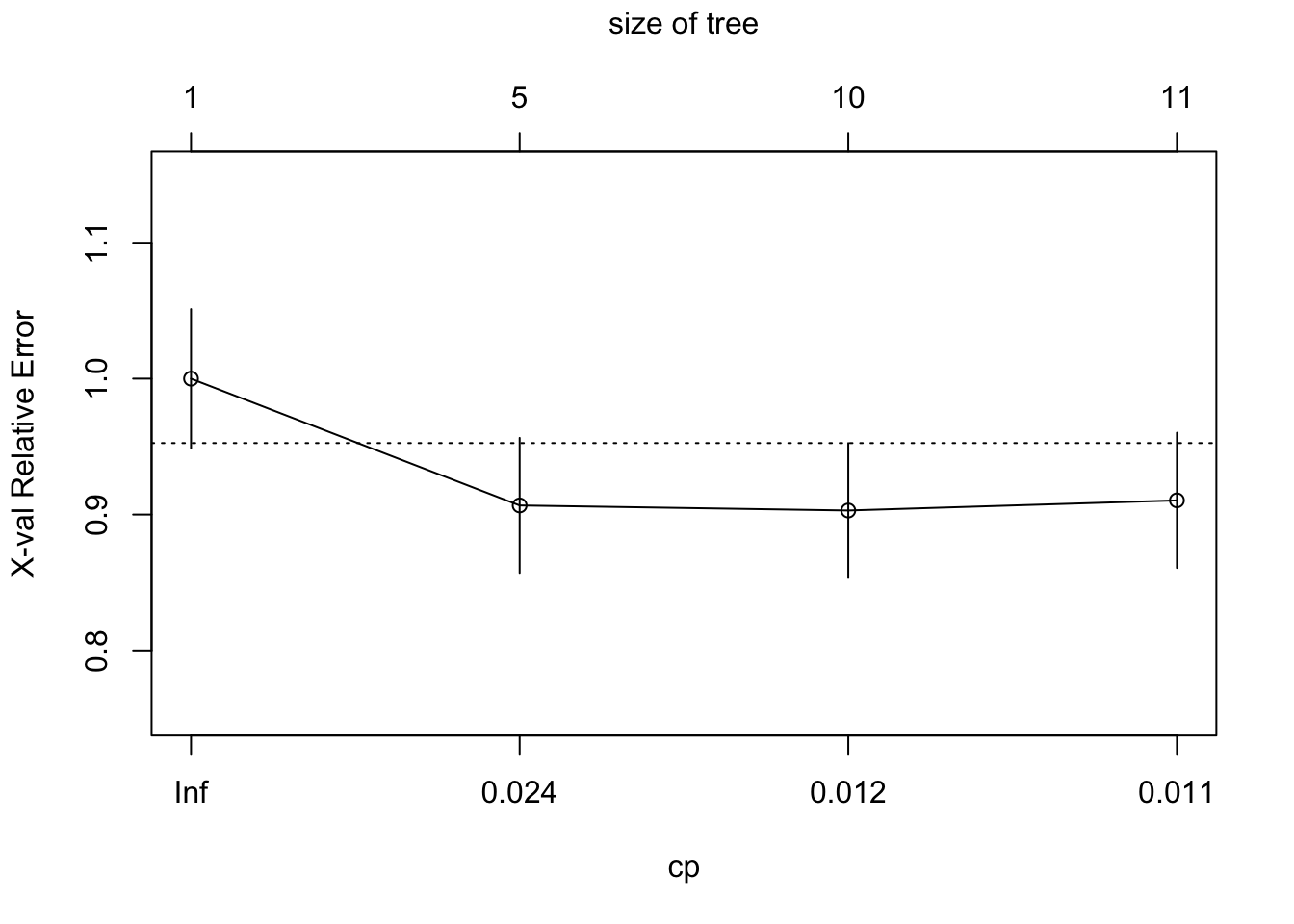
model_pruned <- prune(credit_model, cp = 0.013682 )
credit_pred_pruned <- predict(model_pruned, credit_test,type = "class")
CrossTable(credit_test$default, credit_pred_pruned,
prop.chisq = FALSE, prop.c = FALSE, prop.r = FALSE,
dnn = c('actual default', 'predicted default'))##
##
## Cell Contents
## |-------------------------|
## | N |
## | N / Table Total |
## |-------------------------|
##
##
## Total Observations in Table: 100
##
##
## | predicted default
## actual default | no | yes | Row Total |
## ---------------|-----------|-----------|-----------|
## no | 62 | 6 | 68 |
## | 0.620 | 0.060 | |
## ---------------|-----------|-----------|-----------|
## yes | 15 | 17 | 32 |
## | 0.150 | 0.170 | |
## ---------------|-----------|-----------|-----------|
## Column Total | 77 | 23 | 100 |
## ---------------|-----------|-----------|-----------|
##
##