11 Redes neuronales

A este tipo de algorimos se les suele llamar de “caja negra”. La caja negra se debe a que los modelos subyacentes se basan en sistemas matemáticos complejos y los resultados son difíciles de interpretar.
Aunque puede no ser factible interpretar los modelos de caja negra, es peligroso aplicar los métodos a ciegas.

11.1 Entendiendo una red neuronal

Una Red Neural Artificial (ANN) modela la relación entre un conjunto de señales de entrada y una señal de salida.
ANN usa una red de neuronas o nodos artificiales para resolver problemas de aprendizaje.

En términos generales, las RNA (ANN) son aprendices versátiles que se pueden aplicar a casi cualquier tarea de aprendizaje: clasificación, predicción numérica e incluso reconocimiento de patrones no supervisados.

Las RNA se aplican mejor a problemas donde los datos de entrada y los datos de salida son bien entendidos o al menos bastante simples, sin embargo, el proceso que relaciona la entrada con la salida es extremadamente complejo. Como método de caja negra, funcionan bien para este tipo de problemas de caja negra.

El diagrama de red dirigida define una relación entre las señales de entrada recibidas por los nodos (variables $x$) y la señal de salida (variable $y$).

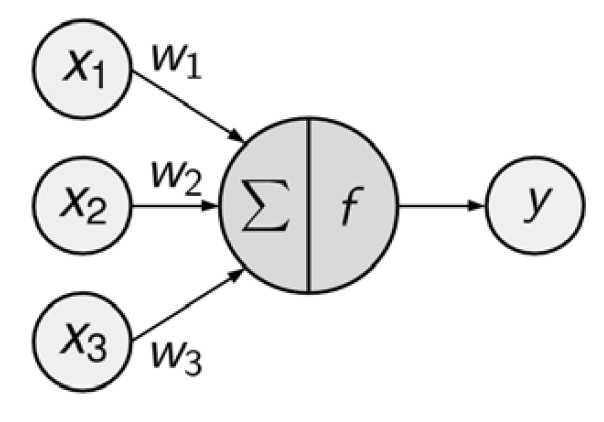
Neurona

La señal de cada nodo se pondera (valores $w$) según su importancia; ignore por ahora cómo se determinan estos pesos. Las señales de entrada son sumadas por el cuerpo de la célula y la señal se transmite de acuerdo con una función de activación indicada por $f$.

Una neurona artificial típica con $n$ nodos de entrada puede representarse mediante la siguiente fórmula. Los pesos $w$ permiten que cada una de las $n$ entradas, ($x$), contribuya una cantidad mayor o menor a la suma de las señales de entrada. El total neto es utilizado por la función de activación $f(x)$, y la señal resultante, $y(x)$, es la salida.

\[ y(x) = f\left(\sum_i^nw_ix_i\right) \]

Aunque existen numerosas variantes de redes neuronales, cada una se puede definir en términos de las siguientes características:

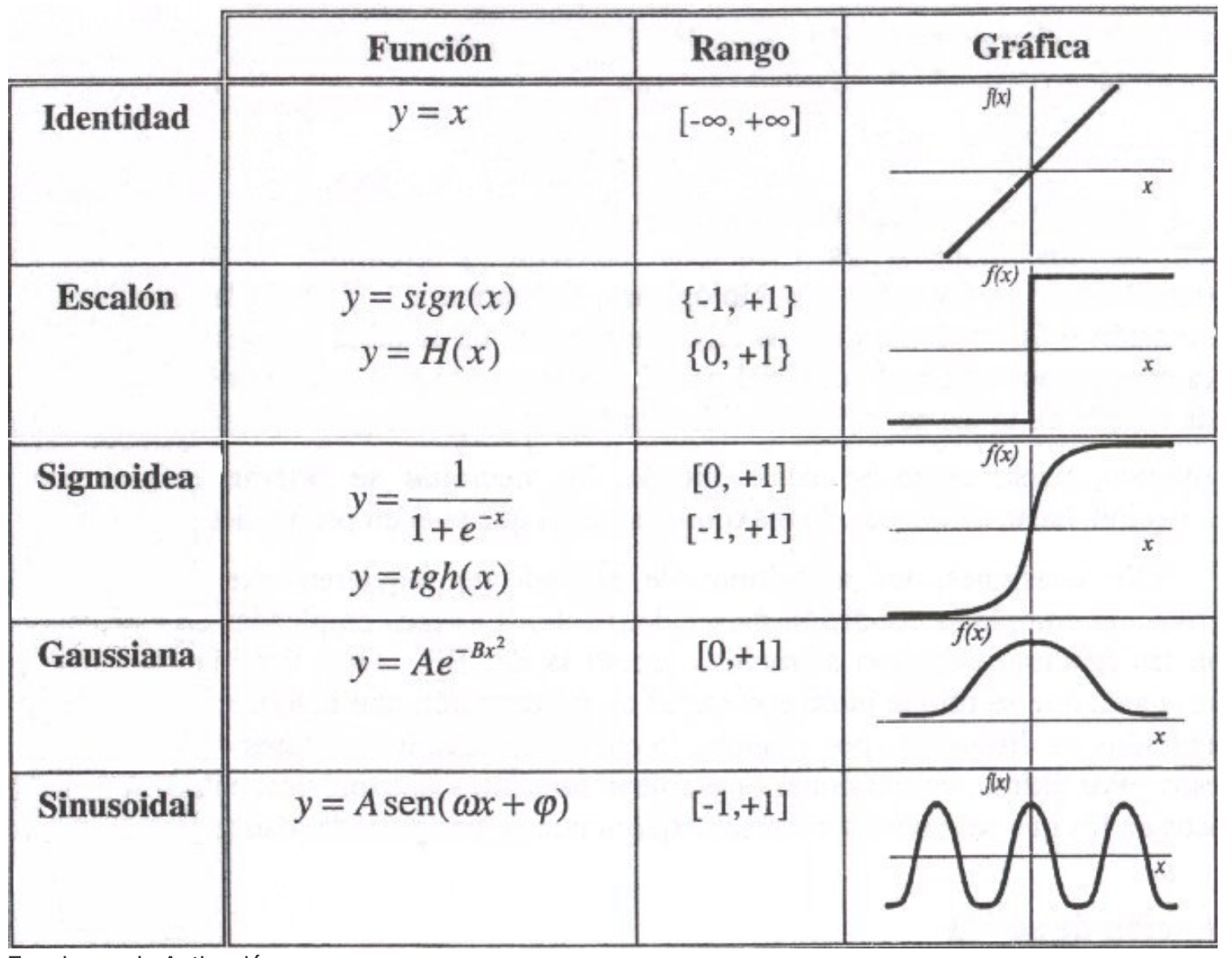
Una función de activación, que transforma la señal de entrada neta de una neurona en una sola señal de salida para ser transmitida en la red

Funciones de actvación {width=60% height = 80%}

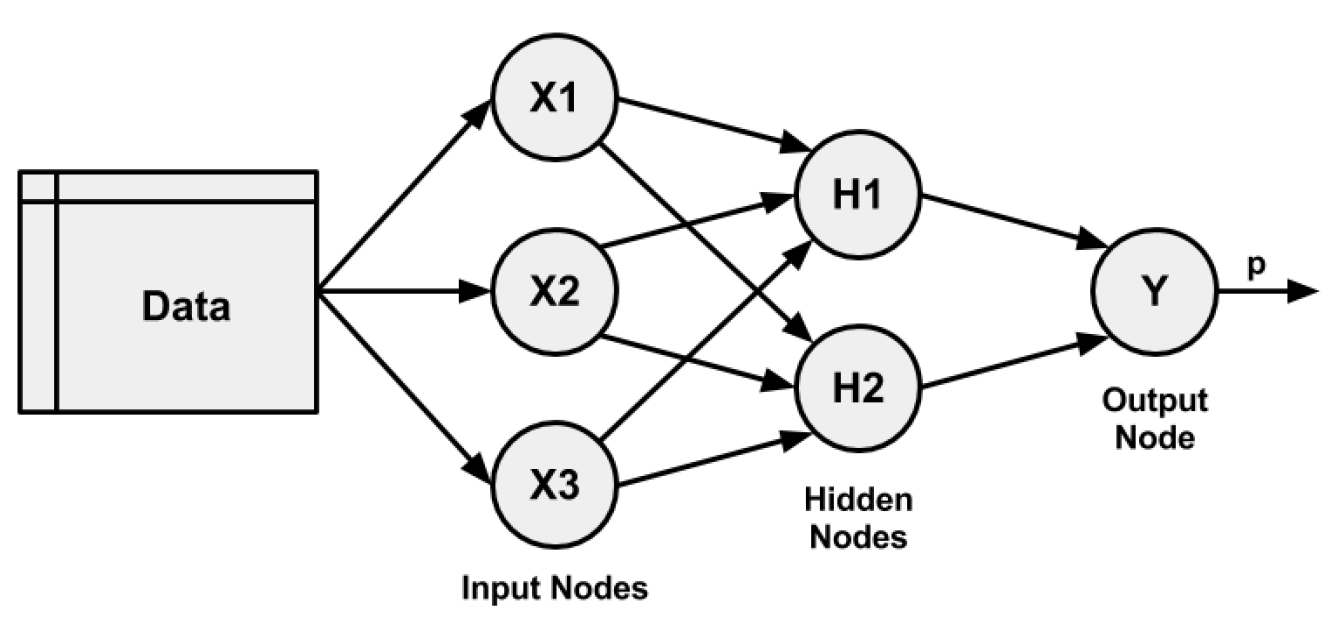
Una topología de red (o arquitectura), que describe el número de neuronas en el modelo, así como el número de capas y la forma en que están conectadas.

Topología de la red {width=60% height = 80%}

El algoritmo de entrenamiento que especifica cómo se establecen los pesos de conexión para activar las neuronas en proporción a la señal de entrada.

Fortalezas	Debilidades
Se puede adaptar a problemas de clasificación o predicción numérica	Reputación de ser computacionalmente intensivo y lento de entrenar, particularmente si la topología de red es compleja
Entre los enfoques de modelado más precisos	Datos de entrenamiento fáciles de sobreestimar o no subestmiar
Hace pocas suposiciones sobre las relaciones subyacentes de los datos	Resultados en un modelo complejo de caja negra que es difícil, si no imposible, de interpretar

11.2 Paso 1: recopilación de datos

El conjunto de datos concretos contiene $1030$ muestras de hormigón, con ocho características que describen los componentes utilizados en la mezcla. Se cree que estas características están relacionadas con la resistencia a la compresión final e incluyen la cantidad (en kilogramos por metro cúbico) de cemento, escoria, cenizas, agua, superplastificante, agregado grueso y agregado fino utilizado en el producto, además de el tiempo de envejecimiento (medido en días).

uu <- "https://raw.githubusercontent.com/vmoprojs/DataLectures/master/concrete.csv"
concrete <- read.csv(url(uu))
# set.seed(12345)
# concrete <- concrete[order(runif(nrow(concrete))), ]
concrete <- concrete[-1]

11.3 Paso 2: Explorar y preparar los datos

str(concrete)

## 'data.frame':    1030 obs. of  9 variables:
##  $ cement      : num  141 169 250 266 155 ...
##  $ slag        : num  212 42.2 0 114 183.4 ...
##  $ ash         : num  0 124.3 95.7 0 0 ...
##  $ water       : num  204 158 187 228 193 ...
##  $ superplastic: num  0 10.8 5.5 0 9.1 0 0 6.4 0 9 ...
##  $ coarseagg   : num  972 1081 957 932 1047 ...
##  $ fineagg     : num  748 796 861 670 697 ...
##  $ age         : int  28 14 28 28 28 90 7 56 28 28 ...
##  $ strength    : num  29.9 23.5 29.2 45.9 18.3 ...

Las nueve variables en los datos corresponden a las ocho características y un resultado, aunque se ha evidenciado un problema. Las redes neuronales funcionan mejor cuando los datos de entrada se escalan a un rango estrecho alrededor de cero, y aquí vemos valores que van desde cero hasta más de mil.

Normalmente, la solución a este problema es reescalar los datos con una función de normalización o estandarización.

Si los datos siguen una curva en forma de campana (una distribución normal), entonces puede tener sentido utilizar la estandarización a través de la función scale () integrada de R.
Por otro lado, si los datos siguen una distribución uniforme o son severamente no normales, entonces la normalización a un rango de 0-1 puede ser más apropiada.

normalize <- function(x) {
return((x - min(x)) / (max(x) - min(x)))
}
concrete_norm <- as.data.frame(lapply(concrete, normalize))
summary(concrete_norm$strength)

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##  0.0000  0.2664  0.4001  0.4172  0.5457  1.0000

En comparación, los valores mínimos y máximos originales fueron 2.33 y 82.6

summary(concrete$strength)

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##    2.33   23.71   34.45   35.82   46.13   82.60

Cualquier transformación aplicada a los datos antes de entrenar el modelo tendrá que aplicarse en reversa más adelante para volver a las unidades de medida originales. Para facilitar el cambio de escala, es conveniente guardar los datos originales, o al menos las estadísticas de resumen de los datos originales.

Dividiremos los datos en un conjunto de capacitación con el 75 por ciento de los ejemplos y un conjunto de prueba con el 25 por ciento.

concrete_train <- concrete_norm[1:773, ]
concrete_test <- concrete_norm[774:1030, ]

11.4 Paso 3: entrenar un modelo en los datos

Para modelar la relación entre los ingredientes usados en el concreto y la resistencia del producto terminado, usaremos una red neuronal feedforward (red que no tiene ciclos) de múltiples capas. El paquete neuralnet (Fritsch and Guenther (2016)) proporciona una implementación estándar y fácil de usar de tales redes. También ofrece una función para trazar la topología de red (más paquetes aquí).

Empezaremos a entrenar la red con solo un nodo oculto

library(neuralnet)

## 
## Attaching package: 'neuralnet'

## The following object is masked from 'package:dplyr':
## 
##     compute

concrete_model <- neuralnet(strength ~ cement + slag +
ash + water + superplastic +
coarseagg + fineagg + age,
data = concrete_train)

Grafiquemos el resultado

plot(concrete_model)

En este modelo simple, hay un nodo de entrada para cada una de las ocho características, seguido de un único nodo oculto y un único nodo de salida que predice la fuerza del concreto.
Los pesos para cada una de las conexiones también se representan, al igual que los términos de sesgo (indicados por los nodos con un 1).
El diagrama también informa el número de pasos de entrenamiento y una medida llamada, la suma de los errores cuadrados (SSE). Estas métricas serán útiles cuando estemos evaluando el rendimiento del modelo.

En ocasiones es importante estimar la complejidad del modelo cuand trabajamos con más datos:

nn_test = function(data)
{
  concrete_model <- neuralnet(strength ~ cement + slag +
ash + water + superplastic +
coarseagg + fineagg + age,
data = data)
}
# devtools::install_github("agenis/GuessCompx")
#library(GuessCompx) # get it by running: install.packages("GuessCompx")
library(neuralnet)
#CompEst(concrete_train, nn_test,plot =FALSE)

11.5 Paso 4: evaluar el rendimiento del modelo

El diagrama de topología de red nos permite observar la caja negra de la ANN, pero no proporciona mucha información sobre qué tan bien el modelo se ajusta a nuestros datos. Para estimar el rendimiento de nuestro modelo, podemos usar la función predict() para generar predicciones en el conjunto de datos de prueba:

predicted_strength <- predict(concrete_model, concrete_test[1:8])

Ten en cuenta que la función de predict() funciona de manera un poco diferente de las funciones de predict() que hemos utilizado hasta ahora. Devuelve una lista con dos componentes: $neuronas, que almacena las neuronas para cada capa en la red, y $net.results, que almacena los valores predichos. Vamos a querer lo último:

# predicted_strength <- model_results$net.result

Debido a que este es un problema de predicción numérica en lugar de un problema de clasificación, no podemos usar una matriz de confusión para examinar la precisión del modelo. En cambio, debemos medir la correlación entre nuestra fuerza del concreto predicha y el valor verdadero. Esto proporciona una idea de la fuerza de la asociación lineal entre las dos variables.

cor(predicted_strength, concrete_test$strength)

##           [,1]
## [1,] 0.8059025

No te alarmes si el resultado difiere. Debido a que la red neuronal comienza con pesos aleatorios, las predicciones pueden variar de un modelo a otro.

Si la correlación es alta implica que el modelo está haciendo un buen trabajo.

11.6 Paso 5: mejorando el ajuste

Como las redes con topologías más complejas son capaces de aprender conceptos más difíciles, veamos qué sucede cuando aumentamos la cantidad de nodos ocultos a cinco.

concrete_model2 <- neuralnet(strength ~ cement + slag +
ash + water + superplastic +
coarseagg + fineagg + age,
data = concrete_train, hidden = 5)

plot(concrete_model2)

Observa que el error informado (medido nuevamente por SSE) se ha reducido.

Comparemos los resultados:

predicted_strength2 <- predict(concrete_model2, concrete_test[1:8])
# predicted_strength2 <- model_results2$net.result
cor(predicted_strength2, concrete_test$strength)

##           [,1]
## [1,] 0.9364437

denormalize <- function(x_norm,x_orig)
{
  #x_norm: normalized dats
  #x_orig: original data
  mmin <- min(x_orig);mmax <- max(x_orig)
  denorm_val <- x_norm*(mmax-mmin)+mmin
  return(denorm_val)
}
library(caret)
R2(denormalize(predicted_strength2,concrete$strength),
   denormalize(concrete_test$strength,concrete$strength))

##           [,1]
## [1,] 0.8769268

Parámetros más importantes

hidden: vector de enteros con el número de neuronas escondidas. Ejemplo, hidden=c(4,3,2) indica que se tiene tres capas ocultas con 4,3, y 2 nodos respectivamente. Por defecto es igual a 1.
act.fct: función de activiación. Se puede usar logistic y tanh, la primera es por defecto.
err.fct: función de pérdida con la que se evalúa el error cometido en las estimación durante la estimación de los pesos $w$. Por defecto es igual a sse (errores al cuadrado).

Ajustemos un modelo con una arquitectura más compleja:

concrete_model3 <- neuralnet(strength ~ cement + slag +
ash + water + superplastic +
coarseagg + fineagg + age,
data = concrete_train, hidden = c(5,2,3),act.fct = "tanh")

plot(concrete_model3)
predicted_strength3 <- predict(concrete_model3, concrete_test[1:8])


R2(denormalize(predicted_strength3,concrete$strength),
   denormalize(concrete_test$strength,concrete$strength))

##           [,1]
## [1,] 0.8491314

11.6.1 Usando `caret`

Como podemos ver, podemos variar los parámetros elegidos para elegir la mejor combinación de, por ejemplo, el número de capas y nodos. Podemos hacerlo con caret

tune.grid.neuralnet <- expand.grid(
  layer1 = 2:3,
  layer2 = 2:3,
  layer3 = 2:3
)

control <- trainControl(method="repeatedcv", number=5)

nnet_caret <- caret::train(strength ~ cement + slag + ash + water + superplastic + coarseagg + fineagg + age, 
               data = concrete_train,
               method = 'neuralnet', 
               linear.output = TRUE, 
               tuneGrid = tune.grid.neuralnet,
               metric = "RMSE",
               trControl = control)


nnet_caret$finalModel$tuneValue # valores de las capas

##   layer1 layer2 layer3
## 7      3      3      2

predicted_strength4 <- predict(nnet_caret,concrete_test[1:8])

c(m1 =R2(denormalize(predicted_strength,concrete$strength),
   denormalize(concrete_test$strength,concrete$strength))
,
m2 = R2(denormalize(predicted_strength2,concrete$strength),
   denormalize(concrete_test$strength,concrete$strength))
,
m3 = R2(denormalize(predicted_strength3,concrete$strength),
   denormalize(concrete_test$strength,concrete$strength))
,
m4 = R2(denormalize(predicted_strength4,concrete$strength),
   denormalize(concrete_test$strength,concrete$strength)))

##        m1        m2        m3        m4 
## 0.6494788 0.8769268 0.8491314 0.8450435

11.6.2 Ejercicio

Usa los datos Hitters (salarios de jugadores de baseball con estadísticas de su rendimiento) cargándolos con:

library(ISLR2)

## 
## Attaching package: 'ISLR2'

## The following objects are masked from 'package:ISLR':
## 
##     Auto, Credit

Gitters <- na.omit(Hitters)

depvar <- "Salary"
X_in <- Gitters[,!(names(Gitters) %in% depvar)]
y <- Gitters[,depvar]
dummies <- dummyVars(~ ., data=X_in)
X_dum <- predict(dummies, X_in)


preprocessParams <- preProcess(X_dum, method = c("center", "scale"))
X <- predict(preprocessParams, X_dum)
y <- scale(y)


set.seed(8519)
index <- createDataPartition(as.numeric(y), p=0.75, list=FALSE)
X_train <- X[ index, ]
X_test <- X[-index, ]
y_train <- y[index]
y_test <- y[-index]

Debes predecir su salario usando regresión lineal múltiple y neuralnet. ¿Cuál es mejor? ¿Por qué?

11.7 Redes neuronales convolucionales

Conjunto de datos de 50.000 imágenes de entrenamiento en color de 32x32, etiquetadas en más de 100 categorías y 10.000 imágenes de prueba.

Son 20 clases de mamíferos (ejemplo: acuáticos), con 5 tipos (castor, delfín, nutria, foca, ballena), 100 etiquetas en total.

Nota: el siguiente enlace tiene las instrucciones para instalar tensorflow y keras: https://tensorflow.rstudio.com/install/

# install.packages("keras")
# install_keras()
# library(tensorflow)
# install_tensorflow()
# https://tensorflow.rstudio.com/install/
library(keras)

## 
## Attaching package: 'keras'

## The following object is masked _by_ '.GlobalEnv':
## 
##     normalize

cifar100 <- dataset_cifar100()
names(cifar100)

## [1] "train" "test"

table(cifar100$train$y)

## 
##   0   1   2   3   4   5   6   7   8   9  10  11  12  13  14  15  16  17  18  19  20  21  22  23 
## 500 500 500 500 500 500 500 500 500 500 500 500 500 500 500 500 500 500 500 500 500 500 500 500 
##  24  25  26  27  28  29  30  31  32  33  34  35  36  37  38  39  40  41  42  43  44  45  46  47 
## 500 500 500 500 500 500 500 500 500 500 500 500 500 500 500 500 500 500 500 500 500 500 500 500 
##  48  49  50  51  52  53  54  55  56  57  58  59  60  61  62  63  64  65  66  67  68  69  70  71 
## 500 500 500 500 500 500 500 500 500 500 500 500 500 500 500 500 500 500 500 500 500 500 500 500 
##  72  73  74  75  76  77  78  79  80  81  82  83  84  85  86  87  88  89  90  91  92  93  94  95 
## 500 500 500 500 500 500 500 500 500 500 500 500 500 500 500 500 500 500 500 500 500 500 500 500 
##  96  97  98  99 
## 500 500 500 500

x_train <- cifar100$train$x
g_train <- cifar100$train$y
x_test <- cifar100$test$x
g_test <- cifar100$test$y
dim(x_train)

## [1] 50000    32    32     3

range(x_train[1,,, 1])

## [1]  13 255

El conjunto de 50.000 imágenes de formación tiene cuatro dimensiones:

Cada imagen de tres colores se representa como un conjunto de tres canales, cada uno de los cuales consta de $32\times 32$ píxeles de ocho bits.

Estandarizamos, pero manteniendo la estructura de la matriz. Codificamos la respuesta one-hot para producir una matriz binaria de 100 columnas.

one_hot_encode <- function(class_vector, num_classes = NULL) {
  class_vector <- as.integer(class_vector)
  if (is.null(num_classes)) {
    num_classes <- max(class_vector) + 1
  }
  binary_matrix <- matrix(0, nrow = length(class_vector), ncol = num_classes)
  for (i in seq_along(class_vector)) {
    binary_matrix[i, class_vector[i] + 1] <- 1
  }
  return(binary_matrix)
}

x_train <- x_train/255 # se divide para estandarizar, [0,1]
x_test <- x_test/255
# y_train <- to_categorical(y = as.integer(g_train),num_classes = 100)
y_train <- one_hot_encode(class_vector = g_train,num_classes = 100)
dim(y_train)

## [1] 50000   100

Antes de comenzar, miramos algunas de las imágenes de entrenamiento usando el paquete jpeg

library(jpeg)
par(mar = c(0, 0, 0, 0), mfrow = c(5, 5))
index <- sample(seq(50000), 25)
for (i in index) plot(as.raster(x_train[i,,, ]))

La función as.raster() convierte el mapa de características (x_train) para que pueda trazarse como una imagen en color.

Aquí especificamos una CNN de tamaño moderado con fines de demostración.

# model <- keras_model_sequential() %>%
#    layer_conv_2d(filters = 32, kernel_size = c(3, 3),
#       padding = "same", activation = "relu",
#       input_shape = c(32, 32, 3)) %>%
#    layer_max_pooling_2d(pool_size = c(2, 2)) %>%
#    layer_conv_2d(filters = 64, kernel_size = c(3, 3),
#       padding = "same", activation = "relu") %>%
#    layer_max_pooling_2d(pool_size = c(2, 2)) %>%
#    layer_conv_2d(filters = 128, kernel_size = c(3, 3),
#       padding = "same", activation = "relu") %>%
#    layer_max_pooling_2d(pool_size = c(2, 2)) %>%
#    layer_conv_2d(filters = 256, kernel_size = c(3, 3),
#       padding = "same", activation = "relu") %>%
#    layer_max_pooling_2d(pool_size = c(2, 2)) %>%
#    layer_flatten() %>%
#    layer_dropout(rate = 0.5) %>%
#    layer_dense(units = 512, activation = "relu") %>%
#    layer_dense(units = 100, activation = "softmax")


model <- keras_model_sequential() %>%
  layer_conv_2d(filters = 32, kernel_size = c(3, 3),
    padding = "same", activation = "relu", input_shape = c(32, 32, 3)) %>%
  layer_max_pooling_2d(pool_size = c(2, 2)) %>%
  layer_conv_2d(filters = 64, kernel_size = c(3, 3),
    padding = "same", activation = "relu") %>%
  layer_max_pooling_2d(pool_size = c(2, 2)) %>%
  layer_conv_2d(filters = 128, kernel_size = c(3, 3),
    padding = "same", activation = "relu") %>%
  layer_max_pooling_2d(pool_size = c(2, 2)) %>%
  layer_conv_2d(filters = 256, kernel_size = c(3, 3),
    padding = "same", activation = "relu") %>%
  layer_max_pooling_2d(pool_size = c(2, 2)) %>%
  layer_flatten() %>%
  layer_dense(units = 512, activation = "relu") %>%
  layer_dropout(rate = 0.5) %>%
  layer_dense(units = 100, activation = "softmax")

summary(model)

## Model: "sequential"
## ___________________________________________________________________________________________________
##  Layer (type)                               Output Shape                            Param #        
## ===================================================================================================
##  conv2d_3 (Conv2D)                          (None, 32, 32, 32)                      896            
##  max_pooling2d_3 (MaxPooling2D)             (None, 16, 16, 32)                      0              
##  conv2d_2 (Conv2D)                          (None, 16, 16, 64)                      18496          
##  max_pooling2d_2 (MaxPooling2D)             (None, 8, 8, 64)                        0              
##  conv2d_1 (Conv2D)                          (None, 8, 8, 128)                       73856          
##  max_pooling2d_1 (MaxPooling2D)             (None, 4, 4, 128)                       0              
##  conv2d (Conv2D)                            (None, 4, 4, 256)                       295168         
##  max_pooling2d (MaxPooling2D)               (None, 2, 2, 256)                       0              
##  flatten (Flatten)                          (None, 1024)                            0              
##  dense_1 (Dense)                            (None, 512)                             524800         
##  dropout (Dropout)                          (None, 512)                             0              
##  dense (Dense)                              (None, 100)                             51300          
## ===================================================================================================
## Total params: 964516 (3.68 MB)
## Trainable params: 964516 (3.68 MB)
## Non-trainable params: 0 (0.00 Byte)
## ___________________________________________________________________________________________________

Observa que usamos el argumento padding =" same " para layer_conv_2D(), que asegura que los canales de salida tengan la misma dimensión que los canales de entrada.
Hay 32 canales en la primera capa oculta, en contraste con los tres canales en la capa de entrada. Usamos un filtro de convolución de $3\times 3$ para cada canal en todas las capas.
A cada convolución le sigue una capa de agrupación máxima de bloques de $2\times 2$.
Al mirar el resumen, podemos ver que los canales se reducen a la mitad en ambas dimensiones después de cada una de estas operaciones de agrupación.
Después del último de estos tenemos una capa con 256 canales de dimensión $2\times 2$.
A continuación, se aplanan a una capa densa de tamaño 1.024: en otras palabras,cada una de las matrices de $2\times 2$ se convierte en un vector de $4$ y se coloca una al lado de la otra en una capa.
A esto le sigue una capa de regularización, luego otra capa densa de tamaño 512 (relu), que finalmente alcanza la capa de salida softmax.

Finalmente, especificamos el algoritmo de ajuste y ajustamos el modelo.

library(caret)
library(ISLR2)
model %>% compile(loss = "categorical_crossentropy",
    optimizer = optimizer_rmsprop(), metrics = c("accuracy"))
#history <- model %>% fit(x_train, y_train, epochs = 30,
history <- model %>% fit(x_train, y_train, epochs = 1,
    batch_size = 128, validation_split = 0.2)

## 313/313 - 45s - loss: 4.3178 - accuracy: 0.0406 - val_loss: 4.0742 - val_accuracy: 0.0772 - 45s/epoch - 142ms/step

sol <- model %>% predict(x_test) %>% k_argmax() %>% as.integer()

## 313/313 - 4s - 4s/epoch - 11ms/step

sum(diag(table(sol,g_test)))/nrow(g_test)

## [1] 0.013

loss=categorical_crossentropy es una función de pérdida que se usa para clasificación multiclase.
optimizer=optimizer_rmsprop() indica el algoritmo de optimización.
metrics. Lista de métricas que el modelo evaluará durante el entrenamiento y las pruebas.
fit ajusta el modelo.
epochs. Una Época es cuando un conjunto de datos ENTERO se pasa hacia adelante y hacia atrás a través de la red neuronal solo UNA VEZ. Dado que una época es demasiado grande para alimentar la computadora a la vez, la dividimos en varios lotes (batch) más pequeños.
batch_size: tamaño del lote. Número total de datos de entrenamiento presentes en un solo lote.
validation_split. Está entre 0 y 1. Es la fracción de los datos de entrenamiento que se utilizarán como datos de validación.