18 DBSCAN

Es un algoritmo no supervisado que tienen por objetivo descubrir grupos a partir de formas arbitrarias de cualquier conjunto de datos y al mismo tiempo puede distinguir noise points que no forman parte de ningún grupo.

Parámetros

  • Epsilon (\(\epsilon\)): define el radio de una bola.
  • MinPts: Número mínimo de puntos requeridos dentro de la bola de radio \(\epsilon\)

Definiciones:

  • Bola Cerrada: \(B_{\epsilon}(p)=B(p;\epsilon)=\{x\in X\mid d(x,p)\leq \epsilon\}\), donde \(p\) es el centro y \(\epsilon\) es el radio
  • Core point: Si, dentro de la bola, contiene un número de puntos mayor o igual a MinPts
  • Border point: Si, dentro de la bola, contiene al menos un core point
  • Noise point: Si, dentro de la bola, no contiene ningún core point
uu = "https://raw.githubusercontent.com/vmoprojs/DataLectures/master/Mall_Customers.csv"
datos = read.csv(url(uu))
library(dbscan)

dbDat <- datos[,4:5]

#Exploramos los datos
summary(dist(dbDat))
##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##    0.00   26.02   45.00   45.60   60.96  143.42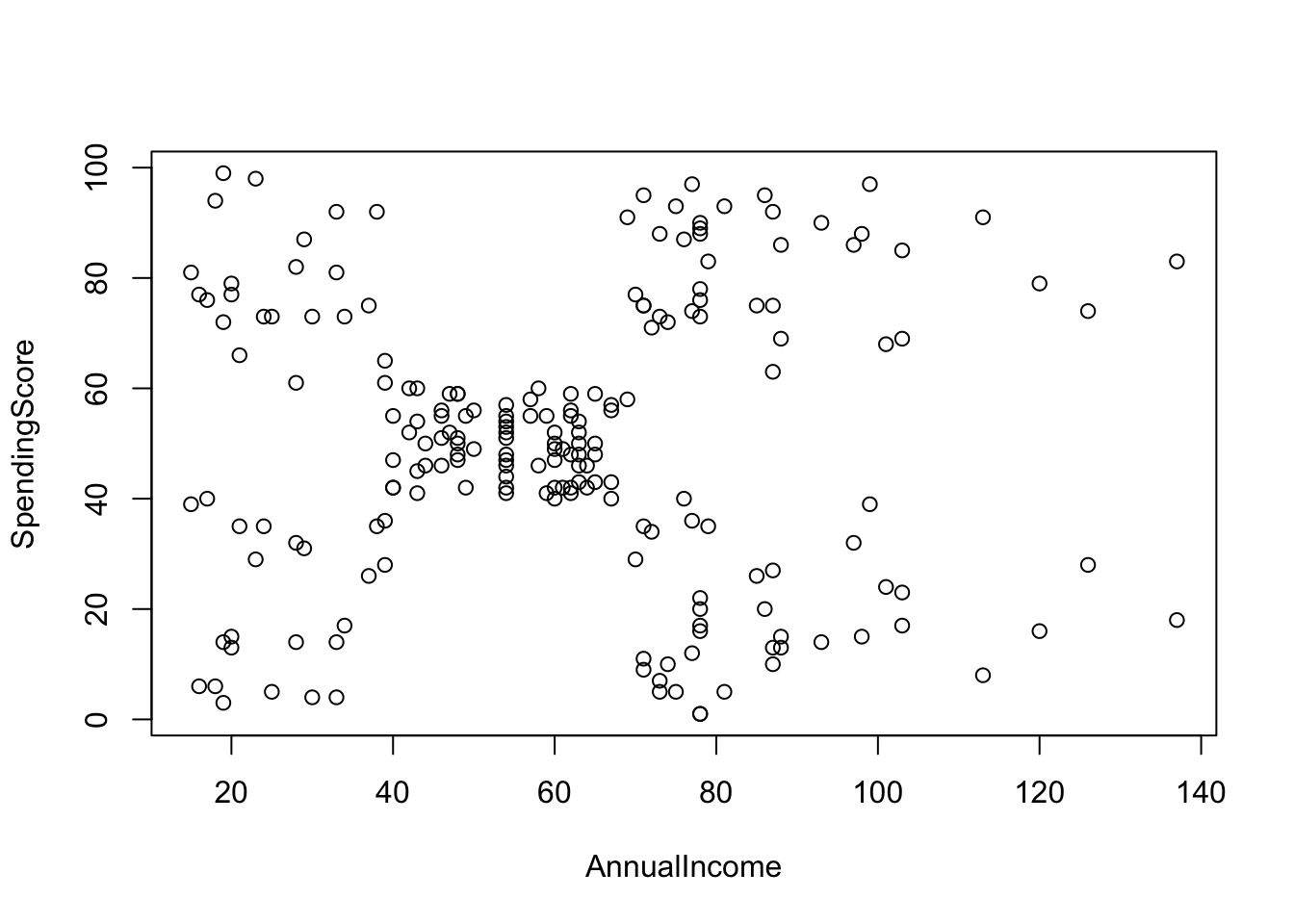
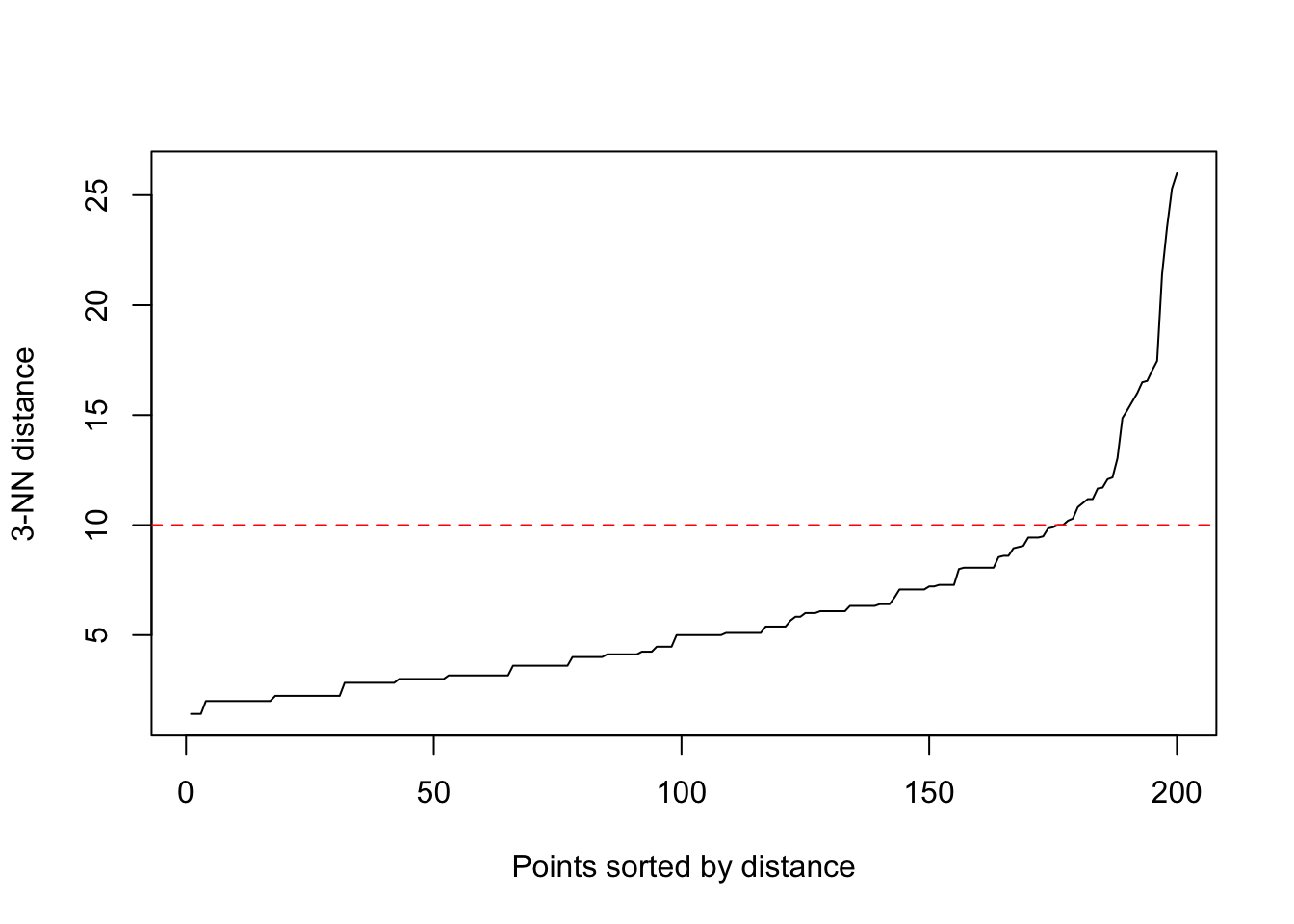
plot(dbDat)

# Guiamos la decision de EPS
kNNdistplot(dbDat,k=3);abline(h=10, lty=2, col="red")

Ejecutamos el algoritmo

library(factoextra)
set.seed(123) 
f<- fpc::dbscan(dbDat, eps=10, MinPts = 3) #
f
## dbscan Pts=200 MinPts=3 eps=10
##         0   1 2  3  4
## border 10   2 0  1  1
## seed    0 124 3 32 27
## total  10 126 3 33 28
d<-dbscan(dbDat,10,3) #
d
## DBSCAN clustering for 200 objects.
## Parameters: eps = 10, minPts = 3
## Using euclidean distances and borderpoints = TRUE
## The clustering contains 4 cluster(s) and 10 noise points.
## 
##   0   1   2   3   4 
##  10 126   3  33  28 
## 
## Available fields: cluster, eps, minPts, metric, borderPoints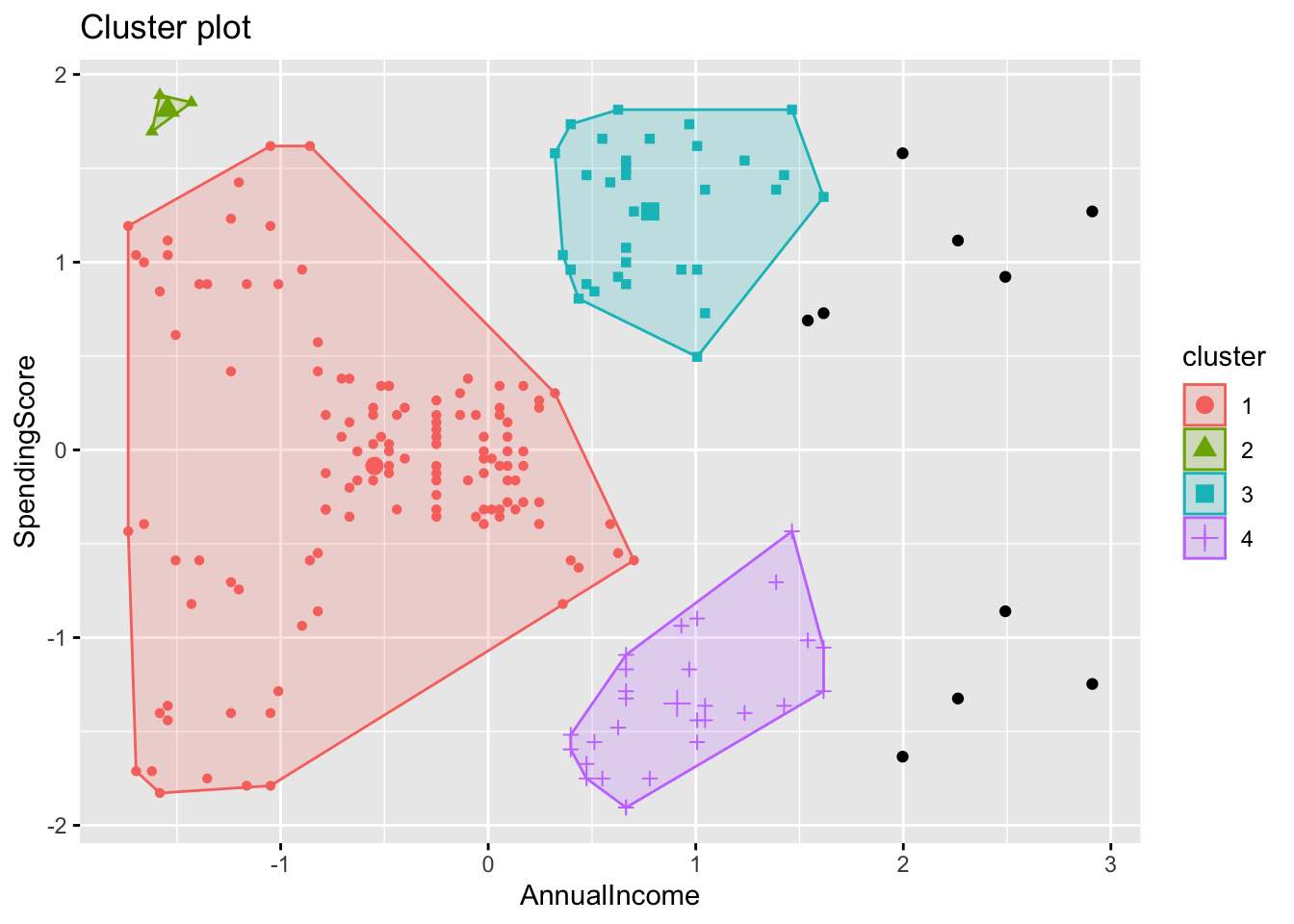
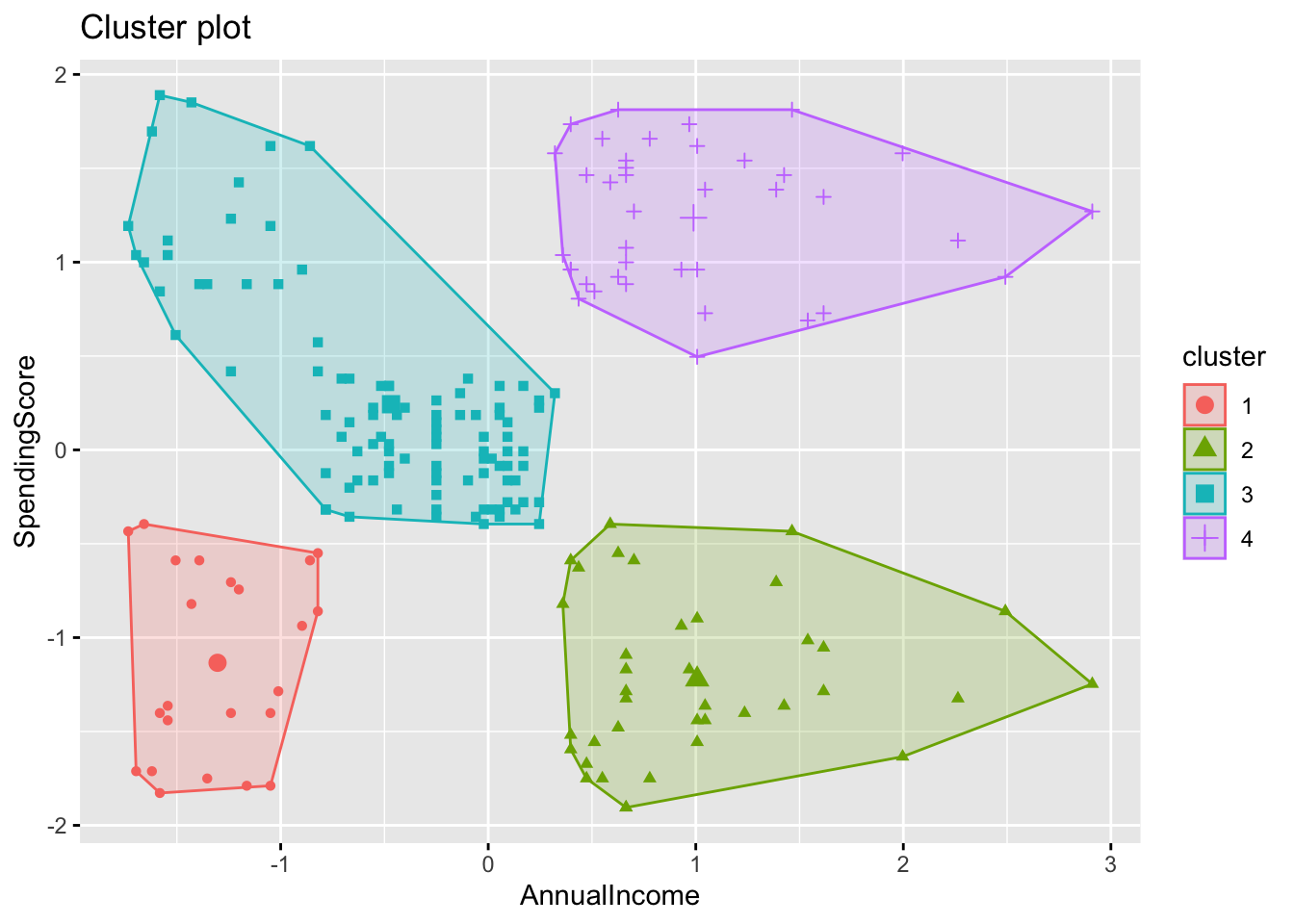
#Graficos de los cluster
fviz_cluster(f, dbDat, geom="point")

km <- kmeans(dbDat, 4)
fviz_cluster(km, dbDat, geom="point")

Ventajas (Kassambara (2017))

  • A diferencia del método K-medias, DBSCAN no requiere que el usuario especifique el número de clusters como input.

  • DBSCAN puede encontrar cualquier forma de clusters. El cluster no necesariamente debe ser circular.

  • DBSCAN puede identificar los valores atípicos (outliers)

Desventajas

  • No es un método absolutamente determinístico. Los objetos bordes, que son alcanzables desde más de un cluster pueden asignarse a uno u otro en función del orden en el que se visite los puntos.

  • No genera buenos resultados cuando la densidad de los grupos es muy distinta, ya que no es posible encontrar parámetros \(\epsilon\) y MinPts que sirvan para todos a la vez.

18.1 Ejercicios

La descripción de los datos del siguiente ejercicio se encuentra en: (https://github.com/vmoprojs/DataLectures/blob/master/world_data.txt)

uu <- "https://raw.githubusercontent.com/vmoprojs/DataLectures/master/world_data.csv"

datos <- read.csv(uu,sep = ";")

Usando las variables de Real GDP, employment and population levels, realizar un análisis de conglomerados para los años 2010 y 2017. Específicamente, aplique k-means y dbscan. Comente sus resultados respecto al grupo que pertenece Ecuador en estos años para cada método.

table(datos$year)
## 
## 1950 1951 1952 1953 1954 1955 1956 1957 1958 1959 1960 1961 1962 1963 1964 1965 1966 1967 1968 
##  182  182  182  182  182  182  182  182  182  182  182  182  182  182  182  182  182  182  182 
## 1969 1970 1971 1972 1973 1974 1975 1976 1977 1978 1979 1980 1981 1982 1983 1984 1985 1986 1987 
##  182  182  182  182  182  182  182  182  182  182  182  182  182  182  182  182  182  182  182 
## 1988 1989 1990 1991 1992 1993 1994 1995 1996 1997 1998 1999 2000 2001 2002 2003 2004 2005 2006 
##  182  182  182  182  182  182  182  182  182  182  182  182  182  182  182  182  182  182  182 
## 2007 2008 2009 2010 2011 2012 2013 2014 2015 2016 2017 
##  182  182  182  182  182  182  182  182  182  182  182
vars <- c("rgdpe","rgdpo","pop","emp","avh","hc")
df1 <- datos[datos$year == 2010,vars]
df2 <- datos[datos$year == 2017,vars]