5 Máquinas de soporte vectorial
Librerías usadas
5.1 Maximal Margin classifier
En dos dimensiones, un hiperplano se define como:
\[ \beta_0 +\beta_1X_1+\beta_2X_2=0 \]
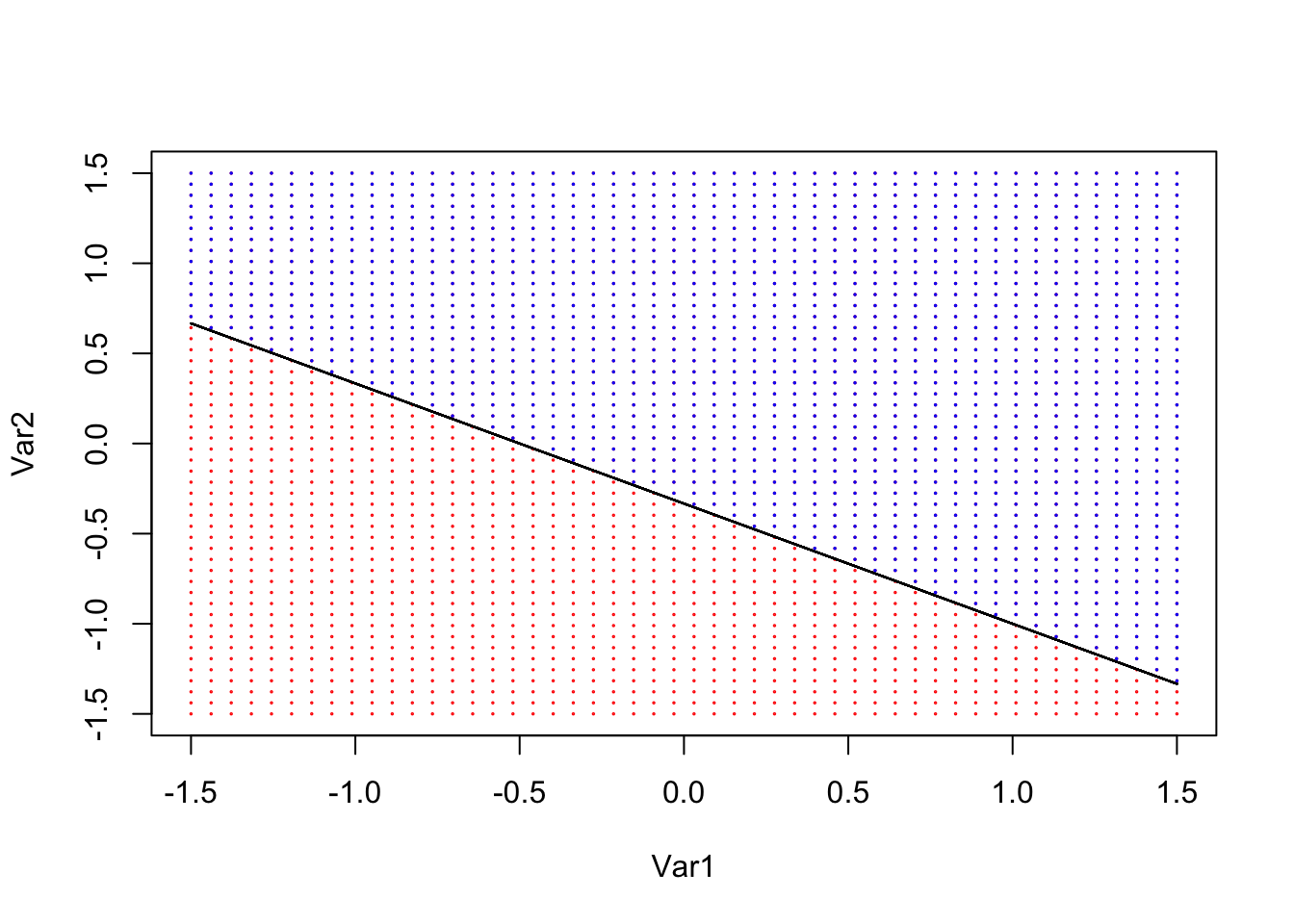
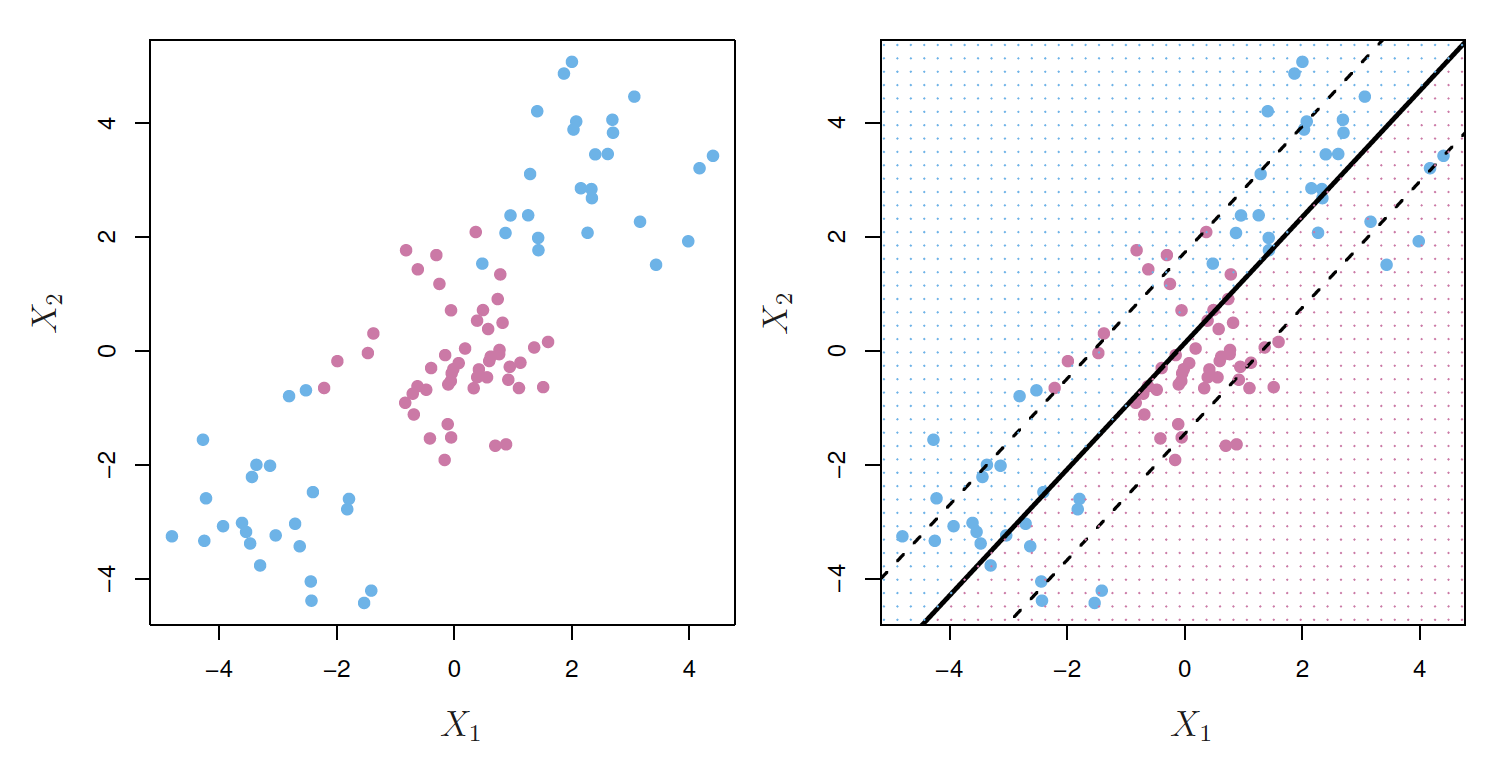
Supongamos que es posible construir un hiperplano que separe perfectamente las observaciones de entrenamiento de acuerdo con sus etiquetas de la variable de respuesta. En el panel de la izquierda de la siguiente Figura se muestran ejemplos de tres de estos hiperplanos separadores.
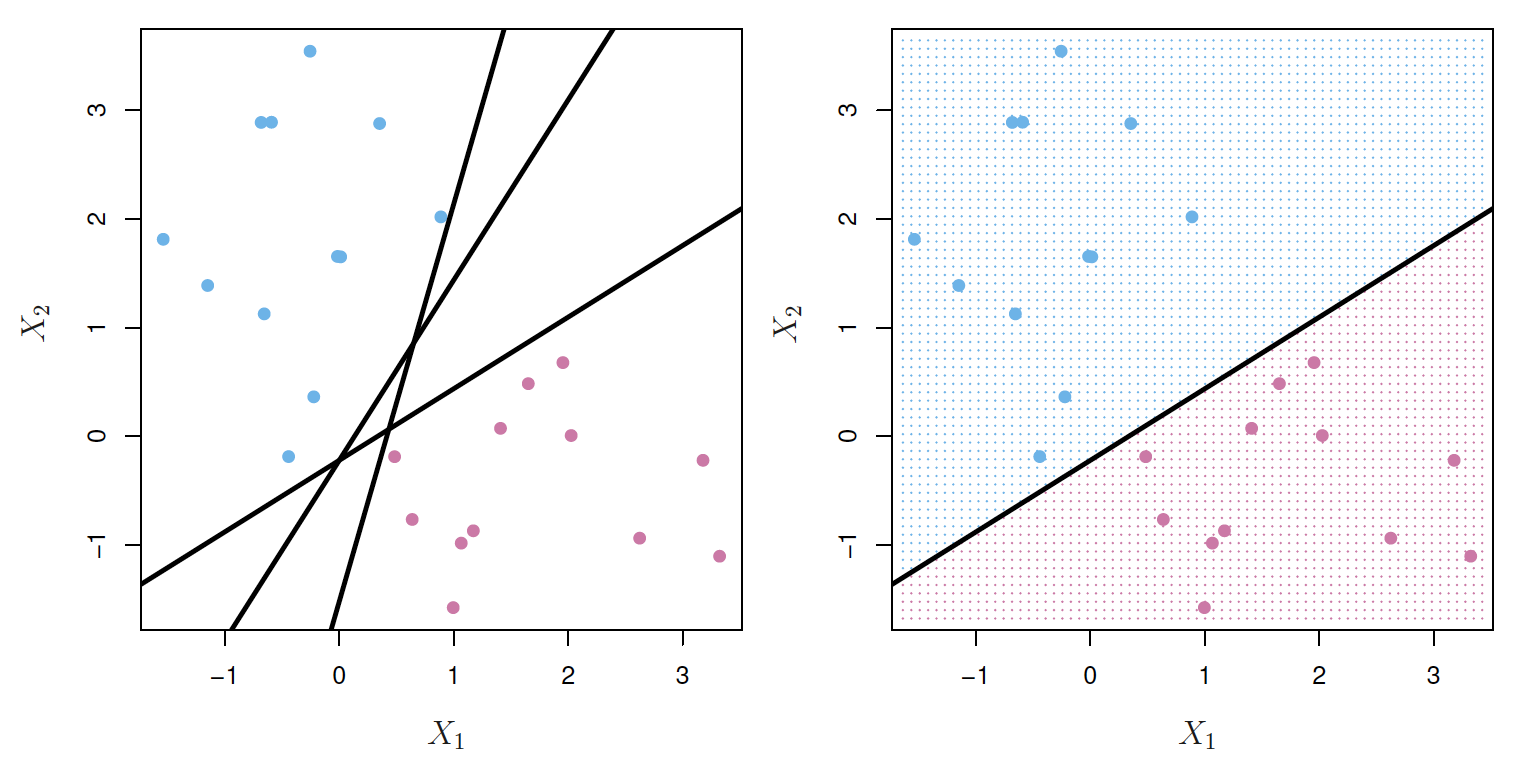
Izquierda: Hay dos clases de observaciones, que se muestran en azul y en violeta, cada una de las cuales tiene medidas en dos variables. Tres hiperplanos que se separan, de los muchos posibles, se muestran en negro. Derecha: se muestra un hiperplano de separación en negro. La cuadrícula azul y violeta indica la regla de decisión tomada por un clasificador basado en este hiperplano separador: una observación de prueba que cae en la parte azul de la cuadrícula se asignará a la clase azul y una observación de prueba que cae en la parte púrpura de la cuadrícula se asignará a la clase púrpura.
En general tenemos:
\[ \beta_0 +\beta_1x_{i1}+\beta_2x_{i2}+\cdots+x_{ip}> \quad \text{if } y_i=1 \]
\[ \beta_0 +\beta_1x_{i1}+\beta_2x_{i2}+\cdots+x_{ip}<0 \quad \text{if } y_i=-1 \]
\[ y_i(\beta_0 +\beta_1x_{i1}+\beta_2x_{i2}+\cdots+x_{ip})>0 \]
Una elección natural es el hiperplano de margen máximo (también conocido como el hiperplano de separación óptimo), que es el hiperplano de separación que está más alejado de las observaciones de entrenamiento.
Es decir, podemos calcular la distancia (perpendicular) desde cada observación de entrenamiento a un hiperplano de separación dado; la distancia más pequeña es la distancia mínima desde las observaciones al hiperplano, y se conoce como margen.
El hiperplano de margen máximo es el hiperplano de separación para el que el margen es mayor, es decir, es el hiperplano que tiene la distancia mínima más lejana a las observaciones de entrenamiento. A continuación, podemos clasificar una observación de prueba en función de qué lado del hiperplano de margen máximo se encuentra. Esto se conoce como clasificador de margen máximo. Esperamos que un clasificador que tenga un gran margen en los datos de entrenamiento también tenga un gran margen en los datos de la prueba y, por lo tanto, clasifique las observaciones de la prueba correctamente. Aunque el clasificador de margen máximo a menudo tiene éxito, también puede provocar un ajuste excesivo cuando \(p\) es grande.
Al examinar la siguiente figura, vemos que tres observaciones de entrenamiento son equidistantes del hiperplano del margen máximo y se encuentran a lo largo de las líneas discontinuas que indican el ancho del margen. Estas tres observaciones se conocen como vectores de soporte, ya que son vectores en el espacio p-dimensional (en la Figura, \(p = 2\)) y soportan el hiperplano de margen máximo en el sentido de que si estos puntos se movieron ligeramente, entonces el margen máximo el hiperplano también se movería.
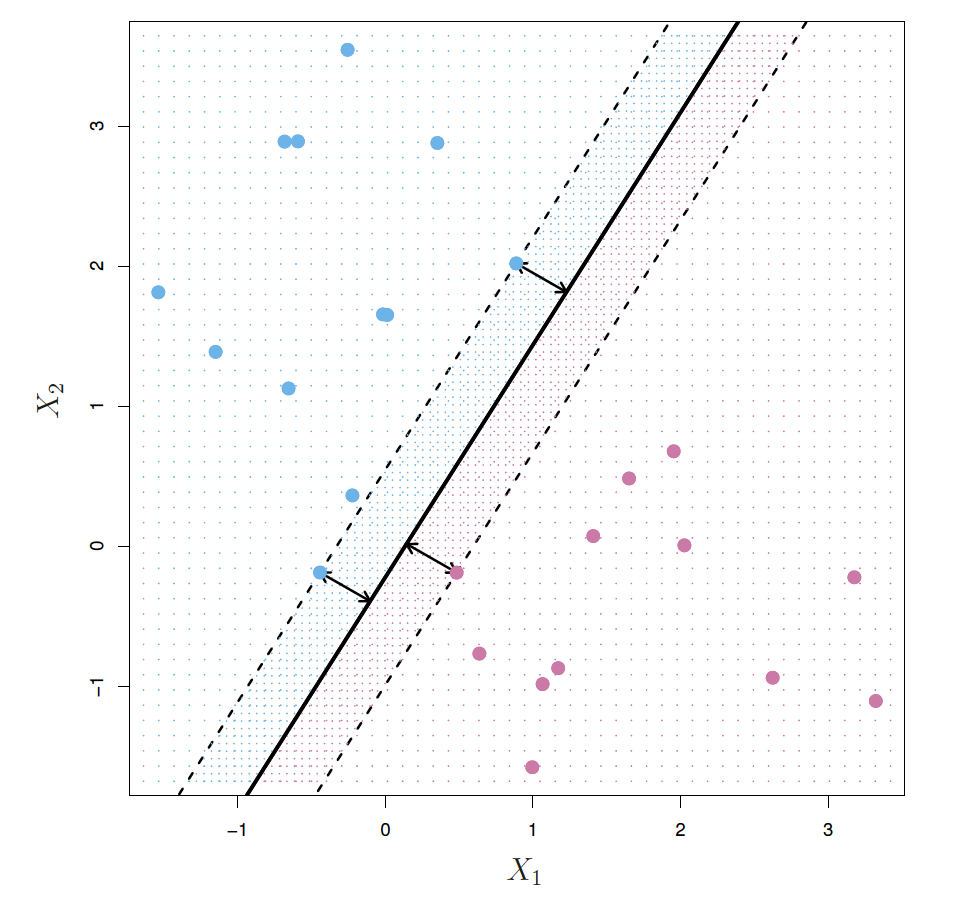
- Hay dos clases de observaciones, que se muestran en azul y en violeta.
- El hiperplano de margen máximo se muestra como una línea continua.
- El margen es la distancia desde la línea continua a cualquiera de las líneas discontinuas.
- Los dos puntos azules y el punto púrpura que se encuentran en las líneas punteadas son los vectores de apoyo (soporte), y la distancia desde esos puntos al hiperplano se indica mediante flechas.
- La cuadrícula violeta y azul indica la regla de decisión tomada por un clasificador basado en este hiperplano.
5.2 Support vector classifiers
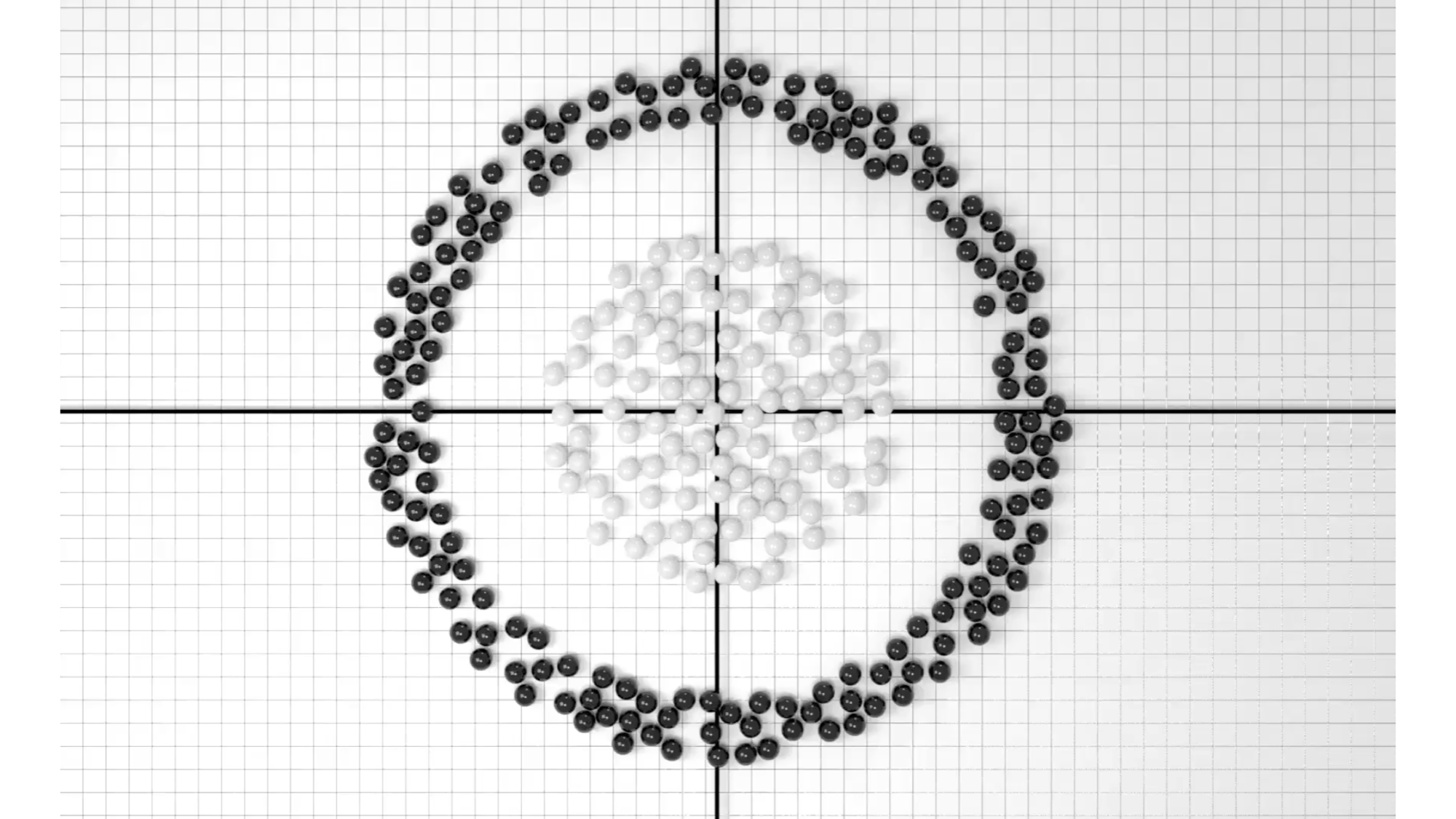
Hay dos clases de observaciones, que se muestran en azul y en violeta. En este caso, las dos clases no son separables por un hiperplano, por lo que no se puede utilizar el clasificador de margen máximo.
Podría valer la pena clasificar erróneamente algunas observaciones de entrenamiento para hacer un mejor trabajo en la clasificación de las observaciones restantes.
El clasificador de vectores de soporte, a veces llamado clasificador de margen suave, hace exactamente esto. En lugar de buscar el mayor margen posible para que cada observación no solo esté en el lado correcto del hiperplano sino también en el lado correcto del margen, permitimos que algunas observaciones estén en el lado incorrecto del margen, o incluso en el lado incorrecto. lado del hiperplano.
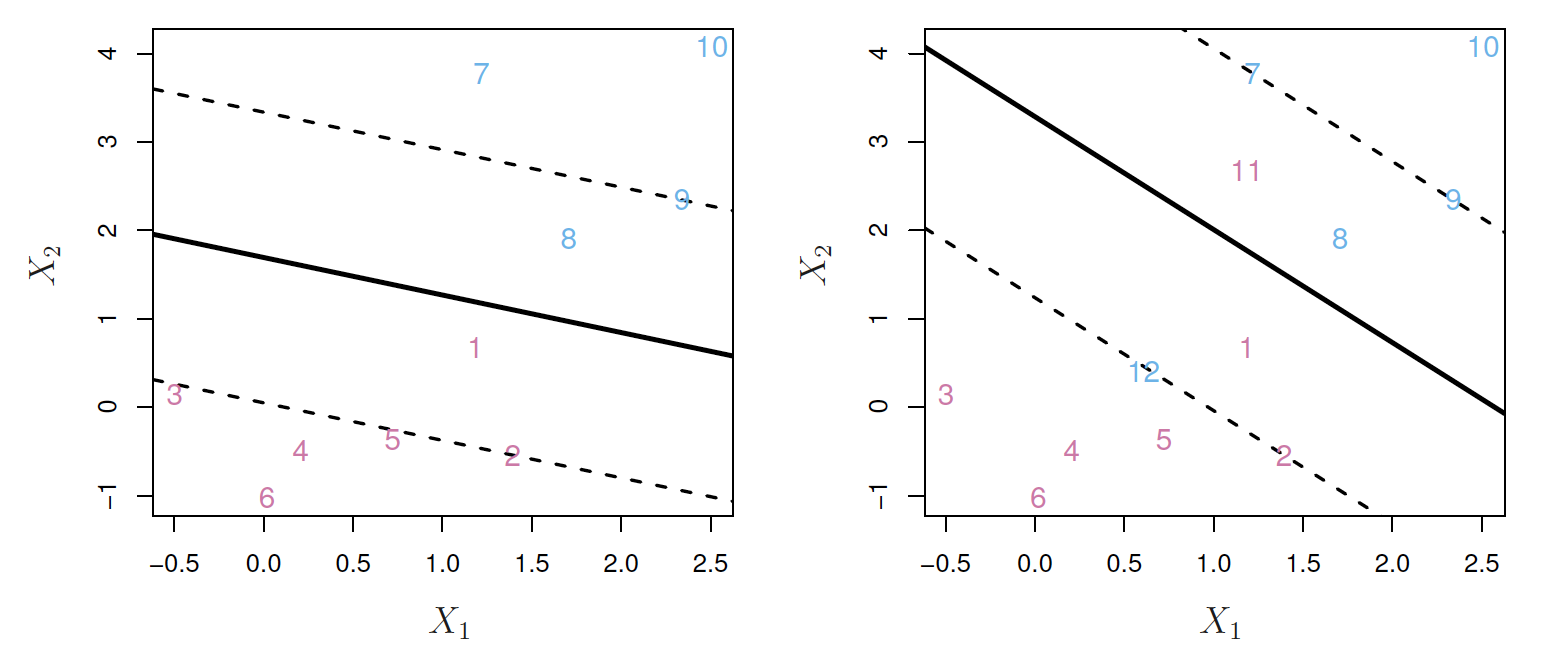Izquierda: Un clasificador de vectores de soporte se ajusta para un pequeño conjunto de datos. Observaciones violetas: Observaciones 3; 4; 5 y 6 están en el lado correcto del margen, la observación 2 está en el margen y la observación 1 está en el lado incorrecto del margen. Observaciones azules: las observaciones 7 y 10 están en el lado correcto del margen, la observación 9 está en el margen y la observación 8 está en el lado incorrecto del margen. No hay observaciones en el lado equivocado del hiperplano. Derecha: Igual que el panel izquierdo con dos puntos adicionales, 11 y 12. Estas dos observaciones están en el lado equivocado del hiperplano y en el lado equivocado del margen.
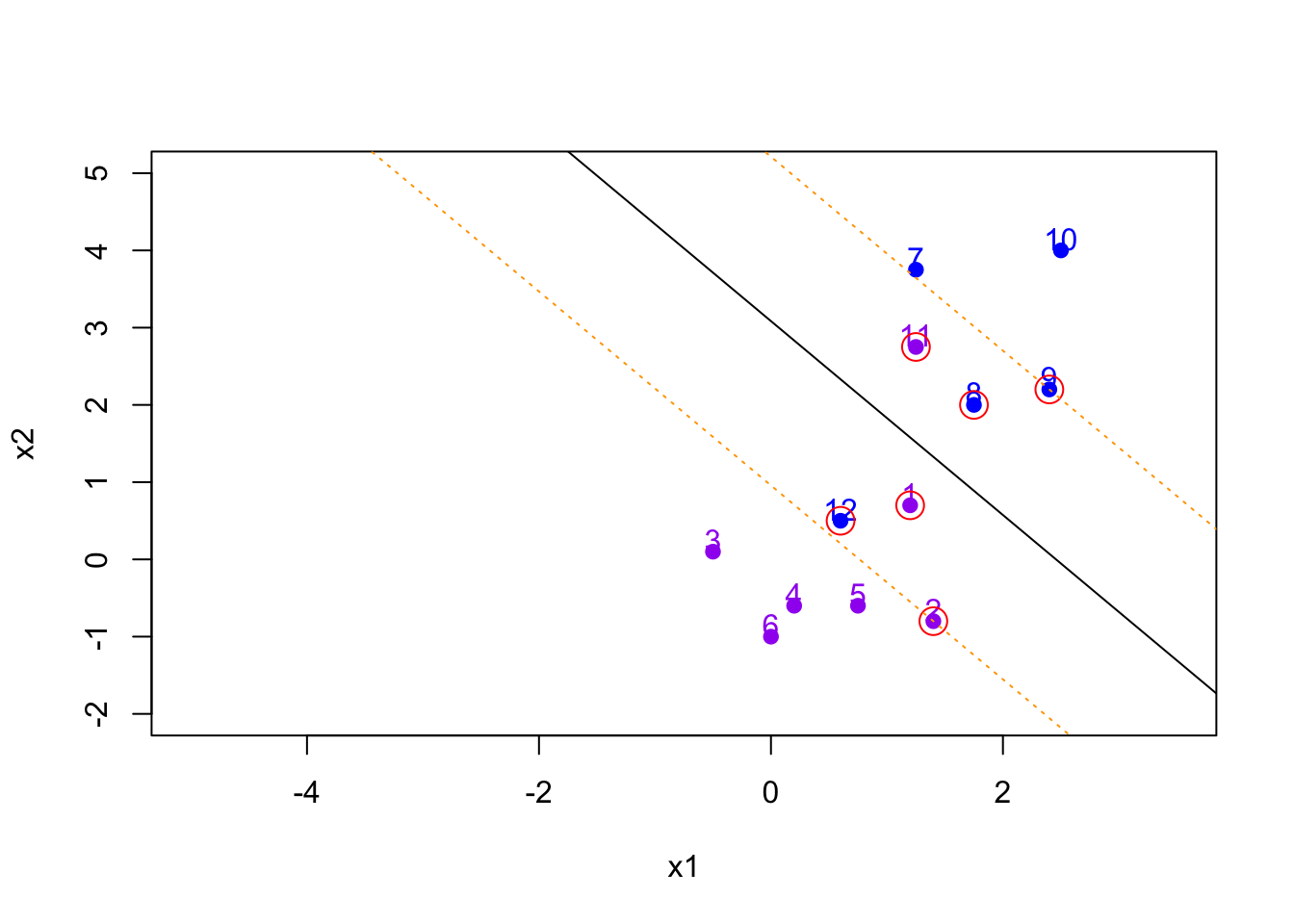
Izquierda: Las observaciones se dividen en dos clases, con un límite no lineal entre ellas.
Derecha: El clasificador de vectores de soporte busca un límite lineal y, en consecuencia, funciona muy mal.
5.3 Support vector machines
Datos de https://archive.ics.uci.edu/ml/datasets/Credit+Approval
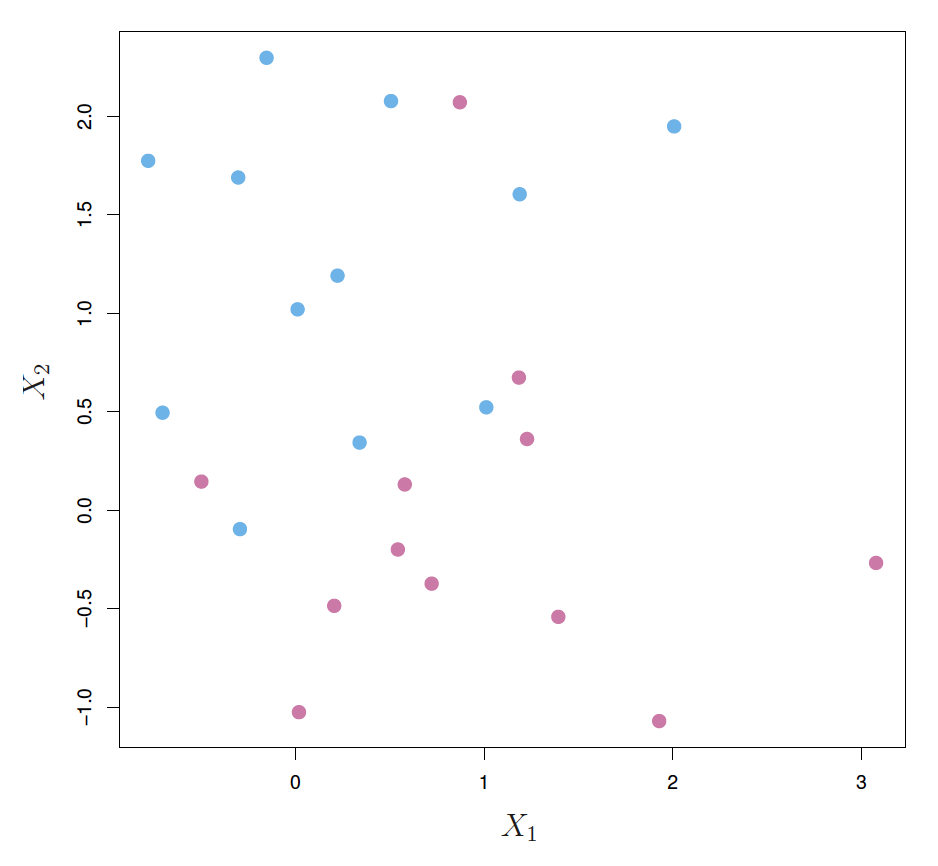
¿Son linealmente separables?
uu <- "https://raw.githubusercontent.com/vmoprojs/DataLectures/master/challengePredTrain.xlsx"
credAp <- rio::import(uu)
credAp$No. <- NULL
credAp$DPTO_Domicilio <- NULL
library(dplyr)
credAp = credAp %>% mutate(Ingreso = case_when(Ingreso<=1500~"B",
Ingreso<=50000~"A"))
# Identificamos factores:
VarsClass <- sapply(credAp,class)
credAp[which(VarsClass=="character")] <- lapply(credAp[which(VarsClass=="character")],factor)
library(caret)
vp <- 16
dummies <- dummyVars(~ ., data=credAp[,-vp])
c2 <- predict(dummies, credAp[,-vp])
d_credAp <- as.data.frame(cbind(credAp$Ingreso, c2))
names(d_credAp)[1] <- "Ingreso"set.seed(8519)
st <- sample(0:1, size = nrow(d_credAp),prob= c(0.7,.3),replace = TRUE)
train <- d_credAp[st==0,]
test <- d_credAp[st==1,]
plot(train[,c("EdadAnio","VarMax_3_4a18M")],col = (train[,"Ingreso"]))
library (e1071)
svmfit <- svm(factor(Ingreso)~., data=train , kernel ="linear", cost =5, scale = TRUE )\[ K(x_i,x_{i'}) =\sum_{j=1}^{p}x_{ij}x_{i'j} \]
Graficamos el resultado
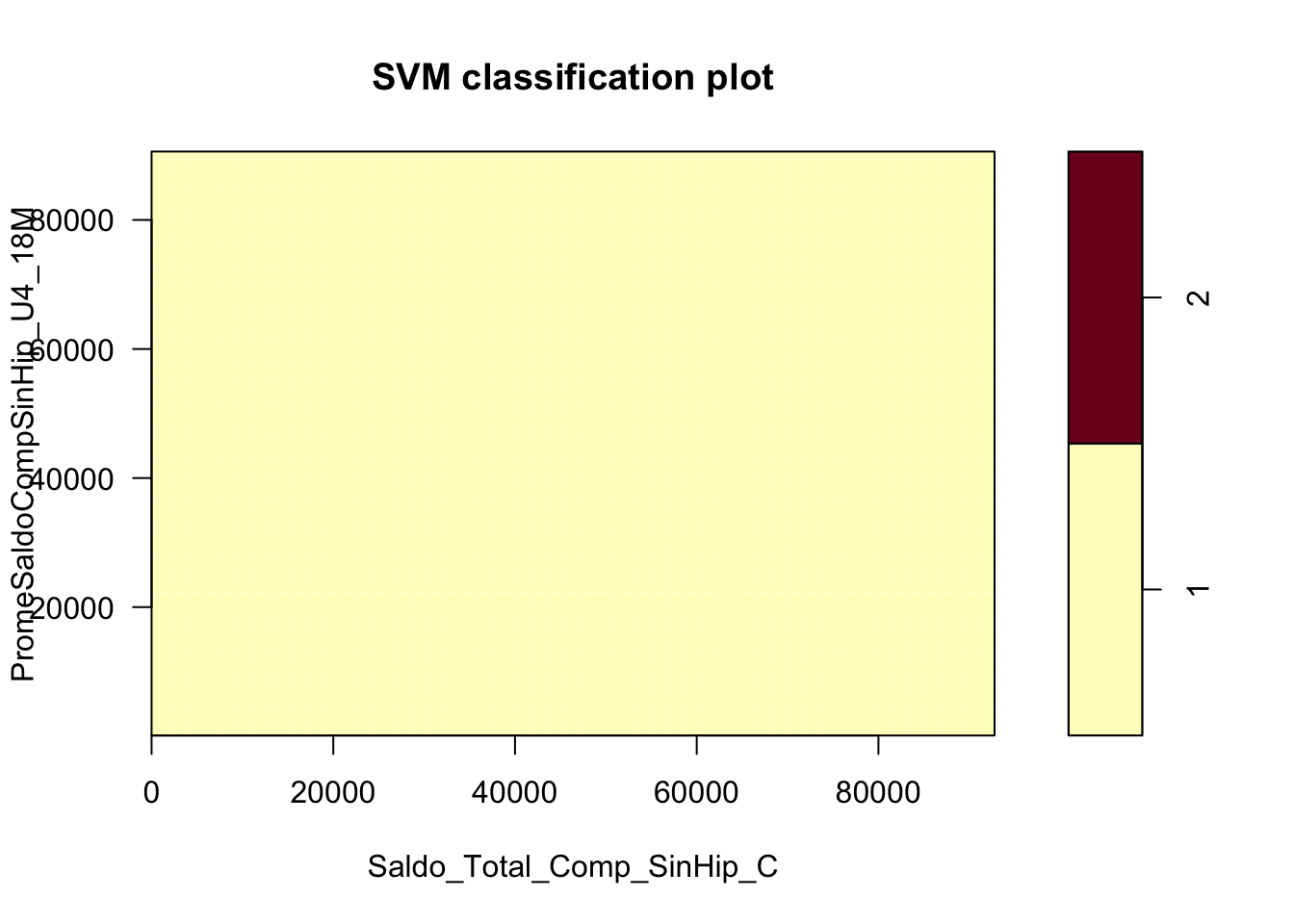
Vectores de soporte:
##
## Call:
## svm(formula = factor(Ingreso) ~ ., data = train, kernel = "linear", cost = 5, scale = TRUE)
##
##
## Parameters:
## SVM-Type: C-classification
## SVM-Kernel: linear
## cost: 5
##
## Number of Support Vectors: 1173
##
## ( 614 559 )
##
##
## Number of Classes: 2
##
## Levels:
## 1 2# ****** A "mano":
# "coefs" ya tiene la multiplicacion de la respuesta por los pesos, solo falta multiplicar por los vectores de soporte:
W <- t(svmfit$SV) %*% svmfit$coefs
# El intercepto:
b <- -svmfit$rho
# XW:
sol_manual <- as.matrix(cbind(1,scale(train[,-1]))) %*% cbind(c(b,W))
# Comparamos los resultados
table(sol_manual<0,(svmfit$fitted)) ##
## 1 2
## FALSE 1858 0
## TRUE 0 367Otro Kernel
\[ K(x_i,x_{i'}) = exp(-\gamma\sum_{j=1}^{p}(x_{ij}-x_{i'j})^2) \]
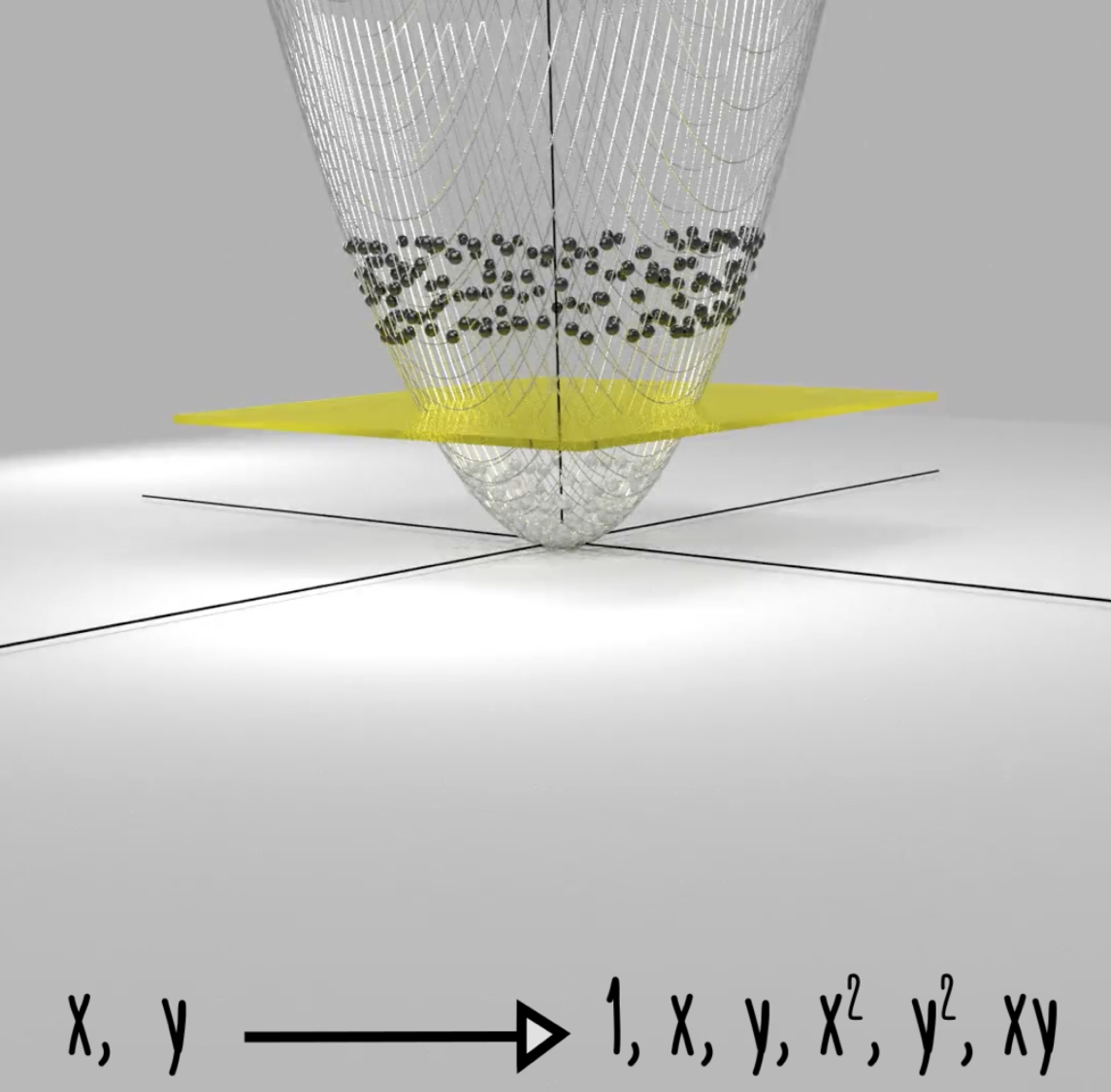
svmfitRad<- svm(factor(Ingreso)~., data=train , kernel ="radial", gamma = 1,cost =0.5,
scale = TRUE )
summary(svmfitRad)##
## Call:
## svm(formula = factor(Ingreso) ~ ., data = train, kernel = "radial", gamma = 1, cost = 0.5,
## scale = TRUE)
##
##
## Parameters:
## SVM-Type: C-classification
## SVM-Kernel: radial
## cost: 0.5
##
## Number of Support Vectors: 2074
##
## ( 1516 558 )
##
##
## Number of Classes: 2
##
## Levels:
## 1 2tune.outRad <- tune(svm ,factor(Ingreso) ~., data=train , kernel ="radial",ranges= list(cost=c(1,5,10 ) ))
bestmodRad = tune.outRad$best.model
summary ( bestmodRad )##
## Call:
## best.tune(METHOD = svm, train.x = factor(Ingreso) ~ ., data = train, ranges = list(cost = c(1,
## 5, 10)), kernel = "radial")
##
##
## Parameters:
## SVM-Type: C-classification
## SVM-Kernel: radial
## cost: 5
##
## Number of Support Vectors: 1189
##
## ( 689 500 )
##
##
## Number of Classes: 2
##
## Levels:
## 1 2ypredRad <- predict(bestmodRad, test)
tt <- table ( predict =ypredRad , truth = test$Ingreso)
caret::confusionMatrix(tt)## Confusion Matrix and Statistics
##
## truth
## predict 1 2
## 1 695 140
## 2 61 73
##
## Accuracy : 0.7926
## 95% CI : (0.7657, 0.8177)
## No Information Rate : 0.7802
## P-Value [Acc > NIR] : 0.1866
##
## Kappa : 0.3023
##
## Mcnemar's Test P-Value : 3.762e-08
##
## Sensitivity : 0.9193
## Specificity : 0.3427
## Pos Pred Value : 0.8323
## Neg Pred Value : 0.5448
## Prevalence : 0.7802
## Detection Rate : 0.7172
## Detection Prevalence : 0.8617
## Balanced Accuracy : 0.6310
##
## 'Positive' Class : 1
## 5.3.1 Ejercicio 1
Cambia el kernel a uno polinómico y compara los resultados. ¿Con qué modelo te quedas? (usa la Specificity como criterio de decisión)