9 GAM
Paquetes de esta sección
Proveen un marco general para extender el modelo linear estándar permitiéndo funciones no lineales para cada variable, conservando aditividad.
Tal como los modelos lineales, los modelos GAM pueden aplicarse a respuestas cuantitativas o cualitativas. Veremos un ejemplo en cada caso.
9.1 GAMs en regresión
Una forma de extnder el modelo de regresión lineal,
\[ y_i = \beta_0+\beta_1x_{i1}+\ldots+\beta_px_{ip}+\epsilon_i \]
para permitir relaciones no lineales entre cara caracerística y la respuesta es reemplazar cada componente lineal \(\beta_jx_{ij}\) con una función no lineal \(f_j(x_{ij})\) (suave). Podemos escribir el modelo como:
\[ y_i= \beta_0 + \sum_{j=1}^{p}f_j(x_{ij})+\epsilon_i \]
\[ = \beta_0 + f_1(x_{i1})+ f_2(x_{i2})+\cdots+f_p(x_{ip})\epsilon_i \]
Notemos que es aditivo porque podemos calcular funciones separadas para cada variable y luego agregar todas las contribuciones.
Lo que hemos revisado de polinomios locales puede usarse sin problema para especificar cada función.
9.1.1 Ejemplo
Ajustemos el modelo:
\[ wage = \beta_0 + f_1(year) + f_2(age) + f_3(education) + \epsilon \]
Cargamos y revisamos los datos:
## 'data.frame': 3000 obs. of 11 variables:
## $ year : int 2006 2004 2003 2003 2005 2008 2009 2008 2006 2004 ...
## $ age : int 18 24 45 43 50 54 44 30 41 52 ...
## $ maritl : Factor w/ 5 levels "1. Never Married",..: 1 1 2 2 4 2 2 1 1 2 ...
## $ race : Factor w/ 4 levels "1. White","2. Black",..: 1 1 1 3 1 1 4 3 2 1 ...
## $ education : Factor w/ 5 levels "1. < HS Grad",..: 1 4 3 4 2 4 3 3 3 2 ...
## $ region : Factor w/ 9 levels "1. New England",..: 2 2 2 2 2 2 2 2 2 2 ...
## $ jobclass : Factor w/ 2 levels "1. Industrial",..: 1 2 1 2 2 2 1 2 2 2 ...
## $ health : Factor w/ 2 levels "1. <=Good","2. >=Very Good": 1 2 1 2 1 2 2 1 2 2 ...
## $ health_ins: Factor w/ 2 levels "1. Yes","2. No": 2 2 1 1 1 1 1 1 1 1 ...
## $ logwage : num 4.32 4.26 4.88 5.04 4.32 ...
## $ wage : num 75 70.5 131 154.7 75 ...Ajustamos el modelo con splines naturales (cúbicos) para las dos primeras funciones y una constante para cada nivel de la tercera usando variables dicotómicas:
##
## Call:
## lm(formula = wage ~ ns(year, 4) + ns(age, 5) + education, data = Wage)
##
## Residuals:
## Min 1Q Median 3Q Max
## -120.513 -19.608 -3.583 14.112 214.535
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 46.949 4.704 9.980 < 2e-16 ***
## ns(year, 4)1 8.625 3.466 2.488 0.01289 *
## ns(year, 4)2 3.762 2.959 1.271 0.20369
## ns(year, 4)3 8.127 4.211 1.930 0.05375 .
## ns(year, 4)4 6.806 2.397 2.840 0.00455 **
## ns(age, 5)1 45.170 4.193 10.771 < 2e-16 ***
## ns(age, 5)2 38.450 5.076 7.575 4.78e-14 ***
## ns(age, 5)3 34.239 4.383 7.813 7.69e-15 ***
## ns(age, 5)4 48.678 10.572 4.605 4.31e-06 ***
## ns(age, 5)5 6.557 8.367 0.784 0.43328
## education2. HS Grad 10.983 2.430 4.520 6.43e-06 ***
## education3. Some College 23.473 2.562 9.163 < 2e-16 ***
## education4. College Grad 38.314 2.547 15.042 < 2e-16 ***
## education5. Advanced Degree 62.554 2.761 22.654 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 35.16 on 2986 degrees of freedom
## Multiple R-squared: 0.293, Adjusted R-squared: 0.2899
## F-statistic: 95.2 on 13 and 2986 DF, p-value: < 2.2e-16Vemos que el modelo es significativo. Veamos puntos de influencia:
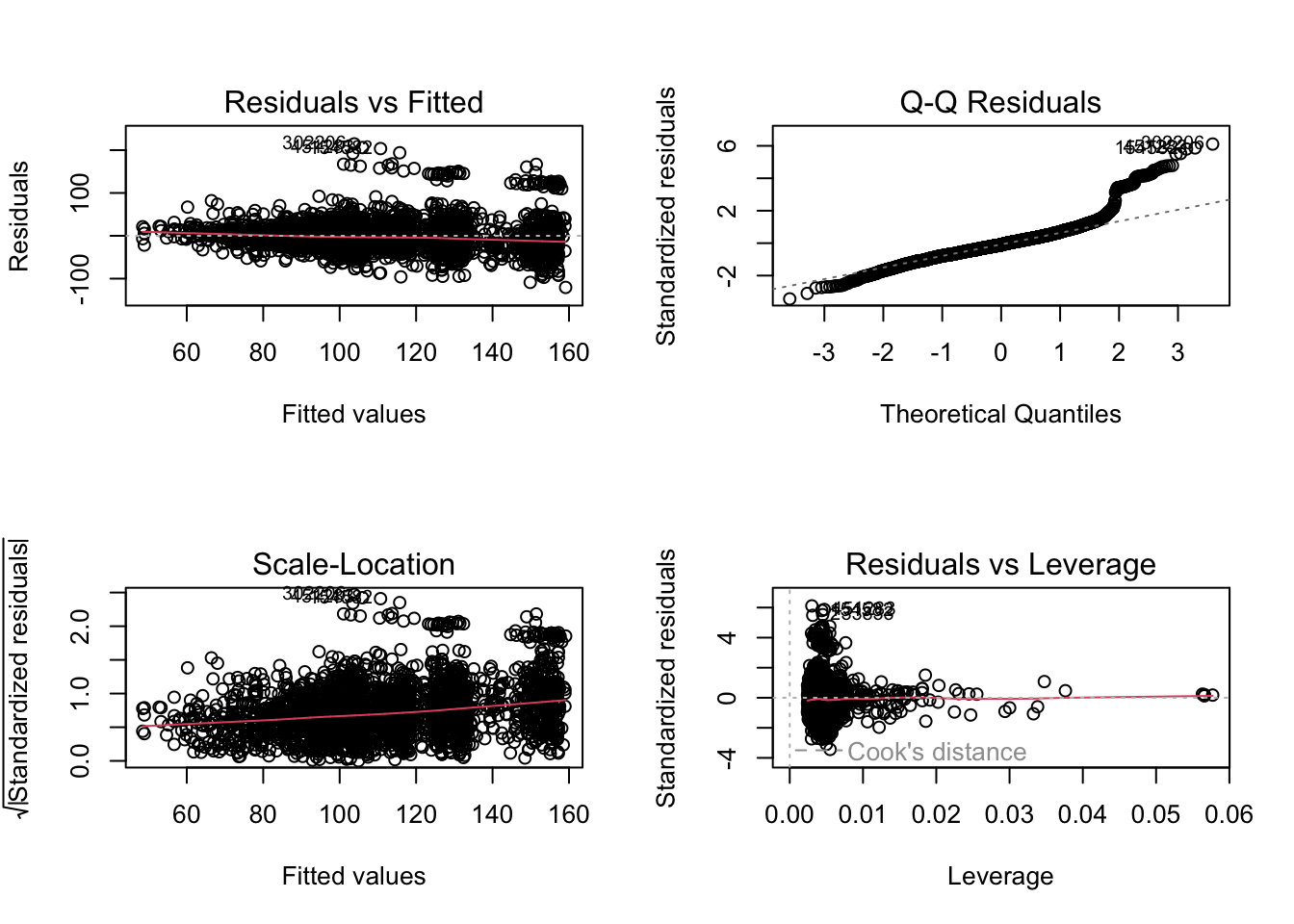
Ahora las relaciones entre las variables
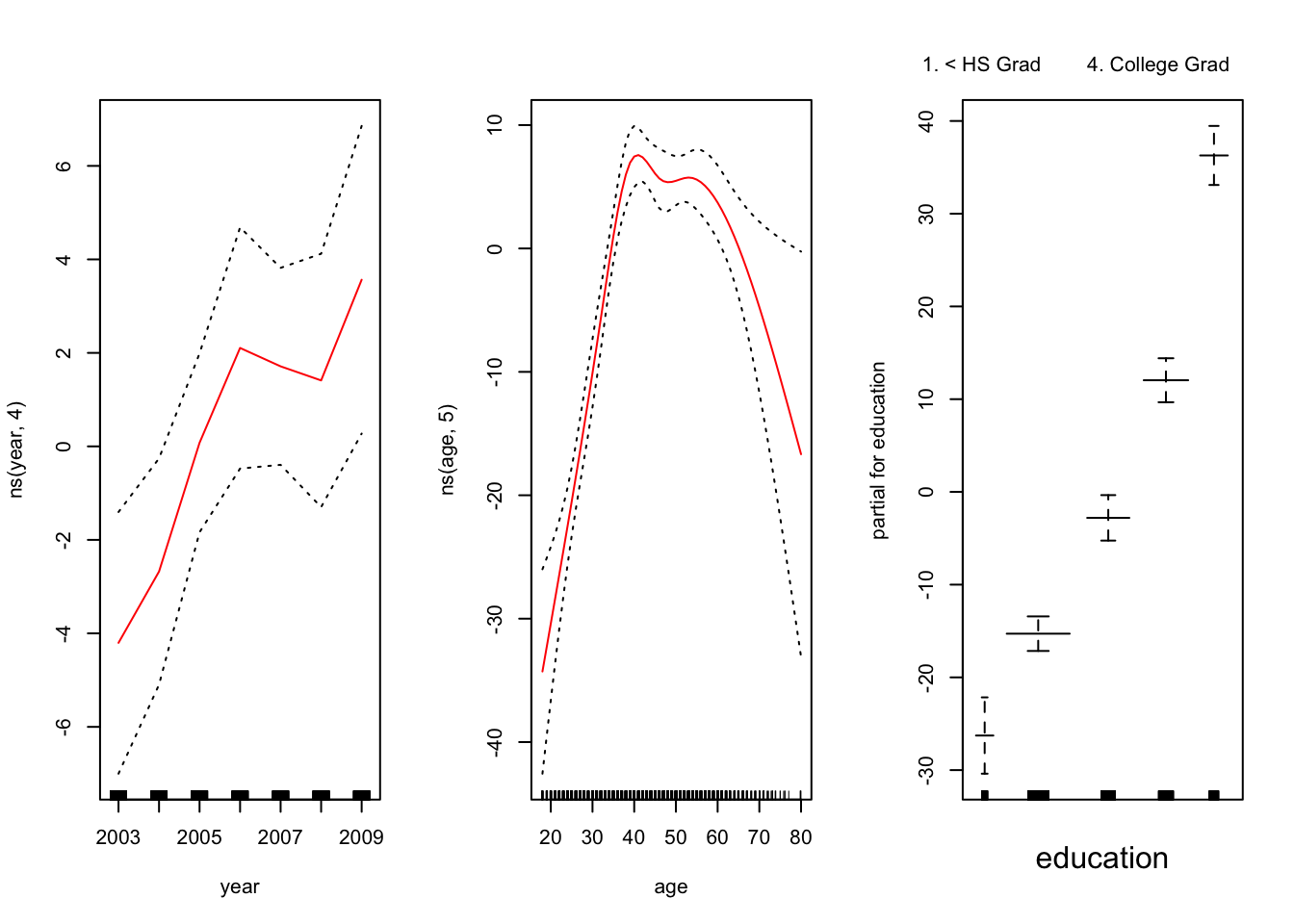
El panel de la izquierda indica que manteniendo la edad y la educación fijas, el salario tiende a aumentar ligeramente con el año; esto puede ser debido a la inflación.
El panel central indica que la educación y el año se mantienen fijos, el salario tiende a ser más alto para los valores intermedios de la edad, y más bajo para los muy jóvenes y muy viejos.
El panel de la derecha indica que el año y la edad se mantienen fijos, el salario tiende a aumentar con la educación: Cuanto más educada es una persona, mayor es su salario, en promedio. Todos estos hallazgos son intuitivos.
Backfitting: Este método se ajusta a un modelo que involucra múltiples predictores mediante la actualización repetida del ajuste para cada predictor de uno en uno, manteniendo los otros fijos. La belleza de este enfoque es que cada vez que actualizamos una función, simplemente aplicamos el método de ajuste para esa variable a un residuo parcial (\(r_i = y_i-f_1(x_{i1})-f_2(x_{i2})\)).
9.2 Ventajas y desventajas de los GAMs
Los GAM nos permiten ajustar un \(f_j\) no lineal en cada \(X_j\), de modo que podamos modelar automáticamente las relaciones no lineales que la regresión lineal estándar fallará. Esto significa que no necesitamos probar manualmente diferentes transformaciones en cada variable individualmente.
Los ajustes no lineales pueden potencialmente hacer predicciones más precisas para la respuesta Y.
Debido a que el modelo es aditivo, aún podemos examinar el efecto de cada \(X_j\) en \(Y\) individualmente mientras mantenemos todas las demás variables fijas. Por lo tanto, si estamos interesados en la inferencia, los GAM proporcionan una representación útil.
La suavidad de la función \(f_j\) para la variable \(X_j\) se puede resumir mediante grados de libertad.
La principal limitación de los GAM es que el modelo está restringido para ser aditivo. Con muchas variables, las interacciones importantes se pueden perder. Sin embargo, al igual que con la regresión lineal, podemos agregar manualmente términos de \(X_j\times X_k\). Además, podemos agregar funciones de interacción de baja dimensión de la forma \(f_{jk} (X_j, X_k)\) en el modelo; dichos términos pueden ajustarse utilizando suavizadores bidimensionales, como la regresión local, o splines bidimensionales (no se tratan aquí).
9.3 GAMS en clasificación
También se pueden usar cuando la respuesta es cualitativa. Se asume que \(Y\) toma valores cero o uno, y sea \(p(X) = Pr(Y = 1|X)\) la probabilidad condicional dado los preditores de que \(Y\) sea \(1\). Recodemos el modelo logístico:
\[ log\left(\frac{p(X)}{1-p(X)}\right) = \beta_0+\beta_1X_1+\cdots+\beta_pX_p \]
El logit es el logaritmo de los odds de \(Pr(Y = 1|X)\) vs \(Pr(Y = 0|X)\) que se representa como una función lineal de los predictores en la ecuación anterior.
Se puede extender usando relaciones no lineales de los predictores.
\[ log\left(\frac{p(X)}{1-p(X)}\right) = \beta_0+f_1(X_1)+\cdots+f_p(X_p) \]
Esta ecuación representa un modelo GAM logístico.
9.3.1 Ejemplo
Ajustamos un GAM a los datos de Salario para predecir la probabilidad de que los ingresos de una persona superen los \(\$250,000\) por año. El GAM que ajustamos toma la forma.
\[ log\left(\frac{p(X)}{1-p(X)}\right) = \beta_0+\beta_1\texttt{year}+f_1(\texttt{age})+f_3(\texttt{education}) \]
donde
\[ p(X)=Pr(\texttt{wage}>250|\texttt{year,age,education}) \]
gam.lr <- gam(I(wage > 250) ~ year + s(age, df = 5) + education,
family = binomial, data = Wage)
summary(gam.lr)##
## Call: gam(formula = I(wage > 250) ~ year + s(age, df = 5) + education,
## family = binomial, data = Wage)
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -0.58206 -0.26780 -0.12341 -0.08241 3.31242
##
## (Dispersion Parameter for binomial family taken to be 1)
##
## Null Deviance: 730.5345 on 2999 degrees of freedom
## Residual Deviance: 602.4588 on 2989 degrees of freedom
## AIC: 624.4586
##
## Number of Local Scoring Iterations: NA
##
## Anova for Parametric Effects
## Df Sum Sq Mean Sq F value Pr(>F)
## year 1 0.48 0.4845 0.5995 0.43883
## s(age, df = 5) 1 3.83 3.8262 4.7345 0.02964 *
## education 4 65.81 16.4514 20.3569 < 2e-16 ***
## Residuals 2989 2415.55 0.8081
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Anova for Nonparametric Effects
## Npar Df Npar Chisq P(Chi)
## (Intercept)
## year
## s(age, df = 5) 4 10.364 0.03472 *
## education
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Veamos las relaciones entre las variables:
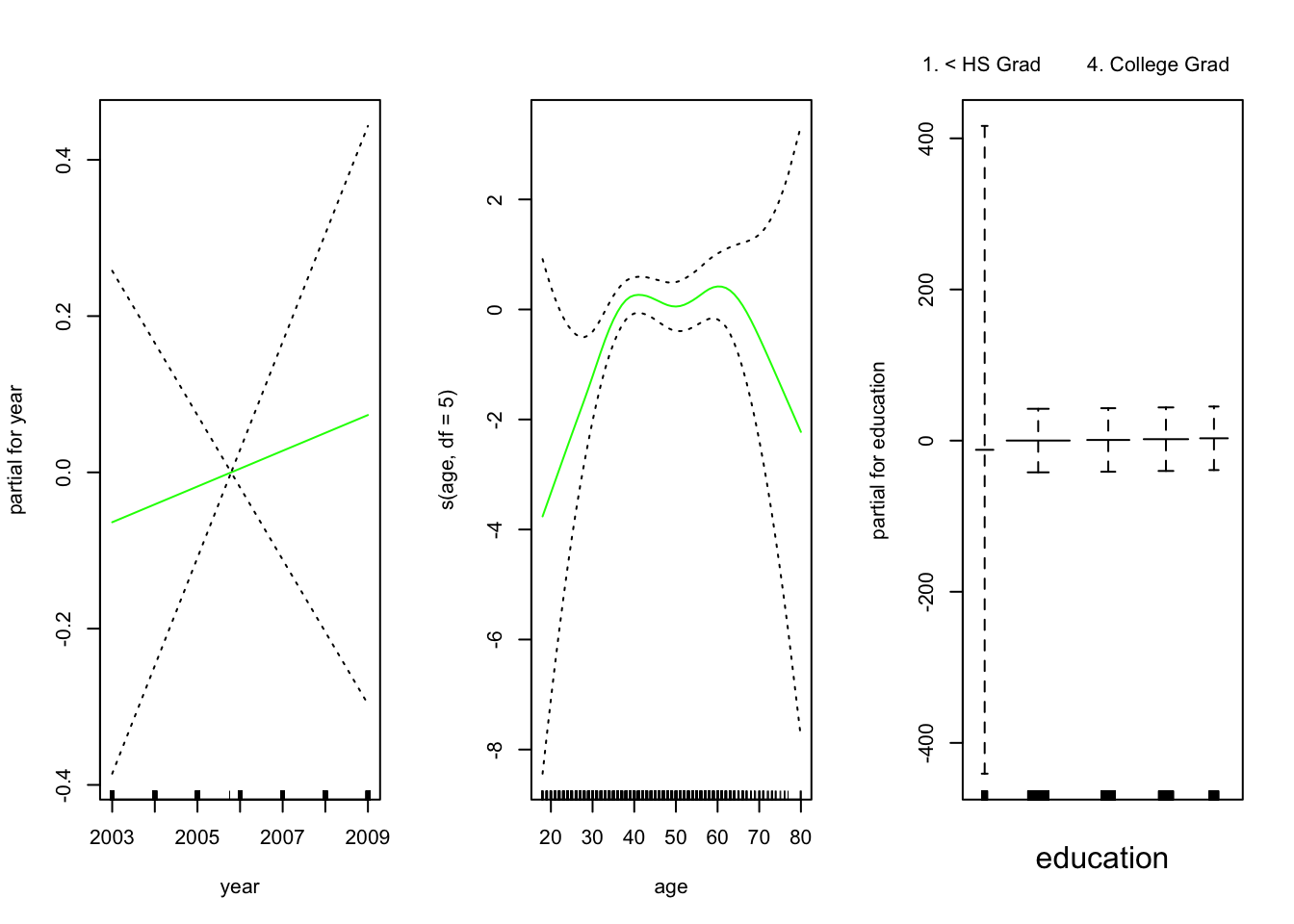
El ajuste resultante se muestra en la figura. El último panel parece sospechoso, con intervalos de confianza muy amplios para el nivel <HS, veamos
##
## education FALSE TRUE
## 1. < HS Grad 268 0
## 2. HS Grad 966 5
## 3. Some College 643 7
## 4. College Grad 663 22
## 5. Advanced Degree 381 45No hay unos para esa categoría: ningún individuo con menos de una educación secundaria gana más de $ 250, 000 por año. Re ajustamos el modelo:
gam.lr.s <- gam(I(wage > 250) ~ year + s(age, df = 5) + education,
family = binomial, data = Wage,
subset = (education != "1. < HS Grad"))
summary(gam.lr.s)##
## Call: gam(formula = I(wage > 250) ~ year + s(age, df = 5) + education,
## family = binomial, data = Wage, subset = (education != "1. < HS Grad"))
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -0.5821 -0.2760 -0.1415 -0.1072 3.3124
##
## (Dispersion Parameter for binomial family taken to be 1)
##
## Null Deviance: 715.5412 on 2731 degrees of freedom
## Residual Deviance: 602.4588 on 2722 degrees of freedom
## AIC: 622.4586
##
## Number of Local Scoring Iterations: NA
##
## Anova for Parametric Effects
## Df Sum Sq Mean Sq F value Pr(>F)
## year 1 0.48 0.4845 0.5459 0.46004
## s(age, df = 5) 1 3.83 3.8262 4.3116 0.03795 *
## education 3 65.80 21.9339 24.7166 8.933e-16 ***
## Residuals 2722 2415.55 0.8874
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Anova for Nonparametric Effects
## Npar Df Npar Chisq P(Chi)
## (Intercept)
## year
## s(age, df = 5) 4 10.364 0.03472 *
## education
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Evaluemos los resultados:
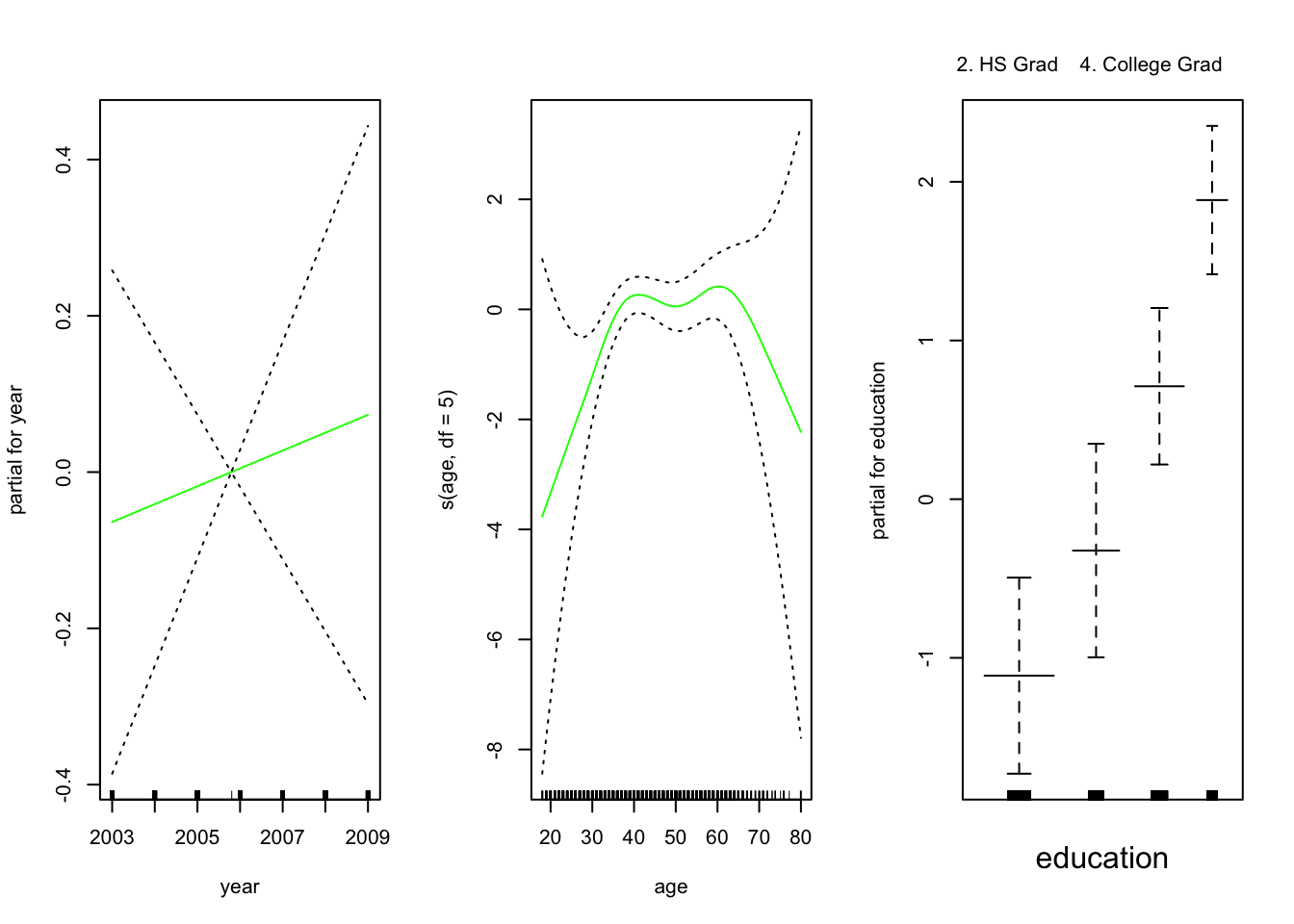
Los tres paneles tienen la misma escala vertical. Esto nos permite evaluar visualmente las contribuciones relativas de cada una de las variables. Observamos que la edad y la educación tienen un efecto mucho mayor que el año en la probabilidad de ser una fuente de ingresos elevada.