16 Conglomerados jerárquicos
El agrupamiento jerárquico es un enfoque alternativo que no requiere que nos comprometamos con una elección particular de \(K\).
El agrupamiento jerárquico tiene una ventaja adicional sobre el agrupamiento de \(K\)-medias en que da como resultado una representación atractiva basada en árboles de las observaciones, llamado dendrograma.
Veremos el enfoque aglomerativo que se construye partiendo de las hojas y combinando ramas hasta el tronco.
16.1 Interpretación
Cada hoja del dendrograma representa una de las \(n\) observaciones.
A medida que subimos por el árbol, algunas hojas comienzan a fusionarse en ramas. Estos corresponden a observaciones que son similares entre sí.
Cuanto antes (más abajo en el árbol) se produzcan fusiones, más similares serán los grupos de observaciones entre sí. Por otro lado, las observaciones que se fusionan más tarde (cerca de la parte superior del árbol) pueden ser bastante diferentes.
La altura de esta fusión, medida en el eje vertical, indica cuán diferentes son las dos observaciones. Por lo tanto, las observaciones que se fusionan en la parte inferior del árbol son bastante similares entre sí, mientras que las observaciones que se fusionan cerca de la parte superior del árbol tenderán a ser bastante diferentes.
16.2 Algoritmo
Comenzar con \(n\) observaciones y una medida (como la distancia euclidiana) de todas las \(n (n − 1)/2\) disimilitudes por pares. Trate cada observación como su propio grupo.
Para \(i=n,n-1,\ldots,2\):
2.1. Examinar todas las diferencias entre grupos por pares entre los \(i\) grupos e identificar el par de grupos que son menos diferentes (es decir, más similares). Fusiona estos dos grupos. La diferencia entre estos dos grupos indica la altura en el dendrograma a la que debe colocarse la fusión.
2.2 Calcule las nuevas diferencias entre grupos por pares entre los \(i - 1\) grupos restantes.
16.2.1 Funciones para fusionar grupos
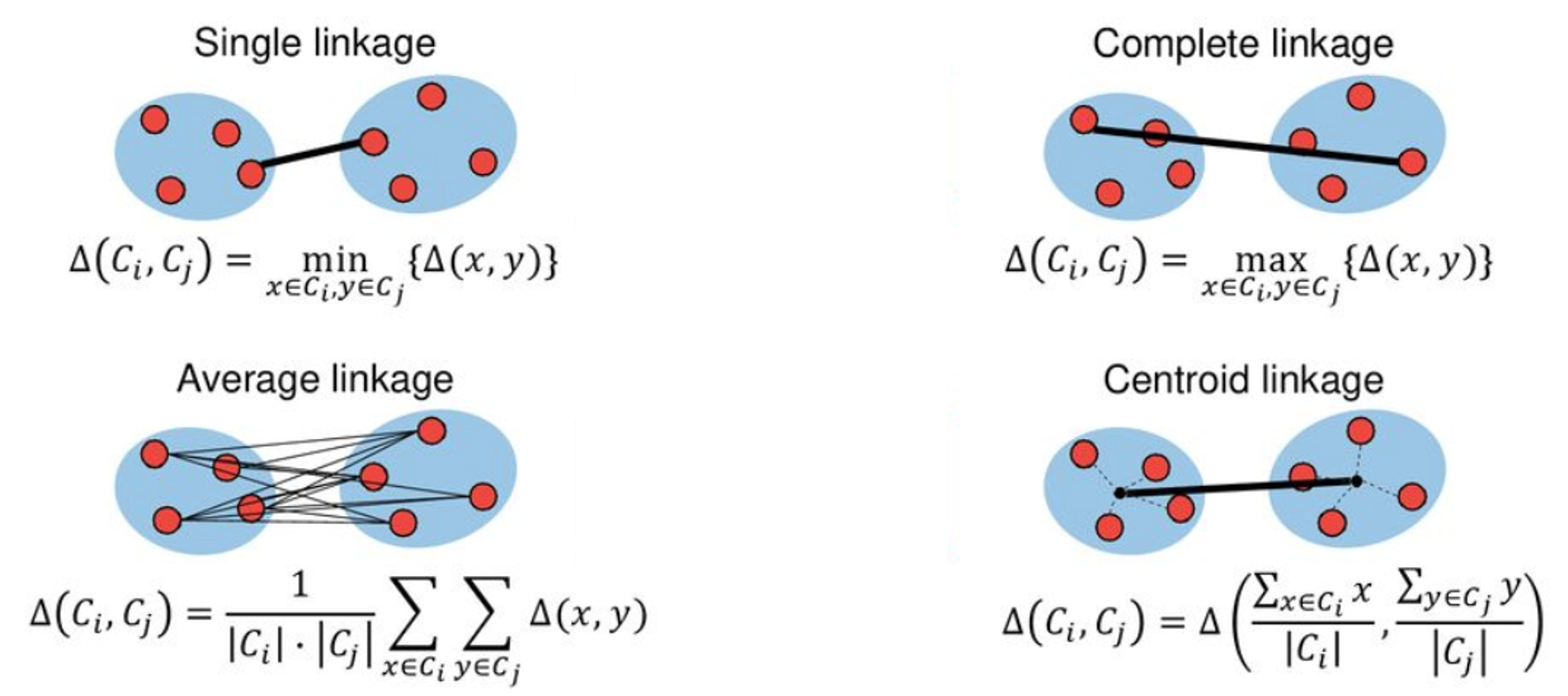
Complete: Disimilitud máxima entre conglomerados. Calcule todas las diferencias por pares entre las observaciones en el grupo \(A\) y las observaciones en el grupo \(B\), y registre la mayor de estas diferencias.
Single: Disimilitud mínima entre conglomerados. Calcule todas las diferencias por pares entre las observaciones en el grupo \(A\) y las observaciones en el grupo \(B\), y registre la más pequeña de estas diferencias. El enlace único puede dar como resultado conglomerados extendidos y finales en los que las observaciones individuales se fusionan una a la vez.
Average: Diferencia media entre grupos. Calcule todas las diferencias por pares entre las observaciones en el grupo \(A\) y las observaciones en el grupo \(B\), y registre el promedio de estas diferencias.
Centroid: Disimilitud entre el centroide para el grupo \(A\) (un vector de medias de longitud \(p\)) y el centroide para el grupo \(B\).
x = crime_s
hc.complete <- hclust(dist(x), method = "complete")
hc.average <- hclust ( dist (x), method = "average")
hc.single <- hclust ( dist (x), method = "single")par ( mfrow = c(1, 3))
plot (hc.complete,main = "Complete Linkage", xlab = "", sub = "", cex = .9)
plot (hc.average,main = "Average Linkage",xlab = "", sub = "", cex = .9)
plot (hc.single , main = "Single Linkage",xlab = "", sub = "", cex = .9)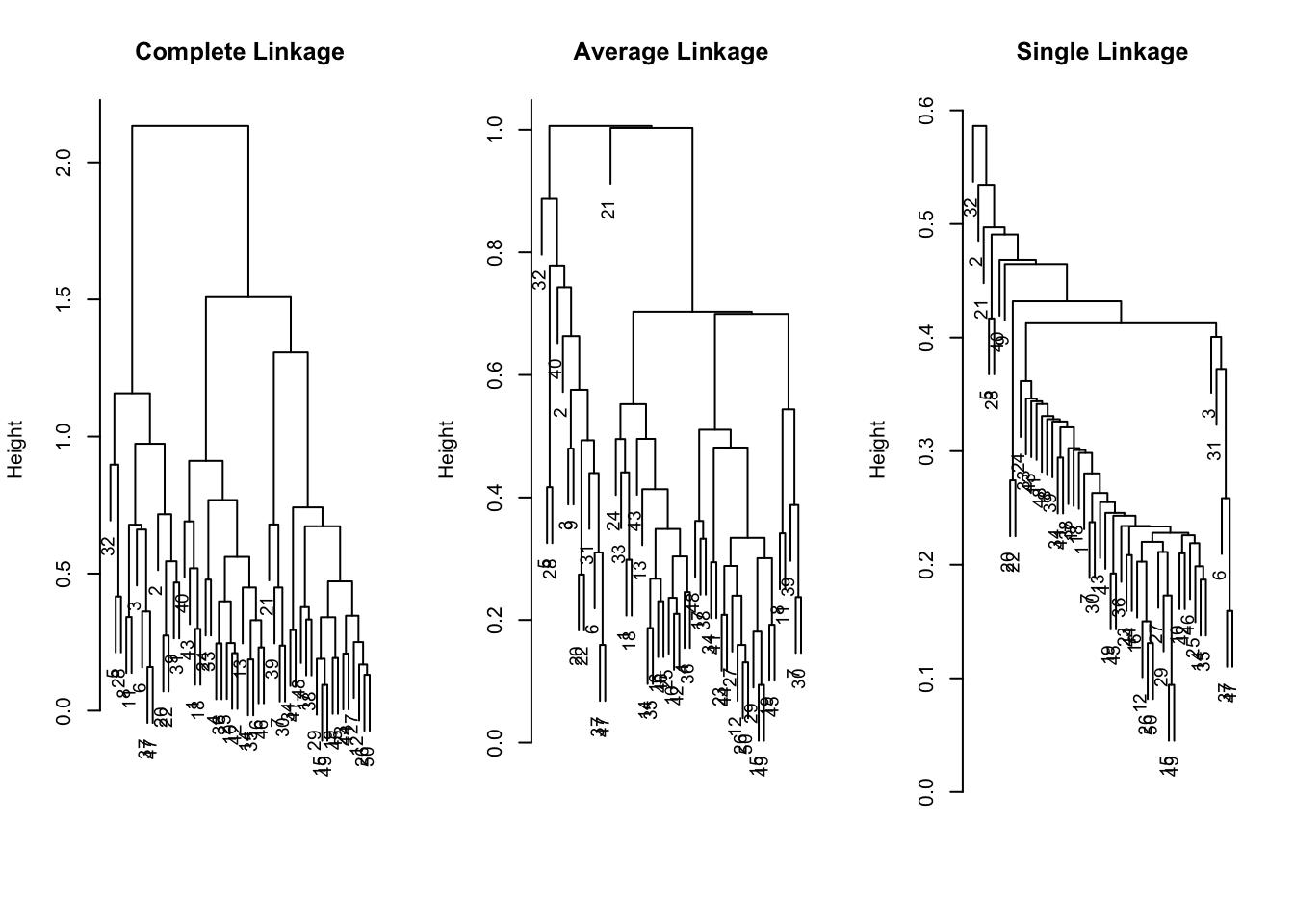
Para determinar las etiquetas de grupo para cada observación asociada con un corte dado del dendrograma, podemos usar la función cutree():
## [1] 1 2 2 1 2 2 1 2 2 1 2 1 1 1 1 1 1 1 1 2 1 2 1 1 1 1 1 2 1 1 2 2 1 1 1 1
## [37] 2 1 1 1 1 1 1 1 1 1 2 1 1 1## [1] 1 2 2 1 2 2 1 1 2 1 1 1 1 1 1 1 1 1 1 2 1 2 1 1 1 1 1 2 1 1 2 2 1 1 1 1
## [37] 2 1 1 2 1 1 1 1 1 1 2 1 1 1## [1] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 1 1 1
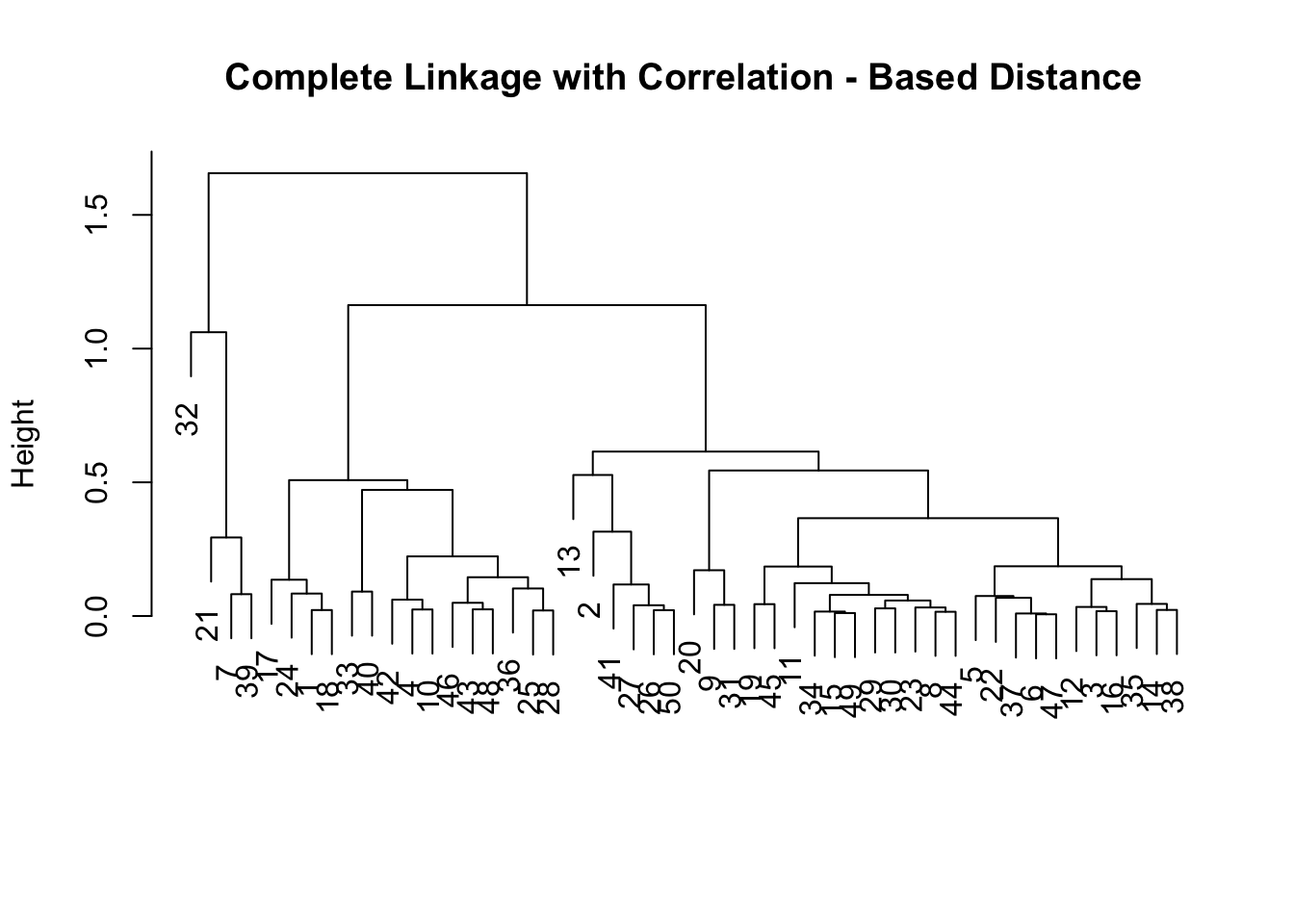
## [37] 1 1 1 1 1 1 1 1 1 1 1 1 1 1Se puede aplicar este método en el contexto de buscar conglomerados por filas. En nuestro ejemplo, se encontrarían dominios geográficos con más tendencia a ciertos crímenes (también se aplicar cuando se tiene datos de compras de clientes en diferentes ítems, en ese contexto la distancia basada en correlación revelaría clientes con preferencias similares).
La distancia basada en correlación se puede calcular usando la función as.dist(), que convierte una matriz simétrica cuadrada arbitraria en una forma que la función hclust() reconoce como una matriz de distancia.
dd <- as.dist (1 - cor (t(x)))
plot(hclust (dd , method = "complete"), main = " Complete Linkage with Correlation - Based Distance ",xlab = "", sub = "")