A Estadística descriptiva & distribuciones de probabilidad
¿Qué relación tienen Charles Darwin, Francis Galton y Karl Pearson?



Charles Darwin (1809-1882), Fracis Galton (1822-1911), Karl Pearson (1857-1936)
Galton nace en Birmingham (Inglaterra). Viaja por el mundo realizando estudios en geografía y en 1850 se le otorga la medalla de oro de la Royal Geographical Society.
Influenciado por su primo, Charles Darwin, dedica la segunda parte de su vida a probar la teoría de la evolución
Detectó que padres de estatura pequeña tenían hijos ligeramente más altos y que padres altos tenían hijos ligeramente más bajos. De ahí la palabra regresión (Gorroochurn (2016)).
A.1 ¿Qué es la estadística?
- El siglo XIX es el punto de encuentro entre dos disciplinas que evolucionaron independientemente: el cálculo de probabilidades o teoría matemática de los juegos de azar (derivada del vocablo árabe al zhar, que signigica dado), que nace en el siglo XVII y la Estadística (o ciencia del Estado, del latín Status).
La Estadística es la ciencia cuyo objetivo es reunir una información cuantitativa concerniente a individuos, grupos, series de hechos, etc. y deducir de ello, gracias al análisis de estos datos, unos significados precisos o unas previsiones para el futuro (Galindo (2015))
A.1.1 Clasificación
La Estadística Descriptiva o Análisis Exporatorio de Datos, resume y describe datos a través de la presentación de información en forma de tablas y gráficos.
La Estadística Inferencial: va más allá de los datos. Trata, a partir de una muestra, determinar características de una población objetivo de investigación.
A.1.2 Definiciones básicas
Unidad muestral o experimental: Una unidad es una persona, animal, planta o cosa que es examinada por un investigador; es el objeto básico sobre el cual el estudio o experimento se lleva a cabo.
Población o universo: Es una colección completa de personas, animales, plantas o cosas, con el objeto de obtener conclusiones sobre la población de la cual proviene.
Muestra: Es un grupo de unidades seleccionadas de la población de acuerdo con un plan o regla, con el objeto de obtener conlusiones sobre la población de la cual proviene.
Tamaño muestral: número de unidades que constituyen la muestra.
A.1.3 Ejemplos (¿Cuál es la población? ¿Cuál es la unidad muestral?):
- La dueña de un almacén desea estimar el gasto medio de compra de sus clientes en su almacén en el último año.
- En un estudio se desea conocer el rating de sintonía de los canales de televisión de una ciudad.
A.1.4 Datos y escalas de medición
A.1.4.1 Números índice
- Simple
\[ I_{0}^{t}(X) = \frac{X_t}{X_0}100 \]
- En cadena
\[ IC^{t}(X) = \frac{X_t}{X_{t-1}}100 \]
- Tasa de variación
\[ Tasa_{t_1}^{t_2}(X) = \frac{X_{t_2}-X_{t_1}}{X_{t_1}} \]
- Tasa media de variación (entre \([t,t+k]\))
\[ T_k = \left(\sqrt[k]{\frac{X_{t+k}}{X_t}-1}\right)100 \]
A.1.5 Tipos de variables
Variable estadística: Es una característica de los individuos que puede ser observada o medida.
¿Qué es un dato? medición o valor de una variable estadística.
Cualitativas (descriptivas o categóricas): comprenden etiquetas o nombres que se usan para identificar un atributo de cada elemento. Ejemplos: sexo, profesión, marca de ropa.
Cuantitativas (numéricas): Describen características medibles. Ejemplos: número de hijos, número de páginas de un libro.
Discretas: son discretas si sus valores pueden ser contados (pertenecen a los números enteros). Ejemplo: clientes que entran a un almacén, número de errores ortográficos.
Continuas: sus valores pueden tomar cualquier valor en un intervalo considerado (pertenecen a los números reales). Ejemplos: edad, perso, talla.
A.1.6 Escalas de medición
La medición es el proceso de asignar un valor a una variable de un elemento de observación. Este proceso usa diferentes escalas:
Nominal: a los datos se les puede asignar un código, en la forma de un número, donde los números son simplemente una etiqueta. Únicamente pueden ser contados, no pueden ser ordenados ni medidos. Ejemplo: sexo, estado civil.
Ordinal: si a los datos se les puede asociar un orden o asociar una escala. Pueden ser contados y ordenados, pero no pueden ser medidos. Ejemplo: escalas de películas, del 1 al 5.
Intervalo: si los datos pueden tomar cualquier valor dentro de un intervalo finito o infinito, existe un cero relativo. Pueden ser contados y ordenados; son válidas la suma y la resta, la multiplicación y la división. Ejemplos: temperatura (cero no significa ausencia de temperatura). Puntajes en pruebas (cero no significa que no sabe nada).
Razón: si los datos pueden tomar cualquier valor dentro de un intervalo finito o infinito, existe un cero absoluto. Pueden ser contados y ordenados; son válidas la suma, resta, multiplicación y división. Ejemplos: estatura, velocidad, edad.
A.2 Características de los datos
Localización: es la posición relativa que presentan un conjunto de datos. En general, se mide por el punto medio del conjunto de datos.
Dispersión: Los valores obtenidos en una muestra no son todos iguales. La variación entre estos valores se denomina dispersión. Se trata de detectar el grado de discrepancia entre los datos individuales al rededor del centro de las observaciones.
Simetría y asimetría: Son simétricos cuando los datos están distribuidos de la misma manera sobre y debajo del punto medio. En los asimétricos hay más agrupamiento de un lado del punto medio.
A.3 Distribución de frecuencias
Es la agrupación de datos en categorías mutuamente excluyentes que indican el número de observaciones en cada categoría. Esto proporciona un valor añadido a la agrupación de datos. La distribución de frecuencias presenta las observaciones clasificadas de modo que se pueda ver el número existente en cada clase.
Se puede elaborar una tabla de frecuencias para datos nominales y ordinales. Si los datos son continuos, ¿Qué debemos hacer?
A.3.1 Elaboración de una tabla de frecuencias
Supongamos que tenemos un conjunto de \(n\) datos, que toman \(k\) valores distintos: \(x_1,x_2,,\ldots,x_k\).
Se ordena los \(x_i\) datos en una columna de forma ascendente y se cuenta cuántas veces aparece cada valor, ésta es su frecuencia absoluta \(n_i\) que se coloca en una columna contigua. Note que \(\sum_{i=1}^{k}n_i=n\).
Una tercera columna tiene la frecuencia relativa \(f\) que resulta de \(f_i = \frac{n_i}{n}\). Note que verse como un porcentaje.
Se pueden agregar dos columnas más, de las frecuencias acumuladas absoluta y relativa respectivamente.
Es decir:
| Valor de la variable (\(x_i\)) | Frec. Absoluta (\(n_i\)) | Frec. Relativa (\(f_i = \frac{n_i}{n}\)) | Fre. Abs. Acumulada (\(N_i\)) | Frec. Rel. Acumulada (\(F_i\)) |
|---|---|---|---|---|
| \(x_1\) | \(n_1\) | \(f_1\) | \(N_1 = n_1\) | \(F_1=f_1\) |
| \(x_2\) | \(n_2\) | \(f_2\) | \(N_2 = N_1+n_2\) | \(F_2 = F_1+f_2\) |
| \(\vdots\) | \(\vdots\) | \(\vdots\) | \(\vdots\) | \(\vdots\) |
| \(x_k\) | \(n_k\) | \(f_k\) | \(N_k = N_{k-1}+n_k\) | \(F_k = F_{k-1}+f_k\) |
| TOTAL | n | 1 |
Ejemplo para variable discreta y continua
A.4 Representaciones gráficas de los datos
A.4.1 Gráfico de sectores y de barras
Ambos suelen usarse para representar gráficamente datos nominales u ordinales.
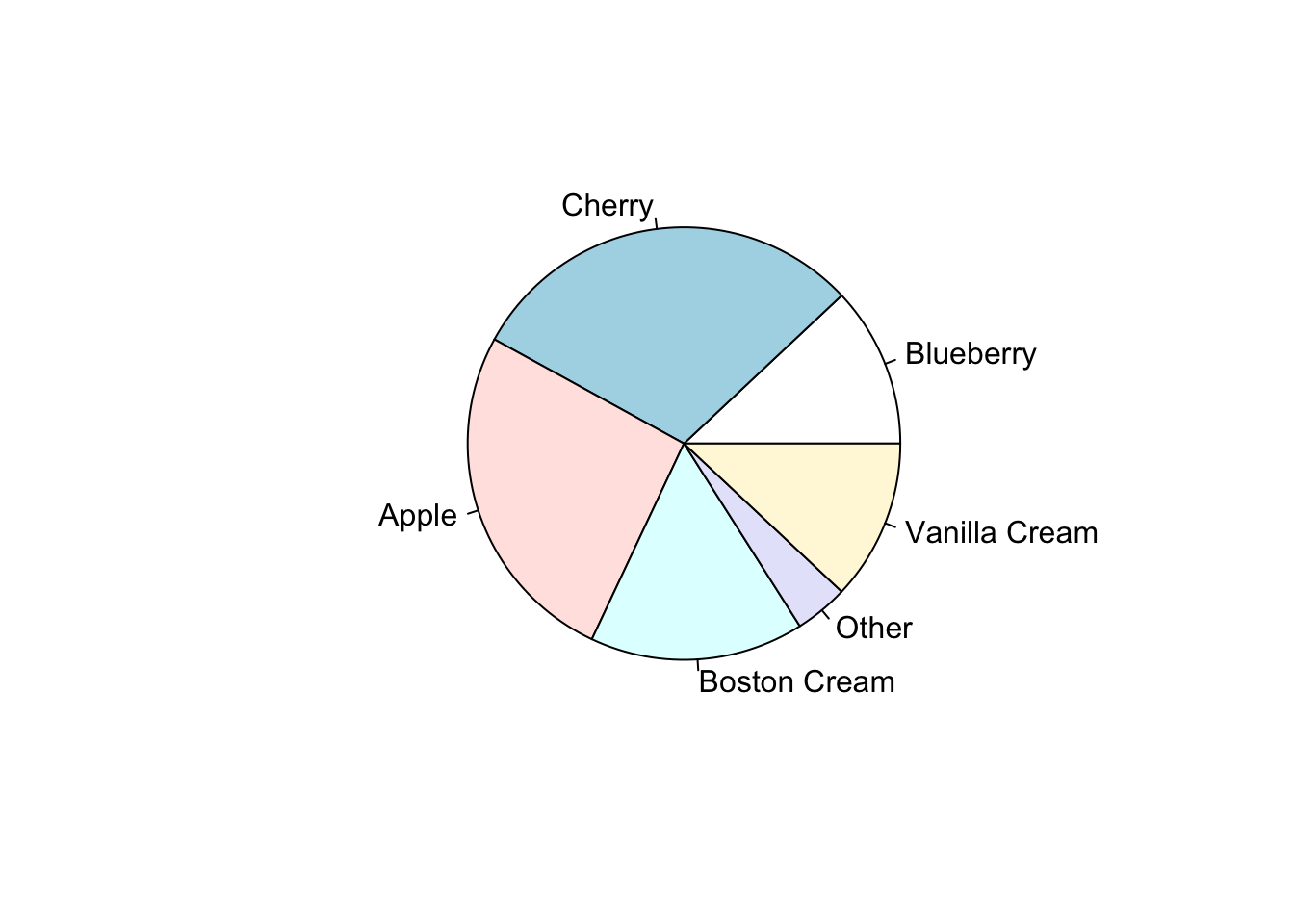
- El gráfico de sectores (pastel) es un círculo dividido en segmentos donde cada uno de los sectores es proporcional a la frecuencia relativa de esa categoría.
- El gráfico de barras se muestra mediante recángulos del mismo ancho, cada uno de los cuales representa una categoría. La longitud (y por tanto el área) de cada uno es proporcional al número de casos que representa.
Si la variable tiene orden, se respecta en el gráfico.Pueden darse como filas o columnas.
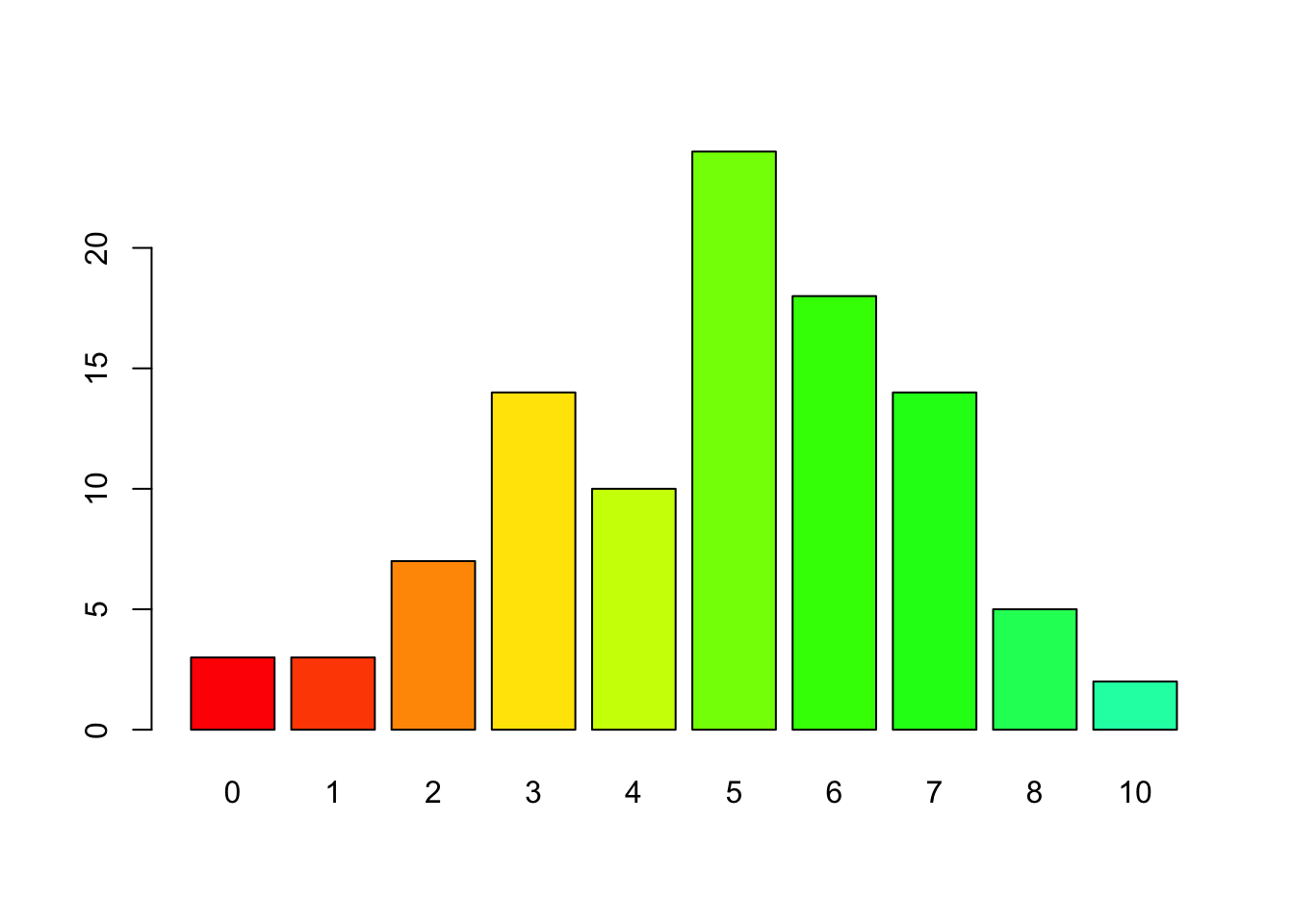
Ejemplo: representar los siguientes datos como gráfico de sectores y barras:
## Marca N.Respuestas Porcentaje
## 1 Toshiba 135 42
## 2 Dell 76 23
## 3 HP 53 16
## 4 Lenovo 43 13
## 5 No sabe 19 6A.5 Medidas de locación
Ante un conjunto de observaciones, es de interés el valor en torno al cual se agrupan la mayoría o el centro del conjunto. Las medidas que permiten hacerlo se llaman medidas de localización o medidas de tendencia central.
A.5.1 Media
Promedio o media: notado como \(\bar{x}\), de un conjunto de \(n\) datos \(x_1,x_2,\ldots,x_n\) es igual a la suma de valores dividido para \(n\).
\[ \bar{x} = \frac{x_1+x_2+\ldots+x_n}{n}=\frac{\sum_{i=1}^nx_i}{n} \]
- Si las observaciones están agrupadas en una tabla de frecuencia de datos individuales de \(k\) valores, el promedio se calcula
\[ \bar{x} =\frac{\sum_{i=1}^kn_ix_i}{n} \] donde \(n = {\sum_{i=1}^kn_i}\).
- Si las observaciones están agrupadas en una tabla de frecuencias agrupadas por clases, se calcula el punto promedio de cada clase \(x_i = \frac{l_i+s_i}{2}\) (\(i = 1,2,\ldots,k\)), donde \(l_i\) y \(s_i\) son la cota inferior y superor de cada clase respectivamente. El promedio es
\[ \bar{x} =\frac{\sum_{i=1}^kn_ix_i}{n} \]
Ventajas y desventajas del promedio:
- Se expresan en las mismas unidades quela variable
- En su cálculo intervienen todos los valores de la distribución
- Es el centro de gravedad de toda la distribución
- Es único
- Su principal inconveniente es que se ve afectado por valores atípicos
A.5.2 Mediana
La mediana de un conjunto de datos \(x_1+x_2+\ldots+x_n\) es el valor que se encuentra en el punto medio, cuando se ordenan los valores de menor a mayor.
Se nota como \(Q_2\) o Med y tiene la propiedad de que a cada lado se encuentra el 50% de los datos.
Si los datos están están resumidos en una tabla de distribución de frecuencias por clases:
\[ Med = L_{i-1}+\frac{n/2-N_{i-1}}{n_i}A \]
Ejemplo:
| Ingreso anual | Numero de personas (\(n_i\)) | Frecuencia acumulada (\(N_i\)) |
|---|---|---|
| 6800-8000 | 3 | 3 |
| 8000-10400 | 20 | 23 |
| 10400-12800 | 35 | 58 |
| 12800-16500 | 25 | 83 |
| 16500-20000 | 15 | 98 |
| 20000-26000 | 2 | 100 |
\[ Med = 10400+\frac{100/2-23}{35}(2400) = 12251 \]
A.5.3 Moda
Es el valor que tiene la mayor frecuencia absoluta
Se la nota como Mo. Para calcularla es últil realizar una tabla de frecuencia de los datos.
Si los datos están están resumidos en una tabla de distribución de frecuencias por clases:
\[ Mo = L_{i-1}+\frac{d1}{d1+d2}A \]
Usando los datos de la tabla anterior:
\[ Mo = 10400+\frac{35-20}{(35-20)+(35-25)}2400=11840 \]
A.5.4 Media geométrica
Notada como \(\bar{MG}\) de un conjunto de \(n\) mediciones \(x_1+x_2+\ldots+x_n\), es igual a la raíz enésima de su producto. Es decir,
\[ \bar{MG} = (x_1\times x_2\times\ldots\times x_n)^{1/n} \]
Si las observaciones están agrupadas en una tabla de frecuencias de datos individuales,
\[ \bar{MG} = (x_1^{n_1}\times x_2^{n_2}\times\ldots\times x_k^{n_k})^{1/n} \]
Si los datos están agrupados por clases, el cáculo es el mismo anterior, pero \(x_i\) es el punto medio de la clase.
Tiene las mismas ventajas de la media, pero
- Es menos sensible a datos atípicos
- Solo se puede calcular cuando hay datos positivos
- Se recomienda su uso cuando la variable presenta variacionas acumuladas: porcentajes, tasas de variación.
A.5.5 Cuantiles
Un cuantil divide la distribución de los datos en una proporción específica, el cuantil es el dato que corresponde a dicha división.
El cuantil de orden \(p\) de una distribución (con \(0 < p < 1\)) es el valor de la variable \(x_{p}\) que marca un corte de modo que una proporción \(p\) de valores de la población es menor o igual que \(x_{p}\). Por ejemplo, el cuantil de orden \(0.36\) dejaría un 36% de valores por debajo y el cuantil de orden \(0.50\) se corresponde con la mediana de la distribución.
Los cuantiles suelen usarse por grupos que dividen la distribución en partes iguales; entendidas estas como intervalos que comprenden la misma proporción de valores. Los más usados son:
- Los cuartiles, que dividen a la distribución en cuatro partes (corresponden a los cuantiles \(0.25\); \(0.50\) y \(0.75\));
- Los quintiles, que dividen a la distribución en cinco partes (corresponden a los cuantiles \(0.20\); \(0.40\); \(0.60\) y \(0.80\));
- Los deciles, que dividen a la distribución en diez partes;
- Los percentiles, que dividen a la distribución en cien partes.
A.6 Medidas de dispersión
Estas medidas permiten estimar el grado de dispersión de las observaciones al rededor del centro.
Son números reales no negativos, su valor es igual a cero cuando los datos son iguales. Si los datos están muy grupados, la medida será baja; será alta caso contrario.
A.6.1 La desviación estándar
Fue introducida por Karl Person en 1894 y se define:
La desviación estándar (o desviación típica), notada por \(s\), de un conjunto de \(n\) mediciones \(x_1+x_2+\ldots+x_n\) es la raíz cuadrada de las desviaciones de las mediciones, respecto al promedio \(\bar{x}\), dividida entre \(n-1\); es decir
\[ s = \sqrt{\frac{1}{n-1}\sum_{i = 1}^{n}(x_i-\bar{x})^2} \]
- Se expresa en las mismas unidades que los datos originales
- En su cálculo intervienen todos los valores de la distribución
- Es única
- Se ve afectada por valores atípicos
A.7 Notación de probabilidad
- El espacio muestral, \(\Omega\), es la colección de posibles resultados de un experimento
- Ejemplo: lanzamiento de un dado \(\Omega = \{1,2,3,4,5,6\}\)
- Un evento, digamos \(E\), es un subconjunto de \(\Omega\)
- Ejemplo: el resultado de un lanzamiento es par \(E = \{2,4,6\}\)
- Un evento elemental o simple es un resultado particular de un experimento
- Ejemplo: el resultado de un lanzamiento es cuatro \(\omega = 4\)
- \(\emptyset\) se denomina un evento nulo o conjunto vacío
A.8 Interpretación de los operadores de conjuntos
- \(\omega \in E\) implica que \(E\) ocurre cuando \(\omega\) ocurre
- \(\omega \not\in E\) implica que \(E\) no occurre cuando \(\omega\) ocurre
- \(E \subset F\) implica que la ocurrencia de \(E\) implica la ocurrencia de \(F\)
- \(E \cap F\) implica el evento en que ambos \(E\) y \(F\) occurren
- \(E \cup F\) implica el evento en que al menos uno de los dos ocurra \(E\) or \(F\)
- \(E \cap F=\emptyset\) significa que \(E\) y \(F\) son mutuamente excluyentes, o no puenden ocurrir ambos
- \(E^c\) o \(\bar E\) es el evento que \(E\) no ocurre
A.9 Funciones importantes
Una medida de probabilidad, \(P\), es una función de una colección posible de eventos tal que
- Para un evento \(E\subset \Omega\), \(0 \leq P(E) \leq 1\)
- \(P(\Omega) = 1\)
- Si \(E_1\) and \(E_2\) son eventos mutuamente excluyentes \(P(E_1 \cup E_2) = P(E_1) + P(E_2)\).
El punto 3 de la definición implica aditividad finita
\[ P(\cup_{i=1}^n A_i) = \sum_{i=1}^n P(A_i) \] donde los eventos \(\{A_i\}\) son mutuamente excluyentes.
A.10 Algunas consecuencias
- \(P(\emptyset) = 0\)
- \(P(E) = 1 - P(E^c)\)
- \(P(A \cup B) = P(A) + P(B) - P(A \cap B)\)
- if \(A \subset B\) then \(P(A) \leq P(B)\)
- \(P\left(A \cup B\right) = 1 - P(A^c \cap B^c)\)
- \(P(A \cap B^c) = P(A) - P(A \cap B)\)
- \(P(\cup_{i=1}^n E_i) \leq \sum_{i=1}^n P(E_i)\)
- \(P(\cup_{i=1}^n E_i) \geq \max_i P(E_i)\)
A.10.1 Ejemplo
La National Sleep Foundation (www.sleepfoundation.org) informa que alrededor del 3% de la población estadounidense tiene apnea del sueño. También informan que alrededor del 10% de la población de América del Norte y Europa tiene síndrome de piernas inquietas. ¿Implica esto que el 13% de las personas tendrá al menos un problema de sueño de este tipo?
A.10.2 Respuesta
No, los eventos no son mutuamente excluyentes. Veamos:
\[\begin{eqnarray*} A_1 & = & \{\mbox{Persona con apnea del sueño}\} \\ A_2 & = & \{\mbox{Persona con RLS}\} \\ \end{eqnarray*}\]
Luego
\[\begin{eqnarray*} P(A_1 \cup A_2 ) & = & P(A_1) + P(A_2) - P(A_1 \cap A_2) \\ & = & 0.13 - \mbox{Probabilidad de tener ambos}\\ \end{eqnarray*}\]
Una porción de la población tiene ambos
A.11 Variables aleatorias
- Una variable aleatoria es un resultado numérico de un experimento.
- Las variables aleatorias que estudiamos tienen dos variantes: discretas or continuas.
- Las v.a discretas son las que tienen un número contable de posibilidades.
- \(P(X = k)\)
- Las v.a. continuas toman valores en los reales o un subconjunto de los reales.
- \(P(X \in A)\)
A.12 Ejemplos de v.a.
- Los resultados \((0-1)\) del lanzamiento de una moneda
- Los resultados del lanzamiento de un dado
- El índice de masa corpotal de una persona en una toma futura a la línea base
- El estado de hipertensión de una persona seleccionada al alzar de una población
A.13 Función de masa de probabilidad \(p(x)\)
Una función de masa de probabilidad evaluada en un valor corresponde a la probabilidad que una v.a. toma ese valor. Para se una función válida, se debe satisfacer:
- \(p(x) \geq 0\) for all \(x\)
- \(\sum_{x} p(x) = 1\)
La suma se toma sobre todos los valores de \(x\).
A.13.1 Ejemplo
Sea \(X\) el resultado del lanzamiento de una moneda donde \(X=0\) representa sello y \(X = 1\) representa cara. \[ p(x) = (1/2)^{x} (1/2)^{1-x} ~~\mbox{ for }~~x = 0,1 \] Suponga que no sabemos si la moneda es justa. Sea \(\theta\) la probabilidad de que salga cara se expresa como una proporción (entre 0 y 1). \[ p(x) = \theta^{x} (1 - \theta)^{1-x} ~~\mbox{ for }~~x = 0,1 \]
A.14 Función de densidad
Una función de densidad (pdf), es una función asociada con una v.a. continua
Las areas debajo las pdfs corresponden a las probabilidades de esa v.a.
La función \(f\) debe satisfacer
\(f(x) \geq 0\) para todo \(x\)
El área debajo de \(f(x)\) es uno.
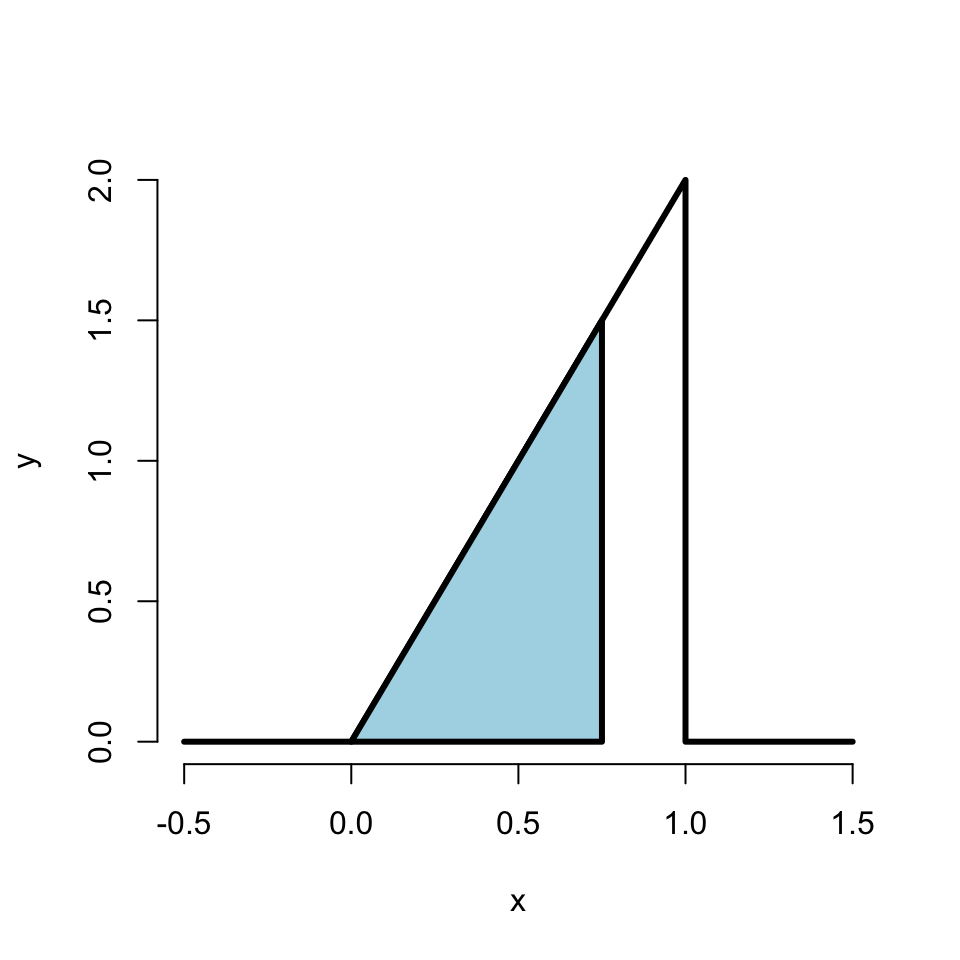
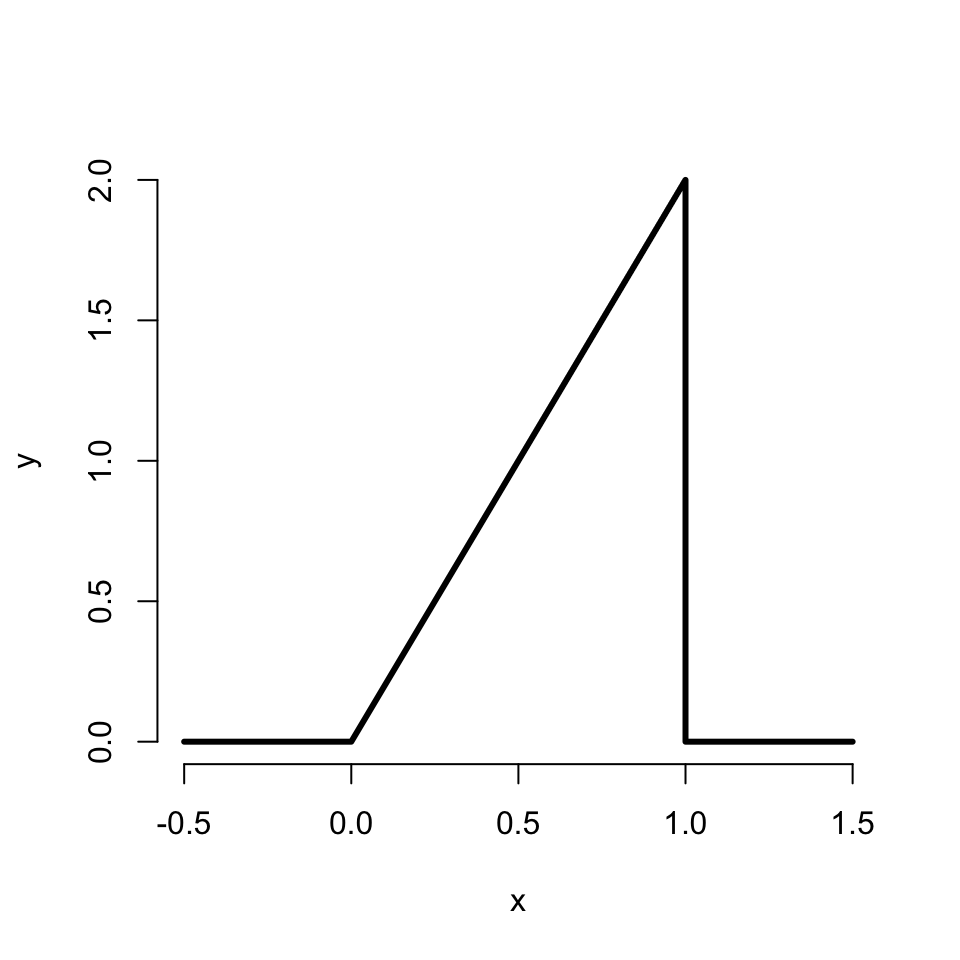
| ### Ejemplo |
| Suppose that the proportion of help calls that get addressed in a random day by a help line is given by \[ f(x) = \left\{\begin{array}{ll} 2 x & \mbox{ for } 1 > x > 0 \\ 0 & \mbox{ otherwise} \end{array} \right. \] |
| ¿Es esta una densidad válida? |
A.15 Función de distribución acumulada
La función de distribución acumulada (CDF) de una v.a. \(X\) se define como la función \[ F(x) = P(X \leq x) \]
Esta definición aplica indistintamente de si \(X\) es discreta o continua.
La función de supervivencia de una v.a. \(X\) es definida como
\[ S(x) = P(X > x) \] - Note que \(S(x) = 1 - F(x)\) - Para v.a. continuas, la función de densidad es la derivada de la acumulada
A.16 Cuantiles
- El cuantil \(\alpha^{th}\) de una distribución con función de distribución \(F\) es el punto \(x_\alpha\) tal que
\[ F(x_\alpha) = \alpha \]
Un percentil es simplemente un cuantil con \(\alpha\) expresado como porcentaje.
La mediana es el percentil \(50^{th}\).
A.17 Nociones de Muestreo
A.17.1 ¿Muestra o Censo?
¿Cuántas veces aparece la letra N __?
EU VIM COM A NAÇÃO ZUMBI / AO SEU OUVIDO FALAR / QUERO VER A POEIRA SUBIR / E MUITA FUMAÇA NO AR / CHEGUEI COM O MEU UNIVERSO / E ATERRISO NO SEU PENSAMENTO / TRAGO AS LUZES DOS POSTES NOS OLHOS / RIOS E PONTES NO CORAÇÃO / PERNAMBUCO EM BAIXO DOS PÉS / E MINHA MENTE NA IMENSIDÃO
A.17.2 Reseña histórica
| Año | Hito |
|---|---|
| 1662 | Primera estimación mediante razonamiento estadístico (en el sentido actual) a partir de una muestra (Graunt (1665)) |
| 1991 | Se demuestra empíricamente que, seleccionando muestras estratificadas, se obtienen mejores resultados en las estimaciones de medias y totales (Kiaer (1901)) |
| 1906 | Uso de aproximaciones de la distribución normal para la estimación de proporciones y propuesta de fórmula para estimación de varianza en muestreo estratificado (A. L. Bowley (1906)) |
| 1926 | Propuesta de métodos de selección representativos con probabilidades de inclusión iguales (A. Bowley (1926)) |
| 1927 | Publicación de tablas de números aleatorios (Tippett (1927)) |
| 1927 | Se publica el artículo considerado como uno de los pilares del muestreo como se conoce hoy en día. Libera el muestreo de las probabilidades de inclusión iguales. Introdujo en su artículo las ideas de eficiencia, asignación óptima, generalización del teorema de Markov, muestreo por conglomerados y presenta un caso donde el muestreo por conveniencia lleva a resultados equivocados (Neyman (1934)) |
| 1952 | Se completa el fundamento de la inferencia basada en el diseño. Se proporciona un marco de trabajo para la teoría de muestreo proporcional sin reemplazo (Horvitz (1952)) |
| 1955 | Pone en tela de juicio el concepto de eficiencia al que Neyman se refería; se prueba que, bajo la inferencia basada en el diseño de muestreo, no existe un estimador insesgado de varianza mínima (V. P. Godambe (1955)) |
| 1960 | Ejemplo pionero de inferencia basada en modelos. Trabajo realizado para estimar variabilidad espacial (Matérn (1960)) |
| 1977 | Se sugiere que se debe buscar una manera para que los estimadores tengan sentido en ambas doctrinas (V. Godambe and Thompson (1977)) |
| 1992 | Se publica Model Assited Survey Sampling, aquí la inferencia se basa en el diseño pero la estrategia de muestreo se complementa con un modelo para la estimación del parámetro de interés. (Sarndal (1992)) |
- 1662-1952: se caracteriza por tener a la IBDI como predominante, ya al final de intervalo es donde se empieza a cuestionar fuertemente esta perspectiva.
- 1952-1976: la discusión sobre la pertinencia de la IBDI o la IBMO está puesta sobre la mesa en diferentes congresos internacionales de estadística.
- Desde 1977: con la aparición del libro Model Assited Survey Sampling, de C.E. Särndal, se empieza a visualizar una reconciliación entre ambas posturas.
A.17.3 Diseño muestral
¿Cuál es la variable aleatoria?
Sea \(\mathcal{U} = \{u_1,\ldots,u_k,\ldots,u_N\}\) una población finita de \(N\) elementos con etiquetas \(k=1\ldots,N\). \(Y\) es la variable de estudio -cualitativa o cuantitativa-.
\(Y_k\) denota el valor del \(k\)-ésimo elemento de la población \(\mathcal{U}\).
\(X_k'\) un vector de información auxiliar de dimensión \(p\times1\).
Así, el objetivo es la estimación de una función \(g(T_y)\), donde los casos más usados son,
- \(T_y = \sum_{k\in\mathcal{U}}Y_k\) para el total,
- \(g(T_y) = T_y/N\) para la media y
- \(g(T_y) = T_y/T_x=R\) para la razón.
Sea \(\Omega\) el conjunto de todas las muestras posibles y sea \(p(\cdot)\) una función tal que \(p(s)\) devuelve la probabilidad de seleccionar cualquier muestra \(s\) de la variable aleatoria \(S\) (la función \(p(\cdot)\), también conocida como diseño muestral, determina la distribución de probabilidad de \(S\)).
Sea \(I_k\) una variable aleatoria de inclusión muestral (\(I_k=1\) si se selecciona el \(k\)-ésimo elemento o \(I_k=0\) en caso contrario). La probabilidad de que un elemento \(k\) sea incluido en la muestra bajo un diseño \(p(\cdot)\) es:
\[\begin{equation}\label{RL_eq:001} \pi_k = Prob(I_k = 1) = \sum_{S\in\Omega}I_kp(s) = \sum_{S\in\Omega_k}p(s) \end{equation}\]
donde \(S\in\Omega_k\) denota que la suma es sobre todas las muestras \(s\) que contienen un \(k\) dado. Finalmente, \(\nu = \sum_{k\in\mathcal{U}}I_k\) denota el número de elementos distintos en una muestra de tamaño \(n\) (Para más detalle y ejemplos véase (Sarndal (1992)) y (Gregoire (1998)).).
A.17.3.1 Un ejemplo ilustrativo:
Usando la librería TeachingSampling (Gutierrez-Rojas (2015))
library(TeachingSampling)
U <- c("Sofía", "Cynthia", "Fausto", "Den", "Mario")
N <- length(U)
# El tamaño de la muestra es n=2
n <- 2
# Cálculo del soporte:
Support(N,n,U)## [,1] [,2]
## [1,] "Sofía" "Cynthia"
## [2,] "Sofía" "Fausto"
## [3,] "Sofía" "Den"
## [4,] "Sofía" "Mario"
## [5,] "Cynthia" "Fausto"
## [6,] "Cynthia" "Den"
## [7,] "Cynthia" "Mario"
## [8,] "Fausto" "Den"
## [9,] "Fausto" "Mario"
## [10,] "Den" "Mario"# p es la prob de selección de cada muestra
# p <- rep(1,10)/10
p <- c(.13,.2,.15,.1,.15,.04,.02,.06,.07,.08)
# Note que los elementos suman 1 y ninguno es negativo
sum(p)## [1] 1## X1 X2 p X1.1 X2.1 X3 X4 X5
## 1 Sofía Cynthia 0.13 1 1 0 0 0
## 2 Sofía Fausto 0.20 1 0 1 0 0
## 3 Sofía Den 0.15 1 0 0 1 0
## 4 Sofía Mario 0.10 1 0 0 0 1
## 5 Cynthia Fausto 0.15 0 1 1 0 0
## 6 Cynthia Den 0.04 0 1 0 1 0
## 7 Cynthia Mario 0.02 0 1 0 0 1
## 8 Fausto Den 0.06 0 0 1 1 0
## 9 Fausto Mario 0.07 0 0 1 0 1
## 10 Den Mario 0.08 0 0 0 1 1## [1] 0.58 0.34 0.48 0.33 0.27## [1] 2## [1] 47.2# Se realiza la muestra
s <- c("Sofía","Mario")
ys <- y[s]
pik_s <- pik[s]
(round(HT <- sum(ys / pik_s)/5,2))## [1] 36.96# ¿Por qué es insesgado?
PIK <- matrix(rep(pik,10),ncol=5,byrow=TRUE)
Y <- matrix(rep(y,10),ncol=5,byrow=TRUE)
Y <- (Y)/(Ind*PIK)
Y[Y == Inf] = 0
# Todas las posibles muestras:
round(apply(Y,1,mean),2)## [1] 31.03 30.20 64.97 36.96 39.17 73.94 45.93 73.11 45.09 79.87## [1] 47.2