6.2 Principal Component Analysis（主成分分析）

主成分分析は，多数の変数で表現されている情報をできるだけ少ない変数に縮約して表現する手法です。情報を集約する際には，できるだけ元の情報を損なわないような方法がとられます。複雑なデータを単純な形にまとめることで，データに対する理解を助けます。

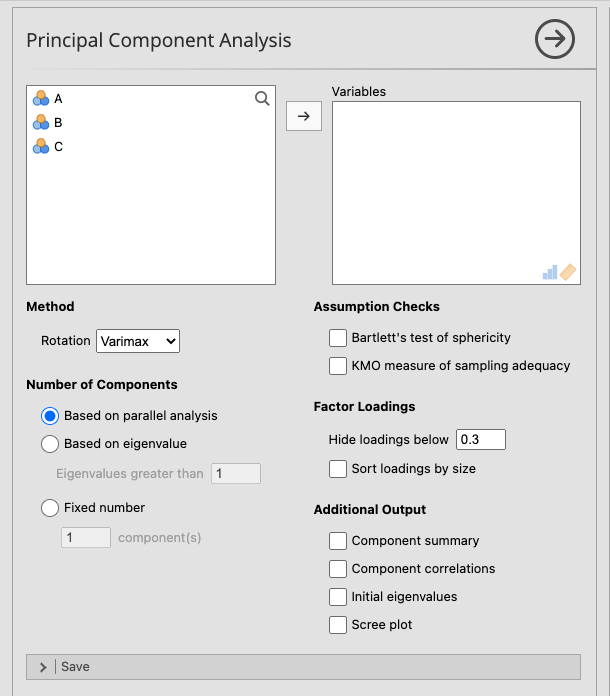
図6.4: Principal Component Analysis

• Method（方法）
  • Rotation（回転）　主成分の回転法を設定します。
    • None（回転なし）　回転を行いません。
    • Varimax（バリマックス法）　バリマックス法による回転を行います（直交回転）。
    • Quartimax（クォーティマックス法）　クォーティマックス法による回転を行います（直交回転）。
    • Promax（プロマックス法）　プロマックス法による回転を行います（斜交回転）。
    • Oblimin（オブリミン法）　オブリミン法による回転を行います（斜交回転）。
    • Simplimax（シンプリマックス法）　シンプリマックス法による回転を行います（斜交回転）。
• Number of Components（主成分の個数）
  • Based on parallel analysis（平行分析に基づいて決定）　平行分析の結果をもとに主成分の個数を決定します。
  • Based on eigenvalue（固有値に基づいて決定）　固有値の大きさが指定値以上主成分を採用します。
  • Fixed number（個数指定）　主成分の個数を直接指定します。
    • [   ] component(s)　主成分の個数を数値指定します。
• Assumption Checks（前提チェック）
  • Bartlett’s test of sphericity（バートレットの球面性検定）　バートレットの球面性検定を実施します。
  • KMO measure of sampling adequacy（KMO標本妥当性指標）　標本妥当性指標（MSA）を算出します。
• Factor Loadings（因子負荷）
  • Hide loadings below [   ]（これ未満の負荷を隠す）　指定した値より絶対値が小さい負荷量を非表示にします。
  • Sort loadings by size（負荷量の大きさで並び替え）　負荷量の絶対値が大きい順に変数を並び替えて表示します。
• Additional Output（追加の出力）
  • Component summary（主成分の要約）　各主成分について要約量を算出します。
  • Component correlations（主成分の相関）　各主成分の間の相関を算出します。
  • Initial eigenvalues（回転前の固有値）　回転前の固有値とその寄与率，累積寄与率を算出します。
  • Scree plot（スクリープロット）　スクリープロットを表示します。
• | Save（保存）　分析結果を新たな変数に保存します。

6.2.1 Save（保存）

分析結果を新たな変数として保存します。

図6.5: Save

• Component scores（主成分得点）　主成分得点を新たな変数として保存します。