3.6 One-Way ANOVA [Kruskal-Wallis]（クラスカル=ウォリス検定）

クラスカル=ウォリス検定は，連続型（inline）の従属変数と名義型（inline）または順序型（inline）の説明変数（独立変数）の関係について検討する際に使用されます。分散分析（ANOVA）とよく似た分析手法ですが，ノンパラメトリック検定であるために分析に必要な前提条件が少なくて済むという利点があります。ただし，分析に使用できる独立変数は1つに限定されます。

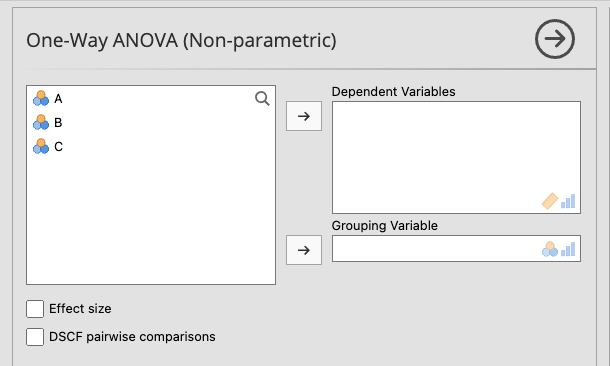
**Kruskal-Wallis**

図3.24: Kruskal-Wallis

  • Dependent Variables（従属変数）　分析対象の測定値が入力されている変数を指定します。
  • Grouping Variable（グループ変数）　グループの値が入力されている変数を指定します。
  • Effect size（効果量）　効果量\(\varepsilon^2\)（イプシロン2乗）の値を算出します。
  • DSCF pairwise comparisons（多重比較）　ドゥワス=スティール=クリッチロウ=フリグナー法（DSCF法）による多重比較を実施します。