3.5 MANCOVA(多変量共分散分析)
多変量共分散分析(MANCOVA)は,複数の従属変数と1つ以上の独立変数の関係について検討する際に使用されます。また,多変量共分散分析で共変量を使用しない場合は多変量分散分析(MANOVA)と呼ばれます。
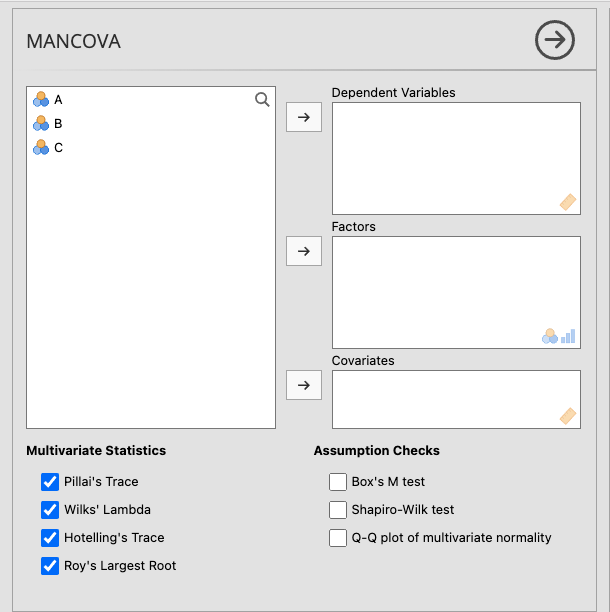
図3.23: MANCOVA
Dependent Variables(従属変数) 分析対象の測定値が入力されている変数を指定します。
Factors(要因) 分析の独立変数(実験条件など)を指定します。
Covariates(共変量) 共変量として使用する変数を指定します。
Multivariate Statistics(多変量統計量) 多変量統計量を算出します。
- Pillai’s Trace(ピライのトレース) ピライのトレースとそれに基づくF値を算出します。
- Wilks’s Lambda(ウィルクスのラムダ) ウィルクスのラムダとそれに基づくF値を算出します。
- Hotelling’s Trace(ホテリングのトレース) ホテリングのトレースとそれに基づくF値を算出します。
- Roy’s Largest Root(ロイの最大根) ロイの最大根とそれに基づくF値を算出します。
Assumption Checks(前提条件チェック) 正規性の検定など,分析の前提条件をチェックします。
- Box’s M test(ボックスのM検定) 「すべてのグループにおいて分散共分散行列が等しい」という帰無仮説について検定を行います。
- Shapiro-Wilk test(シャピロ=ウィルク検定) 「データが多変量正規分布である」という仮説について検定を行います。
- Q-Q plot of multivariate normality(多変量正規Q-Qプロット) 多変量正規Q-Qプロットを作成します。