3.1 One-Way ANOVA（1要因分散分析）

この「1要因分散分析」メニューは，「通常の」分散分析の手順を単純化したものです。説明変数（独立変数）は1種類しか使用できませんが，ウェルチ法による分析も可能です。ウェルチ法による分散分析は，「すべてのグループで分散が等しい」という仮定が必要ないという点に強みがあります。

また，このメニューでは従属変数を複数指定することもできますが，その場合には従属変数ごとに個別に分析が実行されます。

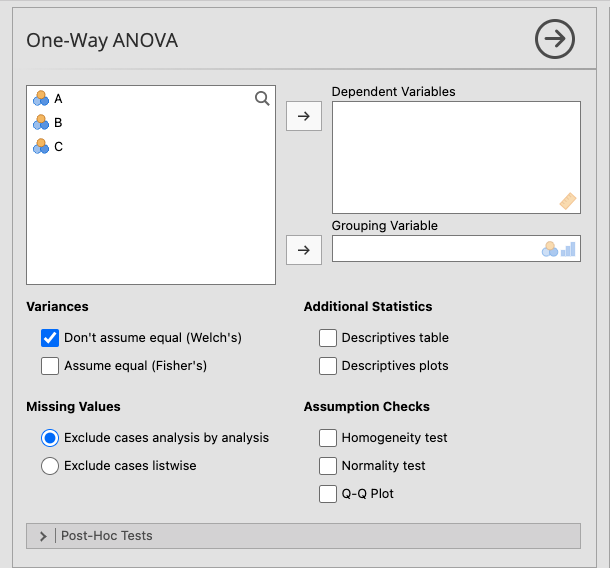
図3.1: One-Way ANOVA

• Dependent Variables（従属変数）　分析対象の測定値が入力されている変数を指定します。

• Grouping Variable（グループ変数）　グループの値が入力されている変数を指定します。

• Variances（分散）　分析における分散の扱い方について設定します。

  • Don’tassume equal (Welch’s)　各グループの分散が等しいと想定しない形で分析を行います（ウェルチの検定）
  • Assume equal (Fisher’s)　各グループで分散が等しいという仮定の元に分析を行います（フィッシャーの検定）

• Missing Values（欠損値）　欠損値の処理方法について設定します。

  • Exclude cases analysis by analysis（分析ごとに除外）
  • Exclude cases listwise（行全体を除外）

• Additional Statistics（追加の統計量）　記述統計量の算出と表示に関する設定を行います。

  • Descriptives table（記述統計量の表）
  • Descriptives plots（記述統計量の図）

• Assumption Checks（前提チェック）　分散分析の前提が満たされているかどうかを確かめます。

  • Homogeniety test（等質性検定）　分散の等質性についての検定を行います。
  • Normality test（正規性検定）　データの正規性についての検定を行います。
  • Q-Q Plot（Q-Qプロット）　正規Q-Qプロットを作成します。

• | Post Hoc Tests（事後検定）　分散分析の事後検定に関する設定を行います。

3.1.1 Post-Hoc Tests（事後検定）

主効果が有意であった場合の事後検定についての設定です。

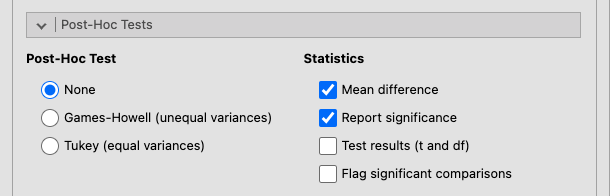
図3.2: Post-Hoc Tests

• Post-Hoc Test（事後検定）　事後検定についての設定を行います。
  • None（なし）　事後検定を行いません。
  • Games-Howell (unequal variances)　ゲームス=ハウエル法による多重比較を行います。この方法では分散の等質性を仮定しません。
  • Tukey (equal variances)　テューキー法による多重比較を行います。この方法では各条件の分散が等質であることが前提となります。
• Statistics（統計量）　事後検定の統計量に関する設定を行います。
  • Mean difference（平均値の差）　条件間の平均値の差を算出します。
  • Report significance（有意確率の報告）　検定統計量の有意確率（p値）を表示します。
  • Test results (t and df)（検定結果：tと自由度）　検定統計量と自由度を表示します。
  • Flag significant comparisons（差が有意なペアにマーク）　差が有意であったペアに「*」などの印をつけて示します。