1.1 Descriptives（記述統計量）

記述統計量メニューには，要約統計量算出の機能，データ分布や分布の形を視覚化するのための機能が集められています。より複雑な分析を実施する前に，データの記述統計量にしっかり目を通しておくのはよいことです。

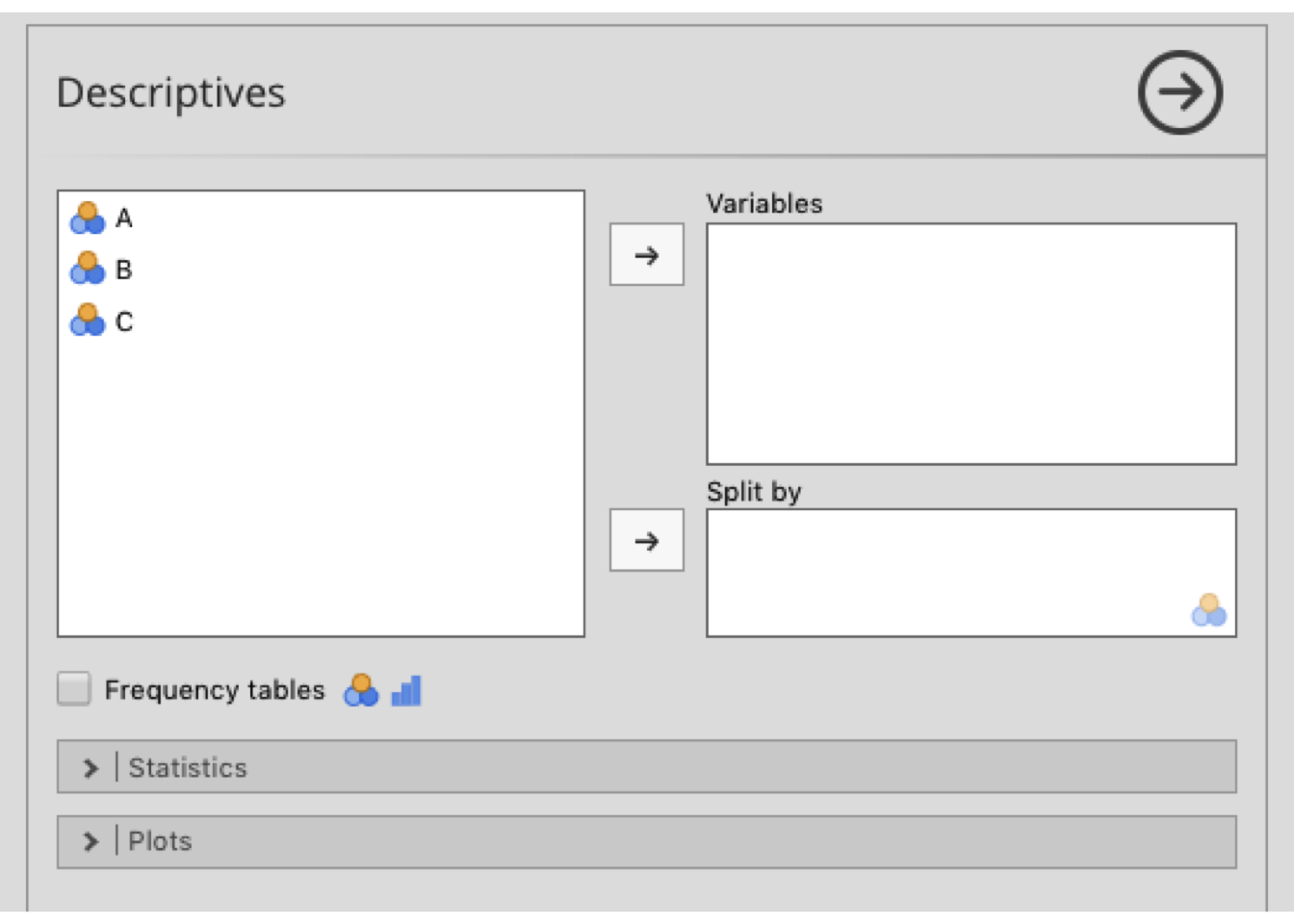
図1.1: Descriptives

Variables（変数）　記述統計量の算出を行う変数を指定します。

Split by（グールプ変数）　グループごとに記述統計量を算出したい場合，ここにグールプ変数（名義型 inline

）を指定します。

Frequency tables（度数分布表）　記述統計量算出の対象が「名義型 inline

」または「順序型

」変数の場合，ここにチェックを入れることで度数分布表が作成されます。

| Statistics（統計量）　算出する統計量に関するオプション設定を行います。

| Plots（作図）　作図のオプションを設定します。

1.1.1 Statistics（統計量）

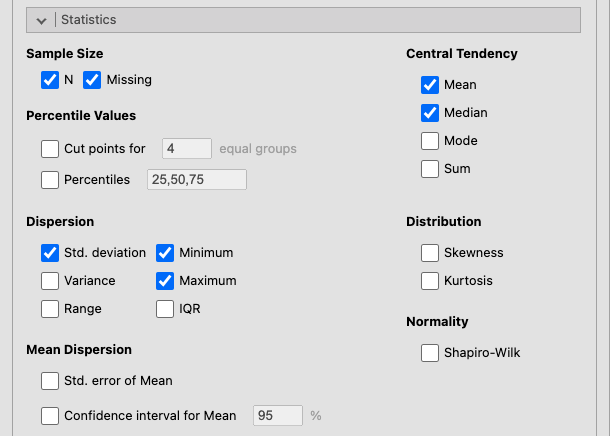
図1.2: Statistics

Sample Size（標本サイズ）
- N（測定値の個数）　分析変数に含まれるデータ総数を表示します。
- Missing（欠損値）　分析変数に含まれる欠損値の個数を表示します。
Percentile Values（パーセンタイル値）
- Cut points for [ ] equal groups（ｎ分位数）　データ全体をn等分する位置にある値を算出します。初期値は「4」に設定されています。
- Percentiles（四分位数）　値の小さい方から数えてn%の位置にある値を算出します。複数のパーセント点を指定する場合は，それらの値をコンマで区切って入力します。初期値は「25,50,75」に設定されています。
Dispersion（ばらつき）
- Std. deviation（標準偏差）　標準偏差を算出します。
- Variance（分散）　分散を算出します。
- Range（範囲）　範囲（最大値 – 最小値の幅）を算出します。
- Minimum（最小値）　最小値を求めます。
- Maximum（最大値）　最大値を求めます。
- IQR（四分位範囲）　四分位範囲（第3四分位 – 第1四分位）を算出します。
Mean Dispersion（平均値のばらつき）
- Std. error of Mean（平均値の標準誤差）　平均値の推定における標準誤差を算出します。
- Confidence interval for Mean [ ]%（平均値の[ ]％信頼区間）　平均値の信頼区間（下限値と上限値）を算出します。
Central Tendency（中心傾向）
- Mean（平均値）　平均値を算出します。
- Median（中央値）　中央値を算出します。
- Mode（最頻値）　中央値を算出します。
- Sum（合計値）　合計値を算出します。
Distribution（分布）
- Skewness（歪度）　歪度（分布が左右対称からずれている程度）を算出します。
- Kurtosis（尖度）　尖度（分布が中心に集中している程度）を算出します。
Normality（正規性）
- Shapiro-Wilk（シャピロ・ウィルク検定）　分布が正規分布からずれているかどうかを検定します。

1.1.2 Plots（作図）

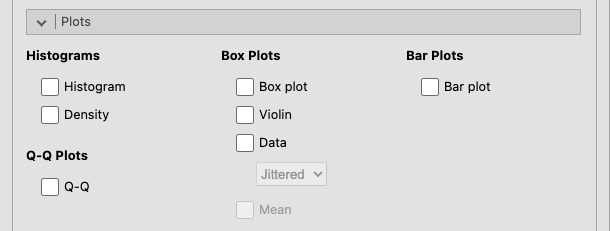
図1.3: Plots

Histograms（ヒストグラム）
- Histogram（ヒストグラム）　度数分布をヒストグラムとして図示します。
  
  図1.4: ヒストグラム
- Density（密度曲線）　度数分布をカーネル平滑化した密度曲線グラフを作成します。
  
  図1.5: 密度曲線
Q-Q Plots（Q-Qプロット）
- Q-Q（正規Q-Qプロット）　正規Q-Qプロットを作成します。