5.3 Compare E3 fit
5.3.0.1 ../out/G2t_T48_L30_msq0-4.900000_msq1-4.650000_l02.500000_l12.500000_mu5.000000_g0.000000_rep0_output
E3_0(L30T48) = 0.4267(21) -0.00017504(31) -0.0050007(67) \(\chi^2/dof=\) 0.79501
E3_0_vev(L30T48) = 0.3961(10) 0.00018161(33) 0.0003(14) 0.0002232(56) \(\chi^2/dof=\) 0.00092646
E3_0_p1(L30T48) = 0.51771(77) 750.1(0.6)e-7 0.0011876(21) 0.000433(65) \(\chi^2/dof=\) 0.051193
E3_0_p1_vev(L30T48) = 0.51533(74) 753.8(0.6)e-7 0.0008189(36) 0.00028(10) 38.8(0.2)e-6 \(\chi^2/dof=\) 0.027218
E3_0_p11(L30T48) = 0.5914(14) 655.7(0.9)e-7 0.0010358(33) -0.00062(12) \(\chi^2/dof=\) 0.099175
E3_0_p11_vev(L30T48) = 0.5876(13) 661.1(0.8)e-7 0.0001563(89) 0.00037(19) 462.9(0.7)e-7 \(\chi^2/dof=\) 0.064069
E3_0_p111(L30T48) = 0.6476(30) 60.2(0.2)e-6 0.0009396(65) 0.00090(26) \(\chi^2/dof=\) 0.043747
E3_0_p111_vev(L30T48) = 0.6449(29) 60.6(0.2)e-6 0.7(0.4)e-4 0.00077(29) 42.5(0.2)e-6 \(\chi^2/dof=\) 0.03665
E3_0_A1(L30T48) = 0.11358(11) 6050.8(0.7)e-8 0.0009869(12) -0.1(1.0)e-5 \(\chi^2/dof=\) 145.18
E3_0_A1_vev(L30T48) = 0.6364(56) 386.9(0.6)e-7 0.0(0.1)e-6 0.006092(20) 647.3(0.1)e-7 \(\chi^2/dof=\) 0.15683
5.3.1 plotting the exponential for A1
\(E_{3A1}\)= 0.72 this is an estimate
\(E_{\phi_0}\)= 0.1283262
\(E_{A1}\)= 0.4956415
\(E_{\phi_0}(p_x)\)= 0.2448188
\(E_{2\phi_0}(p_x)\)= 0.3768698
\(E_{2\phi_0}(0)\)= 0.2604283
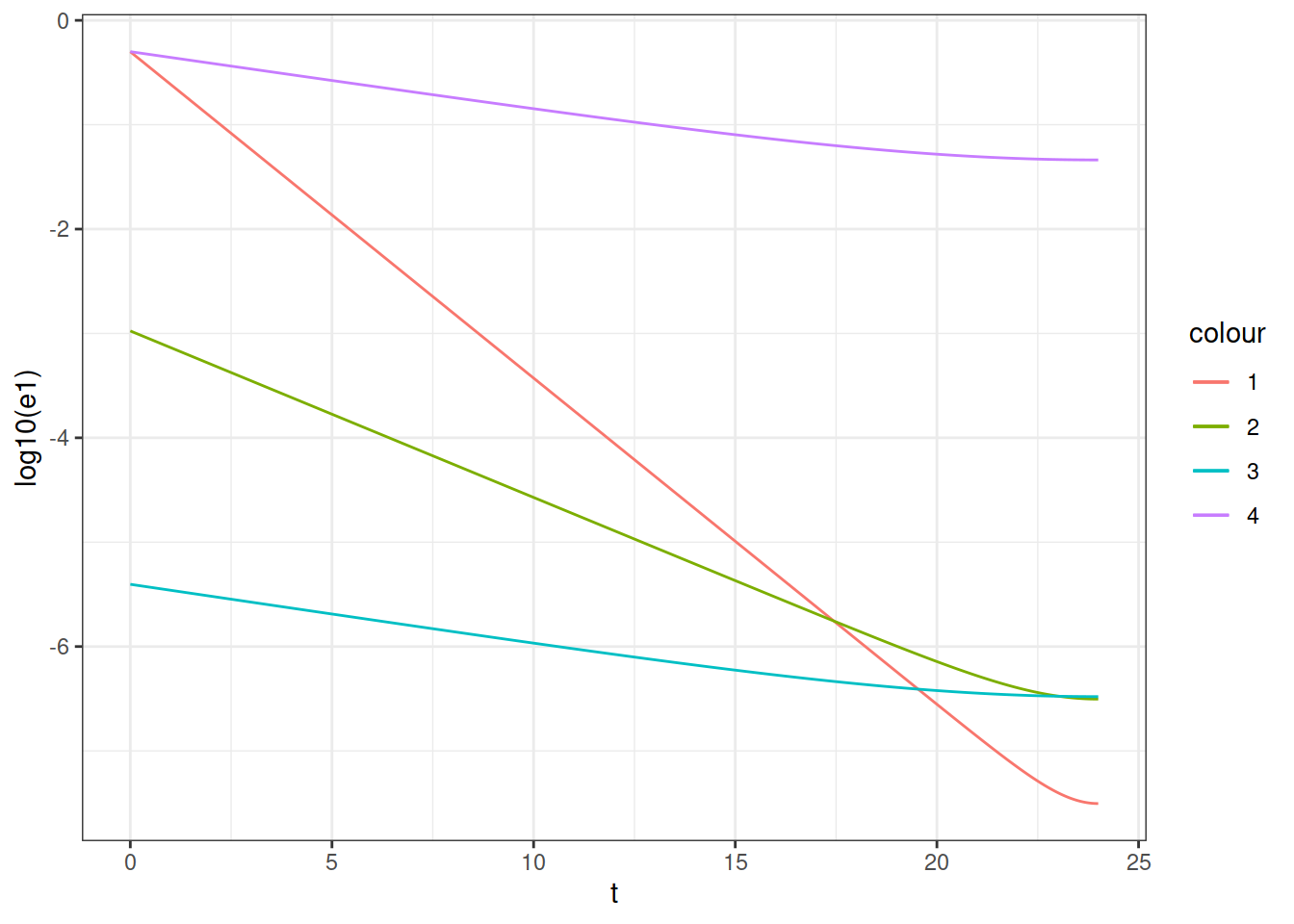
Contribution 4 is the dominant
5.3.2 plotting the exponential for p=(1,0,0)
e1<-c()
e2<-c()
e3<-c()
e4<-c()
T<-48
L<-30
tf<-16
#read the energies
dir<-"../out"
file=sprintf("%s/G2t_T%d_L%d_msq0-4.900000_msq1-4.650000_l02.500000_l12.500000_mu5.000000_g0.000000_rep0_output",dir,T,L)
mt<-read_df(file)
all_obs<- get_all_corr(mt)
E3_0_p1=get_energy("E3_0_p1",all_obs,mt)[1]
E1_0=get_energy("E1_0",all_obs,mt)[1]
E2_0_p1=get_energy("E2_0_p1",all_obs,mt)[1]
E1_0_p1=get_energy("E1_0_p1",all_obs,mt)[1]
E2_0=get_energy("E2_0",all_obs,mt)[1]
cat("$E_{3\\phi_0}(p)$=",E3_0_p1,"\n\n" )\(E_{3\phi_0}(p)\)= 0.5177052
cat("$E_{\\phi_0}$=",E1_0,"\n\n" )\(E_{\phi_0}\)= 0.1283262
cat("$E_{2\\phi_0}(p_x)$=",E2_0_p1,"\n\n" )\(E_{2\phi_0}(p_x)\)= 0.3768698
cat("$E_{\\phi_0}(p_x)$=",E1_0_p1,"\n\n" )\(E_{\phi_0}(p_x)\)= 0.2448188
cat("$E_{2\\phi_0}(0)$=",E2_0,"\n\n" )\(E_{2\phi_0}(0)\)= 0.2604283
t<-c(0:480)/20
e1<-c(e1, exp(-E3_0_p1*T/2) *cosh(E3_0_p1*(t-T/2) ) )
e2<-c(e2, exp(-(E1_0+E2_0_p1 ) *T/2) *cosh((E1_0-E2_0_p1)*(t-T/2) ) )
e3<-c(e3, exp(-(E1_0_p1+E2_0 ) *T/2) *cosh((E1_0_p1-E2_0)*(t-T/2) ) )
e4<-c(e4, exp(-(E1_0_p1) *T/2) *cosh((E1_0_p1)*(t-T/2) ) )
gg<-ggplot()+geom_line(aes(x=t,y=log10(e1), color="1"))
gg<- gg +geom_line(aes(x=t,y=log10(e2), color="2"))
gg<- gg +geom_line(aes(x=t,y=log10(e3), color="3"))+theme_bw()
gg<- gg +geom_line(aes(x=t,y=log10(e4), color="4"))
gg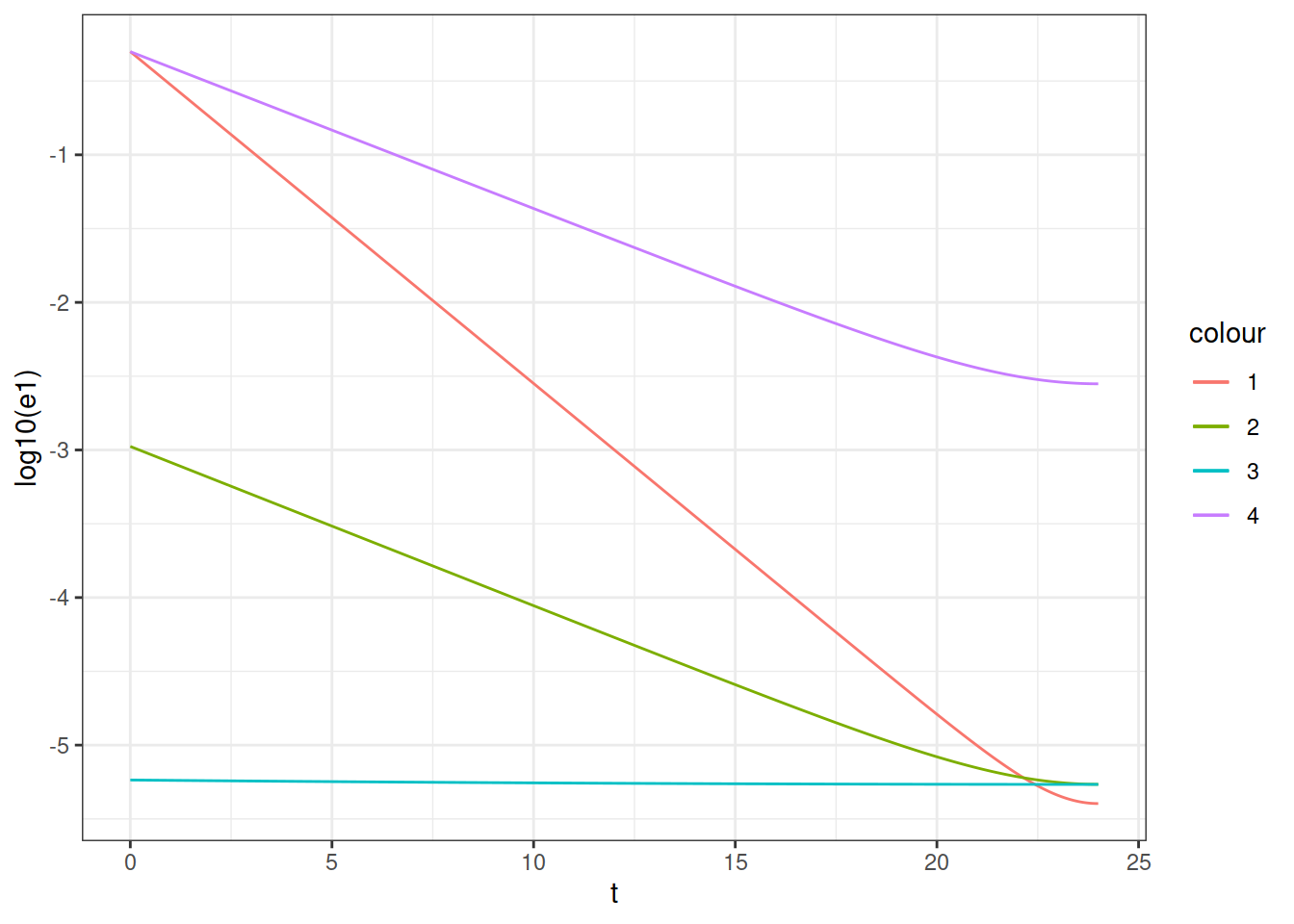
The contribution 4 is dominant but has the same time dependence of contribution 2.