Chapter 37: quaternion

37.1 TaylorCatAlice

https://www.bilibili.com/video/BV1PV411P7w4

曹則賢 2022 跨年演說

https://www.bilibili.com/video/BV1qa411B792

https://en.wikipedia.org/wiki/Blackboard_bold

37.1.1 complex / dionion / bionion

\[ \begin{aligned} & c=a+b\mathrm{i}=a+\mathrm{i}b,\begin{cases} c\in\mathbb{C}\\ \mathrm{i}^{2}=-1\\ a,b\in\mathbb{R} & \Leftrightarrow\left\langle a,b\right\rangle \in\mathbb{R}^{2} \end{cases}\\ = & z=x+y\mathrm{i}=x+\mathrm{i}y,\begin{cases} z\in\mathbb{C}\\ \mathrm{i}^{2}=-1\\ x,y\in\mathbb{R} & \Leftrightarrow\left\langle x,y\right\rangle \in\mathbb{R}^{2} \end{cases}\\ = & \sqrt{x^{2}+y^{2}}\left(\dfrac{x}{\sqrt{x^{2}+y^{2}}}+\dfrac{y}{\sqrt{x^{2}+y^{2}}}\mathrm{i}\right)=r\left(\cos\theta+\mathrm{i}\sin\theta\right)=r\mathrm{e}^{\mathrm{i}\theta} \end{aligned} \]

Also see complex group representation^[40.7].

37.1.2 trionion / triernion / triplex / ternion

https://zh.wikipedia.org/zh-tw/%E4%B8%89%E5%85%83%E6%95%B8

https://math.stackexchange.com/questions/1784166/why-are-there-no-triernions-3-dimensional-analogue-of-complex-numbers-quate

https://math.stackexchange.com/questions/32100/is-there-a-third-dimension-of-numbers/4453131

\[ \begin{aligned} & t=a+b\mathrm{i}+c\mathrm{j}=a+\mathrm{i}b+\mathrm{j}c,\begin{cases} t\in\mathbb{T}\\ \mathrm{i}^{2}=-1\\ \mathrm{j}^{2}=-1 \end{cases}\\ = & w=x+y\mathrm{i}+z\mathrm{j}=x+\mathrm{i}y+\mathrm{j}z,\begin{cases} w\in\mathbb{T}\\ \mathrm{i}^{2}=-1\\ \mathrm{j}^{2}=-1 \end{cases}\\ = & \sqrt{x^{2}+y^{2}+z^{2}}\left(\dfrac{x}{\sqrt{x^{2}+y^{2}+z^{2}}}+\dfrac{y}{\sqrt{x^{2}+y^{2}+z^{2}}}\mathrm{i}+\dfrac{z}{\sqrt{x^{2}+y^{2}+z^{2}}}\mathrm{j}\right)=? \end{aligned} \]

\[ \begin{cases} A\left(BC\right)=\left(AB\right)C & \left(a\right)\text{associativity}\\ A\left(B+C\right)=AB+AC & \left(d\right)\text{distributivity} \end{cases} \]

\[ \begin{aligned} \mathbb{T}\ni\mathrm{i}\mathrm{j}= & X+Y\mathrm{i}+Z\mathrm{j}\in\mathbb{T}\\ -\mathrm{j}=\left(\mathrm{i}^{2}\right)\mathrm{j}\overset{\left(a\right)}{=}\mathrm{i}\left(\mathrm{i}\mathrm{j}\right)= & \mathrm{i}\left(X+Y\mathrm{i}+Z\mathrm{j}\right)\overset{\left(d\right)}{=}-Y+X\mathrm{i}+Z\mathrm{i}\mathrm{j}\\ \mathrm{i}\mathrm{j}= & \dfrac{Y}{Z}-\dfrac{X}{Z}\mathrm{i}-\dfrac{1}{Z}\mathrm{j}\Rightarrow\begin{cases} X=\dfrac{Y}{Z}\\ Y=-\dfrac{X}{Z}\\ Z=-\dfrac{1}{Z} & \Rightarrow Z^{2}=-1\Rightarrow Z\notin\mathbb{R} \end{cases}\\ -\mathrm{i}=\mathrm{i}\left(\mathrm{j}^{2}\right)\overset{\left(a\right)}{=}\left(\mathrm{i}\mathrm{j}\right)\mathrm{j}= & \left(X+Y\mathrm{i}+Z\mathrm{j}\right)\mathrm{j}\overset{\left(d\right)}{=}-Z+X\mathrm{j}+Y\mathrm{i}\mathrm{j}\\ \mathrm{i}\mathrm{j}= & \dfrac{Z}{Y}-\dfrac{1}{Y}\mathrm{i}-\dfrac{X}{Y}\mathrm{j}\Rightarrow\begin{cases} X=\dfrac{Z}{Y}\\ Y=-\dfrac{1}{Y} & \Rightarrow Y^{2}=-1\Rightarrow Y\notin\mathbb{R}\\ Z=-\dfrac{X}{Y} \end{cases} \end{aligned} \]

37.1.3 quaternion

https://en.wikipedia.org/wiki/Quaternion

\[ \begin{aligned} & q=a+b\mathrm{i}+c\mathrm{j}+d\mathrm{k}=a+\mathrm{i}b+\mathrm{j}c+\mathrm{k}d,\begin{cases} q\in\mathbb{H}\\ a,b,c,d\in\mathbb{R} & \Leftrightarrow\left\langle a,b,c,d\right\rangle \in\mathbb{R}^{4} \end{cases}\\ = & w=t+x\mathrm{i}+y\mathrm{j}+z\mathrm{k}=t+\mathrm{i}x+\mathrm{j}y+\mathrm{k}z,\begin{cases} w\in\mathbb{H}\\ t,x,y,z\in\mathbb{R} & \Leftrightarrow\left\langle t,x,y,z\right\rangle \in\mathbb{R}^{4} \end{cases}\\ = & ? \end{aligned} \]

\[ \begin{aligned} & q=a+b\mathrm{i}+c\mathrm{j}+d\mathrm{k}=a+\mathrm{i}b+\mathrm{j}c+\mathrm{k}d,\begin{cases} q\in\mathbb{H}\\ \mathrm{i}^{2}=\mathrm{j}^{2}=\mathrm{k}^{2}=-1=\mathrm{i}\mathrm{j}\mathrm{k} & \Rightarrow\mathrm{i}\mathrm{j}=\mathrm{k}\\ a,b,c,d\in\mathbb{R} & \Leftrightarrow\left\langle a,b,c,d\right\rangle \in\mathbb{R}^{4} \end{cases}\\ = & w=t+x\mathrm{i}+y\mathrm{j}+z\mathrm{k}=t+\mathrm{i}x+\mathrm{j}y+\mathrm{k}z,\begin{cases} w\in\mathbb{H}\\ \mathrm{i}^{2}=\mathrm{j}^{2}=\mathrm{k}^{2}=-1=\mathrm{i}\mathrm{j}\mathrm{k} & \Rightarrow\mathrm{i}\mathrm{j}=\mathrm{k}\\ t,x,y,z\in\mathbb{R} & \Leftrightarrow\left\langle t,x,y,z\right\rangle \in\mathbb{R}^{4} \end{cases}\\ = & t+\begin{pmatrix}\mathrm{i} & \mathrm{j} & \mathrm{k}\end{pmatrix}\begin{pmatrix}x\\ y\\ z \end{pmatrix}=x_{{\scriptscriptstyle 0}}+\begin{pmatrix}\boldsymbol{i} & \boldsymbol{j} & \boldsymbol{k}\end{pmatrix}\begin{pmatrix}x\\ y\\ z \end{pmatrix}=x_{{\scriptscriptstyle 0}}+\begin{pmatrix}\boldsymbol{e}_{{\scriptscriptstyle 1}} & \boldsymbol{e}_{{\scriptscriptstyle 2}} & \boldsymbol{e}_{{\scriptscriptstyle 3}}\end{pmatrix}\begin{pmatrix}x_{{\scriptscriptstyle 1}}\\ x_{{\scriptscriptstyle 2}}\\ x_{{\scriptscriptstyle 3}} \end{pmatrix}=x_{{\scriptscriptstyle 0}}+\boldsymbol{x},\begin{cases} \boldsymbol{e}_{{\scriptscriptstyle 1}}=\boldsymbol{i}=\mathrm{i}\\ \boldsymbol{e}_{{\scriptscriptstyle 2}}=\boldsymbol{j}=\mathrm{j}\\ \boldsymbol{e}_{{\scriptscriptstyle 3}}=\boldsymbol{k}=\mathrm{k} \end{cases}\\ = & t+\dfrac{\mathrm{i}x+\mathrm{j}y+\mathrm{k}z}{r}r,\begin{cases} r^{2}=x^{2}+y^{2}+z^{2} & \left|q\right|^{2}=t^{2}+r^{2}\\ \left\Vert \boldsymbol{n}\right\Vert ^{2}=\left(\dfrac{\mathrm{i}x+\mathrm{j}y+\mathrm{k}z}{r}\right)^{2}=-1 \end{cases}\\ = & \sqrt{t^{2}+r^{2}}\left(\dfrac{t}{\sqrt{t^{2}+r^{2}}}+\boldsymbol{n}\dfrac{r}{\sqrt{t^{2}+r^{2}}}\right)=\left|q\right|\left(\cos\dfrac{\theta}{2}+\boldsymbol{n}\sin\dfrac{\theta}{2}\right)=\left|q\right|\mathrm{e}^{\boldsymbol{n}\frac{\theta}{2}} \end{aligned} \]

The quaternion set is denoted \(\mathbb{H}\) for Sir R.W. Hamilton, because he suddenly and strikingly realized

\[ \begin{cases} \mathrm{i}\mathrm{j}=\mathrm{k}\\ \mathrm{k}\in\mathbb{H} \end{cases}\Rightarrow\mathrm{i}\mathrm{j}\in\mathbb{H}\text{ for closure property} \]

for the sake of rigorosity, see group theory^[40]

\[ \mathrm{k}^{2}=-1 \]

\[ \begin{aligned} \mathrm{i}\mathrm{j} & =\mathrm{k}\\ \mathrm{i}\mathrm{j}\mathrm{k}=\mathrm{i}\left(\mathrm{j}\mathrm{k}\right)\overset{\left(a\right)}{=}\left(\mathrm{i}\mathrm{j}\right)\mathrm{k} & =\mathrm{k}\mathrm{k}=\mathrm{k}^{2}=-1\\ \mathrm{k}\mathrm{i}\mathrm{j}=\left(\mathrm{k}\mathrm{i}\right)\mathrm{j}\overset{\left(a\right)}{=}\mathrm{k}\left(\mathrm{i}\mathrm{j}\right) & =\mathrm{k}\mathrm{k}=\mathrm{k}^{2}=-1 \end{aligned} \]

\[ \begin{aligned} \mathrm{i}\mathrm{j} & =\mathrm{k}\\ -\mathrm{j}=\left(\mathrm{i}^{2}\right)\mathrm{j}\overset{\left(a\right)}{=}\mathrm{i}\left(\mathrm{i}\mathrm{j}\right) & =\mathrm{i}\mathrm{k}\\ -\mathrm{i}=\mathrm{i}\left(\mathrm{j}^{2}\right)\overset{\left(a\right)}{=}\left(\mathrm{i}\mathrm{j}\right)\mathrm{j} & =\mathrm{k}\mathrm{j} \end{aligned} \]

\[ \begin{aligned} -\mathrm{j}=\left(\mathrm{i}^{2}\right)\mathrm{j}\overset{\left(a\right)}{=}\mathrm{i}\left(\mathrm{i}\mathrm{j}\right) & =\mathrm{i}\mathrm{k}\\ 1=-\mathrm{j}^{2}=\mathrm{j}\left(-\mathrm{j}\right) & =\mathrm{j}\left(\mathrm{i}\mathrm{k}\right)\overset{\left(a\right)}{=}\left(\mathrm{j}\mathrm{i}\right)\mathrm{k}\\ \mathrm{k}=\left[1\right]\mathrm{k} & =\left[\left(\mathrm{j}\mathrm{i}\right)\mathrm{k}\right]\mathrm{k}\overset{\left(a\right)}{=}\left(\mathrm{j}\mathrm{i}\right)\left(\mathrm{k}^{2}\right)=\left(\mathrm{j}\mathrm{i}\right)\left(-1\right)\\ -\mathrm{k} & =\mathrm{j}\mathrm{i}\\ -\mathrm{i}=\mathrm{i}\left(\mathrm{j}^{2}\right)\overset{\left(a\right)}{=}\left(\mathrm{i}\mathrm{j}\right)\mathrm{j} & =\mathrm{k}\mathrm{j}\\ 1=\left(-\mathrm{i}\right)\mathrm{i} & =\left(\mathrm{k}\mathrm{j}\right)\mathrm{i}\overset{\left(a\right)}{=}\mathrm{k}\left(\mathrm{j}\mathrm{i}\right)=\mathrm{k}\mathrm{j}\mathrm{i}\\ 1 & =\mathrm{k}\mathrm{j}\mathrm{i} \end{aligned} \]

There is no more commutativity^[37.1.3.2.1], i.e.

\[ AB\not\equiv BA \]

but

\[ AB+BA=0\Leftrightarrow AB=-BA \] satisfying anticommutativity^[37.1.3.2.2].

\[ \begin{aligned} \begin{cases} \mathrm{i}\mathrm{j}=\mathrm{k}\\ \mathrm{j}\mathrm{i}=-\mathrm{k} \end{cases}\Leftrightarrow & \mathrm{j}\mathrm{i}=-\mathrm{k}=-\mathrm{i}\mathrm{j}\\ \Rightarrow & \mathrm{j}\mathrm{i}=-\mathrm{i}\mathrm{j}\\ \Leftrightarrow & \mathrm{i}\mathrm{j}+\mathrm{j}\mathrm{i}=0 \end{aligned} \]

\[ \begin{aligned} \begin{cases} \mathrm{k}\mathrm{i}\mathrm{j}=-1\\ \mathrm{k}\mathrm{j}\mathrm{i}=1 \end{cases}\Leftrightarrow & \mathrm{k}\mathrm{i}\mathrm{j}=-1=-\mathrm{k}\mathrm{j}\mathrm{i}\\ \Rightarrow & \mathrm{k}\mathrm{i}\mathrm{j}=-\mathrm{k}\mathrm{j}\mathrm{i}\\ \Leftrightarrow & \mathrm{k}\mathrm{i}\mathrm{j}+\mathrm{k}\mathrm{j}\mathrm{i}=0 \end{aligned} \]

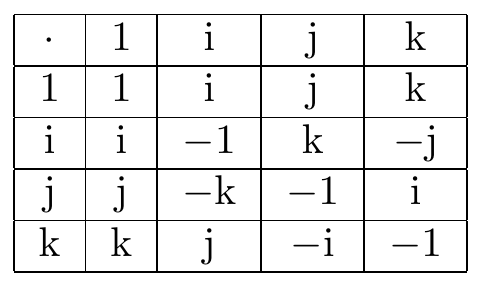
Fig. 24.1: quaternion multiplication table

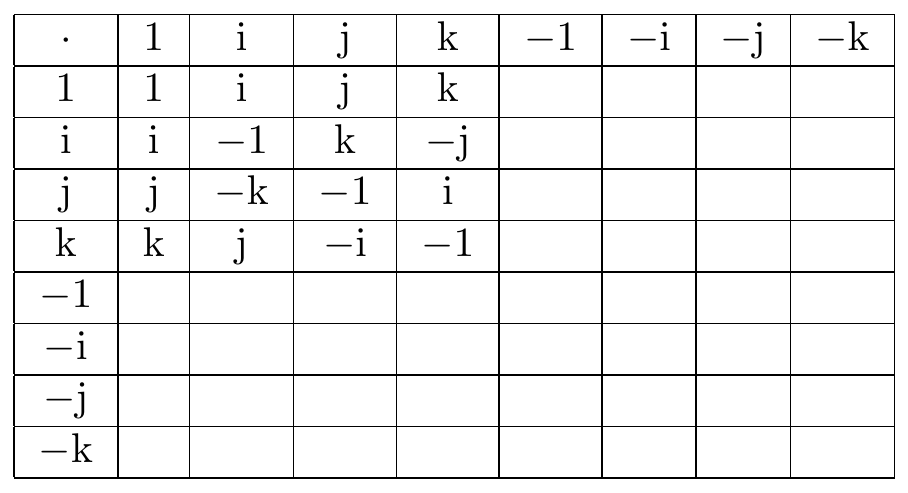
Fig. 30.2: quaternion basis group table

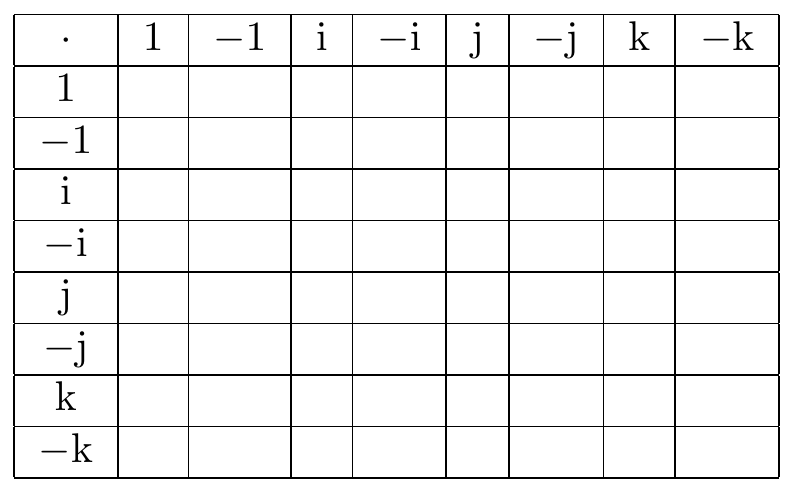
Fig. 17.1: quaternion basis group table 2

37.1.3.1 true origin of ( dot product & cross product ) / ( inner product & outer product )

product of two pure imaginary quaternions

\[ \begin{aligned} \boldsymbol{x}_{{\scriptscriptstyle 1}}\boldsymbol{x}_{{\scriptscriptstyle 2}}= & \left(x_{{\scriptscriptstyle 1}{\scriptscriptstyle 1}}\mathrm{i}+x_{{\scriptscriptstyle 1}{\scriptscriptstyle 2}}\mathrm{j}+x_{{\scriptscriptstyle 1}{\scriptscriptstyle 3}}\mathrm{k}\right)\left(x_{{\scriptscriptstyle 2}{\scriptscriptstyle 1}}\mathrm{i}+x_{{\scriptscriptstyle 2}{\scriptscriptstyle 2}}\mathrm{j}+x_{{\scriptscriptstyle 2}{\scriptscriptstyle 3}}\mathrm{k}\right)\\ = & x_{{\scriptscriptstyle 1}{\scriptscriptstyle 1}}x_{{\scriptscriptstyle 2}{\scriptscriptstyle 1}}\mathrm{i}^{{\scriptscriptstyle 2}}+x_{{\scriptscriptstyle 1}{\scriptscriptstyle 1}}x_{{\scriptscriptstyle 2}{\scriptscriptstyle 2}}\mathrm{i}\mathrm{j}+x_{{\scriptscriptstyle 1}{\scriptscriptstyle 1}}x_{{\scriptscriptstyle 2}{\scriptscriptstyle 3}}\mathrm{i}\mathrm{k}\\ + & x_{{\scriptscriptstyle 1}{\scriptscriptstyle 2}}x_{{\scriptscriptstyle 2}{\scriptscriptstyle 1}}\mathrm{j}\mathrm{i}+x_{{\scriptscriptstyle 1}{\scriptscriptstyle 2}}x_{{\scriptscriptstyle 2}{\scriptscriptstyle 2}}\mathrm{j}^{{\scriptscriptstyle 2}}+x_{{\scriptscriptstyle 1}{\scriptscriptstyle 2}}x_{{\scriptscriptstyle 2}{\scriptscriptstyle 3}}\mathrm{j}\mathrm{k}\\ + & x_{{\scriptscriptstyle 1}{\scriptscriptstyle 3}}x_{{\scriptscriptstyle 2}{\scriptscriptstyle 1}}\mathrm{k}\mathrm{i}+x_{{\scriptscriptstyle 1}{\scriptscriptstyle 3}}x_{{\scriptscriptstyle 2}{\scriptscriptstyle 2}}\mathrm{k}\mathrm{j}+x_{{\scriptscriptstyle 1}{\scriptscriptstyle 3}}x_{{\scriptscriptstyle 2}{\scriptscriptstyle 3}}\mathrm{k}^{{\scriptscriptstyle 2}}\\ = & -\left(x_{{\scriptscriptstyle 1}{\scriptscriptstyle 1}}x_{{\scriptscriptstyle 2}{\scriptscriptstyle 1}}+x_{{\scriptscriptstyle 1}{\scriptscriptstyle 2}}x_{{\scriptscriptstyle 2}{\scriptscriptstyle 2}}+x_{{\scriptscriptstyle 1}{\scriptscriptstyle 3}}x_{{\scriptscriptstyle 2}{\scriptscriptstyle 3}}\right)\\ + & \left(x_{{\scriptscriptstyle 1}{\scriptscriptstyle 2}}x_{{\scriptscriptstyle 2}{\scriptscriptstyle 3}}-x_{{\scriptscriptstyle 1}{\scriptscriptstyle 3}}x_{{\scriptscriptstyle 2}{\scriptscriptstyle 2}}\right)\mathrm{j}\mathrm{k}+\left(x_{{\scriptscriptstyle 1}{\scriptscriptstyle 3}}x_{{\scriptscriptstyle 2}{\scriptscriptstyle 1}}-x_{{\scriptscriptstyle 1}{\scriptscriptstyle 1}}x_{{\scriptscriptstyle 2}{\scriptscriptstyle 3}}\right)\mathrm{k}\mathrm{i}+\left(x_{{\scriptscriptstyle 1}{\scriptscriptstyle 1}}x_{{\scriptscriptstyle 2}{\scriptscriptstyle 2}}-x_{{\scriptscriptstyle 1}{\scriptscriptstyle 2}}x_{{\scriptscriptstyle 2}{\scriptscriptstyle 1}}\right)\mathrm{i}\mathrm{j}\\ = & -\left(x_{{\scriptscriptstyle 1}{\scriptscriptstyle 1}}x_{{\scriptscriptstyle 2}{\scriptscriptstyle 1}}+x_{{\scriptscriptstyle 1}{\scriptscriptstyle 2}}x_{{\scriptscriptstyle 2}{\scriptscriptstyle 2}}+x_{{\scriptscriptstyle 1}{\scriptscriptstyle 3}}x_{{\scriptscriptstyle 2}{\scriptscriptstyle 3}}\right)\\ + & \left(x_{{\scriptscriptstyle 1}{\scriptscriptstyle 2}}x_{{\scriptscriptstyle 2}{\scriptscriptstyle 3}}-x_{{\scriptscriptstyle 1}{\scriptscriptstyle 3}}x_{{\scriptscriptstyle 2}{\scriptscriptstyle 2}}\right)\mathrm{i}+\left(x_{{\scriptscriptstyle 1}{\scriptscriptstyle 3}}x_{{\scriptscriptstyle 2}{\scriptscriptstyle 1}}-x_{{\scriptscriptstyle 1}{\scriptscriptstyle 1}}x_{{\scriptscriptstyle 2}{\scriptscriptstyle 3}}\right)\mathrm{j}+\left(x_{{\scriptscriptstyle 1}{\scriptscriptstyle 1}}x_{{\scriptscriptstyle 2}{\scriptscriptstyle 2}}-x_{{\scriptscriptstyle 1}{\scriptscriptstyle 2}}x_{{\scriptscriptstyle 2}{\scriptscriptstyle 1}}\right)\mathrm{k}\\ = & -\left(\boldsymbol{x}_{{\scriptscriptstyle 1}}\cdot\boldsymbol{x}_{{\scriptscriptstyle 2}}\right)+\left(\boldsymbol{x}_{{\scriptscriptstyle 1}}\times\boldsymbol{x}_{{\scriptscriptstyle 2}}\right),\begin{cases} \boldsymbol{x}_{{\scriptscriptstyle 1}}\cdot\boldsymbol{x}_{{\scriptscriptstyle 2}}=x_{{\scriptscriptstyle 1}{\scriptscriptstyle 1}}x_{{\scriptscriptstyle 2}{\scriptscriptstyle 1}}+x_{{\scriptscriptstyle 1}{\scriptscriptstyle 2}}x_{{\scriptscriptstyle 2}{\scriptscriptstyle 2}}+x_{{\scriptscriptstyle 1}{\scriptscriptstyle 3}}x_{{\scriptscriptstyle 2}{\scriptscriptstyle 3}}\\ \boldsymbol{x}_{{\scriptscriptstyle 1}}\times\boldsymbol{x}_{{\scriptscriptstyle 2}}=\begin{vmatrix}\mathrm{i} & \mathrm{j} & \mathrm{k}\\ x_{{\scriptscriptstyle 1}{\scriptscriptstyle 1}} & x_{{\scriptscriptstyle 1}{\scriptscriptstyle 2}} & x_{{\scriptscriptstyle 1}{\scriptscriptstyle 3}}\\ x_{{\scriptscriptstyle 2}{\scriptscriptstyle 1}} & x_{{\scriptscriptstyle 2}{\scriptscriptstyle 2}} & x_{{\scriptscriptstyle 2}{\scriptscriptstyle 3}} \end{vmatrix} \end{cases}\\ = & -\boldsymbol{x}_{{\scriptscriptstyle 1}}\cdot\boldsymbol{x}_{{\scriptscriptstyle 2}}+\boldsymbol{x}_{{\scriptscriptstyle 1}}\times\boldsymbol{x}_{{\scriptscriptstyle 2}} \end{aligned} \]

product of two general quaternions / ordinary quaternions = Grassmann product

\[ \begin{aligned} q_{{\scriptscriptstyle 1}}q_{{\scriptscriptstyle 2}}= & \left(q_{{\scriptscriptstyle 10}}+q_{{\scriptscriptstyle 11}}\mathrm{i}+q_{{\scriptscriptstyle 12}}\mathrm{j}+q_{{\scriptscriptstyle 13}}\mathrm{k}\right)\left(q_{{\scriptscriptstyle 20}}+q_{{\scriptscriptstyle 21}}\mathrm{i}+q_{{\scriptscriptstyle 22}}\mathrm{j}+q_{{\scriptscriptstyle 23}}\mathrm{k}\right)\\ = & \left(x_{{\scriptscriptstyle 10}}+\boldsymbol{x}_{{\scriptscriptstyle 1}}\right)\left(x_{{\scriptscriptstyle 20}}+\boldsymbol{x}_{{\scriptscriptstyle 2}}\right),\begin{cases} x_{{\scriptscriptstyle i\mu}}=q_{{\scriptscriptstyle i\mu}} & \mu\in\left\{ 0\right\} \cup\left(\mathbb{N}\cap\left[1,3\right]\right)\\ \boldsymbol{x}_{{\scriptscriptstyle i}}=x_{{\scriptscriptstyle ij}}\boldsymbol{e}_{{\scriptscriptstyle j}} & i,j\in\mathbb{N}\cap\left[1,3\right],\begin{cases} \boldsymbol{e}_{{\scriptscriptstyle 1}}=\mathrm{i}\\ \boldsymbol{e}_{{\scriptscriptstyle 2}}=\mathrm{j}\\ \boldsymbol{e}_{{\scriptscriptstyle 3}}=\mathrm{k} \end{cases} \end{cases}\\ = & x_{{\scriptscriptstyle 10}}x_{{\scriptscriptstyle 20}}+x_{{\scriptscriptstyle 10}}\boldsymbol{x}_{{\scriptscriptstyle 2}}+x_{{\scriptscriptstyle 20}}\boldsymbol{x}_{{\scriptscriptstyle 1}}+\boldsymbol{x}_{{\scriptscriptstyle 1}}\boldsymbol{x}_{{\scriptscriptstyle 2}}\\ = & x_{{\scriptscriptstyle 10}}x_{{\scriptscriptstyle 20}}+x_{{\scriptscriptstyle 10}}\boldsymbol{x}_{{\scriptscriptstyle 2}}+x_{{\scriptscriptstyle 20}}\boldsymbol{x}_{{\scriptscriptstyle 1}}-\boldsymbol{x}_{{\scriptscriptstyle 1}}\cdot\boldsymbol{x}_{{\scriptscriptstyle 2}}+\boldsymbol{x}_{{\scriptscriptstyle 1}}\times\boldsymbol{x}_{{\scriptscriptstyle 2}}\\ = & \left(x_{{\scriptscriptstyle 10}}x_{{\scriptscriptstyle 20}}-\boldsymbol{x}_{{\scriptscriptstyle 1}}\cdot\boldsymbol{x}_{{\scriptscriptstyle 2}}\right)+\left(x_{{\scriptscriptstyle 10}}\boldsymbol{x}_{{\scriptscriptstyle 2}}+x_{{\scriptscriptstyle 20}}\boldsymbol{x}_{{\scriptscriptstyle 1}}+\boldsymbol{x}_{{\scriptscriptstyle 1}}\times\boldsymbol{x}_{{\scriptscriptstyle 2}}\right)\\ x_{{\scriptscriptstyle 10}}x_{{\scriptscriptstyle 20}}-\boldsymbol{x}_{{\scriptscriptstyle 1}}\cdot\boldsymbol{x}_{{\scriptscriptstyle 2}}= & \begin{pmatrix}q_{{\scriptscriptstyle 10}} & q_{{\scriptscriptstyle 11}} & q_{{\scriptscriptstyle 12}} & q_{{\scriptscriptstyle 13}}\end{pmatrix}\begin{pmatrix}1\\ & -1\\ & & -1\\ & & & -1 \end{pmatrix}\begin{pmatrix}q_{{\scriptscriptstyle 20}}\\ q_{{\scriptscriptstyle 21}}\\ q_{{\scriptscriptstyle 22}}\\ q_{{\scriptscriptstyle 23}} \end{pmatrix}=q_{{\scriptscriptstyle 1}}^{{\scriptscriptstyle \mu}}\eta_{{\scriptscriptstyle \mu\nu}}q_{{\scriptscriptstyle 2}}^{{\scriptscriptstyle \nu}}\\ = & \begin{pmatrix}q_{{\scriptscriptstyle 10}} & q_{{\scriptscriptstyle 11}} & q_{{\scriptscriptstyle 12}} & q_{{\scriptscriptstyle 13}}\end{pmatrix}\begin{pmatrix}1 & 0 & 0 & 0\\ 0 & -1 & 0 & 0\\ 0 & 0 & -1 & 0\\ 0 & 0 & 0 & -1 \end{pmatrix}\begin{pmatrix}q_{{\scriptscriptstyle 20}}\\ q_{{\scriptscriptstyle 21}}\\ q_{{\scriptscriptstyle 22}}\\ q_{{\scriptscriptstyle 23}} \end{pmatrix}=\boldsymbol{q}_{{\scriptscriptstyle 1}}^{\intercal}H\boldsymbol{q}_{{\scriptscriptstyle 2}},H=\left[\eta_{{\scriptscriptstyle \mu\nu}}\right]_{4\times4}=\eta_{{\scriptscriptstyle \mu\nu}} \end{aligned} \]

\[ \begin{aligned} q_{{\scriptscriptstyle 1}}q_{{\scriptscriptstyle 2}}= & \left(x_{{\scriptscriptstyle 10}}x_{{\scriptscriptstyle 20}}-\boldsymbol{x}_{{\scriptscriptstyle 1}}\cdot\boldsymbol{x}_{{\scriptscriptstyle 2}}\right)+\left(x_{{\scriptscriptstyle 10}}\boldsymbol{x}_{{\scriptscriptstyle 2}}+x_{{\scriptscriptstyle 20}}\boldsymbol{x}_{{\scriptscriptstyle 1}}+\boldsymbol{x}_{{\scriptscriptstyle 1}}\times\boldsymbol{x}_{{\scriptscriptstyle 2}}\right)\\ QP= & \left(Q_{{\scriptscriptstyle 0}}P_{{\scriptscriptstyle 0}}-\boldsymbol{Q}\cdot\boldsymbol{P}\right)+\left(Q_{{\scriptscriptstyle 0}}\boldsymbol{P}+P_{{\scriptscriptstyle 0}}\boldsymbol{Q}+\boldsymbol{Q}\times\boldsymbol{P}\right) \end{aligned} \]

\[ ab=\left(a_{{\scriptscriptstyle 0}}b_{{\scriptscriptstyle 0}}-\boldsymbol{a}\cdot\boldsymbol{b}\right)+\left(a_{{\scriptscriptstyle 0}}\boldsymbol{b}+b_{{\scriptscriptstyle 0}}\boldsymbol{a}+\boldsymbol{a}\times\boldsymbol{b}\right) \]

Minkowski metric tensor

\[ \eta=H=\left[\eta_{{\scriptscriptstyle \mu\nu}}\right]_{4\times4}=\begin{pmatrix}1 & 0 & 0 & 0\\ 0 & -1 & 0 & 0\\ 0 & 0 & -1 & 0\\ 0 & 0 & 0 & -1 \end{pmatrix}=\begin{pmatrix}1\\ & -1\\ & & -1\\ & & & -1 \end{pmatrix}=\eta_{{\scriptscriptstyle \mu\nu}} \]

and quaternions as 4-vectors or four-vectors

\[ \boldsymbol{q}_{{\scriptscriptstyle 1}}^{\intercal}=\begin{pmatrix}q_{{\scriptscriptstyle 10}} & q_{{\scriptscriptstyle 11}} & q_{{\scriptscriptstyle 12}} & q_{{\scriptscriptstyle 13}}\end{pmatrix} \]

\[ \boldsymbol{q}_{{\scriptscriptstyle 2}}=\begin{pmatrix}q_{{\scriptscriptstyle 20}}\\ q_{{\scriptscriptstyle 21}}\\ q_{{\scriptscriptstyle 22}}\\ q_{{\scriptscriptstyle 23}} \end{pmatrix} \]

37.1.3.2 commutativity vs. anticommutativity

37.1.3.2.1 commutativity

交換律 = 交換性 = 對易性

\[ AB=BA\Leftrightarrow AB-BA=0 \]

\[ AB=BA\Rightarrow AB\equiv BA \]

37.1.3.2.2 anticommutativity

反交換律 = 反交換性 = 反對易性

\[ AB+BA=0\Leftrightarrow AB=-BA \]

\[ AB=-BA\Rightarrow AB\not\equiv BA \]

37.1.3.3 bracket

37.1.3.3.1 self-invented bracket

自創括號 = 自創括

37.1.3.3.1.1 commutative bracket

交換括號 = 對易式

\[ \left[X,Y\right]=\dfrac{XY-YX}{2} \]

37.1.3.3.1.2 anticommutative bracket

反交換括號 = 反對易式

\[ \left\{ X,Y\right\} =\dfrac{XY+YX}{2} \]

37.1.3.3.2 Poisson bracket

https://en.wikipedia.org/wiki/Poisson_bracket

37.1.3.3.3 Lagrange bracket

37.1.3.3.4 Lie bracket

37.1.3.4 triple product

product = double product = Grassmann product

\[ \begin{aligned} ab= & \left(a_{{\scriptscriptstyle 0}}b_{{\scriptscriptstyle 0}}-\boldsymbol{a}\cdot\boldsymbol{b}\right)+\left(a_{{\scriptscriptstyle 0}}\boldsymbol{b}+b_{{\scriptscriptstyle 0}}\boldsymbol{a}+\boldsymbol{a}\times\boldsymbol{b}\right)\\ \overset{\begin{cases} a_{0}=0\\ b_{0}=0 \end{cases}}{=} & \left(00-\boldsymbol{a}\cdot\boldsymbol{b}\right)+\left(0\boldsymbol{b}+0\boldsymbol{a}+\boldsymbol{a}\times\boldsymbol{b}\right)\\ = & -\boldsymbol{a}\cdot\boldsymbol{b}+\boldsymbol{a}\times\boldsymbol{b} \end{aligned} \]

pure imaginary product can get both ( real & imaginary ) / ( scalar & vector ) parts

\[ ab=\boldsymbol{a}\boldsymbol{b}=-\boldsymbol{a}\cdot\boldsymbol{b}+\boldsymbol{a}\times\boldsymbol{b},\begin{cases} a=0+\boldsymbol{a}=\boldsymbol{a}\\ b=0+\boldsymbol{b}=\boldsymbol{b} \end{cases} \]

triple product

https://en.wikipedia.org/wiki/Triple_product

pure imaginary

\[ \begin{cases} a=0+\boldsymbol{a}=\boldsymbol{a}\\ b=0+\boldsymbol{b}=\boldsymbol{b}\\ c=0+\boldsymbol{c}=\boldsymbol{c} \end{cases} \]

\[ \begin{aligned} abc=\boldsymbol{a}\boldsymbol{b}\boldsymbol{c}= & \left(\boldsymbol{a}\boldsymbol{b}\right)\boldsymbol{c}=\left(-\boldsymbol{a}\cdot\boldsymbol{b}+\boldsymbol{a}\times\boldsymbol{b}\right)\boldsymbol{c}\\ = & \boldsymbol{a}\left(\boldsymbol{b}\boldsymbol{c}\right)=\boldsymbol{a}\left(-\boldsymbol{b}\cdot\boldsymbol{c}+\boldsymbol{b}\times\boldsymbol{c}\right) \end{aligned} \]

\[ \begin{aligned} \boldsymbol{a}\boldsymbol{b}\boldsymbol{c}=\left(\boldsymbol{a}\boldsymbol{b}\right)\boldsymbol{c}= & \left(-\boldsymbol{a}\cdot\boldsymbol{b}+\boldsymbol{a}\times\boldsymbol{b}\right)\boldsymbol{c}\\ = & -\left(\boldsymbol{a}\cdot\boldsymbol{b}\right)\boldsymbol{c}+\left(\boldsymbol{a}\times\boldsymbol{b}\right)\boldsymbol{c}\\ = & -\left(\boldsymbol{a}\cdot\boldsymbol{b}\right)\boldsymbol{c}+\left(-\left(\boldsymbol{a}\times\boldsymbol{b}\right)\cdot\boldsymbol{c}+\left(\boldsymbol{a}\times\boldsymbol{b}\right)\times\boldsymbol{c}\right)\\ = & \left[-\left(\boldsymbol{a}\times\boldsymbol{b}\right)\cdot\boldsymbol{c}\right]+\left[\left(\boldsymbol{a}\times\boldsymbol{b}\right)\times\boldsymbol{c}-\left(\boldsymbol{a}\cdot\boldsymbol{b}\right)\boldsymbol{c}\right]\\ =\boldsymbol{a}\left(\boldsymbol{b}\boldsymbol{c}\right)= & \boldsymbol{a}\left(-\boldsymbol{b}\cdot\boldsymbol{c}+\boldsymbol{b}\times\boldsymbol{c}\right)\\ = & -\boldsymbol{a}\left(\boldsymbol{b}\cdot\boldsymbol{c}\right)+\boldsymbol{a}\left(\boldsymbol{b}\times\boldsymbol{c}\right)\\ = & -\boldsymbol{a}\left(\boldsymbol{b}\cdot\boldsymbol{c}\right)+\left(-\boldsymbol{a}\cdot\left(\boldsymbol{b}\times\boldsymbol{c}\right)+\boldsymbol{a}\times\left(\boldsymbol{b}\times\boldsymbol{c}\right)\right)\\ = & \left[-\boldsymbol{a}\cdot\left(\boldsymbol{b}\times\boldsymbol{c}\right)\right]+\left[\boldsymbol{a}\times\left(\boldsymbol{b}\times\boldsymbol{c}\right)-\boldsymbol{a}\left(\boldsymbol{b}\cdot\boldsymbol{c}\right)\right] \end{aligned} \]

by comparing ( real & imaginary ) / ( scalar & vector ) parts,

\[ \begin{aligned} & \begin{cases} -\left(\boldsymbol{a}\times\boldsymbol{b}\right)\cdot\boldsymbol{c}=-\boldsymbol{a}\cdot\left(\boldsymbol{b}\times\boldsymbol{c}\right)\\ \left(\boldsymbol{a}\times\boldsymbol{b}\right)\times\boldsymbol{c}-\left(\boldsymbol{a}\cdot\boldsymbol{b}\right)\boldsymbol{c}=\boldsymbol{a}\times\left(\boldsymbol{b}\times\boldsymbol{c}\right)-\boldsymbol{a}\left(\boldsymbol{b}\cdot\boldsymbol{c}\right) \end{cases}\\ \Rightarrow & \begin{cases} \left(\boldsymbol{a}\times\boldsymbol{b}\right)\cdot\boldsymbol{c}=\boldsymbol{a}\cdot\left(\boldsymbol{b}\times\boldsymbol{c}\right) & \left(s\right)\\ \left(\boldsymbol{a}\times\boldsymbol{b}\right)\times\boldsymbol{c}-\left(\boldsymbol{a}\cdot\boldsymbol{b}\right)\boldsymbol{c}=\boldsymbol{a}\times\left(\boldsymbol{b}\times\boldsymbol{c}\right)-\boldsymbol{a}\left(\boldsymbol{b}\cdot\boldsymbol{c}\right) & \left(v\right) \end{cases} \end{aligned} \]

permutation

\[ \sigma=\begin{pmatrix}x_{{\scriptscriptstyle 1}} & x_{{\scriptscriptstyle 2}} & \cdots\\ \sigma\left(x_{{\scriptscriptstyle 1}}\right) & \sigma\left(x_{{\scriptscriptstyle 2}}\right) & \cdots \end{pmatrix} \]

\[ \begin{pmatrix}a & b & c\\ a & b & c \end{pmatrix},\begin{pmatrix}a & b & c\\ b & c & a \end{pmatrix},\begin{pmatrix}a & b & c\\ c & a & b \end{pmatrix},\begin{pmatrix}a & b & c\\ a & c & b \end{pmatrix},\begin{pmatrix}a & b & c\\ b & a & c \end{pmatrix},\begin{pmatrix}a & b & c\\ c & b & a \end{pmatrix} \]

\[ \begin{aligned} \left(s\right)\Rightarrow & \begin{cases} \left(\boldsymbol{a}\times\boldsymbol{b}\right)\cdot\boldsymbol{c}=\boldsymbol{a}\cdot\left(\boldsymbol{b}\times\boldsymbol{c}\right) & \begin{pmatrix}a & b & c\\ a & b & c \end{pmatrix},s_{{\scriptscriptstyle 1}}\\ \left(\boldsymbol{b}\times\boldsymbol{c}\right)\cdot\boldsymbol{a}=\boldsymbol{b}\cdot\left(\boldsymbol{c}\times\boldsymbol{a}\right) & \begin{pmatrix}a & b & c\\ b & c & a \end{pmatrix},s_{{\scriptscriptstyle 2}}\\ \left(\boldsymbol{c}\times\boldsymbol{a}\right)\cdot\boldsymbol{b}=\boldsymbol{c}\cdot\left(\boldsymbol{a}\times\boldsymbol{b}\right) & \begin{pmatrix}a & b & c\\ c & a & b \end{pmatrix},s_{{\scriptscriptstyle 3}}\\ \left(\boldsymbol{b}\times\boldsymbol{a}\right)\cdot\boldsymbol{c}=\boldsymbol{b}\cdot\left(\boldsymbol{a}\times\boldsymbol{c}\right) & \begin{pmatrix}a & b & c\\ b & a & c \end{pmatrix},s_{{\scriptscriptstyle 4}}\\ \left(\boldsymbol{a}\times\boldsymbol{c}\right)\cdot\boldsymbol{b}=\boldsymbol{a}\cdot\left(\boldsymbol{c}\times\boldsymbol{b}\right) & \begin{pmatrix}a & b & c\\ a & c & b \end{pmatrix},s_{{\scriptscriptstyle 5}}\\ \left(\boldsymbol{c}\times\boldsymbol{b}\right)\cdot\boldsymbol{a}=\boldsymbol{c}\cdot\left(\boldsymbol{b}\times\boldsymbol{a}\right) & \begin{pmatrix}a & b & c\\ c & b & a \end{pmatrix},s_{{\scriptscriptstyle 6}} \end{cases}\\ \overset{\cdot\text{ commutative}}{\Rightarrow} & \left(\boldsymbol{a}\times\boldsymbol{b}\right)\cdot\boldsymbol{c}\overset{s_{{\scriptscriptstyle 1}}}{=}\left(\boldsymbol{b}\times\boldsymbol{c}\right)\cdot\boldsymbol{a}\overset{s_{{\scriptscriptstyle 2}}}{=}\left(\boldsymbol{c}\times\boldsymbol{a}\right)\cdot\boldsymbol{b}\overset{s_{{\scriptscriptstyle 3}}}{=}\left(\boldsymbol{a}\times\boldsymbol{b}\right)\cdot\boldsymbol{c}\\ \overset{\times\text{ anticommutative}}{=} & -\left(\boldsymbol{b}\times\boldsymbol{a}\right)\cdot\boldsymbol{c}\overset{s_{{\scriptscriptstyle 6}}}{=}-\left(\boldsymbol{c}\times\boldsymbol{b}\right)\cdot\boldsymbol{a}\overset{s_{{\scriptscriptstyle 5}}}{=}-\left(\boldsymbol{a}\times\boldsymbol{c}\right)\cdot\boldsymbol{b}\overset{s_{{\scriptscriptstyle 4}}}{=}-\left(\boldsymbol{b}\times\boldsymbol{a}\right)\cdot\boldsymbol{c}\\ \Leftrightarrow & \boldsymbol{a}\cdot\left(\boldsymbol{b}\times\boldsymbol{c}\right)=\boldsymbol{b}\cdot\left(\boldsymbol{c}\times\boldsymbol{a}\right)=\boldsymbol{c}\cdot\left(\boldsymbol{a}\times\boldsymbol{b}\right)\\ = & -\boldsymbol{a}\cdot\left(\boldsymbol{c}\times\boldsymbol{b}\right)=-\boldsymbol{b}\cdot\left(\boldsymbol{a}\times\boldsymbol{c}\right)=-\boldsymbol{c}\cdot\left(\boldsymbol{b}\times\boldsymbol{a}\right) \end{aligned} \]

\[ \begin{aligned} \left(v\right)\Rightarrow & \begin{cases} \left(\boldsymbol{a}\times\boldsymbol{b}\right)\times\boldsymbol{c}-\left(\boldsymbol{a}\cdot\boldsymbol{b}\right)\boldsymbol{c}=\boldsymbol{a}\times\left(\boldsymbol{b}\times\boldsymbol{c}\right)-\boldsymbol{a}\left(\boldsymbol{b}\cdot\boldsymbol{c}\right) & \begin{pmatrix}a & b & c\\ a & b & c \end{pmatrix},v_{{\scriptscriptstyle 1}}\\ \left(\boldsymbol{b}\times\boldsymbol{c}\right)\times\boldsymbol{a}-\left(\boldsymbol{b}\cdot\boldsymbol{c}\right)\boldsymbol{a}=\boldsymbol{b}\times\left(\boldsymbol{c}\times\boldsymbol{a}\right)-\boldsymbol{b}\left(\boldsymbol{c}\cdot\boldsymbol{a}\right) & \begin{pmatrix}a & b & c\\ b & c & a \end{pmatrix},v_{{\scriptscriptstyle 2}}\\ \left(\boldsymbol{c}\times\boldsymbol{a}\right)\times\boldsymbol{b}-\left(\boldsymbol{c}\cdot\boldsymbol{a}\right)\boldsymbol{b}=\boldsymbol{c}\times\left(\boldsymbol{a}\times\boldsymbol{b}\right)-\boldsymbol{c}\left(\boldsymbol{a}\cdot\boldsymbol{b}\right) & \begin{pmatrix}a & b & c\\ c & a & b \end{pmatrix},v_{{\scriptscriptstyle 3}}\\ \left(\boldsymbol{b}\times\boldsymbol{a}\right)\times\boldsymbol{c}-\left(\boldsymbol{b}\cdot\boldsymbol{a}\right)\boldsymbol{c}=\boldsymbol{b}\times\left(\boldsymbol{a}\times\boldsymbol{c}\right)-\boldsymbol{b}\left(\boldsymbol{a}\cdot\boldsymbol{c}\right) & \begin{pmatrix}a & b & c\\ b & a & c \end{pmatrix},v_{{\scriptscriptstyle 4}}\\ \left(\boldsymbol{a}\times\boldsymbol{c}\right)\times\boldsymbol{b}-\left(\boldsymbol{a}\cdot\boldsymbol{c}\right)\boldsymbol{b}=\boldsymbol{a}\times\left(\boldsymbol{c}\times\boldsymbol{b}\right)-\boldsymbol{a}\left(\boldsymbol{c}\cdot\boldsymbol{b}\right) & \begin{pmatrix}a & b & c\\ a & c & b \end{pmatrix},v_{{\scriptscriptstyle 5}}\\ \left(\boldsymbol{c}\times\boldsymbol{b}\right)\times\boldsymbol{a}-\left(\boldsymbol{c}\cdot\boldsymbol{b}\right)\boldsymbol{a}=\boldsymbol{c}\times\left(\boldsymbol{b}\times\boldsymbol{a}\right)-\boldsymbol{c}\left(\boldsymbol{b}\cdot\boldsymbol{a}\right) & \begin{pmatrix}a & b & c\\ c & b & a \end{pmatrix},v_{{\scriptscriptstyle 6}} \end{cases}\\ \Rightarrow & \begin{cases} -Z-C=X-A & v_{{\scriptscriptstyle 1}}\\ -X-A=Y-B & v_{{\scriptscriptstyle 2}}\\ -Y-B=Z-C & v_{{\scriptscriptstyle 3}}\\ Z-C=-Y-B & v_{{\scriptscriptstyle 4}}\\ Y-B=-X-A & v_{{\scriptscriptstyle 5}}\\ X-A=-Z-C & v_{{\scriptscriptstyle 6}} \end{cases},\begin{cases} \cdot\text{ and scalar-vector product} & \text{commutative}\\ \times & \text{anticommutative} \end{cases},\\ & \begin{cases} X=\boldsymbol{a}\times\left(\boldsymbol{b}\times\boldsymbol{c}\right)=-\left(\boldsymbol{b}\times\boldsymbol{c}\right)\times\boldsymbol{a}=-\boldsymbol{a}\times\left(\boldsymbol{c}\times\boldsymbol{b}\right)=\left(\boldsymbol{c}\times\boldsymbol{b}\right)\times\boldsymbol{a}\\ Y=\boldsymbol{b}\times\left(\boldsymbol{c}\times\boldsymbol{a}\right)=-\left(\boldsymbol{c}\times\boldsymbol{a}\right)\times\boldsymbol{b}=-\boldsymbol{b}\times\left(\boldsymbol{a}\times\boldsymbol{c}\right)=\left(\boldsymbol{a}\times\boldsymbol{c}\right)\times\boldsymbol{b}\\ Z=\boldsymbol{c}\times\left(\boldsymbol{a}\times\boldsymbol{b}\right)=-\left(\boldsymbol{a}\times\boldsymbol{b}\right)\times\boldsymbol{c}=-\boldsymbol{c}\times\left(\boldsymbol{b}\times\boldsymbol{a}\right)=\left(\boldsymbol{b}\times\boldsymbol{a}\right)\times\boldsymbol{c}\\ A=\boldsymbol{a}\left(\boldsymbol{b}\cdot\boldsymbol{c}\right)=\boldsymbol{a}\left(\boldsymbol{c}\cdot\boldsymbol{b}\right)=\left(\boldsymbol{c}\cdot\boldsymbol{b}\right)\boldsymbol{a}=\left(\boldsymbol{b}\cdot\boldsymbol{c}\right)\boldsymbol{a}\\ B=\boldsymbol{b}\left(\boldsymbol{c}\cdot\boldsymbol{a}\right)=\boldsymbol{b}\left(\boldsymbol{a}\cdot\boldsymbol{c}\right)=\left(\boldsymbol{a}\cdot\boldsymbol{c}\right)\boldsymbol{b}=\left(\boldsymbol{c}\cdot\boldsymbol{a}\right)\boldsymbol{b}\\ C=\boldsymbol{c}\left(\boldsymbol{a}\cdot\boldsymbol{b}\right)=\boldsymbol{c}\left(\boldsymbol{b}\cdot\boldsymbol{a}\right)=\left(\boldsymbol{b}\cdot\boldsymbol{a}\right)\boldsymbol{c}=\left(\boldsymbol{a}\cdot\boldsymbol{b}\right)\boldsymbol{c} \end{cases}\\ \Rightarrow & \begin{cases} -Z-C=X-A & v_{{\scriptscriptstyle 1}}=v_{{\scriptscriptstyle 6}}\\ -X-A=Y-B & v_{{\scriptscriptstyle 2}}=v_{{\scriptscriptstyle 5}}\\ -Y-B=Z-C & v_{{\scriptscriptstyle 3}}=v_{{\scriptscriptstyle 4}} \end{cases}\Leftrightarrow\begin{cases} Z+X=A-C\\ X+Y=B-A\\ Y+Z=C-B \end{cases}\Leftrightarrow\begin{cases} X+Y=B-A\\ Y+Z=C-B\\ Z+X=A-C \end{cases}\\ \Leftrightarrow & \begin{cases} 2\left(X+Y+Z\right)=0 & \Rightarrow X+Y+Z=0\\ Y+Z=C-B & \Rightarrow X=B-C\Leftrightarrow\boldsymbol{a}\times\left(\boldsymbol{b}\times\boldsymbol{c}\right)=\boldsymbol{b}\left(\boldsymbol{c}\cdot\boldsymbol{a}\right)-\boldsymbol{c}\left(\boldsymbol{a}\cdot\boldsymbol{b}\right)\text{ "back cab"}\\ Z+X=A-C & \Rightarrow Y=C-A\Leftrightarrow\boldsymbol{b}\times\left(\boldsymbol{c}\times\boldsymbol{a}\right)=\boldsymbol{c}\left(\boldsymbol{a}\cdot\boldsymbol{b}\right)-\boldsymbol{a}\left(\boldsymbol{b}\cdot\boldsymbol{c}\right)\\ X+Y=B-A & \Rightarrow Z=A-B\Leftrightarrow\boldsymbol{c}\times\left(\boldsymbol{a}\times\boldsymbol{b}\right)=\boldsymbol{a}\left(\boldsymbol{b}\cdot\boldsymbol{c}\right)-\boldsymbol{b}\left(\boldsymbol{c}\cdot\boldsymbol{a}\right) \end{cases} \end{aligned} \]

37.1.3.5 differential operator

https://en.wikipedia.org/wiki/Differential_operator

37.1.3.5.1 4-differential operator

4-differential operator / four-differential operator = d’Alembert operator

\[ \begin{aligned} \mathrm{D}= & \dfrac{\partial}{\partial t}+\mathrm{i}\dfrac{\partial}{\partial x}+\mathrm{j}\dfrac{\partial}{\partial y}+\mathrm{k}\dfrac{\partial}{\partial z}=\partial_{{\scriptscriptstyle t}}+\mathrm{i}\partial_{{\scriptscriptstyle x}}+\mathrm{j}\partial_{{\scriptscriptstyle y}}+\mathrm{k}\partial_{z}\\ = & \dfrac{\partial}{\partial t}+\boldsymbol{i}\dfrac{\partial}{\partial x}+\boldsymbol{j}\dfrac{\partial}{\partial y}+\boldsymbol{k}\dfrac{\partial}{\partial z}=\partial_{{\scriptscriptstyle t}}+\boldsymbol{i}\partial_{{\scriptscriptstyle x}}+\boldsymbol{j}\partial_{{\scriptscriptstyle y}}+\boldsymbol{k}\partial_{z}\\ = & \dfrac{\partial}{\partial x_{{\scriptscriptstyle 0}}}+\boldsymbol{e}_{{\scriptscriptstyle 1}}\dfrac{\partial}{\partial x_{{\scriptscriptstyle 1}}}+\boldsymbol{e}_{{\scriptscriptstyle 2}}\dfrac{\partial}{\partial x_{{\scriptscriptstyle 2}}}+\boldsymbol{e}_{{\scriptscriptstyle 3}}\dfrac{\partial}{\partial x_{{\scriptscriptstyle 3}}}=\partial_{{\scriptscriptstyle 0}}+\boldsymbol{e}_{{\scriptscriptstyle i}}\partial_{{\scriptscriptstyle i}}=\partial_{{\scriptscriptstyle 0}}+\boldsymbol{\nabla} \end{aligned} \]

\[ \mathrm{D}=\partial_{{\scriptscriptstyle 0}}+\mathrm{i}\partial_{{\scriptscriptstyle 1}}+\mathrm{j}\partial_{{\scriptscriptstyle 2}}+\mathrm{k}\partial_{{\scriptscriptstyle 3}}=\partial_{{\scriptscriptstyle 0}}+\boldsymbol{\nabla}=\mathrm{D}_{{\scriptscriptstyle 0}}+\boldsymbol{\mathrm{D}} \]

37.1.3.5.2 nabla

nabla = spatial differential operator = 3-differential operator / three-differential operator

\[ \boldsymbol{\nabla}=\boldsymbol{e}_{{\scriptscriptstyle i}}\partial_{{\scriptscriptstyle i}}=\sum_{i=1}^{3}\boldsymbol{e}_{{\scriptscriptstyle i}}\partial_{{\scriptscriptstyle i}}=\sum_{i=1}^{3}\boldsymbol{e}_{{\scriptscriptstyle i}}\dfrac{\partial}{\partial x_{{\scriptscriptstyle i}}}=\begin{pmatrix}\dfrac{\partial}{\partial x} & \dfrac{\partial}{\partial y} & \dfrac{\partial}{\partial z}\end{pmatrix}^{\intercal}=\begin{pmatrix}\dfrac{\partial}{\partial x}\\ \dfrac{\partial}{\partial y}\\ \dfrac{\partial}{\partial z} \end{pmatrix} \]

37.1.3.5.3 Laplace operator

Laplace operator = Laplacian

\[ \triangle=\boldsymbol{\nabla}^{2}=\boldsymbol{\nabla}\cdot\boldsymbol{\nabla}=\dfrac{\partial^{2}}{\partial x^{2}}+\dfrac{\partial^{2}}{\partial y^{2}}+\dfrac{\partial^{2}}{\partial z^{2}} \]

37.1.3.5.4 d’Alembert operator

\[ \square=\square_{{\scriptscriptstyle c}}=\dfrac{1}{c^{2}}\dfrac{\partial^{2}}{\partial t^{2}}-\dfrac{\partial^{2}}{\partial x^{2}}-\dfrac{\partial^{2}}{\partial y^{2}}-\dfrac{\partial^{2}}{\partial z^{2}}=\dfrac{1}{c^{2}}\dfrac{\partial^{2}}{\partial t^{2}}-\triangle=\dfrac{1}{c^{2}}\dfrac{\partial^{2}}{\partial t^{2}}-\boldsymbol{\nabla}^{2} \]

\[ \square_{{\scriptscriptstyle 1}}=\square_{{\scriptscriptstyle c=1}}=\dfrac{\partial^{2}}{\partial t^{2}}-\dfrac{\partial^{2}}{\partial x^{2}}-\dfrac{\partial^{2}}{\partial y^{2}}-\dfrac{\partial^{2}}{\partial z^{2}}=\dfrac{\partial^{2}}{\partial t^{2}}-\triangle=\dfrac{\partial^{2}}{\partial t^{2}}-\boldsymbol{\nabla}^{2} \]

37.1.3.6 electromagnetism

Maxwell

37.1.3.6.1 4-potential

electromagnetic 4-potential / four-potential

\[ A=A_{{\scriptscriptstyle 0}}++\mathrm{i}A_{{\scriptscriptstyle 1}}+\mathrm{j}A_{{\scriptscriptstyle 2}}+\mathrm{k}A_{{\scriptscriptstyle 3}}=A_{0}+\boldsymbol{A} \]

4-differential operator^[37.1.3.5.1]

\[ QP=\left(Q_{{\scriptscriptstyle 0}}P_{{\scriptscriptstyle 0}}-\boldsymbol{Q}\cdot\boldsymbol{P}\right)+\left(Q_{{\scriptscriptstyle 0}}\boldsymbol{P}+P_{{\scriptscriptstyle 0}}\boldsymbol{Q}+\boldsymbol{Q}\times\boldsymbol{P}\right) \]

commutative bracket^{[37.1.3.3.1.1]}

\[ \begin{aligned} \left[\mathrm{D},A\right]= & \dfrac{\mathrm{D}A-A\mathrm{D}}{2}\\ 2\left[\mathrm{D},A\right]= & \mathrm{D}A-A\mathrm{D}\\ = & \left(\partial_{{\scriptscriptstyle 0}}+\mathrm{i}\partial_{{\scriptscriptstyle 1}}+\mathrm{j}\partial_{{\scriptscriptstyle 2}}+\mathrm{k}\partial_{{\scriptscriptstyle 3}}\right)\left(A_{{\scriptscriptstyle 0}}++\mathrm{i}A_{{\scriptscriptstyle 1}}+\mathrm{j}A_{{\scriptscriptstyle 2}}+\mathrm{k}A_{{\scriptscriptstyle 3}}\right)\\ - & \left(A_{{\scriptscriptstyle 0}}++\mathrm{i}A_{{\scriptscriptstyle 1}}+\mathrm{j}A_{{\scriptscriptstyle 2}}+\mathrm{k}A_{{\scriptscriptstyle 3}}\right)\left(\partial_{{\scriptscriptstyle 0}}+\mathrm{i}\partial_{{\scriptscriptstyle 1}}+\mathrm{j}\partial_{{\scriptscriptstyle 2}}+\mathrm{k}\partial_{{\scriptscriptstyle 3}}\right)\\ \mathrm{D}A= & \left(\mathrm{D}_{{\scriptscriptstyle 0}}A_{{\scriptscriptstyle 0}}-\boldsymbol{\mathrm{D}}\cdot\boldsymbol{A}\right)+\left(\mathrm{D}_{{\scriptscriptstyle 0}}\boldsymbol{A}+A_{{\scriptscriptstyle 0}}\boldsymbol{\mathrm{D}}+\boldsymbol{\mathrm{D}}\times\boldsymbol{A}\right)\\ = & \left(\mathrm{D}_{{\scriptscriptstyle 0}}A_{{\scriptscriptstyle 0}}-\boldsymbol{\mathrm{D}}\cdot\boldsymbol{A}\right)+\left(\mathrm{D}_{{\scriptscriptstyle 0}}\boldsymbol{A}+\boldsymbol{\mathrm{D}}A_{{\scriptscriptstyle 0}}+\boldsymbol{\mathrm{D}}\times\boldsymbol{A}\right)\\ = & \mathrm{D}_{{\scriptscriptstyle 0}}\left(A_{{\scriptscriptstyle 0}}+\boldsymbol{A}\right)-\boldsymbol{\mathrm{D}}\cdot\boldsymbol{A}+\boldsymbol{\mathrm{D}}A_{{\scriptscriptstyle 0}}+\boldsymbol{\mathrm{D}}\times\boldsymbol{A}\\ = & \mathrm{D}_{{\scriptscriptstyle 0}}A-\boldsymbol{\mathrm{D}}\cdot\boldsymbol{A}+\boldsymbol{\mathrm{D}}A_{{\scriptscriptstyle 0}}+\boldsymbol{\mathrm{D}}\times\boldsymbol{A}\\ = & \partial_{{\scriptscriptstyle 0}}A-\boldsymbol{\nabla}\cdot\boldsymbol{A}+\boldsymbol{\nabla}A_{{\scriptscriptstyle 0}}+\boldsymbol{\nabla}\times\boldsymbol{A}\\ A\mathrm{D}= & \left(A_{{\scriptscriptstyle 0}}\mathrm{D}_{{\scriptscriptstyle 0}}-\boldsymbol{A}\cdot\boldsymbol{\mathrm{D}}\right)+\left(A_{{\scriptscriptstyle 0}}\boldsymbol{\mathrm{D}}+\mathrm{D}_{{\scriptscriptstyle 0}}\boldsymbol{A}+\boldsymbol{A}\times\boldsymbol{\mathrm{D}}\right)\\ = & \left(\mathrm{D}_{{\scriptscriptstyle 0}}A_{{\scriptscriptstyle 0}}-\boldsymbol{\mathrm{D}}\cdot\boldsymbol{A}\right)+\left(\boldsymbol{\mathrm{D}}A_{{\scriptscriptstyle 0}}+\mathrm{D}_{{\scriptscriptstyle 0}}\boldsymbol{A}-\boldsymbol{\mathrm{D}}\times\boldsymbol{A}\right)\\ = & \left(\mathrm{D}_{{\scriptscriptstyle 0}}A_{{\scriptscriptstyle 0}}-\boldsymbol{\mathrm{D}}\cdot\boldsymbol{A}\right)+\left(\mathrm{D}_{{\scriptscriptstyle 0}}\boldsymbol{A}+\boldsymbol{\mathrm{D}}A_{{\scriptscriptstyle 0}}-\boldsymbol{\mathrm{D}}\times\boldsymbol{A}\right)\\ = & \mathrm{D}_{{\scriptscriptstyle 0}}\left(A_{{\scriptscriptstyle 0}}+\boldsymbol{A}\right)-\boldsymbol{\mathrm{D}}\cdot\boldsymbol{A}+\boldsymbol{\mathrm{D}}A_{{\scriptscriptstyle 0}}-\boldsymbol{\mathrm{D}}\times\boldsymbol{A}\\ = & \mathrm{D}_{{\scriptscriptstyle 0}}A-\boldsymbol{\mathrm{D}}\cdot\boldsymbol{A}+\boldsymbol{\mathrm{D}}A_{{\scriptscriptstyle 0}}-\boldsymbol{\mathrm{D}}\times\boldsymbol{A}\\ = & \partial_{{\scriptscriptstyle 0}}A-\boldsymbol{\nabla}\cdot\boldsymbol{A}+\boldsymbol{\nabla}A_{{\scriptscriptstyle 0}}-\boldsymbol{\nabla}\times\boldsymbol{A} \end{aligned} \]

\[ \begin{aligned} \mathrm{D}A= & \mathrm{D}_{{\scriptscriptstyle 0}}A-\boldsymbol{\mathrm{D}}\cdot\boldsymbol{A}+\boldsymbol{\mathrm{D}}A_{{\scriptscriptstyle 0}}+\boldsymbol{\mathrm{D}}\times\boldsymbol{A}=\partial_{{\scriptscriptstyle 0}}A-\boldsymbol{\nabla}\cdot\boldsymbol{A}+\boldsymbol{\nabla}A_{{\scriptscriptstyle 0}}+\boldsymbol{\nabla}\times\boldsymbol{A}\\ A\mathrm{D}= & \mathrm{D}_{{\scriptscriptstyle 0}}A-\boldsymbol{\mathrm{D}}\cdot\boldsymbol{A}+\boldsymbol{\mathrm{D}}A_{{\scriptscriptstyle 0}}-\boldsymbol{\mathrm{D}}\times\boldsymbol{A}=\partial_{{\scriptscriptstyle 0}}A-\boldsymbol{\nabla}\cdot\boldsymbol{A}+\boldsymbol{\nabla}A_{{\scriptscriptstyle 0}}-\boldsymbol{\nabla}\times\boldsymbol{A} \end{aligned} \]

\[ \begin{aligned} & \mathrm{D}A-A\mathrm{D}=2\boldsymbol{\mathrm{D}}\times\boldsymbol{A}=2\boldsymbol{\nabla}\times\boldsymbol{A}\\ \left[\mathrm{D},A\right]= & \dfrac{\mathrm{D}A-A\mathrm{D}}{2}=\boldsymbol{\mathrm{D}}\times\boldsymbol{A}=\boldsymbol{\nabla}\times\boldsymbol{A} \end{aligned} \]

anticommutative bracket^{[37.1.3.3.1.2]}

\[ \begin{aligned} & \mathrm{D}A+A\mathrm{D}=2\left(\mathrm{D}_{{\scriptscriptstyle 0}}A-\boldsymbol{\mathrm{D}}\cdot\boldsymbol{A}+\boldsymbol{\mathrm{D}}A_{{\scriptscriptstyle 0}}\right)=2\left(\partial_{{\scriptscriptstyle 0}}A-\boldsymbol{\nabla}\cdot\boldsymbol{A}+\boldsymbol{\nabla}A_{{\scriptscriptstyle 0}}\right)\\ \left\{ \mathrm{D},A\right\} = & \dfrac{\mathrm{D}A+A\mathrm{D}}{2}=\mathrm{D}_{{\scriptscriptstyle 0}}A-\boldsymbol{\mathrm{D}}\cdot\boldsymbol{A}+\boldsymbol{\mathrm{D}}A_{{\scriptscriptstyle 0}}=\partial_{{\scriptscriptstyle 0}}A-\boldsymbol{\nabla}\cdot\boldsymbol{A}+\boldsymbol{\nabla}A_{{\scriptscriptstyle 0}} \end{aligned} \]

commutation and anticommutation on differential operator and any quaternion

or more evident

\[ \begin{aligned} \left[\mathrm{D},Q\right]= & \boldsymbol{\nabla}\times\boldsymbol{Q}\\ \left\{ \mathrm{D},Q\right\} = & \partial_{{\scriptscriptstyle 0}}Q-\boldsymbol{\nabla}\cdot\boldsymbol{Q}+\boldsymbol{\nabla}Q_{{\scriptscriptstyle 0}}\\ = & \partial_{{\scriptscriptstyle 0}}\left(Q_{{\scriptscriptstyle 0}}+\boldsymbol{Q}\right)-\boldsymbol{\nabla}\cdot\boldsymbol{Q}+\boldsymbol{\nabla}Q_{{\scriptscriptstyle 0}}\\ = & \left(\partial_{{\scriptscriptstyle 0}}Q_{{\scriptscriptstyle 0}}-\boldsymbol{\nabla}\cdot\boldsymbol{Q}\right)+\left(\partial_{{\scriptscriptstyle 0}}\boldsymbol{Q}+\boldsymbol{\nabla}Q_{{\scriptscriptstyle 0}}\right)\\ = & \left(\dfrac{\partial Q_{{\scriptscriptstyle 0}}}{\partial t}-\boldsymbol{\nabla}\cdot\boldsymbol{Q}\right)+\left(\dfrac{\partial\boldsymbol{Q}}{\partial t}+\boldsymbol{\nabla}Q_{{\scriptscriptstyle 0}}\right) \end{aligned} \]

37.1.3.6.2 Maxwell compromise for both quaternion and 3-vector

electric potential and vector potential

\[ A=A_{{\scriptscriptstyle 0}}++\mathrm{i}A_{{\scriptscriptstyle 1}}+\mathrm{j}A_{{\scriptscriptstyle 2}}+\mathrm{k}A_{{\scriptscriptstyle 3}}=A_{0}+\boldsymbol{A}=U+\boldsymbol{A} \]

electric quaternion and electric field

\[ \begin{aligned} E= & -\left\{ \mathrm{D},A\right\} \\ = & -\left(\partial_{{\scriptscriptstyle 0}}A-\boldsymbol{\nabla}\cdot\boldsymbol{A}+\boldsymbol{\nabla}A_{{\scriptscriptstyle 0}}\right)\\ = & -\partial_{{\scriptscriptstyle 0}}A+\boldsymbol{\nabla}\cdot\boldsymbol{A}-\boldsymbol{\nabla}A_{{\scriptscriptstyle 0}}\\ = & -\partial_{{\scriptscriptstyle t}}\left(U+\boldsymbol{A}\right)+\boldsymbol{\nabla}\cdot\boldsymbol{A}-\boldsymbol{\nabla}U\\ = & -\dfrac{\partial U}{\partial t}+\boldsymbol{\nabla}\cdot\boldsymbol{A}-\boldsymbol{\nabla}U-\dfrac{\partial\boldsymbol{A}}{\partial t}\\ = & E_{{\scriptscriptstyle 0}}+\boldsymbol{E},\begin{cases} E_{{\scriptscriptstyle 0}}=-\dfrac{\partial U}{\partial t}+\boldsymbol{\nabla}\cdot\boldsymbol{A}\\ \boldsymbol{E}=-\boldsymbol{\nabla}U-\dfrac{\partial\boldsymbol{A}}{\partial t} & \text{electric field 3-vector} \end{cases} \end{aligned} \]

magnetic field

\[ B=\left[\mathrm{D},A\right]=\boldsymbol{\nabla}\times\boldsymbol{A}=\begin{vmatrix}\boldsymbol{i} & \boldsymbol{j} & \boldsymbol{k}\\ \dfrac{\partial}{\partial x} & \dfrac{\partial}{\partial y} & \dfrac{\partial}{\partial z}\\ A_{{\scriptscriptstyle 1}} & A_{{\scriptscriptstyle 2}} & A_{{\scriptscriptstyle 3}} \end{vmatrix}=\boldsymbol{B} \]

Work on time? Yes.

\[ qE=qE_{{\scriptscriptstyle 0}}+q\boldsymbol{E}=qE_{{\scriptscriptstyle 0}}+\boldsymbol{F}_{E} \]

force equivalent on time

\[ qE_{{\scriptscriptstyle 0}} \]

\[ \begin{cases} E=-\left\{ \mathrm{D},A\right\} =E_{{\scriptscriptstyle 0}}+\boldsymbol{E}\\ B=+\left[\mathrm{D},A\right]=B_{{\scriptscriptstyle 0}}+\boldsymbol{B}=0+\boldsymbol{B}=\boldsymbol{B} & B_{{\scriptscriptstyle 0}}=0 \end{cases} \]

for any quaternion commutating and anticommutating with differential operator

\[ \begin{cases} \left[\mathrm{D},E\right]=\boldsymbol{\nabla}\times\boldsymbol{E}=\left(0\right)+\left(\boldsymbol{\nabla}\times\boldsymbol{E}\right)\\ \left\{ \mathrm{D},E\right\} =\left(\partial_{{\scriptscriptstyle 0}}E_{{\scriptscriptstyle 0}}-\boldsymbol{\nabla}\cdot\boldsymbol{E}\right)+\left(\partial_{{\scriptscriptstyle 0}}\boldsymbol{E}+\boldsymbol{\nabla}E_{{\scriptscriptstyle 0}}\right)=\left(\dfrac{\partial E_{{\scriptscriptstyle 0}}}{\partial t}-\boldsymbol{\nabla}\cdot\boldsymbol{E}\right)+\left(\dfrac{\partial\boldsymbol{E}}{\partial t}+\boldsymbol{\nabla}E_{{\scriptscriptstyle 0}}\right)\\ \left[\mathrm{D},B\right]=\boldsymbol{\nabla}\times\boldsymbol{B}=\left(0\right)+\left(\boldsymbol{\nabla}\times\boldsymbol{B}\right)\\ \left\{ \mathrm{D},B\right\} =\left(\partial_{{\scriptscriptstyle 0}}B_{{\scriptscriptstyle 0}}-\boldsymbol{\nabla}\cdot\boldsymbol{B}\right)+\left(\partial_{{\scriptscriptstyle 0}}\boldsymbol{B}+\boldsymbol{\nabla}B_{{\scriptscriptstyle 0}}\right)\overset{B_{{\scriptscriptstyle 0}}=0}{=}-\boldsymbol{\nabla}\cdot\boldsymbol{B}+\partial_{{\scriptscriptstyle 0}}\boldsymbol{B}=\left(-\boldsymbol{\nabla}\cdot\boldsymbol{B}\right)+\left(\dfrac{\partial\boldsymbol{B}}{\partial t}\right) \end{cases} \]

by comparing ( real & imaginary ) / ( scalar & vector ) parts,

Maxwell equations without source terms

\[ \begin{aligned} & \begin{cases} \left[\mathrm{D},B\right]=+\left\{ \mathrm{D},E\right\} & \Leftrightarrow\left(0\right)+\left(\boldsymbol{\nabla}\times\boldsymbol{B}\right)=\left(\dfrac{\partial E_{{\scriptscriptstyle 0}}}{\partial t}-\boldsymbol{\nabla}\cdot\boldsymbol{E}\right)+\left(\dfrac{\partial\boldsymbol{E}}{\partial t}+\boldsymbol{\nabla}E_{{\scriptscriptstyle 0}}\right)\\ \left[\mathrm{D},E\right]=-\left\{ \mathrm{D},B\right\} & \Leftrightarrow\left(0\right)+\left(\boldsymbol{\nabla}\times\boldsymbol{E}\right)=\left(-\boldsymbol{\nabla}\cdot\boldsymbol{B}\right)+\left(\dfrac{\partial\boldsymbol{B}}{\partial t}\right) \end{cases}\\ \Leftrightarrow & \begin{cases} \dfrac{\partial E_{{\scriptscriptstyle 0}}}{\partial t}-\boldsymbol{\nabla}\cdot\boldsymbol{E}=0 & \Leftrightarrow\boldsymbol{\nabla}\cdot\boldsymbol{E}=\dfrac{\partial E_{{\scriptscriptstyle 0}}}{\partial t}\\ \dfrac{\partial\boldsymbol{E}}{\partial t}+\boldsymbol{\nabla}E_{{\scriptscriptstyle 0}}=\boldsymbol{\nabla}\times\boldsymbol{B} & \Leftrightarrow\boldsymbol{\nabla}\times\boldsymbol{B}=\dfrac{\partial\boldsymbol{E}}{\partial t}+\boldsymbol{\nabla}E_{{\scriptscriptstyle 0}}\text{ 動電生磁}\\ -\boldsymbol{\nabla}\cdot\boldsymbol{B}=0 & \Leftrightarrow\boldsymbol{\nabla}\cdot\boldsymbol{B}=0\\ \dfrac{\partial\boldsymbol{B}}{\partial t}=\boldsymbol{\nabla}\times\boldsymbol{E} & \Leftrightarrow\boldsymbol{\nabla}\times\boldsymbol{E}=\dfrac{\partial\boldsymbol{B}}{\partial t}\text{ 動磁生電} \end{cases} \end{aligned} \]

37.1.3.7 Joule heat vs. Thomson heat (Kelvin heat?)

The Lord Kelvin = William Thomson

37.1.3.7.1 thermoelectric effect

thermoelectric effect = Seebeck effect = Peltier effect = Thomson effect

37.1.3.8 source term

\[ J=J_{{\scriptscriptstyle 0}}+\mathrm{i}J_{{\scriptscriptstyle 1}}+\mathrm{j}J_{{\scriptscriptstyle 2}}+\mathrm{k}J_{{\scriptscriptstyle 3}}=J_{{\scriptscriptstyle 0}}+\boldsymbol{J}=\rho+\boldsymbol{J} \]

Maxwell equations with source terms

\[ \begin{aligned} & \begin{cases} \left[\mathrm{D},B\right]=J+\left\{ \mathrm{D},E\right\} & \Leftrightarrow\left(0\right)+\left(\boldsymbol{\nabla}\times\boldsymbol{B}\right)=\left(\rho+\dfrac{\partial E_{{\scriptscriptstyle 0}}}{\partial t}-\boldsymbol{\nabla}\cdot\boldsymbol{E}\right)+\left(\boldsymbol{J}+\dfrac{\partial\boldsymbol{E}}{\partial t}+\boldsymbol{\nabla}E_{{\scriptscriptstyle 0}}\right)\\ \left[\mathrm{D},E\right]=0-\left\{ \mathrm{D},B\right\} & \Leftrightarrow\left(0\right)+\left(\boldsymbol{\nabla}\times\boldsymbol{E}\right)=\left(-\boldsymbol{\nabla}\cdot\boldsymbol{B}\right)+\left(\dfrac{\partial\boldsymbol{B}}{\partial t}\right) \end{cases}\\ \Leftrightarrow & \begin{cases} \rho+\dfrac{\partial E_{{\scriptscriptstyle 0}}}{\partial t}-\boldsymbol{\nabla}\cdot\boldsymbol{E}=0 & \Leftrightarrow\boldsymbol{\nabla}\cdot\boldsymbol{E}=\rho+\dfrac{\partial E_{{\scriptscriptstyle 0}}}{\partial t}\\ \boldsymbol{J}+\dfrac{\partial\boldsymbol{E}}{\partial t}+\boldsymbol{\nabla}E_{{\scriptscriptstyle 0}}=\boldsymbol{\nabla}\times\boldsymbol{B} & \Leftrightarrow\boldsymbol{\nabla}\times\boldsymbol{B}=\boldsymbol{J}+\dfrac{\partial\boldsymbol{E}}{\partial t}+\boldsymbol{\nabla}E_{{\scriptscriptstyle 0}}\text{ 動電生磁}\\ -\boldsymbol{\nabla}\cdot\boldsymbol{B}=0 & \Leftrightarrow\boldsymbol{\nabla}\cdot\boldsymbol{B}=0\\ \dfrac{\partial\boldsymbol{B}}{\partial t}=\boldsymbol{\nabla}\times\boldsymbol{E} & \Leftrightarrow\boldsymbol{\nabla}\times\boldsymbol{E}=\dfrac{\partial\boldsymbol{B}}{\partial t}\text{ 動磁生電} \end{cases} \end{aligned} \]

37.1.4 quaternion group

https://en.wikipedia.org/wiki/Quaternion_group

group theory^[40]

or please first see quaternion group representation^[40.8].

https://www.bilibili.com/video/BV1rj41117VW

37.1.4.1 2D rotation

37.1.4.1.1 matrix

\[ \boldsymbol{r}=\left(x,y\right)=\left\langle x,y\right\rangle =\begin{pmatrix}x\\ y \end{pmatrix}=\begin{pmatrix}r\cos\alpha\\ r\sin\alpha \end{pmatrix} \]

\[ \boldsymbol{r}^{\prime}=\left(x^{\prime},y^{\prime}\right)=\left\langle x^{\prime},y^{\prime}\right\rangle =\begin{pmatrix}x^{\prime}\\ y^{\prime} \end{pmatrix}=\begin{pmatrix}r\cos\left(\alpha+\theta\right)\\ r\sin\left(\alpha+\theta\right) \end{pmatrix} \]

\[ \begin{aligned} \boldsymbol{r}^{\prime}= & \begin{pmatrix}r\cos\left(\alpha+\theta\right)\\ r\sin\left(\alpha+\theta\right) \end{pmatrix}=r\begin{pmatrix}\cos\left(\alpha+\theta\right)\\ \sin\left(\alpha+\theta\right) \end{pmatrix}\\ = & r\begin{pmatrix}\cos\alpha\cos\theta-\sin\alpha\sin\theta\\ \sin\alpha\cos\theta+\cos\alpha\sin\theta \end{pmatrix}=r\begin{pmatrix}\cos\theta\cos\alpha-\sin\theta\sin\alpha\\ \sin\theta\cos\alpha+\cos\theta\sin\alpha \end{pmatrix}\\ = & r\begin{pmatrix}\cos\theta & -\sin\theta\\ \sin\theta & \cos\theta \end{pmatrix}\begin{pmatrix}\cos\alpha\\ \sin\alpha \end{pmatrix}=\begin{pmatrix}\cos\theta & -\sin\theta\\ \sin\theta & \cos\theta \end{pmatrix}\begin{pmatrix}r\cos\alpha\\ r\sin\alpha \end{pmatrix}\\ = & R\boldsymbol{r},\begin{cases} R=\begin{pmatrix}\cos\theta & -\sin\theta\\ \sin\theta & \cos\theta \end{pmatrix}=R\left(\theta\right)=R_{{\scriptscriptstyle \theta}}\\ \boldsymbol{r}=\begin{pmatrix}r\cos\alpha\\ r\sin\alpha \end{pmatrix},\boldsymbol{r}^{\prime}=\begin{pmatrix}r\cos\left(\alpha+\theta\right)\\ r\sin\left(\alpha+\theta\right) \end{pmatrix} \end{cases} \end{aligned} \]

orthonormal matrix

\[ \boldsymbol{r}^{\prime}=O\boldsymbol{r} \]

\[ \begin{aligned} \left|\boldsymbol{r}^{\prime}\right|^{2}= & \left|\boldsymbol{r}\right|^{2}\\ \boldsymbol{r}^{\prime}\cdot\boldsymbol{r}^{\prime}= & \boldsymbol{r}\cdot\boldsymbol{r}\\ \boldsymbol{r}^{\prime\intercal}\boldsymbol{r}^{\prime}= & \boldsymbol{r}^{\intercal}\boldsymbol{r}\\ \left(O\boldsymbol{r}\right)^{\intercal}\left(O\boldsymbol{r}\right)=\\ \boldsymbol{r}^{\intercal}O^{\intercal}O\boldsymbol{r}=\\ \boldsymbol{r}^{\intercal}O^{\intercal}O\boldsymbol{r}= & \boldsymbol{r}^{\intercal}\boldsymbol{r}\\ O^{\intercal}O= & 1=I=I_{{\scriptscriptstyle 2}} \end{aligned} \]

\[ \begin{aligned} R^{\intercal}R= & \begin{pmatrix}\cos\theta & -\sin\theta\\ \sin\theta & \cos\theta \end{pmatrix}^{\intercal}\begin{pmatrix}\cos\theta & -\sin\theta\\ \sin\theta & \cos\theta \end{pmatrix}\\ = & \begin{pmatrix}\cos\theta & \sin\theta\\ -\sin\theta & \cos\theta \end{pmatrix}\begin{pmatrix}\cos\theta & -\sin\theta\\ \sin\theta & \cos\theta \end{pmatrix}\\ = & \begin{pmatrix}\cos^{2}\theta+\sin^{2}\theta & -\cos\theta\sin\theta+\sin\theta\cos\theta\\ -\sin\theta\cos\theta+\cos\theta\sin\theta & \sin^{2}\theta+\cos^{2}\theta \end{pmatrix}\\ = & \begin{pmatrix}1 & 0\\ 0 & 1 \end{pmatrix}=1=I\\ R^{\intercal}R= & 1\Rightarrow R\in\left\{ O\middle|O^{\intercal}O=1\right\} \end{aligned} \]

https://en.wikipedia.org/wiki/Transformation_matrix#Affine_transformations

reflection matrix

\[ \begin{cases} P_{{\scriptscriptstyle x}}=\begin{pmatrix}-1 & 0\\ 0 & 1 \end{pmatrix} & P_{{\scriptscriptstyle x}}^{\intercal}P_{{\scriptscriptstyle x}}=P_{{\scriptscriptstyle x}}^{2}=\begin{pmatrix}-1 & 0\\ 0 & 1 \end{pmatrix}^{2}=\begin{pmatrix}1 & 0\\ 0 & 1 \end{pmatrix}=1\Rightarrow P_{{\scriptscriptstyle x}}\in\left\{ O\middle|O^{\intercal}O=1\right\} \\ P_{{\scriptscriptstyle y}}=\begin{pmatrix}1 & 0\\ 0 & -1 \end{pmatrix} & P_{{\scriptscriptstyle y}}^{\intercal}P_{{\scriptscriptstyle y}}=P_{{\scriptscriptstyle y}}^{2}=\begin{pmatrix}1 & 0\\ 0 & -1 \end{pmatrix}^{2}=\begin{pmatrix}1 & 0\\ 0 & 1 \end{pmatrix}=1\Rightarrow P_{{\scriptscriptstyle y}}\in\left\{ O\middle|O^{\intercal}O=1\right\} \end{cases} \]

translation matrix?

\[ \begin{pmatrix}0 & 1\\ 1 & 0 \end{pmatrix}\begin{pmatrix}0 & 1\\ 1 & 0 \end{pmatrix}=\begin{pmatrix}1 & 0\\ 0 & 1 \end{pmatrix}=1 \]

\[ \begin{pmatrix}0 & -1\\ -1 & 0 \end{pmatrix}\begin{pmatrix}0 & -1\\ -1 & 0 \end{pmatrix}=\begin{pmatrix}1 & 0\\ 0 & 1 \end{pmatrix}=1 \]

\(O\left(2\right)\) group

\[ \begin{aligned} O\left(2\right)=&\left\{ 1,R,P_{{\scriptscriptstyle x}},P_{{\scriptscriptstyle y}}\right\} \\=&\left\{ I_{{\scriptscriptstyle 2}},R_{{\scriptscriptstyle \theta}},P_{{\scriptscriptstyle x}},P_{{\scriptscriptstyle y}}\right\} \subseteq\left\{ O\middle|O^{\intercal}O=1\right\} \end{aligned} \]

\[ \begin{aligned} 1= & O^{\intercal}O\\ 1= & \det1=\det I=\det\left(I_{{\scriptscriptstyle 2}}\right)\\ = & \det\left(O^{\intercal}O\right)=\left(\det O^{\intercal}\right)\left(\det O\right)=\left(\det O\right)\left(\det O\right)=\left(\det O\right)^{2}\\ 1= & \left(\det O\right)^{2}\\ \det O= & \pm1 \end{aligned} \]

\[ \det R=\det R_{{\scriptscriptstyle \theta}}=\begin{vmatrix}\cos\theta & -\sin\theta\\ \sin\theta & \cos\theta \end{vmatrix}=\cos^{2}\theta-\left(-\sin^{2}\theta\right)=\cos^{2}\theta+\sin^{2}\theta=1 \]

\[ \begin{cases} P_{{\scriptscriptstyle x}}=\begin{pmatrix}-1 & 0\\ 0 & 1 \end{pmatrix} & \det P_{{\scriptscriptstyle x}}=-1\\ P_{{\scriptscriptstyle y}}=\begin{pmatrix}1 & 0\\ 0 & -1 \end{pmatrix} & \det P_{{\scriptscriptstyle y}}=-1 \end{cases} \]

special orthonormal group of degree 2

\[ \begin{aligned} SO\left(2\right)= & \left\{ 1,R\right\} =\left\{ I_{{\scriptscriptstyle 2}},R_{{\scriptscriptstyle \theta}}\right\} \subseteq\left\{ O\middle|\begin{cases} O^{\intercal}O=1 & O\\ \det O=1 & S \end{cases}\right\} \\ \subset & \left\{ 1,R,P_{{\scriptscriptstyle x}},P_{{\scriptscriptstyle y}}\right\} =O\left(2\right)\subseteq\left\{ O\middle|O^{\intercal}O=1\right\} \end{aligned} \]

37.1.4.1.2 complex

\[ z=r\left(\cos\alpha+\mathrm{i}\sin\alpha\right)=r\mathrm{e}^{\mathrm{i}\alpha} \]

\[ z^{\prime}=r\left(\cos\left(\alpha+\theta\right)+\mathrm{i}\sin\left(\alpha+\theta\right)\right)=r\mathrm{e}^{\mathrm{i}\left(\alpha+\theta\right)} \]

\[ \begin{aligned} z^{\prime}= & z_{{\scriptscriptstyle \theta}}z\\ z_{{\scriptscriptstyle \theta}}= & \dfrac{z^{\prime}}{z}=\dfrac{r^{\prime}\mathrm{e}^{\mathrm{i}\left(\alpha+\theta\right)}}{r\mathrm{e}^{\mathrm{i}\alpha}}=\dfrac{r^{\prime}}{r}\mathrm{e}^{\mathrm{i}\theta}=\dfrac{r^{\prime}}{r}\left(\cos\theta+\mathrm{i}\sin\theta\right) \end{aligned} \]

\[ \begin{aligned} z_{{\scriptscriptstyle \theta}}z= & \left[\dfrac{r^{\prime}}{r}\left(\cos\theta+\mathrm{i}\sin\theta\right)\right]\left[r\left(\cos\alpha+\mathrm{i}\sin\alpha\right)\right]\\ = & r^{\prime}\left[\left(\cos\theta\cos\alpha-\sin\theta\sin\alpha\right)+\mathrm{i}\left(\sin\theta\cos\alpha+\cos\theta\sin\alpha\right)\right]\\ = & r^{\prime}\left[\cos\left(\alpha+\theta\right)+\mathrm{i}\sin\left(\alpha+\theta\right)\right]=z^{\prime} \end{aligned} \]

\[ \hat{z}_{{\scriptscriptstyle \theta}}=z_{{\scriptscriptstyle \theta}}\left(\dfrac{r^{\prime}}{r}=1\right)=\mathrm{e}^{\mathrm{i}\theta}=\cos\theta+\mathrm{i}\sin\theta \]

\[ \hat{z}_{{\scriptscriptstyle \theta}}^{*}=\overline{\hat{z}_{{\scriptscriptstyle \theta}}}=\mathrm{e}^{-\mathrm{i}\theta}=\cos\theta-\mathrm{i}\sin\theta \]

\[ \hat{z}_{{\scriptscriptstyle \theta}}^{*}\hat{z}_{{\scriptscriptstyle \theta}}=\mathrm{e}^{\mathrm{i}\theta}\mathrm{e}^{-\mathrm{i}\theta}=\mathrm{e}^{\mathrm{i}\theta+\left(-\mathrm{i}\theta\right)}=\mathrm{e}^{\mathrm{i}0}=\mathrm{e}^{0}=1 \]

unitary group of degree 1

\[ U\left(1\right)=\left\{ 1,\hat{z}_{{\scriptscriptstyle \theta}}\right\} =\left\{ \mathrm{e}^{\mathrm{i}0},\mathrm{e}^{\mathrm{i}\theta}\right\} \]

37.1.4.1.3 \(SO\left(2\right)\cong U\left(1\right)\)

\(\mathbb{C}\leftrightarrow\mathcal{M}_{2\times2}\left(\mathbb{R}\right)=\mathcal{M}_{2}\left(\mathbb{R}\right)\) complex group representation^[40.7]

\[ x+y\mathrm{i}\leftrightarrow\begin{pmatrix}x & -y\\ y & x \end{pmatrix}=xI+yJ \]

\[ \begin{aligned} U\left(1\right)= & \left\{ 1,\hat{z}_{{\scriptscriptstyle \theta}}\right\} =\left\{ \mathrm{e}^{\mathrm{i}0},\mathrm{e}^{\mathrm{i}\theta}\right\} \\ = & \left\{ \cos0+\mathrm{i}\sin0,\cos\theta+\mathrm{i}\sin\theta\right\} \\ \leftrightarrow & \left\{ \begin{pmatrix}1 & 0\\ 0 & 1 \end{pmatrix}\cos0+\begin{pmatrix}0 & -1\\ 1 & 0 \end{pmatrix}\sin0,\begin{pmatrix}1 & 0\\ 0 & 1 \end{pmatrix}\cos\theta+\begin{pmatrix}0 & -1\\ 1 & 0 \end{pmatrix}\sin\theta\right\} \\ = & \left\{ \begin{pmatrix}1 & 0\\ 0 & 1 \end{pmatrix}1+\begin{pmatrix}0 & -1\\ 1 & 0 \end{pmatrix}0,\begin{pmatrix}1 & 0\\ 0 & 1 \end{pmatrix}\cos\theta+\begin{pmatrix}0 & -1\\ 1 & 0 \end{pmatrix}\sin\theta\right\} \\ = & \left\{ \begin{pmatrix}1 & 0\\ 0 & 1 \end{pmatrix},\begin{pmatrix}\cos\theta & -\sin\theta\\ \sin\theta & \cos\theta \end{pmatrix}\right\} =\left\{ I_{{\scriptscriptstyle 2}},R_{{\scriptscriptstyle \theta}}\right\} =\left\{ 1,R\right\} =SO\left(2\right)\\ U\left(1\right)\cong & SO\left(2\right)\Leftrightarrow SO\left(2\right)\cong U\left(1\right) \end{aligned} \]

unitary group of degree 1 and special orthonormal group of degree 2 are isomorphism

37.1.4.2 3D rotation

37.1.4.2.1 matrix

37.1.4.2.1.1 construction with 2D rotation matrix

\[ \begin{aligned} \boldsymbol{r}^{\prime}= & \begin{pmatrix}r\cos\left(\alpha+\theta\right)\\ r\sin\left(\alpha+\theta\right)\\ z^{\prime} \end{pmatrix}\overset{z^{\prime}=z}{=}\begin{pmatrix}r\cos\left(\alpha+\theta\right)\\ r\sin\left(\alpha+\theta\right)\\ z \end{pmatrix}=\begin{pmatrix}R\left(\theta\right)\\ & 1 \end{pmatrix}\begin{pmatrix}r\cos\alpha\\ r\sin\alpha\\ z \end{pmatrix}\\ = & \begin{pmatrix}\cos\theta & -\sin\theta & 0\\ \sin\theta & \cos\theta & 0\\ 0 & 0 & 1 \end{pmatrix}\begin{pmatrix}r\cos\alpha\\ r\sin\alpha\\ z \end{pmatrix}=R_{{\scriptscriptstyle z}}\left(\theta\right)\boldsymbol{r},\begin{cases} R_{{\scriptscriptstyle z}}\left(\theta\right)=\begin{pmatrix}\cos\theta & -\sin\theta & 0\\ \sin\theta & \cos\theta & 0\\ 0 & 0 & 1 \end{pmatrix}\\ \boldsymbol{r}=\begin{pmatrix}r\cos\alpha\\ r\sin\alpha\\ z \end{pmatrix} \end{cases} \end{aligned} \]

\[ \begin{aligned} \boldsymbol{r}^{\prime}= & \begin{pmatrix}x^{\prime}\\ r\cos\left(\alpha+\theta\right)\\ r\sin\left(\alpha+\theta\right) \end{pmatrix}\overset{x^{\prime}=x}{=}\begin{pmatrix}x\\ r\cos\left(\alpha+\theta\right)\\ r\sin\left(\alpha+\theta\right) \end{pmatrix}=\begin{pmatrix}1\\ & R\left(\theta\right) \end{pmatrix}\begin{pmatrix}x\\ r\cos\alpha\\ r\sin\alpha \end{pmatrix}\\ = & \begin{pmatrix}1 & 0 & 0\\ 0 & \cos\theta & -\sin\theta\\ 0 & \sin\theta & \cos\theta \end{pmatrix}\begin{pmatrix}x\\ r\cos\alpha\\ r\sin\alpha \end{pmatrix}=R_{{\scriptscriptstyle x}}\left(\theta\right)\boldsymbol{r},\begin{cases} R_{{\scriptscriptstyle x}}\left(\theta\right)=\begin{pmatrix}1 & 0 & 0\\ 0 & \cos\theta & -\sin\theta\\ 0 & \sin\theta & \cos\theta \end{pmatrix}\\ \boldsymbol{r}=\begin{pmatrix}x\\ r\cos\alpha\\ r\sin\alpha \end{pmatrix} \end{cases} \end{aligned} \]

\[ \begin{aligned} \boldsymbol{r}^{\prime}= & \begin{pmatrix}r\sin\left(\alpha+\theta\right)\\ y^{\prime}\\ r\cos\left(\alpha+\theta\right) \end{pmatrix}\overset{y^{\prime}=y}{=}\begin{pmatrix}r\sin\left(\alpha+\theta\right)\\ y\\ r\cos\left(\alpha+\theta\right) \end{pmatrix}\\ = & \begin{pmatrix}\cos\theta & 0 & \sin\theta\\ 0 & 1 & 0\\ -\sin\theta & 0 & \cos\theta \end{pmatrix}\begin{pmatrix}r\sin\alpha\\ y\\ r\cos\alpha \end{pmatrix}=R_{{\scriptscriptstyle y}}\left(\theta\right)\boldsymbol{r},\begin{cases} R_{{\scriptscriptstyle y}}\left(\theta\right)=\begin{pmatrix}\cos\theta & 0 & \sin\theta\\ 0 & 1 & 0\\ -\sin\theta & 0 & \cos\theta \end{pmatrix}\\ \boldsymbol{r}=\begin{pmatrix}r\sin\alpha\\ y\\ r\cos\alpha \end{pmatrix} \end{cases} \end{aligned} \]

37.1.4.2.1.2 Euler angle

\(z\rightarrow x\rightarrow z:\alpha\rightarrow\beta\rightarrow\gamma\)

\[ \begin{aligned} & R_{{\scriptscriptstyle z}}\left(\gamma\right)R_{{\scriptscriptstyle x}}\left(\beta\right)R_{{\scriptscriptstyle z}}\left(\alpha\right)\\ = & \begin{pmatrix}\cos\gamma & -\sin\gamma & 0\\ \sin\gamma & \cos\gamma & 0\\ 0 & 0 & 1 \end{pmatrix}\begin{pmatrix}1 & 0 & 0\\ 0 & \cos\beta & -\sin\beta\\ 0 & \sin\beta & \cos\beta \end{pmatrix}\begin{pmatrix}\cos\alpha & -\sin\alpha & 0\\ \sin\alpha & \cos\alpha & 0\\ 0 & 0 & 1 \end{pmatrix}\\ = & \begin{pmatrix}\cos\gamma & -\sin\gamma & 0\\ \sin\gamma & \cos\gamma & 0\\ 0 & 0 & 1 \end{pmatrix}\begin{pmatrix}\cos\alpha & -\sin\alpha & 0\\ \cos\beta\sin\alpha & \cos\beta\cos\alpha & -\sin\beta\\ \sin\beta\sin\alpha & \sin\beta\cos\alpha & \cos\beta \end{pmatrix}\\ = & \begin{pmatrix}\cos\gamma\cos\alpha-\sin\gamma\cos\beta\sin\alpha & -\cos\gamma\sin\alpha-\sin\gamma\cos\beta\cos\alpha & \sin\gamma\sin\beta\\ \sin\gamma\cos\alpha+\cos\gamma\cos\beta\sin\alpha & -\sin\gamma\sin\alpha-\cos\gamma\cos\beta\cos\alpha & -\cos\gamma\sin\beta\\ \sin\beta\sin\alpha & \sin\beta\cos\alpha & \cos\beta \end{pmatrix} \end{aligned} \]

\(x\rightarrow y\rightarrow z:\alpha\rightarrow\beta\rightarrow\gamma\)

\[ \begin{aligned} & R_{{\scriptscriptstyle z}}\left(\gamma\right)R_{{\scriptscriptstyle y}}\left(\beta\right)R_{{\scriptscriptstyle x}}\left(\alpha\right)\\ = & \begin{pmatrix}\cos\gamma & -\sin\gamma & 0\\ \sin\gamma & \cos\gamma & 0\\ 0 & 0 & 1 \end{pmatrix}\begin{pmatrix}\cos\beta & 0 & \sin\beta\\ 0 & 1 & 0\\ -\sin\beta & 0 & \cos\beta \end{pmatrix}\begin{pmatrix}1 & 0 & 0\\ 0 & \cos\alpha & -\sin\alpha\\ 0 & \sin\alpha & \cos\alpha \end{pmatrix}\\ = & \begin{pmatrix}\cos\gamma & -\sin\gamma & 0\\ \sin\gamma & \cos\gamma & 0\\ 0 & 0 & 1 \end{pmatrix}\begin{pmatrix}\cos\beta & \sin\beta\sin\alpha & \sin\beta\cos\alpha\\ 0 & \cos\alpha & -\sin\alpha\\ -\sin\beta & \cos\beta\sin\alpha & \cos\beta\cos\alpha \end{pmatrix}\\ = & \begin{pmatrix}\cos\gamma\cos\beta & \cos\gamma\sin\beta\sin\alpha-\sin\gamma\cos\alpha & \cos\gamma\sin\beta\cos\alpha+\sin\gamma\sin\alpha\\ \sin\gamma\cos\beta & \sin\gamma\sin\beta\sin\alpha+\cos\gamma\cos\alpha & \sin\gamma\sin\beta\cos\alpha-\cos\gamma\sin\alpha\\ -\sin\beta & \cos\beta\sin\alpha & \cos\beta\cos\alpha \end{pmatrix} \end{aligned} \]

37.1.4.2.1.3 3D rotation about an arbitrary axis

https://math.stackexchange.com/questions/4550704/rotation-around-an-arbitrary-axis

spherical coordinate unit vector

\[ \begin{cases} \hat{x}=r\sin\theta\cos\phi & \overset{r=1}{=}\sin\theta\cos\phi\\ \hat{y}=r\sin\theta\sin\phi & \overset{r=1}{=}\sin\theta\sin\phi\\ \hat{z}=r\cos\theta & \overset{r=1}{=}\cos\theta \end{cases} \]

although I prefer \(\theta\) and \(\phi\) switched back to be compatible with 2D coordinate

\[ \begin{cases} \hat{x}=r\sin\phi\cos\theta & \overset{r=1}{=}\sin\phi\cos\theta\\ \hat{y}=r\sin\phi\sin\theta & \overset{r=1}{=}\sin\phi\sin\theta\\ \hat{z}=r\cos\phi & \overset{r=1}{=}\cos\phi \end{cases} \]

or \(\cos\) first in \(x,y\)-plane

\[ \begin{cases} \hat{x}=r\cos\phi\cos\theta & \overset{r=1}{=}\cos\phi\cos\theta\\ \hat{y}=r\cos\phi\sin\theta & \overset{r=1}{=}\cos\phi\sin\theta\\ \hat{z}=r\sin\phi & \overset{r=1}{=}\sin\phi \end{cases} \]

still use the most convention

\[ \hat{\boldsymbol{n}}=\begin{pmatrix}\hat{x}\\ \hat{y}\\ \hat{z} \end{pmatrix}=\begin{pmatrix}\sin\theta\cos\phi\\ \sin\theta\sin\phi\\ \cos\theta \end{pmatrix} \]

\[ \begin{cases} \hat{\boldsymbol{n}}=\begin{pmatrix}\sin\theta\cos\phi\\ \sin\theta\sin\phi\\ \cos\theta \end{pmatrix}\\ \hat{\boldsymbol{u}}=\begin{pmatrix}\cos\theta\cos\phi\\ \cos\theta\sin\phi\\ -\sin\theta \end{pmatrix}\Leftarrow\cos\theta\sin\theta-\cos\theta\sin\theta=0\Rightarrow & \hat{\boldsymbol{u}}\cdot\hat{\boldsymbol{n}}=0\Leftrightarrow\hat{\boldsymbol{u}}\perp\hat{\boldsymbol{n}}\\ \hat{\boldsymbol{v}}=\hat{\boldsymbol{n}}\times\hat{\boldsymbol{u}}=\begin{vmatrix}\boldsymbol{i} & \boldsymbol{j} & \boldsymbol{k}\\ \sin\theta\cos\phi & \sin\theta\sin\phi & \cos\theta\\ \cos\theta\cos\phi & \cos\theta\sin\phi & -\sin\theta \end{vmatrix}=\begin{pmatrix}-\sin\phi\\ \cos\phi\\ 0 \end{pmatrix} & \Rightarrow\begin{cases} \hat{\boldsymbol{v}}\perp\hat{\boldsymbol{n}}\\ \hat{\boldsymbol{v}}\perp\hat{\boldsymbol{u}} \end{cases} \end{cases} \]

\[ S=\left\{ \hat{\boldsymbol{n}},\hat{\boldsymbol{u}},\hat{\boldsymbol{v}}\right\} =\left\{ \hat{\boldsymbol{u}},\hat{\boldsymbol{v}},\hat{\boldsymbol{n}}\right\} \text{ is a basis of the spherical coordinate} \]

\[ \left[\boldsymbol{V}\right]_{S}=\begin{pmatrix}u\\ v\\ n \end{pmatrix} \]

\[ \begin{aligned} \boldsymbol{V}= & \begin{pmatrix}\hat{\boldsymbol{u}} & \hat{\boldsymbol{v}} & \hat{\boldsymbol{n}}\end{pmatrix}\begin{pmatrix}u\\ v\\ n \end{pmatrix}=u\hat{\boldsymbol{u}}+v\hat{\boldsymbol{v}}+n\hat{\boldsymbol{n}}\\ = & \begin{pmatrix}\cos\theta\cos\phi & -\sin\phi & \sin\theta\cos\phi\\ \cos\theta\sin\phi & \cos\phi & \sin\theta\sin\phi\\ -\sin\theta & 0 & \cos\theta \end{pmatrix}\begin{pmatrix}u\\ v\\ n \end{pmatrix}=S\left[\boldsymbol{V}\right]_{S}\\ \begin{pmatrix}u\\ v\\ n \end{pmatrix}= & \begin{pmatrix}\cos\theta\cos\phi & -\sin\phi & \sin\theta\cos\phi\\ \cos\theta\sin\phi & \cos\phi & \sin\theta\sin\phi\\ -\sin\theta & 0 & \cos\theta \end{pmatrix}^{-1}\boldsymbol{V}\\ \left[\boldsymbol{V}\right]_{S}= & S^{-1}\boldsymbol{V} \end{aligned} \]

\[ \begin{aligned} S^{-1}= & \begin{pmatrix}\cos\theta\cos\phi & -\sin\phi & \sin\theta\cos\phi\\ \cos\theta\sin\phi & \cos\phi & \sin\theta\sin\phi\\ -\sin\theta & 0 & \cos\theta \end{pmatrix}^{-1},S\in\left\{ O\middle|O^{\intercal}O=1\right\} \\ = & \begin{pmatrix}\cos\theta\cos\phi & -\sin\phi & \sin\theta\cos\phi\\ \cos\theta\sin\phi & \cos\phi & \sin\theta\sin\phi\\ -\sin\theta & 0 & \cos\theta \end{pmatrix}^{\intercal}\\ = & \begin{pmatrix}\cos\theta\cos\phi & \cos\theta\sin\phi & -\sin\theta\\ -\sin\phi & \cos\phi & 0\\ \sin\theta\cos\phi & \sin\theta\sin\phi & \cos\theta \end{pmatrix}=\begin{pmatrix}\hat{\boldsymbol{u}}^{\intercal}\\ \hat{\boldsymbol{v}}^{\intercal}\\ \hat{\boldsymbol{n}}^{\intercal} \end{pmatrix}\\ S^{-1}S= & \begin{pmatrix}\cos\theta\cos\phi & \cos\theta\sin\phi & -\sin\theta\\ -\sin\phi & \cos\phi & 0\\ \sin\theta\cos\phi & \sin\theta\sin\phi & \cos\theta \end{pmatrix}\begin{pmatrix}\cos\theta\cos\phi & -\sin\phi & \sin\theta\cos\phi\\ \cos\theta\sin\phi & \cos\phi & \sin\theta\sin\phi\\ -\sin\theta & 0 & \cos\theta \end{pmatrix}\\ = & \begin{pmatrix}1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{pmatrix}=1 \end{aligned} \]

\(\hat{\boldsymbol{n}}\) as \(z\) direction

\[ \begin{aligned} \left[\boldsymbol{V}\right]_{S}= & S^{-1}\boldsymbol{V}\\ \left[\boldsymbol{V}^{\prime}\right]_{S}=R_{{\scriptscriptstyle z}}\left(\gamma\right)\left[\boldsymbol{V}\right]_{S}= & R_{{\scriptscriptstyle z}}\left(\gamma\right)S^{-1}\boldsymbol{V}\\ \boldsymbol{V}^{\prime}=S\left[\boldsymbol{V}^{\prime}\right]_{S}= & SR_{{\scriptscriptstyle z}}\left(\gamma\right)\left[\boldsymbol{V}\right]_{S}=SR_{{\scriptscriptstyle z}}\left(\gamma\right)S^{-1}\boldsymbol{V}\\ \boldsymbol{V}^{\prime}= & SR_{{\scriptscriptstyle z}}\left(\gamma\right)S^{-1}\boldsymbol{V} \end{aligned} \] https://www.symbolab.com/

\[ \begin{aligned} & SR_{{\scriptscriptstyle z}}\left(\gamma\right)S^{-1}\\ = & \begin{pmatrix}\cos\theta\cos\phi & -\sin\phi & \sin\theta\cos\phi\\ \cos\theta\sin\phi & \cos\phi & \sin\theta\sin\phi\\ -\sin\theta & 0 & \cos\theta \end{pmatrix}\begin{pmatrix}\cos\gamma & -\sin\gamma & 0\\ \sin\gamma & \cos\gamma & 0\\ 0 & 0 & 1 \end{pmatrix}\begin{pmatrix}\cos\theta\cos\phi & \cos\theta\sin\phi & -\sin\theta\\ -\sin\phi & \cos\phi & 0\\ \sin\theta\cos\phi & \sin\theta\sin\phi & \cos\theta \end{pmatrix}\\ = & \begin{pmatrix}c_{1}c_{2} & -s_{2} & s_{1}c_{2}\\ c_{1}s_{2} & c_{2} & s_{1}s_{2}\\ -s_{1} & 0 & c_{1} \end{pmatrix}\begin{pmatrix}c_{3} & -s_{3} & 0\\ s_{3} & c_{3} & 0\\ 0 & 0 & 1 \end{pmatrix}\begin{pmatrix}c_{1}c_{2} & c_{1}s_{2} & -s_{1}\\ -s_{2} & c_{2} & 0\\ s_{1}c_{2} & s_{1}s_{2} & c_{1} \end{pmatrix},\begin{cases} c_{1}=\cos\theta & s_{1}=\sin\theta\\ c_{2}=\cos\phi & s_{2}=\sin\phi\\ c_{3}=\cos\gamma & s_{3}=\sin\gamma \end{cases}\\ = & \begin{pmatrix}c_{1}c_{2} & -s_{2} & s_{1}c_{2}\\ c_{1}s_{2} & c_{2} & s_{1}s_{2}\\ -s_{1} & 0 & c_{1} \end{pmatrix}\begin{pmatrix}c_{3}c_{1}c_{2}+s_{3}s_{2} & c_{3}c_{1}s_{2}-c_{2}s_{3} & -c_{3}s_{1}\\ c_{1}c_{2}s_{3}-c_{3}s_{2} & c_{3}c_{2}+c_{1}s_{3}s_{2} & -s_{3}s_{1}\\ c_{2}s_{1} & s_{2}s_{1} & c_{1} \end{pmatrix}\\ = & \begin{pmatrix}c_{1}^{2}c_{2}^{2}c_{3}+c_{3}s_{2}^{2}+c_{2}^{2}s_{1}^{2} & c_{1}s_{2}\left(c_{1}c_{2}c_{3}-s_{2}s_{3}\right)+c_{2}\left(-c_{1}c_{2}s_{3}-c_{3}s_{2}\right)+c_{2}s_{2}s_{1}^{2} & c_{1}c_{2}s_{1}-s_{1}\left(c_{1}c_{2}c_{3}-s_{2}s_{3}\right)\\ c_{1}c_{2}\left(c_{1}c_{3}s_{2}+c_{2}s_{3}\right)-s_{2}\left(c_{2}c_{3}-c_{1}s_{2}s_{3}\right)+c_{2}s_{2}s_{1}^{2} & c_{1}^{2}c_{3}s_{2}^{2}+s_{2}^{2}s_{1}^{2}+c_{2}^{2}c_{3} & c_{1}s_{2}s_{1}-s_{1}\left(c_{1}c_{3}s_{2}+c_{2}s_{3}\right)\\ -c_{1}c_{2}c_{3}s_{1}-s_{2}s_{1}s_{3}+c_{1}c_{2}s_{1} & -c_{1}c_{3}s_{2}s_{1}+c_{2}s_{1}s_{3}+c_{1}s_{2}s_{1} & c_{3}s_{1}^{2}+c_{1}^{2} \end{pmatrix} \end{aligned} \]

37.1.4.2.2 quaternion

https://math.stackexchange.com/questions/328117/how-does-one-derive-this-rotation-quaternion-formula

\[ q_{{\scriptscriptstyle 1}}q_{{\scriptscriptstyle 2}}=\left(x_{{\scriptscriptstyle 10}}x_{{\scriptscriptstyle 20}}-\boldsymbol{x}_{{\scriptscriptstyle 1}}\cdot\boldsymbol{x}_{{\scriptscriptstyle 2}}\right)+\left(x_{{\scriptscriptstyle 10}}\boldsymbol{x}_{{\scriptscriptstyle 2}}+x_{{\scriptscriptstyle 20}}\boldsymbol{x}_{{\scriptscriptstyle 1}}+\boldsymbol{x}_{{\scriptscriptstyle 1}}\times\boldsymbol{x}_{{\scriptscriptstyle 2}}\right) \]

\[ q=q_{{\scriptscriptstyle 0}}+\boldsymbol{q}=q_{{\scriptscriptstyle 0}}+q_{{\scriptscriptstyle 1}}\mathrm{i}+q_{{\scriptscriptstyle 2}}\mathrm{j}+q_{{\scriptscriptstyle 3}}\mathrm{k}=q_{{\scriptscriptstyle 0}}+q_{{\scriptscriptstyle 1}}\boldsymbol{\mathrm{i}}+q_{{\scriptscriptstyle 2}}\boldsymbol{\mathrm{j}}+q_{{\scriptscriptstyle 3}}\boldsymbol{\mathrm{k}} \]

\[ \begin{aligned} q^{*}=\overline{q}= & \overline{q_{{\scriptscriptstyle 0}}+\boldsymbol{q}}=q_{{\scriptscriptstyle 0}}-\boldsymbol{q}\\ = & \overline{q_{{\scriptscriptstyle 0}}+q_{{\scriptscriptstyle 1}}\mathrm{i}+q_{{\scriptscriptstyle 2}}\mathrm{j}+q_{{\scriptscriptstyle 3}}\mathrm{k}}=q_{{\scriptscriptstyle 0}}-q_{{\scriptscriptstyle 1}}\mathrm{i}-q_{{\scriptscriptstyle 2}}\mathrm{j}-q_{{\scriptscriptstyle 3}}\mathrm{k}\\ = & q_{{\scriptscriptstyle 0}}-q_{{\scriptscriptstyle 1}}\boldsymbol{\mathrm{i}}-q_{{\scriptscriptstyle 2}}\boldsymbol{\mathrm{j}}-q_{{\scriptscriptstyle 3}}\boldsymbol{\mathrm{k}} \end{aligned} \]

\[ v=v_{{\scriptscriptstyle 0}}+\boldsymbol{v}=v_{{\scriptscriptstyle 0}}+v_{{\scriptscriptstyle 1}}\mathrm{i}+v_{{\scriptscriptstyle 2}}\mathrm{j}+v_{{\scriptscriptstyle 3}}\mathrm{k}=v_{{\scriptscriptstyle 0}}+v_{{\scriptscriptstyle 1}}\boldsymbol{\mathrm{i}}+v_{{\scriptscriptstyle 2}}\boldsymbol{\mathrm{j}}+v_{{\scriptscriptstyle 3}}\boldsymbol{\mathrm{k}} \]

\[ \boldsymbol{v}=v_{{\scriptscriptstyle 1}}\mathrm{i}+v_{{\scriptscriptstyle 2}}\mathrm{j}+v_{{\scriptscriptstyle 3}}\mathrm{k}=v_{{\scriptscriptstyle 1}}\boldsymbol{\mathrm{i}}+v_{{\scriptscriptstyle 2}}\boldsymbol{\mathrm{j}}+v_{{\scriptscriptstyle 3}}\boldsymbol{\mathrm{k}} \]

\[ \begin{aligned} qv= & \left(q_{{\scriptscriptstyle 0}}v_{{\scriptscriptstyle 0}}-\boldsymbol{q}\cdot\boldsymbol{v}\right)+\left(q_{{\scriptscriptstyle 0}}\boldsymbol{v}+v_{{\scriptscriptstyle 0}}\boldsymbol{q}+\boldsymbol{q}\times\boldsymbol{v}\right)\\ & \overset{v_{{\scriptscriptstyle 0}}=0}{=}\left(q_{{\scriptscriptstyle 0}}0-\boldsymbol{q}\cdot\boldsymbol{v}\right)+\left(q_{{\scriptscriptstyle 0}}\boldsymbol{v}+0\boldsymbol{q}+\boldsymbol{q}\times\boldsymbol{v}\right)\\ & =\left(-\boldsymbol{q}\cdot\boldsymbol{v}\right)+\left(q_{{\scriptscriptstyle 0}}\boldsymbol{v}+\boldsymbol{q}\times\boldsymbol{v}\right)\\ q\boldsymbol{v}= & \left(-\boldsymbol{q}\cdot\boldsymbol{v}\right)+\left(q_{{\scriptscriptstyle 0}}\boldsymbol{v}+\boldsymbol{q}\times\boldsymbol{v}\right) \end{aligned} \]

\[ \begin{aligned} v\overline{q}= & \left(v_{{\scriptscriptstyle 0}}q_{{\scriptscriptstyle 0}}-\boldsymbol{v}\cdot\overline{\boldsymbol{q}}\right)+\left(v_{{\scriptscriptstyle 0}}\overline{\boldsymbol{q}}+q_{{\scriptscriptstyle 0}}\boldsymbol{v}+\boldsymbol{v}\times\overline{\boldsymbol{q}}\right)\\ & \overset{v_{{\scriptscriptstyle 0}}=0}{=}\left(0q_{{\scriptscriptstyle 0}}-\boldsymbol{v}\cdot\overline{\boldsymbol{q}}\right)+\left(0\overline{\boldsymbol{q}}+q_{{\scriptscriptstyle 0}}\boldsymbol{v}+\boldsymbol{v}\times\overline{\boldsymbol{q}}\right)\\ & =\left(-\boldsymbol{v}\cdot\overline{\boldsymbol{q}}\right)+\left(q_{{\scriptscriptstyle 0}}\boldsymbol{v}+\boldsymbol{v}\times\overline{\boldsymbol{q}}\right)\\ & =\left(-\boldsymbol{v}\cdot\left(-\boldsymbol{q}\right)\right)+\left(q_{{\scriptscriptstyle 0}}\boldsymbol{v}+\boldsymbol{v}\times\left(-\boldsymbol{q}\right)\right)\\ & =\left(\boldsymbol{v}\cdot\boldsymbol{q}\right)+\left(q_{{\scriptscriptstyle 0}}\boldsymbol{v}-\boldsymbol{v}\times\boldsymbol{q}\right)\\ \boldsymbol{v}\overline{q}= & \left(\boldsymbol{v}\cdot\boldsymbol{q}\right)+\left(q_{{\scriptscriptstyle 0}}\boldsymbol{v}-\boldsymbol{v}\times\boldsymbol{q}\right) \end{aligned} \]

https://math.stackexchange.com/questions/41574/can-eulers-identity-be-extended-to-quaternions

\[ \begin{aligned} q= & a+b\mathrm{i}+c\mathrm{j}+d\mathrm{k}=a+\mathrm{i}b+\mathrm{j}c+\mathrm{k}d\\ = & a+r\dfrac{\mathrm{i}b+\mathrm{j}c+\mathrm{k}d}{r},r^{2}=b^{2}+c^{2}+d^{2}\\ = & a+\theta\dfrac{\mathrm{i}b+\mathrm{j}c+\mathrm{k}d}{\theta},\theta^{2}=b^{2}+c^{2}+d^{2} \end{aligned} \]

\[ \begin{aligned} \left(\dfrac{\mathrm{i}b+\mathrm{j}c+\mathrm{k}d}{r}\right)^{2}= & \dfrac{-b^{2}-c^{2}-d^{2}+bc\left(\mathrm{i}\mathrm{j}+\mathrm{j}\mathrm{i}\right)+cd\left(\mathrm{j}\mathrm{k}+\mathrm{k}\mathrm{j}\right)+db\left(\mathrm{k}\mathrm{i}+\mathrm{i}\mathrm{k}\right)}{r^{2}}\\ = & \dfrac{-b^{2}-c^{2}-d^{2}+bc\left(\mathrm{k}-\mathrm{k}\right)+cd\left(\mathrm{i}-\mathrm{i}\right)+db\left(\mathrm{j}-\mathrm{j}\right)}{r^{2}}\\ = & \dfrac{-b^{2}-c^{2}-d^{2}+bc0+cd0+db0}{r^{2}}=\dfrac{-b^{2}-c^{2}-d^{2}}{r^{2}}\\ = & \dfrac{-b^{2}-c^{2}-d^{2}}{b^{2}+c^{2}+d^{2}}=-1\\ \dfrac{\mathrm{i}b+\mathrm{j}c+\mathrm{k}d}{r}= & \pm\sqrt{-1} \end{aligned} \]

\[ \begin{aligned} \mathrm{e}^{q}= & \mathrm{e}^{a+\mathrm{i}b+\mathrm{j}c+\mathrm{k}d}\\ = & \mathrm{e}^{a+r\sqrt{-1}}=\mathrm{e}^{a}\mathrm{e}^{r\sqrt{-1}}=\mathrm{e}^{a+\theta\sqrt{-1}}=\mathrm{e}^{a}\mathrm{e}^{\theta\sqrt{-1}}\\ = & \mathrm{e}^{a}\left(\cos r+\sqrt{-1}\sin r\right)=\mathrm{e}^{a}\left(\cos\theta+\sqrt{-1}\sin\theta\right)\\ = & \mathrm{e}^{a}\left(\cos r+\dfrac{\mathrm{i}b+\mathrm{j}c+\mathrm{k}d}{r}\sin r\right)=\mathrm{e}^{a}\left[\cos r+\left(\mathrm{i}b+\mathrm{j}c+\mathrm{k}d\right)\dfrac{\sin r}{r}\right]\\ = & \mathrm{e}^{a}\left(\cos\theta+\dfrac{\mathrm{i}b+\mathrm{j}c+\mathrm{k}d}{\theta}\sin\theta\right)=\mathrm{e}^{a}\left[\cos\theta+\left(\mathrm{i}b+\mathrm{j}c+\mathrm{k}d\right)\dfrac{\sin\theta}{\theta}\right] \end{aligned} \]

\[ \begin{aligned} q= & a+b\mathrm{i}+c\mathrm{j}+d\mathrm{k}=a+\mathrm{i}b+\mathrm{j}c+\mathrm{k}d\\ = & a+r\dfrac{\mathrm{i}b+\mathrm{j}c+\mathrm{k}d}{r},r^{2}=b^{2}+c^{2}+d^{2}\\ = & \sqrt{a^{2}+r^{2}}\left(\dfrac{a}{\sqrt{a^{2}+r^{2}}}+\dfrac{\mathrm{i}b+\mathrm{j}c+\mathrm{k}d}{r}\dfrac{r}{\sqrt{a^{2}+r^{2}}}\right)\\ = & \rho\left(\cos\phi+\sqrt{-1}\sin\phi\right),\begin{cases} \rho=\sqrt{a^{2}+r^{2}}\\ \tan\phi=\dfrac{r}{a}\Leftrightarrow\phi=\arctan\dfrac{r}{a} \end{cases}\\ = & \rho\mathrm{e}^{\phi\sqrt{-1}}\\ q= & \rho\mathrm{e}^{\phi\sqrt{-1}},\begin{cases} q=a+\mathrm{i}b+\mathrm{j}c+\mathrm{k}d\\ \rho=\sqrt{a^{2}+r^{2}}=\sqrt{a^{2}+b^{2}+c^{2}+d^{2}}\\ \tan\phi=\dfrac{r}{a}\Leftrightarrow\phi=\arctan\dfrac{r}{a}=\arctan\dfrac{\pm\sqrt{b^{2}+c^{2}+d^{2}}}{a} \end{cases} \end{aligned} \]

\[ \begin{aligned} \rho\mathrm{e}^{-\phi\sqrt{-1}}= & \rho\left[\cos\left(-\phi\right)+\sqrt{-1}\sin\left(-\phi\right)\right]\\ = & \rho\left[\cos\phi-\sqrt{-1}\sin\phi\right]\\ = & \sqrt{a^{2}+r^{2}}\left[\dfrac{a}{\sqrt{a^{2}+r^{2}}}-\dfrac{\mathrm{i}b+\mathrm{j}c+\mathrm{k}d}{r}\dfrac{r}{\sqrt{a^{2}+r^{2}}}\right]\\ = & a-\left(\mathrm{i}b+\mathrm{j}c+\mathrm{k}d\right)=a-\mathrm{i}b-\mathrm{j}c-\mathrm{k}d=\overline{q}=q^{*} \end{aligned} \]

37.1.5 octonion

37.2 Krasjet

https://github.com/Krasjet/quaternion

https://krasjet.github.io/quaternion/

https://krasjet.github.io/quaternion/bonus_gimbal_lock.pdf

37.2.1 Rodrigues rotation

\[ \boldsymbol{v}\rightarrow\boldsymbol{v}^{\prime} \]

\[ \boldsymbol{v}\xrightarrow{\text{rotate about }\boldsymbol{u}}\boldsymbol{v}^{\prime} \]

\[ \boldsymbol{v}\xrightarrow{\text{rotate about }\boldsymbol{n}}\boldsymbol{v}^{\prime} \]

\[ \begin{cases} \boldsymbol{v}=\boldsymbol{v}_{{\scriptscriptstyle \parallel\boldsymbol{n}}}+\boldsymbol{v}_{{\scriptscriptstyle \perp\boldsymbol{n}}}=\boldsymbol{v}_{{\scriptscriptstyle \parallel}}+\boldsymbol{v}_{{\scriptscriptstyle \perp}} & \Rightarrow\boldsymbol{v}_{{\scriptscriptstyle \perp}}=\boldsymbol{v}-\boldsymbol{v}_{{\scriptscriptstyle \parallel}}\\ \boldsymbol{v}^{\prime}=\boldsymbol{v}_{{\scriptscriptstyle \parallel\boldsymbol{n}}}^{\prime}+\boldsymbol{v}_{{\scriptscriptstyle \perp\boldsymbol{n}}}^{\prime}=\boldsymbol{v}_{{\scriptscriptstyle \parallel}}^{\prime}+\boldsymbol{v}_{{\scriptscriptstyle \perp}}^{\prime} & \Rightarrow\boldsymbol{v}_{{\scriptscriptstyle \perp}}^{\prime}=\boldsymbol{v}^{\prime}-\boldsymbol{v}_{{\scriptscriptstyle \parallel}}^{\prime} \end{cases} \]

\[ \begin{aligned} \boldsymbol{v}_{{\scriptscriptstyle \parallel\hat{\boldsymbol{n}}}}=\boldsymbol{v}_{{\scriptscriptstyle \parallel}}= & \mathrm{proj}_{\hat{{\scriptscriptstyle \boldsymbol{n}}}}\boldsymbol{v}=\dfrac{\boldsymbol{v}\cdot\hat{\boldsymbol{n}}}{\left\Vert \hat{\boldsymbol{n}}\right\Vert }\hat{\boldsymbol{n}}\overset{\left\Vert \hat{\boldsymbol{n}}\right\Vert =1}{=}\left(\boldsymbol{v}\cdot\hat{\boldsymbol{n}}\right)\hat{\boldsymbol{n}}=\boldsymbol{v}\cdot\hat{\boldsymbol{n}}\hat{\boldsymbol{n}}\\ = & \dfrac{\boldsymbol{v}\cdot\hat{\boldsymbol{n}}}{\left\Vert \hat{\boldsymbol{n}}\right\Vert }\dfrac{\hat{\boldsymbol{n}}}{\left\Vert \hat{\boldsymbol{n}}\right\Vert }=\dfrac{\boldsymbol{v}\cdot\hat{\boldsymbol{n}}}{\left\Vert \hat{\boldsymbol{n}}\right\Vert ^{2}}\hat{\boldsymbol{n}}\overset{\left\Vert \hat{\boldsymbol{n}}\right\Vert =1}{=}\left(\boldsymbol{v}\cdot\hat{\boldsymbol{n}}\right)\hat{\boldsymbol{n}}=\boldsymbol{v}\cdot\hat{\boldsymbol{n}}\hat{\boldsymbol{n}} \end{aligned} \]

\[ \boldsymbol{n}=\hat{\boldsymbol{n}} \]

\[ \begin{aligned} \boldsymbol{v}_{{\scriptscriptstyle \parallel\boldsymbol{n}}}=\boldsymbol{v}_{{\scriptscriptstyle \parallel}}= & \mathrm{proj}_{{\scriptscriptstyle \boldsymbol{n}}}\boldsymbol{v}=\dfrac{\boldsymbol{v}\cdot\boldsymbol{n}}{\left\Vert \boldsymbol{n}\right\Vert }\hat{\boldsymbol{n}}\overset{\left\Vert \boldsymbol{n}\right\Vert =1}{=}\left(\boldsymbol{v}\cdot\hat{\boldsymbol{n}}\right)\hat{\boldsymbol{n}}=\boldsymbol{v}\cdot\hat{\boldsymbol{n}}\hat{\boldsymbol{n}}\\ = & \dfrac{\boldsymbol{v}\cdot\boldsymbol{n}}{\left\Vert \boldsymbol{n}\right\Vert }\dfrac{\boldsymbol{n}}{\left\Vert \boldsymbol{n}\right\Vert }=\dfrac{\boldsymbol{v}\cdot\boldsymbol{n}}{\left\Vert \boldsymbol{n}\right\Vert ^{2}}\boldsymbol{n}\overset{\left\Vert \boldsymbol{n}\right\Vert =1}{=}\left(\boldsymbol{v}\cdot\boldsymbol{n}\right)\boldsymbol{n}=\boldsymbol{v}\cdot\boldsymbol{n}\boldsymbol{n} \end{aligned} \]

\[ \boldsymbol{v}_{{\scriptscriptstyle \parallel}}=\left(\boldsymbol{v}\cdot\boldsymbol{n}\right)\boldsymbol{n} \]

\[ \boldsymbol{v}_{{\scriptscriptstyle \perp}}=\boldsymbol{v}-\boldsymbol{v}_{{\scriptscriptstyle \parallel}}=\boldsymbol{v}-\left(\boldsymbol{v}\cdot\boldsymbol{n}\right)\boldsymbol{n} \]

\[ \boldsymbol{v}_{{\scriptscriptstyle \parallel}}+\boldsymbol{v}_{{\scriptscriptstyle \perp}}=\boldsymbol{v}\xrightarrow{\text{rotate about }\boldsymbol{n}}\boldsymbol{v}^{\prime}=\boldsymbol{v}_{{\scriptscriptstyle \parallel}}^{\prime}+\boldsymbol{v}_{{\scriptscriptstyle \perp}}^{\prime} \]

\[ \boldsymbol{v}_{{\scriptscriptstyle \parallel}}\xrightarrow{\text{rotate about }\boldsymbol{n}}\boldsymbol{v}_{{\scriptscriptstyle \parallel}}^{\prime} \]

\[ \boldsymbol{v}_{{\scriptscriptstyle \parallel}}=\boldsymbol{v}_{{\scriptscriptstyle \parallel\boldsymbol{n}}}=\boldsymbol{v}_{{\scriptscriptstyle \parallel\boldsymbol{n}}}^{\prime}=\boldsymbol{v}_{{\scriptscriptstyle \parallel}}^{\prime} \]

\[ \boldsymbol{v}_{{\scriptscriptstyle \parallel}}=\boldsymbol{v}_{{\scriptscriptstyle \parallel}}^{\prime} \]

\[ \boldsymbol{v}_{{\scriptscriptstyle \parallel}}^{\prime}=\boldsymbol{v}_{{\scriptscriptstyle \parallel}} \]

\[ \begin{cases} \boldsymbol{u}=\boldsymbol{n}\times\boldsymbol{v}_{{\scriptscriptstyle \perp}} & \begin{cases} \boldsymbol{u}\perp\boldsymbol{n}\\ \boldsymbol{u}\perp\boldsymbol{v}_{{\scriptscriptstyle \perp}} \end{cases}\\ \left\Vert \boldsymbol{u}\right\Vert =\left\Vert \boldsymbol{n}\times\boldsymbol{v}_{{\scriptscriptstyle \perp}}\right\Vert =\left\Vert \boldsymbol{n}\right\Vert \left\Vert \boldsymbol{v}_{{\scriptscriptstyle \perp}}\right\Vert \sin\dfrac{\pi}{2}=\left\Vert \boldsymbol{v}_{{\scriptscriptstyle \perp}}\right\Vert & \begin{cases} \boldsymbol{n}\perp\boldsymbol{v}_{{\scriptscriptstyle \perp}}\\ \left\Vert \boldsymbol{n}\right\Vert =1 \end{cases} \end{cases} \]

\[ \begin{aligned} \boldsymbol{v}_{{\scriptscriptstyle \perp}}^{\prime}= & \boldsymbol{v}_{{\scriptscriptstyle \parallel\boldsymbol{v}_{{\scriptscriptstyle \perp}}}}^{\prime}+\boldsymbol{v}_{{\scriptscriptstyle \parallel\boldsymbol{u}}}^{\prime}\\ = & \left(\cos\theta\right)\boldsymbol{v}_{{\scriptscriptstyle \perp}}+\left(\sin\theta\right)\boldsymbol{u},\theta=\angle\boldsymbol{v}_{{\scriptscriptstyle \perp}}^{\prime}\boldsymbol{v}_{{\scriptscriptstyle \perp}}\\ = & \cos\theta\boldsymbol{v}_{{\scriptscriptstyle \perp}}+\sin\theta\boldsymbol{u}\\ = & \cos\theta\boldsymbol{v}_{{\scriptscriptstyle \perp}}+\sin\theta\left(\boldsymbol{n}\times\boldsymbol{v}_{{\scriptscriptstyle \perp}}\right)\\ \boldsymbol{v}_{{\scriptscriptstyle \perp}}^{\prime}= & \cos\theta\boldsymbol{v}_{{\scriptscriptstyle \perp}}+\sin\theta\left(\boldsymbol{n}\times\boldsymbol{v}_{{\scriptscriptstyle \perp}}\right) \end{aligned} \]

\[ \boldsymbol{v}_{{\scriptscriptstyle \perp}}^{\prime}=\cos\theta\boldsymbol{v}_{{\scriptscriptstyle \perp}}+\sin\theta\left(\boldsymbol{n}\times\boldsymbol{v}_{{\scriptscriptstyle \perp}}\right),\theta=\angle\boldsymbol{v}_{{\scriptscriptstyle \perp}}^{\prime}\boldsymbol{v}_{{\scriptscriptstyle \perp}} \]

\[ \boldsymbol{v}_{{\scriptscriptstyle \perp}}^{\prime}=\cos\theta\boldsymbol{v}_{{\scriptscriptstyle \perp}}+\sin\theta\left(\boldsymbol{n}\times\boldsymbol{v}_{{\scriptscriptstyle \perp}}\right) \]

\[ \begin{aligned} \boldsymbol{v}^{\prime}= & \boldsymbol{v}_{{\scriptscriptstyle \parallel}}^{\prime}+\boldsymbol{v}_{{\scriptscriptstyle \perp}}^{\prime},\begin{cases} \boldsymbol{v}_{{\scriptscriptstyle \parallel}}^{\prime}=\boldsymbol{v}_{{\scriptscriptstyle \parallel}}\\ \boldsymbol{v}_{{\scriptscriptstyle \perp}}^{\prime}=\cos\theta\boldsymbol{v}_{{\scriptscriptstyle \perp}}+\sin\theta\left(\boldsymbol{n}\times\boldsymbol{v}_{{\scriptscriptstyle \perp}}\right),\theta=\angle\boldsymbol{v}_{{\scriptscriptstyle \perp}}^{\prime}\boldsymbol{v}_{{\scriptscriptstyle \perp}} \end{cases}\\ = & \boldsymbol{v}_{{\scriptscriptstyle \parallel}}+\cos\theta\boldsymbol{v}_{{\scriptscriptstyle \perp}}+\sin\theta\left(\boldsymbol{n}\times\boldsymbol{v}_{{\scriptscriptstyle \perp}}\right),\theta=\angle\boldsymbol{v}_{{\scriptscriptstyle \perp}}^{\prime}\boldsymbol{v}_{{\scriptscriptstyle \perp}}\\ = & \boldsymbol{v}_{{\scriptscriptstyle \parallel}}+\cos\theta\boldsymbol{v}_{{\scriptscriptstyle \perp}}+\sin\theta\left(\boldsymbol{n}\times\boldsymbol{v}_{{\scriptscriptstyle \perp}}\right),\begin{cases} \boldsymbol{v}_{{\scriptscriptstyle \parallel}}=\left(\boldsymbol{v}\cdot\boldsymbol{n}\right)\boldsymbol{n}\\ \boldsymbol{v}_{{\scriptscriptstyle \perp}}=\boldsymbol{v}-\boldsymbol{v}_{{\scriptscriptstyle \parallel}}=\boldsymbol{v}-\left(\boldsymbol{v}\cdot\boldsymbol{n}\right)\boldsymbol{n} \end{cases}\\ = & \left(\boldsymbol{v}\cdot\boldsymbol{n}\right)\boldsymbol{n}+\cos\theta\left[\boldsymbol{v}-\left(\boldsymbol{v}\cdot\boldsymbol{n}\right)\boldsymbol{n}\right]+\sin\theta\left[\boldsymbol{n}\times\left(\boldsymbol{v}-\boldsymbol{v}_{{\scriptscriptstyle \parallel}}\right)\right]\\ = & \left(\boldsymbol{v}\cdot\boldsymbol{n}\right)\boldsymbol{n}+\cos\theta\boldsymbol{v}-\cos\theta\left(\boldsymbol{v}\cdot\boldsymbol{n}\right)\boldsymbol{n}+\sin\theta\left[\boldsymbol{n}\times\boldsymbol{v}-\boldsymbol{n}\times\boldsymbol{v}_{{\scriptscriptstyle \parallel}}\right]\\ = & \cos\theta\boldsymbol{v}+\left(1-\cos\theta\right)\left(\boldsymbol{v}\cdot\boldsymbol{n}\right)\boldsymbol{n}+\sin\theta\left[\boldsymbol{n}\times\boldsymbol{v}-\boldsymbol{0}\right]\\ = & \cos\theta\boldsymbol{v}+\left(1-\cos\theta\right)\left(\boldsymbol{v}\cdot\boldsymbol{n}\right)\boldsymbol{n}+\sin\theta\boldsymbol{n}\times\boldsymbol{v} \end{aligned} \]

\[ \boldsymbol{v}^{\prime}=\cos\theta\boldsymbol{v}+\left(1-\cos\theta\right)\left(\boldsymbol{v}\cdot\boldsymbol{n}\right)\boldsymbol{n}+\sin\theta\boldsymbol{n}\times\boldsymbol{v} \]

\[ \begin{aligned} \boldsymbol{v}^{\prime}= & \cos\theta\boldsymbol{v}+\left(1-\cos\theta\right)\left(\boldsymbol{v}\cdot\boldsymbol{n}\right)\boldsymbol{n}+\sin\theta\boldsymbol{n}\times\boldsymbol{v}\\ = & \cos\theta\boldsymbol{v}+\left[1-\left(1-2\sin^{2}\dfrac{\theta}{2}\right)\right]\left(\boldsymbol{v}\cdot\boldsymbol{n}\right)\boldsymbol{n}+\left[2\sin\dfrac{\theta}{2}\cos\dfrac{\theta}{2}\right]\boldsymbol{n}\times\boldsymbol{v}\\ = & \cos\theta\boldsymbol{v}+\left[2\sin^{2}\dfrac{\theta}{2}\right]\left(\boldsymbol{v}\cdot\boldsymbol{n}\right)\boldsymbol{n}+\left[2\sin\dfrac{\theta}{2}\cos\dfrac{\theta}{2}\right]\boldsymbol{n}\times\boldsymbol{v}\\ = & \cos\theta\boldsymbol{v}+2\sin\dfrac{\theta}{2}\left[\left(\sin\dfrac{\theta}{2}\right)\left(\boldsymbol{v}\cdot\boldsymbol{n}\right)\boldsymbol{n}+\left(\cos\dfrac{\theta}{2}\right)\boldsymbol{n}\times\boldsymbol{v}\right]\\ = & \cos\theta\boldsymbol{v}+2\sin\dfrac{\theta}{2}\left[\left(\cos\dfrac{\theta}{2}\right)\boldsymbol{n}\times\boldsymbol{v}+\left(\sin\dfrac{\theta}{2}\right)\left(\boldsymbol{v}\cdot\boldsymbol{n}\right)\boldsymbol{n}\right]\\ = & \left[2\cos^{2}\dfrac{\theta}{2}-1\right]\boldsymbol{v}+2\sin\dfrac{\theta}{2}\left[\left(\cos\dfrac{\theta}{2}\right)\boldsymbol{n}\times\boldsymbol{v}+\left(\sin\dfrac{\theta}{2}\right)\left(\boldsymbol{v}\cdot\boldsymbol{n}\right)\boldsymbol{n}\right] \end{aligned} \]

37.2.2 quaternion operation

\[ \begin{aligned} q= & a+b\mathrm{i}+c\mathrm{j}+d\mathrm{k}\\ \varrho= & \alpha+\beta\mathrm{i}+\gamma\mathrm{j}+\delta\mathrm{k} \end{aligned} \]

\[ \begin{aligned} \begin{pmatrix}a\\ b\\ c\\ d \end{pmatrix}\begin{pmatrix}\alpha\\ \beta\\ \gamma\\ \delta \end{pmatrix}\leftarrow q\varrho= & \left(a+b\mathrm{i}+c\mathrm{j}+d\mathrm{k}\right)\left(\alpha+\beta\mathrm{i}+\gamma\mathrm{j}+\delta\mathrm{k}\right)\\ = & a\left(\alpha+\beta\mathrm{i}+\gamma\mathrm{j}+\delta\mathrm{k}\right)\\ + & b\mathrm{i}\left(\alpha+\beta\mathrm{i}+\gamma\mathrm{j}+\delta\mathrm{k}\right)\\ + & c\mathrm{j}\left(\alpha+\beta\mathrm{i}+\gamma\mathrm{j}+\delta\mathrm{k}\right)\\ + & d\mathrm{k}\left(\alpha+\beta\mathrm{i}+\gamma\mathrm{j}+\delta\mathrm{k}\right)\\ = & a\alpha+a\beta\mathrm{i}+a\gamma\mathrm{j}+a\delta\mathrm{k}\\ + & b\alpha\mathrm{i}-b\beta+b\gamma\mathrm{k}-b\delta\mathrm{j}\\ + & c\alpha\mathrm{j}-c\beta\mathrm{k}-c\gamma+c\delta\mathrm{i}\\ + & d\alpha\mathrm{k}+d\beta\mathrm{j}-d\gamma\mathrm{i}-d\delta\\ = & \left(a\alpha-b\beta-c\gamma-d\delta\right)\\ + & \left(b\alpha+a\beta-d\gamma+c\delta\right)\mathrm{i}\\ + & \left(c\alpha+d\beta+a\gamma-b\delta\right)\mathrm{j}\\ + & \left(d\alpha-c\beta+b\gamma+a\delta\right)\mathrm{k}\\ \begin{pmatrix}a & -b & -c & -d\\ b & a & -d & c\\ c & d & a & -b\\ d & -c & b & a \end{pmatrix}\begin{pmatrix}\alpha\\ \beta\\ \gamma\\ \delta \end{pmatrix}\leftarrow\\ = & \left(\alpha a-\beta b-\gamma c-\delta d\right)\\ + & \left(\beta a+\alpha b+\delta c-\gamma d\right)\mathrm{i}\\ + & \left(\gamma a-\delta b+\alpha c+\beta d\right)\mathrm{j}\\ + & \left(\delta a+\gamma b-\beta c+\alpha d\right)\mathrm{k}\\ \begin{pmatrix}\alpha & -\beta & -\gamma & -\delta\\ \beta & \alpha & \delta & -\gamma\\ \gamma & -\delta & \alpha & \beta\\ \delta & \gamma & -\beta & \alpha \end{pmatrix}\begin{pmatrix}a\\ b\\ c\\ d \end{pmatrix}\leftarrow \end{aligned} \]

concept like quaternion group representation^[40.8]

\[ \begin{aligned} L\left(q\right)=Q_{{\scriptscriptstyle l}}=\begin{pmatrix}a & -b & -c & -d\\ b & a & -d & c\\ c & d & a & -b\\ d & -c & b & a \end{pmatrix}= & \begin{pmatrix}1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{pmatrix}a+\begin{pmatrix}0 & -1 & 0 & 0\\ 1 & 0 & 0 & 0\\ 0 & 0 & 0 & -1\\ 0 & 0 & 1 & 0 \end{pmatrix}b\\ + & \begin{pmatrix}0 & 0 & -1 & 0\\ 0 & 0 & 0 & 1\\ 1 & 0 & 0 & 0\\ 0 & -1 & 0 & 0 \end{pmatrix}c+\begin{pmatrix}0 & 0 & 0 & -1\\ 0 & 0 & -1 & 0\\ 0 & 1 & 0 & 0\\ 1 & 0 & 0 & 0 \end{pmatrix}d\\ \leftrightarrow & 1a+\mathrm{i}b+\mathrm{j}c+\mathrm{k}d \end{aligned} \]

\[ \mathrm{i}\mathrm{j}\leftrightarrow\begin{pmatrix}0 & -1 & 0 & 0\\ 1 & 0 & 0 & 0\\ 0 & 0 & 0 & -1\\ 0 & 0 & 1 & 0 \end{pmatrix}\begin{pmatrix}0 & 0 & -1 & 0\\ 0 & 0 & 0 & 1\\ 1 & 0 & 0 & 0\\ 0 & -1 & 0 & 0 \end{pmatrix}=\begin{pmatrix}0 & 0 & 0 & -1\\ 0 & 0 & -1 & 0\\ 0 & 1 & 0 & 0\\ 1 & 0 & 0 & 0 \end{pmatrix}\leftrightarrow\mathrm{k} \] \[ \mathrm{j}\mathrm{i}\leftrightarrow\begin{pmatrix}0 & 0 & -1 & 0\\ 0 & 0 & 0 & 1\\ 1 & 0 & 0 & 0\\ 0 & -1 & 0 & 0 \end{pmatrix}\begin{pmatrix}0 & -1 & 0 & 0\\ 1 & 0 & 0 & 0\\ 0 & 0 & 0 & -1\\ 0 & 0 & 1 & 0 \end{pmatrix}=-\begin{pmatrix}0 & 0 & 0 & -1\\ 0 & 0 & -1 & 0\\ 0 & 1 & 0 & 0\\ 1 & 0 & 0 & 0 \end{pmatrix}\leftrightarrow-\mathrm{k} \] \[ \mathrm{k}\mathrm{i}\leftrightarrow\begin{pmatrix}0 & 0 & 0 & -1\\ 0 & 0 & -1 & 0\\ 0 & 1 & 0 & 0\\ 1 & 0 & 0 & 0 \end{pmatrix}\begin{pmatrix}0 & -1 & 0 & 0\\ 1 & 0 & 0 & 0\\ 0 & 0 & 0 & -1\\ 0 & 0 & 1 & 0 \end{pmatrix}=\begin{pmatrix}0 & 0 & -1 & 0\\ 0 & 0 & 0 & 1\\ 1 & 0 & 0 & 0\\ 0 & -1 & 0 & 0 \end{pmatrix}\leftrightarrow\mathrm{j} \]

\[ Q_{{\scriptscriptstyle l}}=\begin{pmatrix}a & -b & -c & -d\\ b & a & -d & c\\ c & d & a & -b\\ d & -c & b & a \end{pmatrix}=\begin{pmatrix}a & -\begin{pmatrix}b & c & d\end{pmatrix}\\ \begin{pmatrix}b\\ c\\ d \end{pmatrix} & \begin{pmatrix}a & -d & c\\ d & a & -b\\ -c & b & a \end{pmatrix} \end{pmatrix}=\begin{pmatrix}q_{{\scriptscriptstyle 0}} & -\boldsymbol{q}^{\intercal}\\ \boldsymbol{q} & Q_{{\scriptscriptstyle i}} \end{pmatrix},\begin{cases} a=q_{{\scriptscriptstyle 0}}\\ \boldsymbol{q}=\begin{pmatrix}b\\ c\\ d \end{pmatrix}\\ Q_{{\scriptscriptstyle i}}=\begin{pmatrix}a & -d & c\\ d & a & -b\\ -c & b & a \end{pmatrix} \end{cases} \]

Grassmann product

\[ qv\leftrightarrow\begin{pmatrix}a & -b & -c & -d\\ b & a & -d & c\\ c & d & a & -b\\ d & -c & b & a \end{pmatrix}\begin{pmatrix}v_{{\scriptscriptstyle 0}}\\ v_{{\scriptscriptstyle 1}}\\ v_{{\scriptscriptstyle 2}}\\ v_{{\scriptscriptstyle 3}} \end{pmatrix}=Q_{{\scriptscriptstyle l}}v=\begin{pmatrix}q_{{\scriptscriptstyle 0}} & -\boldsymbol{q}^{\intercal}\\ \boldsymbol{q} & Q_{{\scriptscriptstyle i}} \end{pmatrix}\begin{pmatrix}v_{{\scriptscriptstyle 0}}\\ \boldsymbol{v} \end{pmatrix}=\begin{pmatrix}q_{{\scriptscriptstyle 0}}v_{{\scriptscriptstyle 0}}-\boldsymbol{q}^{\intercal}\boldsymbol{v}\\ \boldsymbol{q}v_{{\scriptscriptstyle 0}}+Q_{{\scriptscriptstyle i}}\boldsymbol{v} \end{pmatrix}=\begin{pmatrix}q_{{\scriptscriptstyle 0}}v_{{\scriptscriptstyle 0}}-\boldsymbol{q}\cdot\boldsymbol{v}\\ \boldsymbol{q}v_{{\scriptscriptstyle 0}}+q_{{\scriptscriptstyle 0}}\boldsymbol{v}+\boldsymbol{q}\times\boldsymbol{v} \end{pmatrix} \]

\[ \begin{aligned} R\left(q\right)=Q_{{\scriptscriptstyle r}}=\begin{pmatrix}a & -b & -c & -d\\ b & a & d & -c\\ c & -d & a & b\\ d & c & -b & a \end{pmatrix}= & a\begin{pmatrix}1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{pmatrix}+b\begin{pmatrix}0 & -1 & 0 & 0\\ 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 1\\ 0 & 0 & -1 & 0 \end{pmatrix}\\ + & c\begin{pmatrix}0 & 0 & -1 & 0\\ 0 & 0 & 0 & -1\\ 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 \end{pmatrix}+d\begin{pmatrix}0 & 0 & 0 & -1\\ 0 & 0 & 1 & 0\\ 0 & -1 & 0 & 0\\ 1 & 0 & 0 & 0 \end{pmatrix}\\ \leftrightarrow & a1+b\mathrm{i}+c\mathrm{j}+d\mathrm{k} \end{aligned} \]

\[ \mathrm{i}\mathrm{j}\leftrightarrow\begin{pmatrix}0 & -1 & 0 & 0\\ 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 1\\ 0 & 0 & -1 & 0 \end{pmatrix}\begin{pmatrix}0 & 0 & -1 & 0\\ 0 & 0 & 0 & -1\\ 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 \end{pmatrix}=-\begin{pmatrix}0 & 0 & 0 & -1\\ 0 & 0 & 1 & 0\\ 0 & -1 & 0 & 0\\ 1 & 0 & 0 & 0 \end{pmatrix}\leftrightarrow-\mathrm{k} \]

\[ \mathrm{j}\mathrm{i}\leftrightarrow\begin{pmatrix}0 & 0 & -1 & 0\\ 0 & 0 & 0 & -1\\ 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 \end{pmatrix}\begin{pmatrix}0 & -1 & 0 & 0\\ 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 1\\ 0 & 0 & -1 & 0 \end{pmatrix}=\begin{pmatrix}0 & 0 & 0 & -1\\ 0 & 0 & 1 & 0\\ 0 & -1 & 0 & 0\\ 1 & 0 & 0 & 0 \end{pmatrix}\leftrightarrow\mathrm{k} \]

\[ \mathrm{k}\mathrm{i}\leftrightarrow\begin{pmatrix}0 & 0 & 0 & -1\\ 0 & 0 & 1 & 0\\ 0 & -1 & 0 & 0\\ 1 & 0 & 0 & 0 \end{pmatrix}\begin{pmatrix}0 & -1 & 0 & 0\\ 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 1\\ 0 & 0 & -1 & 0 \end{pmatrix}=-\begin{pmatrix}0 & 0 & -1 & 0\\ 0 & 0 & 0 & -1\\ 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 \end{pmatrix}\leftrightarrow-\mathrm{j} \]

\[ \begin{aligned} R\left(q\right)=Q_{{\scriptscriptstyle r}}=\begin{pmatrix}a & -b & -c & -d\\ b & a & d & -c\\ c & -d & a & b\\ d & c & -b & a \end{pmatrix}\leftrightarrow & \begin{pmatrix}a+bi & -c+di\\ c+di & a-bi \end{pmatrix}\\ = & \begin{pmatrix}\alpha & -\overline{\beta}\\ \beta & \overline{\alpha} \end{pmatrix},\begin{cases} \alpha=a+bi & \overline{\alpha}=a-bi\\ \beta=c+di & \overline{\beta}=c-di \end{cases} \end{aligned} \]

\[ Q_{{\scriptscriptstyle r}}=\begin{pmatrix}a & -b & -c & -d\\ b & a & d & -c\\ c & -d & a & b\\ d & c & -b & a \end{pmatrix}=\begin{pmatrix}a & -\begin{pmatrix}b & c & d\end{pmatrix}\\ \begin{pmatrix}b\\ c\\ d \end{pmatrix} & \begin{pmatrix}a & d & -c\\ -d & a & b\\ c & -b & a \end{pmatrix} \end{pmatrix}=\begin{pmatrix}q_{{\scriptscriptstyle 0}} & -\boldsymbol{q}^{\intercal}\\ \boldsymbol{q} & Q_{{\scriptscriptstyle i}}^{\intercal} \end{pmatrix},\begin{cases} a=q_{{\scriptscriptstyle 0}}\\ \boldsymbol{q}=\begin{pmatrix}b\\ c\\ d \end{pmatrix}\\ Q_{{\scriptscriptstyle i}}=\begin{pmatrix}a & -d & c\\ d & a & -b\\ -c & b & a \end{pmatrix} \end{cases} \]

\[ vq\leftrightarrow\begin{pmatrix}a & -b & -c & -d\\ b & a & d & -c\\ c & -d & a & b\\ d & c & -b & a \end{pmatrix}\begin{pmatrix}v_{{\scriptscriptstyle 0}}\\ v_{{\scriptscriptstyle 1}}\\ v_{{\scriptscriptstyle 2}}\\ v_{{\scriptscriptstyle 3}} \end{pmatrix}=Q_{{\scriptscriptstyle r}}v=\begin{pmatrix}q_{{\scriptscriptstyle 0}} & -\boldsymbol{q}^{\intercal}\\ \boldsymbol{q} & Q_{{\scriptscriptstyle i}}^{\intercal} \end{pmatrix}\begin{pmatrix}v_{{\scriptscriptstyle 0}}\\ \boldsymbol{v} \end{pmatrix}=\begin{pmatrix}v_{{\scriptscriptstyle 0}}q_{{\scriptscriptstyle 0}}-\boldsymbol{q}^{\intercal}\boldsymbol{v}\\ v_{{\scriptscriptstyle 0}}\boldsymbol{q}+Q_{{\scriptscriptstyle i}}^{\intercal}\boldsymbol{v} \end{pmatrix}=\begin{pmatrix}v_{{\scriptscriptstyle 0}}q_{{\scriptscriptstyle 0}}-\boldsymbol{v}\cdot\boldsymbol{q}\\ v_{{\scriptscriptstyle 0}}\boldsymbol{q}+q_{{\scriptscriptstyle 0}}\boldsymbol{v}+\boldsymbol{v}\times\boldsymbol{q} \end{pmatrix}=\begin{pmatrix}q_{{\scriptscriptstyle 0}}v_{{\scriptscriptstyle 0}}-\boldsymbol{q}\cdot\boldsymbol{v}\\ \boldsymbol{q}v_{{\scriptscriptstyle 0}}+q_{{\scriptscriptstyle 0}}\boldsymbol{v}-\boldsymbol{q}\times\boldsymbol{v} \end{pmatrix} \]

\[ \begin{cases} qv\leftrightarrow Q_{{\scriptscriptstyle l}}v=\begin{pmatrix}q_{{\scriptscriptstyle 0}} & -\boldsymbol{q}^{\intercal}\\ \boldsymbol{q} & Q_{{\scriptscriptstyle i}} \end{pmatrix}\begin{pmatrix}v_{{\scriptscriptstyle 0}}\\ \boldsymbol{v} \end{pmatrix}=\begin{pmatrix}q_{{\scriptscriptstyle 0}}v_{{\scriptscriptstyle 0}}-\boldsymbol{q}^{\intercal}\boldsymbol{v}\\ \boldsymbol{q}v_{{\scriptscriptstyle 0}}+Q_{{\scriptscriptstyle i}}\boldsymbol{v} \end{pmatrix}=\begin{pmatrix}q_{{\scriptscriptstyle 0}}v_{{\scriptscriptstyle 0}}-\boldsymbol{q}\cdot\boldsymbol{v}\\ \boldsymbol{q}v_{{\scriptscriptstyle 0}}+q_{{\scriptscriptstyle 0}}\boldsymbol{v}+\boldsymbol{q}\times\boldsymbol{v} \end{pmatrix}=\begin{pmatrix}q_{{\scriptscriptstyle 0}}v_{{\scriptscriptstyle 0}}-\boldsymbol{q}\cdot\boldsymbol{v}\\ \boldsymbol{q}v_{{\scriptscriptstyle 0}}+q_{{\scriptscriptstyle 0}}\boldsymbol{v}+\boldsymbol{q}\times\boldsymbol{v} \end{pmatrix}\\ vq\leftrightarrow Q_{{\scriptscriptstyle r}}v=\begin{pmatrix}q_{{\scriptscriptstyle 0}} & -\boldsymbol{q}^{\intercal}\\ \boldsymbol{q} & Q_{{\scriptscriptstyle i}}^{\intercal} \end{pmatrix}\begin{pmatrix}v_{{\scriptscriptstyle 0}}\\ \boldsymbol{v} \end{pmatrix}=\begin{pmatrix}v_{{\scriptscriptstyle 0}}q_{{\scriptscriptstyle 0}}-\boldsymbol{q}^{\intercal}\boldsymbol{v}\\ v_{{\scriptscriptstyle 0}}\boldsymbol{q}+Q_{{\scriptscriptstyle i}}^{\intercal}\boldsymbol{v} \end{pmatrix}=\begin{pmatrix}v_{{\scriptscriptstyle 0}}q_{{\scriptscriptstyle 0}}-\boldsymbol{v}\cdot\boldsymbol{q}\\ v_{{\scriptscriptstyle 0}}\boldsymbol{q}+\boldsymbol{v}q_{{\scriptscriptstyle 0}}+\boldsymbol{v}\times\boldsymbol{q} \end{pmatrix}=\begin{pmatrix}q_{{\scriptscriptstyle 0}}v_{{\scriptscriptstyle 0}}-\boldsymbol{q}\cdot\boldsymbol{v}\\ \boldsymbol{q}v_{{\scriptscriptstyle 0}}+q_{{\scriptscriptstyle 0}}\boldsymbol{v}-\boldsymbol{q}\times\boldsymbol{v} \end{pmatrix} \end{cases} \]

\[ \begin{cases} qv=\begin{pmatrix}q_{{\scriptscriptstyle 0}}\\ \boldsymbol{q} \end{pmatrix}\begin{pmatrix}v_{{\scriptscriptstyle 0}}\\ \boldsymbol{v} \end{pmatrix}=L\left(q\right)v=Q_{{\scriptscriptstyle l}}v=\begin{pmatrix}q_{{\scriptscriptstyle 0}} & -\boldsymbol{q}^{\intercal}\\ \boldsymbol{q} & Q_{{\scriptscriptstyle i}} \end{pmatrix}\begin{pmatrix}v_{{\scriptscriptstyle 0}}\\ \boldsymbol{v} \end{pmatrix}\\ vq=\begin{pmatrix}v_{{\scriptscriptstyle 0}}\\ \boldsymbol{v} \end{pmatrix}\begin{pmatrix}q_{{\scriptscriptstyle 0}}\\ \boldsymbol{q} \end{pmatrix}=R\left(q\right)v=Q_{{\scriptscriptstyle r}}v=\begin{pmatrix}q_{{\scriptscriptstyle 0}} & -\boldsymbol{q}^{\intercal}\\ \boldsymbol{q} & Q_{{\scriptscriptstyle i}}^{\intercal} \end{pmatrix}\begin{pmatrix}v_{{\scriptscriptstyle 0}}\\ \boldsymbol{v} \end{pmatrix} \end{cases} \]

\[ \begin{aligned} & \begin{cases} \boldsymbol{v}\xrightarrow{\text{rotate about }\boldsymbol{n}}\boldsymbol{v}^{\prime}\\ \begin{cases} \boldsymbol{v}=\boldsymbol{v}_{{\scriptscriptstyle \parallel\boldsymbol{n}}}+\boldsymbol{v}_{{\scriptscriptstyle \perp\boldsymbol{n}}}=\boldsymbol{v}_{{\scriptscriptstyle \parallel}}+\boldsymbol{v}_{{\scriptscriptstyle \perp}}= & \Rightarrow\boldsymbol{v}_{{\scriptscriptstyle \perp}}=\boldsymbol{v}-\boldsymbol{v}_{{\scriptscriptstyle \parallel}}\\ \boldsymbol{v}^{\prime}=\boldsymbol{v}_{{\scriptscriptstyle \parallel\boldsymbol{n}}}^{\prime}+\boldsymbol{v}_{{\scriptscriptstyle \perp\boldsymbol{n}}}^{\prime}=\boldsymbol{v}_{{\scriptscriptstyle \parallel}}^{\prime}+\boldsymbol{v}_{{\scriptscriptstyle \perp}}^{\prime} & \Rightarrow\boldsymbol{v}_{{\scriptscriptstyle \perp}}^{\prime}=\boldsymbol{v}^{\prime}-\boldsymbol{v}_{{\scriptscriptstyle \parallel}}^{\prime} \end{cases}\\ \begin{cases} \boldsymbol{u}=\boldsymbol{n}\times\boldsymbol{v}_{{\scriptscriptstyle \perp}} & \begin{cases} \boldsymbol{u}\perp\boldsymbol{n}\\ \boldsymbol{u}\perp\boldsymbol{v}_{{\scriptscriptstyle \perp}} \end{cases}\\ \left\Vert \boldsymbol{u}\right\Vert =\left\Vert \boldsymbol{n}\times\boldsymbol{v}_{{\scriptscriptstyle \perp}}\right\Vert =\left\Vert \boldsymbol{n}\right\Vert \left\Vert \boldsymbol{v}_{{\scriptscriptstyle \perp}}\right\Vert \sin\dfrac{\pi}{2}=\left\Vert \boldsymbol{v}_{{\scriptscriptstyle \perp}}\right\Vert & \begin{cases} \boldsymbol{n}\perp\boldsymbol{v}_{{\scriptscriptstyle \perp}}\\ \left\Vert \boldsymbol{n}\right\Vert =1 \end{cases} \end{cases}\\ \boldsymbol{v}_{{\scriptscriptstyle \parallel}}^{\prime}=\boldsymbol{v}_{{\scriptscriptstyle \parallel}}\\ \boldsymbol{v}_{{\scriptscriptstyle \perp}}^{\prime}=\cos\theta\boldsymbol{v}_{{\scriptscriptstyle \perp}}+\sin\theta\left(\boldsymbol{n}\times\boldsymbol{v}_{{\scriptscriptstyle \perp}}\right),\theta=\angle\boldsymbol{v}_{{\scriptscriptstyle \perp}}^{\prime}\boldsymbol{v}_{{\scriptscriptstyle \perp}} \end{cases}\\ \leftrightarrow & \begin{cases} v\xrightarrow{\text{rotate about }n}v^{\prime}\\ \begin{cases} v=\begin{pmatrix}0\\ \boldsymbol{v} \end{pmatrix}=\begin{pmatrix}0\\ \boldsymbol{v}_{{\scriptscriptstyle \parallel\boldsymbol{n}}} \end{pmatrix}+\begin{pmatrix}0\\ \boldsymbol{v}_{{\scriptscriptstyle \perp\boldsymbol{n}}} \end{pmatrix}=\begin{pmatrix}0\\ \boldsymbol{v}_{{\scriptscriptstyle \parallel}} \end{pmatrix}+\begin{pmatrix}0\\ \boldsymbol{v}_{{\scriptscriptstyle \perp}} \end{pmatrix}=v_{{\scriptscriptstyle \parallel}}+v_{{\scriptscriptstyle \perp}} & \Rightarrow v_{{\scriptscriptstyle \perp}}=v-v_{{\scriptscriptstyle \parallel}}\\ v^{\prime}=\begin{pmatrix}0\\ \boldsymbol{v}^{\prime} \end{pmatrix}=\begin{pmatrix}0\\ \boldsymbol{v}^{\prime}_{{\scriptscriptstyle \parallel\boldsymbol{n}}} \end{pmatrix}+\begin{pmatrix}0\\ \boldsymbol{v}^{\prime}_{{\scriptscriptstyle \perp\boldsymbol{n}}} \end{pmatrix}=\begin{pmatrix}0\\ \boldsymbol{v}^{\prime}_{{\scriptscriptstyle \parallel}} \end{pmatrix}+\begin{pmatrix}0\\ \boldsymbol{v}^{\prime}_{{\scriptscriptstyle \perp}} \end{pmatrix}=v_{{\scriptscriptstyle \parallel}}^{\prime}+v_{{\scriptscriptstyle \perp}}^{\prime} & \Rightarrow v_{{\scriptscriptstyle \perp}}^{\prime}=v^{\prime}-v_{{\scriptscriptstyle \parallel}}^{\prime} \end{cases}\\ \begin{cases} u=\begin{pmatrix}0\\ \boldsymbol{u} \end{pmatrix}=\begin{pmatrix}0\\ \boldsymbol{n}\times\boldsymbol{v}_{{\scriptscriptstyle \perp}} \end{pmatrix}=\begin{pmatrix}00-0\\ \boldsymbol{n}0+0\boldsymbol{v}_{{\scriptscriptstyle \perp}}+\boldsymbol{n}\times\boldsymbol{v}_{{\scriptscriptstyle \perp}} \end{pmatrix}=\begin{pmatrix}n_{{\scriptscriptstyle 0}}v_{{\scriptscriptstyle \perp}0}-\boldsymbol{n}\cdot\boldsymbol{v}_{{\scriptscriptstyle \perp}}\\ \boldsymbol{n}v_{{\scriptscriptstyle \perp}0}+n_{{\scriptscriptstyle 0}}\boldsymbol{v}_{{\scriptscriptstyle \perp}}+\boldsymbol{n}\times\boldsymbol{v}_{{\scriptscriptstyle \perp}} \end{pmatrix}=nv_{{\scriptscriptstyle \perp}} & \begin{cases} \boldsymbol{u}\perp\boldsymbol{n}\\ \boldsymbol{u}\perp\boldsymbol{v}_{{\scriptscriptstyle \perp}} \end{cases}\\ \left\Vert \boldsymbol{u}\right\Vert =\left\Vert \boldsymbol{n}\times\boldsymbol{v}_{{\scriptscriptstyle \perp}}\right\Vert =\left\Vert \boldsymbol{n}\right\Vert \left\Vert \boldsymbol{v}_{{\scriptscriptstyle \perp}}\right\Vert \sin\dfrac{\pi}{2}=\left\Vert \boldsymbol{v}_{{\scriptscriptstyle \perp}}\right\Vert & \begin{cases} \boldsymbol{n}\perp\boldsymbol{v}_{{\scriptscriptstyle \perp}}\\ \left\Vert \boldsymbol{n}\right\Vert =1 \end{cases} \end{cases}\\ v_{{\scriptscriptstyle \parallel}}^{\prime}=\begin{pmatrix}0\\ \boldsymbol{v}_{{\scriptscriptstyle \parallel}}^{\prime} \end{pmatrix}=\begin{pmatrix}0\\ \boldsymbol{v}_{{\scriptscriptstyle \parallel}} \end{pmatrix}=v_{{\scriptscriptstyle \parallel}}\\ v_{{\scriptscriptstyle \perp}}^{\prime}=\begin{pmatrix}0\\ \boldsymbol{v}_{{\scriptscriptstyle \perp}}^{\prime} \end{pmatrix}=\cos\theta\begin{pmatrix}0\\ \boldsymbol{v}_{{\scriptscriptstyle \perp}} \end{pmatrix}+\sin\theta\begin{pmatrix}0\\ \boldsymbol{n}\times\boldsymbol{v}_{{\scriptscriptstyle \perp}} \end{pmatrix}=\cos\theta v_{{\scriptscriptstyle \perp}}+\sin\theta nv_{{\scriptscriptstyle \perp}}=\left(\cos\theta+\sin\theta n\right)v_{{\scriptscriptstyle \perp}} \end{cases} \end{aligned} \]

\[ v_{{\scriptscriptstyle \perp}}^{\prime}=\left(\cos\theta+\sin\theta n\right)v_{{\scriptscriptstyle \perp}} \]

\[ v_{{\scriptscriptstyle \perp}}^{\prime}=pv_{{\scriptscriptstyle \perp}},p=\cos\theta+\sin\theta n=\cos\theta\begin{pmatrix}1\\ \boldsymbol{0} \end{pmatrix}+\sin\theta\begin{pmatrix}0\\ \boldsymbol{n} \end{pmatrix}=\begin{pmatrix}\cos\theta\\ \sin\theta\boldsymbol{n} \end{pmatrix} \]

\[ p=\begin{pmatrix}p_{{\scriptscriptstyle 0}}\\ \boldsymbol{p} \end{pmatrix}=\begin{pmatrix}\cos\theta\\ \sin\theta\boldsymbol{n} \end{pmatrix}=\cos\theta+\sin\theta n,\left\Vert \boldsymbol{n}\right\Vert =1 \]

\[ \left|p\right|=\left\Vert \begin{pmatrix}\cos\theta\\ \sin\theta\boldsymbol{n} \end{pmatrix}\right\Vert =\sqrt{\begin{pmatrix}\cos\theta\\ \sin\theta\boldsymbol{n} \end{pmatrix}^{\intercal}\begin{pmatrix}\cos\theta\\ \sin\theta\boldsymbol{n} \end{pmatrix}}=\sqrt{\cos^{2}\theta+\sin^{2}\theta\left\Vert \boldsymbol{n}\right\Vert ^{2}}=\sqrt{\cos^{2}\theta+\sin^{2}\theta}=1 \]

\[ \left|p\right|=\left\Vert \begin{pmatrix}\cos\theta\\ \sin\theta\boldsymbol{n} \end{pmatrix}\right\Vert =1 \]

\[ p^{*}=\overline{p}=\begin{pmatrix}p_{{\scriptscriptstyle 0}}\\ -\boldsymbol{p} \end{pmatrix}=\begin{pmatrix}\cos\theta\\ -\sin\theta\boldsymbol{n} \end{pmatrix}=\cos\theta-\sin\theta n \]

\[ \begin{aligned} p^{*}p=\overline{p}p= & \begin{pmatrix}p_{{\scriptscriptstyle 0}}\\ -\boldsymbol{p} \end{pmatrix}\begin{pmatrix}p_{{\scriptscriptstyle 0}}\\ \boldsymbol{p} \end{pmatrix}=\begin{pmatrix}p_{{\scriptscriptstyle 0}}p_{{\scriptscriptstyle 0}}-\left(-\boldsymbol{p}\right)\cdot\boldsymbol{p}\\ -\boldsymbol{p}p_{{\scriptscriptstyle 0}}+p_{{\scriptscriptstyle 0}}\boldsymbol{p}+\left(-\boldsymbol{p}\right)\times\boldsymbol{p} \end{pmatrix}\\ = & \begin{pmatrix}p_{{\scriptscriptstyle 0}}p_{{\scriptscriptstyle 0}}+\boldsymbol{p}\cdot\boldsymbol{p}\\ \boldsymbol{0}+\boldsymbol{0} \end{pmatrix}=p_{{\scriptscriptstyle 0}}p_{{\scriptscriptstyle 0}}+\boldsymbol{p}\cdot\boldsymbol{p}=p_{{\scriptscriptstyle 0}}^{2}+\left\Vert \boldsymbol{p}\right\Vert ^{2}=\left|p\right|^{2}=1^{2}=1\\ = & \begin{pmatrix}p_{{\scriptscriptstyle 0}}p_{{\scriptscriptstyle 0}}-\boldsymbol{p}\cdot\left(-\boldsymbol{p}\right)\\ \boldsymbol{p}p_{{\scriptscriptstyle 0}}+p_{{\scriptscriptstyle 0}}\left(-\boldsymbol{p}\right)+\boldsymbol{p}\times\left(-\boldsymbol{p}\right) \end{pmatrix}=p\overline{p}=pp^{*} \end{aligned} \]

\[ p^{*}p=\overline{p}p=1=p\overline{p}=pp^{*}=\left|p\right|^{2}=p_{{\scriptscriptstyle 0}}^{2}+\left\Vert \boldsymbol{p}\right\Vert ^{2}\Rightarrow p^{*}=\dfrac{1}{p}=p^{-1} \]

\[ \begin{aligned} p^{2}=pp= & \begin{pmatrix}p_{{\scriptscriptstyle 0}}p_{{\scriptscriptstyle 0}}-\boldsymbol{p}\cdot\boldsymbol{p}\\ \boldsymbol{p}p_{{\scriptscriptstyle 0}}+p_{{\scriptscriptstyle 0}}\boldsymbol{p}+\boldsymbol{p}\times\boldsymbol{p} \end{pmatrix}=\begin{pmatrix}\cos^{2}\theta-\sin^{2}\theta\left\Vert \boldsymbol{n}\right\Vert ^{2}\\ 2\left(\sin\theta\boldsymbol{n}\right)\cos\theta+\boldsymbol{0} \end{pmatrix}\\ = & \begin{pmatrix}\cos^{2}\theta-\sin^{2}\theta\\ 2\sin\theta\cos\theta\boldsymbol{n} \end{pmatrix}=\begin{pmatrix}\cos2\theta\\ \sin2\theta\boldsymbol{n} \end{pmatrix}\\ \begin{pmatrix}\cos\theta\\ \sin\theta\boldsymbol{n} \end{pmatrix}^{2}= & \begin{pmatrix}\cos2\theta\\ \sin2\theta\boldsymbol{n} \end{pmatrix}\\ q^{2}=\begin{pmatrix}\cos\dfrac{\theta}{2}\\ \sin\dfrac{\theta}{2}\boldsymbol{n} \end{pmatrix}^{2}= & \begin{pmatrix}\cos\theta\\ \sin\theta\boldsymbol{n} \end{pmatrix}=p \end{aligned} \]

\(qv_{{\scriptscriptstyle \parallel}}=v_{{\scriptscriptstyle \parallel}}q\)

\[ \begin{aligned} \begin{pmatrix}\alpha\\ \beta\boldsymbol{n} \end{pmatrix}v_{{\scriptscriptstyle \parallel\boldsymbol{n}}}= & \begin{pmatrix}\alpha\\ \beta\boldsymbol{n} \end{pmatrix}v_{{\scriptscriptstyle \parallel}}=\begin{pmatrix}\alpha\\ \beta\boldsymbol{n} \end{pmatrix}\begin{pmatrix}0\\ \boldsymbol{v}_{{\scriptscriptstyle \parallel}} \end{pmatrix}\\ = & \begin{pmatrix}\alpha0-\beta\boldsymbol{n}\cdot\boldsymbol{v}_{{\scriptscriptstyle \parallel}}\\ \beta\boldsymbol{n}0+\alpha\boldsymbol{v}_{{\scriptscriptstyle \parallel}}+\beta\boldsymbol{n}\times\boldsymbol{v}_{{\scriptscriptstyle \parallel}} \end{pmatrix}=\begin{pmatrix}-\beta\boldsymbol{n}\cdot\boldsymbol{v}_{{\scriptscriptstyle \parallel}}\\ \alpha\boldsymbol{v}_{{\scriptscriptstyle \parallel}}+\boldsymbol{0} \end{pmatrix}=\begin{pmatrix}-\beta\boldsymbol{n}\cdot\boldsymbol{v}_{{\scriptscriptstyle \parallel}}\\ \alpha\boldsymbol{v}_{{\scriptscriptstyle \parallel}} \end{pmatrix}\\ = & \begin{pmatrix}0\alpha-\boldsymbol{v}_{{\scriptscriptstyle \parallel}}\cdot\beta\boldsymbol{n}\\ \boldsymbol{v}_{{\scriptscriptstyle \parallel}}\alpha+0\beta\boldsymbol{n}+\boldsymbol{v}_{{\scriptscriptstyle \parallel}}\times\beta\boldsymbol{n} \end{pmatrix}=\begin{pmatrix}-\boldsymbol{v}_{{\scriptscriptstyle \parallel}}\cdot\beta\boldsymbol{n}\\ \alpha\boldsymbol{v}_{{\scriptscriptstyle \parallel}}+\boldsymbol{0} \end{pmatrix}=\begin{pmatrix}-\beta\boldsymbol{n}\cdot\boldsymbol{v}_{{\scriptscriptstyle \parallel}}\\ \alpha\boldsymbol{v}_{{\scriptscriptstyle \parallel}} \end{pmatrix}\\ = & \begin{pmatrix}0\\ \boldsymbol{v}_{{\scriptscriptstyle \parallel}} \end{pmatrix}\begin{pmatrix}\alpha\\ \beta\boldsymbol{n} \end{pmatrix}=v_{{\scriptscriptstyle \parallel}}\begin{pmatrix}\alpha\\ \beta\boldsymbol{n} \end{pmatrix}=v_{{\scriptscriptstyle \parallel\boldsymbol{n}}}\begin{pmatrix}\alpha\\ \beta\boldsymbol{n} \end{pmatrix}\\ \begin{pmatrix}\alpha\\ \beta\boldsymbol{n} \end{pmatrix}v_{{\scriptscriptstyle \parallel}}= & v_{{\scriptscriptstyle \parallel}}\begin{pmatrix}\alpha\\ \beta\boldsymbol{n} \end{pmatrix} \end{aligned} \]

\(qv_{{\scriptscriptstyle \perp}}=v_{{\scriptscriptstyle \perp}}q^{*}\)

\[ \begin{aligned} \begin{pmatrix}\alpha\\ \beta\boldsymbol{n} \end{pmatrix}v_{{\scriptscriptstyle \perp\boldsymbol{n}}}= & \begin{pmatrix}\alpha\\ \beta\boldsymbol{n} \end{pmatrix}v_{{\scriptscriptstyle \perp}}=\begin{pmatrix}\alpha\\ \beta\boldsymbol{n} \end{pmatrix}\begin{pmatrix}0\\ \boldsymbol{v}_{{\scriptscriptstyle \perp}} \end{pmatrix}\\ = & \begin{pmatrix}\alpha0-\beta\boldsymbol{n}\cdot\boldsymbol{v}_{{\scriptscriptstyle \perp}}\\ \beta\boldsymbol{n}0+\alpha\boldsymbol{v}_{{\scriptscriptstyle \perp}}+\beta\boldsymbol{n}\times\boldsymbol{v}_{{\scriptscriptstyle \perp}} \end{pmatrix}=\begin{pmatrix}0-0\\ \alpha\boldsymbol{v}_{{\scriptscriptstyle \perp}}+\beta\boldsymbol{n}\times\boldsymbol{v}_{{\scriptscriptstyle \perp}} \end{pmatrix}=\begin{pmatrix}0\\ \alpha\boldsymbol{v}_{{\scriptscriptstyle \perp}}+\boldsymbol{v}_{{\scriptscriptstyle \perp}}\times\left(-\beta\boldsymbol{n}\right) \end{pmatrix}\\ = & \begin{pmatrix}0\alpha-\boldsymbol{v}_{{\scriptscriptstyle \perp}}\cdot\left(-\beta\boldsymbol{n}\right)\\ \boldsymbol{v}_{{\scriptscriptstyle \perp}}\alpha+0\left(-\beta\boldsymbol{n}\right)+\boldsymbol{v}_{{\scriptscriptstyle \perp}}\times\left(-\beta\boldsymbol{n}\right) \end{pmatrix}=\begin{pmatrix}0-0\\ \alpha\boldsymbol{v}_{{\scriptscriptstyle \perp}}+\boldsymbol{v}_{{\scriptscriptstyle \perp}}\times\left(-\beta\boldsymbol{n}\right) \end{pmatrix}=\begin{pmatrix}0\\ \alpha\boldsymbol{v}_{{\scriptscriptstyle \perp}}+\beta\boldsymbol{n}\times\boldsymbol{v}_{{\scriptscriptstyle \perp}} \end{pmatrix}\\ = & \begin{pmatrix}0\\ \boldsymbol{v}_{{\scriptscriptstyle \perp}} \end{pmatrix}\begin{pmatrix}\alpha\\ -\beta\boldsymbol{n} \end{pmatrix}=v_{{\scriptscriptstyle \perp}}\begin{pmatrix}\alpha\\ -\beta\boldsymbol{n} \end{pmatrix}=v_{{\scriptscriptstyle \perp\boldsymbol{n}}}\begin{pmatrix}\alpha\\ -\beta\boldsymbol{n} \end{pmatrix}\\ \begin{pmatrix}\alpha\\ \beta\boldsymbol{n} \end{pmatrix}v_{{\scriptscriptstyle \perp}}= & v_{{\scriptscriptstyle \perp}}\begin{pmatrix}\alpha\\ -\beta\boldsymbol{n} \end{pmatrix}=v_{{\scriptscriptstyle \perp}}\begin{pmatrix}\alpha\\ \beta\boldsymbol{n} \end{pmatrix}^{*}=v_{{\scriptscriptstyle \perp}}\overline{\begin{pmatrix}\alpha\\ \beta\boldsymbol{n} \end{pmatrix}} \end{aligned} \]

\[ \begin{aligned} q=\cos\dfrac{\theta}{2}+\sin\dfrac{\theta}{2}n\in & \left\{ p\middle|\begin{cases} p=\cos\theta+\sin\theta n\\ n=\begin{pmatrix}0\\ \boldsymbol{n} \end{pmatrix},\left\Vert \boldsymbol{n}\right\Vert =1 \end{cases}\right\} \subset\left\{ \begin{pmatrix}\alpha\\ \beta\boldsymbol{n} \end{pmatrix}\middle|\begin{cases} \alpha,\beta\in\mathbb{R}\\ \left\Vert \boldsymbol{n}\right\Vert =1 \end{cases}\right\} \\ \Rightarrow & \begin{cases} q^{*}q=\overline{q}q=1=q\overline{q}=qq^{*}=\left|q\right|^{2}=q_{{\scriptscriptstyle 0}}^{2}+\left\Vert \boldsymbol{q}\right\Vert ^{2}\Rightarrow q^{*}=\dfrac{1}{q}=q^{-1} & \left(u\right)\text{unit quaternion}\\ qv_{{\scriptscriptstyle \parallel}}=v_{{\scriptscriptstyle \parallel}}q & \left(c\right)\text{commutativity}\\ qv_{{\scriptscriptstyle \perp}}=v_{{\scriptscriptstyle \perp}}q^{*}=v_{{\scriptscriptstyle \perp}}\overline{q}\Leftrightarrow\begin{pmatrix}\cos\dfrac{\theta}{2}\\ \sin\dfrac{\theta}{2}\boldsymbol{n} \end{pmatrix}v_{{\scriptscriptstyle \perp}}=v_{{\scriptscriptstyle \perp}}\begin{pmatrix}\cos\dfrac{\theta}{2}\\ -\sin\dfrac{\theta}{2}\boldsymbol{n} \end{pmatrix} & \left(a\right)\text{anticommutativity} \end{cases} \end{aligned} \]

\[ \begin{aligned} v^{\prime}= & v_{{\scriptscriptstyle \parallel}}^{\prime}+v_{{\scriptscriptstyle \perp}}^{\prime},\begin{cases} v_{{\scriptscriptstyle \parallel}}^{\prime}=v_{{\scriptscriptstyle \parallel}} & q=\cos\dfrac{\theta}{2}+\sin\dfrac{\theta}{2}n,\left|n\right|=1\\ v_{{\scriptscriptstyle \perp}}^{\prime}=pv_{{\scriptscriptstyle \perp}}=q^{2}v_{{\scriptscriptstyle \perp}} & p=q^{2}=\cos\theta+\sin\theta n \end{cases}\\ = & v_{{\scriptscriptstyle \parallel}}+q^{2}v_{{\scriptscriptstyle \perp}}\overset{\left(u\right)}{=}1v_{{\scriptscriptstyle \parallel}}+qqv_{{\scriptscriptstyle \perp}}\\ \overset{\left(a\right)}{=} & qq^{*}v_{{\scriptscriptstyle \parallel}}+qv_{{\scriptscriptstyle \perp}}q^{*}\overset{\left(c\right)}{=}qv_{{\scriptscriptstyle \parallel}}q^{*}+qv_{{\scriptscriptstyle \perp}}q^{*}\\ = & q\left(v_{{\scriptscriptstyle \parallel}}+v_{{\scriptscriptstyle \perp}}\right)q^{*}=q\left(v\right)q^{*}=qvq^{*} \end{aligned} \]

\[ \begin{aligned} v^{\prime}= & qvq^{-1},q=\cos\dfrac{\theta}{2}+\sin\dfrac{\theta}{2}n,\left|n\right|=1\\ = & qvq^{*}=q\left(v_{{\scriptscriptstyle \parallel}}+v_{{\scriptscriptstyle \perp}}\right)q^{*}\\ = & qv_{{\scriptscriptstyle \parallel}}q^{*}+qv_{{\scriptscriptstyle \perp}}q^{*}=qq^{*}v_{{\scriptscriptstyle \parallel}}+qqv_{{\scriptscriptstyle \perp}}=1v_{{\scriptscriptstyle \parallel}}+q^{2}v_{{\scriptscriptstyle \perp}}\\ = & v_{{\scriptscriptstyle \parallel}}+pv_{{\scriptscriptstyle \perp}},p=q^{2}=\cos\theta+\sin\theta n \end{aligned} \]

\[ \begin{aligned} v^{\prime}=qvq^{*}=q\left(vq^{*}\right)\leftrightarrow & L\left(q\right)R\left(q^{*}\right)v=Q_{{\scriptscriptstyle l}}Q_{{\scriptscriptstyle r}}v=\begin{pmatrix}q_{{\scriptscriptstyle 0}} & -\boldsymbol{q}^{\intercal}\\ \boldsymbol{q} & Q_{{\scriptscriptstyle i}} \end{pmatrix}\begin{pmatrix}q_{{\scriptscriptstyle 0}} & -\boldsymbol{q}^{\intercal}\\ \boldsymbol{q} & Q_{{\scriptscriptstyle i}}^{\intercal} \end{pmatrix}\begin{pmatrix}v_{{\scriptscriptstyle 0}}\\ \boldsymbol{v} \end{pmatrix}\\ =\left(qv\right)q^{*}\leftrightarrow & R\left(q^{*}\right)L\left(q\right)v=Q_{{\scriptscriptstyle r}}Q_{{\scriptscriptstyle l}}v=\begin{pmatrix}q_{{\scriptscriptstyle 0}} & -\boldsymbol{q}^{\intercal}\\ \boldsymbol{q} & Q_{{\scriptscriptstyle i}}^{\intercal} \end{pmatrix}\begin{pmatrix}q_{{\scriptscriptstyle 0}} & -\boldsymbol{q}^{\intercal}\\ \boldsymbol{q} & Q_{{\scriptscriptstyle i}} \end{pmatrix}\begin{pmatrix}v_{{\scriptscriptstyle 0}}\\ \boldsymbol{v} \end{pmatrix}\\ \begin{pmatrix}q_{{\scriptscriptstyle 0}} & -\boldsymbol{q}^{\intercal}\\ \boldsymbol{q} & Q_{{\scriptscriptstyle i}} \end{pmatrix}\begin{pmatrix}q_{{\scriptscriptstyle 0}} & -\boldsymbol{q}^{\intercal}\\ \boldsymbol{q} & Q_{{\scriptscriptstyle i}}^{\intercal} \end{pmatrix}= & \begin{pmatrix}q_{{\scriptscriptstyle 0}}^{2}-\boldsymbol{q}^{\intercal}\boldsymbol{q} & -q_{{\scriptscriptstyle 0}}\boldsymbol{q}^{\intercal}-\boldsymbol{q}^{\intercal}Q_{{\scriptscriptstyle i}}^{\intercal}\\ \boldsymbol{q}q_{{\scriptscriptstyle 0}}+Q_{{\scriptscriptstyle i}}\boldsymbol{q} & -\boldsymbol{q}\boldsymbol{q}^{\intercal}+Q_{{\scriptscriptstyle i}}Q_{{\scriptscriptstyle i}}^{\intercal} \end{pmatrix}=L\left(q\right)R\left(q^{*}\right)\\ \begin{pmatrix}q_{{\scriptscriptstyle 0}} & -\boldsymbol{q}^{\intercal}\\ \boldsymbol{q} & Q_{{\scriptscriptstyle i}}^{\intercal} \end{pmatrix}\begin{pmatrix}q_{{\scriptscriptstyle 0}} & -\boldsymbol{q}^{\intercal}\\ \boldsymbol{q} & Q_{{\scriptscriptstyle i}} \end{pmatrix}= & \begin{pmatrix}q_{{\scriptscriptstyle 0}}^{2}-\boldsymbol{q}^{\intercal}\boldsymbol{q} & -q_{{\scriptscriptstyle 0}}\boldsymbol{q}^{\intercal}-\boldsymbol{q}^{\intercal}Q_{{\scriptscriptstyle i}}\\ \boldsymbol{q}q_{{\scriptscriptstyle 0}}+Q_{{\scriptscriptstyle i}}^{\intercal}\boldsymbol{q} & -\boldsymbol{q}\boldsymbol{q}^{\intercal}+Q_{{\scriptscriptstyle i}}^{\intercal}Q_{{\scriptscriptstyle i}} \end{pmatrix}=R\left(q^{*}\right)L\left(q\right) \end{aligned} \]

\[ \begin{aligned} q= & a+b\mathrm{i}+c\mathrm{j}+d\mathrm{k}=\cos\dfrac{\theta}{2}+\sin\dfrac{\theta}{2}n=\cos\dfrac{\theta}{2}+b\mathrm{i}+c\mathrm{j}+d\mathrm{k}\\ \Rightarrow Q_{{\scriptscriptstyle i}}Q_{{\scriptscriptstyle i}}^{\intercal}= & \begin{pmatrix}a & -d & c\\ d & a & -b\\ -c & b & a \end{pmatrix}\begin{pmatrix}a & d & -c\\ -d & a & b\\ c & -b & a \end{pmatrix}=\begin{pmatrix}a^{2}+d^{2}+c^{2} & -cb & -db\\ -cb & d^{2}+a^{2}+b^{2} & -dc\\ -db & -dc & c^{2}+b^{2}+a^{2} \end{pmatrix}\\ =Q_{{\scriptscriptstyle i}}^{\intercal}Q_{{\scriptscriptstyle i}}= & \begin{pmatrix}a & d & -c\\ -d & a & b\\ c & -b & a \end{pmatrix}\begin{pmatrix}a & -d & c\\ d & a & -b\\ -c & b & a \end{pmatrix}=\begin{pmatrix}a^{2}+d^{2}+c^{2} & -cb & -db\\ -cb & d^{2}+a^{2}+b^{2} & -dc\\ -db & -dc & c^{2}+b^{2}+a^{2} \end{pmatrix}\\ \boldsymbol{q}^{\intercal}Q_{{\scriptscriptstyle i}}^{\intercal}= & \begin{pmatrix}b & c & d\end{pmatrix}\begin{pmatrix}a & d & -c\\ -d & a & b\\ c & -b & a \end{pmatrix}=\begin{pmatrix}ba & ca & da\end{pmatrix}\\ =\boldsymbol{q}^{\intercal}Q_{{\scriptscriptstyle i}}= & \begin{pmatrix}b & c & d\end{pmatrix}\begin{pmatrix}a & -d & c\\ d & a & -b\\ -c & b & a \end{pmatrix}=\begin{pmatrix}ba & ca & da\end{pmatrix}\\ Q_{{\scriptscriptstyle i}}\boldsymbol{q}= & \begin{pmatrix}a & -d & c\\ d & a & -b\\ -c & b & a \end{pmatrix}\begin{pmatrix}b\\ c\\ d \end{pmatrix}=\begin{pmatrix}ab\\ ac\\ ad \end{pmatrix}\\ =Q_{{\scriptscriptstyle i}}^{\intercal}\boldsymbol{q}= & \begin{pmatrix}a & d & -c\\ -d & a & b\\ c & -b & a \end{pmatrix}\begin{pmatrix}b\\ c\\ d \end{pmatrix}=\begin{pmatrix}ab\\ ac\\ ad \end{pmatrix} \end{aligned} \]

\[ \begin{aligned} & \begin{pmatrix}q_{{\scriptscriptstyle 0}} & -\boldsymbol{q}^{\intercal}\\ \boldsymbol{q} & Q_{{\scriptscriptstyle i}} \end{pmatrix}\begin{pmatrix}q_{{\scriptscriptstyle 0}} & -\boldsymbol{q}^{\intercal}\\ \boldsymbol{q} & Q_{{\scriptscriptstyle i}}^{\intercal} \end{pmatrix}=\begin{pmatrix}q_{{\scriptscriptstyle 0}}^{2}-\boldsymbol{q}^{\intercal}\boldsymbol{q} & -q_{{\scriptscriptstyle 0}}\boldsymbol{q}^{\intercal}-\boldsymbol{q}^{\intercal}Q_{{\scriptscriptstyle i}}^{\intercal}\\ \boldsymbol{q}q_{{\scriptscriptstyle 0}}+Q_{{\scriptscriptstyle i}}\boldsymbol{q} & -\boldsymbol{q}\boldsymbol{q}^{\intercal}+Q_{{\scriptscriptstyle i}}Q_{{\scriptscriptstyle i}}^{\intercal} \end{pmatrix}=L\left(q\right)R\left(q^{*}\right)\\ = & \begin{pmatrix}q_{{\scriptscriptstyle 0}} & -\boldsymbol{q}^{\intercal}\\ \boldsymbol{q} & Q_{{\scriptscriptstyle i}}^{\intercal} \end{pmatrix}\begin{pmatrix}q_{{\scriptscriptstyle 0}} & -\boldsymbol{q}^{\intercal}\\ \boldsymbol{q} & Q_{{\scriptscriptstyle i}} \end{pmatrix}=\begin{pmatrix}q_{{\scriptscriptstyle 0}}^{2}-\boldsymbol{q}^{\intercal}\boldsymbol{q} & -q_{{\scriptscriptstyle 0}}\boldsymbol{q}^{\intercal}-\boldsymbol{q}^{\intercal}Q_{{\scriptscriptstyle i}}\\ \boldsymbol{q}q_{{\scriptscriptstyle 0}}+Q_{{\scriptscriptstyle i}}^{\intercal}\boldsymbol{q} & -\boldsymbol{q}\boldsymbol{q}^{\intercal}+Q_{{\scriptscriptstyle i}}^{\intercal}Q_{{\scriptscriptstyle i}} \end{pmatrix}=R\left(q^{*}\right)L\left(q\right)\\ \Downarrow\\ L\left(q\right)R\left(q^{*}\right)= & R\left(q^{*}\right)L\left(q\right)\\ \updownarrow\\ v^{\prime}=qvq^{*}=q\left(vq^{*}\right)= & \left(qv\right)q^{*} \end{aligned} \]

\[ a=\cos\dfrac{\theta}{2}\Rightarrow\theta=2\arccos a=2\cos^{-1}a \]

\[ \sin\dfrac{\theta}{2}n=\sin\dfrac{2\arccos a}{2}n=\sin\left(\cos^{-1}a\right)n \]

\[ n=\begin{pmatrix}0\\ \boldsymbol{n} \end{pmatrix}=\begin{pmatrix}0\\ \hat{\boldsymbol{n}} \end{pmatrix},\left\Vert \boldsymbol{n}\right\Vert =1,\boldsymbol{n}=\begin{pmatrix}\sin\gamma\cos\varphi\\ \sin\gamma\sin\varphi\\ \cos\gamma \end{pmatrix},\begin{cases} \varphi=\angle\hat{\boldsymbol{n}}_{{\scriptscriptstyle xy}}\hat{\boldsymbol{x}}\\ \gamma=\angle\hat{\boldsymbol{n}}\hat{\boldsymbol{z}} \end{cases} \]

\[ \begin{aligned} q= & a+b\mathrm{i}+c\mathrm{j}+d\mathrm{k}\\ = & \cos\dfrac{\theta}{2}+\sin\dfrac{\theta}{2}n,n=\begin{pmatrix}0\\ \boldsymbol{n} \end{pmatrix}=\begin{pmatrix}0\\ \hat{\boldsymbol{n}} \end{pmatrix}=\begin{pmatrix}0\\ \sin\gamma\cos\varphi\\ \sin\gamma\sin\varphi\\ \cos\gamma \end{pmatrix},\left\Vert \boldsymbol{n}\right\Vert =1,\begin{cases} \varphi=\angle\hat{\boldsymbol{n}}_{{\scriptscriptstyle xy}}\hat{\boldsymbol{x}}\\ \gamma=\angle\hat{\boldsymbol{n}}\hat{\boldsymbol{z}} \end{cases}\\ = & \cos\dfrac{\theta}{2}+\sin\dfrac{\theta}{2}\boldsymbol{n},\boldsymbol{n}=\left(\sin\gamma\cos\varphi\right)\mathrm{i}+\left(\sin\gamma\sin\varphi\right)\mathrm{j}+\left(\cos\gamma\right)\mathrm{k}\\ = & \cos\dfrac{\theta}{2}+\sin\dfrac{\theta}{2}\left[\left(\sin\gamma\cos\varphi\right)\mathrm{i}+\left(\sin\gamma\sin\varphi\right)\mathrm{j}+\left(\cos\gamma\right)\mathrm{k}\right]\\ = & \cos\dfrac{\theta}{2}+\boldsymbol{n}\sin\dfrac{\theta}{2}\\ q^{-1}=q^{*}= & \cos\dfrac{\theta}{2}-\boldsymbol{n}\sin\dfrac{\theta}{2}\\ = & \cos\dfrac{\theta}{2}-\sin\dfrac{\theta}{2}\left[\left(\sin\gamma\cos\varphi\right)\mathrm{i}+\left(\sin\gamma\sin\varphi\right)\mathrm{j}+\left(\cos\gamma\right)\mathrm{k}\right]\\ \boldsymbol{v}^{\prime}=v^{\prime}= & qvq^{-1}=q\boldsymbol{v}q^{-1},\begin{cases} v=\boldsymbol{v}=v_{{\scriptscriptstyle 1}}\mathrm{i}+v_{{\scriptscriptstyle 2}}\mathrm{j}+v_{{\scriptscriptstyle 3}}\mathrm{k}\\ v^{\prime}=\boldsymbol{v}^{\prime}=v_{{\scriptscriptstyle 1}}^{\prime}\mathrm{i}+v_{{\scriptscriptstyle 2}}^{\prime}\mathrm{j}+v_{{\scriptscriptstyle 3}}^{\prime}\mathrm{k} \end{cases}\\ = & \left\{ \cos\dfrac{\theta}{2}+\sin\dfrac{\theta}{2}\left[\left(\sin\gamma\cos\varphi\right)\mathrm{i}+\left(\sin\gamma\sin\varphi\right)\mathrm{j}+\left(\cos\gamma\right)\mathrm{k}\right]\right\} \boldsymbol{v}\\ & \left\{ \cos\dfrac{\theta}{2}-\sin\dfrac{\theta}{2}\left[\left(\sin\gamma\cos\varphi\right)\mathrm{i}+\left(\sin\gamma\sin\varphi\right)\mathrm{j}+\left(\cos\gamma\right)\mathrm{k}\right]\right\} \\ = & q\left(\theta,\gamma,\varphi\right)\boldsymbol{v}q^{-1}\left(\theta,\gamma,\varphi\right)\\ = & \left\{ \cos\dfrac{\theta}{2}+\sin\dfrac{\theta}{2}\left[n_{{\scriptscriptstyle x}}\mathrm{i}+n_{{\scriptscriptstyle y}}\mathrm{j}+n_{{\scriptscriptstyle z}}\mathrm{k}\right]\right\} \boldsymbol{v}\left\{ \cos\dfrac{\theta}{2}-\sin\dfrac{\theta}{2}\left[n_{{\scriptscriptstyle x}}\mathrm{i}+n_{{\scriptscriptstyle y}}\mathrm{j}+n_{{\scriptscriptstyle z}}\mathrm{k}\right]\right\} \\ = & \left\{ \cos\dfrac{\theta}{2}+\sin\dfrac{\theta}{2}\left[n_{{\scriptscriptstyle x}}\mathrm{i}\pm\sqrt{1-n_{{\scriptscriptstyle x}}^{2}-n_{{\scriptscriptstyle z}}^{2}}\mathrm{j}+n_{{\scriptscriptstyle z}}\mathrm{k}\right]\right\} \boldsymbol{v}\\ & \left\{ \cos\dfrac{\theta}{2}-\sin\dfrac{\theta}{2}\left[n_{{\scriptscriptstyle x}}\mathrm{i}\pm\sqrt{1-n_{{\scriptscriptstyle x}}^{2}-n_{{\scriptscriptstyle z}}^{2}}\mathrm{j}+n_{{\scriptscriptstyle z}}\mathrm{k}\right]\right\} \\ = & q\left(\theta,n_{{\scriptscriptstyle z}},n_{{\scriptscriptstyle x}}\right)\boldsymbol{v}q^{-1}\left(\theta,n_{{\scriptscriptstyle z}},n_{{\scriptscriptstyle x}}\right) \end{aligned} \]

\[ \boldsymbol{v}^{\prime}=v^{\prime}=qvq^{-1}=q\boldsymbol{v}q^{-1},\begin{cases} v=\boldsymbol{v}=v_{{\scriptscriptstyle 1}}\mathrm{i}+v_{{\scriptscriptstyle 2}}\mathrm{j}+v_{{\scriptscriptstyle 3}}\mathrm{k}\\ v^{\prime}=\boldsymbol{v}^{\prime}=v_{{\scriptscriptstyle 1}}^{\prime}\mathrm{i}+v_{{\scriptscriptstyle 2}}^{\prime}\mathrm{j}+v_{{\scriptscriptstyle 3}}^{\prime}\mathrm{k}\\ q=\cos\dfrac{\theta}{2}+\sin\dfrac{\theta}{2}\left[\left(\sin\gamma\cos\varphi\right)\mathrm{i}+\left(\sin\gamma\sin\varphi\right)\mathrm{j}+\left(\cos\gamma\right)\mathrm{k}\right]\\ q^{-1}=\cos\dfrac{\theta}{2}-\sin\dfrac{\theta}{2}\left[\left(\sin\gamma\cos\varphi\right)\mathrm{i}+\left(\sin\gamma\sin\varphi\right)\mathrm{j}+\left(\cos\gamma\right)\mathrm{k}\right] \end{cases} \]

37.2.3 matrix form

\[ q\overset{\left|q\right|=1}{=}a+b\mathrm{i}+c\mathrm{j}+d\mathrm{k},\begin{cases} a=\cos\dfrac{\theta}{2}\\ b=\sin\dfrac{\theta}{2}\sin\gamma\cos\varphi\\ c=\sin\dfrac{\theta}{2}\sin\gamma\sin\varphi\\ d=\sin\dfrac{\theta}{2}\cos\gamma \end{cases} \]

\[ L\left(q\right)=Q_{{\scriptscriptstyle l}}=\begin{pmatrix}a & -b & -c & -d\\ b & a & -d & c\\ c & d & a & -b\\ d & -c & b & a \end{pmatrix} \]

\[ R\left(q\right)=Q_{{\scriptscriptstyle r}}=\begin{pmatrix}a & -b & -c & -d\\ b & a & d & -c\\ c & -d & a & b\\ d & c & -b & a \end{pmatrix} \]

\[ R\left(q^{*}\right)=\begin{pmatrix}a & b & c & d\\ -b & a & -d & c\\ -c & d & a & -b\\ -d & -c & b & a \end{pmatrix} \]

\[ \begin{aligned} v^{\prime}=qvq^{*}=\left(qv\right)q^{*}\leftrightarrow & R\left(q^{*}\right)L\left(q\right)v\\ =q\left(vq^{*}\right)\leftrightarrow & L\left(q\right)R\left(q^{*}\right)v\\ = & \begin{pmatrix}a & -b & -c & -d\\ b & a & -d & c\\ c & d & a & -b\\ d & -c & b & a \end{pmatrix}\begin{pmatrix}a & b & c & d\\ -b & a & -d & c\\ -c & d & a & -b\\ -d & -c & b & a \end{pmatrix}v\\ = & \begin{pmatrix}a^{2}+b^{2}+c^{2}+d^{2} & 0 & 0 & 0\\ 0 & b^{2}+a^{2}-d^{2}-c^{2} & -2ad+2bc & 2ac+2bd\\ 0 & 2ad+2bc & c^{2}-d^{2}+a^{2}-b^{2} & 2cd-2ab\\ 0 & -2ac+2bd & 2cd+2ab & d^{2}-c^{2}-b^{2}+a^{2} \end{pmatrix}v\\ = & \begin{pmatrix}1 & 0 & 0 & 0\\ 0 & 1-2\left(d^{2}+c^{2}\right) & 2\left(bc-ad\right) & 2\left(bd+ac\right)\\ 0 & 2\left(bc+ad\right) & 1-2\left(d^{2}+b^{2}\right) & 2\left(cd-ab\right)\\ 0 & 2\left(bd-ac\right) & 2\left(cd+ab\right) & 1-2\left(c^{2}+b^{2}\right) \end{pmatrix}v\\ \begin{pmatrix}0\\ \boldsymbol{v}^{\prime} \end{pmatrix}= & \begin{pmatrix}1 & 0 & 0 & 0\\ 0 & 1-2\left(d^{2}+c^{2}\right) & 2\left(bc-ad\right) & 2\left(bd+ac\right)\\ 0 & 2\left(bc+ad\right) & 1-2\left(d^{2}+b^{2}\right) & 2\left(cd-ab\right)\\ 0 & 2\left(bd-ac\right) & 2\left(cd+ab\right) & 1-2\left(c^{2}+b^{2}\right) \end{pmatrix}\begin{pmatrix}0\\ \boldsymbol{v} \end{pmatrix} \end{aligned} \]

\[ \boldsymbol{v}^{\prime}=\begin{pmatrix}1-2\left(d^{2}+c^{2}\right) & 2\left(bc-ad\right) & 2\left(bd+ac\right)\\ 2\left(bc+ad\right) & 1-2\left(d^{2}+b^{2}\right) & 2\left(cd-ab\right)\\ 2\left(bd-ac\right) & 2\left(cd+ab\right) & 1-2\left(c^{2}+b^{2}\right) \end{pmatrix}\boldsymbol{v} \]

37.2.4 exponential form

\[ \begin{aligned} q= & a+b\mathrm{i}+c\mathrm{j}+d\mathrm{k}=a+\mathrm{i}b+\mathrm{j}c+\mathrm{k}d\\ = & a+r\dfrac{\mathrm{i}b+\mathrm{j}c+\mathrm{k}d}{r},r^{2}=b^{2}+c^{2}+d^{2}\\ \overset{\left|q\right|=1}{=} & \cos\dfrac{\theta}{2}+\sin\dfrac{\theta}{2}\boldsymbol{n},\begin{cases} a=\cos\dfrac{\theta}{2} & \cos\dfrac{\theta}{2}=a\\ r=\sin\dfrac{\theta}{2} & \sin\dfrac{\theta}{2}=r\\ \dfrac{\mathrm{i}b+\mathrm{j}c+\mathrm{k}d}{r}=\boldsymbol{n} & \boldsymbol{n}=\dfrac{\mathrm{i}b+\mathrm{j}c+\mathrm{k}d}{r} \end{cases} \end{aligned} \]

\[ \begin{aligned} \left\Vert \boldsymbol{n}\right\Vert ^{2}=\left(\dfrac{\mathrm{i}b+\mathrm{j}c+\mathrm{k}d}{r}\right)^{2}= & \dfrac{-b^{2}-c^{2}-d^{2}+bc\left(\mathrm{i}\mathrm{j}+\mathrm{j}\mathrm{i}\right)+cd\left(\mathrm{j}\mathrm{k}+\mathrm{k}\mathrm{j}\right)+db\left(\mathrm{k}\mathrm{i}+\mathrm{i}\mathrm{k}\right)}{r^{2}}\\ = & \dfrac{-b^{2}-c^{2}-d^{2}+bc\left(\mathrm{k}-\mathrm{k}\right)+cd\left(\mathrm{i}-\mathrm{i}\right)+db\left(\mathrm{j}-\mathrm{j}\right)}{r^{2}}\\ = & \dfrac{-b^{2}-c^{2}-d^{2}+bc0+cd0+db0}{r^{2}}=\dfrac{-b^{2}-c^{2}-d^{2}}{r^{2}}\\ = & \dfrac{-b^{2}-c^{2}-d^{2}}{b^{2}+c^{2}+d^{2}}=-1\\ \boldsymbol{n}=\dfrac{\mathrm{i}b+\mathrm{j}c+\mathrm{k}d}{r}= & \pm\sqrt{-1} \end{aligned} \]

\[ \begin{aligned} q= & a+b\mathrm{i}+c\mathrm{j}+d\mathrm{k}=a+\mathrm{i}b+\mathrm{j}c+\mathrm{k}d\\ = & a+r\dfrac{\mathrm{i}b+\mathrm{j}c+\mathrm{k}d}{r},r^{2}=b^{2}+c^{2}+d^{2}\\ = & \sqrt{a^{2}+r^{2}}\left(\dfrac{a}{\sqrt{a^{2}+r^{2}}}+\dfrac{\mathrm{i}b+\mathrm{j}c+\mathrm{k}d}{r}\dfrac{r}{\sqrt{a^{2}+r^{2}}}\right)\\ = & \rho\left(\cos\phi+\sqrt{-1}\sin\phi\right),\begin{cases} \rho=\sqrt{a^{2}+r^{2}}\\ \tan\phi=\dfrac{r}{a}\Leftrightarrow\phi=\arctan\dfrac{r}{a}=\dfrac{\theta}{2} \end{cases}\\ = & \rho\mathrm{e}^{\phi\sqrt{-1}}\overset{\left|q\right|=1}{=}\left|q\right|\mathrm{e}^{\boldsymbol{n}\frac{\theta}{2}}=\mathrm{e}^{\boldsymbol{n}\frac{\theta}{2}}\\ q= & \rho\mathrm{e}^{\phi\sqrt{-1}}\overset{\left|q\right|=1}{=}\mathrm{e}^{\boldsymbol{n}\frac{\theta}{2}},\begin{cases} q=a+\mathrm{i}b+\mathrm{j}c+\mathrm{k}d\\ \rho=\sqrt{a^{2}+r^{2}}=\left|q\right|=\sqrt{a^{2}+b^{2}+c^{2}+d^{2}}=1\\ \tan\dfrac{\theta}{2}=\dfrac{r}{a}\Leftrightarrow\dfrac{\theta}{2}=\arctan\dfrac{r}{a}=\arctan\dfrac{\pm\sqrt{b^{2}+c^{2}+d^{2}}}{a} \end{cases} \end{aligned} \]

\[ \begin{aligned} \boldsymbol{v}^{\prime}=v^{\prime}= & qvq^{-1}=q\boldsymbol{v}q^{-1},\begin{cases} v=\boldsymbol{v}=v_{{\scriptscriptstyle 1}}\mathrm{i}+v_{{\scriptscriptstyle 2}}\mathrm{j}+v_{{\scriptscriptstyle 3}}\mathrm{k}\\ v^{\prime}=\boldsymbol{v}^{\prime}=v_{{\scriptscriptstyle 1}}^{\prime}\mathrm{i}+v_{{\scriptscriptstyle 2}}^{\prime}\mathrm{j}+v_{{\scriptscriptstyle 3}}^{\prime}\mathrm{k} \end{cases},\boldsymbol{n}=\begin{pmatrix}\sin\gamma\cos\varphi\\ \sin\gamma\sin\varphi\\ \cos\gamma \end{pmatrix},\begin{cases} \varphi=\angle\hat{\boldsymbol{n}}_{{\scriptscriptstyle xy}}\hat{\boldsymbol{x}}\\ \gamma=\angle\hat{\boldsymbol{n}}\hat{\boldsymbol{z}} \end{cases}\\ = & \left\{ \cos\dfrac{\theta}{2}+\sin\dfrac{\theta}{2}\left[\left(\sin\gamma\cos\varphi\right)\mathrm{i}+\left(\sin\gamma\sin\varphi\right)\mathrm{j}+\left(\cos\gamma\right)\mathrm{k}\right]\right\} \boldsymbol{v}\\ & \left\{ \cos\dfrac{\theta}{2}-\sin\dfrac{\theta}{2}\left[\left(\sin\gamma\cos\varphi\right)\mathrm{i}+\left(\sin\gamma\sin\varphi\right)\mathrm{j}+\left(\cos\gamma\right)\mathrm{k}\right]\right\} \\ = & q\left(\theta,\gamma,\varphi\right)\boldsymbol{v}q^{-1}\left(\theta,\gamma,\varphi\right)=q\left(\dfrac{\theta}{2},\gamma,\varphi\right)\boldsymbol{v}q^{-1}\left(\dfrac{\theta}{2},\gamma,\varphi\right)\\ = & \left\{ \cos\dfrac{\theta}{2}+\sin\dfrac{\theta}{2}\left[n_{{\scriptscriptstyle x}}\mathrm{i}+n_{{\scriptscriptstyle y}}\mathrm{j}+n_{{\scriptscriptstyle z}}\mathrm{k}\right]\right\} \boldsymbol{v}\left\{ \cos\dfrac{\theta}{2}-\sin\dfrac{\theta}{2}\left[n_{{\scriptscriptstyle x}}\mathrm{i}+n_{{\scriptscriptstyle y}}\mathrm{j}+n_{{\scriptscriptstyle z}}\mathrm{k}\right]\right\} \\ = & \left\{ \cos\dfrac{\theta}{2}+\sin\dfrac{\theta}{2}\left[n_{{\scriptscriptstyle x}}\mathrm{i}\pm\sqrt{1-n_{{\scriptscriptstyle x}}^{2}-n_{{\scriptscriptstyle z}}^{2}}\mathrm{j}+n_{{\scriptscriptstyle z}}\mathrm{k}\right]\right\} \boldsymbol{v}\\ & \left\{ \cos\dfrac{\theta}{2}-\sin\dfrac{\theta}{2}\left[n_{{\scriptscriptstyle x}}\mathrm{i}\pm\sqrt{1-n_{{\scriptscriptstyle x}}^{2}-n_{{\scriptscriptstyle z}}^{2}}\mathrm{j}+n_{{\scriptscriptstyle z}}\mathrm{k}\right]\right\} \\ = & \left\{ \cos\dfrac{\theta}{2}+\sin\dfrac{\theta}{2}\left[n_{{\scriptscriptstyle x}}\mathrm{i}+n_{{\scriptscriptstyle y}}\mathrm{j}\pm\sqrt{1-n_{{\scriptscriptstyle x}}^{2}-n_{{\scriptscriptstyle y}}^{2}}\mathrm{k}\right]\right\} \boldsymbol{v}\\ & \left\{ \cos\dfrac{\theta}{2}-\sin\dfrac{\theta}{2}\left[n_{{\scriptscriptstyle x}}\mathrm{i}+n_{{\scriptscriptstyle y}}\mathrm{j}\pm\sqrt{1-n_{{\scriptscriptstyle x}}^{2}-n_{{\scriptscriptstyle y}}^{2}}\mathrm{k}\right]\right\} \\ = & q\left(n_{{\scriptscriptstyle x}},n_{{\scriptscriptstyle y}},\theta\right)\boldsymbol{v}q^{-1}\left(n_{{\scriptscriptstyle x}},n_{{\scriptscriptstyle y}},\theta\right)=q\left(n_{{\scriptscriptstyle x}},n_{{\scriptscriptstyle y}},\dfrac{\theta}{2}\right)\boldsymbol{v}q^{-1}\left(n_{{\scriptscriptstyle x}},n_{{\scriptscriptstyle y}},\dfrac{\theta}{2}\right)\\ = & \mathrm{e}^{\boldsymbol{n}\frac{\theta}{2}}\boldsymbol{v}\mathrm{e}^{-\boldsymbol{n}\frac{\theta}{2}} \end{aligned} \]

\[ \begin{aligned} \boldsymbol{v}^{\prime}= & q\boldsymbol{v}q^{-1},\\ & \begin{cases} q=q\left(n_{{\scriptscriptstyle x}},n_{{\scriptscriptstyle y}},\theta\right) & =\cos\dfrac{\theta}{2}+\sin\dfrac{\theta}{2}\left[n_{{\scriptscriptstyle x}}\mathrm{i}+n_{{\scriptscriptstyle y}}\mathrm{j}\pm\sqrt{1-n_{{\scriptscriptstyle x}}^{2}-n_{{\scriptscriptstyle y}}^{2}}\mathrm{k}\right]\\ q^{-1}=q^{*}=\overline{q} & =\cos\dfrac{\theta}{2}-\sin\dfrac{\theta}{2}\left[n_{{\scriptscriptstyle x}}\mathrm{i}+n_{{\scriptscriptstyle y}}\mathrm{j}\pm\sqrt{1-n_{{\scriptscriptstyle x}}^{2}-n_{{\scriptscriptstyle y}}^{2}}\mathrm{k}\right] \end{cases},\\ & \begin{cases} n_{{\scriptscriptstyle x}} & =\sin\gamma\cos\varphi\\ n_{{\scriptscriptstyle y}} & =\sin\gamma\sin\varphi \end{cases}\Rightarrow\pm\sqrt{1-n_{{\scriptscriptstyle x}}^{2}-n_{{\scriptscriptstyle y}}^{2}}=n_{{\scriptscriptstyle z}}=\cos\gamma \end{aligned} \]

\[ \boldsymbol{v}^{\prime}=\mathrm{e}^{\boldsymbol{n}\frac{\theta}{2}}\boldsymbol{v}\mathrm{e}^{-\boldsymbol{n}\frac{\theta}{2}} \]

general quaternion exponential form

\[ \begin{aligned} q= & \rho\mathrm{e}^{\phi\sqrt{-1}}=\left|q\right|\mathrm{e}^{\boldsymbol{n}\phi},\begin{cases} q=a+\mathrm{i}b+\mathrm{j}c+\mathrm{k}d=a+r\dfrac{\mathrm{i}b+\mathrm{j}c+\mathrm{k}d}{r}=a+r\boldsymbol{n}\\ \rho=\sqrt{a^{2}+r^{2}}=\left|q\right|=\sqrt{a^{2}+b^{2}+c^{2}+d^{2}}\\ \tan\phi=\dfrac{r}{a}\Leftrightarrow\phi=\arctan\dfrac{r}{a}=\arctan\dfrac{\pm\sqrt{b^{2}+c^{2}+d^{2}}}{a} \end{cases}\\ = & \mathrm{e}^{\ln\left|q\right|}\mathrm{e}^{\boldsymbol{n}\phi}=\mathrm{e}^{\ln\left|q\right|+\boldsymbol{n}\phi} \end{aligned} \]

37.2.5 double cover

https://www.bilibili.com/video/BV1rj41117VW/?t=15m15s

\[ \begin{array}{cccccccccccccccccc} \theta & 0 & \rightarrow & \dfrac{\pi}{2} & \rightarrow & \pi & \rightarrow & \dfrac{3\pi}{2} & \rightarrow & 2\pi & \rightarrow & \dfrac{5\pi}{2} & \rightarrow & 3\pi & \rightarrow & \dfrac{7\pi}{2} & \rightarrow & 4\pi\\ \dfrac{\theta}{2} & 0 & \rightarrow & \dfrac{\pi}{4} & \rightarrow & \dfrac{\pi}{2} & \rightarrow & \dfrac{3\pi}{4} & \rightarrow & \pi & \rightarrow & \dfrac{5\pi}{4} & \rightarrow & \dfrac{3\pi}{2} & \rightarrow & \dfrac{7\pi}{4} & \rightarrow & 2\pi\\ \mathrm{e}^{\boldsymbol{n}\frac{\theta}{2}} & 1 & \rightarrow & \mathrm{e}^{\boldsymbol{n}\frac{\pi}{4}} & \rightarrow & \boldsymbol{n} & \rightarrow & \mathrm{e}^{\boldsymbol{n}\frac{3\pi}{4}} & \rightarrow & -1 & \rightarrow & \mathrm{e}^{\boldsymbol{n}\frac{5\pi}{4}} & \rightarrow & -\boldsymbol{n} & \rightarrow & \mathrm{e}^{\boldsymbol{n}\frac{7\pi}{4}} & \rightarrow & 1\\ \mathrm{e}^{-\boldsymbol{n}\frac{\theta}{2}} & 1 & \rightarrow & \mathrm{e}^{\boldsymbol{n}\frac{-\pi}{4}} & \rightarrow & -\boldsymbol{n} & \rightarrow & \mathrm{e}^{\boldsymbol{n}\frac{-3\pi}{4}} & \rightarrow & -1 & \rightarrow & \mathrm{e}^{\boldsymbol{n}\frac{-5\pi}{4}} & \rightarrow & \boldsymbol{n} & \rightarrow & \mathrm{e}^{\boldsymbol{n}\frac{-7\pi}{4}} & \rightarrow & 1\\ \boldsymbol{v}^{\prime}=\mathrm{e}^{\boldsymbol{n}\frac{\theta}{2}}\boldsymbol{v}\mathrm{e}^{-\boldsymbol{n}\frac{\theta}{2}} & \boldsymbol{v} & \rightarrow & & \rightarrow & -\boldsymbol{n}\boldsymbol{v}\boldsymbol{n} & \rightarrow & & \rightarrow & \boldsymbol{v} & \rightarrow & & \rightarrow & -\boldsymbol{n}\boldsymbol{v}\boldsymbol{n} & \rightarrow & & \rightarrow & \boldsymbol{v} \end{array} \]

\[ SU\left(2\right)=\left\{ 1\left(\cdot\right)1,\mathrm{e}^{\boldsymbol{n}\frac{\theta}{2}}\left(\cdot\right)\mathrm{e}^{-\boldsymbol{n}\frac{\theta}{2}}\right\} \]

3D rotation about an arbitrary axis^{[37.1.4.2.1.3]}

\[ \boldsymbol{V}^{\prime}=SR_{{\scriptscriptstyle z}}\left(\gamma\right)S^{-1}\boldsymbol{V} \]

\[ \boldsymbol{v}^{\prime}=SR_{{\scriptscriptstyle z}}\left(\theta\right)S^{-1}\boldsymbol{v} \]

\[ SO\left(3\right)=\left\{ 1,SR_{{\scriptscriptstyle z}}\left(\theta\right)S^{-1}\right\} =\left\{ \begin{pmatrix}1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{pmatrix},SR_{{\scriptscriptstyle z}}\left(\theta\right)S^{-1}\right\} \]

\[ SU\left(2\right)\cong2\cdot SO\left(3\right) \]

Special unitary group of degree 2 \(SU\left(2\right)\) is the boss of special orthonormal group of degree 3 \(SO\left(3\right)\), \(SU\left(2\right)\) double covers \(SO\left(3\right)\).

https://en.wikipedia.org/wiki/Special_unitary_group#The_group_SU(2)

https://en.wikipedia.org/wiki/Unitary_group

“Particle is group representation, spin is square root of 4-vector.”?

「粒子是群表示，自旋是四維向量開根號。」？

See also spinor^[75] and Lie group^[37.2.8]

https://zhuanlan.zhihu.com/p/143972449

37.2.6 right-hand vs. left-hand coordinates

Krasjet_四元數與三維旋轉 p.63~73

37.2.6.1 clock

\[ \boldsymbol{v}^{\prime}=\mathrm{e}^{\boldsymbol{n}\frac{\theta}{2}}\boldsymbol{v}\mathrm{e}^{-\boldsymbol{n}\frac{\theta}{2}} \]

\[ \boldsymbol{v}^{\prime}=\mathrm{e}^{-\boldsymbol{n}\frac{\theta}{2}}\boldsymbol{v}\mathrm{e}^{\boldsymbol{n}\frac{\theta}{2}} \]

right-hand = anticlockwise

\[ \left[\boldsymbol{v}^{\prime}\right]_{{\scriptscriptstyle R}}=\left[\mathrm{e}^{\boldsymbol{n}\frac{\theta}{2}}\right]_{{\scriptscriptstyle R}}\left[\boldsymbol{v}\right]_{{\scriptscriptstyle R}}\left[\mathrm{e}^{-\boldsymbol{n}\frac{\theta}{2}}\right]_{{\scriptscriptstyle R}} \]

\[ \left[\boldsymbol{v}^{\prime}\right]_{{\scriptscriptstyle L}}=\left[\mathrm{e}^{-\boldsymbol{n}\frac{\theta}{2}}\right]_{{\scriptscriptstyle R}}\left[\boldsymbol{v}\right]_{{\scriptscriptstyle L}}\left[\mathrm{e}^{\boldsymbol{n}\frac{\theta}{2}}\right]_{{\scriptscriptstyle R}} \]

\[ \left[\boldsymbol{v}^{\prime}\right]_{{\scriptscriptstyle L}}=\left[\mathrm{e}^{\boldsymbol{n}\frac{\theta}{2}}\right]_{{\scriptscriptstyle L}}\left[\boldsymbol{v}\right]_{{\scriptscriptstyle L}}\left[\mathrm{e}^{-\boldsymbol{n}\frac{\theta}{2}}\right]_{{\scriptscriptstyle L}} \]

37.2.6.2 Rodrigues rotation in right-hand vs. left-hand coordinates

\[ \boldsymbol{u}=\boldsymbol{n}\times\boldsymbol{v}_{{\scriptscriptstyle \perp}} \]

\[ \left[\boldsymbol{u}\right]_{{\scriptscriptstyle R}}=\left[\boldsymbol{n}\right]_{{\scriptscriptstyle R}}\times_{{\scriptscriptstyle R}}\left[\boldsymbol{v}_{{\scriptscriptstyle \perp}}\right]_{{\scriptscriptstyle R}}=\left[\boldsymbol{n}\right]_{{\scriptscriptstyle L}}\times_{{\scriptscriptstyle L}}\left[\boldsymbol{v}_{{\scriptscriptstyle \perp}}\right]_{{\scriptscriptstyle L}}=\left[\boldsymbol{u}\right]_{{\scriptscriptstyle L}} \]

\[ \begin{pmatrix}0\\ 1\\ 0 \end{pmatrix}=\begin{pmatrix}0\\ 0\\ 1 \end{pmatrix}\times_{{\scriptscriptstyle R}}\begin{pmatrix}1\\ 0\\ 0 \end{pmatrix}=\begin{pmatrix}0\\ 0\\ 1 \end{pmatrix}\times_{{\scriptscriptstyle L}}\begin{pmatrix}1\\ 0\\ 0 \end{pmatrix}=\begin{pmatrix}0\\ 1\\ 0 \end{pmatrix} \]

\[ \left[\left[\boldsymbol{u}\right]_{{\scriptscriptstyle L}}\right]_{{\scriptscriptstyle R}}=-\left[\boldsymbol{u}\right]_{{\scriptscriptstyle R}} \]

\[ \left[\begin{pmatrix}0\\ 1\\ 0 \end{pmatrix}_{{\scriptscriptstyle L}}\right]_{{\scriptscriptstyle R}}=-\begin{pmatrix}0\\ 1\\ 0 \end{pmatrix}=\begin{pmatrix}0\\ -1\\ 0 \end{pmatrix}_{{\scriptscriptstyle R}} \]

\[ \det O=\pm1 \]

\(\det O=-1\) will change handedness of the coordinate.

\(q\) or \(q\left(\cdot\right)q^{-1}=\mathrm{e}^{\boldsymbol{n}\frac{\theta}{2}}\left(\cdot\right)\mathrm{e}^{-\boldsymbol{n}\frac{\theta}{2}}\) corresponding 3D manifold is a solid ball by coordinate \(\left(n_{{\scriptscriptstyle x}},n_{{\scriptscriptstyle y}},\theta\right)\)

\[ q=q\left(n_{{\scriptscriptstyle x}},n_{{\scriptscriptstyle y}},\theta\right)=q\left(\begin{pmatrix}n_{{\scriptscriptstyle x}}\\ n_{{\scriptscriptstyle y}}\\ \theta \end{pmatrix}\right)=q\left(\left\langle \begin{array}{c} n_{{\scriptscriptstyle x}}\\ n_{{\scriptscriptstyle y}}\\ \theta \end{array}\right\rangle \right)=q\begin{pmatrix}n_{{\scriptscriptstyle x}}\\ n_{{\scriptscriptstyle y}}\\ \theta \end{pmatrix}=q\begin{pmatrix}\sin\gamma\cos\varphi\\ \sin\gamma\sin\varphi\\ \theta \end{pmatrix},\begin{cases} \gamma\in\left[0,\pi\right]\\ \varphi\in\left[-\pi,\pi\right]\\ \theta\in\left[-\pi,\pi\right] \end{cases} \]

https://www.youtube.com/watch?v=9CBS5CAynBE&list=PLDcSwjT2BF_WDki-WvmJ__Q0nLIHuNPbP&index=4