Chapter 47: Feynman method
47.1 Feynman method of differentiation / derivative technique
https://www.bilibili.com/video/BV1hG411Z7Cb
分式微分不是難而是煩
47.1.1 principle
Theorem 25.1 Feynman method of differentiation / derivative
\[ \begin{array}{c} f\left(t\right)=k\left[u\left(t\right)\right]^{a}\left[v\left(t\right)\right]^{b}\left[w\left(t\right)\right]^{c}\cdots\\ \Downarrow\\ f^{\prime}\left(t\right)=f\left(t\right)\left[a\dfrac{u^{\prime}\left(t\right)}{u\left(t\right)}+b\dfrac{v^{\prime}\left(t\right)}{v\left(t\right)}+c\dfrac{w^{\prime}\left(t\right)}{w\left(t\right)}+\cdots\right] \end{array} \]
Proof:
\[ f\left(t\right)=k\left[u\left(t\right)\right]^{a}\left[v\left(t\right)\right]^{b}\left[w\left(t\right)\right]^{c}\cdots \]
\[ f=ku^{a}v^{b}w^{c}\cdots=k\cdot u^{a}\cdot v^{b}\cdot w^{c}\cdot\cdots \]
\[ \begin{aligned} f= & ku^{a}v^{b}w^{c}\cdots=k\cdot u^{a}\cdot v^{b}\cdot w^{c}\cdot\cdots\\ \ln f= & \ln\left(ku^{a}v^{b}w^{c}\cdots\right)=\ln k+\ln u^{a}+\ln v^{b}+\ln w^{c}+\cdots\\ = & \ln k+a\ln u+b\ln v+c\ln w+\cdots\\ \dfrac{\mathrm{d}}{\mathrm{d}t}\ln f= & \dfrac{\mathrm{d}}{\mathrm{d}t}\left(\ln k+a\ln u+b\ln v+c\ln w+\cdots\right)\\ \dfrac{\dfrac{\mathrm{d}}{\mathrm{d}t}f}{f}= & 0+\dfrac{\mathrm{d}}{\mathrm{d}t}\left(a\ln u\right)+\dfrac{\mathrm{d}}{\mathrm{d}t}\left(b\ln v\right)+\dfrac{\mathrm{d}}{\mathrm{d}t}\left(c\ln w\right)+\cdots\\ = & a\dfrac{\mathrm{d}}{\mathrm{d}t}\ln u+b\dfrac{\mathrm{d}}{\mathrm{d}t}\ln v+c\dfrac{\mathrm{d}}{\mathrm{d}t}\ln w+\cdots\\ = & a\dfrac{\dfrac{\mathrm{d}}{\mathrm{d}t}u}{u}+b\dfrac{\dfrac{\mathrm{d}}{\mathrm{d}t}v}{v}+c\dfrac{\dfrac{\mathrm{d}}{\mathrm{d}t}w}{w}+\cdots\\ \dfrac{f^{\prime}}{f}= & a\dfrac{u^{\prime}}{u}+b\dfrac{v^{\prime}}{v}+c\dfrac{w^{\prime}}{w}+\cdots\\ f^{\prime}= & f\left(a\dfrac{u^{\prime}}{u}+b\dfrac{v^{\prime}}{v}+c\dfrac{w^{\prime}}{w}+\cdots\right)\\ f^{\prime}\left(t\right)= & f\left(t\right)\left[a\dfrac{u^{\prime}\left(t\right)}{u\left(t\right)}+b\dfrac{v^{\prime}\left(t\right)}{v\left(t\right)}+c\dfrac{w^{\prime}\left(t\right)}{w\left(t\right)}+\cdots\right] \end{aligned} \]
\[ \tag*{$\Box$} \]
47.1.2 examples
\(f\left(x\right)=x^{x}\)
\[ \left(x^{x}\right)^{\prime}=x^{x}+x^{x}\ln x \]
\[ \begin{aligned} f\left(x\right)= & x^{x}\\ \ln f\left(x\right)= & x\ln x\\ \dfrac{\mathrm{d}}{\mathrm{d}x}\ln f\left(x\right)= & \dfrac{\mathrm{d}}{\mathrm{d}x}\left[x\ln x\right]\\ \dfrac{f^{\prime}\left(x\right)}{f\left(x\right)}= & \left[x\ln x\right]^{\prime}\\ f^{\prime}\left(x\right)= & f\left(x\right)\left[x\ln x\right]^{\prime}=x^{x}\left[\left(x\right)^{\prime}\ln x+x\left(\ln x\right)^{\prime}\right]\\ = & x^{x}\left[1\ln x+x\dfrac{1}{x}\right]=x^{x}\left[\ln x+1\right]=x^{x}\left[1+\ln x\right]\\ = & x^{x}+x^{x}\ln x \end{aligned} \]
\[ \tag*{$\Box$} \]
\(\Delta\left(\dfrac{1}{r}\right)=\boldsymbol{\nabla}^{2}\left(\dfrac{1}{\sqrt{\boldsymbol{r}^{2}}}\right)=\boldsymbol{\nabla}\cdot\boldsymbol{\nabla}\left(\dfrac{1}{\sqrt{\boldsymbol{r}\cdot\boldsymbol{r}}}\right)=\boldsymbol{\nabla}\cdot\left(\dfrac{\partial}{\partial x},\dfrac{\partial}{\partial y},\dfrac{\partial}{\partial z}\right)\left(\dfrac{1}{\sqrt{x^{2}+y^{2}+z^{2}}}\right)\)
\[ \dfrac{\partial}{\partial x}\dfrac{1}{\sqrt{x^{2}+y^{2}+z^{2}}} \]
\[ \begin{aligned} & \dfrac{\partial}{\partial x}\dfrac{1}{\sqrt{x^{2}+y^{2}+z^{2}}}=\dfrac{\partial}{\partial x}\left[\left(x^{2}+y^{2}+z^{2}\right)^{\frac{-1}{2}}\right]\\ = & \left(x^{2}+y^{2}+z^{2}\right)^{\frac{-1}{2}}\left[\frac{-1}{2}\dfrac{2x}{x^{2}+y^{2}+z^{2}}\right]\\ = & \dfrac{-x}{\left(x^{2}+y^{2}+z^{2}\right)^{\frac{-3}{2}}} \end{aligned} \]
\[ \boldsymbol{\nabla}\left(\dfrac{1}{r}\right)=\boldsymbol{\nabla}\left(\dfrac{1}{\sqrt{\boldsymbol{r}\cdot\boldsymbol{r}}}\right)=\left(\dfrac{\partial}{\partial x},\dfrac{\partial}{\partial y},\dfrac{\partial}{\partial z}\right)\left(\dfrac{1}{\sqrt{x^{2}+y^{2}+z^{2}}}\right)=\left(\dfrac{-x}{\left(x^{2}+y^{2}+z^{2}\right)^{\frac{3}{2}}},\dfrac{-y}{\left(x^{2}+y^{2}+z^{2}\right)^{\frac{3}{2}}},\dfrac{-z}{\left(x^{2}+y^{2}+z^{2}\right)^{\frac{3}{2}}}\right) \]
\[ \begin{aligned} \boldsymbol{\nabla}\cdot\boldsymbol{\nabla}\left(\dfrac{1}{r}\right)= & \boldsymbol{\nabla}\cdot\left(\dfrac{-x}{\left(x^{2}+y^{2}+z^{2}\right)^{\frac{3}{2}}},\dfrac{-y}{\left(x^{2}+y^{2}+z^{2}\right)^{\frac{3}{2}}},\dfrac{-z}{\left(x^{2}+y^{2}+z^{2}\right)^{\frac{3}{2}}}\right)\\ = & \dfrac{\partial}{\partial x}\dfrac{-x}{\left(x^{2}+y^{2}+z^{2}+\epsilon^{2}\right)^{\frac{3}{2}}}+\dfrac{\partial}{\partial y}\dfrac{-y}{\left(x^{2}+y^{2}+z^{2}+\epsilon^{2}\right)^{\frac{3}{2}}}+\dfrac{\partial}{\partial z}\dfrac{-z}{\left(x^{2}+y^{2}+z^{2}+\epsilon^{2}\right)^{\frac{3}{2}}} \end{aligned} \]
\[ \dfrac{\partial}{\partial x}\dfrac{-x}{\left(x^{2}+y^{2}+z^{2}+\epsilon^{2}\right)^{\frac{3}{2}}} \]
\[ \begin{aligned} & \dfrac{\partial}{\partial x}\dfrac{-x}{\left(x^{2}+y^{2}+z^{2}\right)^{\frac{3}{2}}}\\ = & \dfrac{-x}{\left(x^{2}+y^{2}+z^{2}\right)^{\frac{3}{2}}}\left[1\cdot\dfrac{1}{x}+\dfrac{-3}{2}\dfrac{2x}{x^{2}+y^{2}+z^{2}}\right]\\ = & \dfrac{-1}{\left(x^{2}+y^{2}+z^{2}\right)^{\frac{3}{2}}}+\dfrac{3x^{2}}{\left(x^{2}+y^{2}+z^{2}\right)^{\frac{5}{2}}}\\ = & \dfrac{-\left(x^{2}+y^{2}+z^{2}\right)+3x^{2}}{\left(x^{2}+y^{2}+z^{2}\right)^{\frac{5}{2}}}=\dfrac{2x^{2}-y^{2}-z^{2}}{\left(x^{2}+y^{2}+z^{2}\right)^{\frac{5}{2}}} \end{aligned} \]
\[ \begin{aligned} \boldsymbol{\nabla}\cdot\boldsymbol{\nabla}\left(\dfrac{1}{r}\right)= & \dfrac{\partial}{\partial x}\dfrac{-x}{\left(x^{2}+y^{2}+z^{2}+\epsilon^{2}\right)^{\frac{3}{2}}}+\dfrac{\partial}{\partial y}\dfrac{-y}{\left(x^{2}+y^{2}+z^{2}+\epsilon^{2}\right)^{\frac{3}{2}}}+\dfrac{\partial}{\partial z}\dfrac{-z}{\left(x^{2}+y^{2}+z^{2}+\epsilon^{2}\right)^{\frac{3}{2}}}\\ = & \dfrac{+2x^{2}-y^{2}-z^{2}}{\left(x^{2}+y^{2}+z^{2}\right)^{\frac{5}{2}}}+\dfrac{-x^{2}+2y^{2}-z^{2}}{\left(x^{2}+y^{2}+z^{2}\right)^{\frac{5}{2}}}+\dfrac{-x^{2}-y^{2}+2z^{2}}{\left(x^{2}+y^{2}+z^{2}\right)^{\frac{5}{2}}}=0 \end{aligned} \]
\[ \Delta\left(\dfrac{1}{r}\right)=\boldsymbol{\nabla}\cdot\boldsymbol{\nabla}\left(\dfrac{1}{r}\right)=0 \]
\[ \tag*{$\Box$} \]
\(\dfrac{6\left(1+2t^{2}\right)\left(t^{3}-t\right)^{2}}{\sqrt{t+5t^{2}}\left(4t\right)^{\frac{3}{2}}}+\dfrac{\sqrt{1+2t}}{t+\sqrt{1+t^{2}}}\)
\[ \dfrac{\mathrm{d}}{\mathrm{d}t}\left[\dfrac{6\left(1+2t^{2}\right)\left(t^{3}-t\right)^{2}}{\sqrt{t+5t^{2}}\left(4t\right)^{\frac{3}{2}}}+\dfrac{\sqrt{1+2t}}{t+\sqrt{1+t^{2}}}\right] \]
\[ \dfrac{\mathrm{d}}{\mathrm{d}t}\left[\dfrac{6\left(1+2t^{2}\right)\left(t^{3}-t\right)^{2}}{\sqrt{t+5t^{2}}\left(4t\right)^{\frac{3}{2}}}\right] \]
\[ \begin{aligned} & \dfrac{\mathrm{d}}{\mathrm{d}t}\left[\dfrac{6\left(1+2t^{2}\right)\left(t^{3}-t\right)^{2}}{\sqrt{t+5t^{2}}\left(4t\right)^{\frac{3}{2}}}\right]\\ = & \dfrac{6\left(1+2t^{2}\right)\left(t^{3}-t\right)^{2}}{\sqrt{t+5t^{2}}\left(4t\right)^{\frac{3}{2}}}\cdot[\\ = & \dfrac{6\left[1+2t^{2}\right]\left(t^{3}-t\right)^{2}}{\sqrt{t+5t^{2}}\left(4t\right)^{\frac{3}{2}}}\cdot[1\cdot\dfrac{1}{1+2t^{2}}\cdot4t,\left[1+2t^{2}\right]\rightarrow\begin{cases} \text{exponential}: & 1\\ \text{linear to denominator}: & \dfrac{1}{1+2t^{2}}\\ \text{differentiation} & 4t \end{cases}\\ = & \dfrac{6\left(1+2t^{2}\right)\left[\left(t^{3}-t\right)^{2}\right]}{\sqrt{t+5t^{2}}\left(4t\right)^{\frac{3}{2}}}\cdot[\dfrac{4t}{1+2t^{2}}+2\cdot\dfrac{1}{t^{3}-t}\cdot\left(3t^{2}-1\right)\\ & ,\left[\left(t^{3}-t\right)^{2}\right]\rightarrow\begin{cases} \text{exponential}: & 2\\ \text{linear to denominator}: & \dfrac{1}{t^{3}-t}\\ \text{differentiation} & 3t^{2}-1 \end{cases}\\ = & \dfrac{6\left(1+2t^{2}\right)\left(t^{3}-t\right)^{2}}{\left[\sqrt{t+5t^{2}}\right]\left(4t\right)^{\frac{3}{2}}}\cdot[\dfrac{4t}{1+2t^{2}}+\dfrac{6t^{2}-2}{t^{3}-t}+\dfrac{-1}{2}\cdot\dfrac{1}{t+5t^{2}}\cdot\left(1+10t\right)\\ & ,\left[\sqrt{t+5t^{2}}\right]\rightarrow\begin{cases} \text{exponential}: & \dfrac{-1}{2}\\ \text{linear to denominator}: & \dfrac{1}{t+5t^{2}}\\ \text{differentiation} & 1+10t \end{cases}\\ = & \dfrac{6\left(1+2t^{2}\right)\left(t^{3}-t\right)^{2}}{\sqrt{t+5t^{2}}\left[\left(4t\right)^{\frac{3}{2}}\right]}\cdot\left[\dfrac{4t}{1+2t^{2}}+\dfrac{6t^{2}-2}{t^{3}-t}-\dfrac{1+10t}{2t+10t^{2}}+\dfrac{-3}{2}\cdot\dfrac{1}{4t}\cdot4\right]\\ & ,\left[\left(4t\right)^{\frac{3}{2}}\right]\rightarrow\begin{cases} \text{exponential}: & \dfrac{-3}{2}\\ \text{linear to denominator}: & \dfrac{1}{4t}\\ \text{differentiation} & 4 \end{cases}\\ = & \dfrac{6\left(1+2t^{2}\right)\left(t^{3}-t\right)^{2}}{\sqrt{t+5t^{2}}\left(4t\right)^{\frac{3}{2}}}\left[\dfrac{4t}{1+2t^{2}}+\dfrac{6t^{2}-2}{t^{3}-t}-\dfrac{1+10t}{2t+10t^{2}}-\dfrac{3}{2t}\right] \end{aligned} \]
\[ \dfrac{\mathrm{d}}{\mathrm{d}t}\left[\dfrac{\sqrt{1+2t}}{t+\sqrt{1+t^{2}}}\right] \]
\[ \begin{aligned} & \dfrac{\mathrm{d}}{\mathrm{d}t}\left[\dfrac{\sqrt{1+2t}}{t+\sqrt{1+t^{2}}}\right]\\ = & \dfrac{\sqrt{1+2t}}{t+\left[\sqrt{1+t^{2}}\right]}\left[\dfrac{1}{2}\dfrac{2}{1+2t}+\left(-1\right)\dfrac{1+\left[\frac{1}{2}\frac{2t}{\sqrt{1+t^{2}}}\right]}{t+\sqrt{1+t^{2}}}\right] \end{aligned} \]
\[ \tag*{$\Box$} \]
47.2 Feynman method of integration / integral technique
47.2.1 principle
https://www.bilibili.com/video/BV1Lj411L79X/?t=2m38s
https://www.youtube.com/watch?v=GW86SShcYbM
\[ I=\int f\left(x\right)\mathrm{d}x \]
\[ I\left(t\right)=\int f\left(x,t\right)\mathrm{d}x \]
\[ \begin{aligned} I= & \int f\left(x\right)\mathrm{d}x\\ I\left(t\right)= & \int f\left(x,t\right)\mathrm{d}x\\ \dfrac{\mathrm{d}}{\mathrm{d}t}I\left(t\right)=I^{\prime}\left(t\right)= & \dfrac{\mathrm{d}}{\mathrm{d}t}\int f\left(x,t\right)\mathrm{d}x\\ \overset{\text{Lebniz integral rule}}{=} & f\left(x,b\left(x\right),t\right)\dfrac{\mathrm{d}b\left(x\right)}{\mathrm{d}x}-f\left(x,a\left(x\right),t\right)\dfrac{\mathrm{d}a\left(x\right)}{\mathrm{d}x}+\int_{a\left(x\right)}^{b\left(x\right)}\dfrac{\partial}{\partial t}f\left(x,t\right)\mathrm{d}x\\ \overset{\cdots}{=} & \int\dfrac{\partial}{\partial t}f\left(x,t\right)\mathrm{d}x=\int\dfrac{\partial f\left(x,t\right)}{\partial t}\mathrm{d}x=\int f_{{\scriptscriptstyle t}}\left(x,t\right)\mathrm{d}x\\ I\left(t\right)= & \int I^{\prime}\left(t\right)\mathrm{d}t=\int I^{\prime}\left(t\right)\mathrm{d}t+C=\left[\int I^{\prime}\left(t\right)\mathrm{d}t\right]\left(t\right)\\ \Downarrow & \text{ if }f\left(x,t=0\right)=f\left(x,0\right)=f\left(x\right)\\ I\overset{f\left(x,0\right)=f\left(x\right)}{=}I\left(0\right)= & \left[\int I^{\prime}\left(t\right)\mathrm{d}t\right]\left(0\right) \end{aligned} \]
47.2.2 Dirichlet integral
as a example by Feynman method of integration / integral technique
https://en.wikipedia.org/wiki/Dirichlet_integral
https://www.bilibili.com/video/BV1Lj411L79X/?t=4m38s
\(\int_{0}^{\infty}\dfrac{\sin x}{x}\mathrm{d}x\)
https://www.youtube.com/watch?v=ZZccxuOpb4k
https://blog.csdn.net/zhuoqingjoking97298/article/details/127950915
\(\int_{-\infty}^{\infty}\dfrac{\sin x}{x}\mathrm{d}x\)
\[ \int_{-\infty}^{\infty}\dfrac{\sin x}{x}\mathrm{d}x \]
\[ f\left(x\right)=\dfrac{\sin x}{x}\text{ is an even function}\Leftrightarrow f\left(-x\right)=\dfrac{\sin\left(-x\right)}{\left(-x\right)}=\dfrac{-\sin\left(x\right)}{-x}=\dfrac{\sin x}{x}=f\left(x\right) \]
\[ \begin{aligned} \int_{-\infty}^{\infty}\dfrac{\sin x}{x}\mathrm{d}x= & \int_{-\infty}^{0}\dfrac{\sin x}{x}\mathrm{d}x+\int_{0}^{\infty}\dfrac{\sin x}{x}\mathrm{d}x\\ = & \int_{x=-\infty}^{x=0}\dfrac{\sin x}{x}\mathrm{d}x+\int_{0}^{\infty}\dfrac{\sin x}{x}\mathrm{d}x\\ = & \int_{x=-\infty}^{x=0}\dfrac{\sin x}{x}\mathrm{d}x\left(,x^{\prime}=-x\Leftrightarrow x=-x^{\prime}\right)+\int_{0}^{\infty}\dfrac{\sin x}{x}\mathrm{d}x\\ = & \int_{\left(-x^{\prime}\right)=-\infty}^{\left(-x^{\prime}\right)=0}\dfrac{\sin\left(-x^{\prime}\right)}{\left(-x^{\prime}\right)}\mathrm{d}\left(-x^{\prime}\right)+\int_{0}^{\infty}\dfrac{\sin x}{x}\mathrm{d}x\\ = & \int_{x^{\prime}=-\left(-\infty\right)}^{x^{\prime}=-0}\dfrac{-\sin x^{\prime}}{-x^{\prime}}\left(-\mathrm{d}x^{\prime}\right)+\int_{0}^{\infty}\dfrac{\sin x}{x}\mathrm{d}x\\ = & \int_{x^{\prime}=\infty}^{x^{\prime}=0}\dfrac{\sin x^{\prime}}{x^{\prime}}\left(-\mathrm{d}x^{\prime}\right)+\int_{0}^{\infty}\dfrac{\sin x}{x}\mathrm{d}x\\ = & -\int_{x^{\prime}=\infty}^{x^{\prime}=0}\dfrac{\sin x^{\prime}}{x^{\prime}}\mathrm{d}x^{\prime}+\int_{0}^{\infty}\dfrac{\sin x}{x}\mathrm{d}x\\ = & \int_{x^{\prime}=0}^{x^{\prime}=\infty}\dfrac{\sin x^{\prime}}{x^{\prime}}\mathrm{d}x^{\prime}+\int_{0}^{\infty}\dfrac{\sin x}{x}\mathrm{d}x\\ = & \int_{0}^{\infty}\dfrac{\sin x}{x}\mathrm{d}x+\int_{0}^{\infty}\dfrac{\sin x}{x}\mathrm{d}x=2\int_{0}^{\infty}\dfrac{\sin x}{x}\mathrm{d}x \end{aligned} \]
\[ \int_{-\infty}^{\infty}\dfrac{\sin x}{x}\mathrm{d}x=2\int_{0}^{\infty}\dfrac{\sin x}{x}\mathrm{d}x \]
\(\int_{0}^{\infty}\dfrac{\sin x}{x}\mathrm{d}x\)
\[ \begin{aligned} I=\int_{0}^{\infty}\dfrac{\sin x}{x}\mathrm{d}x= & \int_{0}^{\infty}f\left(x\right)\mathrm{d}x,f\left(x\right)=\dfrac{\sin x}{x}\\ \int_{0}^{\infty}\mathrm{e}^{-tx}\dfrac{\sin x}{x}\mathrm{d}x= & \int_{0}^{\infty}\mathrm{e}^{-tx}f\left(x\right)\mathrm{d}x,\text{ Laplacian transform of }f\left(x\right)\\ = & \int_{0}^{\infty}f\left(x,t\right)\mathrm{d}x,\begin{cases} f\left(x,t\right)=\mathrm{e}^{-tx}f\left(x\right)\\ f\left(x,0\right)=\mathrm{e}^{-0x}f\left(x\right)=1\cdot f\left(x\right)=f\left(x\right) & \Downarrow \end{cases}\\ I\left(t\right)= & \int_{0}^{\infty}f\left(x,t\right)\mathrm{d}x=\int_{0}^{\infty}\mathrm{e}^{-tx}f\left(x\right)\mathrm{d}x=\int_{0}^{\infty}\mathrm{e}^{-tx}\dfrac{\sin x}{x}\mathrm{d}x\Rightarrow I\left(0\right)=I\\ \dfrac{\mathrm{d}}{\mathrm{d}t}I\left(t\right)=I^{\prime}\left(t\right)= & \dfrac{\mathrm{d}}{\mathrm{d}t}\int_{0}^{\infty}f\left(x,t\right)\mathrm{d}x=\int_{0}^{\infty}\dfrac{\partial f\left(x,t\right)}{\partial t}\mathrm{d}x=\int_{0}^{\infty}\dfrac{\partial\mathrm{e}^{-tx}\dfrac{\sin x}{x}}{\partial t}\mathrm{d}x\\ = & \int_{0}^{\infty}\dfrac{\sin x}{x}\left[\dfrac{\partial\mathrm{e}^{-tx}}{\partial t}\right]\mathrm{d}x=\int_{0}^{\infty}\dfrac{\sin x}{x}\left[-x\mathrm{e}^{-tx}\right]\mathrm{d}x=\int_{0}^{\infty}\sin x\left[-\mathrm{e}^{-tx}\right]\mathrm{d}x\\ = & -\int_{0}^{\infty}\mathrm{e}^{-tx}\sin x\mathrm{d}x,\text{ Laplacian transform of }-\sin x\\ = & \int_{0}^{\infty}\mathrm{e}^{-tx}\left(-\sin x\right)\mathrm{d}x=\int_{x=0}^{x=\infty}\mathrm{e}^{-tx}\mathrm{d}\cos x,I^{\prime}\left(t\right)=\int_{0}^{\infty}\mathrm{e}^{-tx}\left(-\sin x\right)\mathrm{d}x\\ = & \left[\mathrm{e}^{-tx}\cos x\right]_{x=0}^{x=\infty}-\int_{x=0}^{x=\infty}\cos x\mathrm{d}\mathrm{e}^{-tx}\\ = & \left[\mathrm{e}^{-t\infty}\cos\infty\right]-\left[\mathrm{e}^{-t0}\cos0\right]-\int_{x=0}^{x=\infty}\cos x\left(-t\mathrm{e}^{-tx}\mathrm{d}x\right)\\ = & \left[0\cos\infty\right]-\left[1\cdot1\right]+\int_{0}^{\infty}t\mathrm{e}^{-tx}\cos x\mathrm{d}x\\ = & 0-1+\int_{0}^{\infty}t\mathrm{e}^{-tx}\cos x\mathrm{d}x=-1+\int_{x=0}^{x=\infty}t\mathrm{e}^{-tx}\mathrm{d}\sin x\\ = & -1+\left[t\mathrm{e}^{-tx}\sin x\right]_{x=0}^{x=\infty}-\int_{x=0}^{x=\infty}\sin x\mathrm{d}\left(t\mathrm{e}^{-tx}\right)\\ = & -1+\left[0-0\right]-\int_{0}^{\infty}\sin x\left(t\mathrm{e}^{-tx}\left(-t\right)\mathrm{d}x\right)=-1-\int_{0}^{\infty}t^{2}\mathrm{e}^{-tx}\left(-\sin x\right)\mathrm{d}x\\ = & -1-t^{2}\int_{0}^{\infty}\mathrm{e}^{-tx}\left(-\sin x\right)\mathrm{d}x=-1-t^{2}I^{\prime}\left(t\right)\\ I^{\prime}\left(t\right)= & -1-t^{2}I^{\prime}\left(t\right)\\ I^{\prime}\left(t\right)= & \dfrac{-1}{1+t^{2}}\\ I\left(t\right)= & \int\dfrac{-1}{1+t^{2}}\mathrm{d}t\overset{t=\tan\theta}{=}\int\dfrac{-1}{1+\tan^{2}\theta}\mathrm{d}\tan\theta=-\int\dfrac{1}{\sec^{2}\theta}\sec^{2}\theta\mathrm{d}\theta=-\int\mathrm{d}\theta=-\theta+C\\ = & -\arctan t+C=-\tan^{-1}t+C\\ & \int_{0}^{\infty}\mathrm{e}^{-tx}\dfrac{\sin x}{x}\mathrm{d}x=I\left(t\right)=-\arctan t+C\\ \Downarrow & \Rightarrow I=\int_{0}^{\infty}\dfrac{\sin x}{x}\mathrm{d}x=\int_{0}^{\infty}\mathrm{e}^{-0x}\dfrac{\sin x}{x}\mathrm{d}x=I\left(0\right)=-\arctan0+C=-0+C\Rightarrow C=I\\ \Rightarrow & 0=\int_{0}^{\infty}0\dfrac{\sin x}{x}\mathrm{d}x=\int_{0}^{\infty}\mathrm{e}^{-\infty x}\dfrac{\sin x}{x}\mathrm{d}x=I\left(\infty\right)=-\arctan\infty+C=\dfrac{-\pi}{2}+C\\ & 0=\dfrac{-\pi}{2}+C\Rightarrow C=\dfrac{\pi}{2}\\ I= & I\left(0\right)=C=\dfrac{\pi}{2},I=\int_{0}^{\infty}\dfrac{\sin x}{x}\mathrm{d}x\\ \int_{0}^{\infty}\dfrac{\sin x}{x}\mathrm{d}x= & \dfrac{\pi}{2} \end{aligned} \]
\[ \int_{0}^{\infty}\dfrac{\sin x}{x}\mathrm{d}x=\dfrac{\pi}{2} \]
\[ \int_{-\infty}^{\infty}\dfrac{\sin x}{x}\mathrm{d}x=2\int_{0}^{\infty}\dfrac{\sin x}{x}\mathrm{d}x=2\cdot\dfrac{\pi}{2}=\pi \]
\[ \int_{-\infty}^{\infty}\dfrac{\sin x}{x}\mathrm{d}x=\pi \]
\[ \tag*{$\Box$} \]
47.2.2.2 sinc function
https://en.wikipedia.org/wiki/Sinc_function
https://en.wikipedia.org/wiki/Anti-aliasing_filter
https://en.wikipedia.org/wiki/Borwein_integral
https://blog.udn.com/paraquat/22455342
Fig. 30.2: \(\mathrm{sin}(x)\)
https://tex.stackexchange.com/questions/235006/declaring-sinc-in-tikz
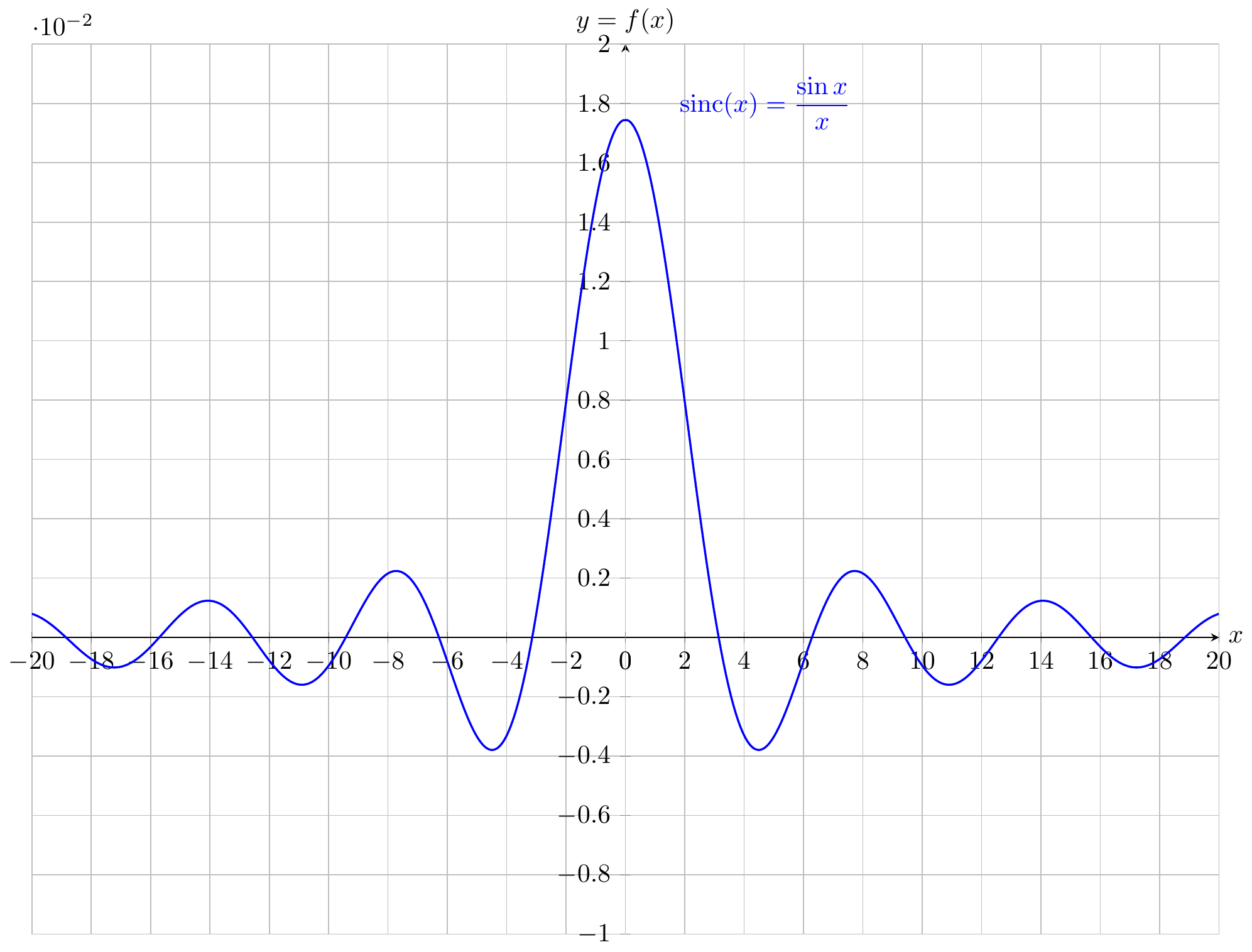
Fig. 17.1: \(\mathrm{sinc}(x)\)
47.2.3 Gaussian integral
https://www.youtube.com/watch?v=jP-6j6mEpRg
\(\int_{-\infty}^{\infty}\mathrm{e}^{-x^{2}}\mathrm{d}x\)
\[ \int_{-\infty}^{\infty}\mathrm{e}^{-x^{2}}\mathrm{d}x \]
\[ f\left(x\right)=\mathrm{e}^{-x^{2}}\text{ is an even function}\Leftrightarrow f\left(-x\right)=\mathrm{e}^{-\left(-x\right)^{2}}=\mathrm{e}^{-x^{2}}=f\left(x\right) \]
\[ \begin{aligned} \int_{-\infty}^{\infty}\mathrm{e}^{-x^{2}}\mathrm{d}x= & \int_{-\infty}^{0}\mathrm{e}^{-x^{2}}\mathrm{d}x+\int_{0}^{\infty}\mathrm{e}^{-x^{2}}\mathrm{d}x\\ = & \int_{x=-\infty}^{x=0}\mathrm{e}^{-x^{2}}\mathrm{d}x+\int_{0}^{\infty}\mathrm{e}^{-x^{2}}\mathrm{d}x\\ = & \int_{x=-\infty}^{x=0}\mathrm{e}^{-x^{2}}\mathrm{d}x\left(,x^{\prime}=-x\Leftrightarrow x=-x^{\prime}\right)+\int_{0}^{\infty}\mathrm{e}^{-x^{2}}\mathrm{d}x\\ = & \int_{\left(-x^{\prime}\right)=-\infty}^{\left(-x^{\prime}\right)=0}\mathrm{e}^{-\left(-x^{\prime}\right)^{2}}\mathrm{d}\left(-x^{\prime}\right)+\int_{0}^{\infty}\mathrm{e}^{-x^{2}}\mathrm{d}x\\ = & \int_{x^{\prime}=-\left(-\infty\right)}^{x^{\prime}=-0}\mathrm{e}^{-\left(x^{\prime}\right)^{2}}\left(-\mathrm{d}x^{\prime}\right)+\int_{0}^{\infty}\mathrm{e}^{-x^{2}}\mathrm{d}x\\ = & \int_{x^{\prime}=\infty}^{x^{\prime}=0}\mathrm{e}^{-\left(x^{\prime}\right)^{2}}\mathrm{d}x^{\prime}+\int_{0}^{\infty}\mathrm{e}^{-x^{2}}\mathrm{d}x\\ = & -\int_{x^{\prime}=\infty}^{x^{\prime}=0}\mathrm{e}^{-\left(x^{\prime}\right)^{2}}\mathrm{d}x^{\prime}+\int_{0}^{\infty}\mathrm{e}^{-x^{2}}\mathrm{d}x\\ = & \int_{x^{\prime}=0}^{x^{\prime}=\infty}\mathrm{e}^{-\left(x^{\prime}\right)^{2}}\mathrm{d}x+\int_{0}^{\infty}\mathrm{e}^{-x^{2}}\mathrm{d}x\\ = & \int_{0}^{\infty}\mathrm{e}^{-x^{2}}\mathrm{d}x+\int_{0}^{\infty}\mathrm{e}^{-x^{2}}\mathrm{d}x=2\int_{0}^{\infty}\mathrm{e}^{-x^{2}}\mathrm{d}x \end{aligned} \]
\[ \int_{-\infty}^{\infty}\mathrm{e}^{-x^{2}}\mathrm{d}x=2\int_{0}^{\infty}\mathrm{e}^{-x^{2}}\mathrm{d}x \]
\(\int_{0}^{\infty}\mathrm{e}^{-x^{2}}\mathrm{d}x\)
\[ I\left(t\right)=\left[\int_{0}^{t}\mathrm{e}^{-x^{2}}\mathrm{d}x\right]^{2} \]
\[ \begin{aligned} I^{\prime}\left(t\right)=\dfrac{\mathrm{d}I\left(t\right)}{\mathrm{d}t}= & \dfrac{\mathrm{d}\left[\int_{0}^{t}\mathrm{e}^{-x^{2}}\mathrm{d}x\right]^{2}}{\mathrm{d}t}=\dfrac{\mathrm{d}\left[\int_{0}^{t}\mathrm{e}^{-x^{2}}\mathrm{d}x\right]^{2}}{\mathrm{d}\left[\int_{0}^{t}\mathrm{e}^{-x^{2}}\mathrm{d}x\right]}\dfrac{\mathrm{d}\left[\int_{0}^{t}\mathrm{e}^{-x^{2}}\mathrm{d}x\right]}{\mathrm{d}t}=2\left[\int_{0}^{t}\mathrm{e}^{-x^{2}}\mathrm{d}x\right]\left[\dfrac{\mathrm{d}}{\mathrm{d}t}\int_{0}^{t}\mathrm{e}^{-x^{2}}\mathrm{d}x\right]\\ = & 2\left[\int_{0}^{t}\mathrm{e}^{-x^{2}}\mathrm{d}x\right]\left[\dfrac{\mathrm{d}}{\mathrm{d}t}\int_{0}^{t}\mathrm{e}^{-x^{2}}\mathrm{d}x\right]\overset{\text{FToC}}{=}2\left[\int_{0}^{t}\mathrm{e}^{-x^{2}}\mathrm{d}x\right]\left[\mathrm{e}^{-t^{2}}\right]\\ = & 2\int_{0}^{t}\mathrm{e}^{-x^{2}}\mathrm{e}^{-t^{2}}\mathrm{d}x=2\int_{0}^{t}\mathrm{e}^{-\left(x^{2}+t^{2}\right)}\mathrm{d}x=2\int_{x=0}^{x=t}\mathrm{e}^{-\left(x^{2}+t^{2}\right)}\mathrm{d}x,x^{\prime}=\dfrac{x}{t}\Leftrightarrow x=tx^{\prime}\\ = & 2\int_{tx^{\prime}=0}^{tx^{\prime}=t}\mathrm{e}^{-\left(\left(tx^{\prime}\right)^{2}+t^{2}\right)}\mathrm{d}tx^{\prime}=2\int_{x^{\prime}=0}^{x^{\prime}=1}\mathrm{e}^{-t^{2}\left(\left(x^{\prime}\right)^{2}+1\right)}t\mathrm{d}x^{\prime}=2\int_{0}^{1}t\mathrm{e}^{-t^{2}\left(x^{2}+1\right)}\mathrm{d}x\\ = & -\int_{0}^{1}\left(-2t\right)\mathrm{e}^{-t^{2}\left(x^{2}+1\right)}\mathrm{d}x=-\int_{0}^{1}\dfrac{\partial}{\partial t}\dfrac{\mathrm{e}^{-t^{2}\left(x^{2}+1\right)}}{x^{2}+1}\mathrm{d}x=-\dfrac{\mathrm{d}}{\mathrm{d}t}\int_{0}^{1}\dfrac{\mathrm{e}^{-t^{2}\left(x^{2}+1\right)}}{x^{2}+1}\mathrm{d}x\\ \left[\int_{0}^{t}\mathrm{e}^{-x^{2}}\mathrm{d}x\right]^{2}= & I\left(t\right)=-\int_{0}^{1}\dfrac{\mathrm{e}^{-t^{2}\left(x^{2}+1\right)}}{x^{2}+1}\mathrm{d}x+C\\ 0=\left[\int_{0}^{0}\mathrm{e}^{-x^{2}}\mathrm{d}x\right]^{2}= & I\left(0\right)=\int_{0}^{1}\dfrac{1}{x^{2}+1}\mathrm{d}x+C\overset{x=\tan\theta}{=}\left[-\arctan x\right]_{0}^{1}+C=\dfrac{-\pi}{4}+C\Rightarrow C=\dfrac{\pi}{4}\\ \left[\int_{0}^{t}\mathrm{e}^{-x^{2}}\mathrm{d}x\right]^{2}= & I\left(t\right)=-\int_{0}^{1}\dfrac{\mathrm{e}^{-t^{2}\left(x^{2}+1\right)}}{x^{2}+1}\mathrm{d}x+C=-\int_{0}^{1}\dfrac{\mathrm{e}^{-t^{2}\left(x^{2}+1\right)}}{x^{2}+1}\mathrm{d}x+\dfrac{\pi}{4}\\ \left[\int_{0}^{\infty}\mathrm{e}^{-x^{2}}\mathrm{d}x\right]^{2}= & \lim_{t\rightarrow\infty}I\left(t\right)=I\left(\infty\right)=-\int_{0}^{1}\dfrac{\mathrm{e}^{-\infty^{2}\left(x^{2}+1\right)}}{x^{2}+1}\mathrm{d}x+\dfrac{\pi}{4}=-\int_{0}^{1}\dfrac{0}{x^{2}+1}\mathrm{d}x+\dfrac{\pi}{4}=\dfrac{\pi}{4}\\ \left[\int_{0}^{\infty}\mathrm{e}^{-x^{2}}\mathrm{d}x\right]^{2}= & \dfrac{\pi}{4}\\ \int_{0}^{\infty}\mathrm{e}^{-x^{2}}\mathrm{d}x= & \dfrac{\sqrt{\pi}}{2} \end{aligned} \]
\[ \int_{0}^{\infty}\mathrm{e}^{-x^{2}}\mathrm{d}x=\dfrac{\sqrt{\pi}}{2} \]
\[ \int_{-\infty}^{\infty}\mathrm{e}^{-x^{2}}\mathrm{d}x=2\int_{0}^{\infty}\mathrm{e}^{-x^{2}}\mathrm{d}x=2\cdot\dfrac{\sqrt{\pi}}{2}=\sqrt{\pi} \]
\[ \int_{-\infty}^{\infty}\mathrm{e}^{-x^{2}}\mathrm{d}x=\sqrt{\pi} \]
\[ \tag*{$\Box$} \]
47.2.4 other examples
https://www.youtube.com/watch?v=GW86SShcYbM
\(\int_{0}^{1}\ln x\mathrm{d}x\)
\[ I=\int_{0}^{1}\ln x\mathrm{d}x=\int_{0}^{1}\ln\left(x\right)\mathrm{d}x,f\left(x\right)=\ln x \]
\[ I\left(t\right)=\int_{0}^{1}\ln tx\mathrm{d}x=\int_{0}^{1}f\left(tx\right)\mathrm{d}x=\int_{0}^{1}f\left(x,t\right)\mathrm{d}x,\begin{cases} f\left(x,t\right)=f\left(tx\right)=\ln tx\\ f\left(x,1\right)=f\left(x\right)=\ln x \end{cases} \]
\[ \begin{aligned} I\left(t\right)= & \int_{0}^{1}f\left(x,t\right)\mathrm{d}x=\int_{0}^{1}f\left(tx\right)\mathrm{d}x=\int_{0}^{1}\ln tx\mathrm{d}x\Rightarrow I\left(1\right)=I\\ \dfrac{\mathrm{d}}{\mathrm{d}t}I\left(t\right)=I^{\prime}\left(t\right)= & \dfrac{\mathrm{d}}{\mathrm{d}t}\int_{0}^{1}f\left(x,t\right)\mathrm{d}x=\int_{0}^{1}\dfrac{\partial f\left(x,t\right)}{\partial t}\mathrm{d}x=\int_{0}^{1}\dfrac{\partial\ln tx}{\partial t}\mathrm{d}x\\ = & \int_{0}^{1}\dfrac{1}{tx}x\mathrm{d}x=\int_{0}^{1}\dfrac{1}{t}\mathrm{d}x=\dfrac{1}{t}\int_{0}^{1}\mathrm{d}x=\dfrac{1}{t}\left[x\right]_{0}^{1}=\dfrac{1}{t}\\ I\left(t\right)= & \int I^{\prime}\left(t\right)\mathrm{d}t=\int\dfrac{1}{t}\mathrm{d}t=\ln\left|t\right|+C\\ \Downarrow & \Rightarrow I=\int_{0}^{1}\ln x\mathrm{d}x=\int_{0}^{1}\ln1x\mathrm{d}x=I\left(1\right)=\ln\left|1\right|+C=0+C\Rightarrow C=I\\ \text{no more known } & \text{boundary condition} \end{aligned} \]
\[ \begin{aligned} \Im\left(t\right)= & \int_{0}^{1}x^{t}\mathrm{d}x=\left[\dfrac{x^{t+1}}{t+1}\right]_{x=0}^{1}=\dfrac{1}{t+1}\\ \dfrac{-1}{\left(t+1\right)^{2}}=\dfrac{\mathrm{d}}{\mathrm{d}t}\dfrac{1}{t+1}=\dfrac{\mathrm{d}}{\mathrm{d}t}\Im\left(t\right)=\Im^{\prime}\left(t\right)= & \dfrac{\mathrm{d}}{\mathrm{d}t}\int_{0}^{1}x^{t}\mathrm{d}x=\int_{0}^{1}\dfrac{\partial x^{t}}{\partial t}\mathrm{d}x=\int_{0}^{1}x^{t}\ln x\mathrm{d}x\\ -1=\left[\dfrac{-1}{\left(t+1\right)^{2}}\right]_{t=0}=\Im^{\prime}\left(0\right)= & \int_{0}^{1}x^{0}\ln x\mathrm{d}x=\int_{0}^{1}1\ln x\mathrm{d}x=\int_{0}^{1}\ln x\mathrm{d}x\\ \int_{0}^{1}\ln x\mathrm{d}x= & -1 \end{aligned} \]
https://zhuanlan.zhihu.com/p/687355703
https://www.zhihu.com/question/646881575/answer/3417318090
TaylorCatAlice: Feynman method of integration and residue theorem
https://www.bilibili.com/video/BV1Lj411L79X
MatheManiac: complex integral
https://www.youtube.com/watch?v=EyBDtUtyshk&list=PLDcSwjT2BF_UDdkQ3KQjX5SRQ2DLLwv0R&index=11
https://www.youtube.com/watch?v=EyBDtUtyshk
47.3 Feynman method of path integral
Elliot Schneider: Physics with Elliot
https://www.youtube.com/watch?v=W8QZ-yxebFA
https://www.youtube.com/watch?v=Se-CpexiJLQ
Feynman method of path integral in quantum dynamics
https://www.youtube.com/watch?v=Sp5SvdDh2u8
history of path integral