Chapter 53: Fourier analysis

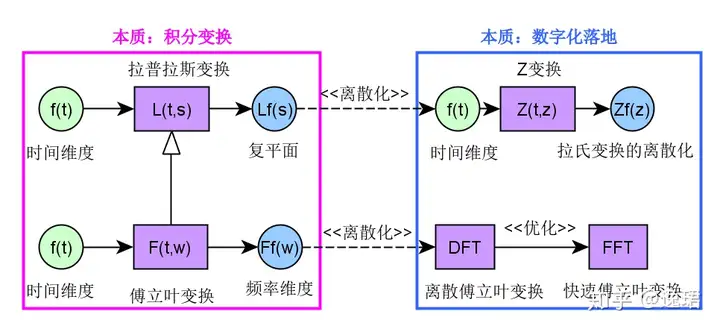
Fig. 24.1: transform relationhsip: Fourier vs Laplace vs Z

https://zhuanlan.zhihu.com/p/342952028

https://zhuanlan.zhihu.com/p/19763358

53.1 basic calculation

\[ \int_{\frac{-\tau}{2}+\psi}^{\frac{\tau}{2}+\psi}\cos\left(n\frac{2\pi}{\tau}t+\phi\right){\rm d}t=\left[\frac{\sin\left(n\frac{2\pi}{\tau}t+\phi\right)}{n\frac{2\pi}{\tau}}\right]_{\frac{-\tau}{2}+\psi}^{\frac{\tau}{2}+\psi}=0 \]

\[ \begin{aligned} \cos\alpha\cos\beta= & \frac{\cos\left(\alpha+\beta\right)+\cos\left(\alpha-\beta\right)}{2}\\ \sin\alpha\sin\beta= & \frac{-\cos\left(\alpha+\beta\right)+\cos\left(\alpha-\beta\right)}{2}\\ \sin\alpha\cos\beta= & \frac{\sin\left(\alpha+\beta\right)+\sin\left(\alpha-\beta\right)}{2}\\ \cos\alpha\sin\beta= & \frac{\sin\left(\alpha+\beta\right)-\sin\left(\alpha-\beta\right)}{2} \end{aligned} \]

\[ \begin{aligned} & \int\cos\left(m\frac{2\pi}{\tau}t\right)\cos\left(n\frac{2\pi}{\tau}t+\phi_{n}\right){\rm d}t\\ = & \begin{cases} \int\cos\phi_{0}{\rm d}t & m=n=0\\ \int\dfrac{\cos\left(\left(m+n\right)\frac{2\pi}{\tau}t+\phi_{n}\right)+\cos\left(\left(m-n\right)\frac{2\pi}{\tau}t-\phi_{n}\right){\rm d}t}{2} & mn\ne0 \end{cases}\\ = & \begin{cases} t\cos\phi_{0} & m=n=0\\ \begin{cases} \int\dfrac{\cos\left(2n\frac{2\pi}{\tau}t+\phi_{n}\right)+\cos\left(-\phi_{n}\right)}{2}{\rm d}t & m=n\\ \int\dfrac{\cos\left(\left(m+n\right)\frac{2\pi}{\tau}t+\phi_{n}\right)+\cos\left(\left(m-n\right)\frac{2\pi}{\tau}t-\phi_{n}\right)}{2}{\rm d}t & m\ne n \end{cases} & mn\ne0 \end{cases}\\ = & \begin{cases} t\cos\phi_{0} & m=n=0\\ \begin{cases} \int\dfrac{\cos\left(2n\frac{2\pi}{\tau}t+\phi_{n}\right)+\cos\phi_{n}}{2}{\rm d}t & m=n\\ \int\dfrac{\cos\left(\left(m+n\right)\frac{2\pi}{\tau}t+\phi_{n}\right)+\cos\left(\left(m-n\right)\frac{2\pi}{\tau}t-\phi_{n}\right)}{2}{\rm d}t & m\ne n \end{cases} & mn\ne0 \end{cases}\\ = & \begin{cases} t\cos\phi_{0} & m=n=0\\ \begin{cases} \int\dfrac{\cos\left(2n\frac{2\pi}{\tau}t+\phi_{n}\right)}{2}{\rm d}t+\frac{t\cos\phi_{n}}{2} & m=n\\ \int\dfrac{\cos\left(\left(m+n\right)\frac{2\pi}{\tau}t+\phi_{n}\right)+\cos\left(\left(m-n\right)\frac{2\pi}{\tau}t-\phi_{n}\right)}{2}{\rm d}t & m\ne n \end{cases} & mn\ne0 \end{cases} \end{aligned} \]

\[ \begin{aligned} & \int_{\frac{-\tau}{2}+\psi}^{\frac{\tau}{2}+\psi}\cos\left(m\frac{2\pi}{\tau}t\right)\cos\left(n\frac{2\pi}{\tau}t+\phi_{n}\right){\rm d}t\\ = & \begin{cases} \tau\cos\phi_{0} & m=n=0\\ \begin{cases} \frac{\tau\cos\phi_{n}}{2} & m=n\\ 0 & m\ne n \end{cases} & mn\ne0 \end{cases}\\ = & \begin{cases} \begin{cases} \tau\cos\phi_{0} & n=0\\ \frac{\tau\cos\phi_{n}}{2} & n\ne0 \end{cases} & m=n\\ 0 & m\ne n \end{cases} \end{aligned} \]

\[ \begin{aligned} & \frac{2}{\tau\cos\phi_{n}}\int_{\frac{-\tau}{2}+\psi}^{\frac{\tau}{2}+\psi}\cos\left(m\frac{2\pi}{\tau}t\right)\cos\left(n\frac{2\pi}{\tau}t+\phi_{n}\right){\rm d}t\\ = & \begin{cases} \begin{cases} 2 & n=0\\ 1 & n\ne0 \end{cases} & m=n\\ 0 & m\ne n \end{cases} \end{aligned} \]

\[ \begin{aligned} & \int_{\frac{-\tau}{2}+\psi}^{\frac{\tau}{2}+\psi}\sin\left(m\frac{2\pi}{\tau}t\right)\cos\left(n\frac{2\pi}{\tau}t+\phi_{n}\right){\rm d}t\\ = & \begin{cases} 0 & m=n\\ 0 & m\ne n \end{cases} \end{aligned} \]

\[ \begin{aligned} & \int_{\frac{-\tau}{2}+\psi}^{\frac{\tau}{2}+\psi}\cos\left(m\frac{2\pi}{\tau}t\right)\sin\left(n\frac{2\pi}{\tau}t+\phi_{n}\right){\rm d}t\\ = & \begin{cases} 0 & m=n\\ 0 & m\ne n \end{cases} \end{aligned} \]

\[ \begin{aligned} \frac{2}{\tau\cos\phi_{n}}\int_{\frac{-\tau}{2}+\psi}^{\frac{\tau}{2}+\psi}\cos\left(m\frac{2\pi}{\tau}t\right)\cos\left(n\frac{2\pi}{\tau}t+\phi_{n}\right){\rm d}t= & \begin{cases} \begin{cases} 2 & n=0\\ 1 & n\ne0 \end{cases} & m=n\\ 0 & m\ne n \end{cases}\\ \frac{2}{\tau\cos\phi_{n}}\int_{\frac{-\tau}{2}+\psi}^{\frac{\tau}{2}+\psi}\sin\left(m\frac{2\pi}{\tau}t\right)\sin\left(n\frac{2\pi}{\tau}t+\phi_{n}\right){\rm d}t= & \begin{cases} 1 & m=n\ne0\\ 0 & \neg\left(m=n\ne0\right) \end{cases}\\ \int_{\frac{-\tau}{2}+\psi}^{\frac{\tau}{2}+\psi}\sin\left(m\frac{2\pi}{\tau}t\right)\cos\left(n\frac{2\pi}{\tau}t+\phi_{n}\right){\rm d}t= & \begin{cases} 0 & m=n\\ 0 & m\ne n \end{cases}\\ \int_{\frac{-\tau}{2}+\psi}^{\frac{\tau}{2}+\psi}\cos\left(m\frac{2\pi}{\tau}t\right)\sin\left(n\frac{2\pi}{\tau}t+\phi_{n}\right){\rm d}t= & \begin{cases} 0 & m=n\\ 0 & m\ne n \end{cases} \end{aligned} \]