Chapter 55: linear algebra

55.1 The Art of Linear Algeba

https://github.com/kenjihiranabe/The-Art-of-Linear-Algebra

https://stackoverflow.com/questions/39173714/r-markdown-can-i-insert-a-pdf-to-the-r-markdown-file-as-an-image

https://stackoverflow.com/a/39177166

55.2 CCJou

https://www.youtube.com/playlist?list=PLP-JUp2VR1LsFtHT-i_vZ3oNFIAc3t_Ju

55.2.1 coordinate

https://www.youtube.com/watch?v=eMUFexQsKXA&list=PLP-JUp2VR1LsFtHT-i_vZ3oNFIAc3t_Ju&index=20

$$\begin{aligned} \boldsymbol{v}= & v^{{\scriptscriptstyle 1}}\boldsymbol{v}_{{\scriptscriptstyle 1}}+v^{{\scriptscriptstyle 2}}\boldsymbol{v}_{{\scriptscriptstyle 2}}+\cdots+v^{{\scriptscriptstyle n}}\boldsymbol{v}_{{\scriptscriptstyle n}}\\ = & v^{{\scriptscriptstyle 1}}\boldsymbol{v}_{{\scriptscriptstyle 1}}+\cdots+v^{{\scriptscriptstyle n}}\boldsymbol{v}_{{\scriptscriptstyle n}}\\ = & c^{{\scriptscriptstyle 1}}\boldsymbol{\beta}_{{\scriptscriptstyle 1}}+\cdots+c^{{\scriptscriptstyle n}}\boldsymbol{\beta}_{{\scriptscriptstyle n}}=c_{{\scriptscriptstyle 1}}\boldsymbol{\beta}_{{\scriptscriptstyle 1}}+\cdots+c_{{\scriptscriptstyle n}}\boldsymbol{\beta}_{{\scriptscriptstyle n}}=B\boldsymbol{c}=B\left[\boldsymbol{v}\right]_{{\scriptscriptstyle B}}\\ = & e^{{\scriptscriptstyle 1}}\hat{\boldsymbol{\beta}}_{{\scriptscriptstyle 1}}+\cdots+e^{{\scriptscriptstyle n}}\hat{\boldsymbol{\beta}}_{{\scriptscriptstyle n}}=e_{{\scriptscriptstyle 1}}\hat{\boldsymbol{\beta}}_{{\scriptscriptstyle 1}}+\cdots+e_{{\scriptscriptstyle n}}\hat{\boldsymbol{\beta}}_{{\scriptscriptstyle n}}\\ = & e^{{\scriptscriptstyle 1}}\hat{\boldsymbol{e}}_{{\scriptscriptstyle 1}}+\cdots+e^{{\scriptscriptstyle n}}\hat{\boldsymbol{e}}_{{\scriptscriptstyle n}}=e_{{\scriptscriptstyle 1}}\hat{\boldsymbol{e}}_{{\scriptscriptstyle 1}}+\cdots+e_{{\scriptscriptstyle n}}\hat{\boldsymbol{e}}_{{\scriptscriptstyle n}}\\ \overset{\text{e.g.}}{=} & e^{{\scriptscriptstyle 1}}\begin{pmatrix}1\\ \vdots\\ 0\\ \vdots\\ 0 \end{pmatrix}_{{\scriptscriptstyle n\times1}}+\cdots+e^{{\scriptscriptstyle n}}\begin{pmatrix}0\\ \vdots\\ 0\\ \vdots\\ 1 \end{pmatrix}_{{\scriptscriptstyle n\times1}}=e_{{\scriptscriptstyle 1}}\begin{pmatrix}1\\ \vdots\\ 0\\ \vdots\\ 0 \end{pmatrix}+\cdots+e_{{\scriptscriptstyle n}}\begin{pmatrix}0\\ \vdots\\ 0\\ \vdots\\ 1 \end{pmatrix}\\ = & \begin{pmatrix}1 & \cdots & 0 & \cdots & 0\\ \vdots & \ddots & \vdots & \ddots & \vdots\\ 0 & \cdots & 1 & \cdots & 0\\ \vdots & \ddots & \vdots & \ddots & \vdots\\ 0 & \cdots & 0 & \cdots & 1 \end{pmatrix}_{{\scriptscriptstyle n\times n}}\begin{pmatrix}e^{{\scriptscriptstyle 1}}\\ \vdots\\ e^{{\scriptscriptstyle j}}\\ \vdots\\ e^{{\scriptscriptstyle n}} \end{pmatrix}_{{\scriptscriptstyle n\times1}}=I_{{\scriptscriptstyle n\times n}}\boldsymbol{e}=I\boldsymbol{e} \end{aligned}$$

$$\begin{aligned} B\boldsymbol{c}= & c^{{\scriptscriptstyle 1}}\begin{pmatrix}|\\ \boldsymbol{\beta}_{{\scriptscriptstyle 1}}\\ | \end{pmatrix}+\cdots+c^{{\scriptscriptstyle j}}\begin{pmatrix}|\\ \boldsymbol{\beta}_{{\scriptscriptstyle j}}\\ | \end{pmatrix}+\cdots+c^{{\scriptscriptstyle n}}\begin{pmatrix}|\\ \boldsymbol{\beta}_{{\scriptscriptstyle n}}\\ | \end{pmatrix}=\begin{pmatrix}| & & | & & |\\ \boldsymbol{\beta}_{{\scriptscriptstyle 1}} & \cdots & \boldsymbol{\beta}_{{\scriptscriptstyle j}} & \cdots & \boldsymbol{\beta}_{{\scriptscriptstyle n}}\\ | & & | & & | \end{pmatrix}\begin{pmatrix}c^{{\scriptscriptstyle 1}}\\ \vdots\\ c^{{\scriptscriptstyle j}}\\ \vdots\\ c^{{\scriptscriptstyle n}} \end{pmatrix}\\ = & c^{{\scriptscriptstyle 1}}\begin{bmatrix}|\\ \boldsymbol{\beta}_{{\scriptscriptstyle 1}}\\ | \end{bmatrix}+\cdots+c^{{\scriptscriptstyle j}}\begin{bmatrix}|\\ \boldsymbol{\beta}_{{\scriptscriptstyle j}}\\ | \end{bmatrix}+\cdots+c^{{\scriptscriptstyle n}}\begin{bmatrix}|\\ \boldsymbol{\beta}_{{\scriptscriptstyle n}}\\ | \end{bmatrix}=\begin{bmatrix}| & & | & & |\\ \boldsymbol{\beta}_{{\scriptscriptstyle 1}} & \cdots & \boldsymbol{\beta}_{{\scriptscriptstyle j}} & \cdots & \boldsymbol{\beta}_{{\scriptscriptstyle n}}\\ | & & | & & | \end{bmatrix}\begin{bmatrix}c^{{\scriptscriptstyle 1}}\\ \vdots\\ c^{{\scriptscriptstyle j}}\\ \vdots\\ c^{{\scriptscriptstyle n}} \end{bmatrix}\\ = & c^{{\scriptscriptstyle 1}}\boldsymbol{\beta}_{{\scriptscriptstyle 1}}+c^{{\scriptscriptstyle 2}}\boldsymbol{\beta}_{{\scriptscriptstyle 2}}+\cdots+c^{{\scriptscriptstyle n}}\boldsymbol{\beta}_{{\scriptscriptstyle n}}=c^{{\scriptscriptstyle 1}}\begin{pmatrix}|\\ \boldsymbol{\beta}_{{\scriptscriptstyle 1}}\\ | \end{pmatrix}+c^{{\scriptscriptstyle 2}}\begin{pmatrix}|\\ \boldsymbol{\beta}_{{\scriptscriptstyle 2}}\\ | \end{pmatrix}+\cdots+c^{{\scriptscriptstyle n}}\begin{pmatrix}|\\ \boldsymbol{\beta}_{{\scriptscriptstyle n}}\\ | \end{pmatrix}=\begin{pmatrix}| & | & & |\\ \boldsymbol{\beta}_{{\scriptscriptstyle 1}} & \boldsymbol{\beta}_{{\scriptscriptstyle 2}} & \cdots & \boldsymbol{\beta}_{{\scriptscriptstyle n}}\\ | & | & & | \end{pmatrix}\begin{pmatrix}c^{{\scriptscriptstyle 1}}\\ c^{{\scriptscriptstyle 2}}\\ \vdots\\ c^{{\scriptscriptstyle n}} \end{pmatrix}\\ = & c^{{\scriptscriptstyle 1}}\boldsymbol{\beta}_{{\scriptscriptstyle 1}}+c^{{\scriptscriptstyle 2}}\boldsymbol{\beta}_{{\scriptscriptstyle 2}}+\cdots+c^{{\scriptscriptstyle n}}\boldsymbol{\beta}_{{\scriptscriptstyle n}}=c^{{\scriptscriptstyle 1}}\begin{bmatrix}|\\ \boldsymbol{\beta}_{{\scriptscriptstyle 1}}\\ | \end{bmatrix}+c^{{\scriptscriptstyle 2}}\begin{bmatrix}|\\ \boldsymbol{\beta}_{{\scriptscriptstyle 2}}\\ | \end{bmatrix}+\cdots+c^{{\scriptscriptstyle n}}\begin{bmatrix}|\\ \boldsymbol{\beta}_{{\scriptscriptstyle n}}\\ | \end{bmatrix}=\begin{bmatrix}| & | & & |\\ \boldsymbol{\beta}_{{\scriptscriptstyle 1}} & \boldsymbol{\beta}_{{\scriptscriptstyle 2}} & \cdots & \boldsymbol{\beta}_{{\scriptscriptstyle n}}\\ | & | & & | \end{bmatrix}\begin{bmatrix}c^{{\scriptscriptstyle 1}}\\ c^{{\scriptscriptstyle 2}}\\ \vdots\\ c^{{\scriptscriptstyle n}} \end{bmatrix}\\ = & c^{{\scriptscriptstyle 1}}\boldsymbol{\beta}_{{\scriptscriptstyle 1}}+\cdots+c^{{\scriptscriptstyle n}}\boldsymbol{\beta}_{{\scriptscriptstyle n}}=c^{{\scriptscriptstyle 1}}\begin{pmatrix}|\\ \boldsymbol{\beta}_{{\scriptscriptstyle 1}}\\ | \end{pmatrix}+\cdots+c^{{\scriptscriptstyle n}}\begin{pmatrix}|\\ \boldsymbol{\beta}_{{\scriptscriptstyle n}}\\ | \end{pmatrix}=\begin{pmatrix}| & & |\\ \boldsymbol{\beta}_{{\scriptscriptstyle 1}} & \cdots & \boldsymbol{\beta}_{{\scriptscriptstyle n}}\\ | & & | \end{pmatrix}\begin{pmatrix}c^{{\scriptscriptstyle 1}}\\ \vdots\\ c^{{\scriptscriptstyle n}} \end{pmatrix}=B\left[\boldsymbol{v}\right]_{{\scriptscriptstyle B}}\\ = & c^{{\scriptscriptstyle 1}}\boldsymbol{\beta}_{{\scriptscriptstyle 1}}+\cdots+c^{{\scriptscriptstyle n}}\boldsymbol{\beta}_{{\scriptscriptstyle n}}=c^{{\scriptscriptstyle 1}}\begin{bmatrix}|\\ \boldsymbol{\beta}_{{\scriptscriptstyle 1}}\\ | \end{bmatrix}+\cdots+c^{{\scriptscriptstyle n}}\begin{bmatrix}|\\ \boldsymbol{\beta}_{{\scriptscriptstyle n}}\\ | \end{bmatrix}=\begin{bmatrix}| & & |\\ \boldsymbol{\beta}_{{\scriptscriptstyle 1}} & \cdots & \boldsymbol{\beta}_{{\scriptscriptstyle n}}\\ | & & | \end{bmatrix}\begin{bmatrix}c^{{\scriptscriptstyle 1}}\\ \vdots\\ c^{{\scriptscriptstyle n}} \end{bmatrix}=\begin{bmatrix}| & & |\\ \boldsymbol{\beta}_{{\scriptscriptstyle 1}} & \cdots & \boldsymbol{\beta}_{{\scriptscriptstyle n}}\\ | & & | \end{bmatrix}\begin{bmatrix}v^{{\scriptscriptstyle 1}}\\ \vdots\\ v^{{\scriptscriptstyle n}} \end{bmatrix}\\ B= & \begin{pmatrix}| & & | & & |\\ \boldsymbol{\beta}_{{\scriptscriptstyle 1}} & \cdots & \boldsymbol{\beta}_{{\scriptscriptstyle j}} & \cdots & \boldsymbol{\beta}_{{\scriptscriptstyle n}}\\ | & & | & & | \end{pmatrix}=\begin{bmatrix}| & & | & & |\\ \boldsymbol{\beta}_{{\scriptscriptstyle 1}} & \cdots & \boldsymbol{\beta}_{{\scriptscriptstyle j}} & \cdots & \boldsymbol{\beta}_{{\scriptscriptstyle n}}\\ | & & | & & | \end{bmatrix}=\begin{bmatrix}| & | & & |\\ \boldsymbol{\beta}_{{\scriptscriptstyle 1}} & \boldsymbol{\beta}_{{\scriptscriptstyle 2}} & \cdots & \boldsymbol{\beta}_{{\scriptscriptstyle n}}\\ | & | & & | \end{bmatrix}=\begin{bmatrix}| & & |\\ \boldsymbol{\beta}_{{\scriptscriptstyle 1}} & \cdots & \boldsymbol{\beta}_{{\scriptscriptstyle n}}\\ | & & | \end{bmatrix}\\ \left[\boldsymbol{v}\right]_{{\scriptscriptstyle B}}= & \boldsymbol{c}=\begin{bmatrix}c^{{\scriptscriptstyle 1}}\\ \vdots\\ c^{{\scriptscriptstyle n}} \end{bmatrix}=\begin{bmatrix}v^{{\scriptscriptstyle 1}}\\ \vdots\\ v^{{\scriptscriptstyle n}} \end{bmatrix}\in F^{n} = \mathbb{F}^n \in\left\{ \mathbb{R}^{n},\mathbb{C}^{n},\cdots\right\} \end{aligned}$$

---

$$\boldsymbol{v}=B\left[\boldsymbol{v}\right]_{{\scriptscriptstyle B}}$$

---

$$\begin{aligned} \boldsymbol{v}= & B\left[\boldsymbol{v}\right]_{{\scriptscriptstyle B}}\\ B^{-1}\boldsymbol{v}= & B^{-1}B\left[\boldsymbol{v}\right]_{{\scriptscriptstyle B}}=I\left[\boldsymbol{v}\right]_{{\scriptscriptstyle B}}=\left[\boldsymbol{v}\right]_{{\scriptscriptstyle B}}\\ \left[\boldsymbol{v}\right]_{{\scriptscriptstyle B}}= & B^{-1}\boldsymbol{v} \end{aligned}$$

---

$$\left[\boldsymbol{v}\right]_{{\scriptscriptstyle B}}=B^{-1}\boldsymbol{v}$$

$$\left[\boldsymbol{v}\right]_{{\scriptscriptstyle B}}=B^{-1}\boldsymbol{v}\in\in F^{n}\in\left\{ \mathbb{R}^{n},\mathbb{C}^{n},\cdots\right\}$$

---

$$\boldsymbol{v}=B\left[\boldsymbol{v}\right]_{{\scriptscriptstyle B}}=B^{\prime}\left[\boldsymbol{v}\right]_{{\scriptscriptstyle B^{\prime}}}$$

---

$$\begin{aligned} B\left[\boldsymbol{v}\right]_{{\scriptscriptstyle B}}= & B^{\prime}\left[\boldsymbol{v}\right]_{{\scriptscriptstyle B^{\prime}}}\\ \left[\boldsymbol{v}\right]_{{\scriptscriptstyle B}}=I\left[\boldsymbol{v}\right]_{{\scriptscriptstyle B}}=B^{-1}B\left[\boldsymbol{v}\right]_{{\scriptscriptstyle B}}= & B^{-1}B^{\prime}\left[\boldsymbol{v}\right]_{{\scriptscriptstyle B^{\prime}}}\\ \left[\boldsymbol{v}\right]_{{\scriptscriptstyle B}}= & B^{-1}B^{\prime}\left[\boldsymbol{v}\right]_{{\scriptscriptstyle B^{\prime}}}\\ B^{\prime}\left[\boldsymbol{v}\right]_{{\scriptscriptstyle B^{\prime}}}= & B\left[\boldsymbol{v}\right]_{{\scriptscriptstyle B}}\\ \left[\boldsymbol{v}\right]_{{\scriptscriptstyle B^{\prime}}}=I\left[\boldsymbol{v}\right]_{{\scriptscriptstyle B^{\prime}}}=B^{\prime-1}B^{\prime}\left[\boldsymbol{v}\right]_{{\scriptscriptstyle B^{\prime}}}= & B^{\prime-1}B\left[\boldsymbol{v}\right]_{{\scriptscriptstyle B}}\\ \left[\boldsymbol{v}\right]_{{\scriptscriptstyle B^{\prime}}}= & B^{\prime-1}B\left[\boldsymbol{v}\right]_{{\scriptscriptstyle B}} \end{aligned}$$

55.2.2 linear transformation

$$\begin{aligned} \boldsymbol{v}= & v^{{\scriptscriptstyle 1}}\boldsymbol{v}_{{\scriptscriptstyle 1}}+\cdots+v^{{\scriptscriptstyle n}}\boldsymbol{v}_{{\scriptscriptstyle n}}=v^{{\scriptscriptstyle j}}\boldsymbol{v}_{{\scriptscriptstyle j}}=\sum_{j=1}^{n}v^{{\scriptscriptstyle j}}\boldsymbol{v}_{{\scriptscriptstyle j}}\\ = & v^{{\scriptscriptstyle 1}}\begin{bmatrix}|\\ \boldsymbol{v}_{{\scriptscriptstyle 1}}\\ | \end{bmatrix}+\cdots+v^{{\scriptscriptstyle n}}\begin{bmatrix}|\\ \boldsymbol{v}_{{\scriptscriptstyle n}}\\ | \end{bmatrix}=\begin{bmatrix}| & & |\\ \boldsymbol{v}_{{\scriptscriptstyle 1}} & \cdots & \boldsymbol{v}_{{\scriptscriptstyle n}}\\ | & & | \end{bmatrix}\begin{bmatrix}v^{{\scriptscriptstyle 1}}\\ \vdots\\ v^{{\scriptscriptstyle n}} \end{bmatrix}=V\left[\boldsymbol{v}\right]_{{\scriptscriptstyle V}}\\ , & \begin{cases} V=\begin{bmatrix}| & & |\\ \boldsymbol{v}_{{\scriptscriptstyle 1}} & \cdots & \boldsymbol{v}_{{\scriptscriptstyle n}}\\ | & & | \end{bmatrix},\mathfrak{V}=\left\{ \boldsymbol{v}_{{\scriptscriptstyle j}}\right\} _{{\scriptscriptstyle j}=1}^{{\scriptscriptstyle n}}=\left\{ \boldsymbol{v}_{{\scriptscriptstyle 1}},\cdots,\boldsymbol{v}_{{\scriptscriptstyle n}}\right\} \\ \left[\boldsymbol{v}\right]_{{\scriptscriptstyle V}}=\begin{bmatrix}v^{{\scriptscriptstyle 1}}\\ \vdots\\ v^{{\scriptscriptstyle n}} \end{bmatrix}\in F^{n}\in\left\{ \mathbb{R}^{n},\mathbb{C}^{n},\cdots\right\} \end{cases}\overset{\text{if }V\text{ invertible}}{\implies}\left[\boldsymbol{v}\right]_{{\scriptscriptstyle V}}=V^{-1}\boldsymbol{v} \end{aligned}$$

$$\backslash\text{mathfrak}V=\mathfrak{V}\text{ vs.}\backslash\text{mathfrak}B=\mathfrak{B}$$

$$\begin{aligned} & \boldsymbol{v}\in\mathcal{V}\overset{T}{\rightarrow}\mathcal{W}\ni\boldsymbol{w}=T\left(\boldsymbol{v}\right)\\ & ,T:\mathcal{V}\rightarrow\mathcal{W}\begin{cases} T\left(\boldsymbol{u}+\boldsymbol{v}\right)=T\left(\boldsymbol{u}\right)+T\left(\boldsymbol{v}\right) & \left(a\right)\text{additivity}\\ T\left(\lambda\boldsymbol{v}\right)=\lambda T\left(\boldsymbol{v}\right) & \left(h\right)\text{homogeneity} \end{cases} \end{aligned}$$

$$\begin{aligned} \boldsymbol{w}=T\left(\boldsymbol{v}\right)= & T\left(v^{{\scriptscriptstyle 1}}\boldsymbol{v}_{{\scriptscriptstyle 1}}+\cdots+v^{{\scriptscriptstyle n}}\boldsymbol{v}_{{\scriptscriptstyle n}}\right)\overset{\left(a\right)}{=}T\left(v^{{\scriptscriptstyle 1}}\boldsymbol{v}_{{\scriptscriptstyle 1}}\right)+\cdots+T\left(v^{{\scriptscriptstyle n}}\boldsymbol{v}_{{\scriptscriptstyle n}}\right)\overset{\left(h\right)}{=}v^{{\scriptscriptstyle 1}}T\left(\boldsymbol{v}_{{\scriptscriptstyle 1}}\right)+\cdots+v^{{\scriptscriptstyle n}}T\left(\boldsymbol{v}_{{\scriptscriptstyle n}}\right)\\ = & v^{{\scriptscriptstyle 1}}\begin{bmatrix}|\\ T\left(\boldsymbol{v}_{{\scriptscriptstyle 1}}\right)\\ | \end{bmatrix}+\cdots+v^{{\scriptscriptstyle n}}\begin{bmatrix}|\\ T\left(\boldsymbol{v}_{{\scriptscriptstyle n}}\right)\\ | \end{bmatrix}=\begin{bmatrix}| & & |\\ T\left(\boldsymbol{v}_{{\scriptscriptstyle 1}}\right) & \cdots & T\left(\boldsymbol{v}_{{\scriptscriptstyle n}}\right)\\ | & & | \end{bmatrix}\begin{bmatrix}v^{{\scriptscriptstyle 1}}\\ \vdots\\ v^{{\scriptscriptstyle n}} \end{bmatrix}=\begin{bmatrix}| & & |\\ T\left(\boldsymbol{v}_{{\scriptscriptstyle 1}}\right) & \cdots & T\left(\boldsymbol{v}_{{\scriptscriptstyle n}}\right)\\ | & & | \end{bmatrix}\left[\boldsymbol{v}\right]_{{\scriptscriptstyle V}} \end{aligned}$$

$$\boldsymbol{w}=T\left(\boldsymbol{v}\right)=\begin{bmatrix}| & & |\\ T\left(\boldsymbol{v}_{{\scriptscriptstyle 1}}\right) & \cdots & T\left(\boldsymbol{v}_{{\scriptscriptstyle n}}\right)\\ | & & | \end{bmatrix}\left[\boldsymbol{v}\right]_{{\scriptscriptstyle V}}=T\left(V\right)\left[\boldsymbol{v}\right]_{{\scriptscriptstyle V}},T\left(V\right)=\begin{bmatrix}| & & |\\ T\left(\boldsymbol{v}_{{\scriptscriptstyle 1}}\right) & \cdots & T\left(\boldsymbol{v}_{{\scriptscriptstyle n}}\right)\\ | & & | \end{bmatrix}$$

---

$$\boldsymbol{w}=T\left(\boldsymbol{v}\right)\overset{\boldsymbol{v}=V\left[\boldsymbol{v}\right]_{{\scriptscriptstyle V}}}{=}T\left(V\left[\boldsymbol{v}\right]_{{\scriptscriptstyle V}}\right)\overset{T\text{ linear}}{=}T\left(V\right)\left[\boldsymbol{v}\right]_{{\scriptscriptstyle V}}$$

---

$$\begin{aligned} T\left(\boldsymbol{v}\right)=\boldsymbol{w}= & w^{{\scriptscriptstyle 1}}\boldsymbol{w}_{{\scriptscriptstyle 1}}+\cdots+w^{{\scriptscriptstyle m}}\boldsymbol{w}_{{\scriptscriptstyle m}}=w^{{\scriptscriptstyle j}}\boldsymbol{w}_{{\scriptscriptstyle j}}=\sum_{j=1}^{n}w^{{\scriptscriptstyle j}}\boldsymbol{w}_{{\scriptscriptstyle j}}\\ = & w^{{\scriptscriptstyle 1}}\begin{bmatrix}|\\ \boldsymbol{w}_{{\scriptscriptstyle 1}}\\ | \end{bmatrix}+\cdots+w^{{\scriptscriptstyle m}}\begin{bmatrix}|\\ \boldsymbol{w}_{{\scriptscriptstyle m}}\\ | \end{bmatrix}=\begin{bmatrix}| & & |\\ \boldsymbol{w}_{{\scriptscriptstyle 1}} & \cdots & \boldsymbol{w}_{{\scriptscriptstyle m}}\\ | & & | \end{bmatrix}\begin{bmatrix}w^{{\scriptscriptstyle 1}}\\ \vdots\\ w^{{\scriptscriptstyle m}} \end{bmatrix}=W\left[\boldsymbol{w}\right]_{{\scriptscriptstyle W}}\overset{\boldsymbol{w}=T\left(\boldsymbol{v}\right)}{=}W\left[T\left(\boldsymbol{v}\right)\right]_{{\scriptscriptstyle W}}\\ , & \begin{cases} W=\begin{bmatrix}| & & |\\ \boldsymbol{w}_{{\scriptscriptstyle 1}} & \cdots & \boldsymbol{w}_{{\scriptscriptstyle m}}\\ | & & | \end{bmatrix},\mathfrak{W}=\left\{ \boldsymbol{w}_{{\scriptscriptstyle j}}\right\} _{{\scriptscriptstyle j}=1}^{{\scriptscriptstyle m}}=\left\{ \boldsymbol{w}_{{\scriptscriptstyle 1}},\cdots,\boldsymbol{w}_{{\scriptscriptstyle m}}\right\} \\ \left[\boldsymbol{w}\right]_{{\scriptscriptstyle W}}=\begin{bmatrix}w^{{\scriptscriptstyle 1}}\\ \vdots\\ w^{{\scriptscriptstyle m}} \end{bmatrix}\in F^{m}\in\left\{ \mathbb{R}^{m},\mathbb{C}^{m},\cdots\right\} \end{cases}\overset{\text{if }W\text{ invertible}}{\implies}\left[\boldsymbol{w}\right]_{{\scriptscriptstyle W}}=W^{-1}\boldsymbol{w} \end{aligned}$$

$$\backslash\text{mathfrak}W=\mathfrak{W}\text{ vs.}\backslash\text{mathfrak}V=\mathfrak{V}$$

$$\begin{aligned} T\left(\boldsymbol{v}_{{\scriptscriptstyle 1}}\right)= & t_{{\scriptscriptstyle 1}}^{{\scriptscriptstyle 1}}\boldsymbol{w}_{{\scriptscriptstyle 1}}+\cdots+t_{{\scriptscriptstyle 1}}^{{\scriptscriptstyle m}}\boldsymbol{w}_{{\scriptscriptstyle m}}=t_{{\scriptscriptstyle 1}}^{{\scriptscriptstyle 1}}\begin{bmatrix}|\\ \boldsymbol{w}_{{\scriptscriptstyle 1}}\\ | \end{bmatrix}+\cdots+t_{{\scriptscriptstyle 1}}^{{\scriptscriptstyle m}}\begin{bmatrix}|\\ \boldsymbol{w}_{{\scriptscriptstyle m}}\\ | \end{bmatrix}\\ = & \begin{bmatrix}| & & |\\ \boldsymbol{w}_{{\scriptscriptstyle 1}} & \cdots & \boldsymbol{w}_{{\scriptscriptstyle m}}\\ | & & | \end{bmatrix}\begin{bmatrix}t_{{\scriptscriptstyle 1}}^{{\scriptscriptstyle 1}}\\ \vdots\\ t_{{\scriptscriptstyle 1}}^{{\scriptscriptstyle m}} \end{bmatrix}=\begin{bmatrix}| & & |\\ \boldsymbol{w}_{{\scriptscriptstyle 1}} & \cdots & \boldsymbol{w}_{{\scriptscriptstyle m}}\\ | & & | \end{bmatrix}\begin{bmatrix}|\\ \left[T\left(\boldsymbol{v}_{{\scriptscriptstyle 1}}\right)\right]_{{\scriptscriptstyle W}}\\ | \end{bmatrix}=W\left[T\left(\boldsymbol{v}_{{\scriptscriptstyle 1}}\right)\right]_{{\scriptscriptstyle W}}\\ \vdots\\ T\left(\boldsymbol{v}_{{\scriptscriptstyle n}}\right)= & t_{{\scriptscriptstyle n}}^{{\scriptscriptstyle 1}}\boldsymbol{w}_{{\scriptscriptstyle 1}}+\cdots+t_{{\scriptscriptstyle n}}^{{\scriptscriptstyle m}}\boldsymbol{w}_{{\scriptscriptstyle m}}=t_{{\scriptscriptstyle n}}^{{\scriptscriptstyle 1}}\begin{bmatrix}|\\ \boldsymbol{w}_{{\scriptscriptstyle 1}}\\ | \end{bmatrix}+\cdots+t_{{\scriptscriptstyle n}}^{{\scriptscriptstyle m}}\begin{bmatrix}|\\ \boldsymbol{w}_{{\scriptscriptstyle m}}\\ | \end{bmatrix}\\ = & \begin{bmatrix}| & & |\\ \boldsymbol{w}_{{\scriptscriptstyle 1}} & \cdots & \boldsymbol{w}_{{\scriptscriptstyle m}}\\ | & & | \end{bmatrix}\begin{bmatrix}t_{{\scriptscriptstyle n}}^{{\scriptscriptstyle 1}}\\ \vdots\\ t_{{\scriptscriptstyle n}}^{{\scriptscriptstyle m}} \end{bmatrix}=\begin{bmatrix}| & & |\\ \boldsymbol{w}_{{\scriptscriptstyle 1}} & \cdots & \boldsymbol{w}_{{\scriptscriptstyle m}}\\ | & & | \end{bmatrix}\begin{bmatrix}|\\ \left[T\left(\boldsymbol{v}_{{\scriptscriptstyle n}}\right)\right]_{{\scriptscriptstyle W}}\\ | \end{bmatrix}=W\left[T\left(\boldsymbol{v}_{{\scriptscriptstyle n}}\right)\right]_{{\scriptscriptstyle W}} \end{aligned}$$

$$\begin{aligned} T\left(V\right)=\begin{bmatrix}| & & |\\ T\left(\boldsymbol{v}_{{\scriptscriptstyle 1}}\right) & \cdots & T\left(\boldsymbol{v}_{{\scriptscriptstyle n}}\right)\\ | & & | \end{bmatrix}= & \begin{bmatrix}| & & |\\ \boldsymbol{w}_{{\scriptscriptstyle 1}} & \cdots & \boldsymbol{w}_{{\scriptscriptstyle m}}\\ | & & | \end{bmatrix}\begin{bmatrix}\begin{bmatrix}t_{{\scriptscriptstyle 1}}^{{\scriptscriptstyle 1}}\\ \vdots\\ t_{{\scriptscriptstyle 1}}^{{\scriptscriptstyle m}} \end{bmatrix} & \cdots & \begin{bmatrix}t_{{\scriptscriptstyle n}}^{{\scriptscriptstyle 1}}\\ \vdots\\ t_{{\scriptscriptstyle n}}^{{\scriptscriptstyle m}} \end{bmatrix}\end{bmatrix}\\ = & \begin{bmatrix}| & & |\\ \boldsymbol{w}_{{\scriptscriptstyle 1}} & \cdots & \boldsymbol{w}_{{\scriptscriptstyle m}}\\ | & & | \end{bmatrix}\begin{bmatrix}t_{{\scriptscriptstyle 1}}^{{\scriptscriptstyle 1}} & \cdots & t_{{\scriptscriptstyle n}}^{{\scriptscriptstyle 1}}\\ \vdots & \ddots & \vdots\\ t_{{\scriptscriptstyle 1}}^{{\scriptscriptstyle m}} & \cdots & t_{{\scriptscriptstyle n}}^{{\scriptscriptstyle m}} \end{bmatrix}\\ = & \begin{bmatrix}| & & |\\ \boldsymbol{w}_{{\scriptscriptstyle 1}} & \cdots & \boldsymbol{w}_{{\scriptscriptstyle m}}\\ | & & | \end{bmatrix}\begin{bmatrix}| & & |\\ \left[T\left(\boldsymbol{v}_{{\scriptscriptstyle 1}}\right)\right]_{{\scriptscriptstyle W}} & \cdots & \left[T\left(\boldsymbol{v}_{{\scriptscriptstyle n}}\right)\right]_{{\scriptscriptstyle W}}\\ | & & | \end{bmatrix}=WT\\ , & \begin{cases} W=\begin{bmatrix}| & & |\\ \boldsymbol{w}_{{\scriptscriptstyle 1}} & \cdots & \boldsymbol{w}_{{\scriptscriptstyle m}}\\ | & & | \end{bmatrix}\\ T=\begin{bmatrix}t_{{\scriptscriptstyle 1}}^{{\scriptscriptstyle 1}} & \cdots & t_{{\scriptscriptstyle n}}^{{\scriptscriptstyle 1}}\\ \vdots & \ddots & \vdots\\ t_{{\scriptscriptstyle 1}}^{{\scriptscriptstyle m}} & \cdots & t_{{\scriptscriptstyle n}}^{{\scriptscriptstyle m}} \end{bmatrix}=\begin{bmatrix}| & & |\\ \left[T\left(\boldsymbol{v}_{{\scriptscriptstyle 1}}\right)\right]_{{\scriptscriptstyle W}} & \cdots & \left[T\left(\boldsymbol{v}_{{\scriptscriptstyle n}}\right)\right]_{{\scriptscriptstyle W}}\\ | & & | \end{bmatrix} \end{cases} \end{aligned}$$

$$T\left(V\right)=\begin{bmatrix}| & & |\\ T\left(\boldsymbol{v}_{{\scriptscriptstyle 1}}\right) & \cdots & T\left(\boldsymbol{v}_{{\scriptscriptstyle n}}\right)\\ | & & | \end{bmatrix}=WT,\begin{cases} W=\begin{bmatrix}| & & |\\ \boldsymbol{w}_{{\scriptscriptstyle 1}} & \cdots & \boldsymbol{w}_{{\scriptscriptstyle m}}\\ | & & | \end{bmatrix}\\ T=\begin{bmatrix}t_{{\scriptscriptstyle 1}}^{{\scriptscriptstyle 1}} & \cdots & t_{{\scriptscriptstyle n}}^{{\scriptscriptstyle 1}}\\ \vdots & \ddots & \vdots\\ t_{{\scriptscriptstyle 1}}^{{\scriptscriptstyle m}} & \cdots & t_{{\scriptscriptstyle n}}^{{\scriptscriptstyle m}} \end{bmatrix}=\begin{bmatrix}| & & |\\ \left[T\left(\boldsymbol{v}_{{\scriptscriptstyle 1}}\right)\right]_{{\scriptscriptstyle W}} & \cdots & \left[T\left(\boldsymbol{v}_{{\scriptscriptstyle n}}\right)\right]_{{\scriptscriptstyle W}}\\ | & & | \end{bmatrix} \end{cases}$$

$$T=\begin{bmatrix}| & & |\\ \left[T\left(\boldsymbol{v}_{{\scriptscriptstyle 1}}\right)\right]_{{\scriptscriptstyle W}} & \cdots & \left[T\left(\boldsymbol{v}_{{\scriptscriptstyle n}}\right)\right]_{{\scriptscriptstyle W}}\\ | & & | \end{bmatrix}\overset{V=\begin{bmatrix}| & & |\\ \boldsymbol{v}_{{\scriptscriptstyle 1}} & \cdots & \boldsymbol{v}_{{\scriptscriptstyle n}}\\ | & & | \end{bmatrix}}{=}\left[T\left(V\right)\right]_{{\scriptscriptstyle W}}$$

---

$$\begin{aligned} T=\left[T\left(V\right)\right]_{{\scriptscriptstyle W}}= & W^{{\scriptscriptstyle -1}}T\left(V\right)=\begin{bmatrix}| & & |\\ \boldsymbol{w}_{{\scriptscriptstyle 1}} & \cdots & \boldsymbol{w}_{{\scriptscriptstyle m}}\\ | & & | \end{bmatrix}^{{\scriptscriptstyle -1}}T\left(V\right),\text{if }W\text{ invertible}\\ = & \begin{bmatrix}| & & |\\ \boldsymbol{w}_{{\scriptscriptstyle 1}} & \cdots & \boldsymbol{w}_{{\scriptscriptstyle m}}\\ | & & | \end{bmatrix}^{{\scriptscriptstyle -1}}T\left(\begin{bmatrix}| & & |\\ \boldsymbol{v}_{{\scriptscriptstyle 1}} & \cdots & \boldsymbol{v}_{{\scriptscriptstyle n}}\\ | & & | \end{bmatrix}\right)\\ = & \begin{bmatrix}| & & |\\ \boldsymbol{w}_{{\scriptscriptstyle 1}} & \cdots & \boldsymbol{w}_{{\scriptscriptstyle m}}\\ | & & | \end{bmatrix}^{{\scriptscriptstyle -1}}\begin{bmatrix}| & & |\\ T\left(\boldsymbol{v}_{{\scriptscriptstyle 1}}\right) & \cdots & T\left(\boldsymbol{v}_{{\scriptscriptstyle n}}\right)\\ | & & | \end{bmatrix}\\ = & W^{{\scriptscriptstyle -1}}\begin{bmatrix}| & & |\\ T\left(\boldsymbol{v}_{{\scriptscriptstyle 1}}\right) & \cdots & T\left(\boldsymbol{v}_{{\scriptscriptstyle n}}\right)\\ | & & | \end{bmatrix}=\begin{bmatrix}| & & |\\ W^{{\scriptscriptstyle -1}}T\left(\boldsymbol{v}_{{\scriptscriptstyle 1}}\right) & \cdots & W^{{\scriptscriptstyle -1}}T\left(\boldsymbol{v}_{{\scriptscriptstyle n}}\right)\\ | & & | \end{bmatrix}\\ = & \begin{bmatrix}| & & |\\ \left[T\left(\boldsymbol{v}_{{\scriptscriptstyle 1}}\right)\right]_{{\scriptscriptstyle W}} & \cdots & \left[T\left(\boldsymbol{v}_{{\scriptscriptstyle n}}\right)\right]_{{\scriptscriptstyle W}}\\ | & & | \end{bmatrix} \end{aligned}$$

---

$$T=\left[T\left(V\right)\right]_{{\scriptscriptstyle W}}=\begin{bmatrix}| & & |\\ \boldsymbol{w}_{{\scriptscriptstyle 1}} & \cdots & \boldsymbol{w}_{{\scriptscriptstyle m}}\\ | & & | \end{bmatrix}^{{\scriptscriptstyle -1}}\begin{bmatrix}| & & |\\ T\left(\boldsymbol{v}_{{\scriptscriptstyle 1}}\right) & \cdots & T\left(\boldsymbol{v}_{{\scriptscriptstyle n}}\right)\\ | & & | \end{bmatrix}=W^{{\scriptscriptstyle -1}}T\left(V\right)$$

---

$$\begin{aligned} T= & \begin{bmatrix}t_{{\scriptscriptstyle 1}}^{{\scriptscriptstyle 1}} & \cdots & t_{{\scriptscriptstyle n}}^{{\scriptscriptstyle 1}}\\ \vdots & \ddots & \vdots\\ t_{{\scriptscriptstyle 1}}^{{\scriptscriptstyle m}} & \cdots & t_{{\scriptscriptstyle n}}^{{\scriptscriptstyle m}} \end{bmatrix}=\begin{bmatrix}| & & |\\ \left[T\left(\boldsymbol{v}_{{\scriptscriptstyle 1}}\right)\right]_{{\scriptscriptstyle W}} & \cdots & \left[T\left(\boldsymbol{v}_{{\scriptscriptstyle n}}\right)\right]_{{\scriptscriptstyle W}}\\ | & & | \end{bmatrix}=\left[T\left(V\right)\right]_{{\scriptscriptstyle W}}\\ = & \begin{bmatrix}| & & |\\ \boldsymbol{t}_{{\scriptscriptstyle 1}} & \cdots & \boldsymbol{t}_{{\scriptscriptstyle n}}\\ | & & | \end{bmatrix}=\begin{bmatrix}| & & |\\ \left[T\left(\boldsymbol{v}_{{\scriptscriptstyle 1}}\right)\right]_{{\scriptscriptstyle W}} & \cdots & \left[T\left(\boldsymbol{v}_{{\scriptscriptstyle n}}\right)\right]_{{\scriptscriptstyle W}}\\ | & & | \end{bmatrix},\boldsymbol{t}_{{\scriptscriptstyle j}}=\left[T\left(\boldsymbol{v}_{{\scriptscriptstyle j}}\right)\right]_{{\scriptscriptstyle W}} \end{aligned}$$

$$\begin{aligned} W\left[\boldsymbol{w}\right]_{{\scriptscriptstyle W}}=\boldsymbol{w}=T\left(\boldsymbol{v}\right)= & T\left(V\right)\left[\boldsymbol{v}\right]_{{\scriptscriptstyle V}}\overset{T\left(V\right)=WT}{=}WT\left[\boldsymbol{v}\right]_{{\scriptscriptstyle V}}=W\left(T\left[\boldsymbol{v}\right]_{{\scriptscriptstyle V}}\right)\\ W\left[\boldsymbol{w}\right]_{{\scriptscriptstyle W}}= & W\left(T\left[\boldsymbol{v}\right]_{{\scriptscriptstyle V}}\right)\\ \left[\boldsymbol{w}\right]_{{\scriptscriptstyle W}}=I\left[\boldsymbol{w}\right]_{{\scriptscriptstyle W}}=W^{{\scriptscriptstyle -1}}W\left[\boldsymbol{w}\right]_{{\scriptscriptstyle W}}= & W^{{\scriptscriptstyle -1}}W\left(T\left[\boldsymbol{v}\right]_{{\scriptscriptstyle V}}\right)=IT\left[\boldsymbol{v}\right]_{{\scriptscriptstyle V}}=T\left[\boldsymbol{v}\right]_{{\scriptscriptstyle V}},\text{if }W\text{ invertible}\\ \left[\boldsymbol{w}\right]_{{\scriptscriptstyle W}}= & T\left[\boldsymbol{v}\right]_{{\scriptscriptstyle V}}\\ \left[T\left(\boldsymbol{v}\right)\right]_{{\scriptscriptstyle W}}\overset{\boldsymbol{w}=T\left(\boldsymbol{v}\right)}{=}\left[\boldsymbol{w}\right]_{{\scriptscriptstyle W}}= & T\left[\boldsymbol{v}\right]_{{\scriptscriptstyle V}}\\ \left[T\left(\boldsymbol{v}\right)\right]_{{\scriptscriptstyle W}}= & T\left[\boldsymbol{v}\right]_{{\scriptscriptstyle V}}\overset{T=\left[T\left(V\right)\right]_{{\scriptscriptstyle W}}}{=}\left[T\left(V\right)\right]_{{\scriptscriptstyle W}}\left[\boldsymbol{v}\right]_{{\scriptscriptstyle V}} \end{aligned}$$

---

$$\begin{aligned} \left[\boldsymbol{w}\right]_{{\scriptscriptstyle W}}= & T\left[\boldsymbol{v}\right]_{{\scriptscriptstyle V}}\\ =\left[T\left(\boldsymbol{v}\right)\right]_{{\scriptscriptstyle W}}= & \left[T\left(V\right)\right]_{{\scriptscriptstyle W}}\left[\boldsymbol{v}\right]_{{\scriptscriptstyle V}} \end{aligned}$$

---

$$\begin{aligned} T=\begin{bmatrix}| & & |\\ \boldsymbol{t}_{{\scriptscriptstyle 1}} & \cdots & \boldsymbol{t}_{{\scriptscriptstyle n}}\\ | & & | \end{bmatrix}= & \begin{bmatrix}\begin{bmatrix}t_{{\scriptscriptstyle 1}}^{{\scriptscriptstyle 1}}\\ \vdots\\ t_{{\scriptscriptstyle 1}}^{{\scriptscriptstyle m}} \end{bmatrix} & \cdots & \begin{bmatrix}t_{{\scriptscriptstyle n}}^{{\scriptscriptstyle 1}}\\ \vdots\\ t_{{\scriptscriptstyle n}}^{{\scriptscriptstyle m}} \end{bmatrix}\end{bmatrix}=\begin{bmatrix}t_{{\scriptscriptstyle 1}}^{{\scriptscriptstyle 1}} & \cdots & t_{{\scriptscriptstyle n}}^{{\scriptscriptstyle 1}}\\ \vdots & \ddots & \vdots\\ t_{{\scriptscriptstyle 1}}^{{\scriptscriptstyle m}} & \cdots & t_{{\scriptscriptstyle n}}^{{\scriptscriptstyle m}} \end{bmatrix},\begin{array}{c} \left[\boldsymbol{w}\right]_{{\scriptscriptstyle W}}=T\left[\boldsymbol{v}\right]_{{\scriptscriptstyle V}}\\ \Updownarrow\\ w^{{\scriptscriptstyle i}}=t_{{\scriptscriptstyle j}}^{{\scriptscriptstyle i}}v^{{\scriptscriptstyle j}}=t^{{\scriptscriptstyle i}}{}_{{\scriptscriptstyle j}}v^{{\scriptscriptstyle j}} \end{array}\\ = & \begin{bmatrix}\begin{bmatrix}t^{{\scriptscriptstyle 1}}{}_{{\scriptscriptstyle 1}}\\ \vdots\\ t^{{\scriptscriptstyle m}}{}_{{\scriptscriptstyle 1}} \end{bmatrix} & \cdots & \begin{bmatrix}t^{{\scriptscriptstyle 1}}{}_{{\scriptscriptstyle n}}\\ \vdots\\ t^{{\scriptscriptstyle m}}{}_{{\scriptscriptstyle n}} \end{bmatrix}\end{bmatrix}=\begin{bmatrix}t^{{\scriptscriptstyle 1}}{}_{{\scriptscriptstyle 1}} & \cdots & t^{{\scriptscriptstyle 1}}{}_{{\scriptscriptstyle n}}\\ \vdots & \ddots & \vdots\\ t^{{\scriptscriptstyle m}}{}_{{\scriptscriptstyle 1}} & \cdots & t^{{\scriptscriptstyle m}}{}_{{\scriptscriptstyle n}} \end{bmatrix}=\left[t^{{\scriptscriptstyle i}}{}_{{\scriptscriptstyle j}}\right]_{{\scriptscriptstyle m\times n}}=\left[t^{{\scriptscriptstyle i}}{}_{{\scriptscriptstyle j}}\right]=t^{{\scriptscriptstyle i}}{}_{{\scriptscriptstyle j}}\\ = & \begin{bmatrix}\begin{bmatrix}t_{{\scriptscriptstyle 11}}\\ \vdots\\ t_{{\scriptscriptstyle m1}} \end{bmatrix} & \cdots & \begin{bmatrix}t_{{\scriptscriptstyle 1n}}\\ \vdots\\ t_{{\scriptscriptstyle mn}} \end{bmatrix}\end{bmatrix}=\begin{bmatrix}t_{{\scriptscriptstyle 11}} & \cdots & t_{{\scriptscriptstyle 1n}}\\ \vdots & \ddots & \vdots\\ t_{{\scriptscriptstyle m1}} & \cdots & t_{{\scriptscriptstyle mn}} \end{bmatrix}=\left[t_{{\scriptscriptstyle ij}}\right]_{{\scriptscriptstyle m\times n}}=\left[t_{{\scriptscriptstyle ij}}\right]=t_{{\scriptscriptstyle ij}} \end{aligned}$$

---

$$T=\begin{bmatrix}| & & |\\ \boldsymbol{t}_{{\scriptscriptstyle 1}} & \cdots & \boldsymbol{t}_{{\scriptscriptstyle n}}\\ | & & | \end{bmatrix}=\begin{bmatrix}t^{{\scriptscriptstyle 1}}{}_{{\scriptscriptstyle 1}} & \cdots & t^{{\scriptscriptstyle 1}}{}_{{\scriptscriptstyle n}}\\ \vdots & \ddots & \vdots\\ t^{{\scriptscriptstyle m}}{}_{{\scriptscriptstyle 1}} & \cdots & t^{{\scriptscriptstyle m}}{}_{{\scriptscriptstyle n}} \end{bmatrix}=\left[t^{{\scriptscriptstyle i}}{}_{{\scriptscriptstyle j}}\right]_{{\scriptscriptstyle m\times n}}=t^{{\scriptscriptstyle i}}{}_{{\scriptscriptstyle j}}$$

---

$$\begin{aligned} T\left(\boldsymbol{v}_{{\scriptscriptstyle 1}}\right)= & t_{{\scriptscriptstyle 1}}{}^{{\scriptscriptstyle 1}}\boldsymbol{w}_{{\scriptscriptstyle 1}}+\cdots+t_{{\scriptscriptstyle 1}}{}^{{\scriptscriptstyle m}}\boldsymbol{w}_{{\scriptscriptstyle m}}=t_{{\scriptscriptstyle 1}}{}^{{\scriptscriptstyle 1}}\begin{bmatrix}|\\ \boldsymbol{w}_{{\scriptscriptstyle 1}}\\ | \end{bmatrix}+\cdots+t_{{\scriptscriptstyle 1}}{}^{{\scriptscriptstyle m}}\begin{bmatrix}|\\ \boldsymbol{w}_{{\scriptscriptstyle m}}\\ | \end{bmatrix}=\begin{bmatrix}| & & |\\ \boldsymbol{w}_{{\scriptscriptstyle 1}} & \cdots & \boldsymbol{w}_{{\scriptscriptstyle m}}\\ | & & | \end{bmatrix}\begin{bmatrix}t_{{\scriptscriptstyle 1}}{}^{{\scriptscriptstyle 1}}\\ \vdots\\ t_{{\scriptscriptstyle 1}}{}^{{\scriptscriptstyle m}} \end{bmatrix}\\ = & W\left[T\left(\boldsymbol{v}_{{\scriptscriptstyle 1}}\right)\right]_{{\scriptscriptstyle W}}\\ \vdots\\ T\left(\boldsymbol{v}_{{\scriptscriptstyle n}}\right)= & t_{{\scriptscriptstyle n}}{}^{{\scriptscriptstyle 1}}\boldsymbol{w}_{{\scriptscriptstyle 1}}+\cdots+t_{{\scriptscriptstyle n}}{}^{{\scriptscriptstyle m}}\boldsymbol{w}_{{\scriptscriptstyle m}}=t_{{\scriptscriptstyle n}}{}^{{\scriptscriptstyle 1}}\begin{bmatrix}|\\ \boldsymbol{w}_{{\scriptscriptstyle 1}}\\ | \end{bmatrix}+\cdots+t_{{\scriptscriptstyle n}}{}^{{\scriptscriptstyle m}}\begin{bmatrix}|\\ \boldsymbol{w}_{{\scriptscriptstyle m}}\\ | \end{bmatrix}=\begin{bmatrix}| & & |\\ \boldsymbol{w}_{{\scriptscriptstyle 1}} & \cdots & \boldsymbol{w}_{{\scriptscriptstyle m}}\\ | & & | \end{bmatrix}\begin{bmatrix}t_{{\scriptscriptstyle n}}{}^{{\scriptscriptstyle 1}}\\ \vdots\\ t_{{\scriptscriptstyle n}}{}^{{\scriptscriptstyle m}} \end{bmatrix}\\ = & W\left[T\left(\boldsymbol{v}_{{\scriptscriptstyle n}}\right)\right]_{{\scriptscriptstyle W}}\\ \Downarrow\\ \begin{bmatrix}| & & |\\ T\left(\boldsymbol{v}_{{\scriptscriptstyle 1}}\right) & \cdots & T\left(\boldsymbol{v}_{{\scriptscriptstyle n}}\right)\\ | & & | \end{bmatrix}= & \begin{array}{c} t_{{\scriptscriptstyle 1}}{}^{{\scriptscriptstyle 1}}\\ \vdots\\ t_{{\scriptscriptstyle n}}{}^{{\scriptscriptstyle 1}} \end{array}\begin{bmatrix}|\\ \boldsymbol{w}_{{\scriptscriptstyle 1}}\\ | \end{bmatrix}\begin{array}{c} +\\ \\ + \end{array}\begin{array}{c} \cdots\\ \curvearrowright\\ \cdots \end{array}\begin{array}{c} +\\ \\ + \end{array}\begin{array}{c} t_{{\scriptscriptstyle 1}}{}^{{\scriptscriptstyle m}}\\ \vdots\\ t_{{\scriptscriptstyle n}}{}^{{\scriptscriptstyle m}} \end{array}\begin{bmatrix}|\\ \boldsymbol{w}_{{\scriptscriptstyle m}}\\ | \end{bmatrix}\\ = & \begin{bmatrix}| & & |\\ \boldsymbol{w}_{{\scriptscriptstyle 1}} & \cdots & \boldsymbol{w}_{{\scriptscriptstyle m}}\\ | & & | \end{bmatrix}\begin{bmatrix}t_{{\scriptscriptstyle 1}}{}^{{\scriptscriptstyle 1}} & \cdots & t_{{\scriptscriptstyle n}}{}^{{\scriptscriptstyle 1}}\\ \vdots & \ddots & \vdots\\ t_{{\scriptscriptstyle 1}}{}^{{\scriptscriptstyle m}} & \cdots & t_{{\scriptscriptstyle n}}{}^{{\scriptscriptstyle m}} \end{bmatrix}=\begin{bmatrix}| & & |\\ \boldsymbol{w}_{{\scriptscriptstyle 1}} & \cdots & \boldsymbol{w}_{{\scriptscriptstyle m}}\\ | & & | \end{bmatrix}\begin{bmatrix}| & & |\\ \boldsymbol{t}_{{\scriptscriptstyle 1}} & \cdots & \boldsymbol{t}_{{\scriptscriptstyle n}}\\ | & & | \end{bmatrix}=WT\\ = & \begin{bmatrix}| & & |\\ \boldsymbol{w}_{{\scriptscriptstyle 1}} & \cdots & \boldsymbol{w}_{{\scriptscriptstyle m}}\\ | & & | \end{bmatrix}\begin{bmatrix}| & & |\\ \left[T\left(\boldsymbol{v}_{{\scriptscriptstyle 1}}\right)\right]_{{\scriptscriptstyle W}} & \cdots & \left[T\left(\boldsymbol{v}_{{\scriptscriptstyle n}}\right)\right]_{{\scriptscriptstyle W}}\\ | & & | \end{bmatrix}=W\left[T\left(V\right)\right]_{{\scriptscriptstyle W}}\\ T\left(V\right)= & WT=W\left[T\left(V\right)\right]_{{\scriptscriptstyle W}} \end{aligned}$$

---

$$\begin{aligned} WT= & T\left(V\right)\\ \Downarrow\\ T= & W^{{\scriptscriptstyle -1}}T\left(V\right) \end{aligned}$$

---

$$T=\begin{bmatrix}t_{{\scriptscriptstyle 1}}{}^{{\scriptscriptstyle 1}} & \cdots & t_{{\scriptscriptstyle n}}{}^{{\scriptscriptstyle 1}}\\ \vdots & \ddots & \vdots\\ t_{{\scriptscriptstyle 1}}{}^{{\scriptscriptstyle m}} & \cdots & t_{{\scriptscriptstyle n}}{}^{{\scriptscriptstyle m}} \end{bmatrix}=\begin{bmatrix}t_{{\scriptscriptstyle 1}}^{{\scriptscriptstyle 1}} & \cdots & t_{{\scriptscriptstyle n}}^{{\scriptscriptstyle 1}}\\ \vdots & \ddots & \vdots\\ t_{{\scriptscriptstyle 1}}^{{\scriptscriptstyle m}} & \cdots & t_{{\scriptscriptstyle n}}^{{\scriptscriptstyle m}} \end{bmatrix}=\begin{bmatrix}| & & |\\ \boldsymbol{t}_{{\scriptscriptstyle 1}} & \cdots & \boldsymbol{t}_{{\scriptscriptstyle n}}\\ | & & | \end{bmatrix}=\left[t_{{\scriptscriptstyle j}}^{{\scriptscriptstyle i}}\right]_{{\scriptscriptstyle m\times n}}=\left[t_{{\scriptscriptstyle j}}{}^{{\scriptscriptstyle i}}\right]_{{\scriptscriptstyle m\times n}}=t_{{\scriptscriptstyle j}}{}^{{\scriptscriptstyle i}}$$

---

$$\left[t_{{\scriptscriptstyle j}}{}^{{\scriptscriptstyle i}}\right]_{{\scriptscriptstyle m\times n}}=\left[t_{{\scriptscriptstyle j}}^{{\scriptscriptstyle i}}\right]_{{\scriptscriptstyle m\times n}}=\left[t^{{\scriptscriptstyle i}}{}_{{\scriptscriptstyle j}}\right]_{{\scriptscriptstyle m\times n}},\begin{cases} w^{{\scriptscriptstyle i}}=t_{{\scriptscriptstyle j}}^{{\scriptscriptstyle i}}v^{{\scriptscriptstyle j}}=t^{{\scriptscriptstyle i}}{}_{{\scriptscriptstyle j}}v^{{\scriptscriptstyle j}}\\ T\left(\boldsymbol{v}_{{\scriptscriptstyle j}}\right)=t_{{\scriptscriptstyle j}}^{{\scriptscriptstyle i}}\boldsymbol{w}_{{\scriptscriptstyle i}}=t_{{\scriptscriptstyle j}}{}^{{\scriptscriptstyle i}}\boldsymbol{w}_{{\scriptscriptstyle i}} \end{cases}$$

---

$$T=\left[t^{{\scriptscriptstyle i}}{}_{{\scriptscriptstyle j}}\right]_{{\scriptscriptstyle m\times n}}=t^{{\scriptscriptstyle i}}{}_{{\scriptscriptstyle j}}\text{ is the matrix representation of the linear transformation }T\left(\cdot\right):\mathcal{V}\rightarrow\mathcal{W}$$

---

Fig. 24.1: coordinate under linear transformation

55.2.3 change of basis

https://www.youtube.com/watch?v=WAtLPk55ljM&list=PLP-JUp2VR1LsFtHT-i_vZ3oNFIAc3t_Ju&index=22

$$\boldsymbol{v}=B\left[\boldsymbol{v}\right]_{{\scriptscriptstyle B}}=B^{\prime}\left[\boldsymbol{v}\right]_{{\scriptscriptstyle B^{\prime}}}$$

---

$$\begin{aligned} B\left[\boldsymbol{v}\right]_{{\scriptscriptstyle B}}= & B^{\prime}\left[\boldsymbol{v}\right]_{{\scriptscriptstyle B^{\prime}}}\\ \left[\boldsymbol{v}\right]_{{\scriptscriptstyle B}}=I\left[\boldsymbol{v}\right]_{{\scriptscriptstyle B}}=B^{-1}B\left[\boldsymbol{v}\right]_{{\scriptscriptstyle B}}= & B^{-1}B^{\prime}\left[\boldsymbol{v}\right]_{{\scriptscriptstyle B^{\prime}}}\\ \left[\boldsymbol{v}\right]_{{\scriptscriptstyle B}}= & B^{-1}B^{\prime}\left[\boldsymbol{v}\right]_{{\scriptscriptstyle B^{\prime}}}\\ B^{\prime}\left[\boldsymbol{v}\right]_{{\scriptscriptstyle B^{\prime}}}= & B\left[\boldsymbol{v}\right]_{{\scriptscriptstyle B}}\\ \left[\boldsymbol{v}\right]_{{\scriptscriptstyle B^{\prime}}}=I\left[\boldsymbol{v}\right]_{{\scriptscriptstyle B^{\prime}}}=B^{\prime-1}B^{\prime}\left[\boldsymbol{v}\right]_{{\scriptscriptstyle B^{\prime}}}= & B^{\prime-1}B\left[\boldsymbol{v}\right]_{{\scriptscriptstyle B}}\\ \left[\boldsymbol{v}\right]_{{\scriptscriptstyle B^{\prime}}}= & B^{\prime-1}B\left[\boldsymbol{v}\right]_{{\scriptscriptstyle B}} \end{aligned}$$

---

$$\begin{aligned} \boldsymbol{v}= & v^{{\scriptscriptstyle 1}}\boldsymbol{v}_{{\scriptscriptstyle 1}}+\cdots+v^{{\scriptscriptstyle n}}\boldsymbol{v}_{{\scriptscriptstyle n}}=v^{{\scriptscriptstyle j}}\boldsymbol{v}_{{\scriptscriptstyle j}}=\sum_{j=1}^{n}v^{{\scriptscriptstyle j}}\boldsymbol{v}_{{\scriptscriptstyle j}}=v^{{\scriptscriptstyle 1}}\begin{bmatrix}|\\ \boldsymbol{v}_{{\scriptscriptstyle 1}}\\ | \end{bmatrix}+\cdots+v^{{\scriptscriptstyle n}}\begin{bmatrix}|\\ \boldsymbol{v}_{{\scriptscriptstyle n}}\\ | \end{bmatrix}=\begin{bmatrix}| & & |\\ \boldsymbol{v}_{{\scriptscriptstyle 1}} & \cdots & \boldsymbol{v}_{{\scriptscriptstyle n}}\\ | & & | \end{bmatrix}\begin{bmatrix}v^{{\scriptscriptstyle 1}}\\ \vdots\\ v^{{\scriptscriptstyle n}} \end{bmatrix}=V\left[\boldsymbol{v}\right]_{{\scriptscriptstyle V}}\\ = & v^{\prime{\scriptscriptstyle 1}}\boldsymbol{v}_{{\scriptscriptstyle 1}}^{\prime}+\cdots+v^{\prime{\scriptscriptstyle n}}\boldsymbol{v}_{{\scriptscriptstyle n}}^{\prime}=v^{\prime{\scriptscriptstyle j}}\boldsymbol{v}_{{\scriptscriptstyle j}}^{\prime}=\sum_{j=1}^{n}v^{\prime{\scriptscriptstyle j}}\boldsymbol{v}_{{\scriptscriptstyle j}}^{\prime}=v^{\prime{\scriptscriptstyle 1}}\begin{bmatrix}|\\ \boldsymbol{v}_{{\scriptscriptstyle 1}}^{\prime}\\ | \end{bmatrix}+\cdots+v^{\prime{\scriptscriptstyle n}}\begin{bmatrix}|\\ \boldsymbol{v}_{{\scriptscriptstyle n}}^{\prime}\\ | \end{bmatrix}=\begin{bmatrix}| & & |\\ \boldsymbol{v}_{{\scriptscriptstyle 1}}^{\prime} & \cdots & \boldsymbol{v}_{{\scriptscriptstyle n}}^{\prime}\\ | & & | \end{bmatrix}\begin{bmatrix}v^{\prime{\scriptscriptstyle 1}}\\ \vdots\\ v^{\prime{\scriptscriptstyle n}} \end{bmatrix}=V^{\prime}\left[\boldsymbol{v}\right]_{{\scriptscriptstyle V^{\prime}}}\\ \boldsymbol{v}= & V\left[\boldsymbol{v}\right]_{{\scriptscriptstyle V}}=V^{\prime}\left[\boldsymbol{v}\right]_{{\scriptscriptstyle V^{\prime}}} \end{aligned}$$

$$\begin{aligned} \boldsymbol{w}= & w^{{\scriptscriptstyle 1}}\boldsymbol{w}_{{\scriptscriptstyle 1}}+\cdots+w^{{\scriptscriptstyle m}}\boldsymbol{w}_{{\scriptscriptstyle m}}=w^{{\scriptscriptstyle j}}\boldsymbol{w}_{{\scriptscriptstyle j}}=\sum_{j=1}^{m}w^{{\scriptscriptstyle j}}\boldsymbol{w}_{{\scriptscriptstyle j}}=w^{{\scriptscriptstyle 1}}\begin{bmatrix}|\\ \boldsymbol{w}_{{\scriptscriptstyle 1}}\\ | \end{bmatrix}+\cdots+w^{{\scriptscriptstyle m}}\begin{bmatrix}|\\ \boldsymbol{w}_{{\scriptscriptstyle m}}\\ | \end{bmatrix}=\begin{bmatrix}| & & |\\ \boldsymbol{w}_{{\scriptscriptstyle 1}} & \cdots & \boldsymbol{w}_{{\scriptscriptstyle m}}\\ | & & | \end{bmatrix}\begin{bmatrix}w^{{\scriptscriptstyle 1}}\\ \vdots\\ w^{{\scriptscriptstyle m}} \end{bmatrix}=W\left[\boldsymbol{w}\right]_{{\scriptscriptstyle W}}\\ = & w^{\prime{\scriptscriptstyle 1}}\boldsymbol{w}_{{\scriptscriptstyle 1}}^{\prime}+\cdots+w^{\prime{\scriptscriptstyle m}}\boldsymbol{w}_{{\scriptscriptstyle m}}^{\prime}=w^{\prime{\scriptscriptstyle j}}\boldsymbol{w}_{{\scriptscriptstyle j}}^{\prime}=\sum_{j=1}^{m}w^{\prime{\scriptscriptstyle j}}\boldsymbol{w}_{{\scriptscriptstyle j}}^{\prime}=w^{\prime{\scriptscriptstyle 1}}\begin{bmatrix}|\\ \boldsymbol{w}_{{\scriptscriptstyle 1}}^{\prime}\\ | \end{bmatrix}+\cdots+w^{\prime{\scriptscriptstyle m}}\begin{bmatrix}|\\ \boldsymbol{w}_{{\scriptscriptstyle m}}^{\prime}\\ | \end{bmatrix}=\begin{bmatrix}| & & |\\ \boldsymbol{w}_{{\scriptscriptstyle 1}}^{\prime} & \cdots & \boldsymbol{w}_{{\scriptscriptstyle m}}^{\prime}\\ | & & | \end{bmatrix}\begin{bmatrix}w^{\prime{\scriptscriptstyle 1}}\\ \vdots\\ w^{\prime{\scriptscriptstyle m}} \end{bmatrix}=W^{\prime}\left[\boldsymbol{w}\right]_{{\scriptscriptstyle W^{\prime}}}\\ \boldsymbol{w}= & W\left[\boldsymbol{w}\right]_{{\scriptscriptstyle W}}=W^{\prime}\left[\boldsymbol{w}\right]_{{\scriptscriptstyle W^{\prime}}} \end{aligned}$$

$$\begin{aligned} \boldsymbol{v}_{{\scriptscriptstyle 1}}= & v_{{\scriptscriptstyle 1}}^{\prime}{}^{{\scriptscriptstyle 1}}\boldsymbol{v}_{{\scriptscriptstyle 1}}^{\prime}+\cdots+v_{{\scriptscriptstyle 1}}^{\prime}{}^{{\scriptscriptstyle n}}\boldsymbol{v}_{{\scriptscriptstyle n}}^{\prime}=v_{{\scriptscriptstyle 1}}^{\prime}{}^{{\scriptscriptstyle 1}}\begin{bmatrix}|\\ \boldsymbol{v}_{{\scriptscriptstyle 1}}^{\prime}\\ | \end{bmatrix}+\cdots+v_{{\scriptscriptstyle 1}}^{\prime}{}^{{\scriptscriptstyle n}}\begin{bmatrix}|\\ \boldsymbol{v}_{{\scriptscriptstyle n}}^{\prime}\\ | \end{bmatrix}=\begin{bmatrix}| & & |\\ \boldsymbol{v}_{{\scriptscriptstyle 1}}^{\prime} & \cdots & \boldsymbol{v}_{{\scriptscriptstyle n}}^{\prime}\\ | & & | \end{bmatrix}\begin{bmatrix}v_{{\scriptscriptstyle 1}}^{\prime}{}^{{\scriptscriptstyle 1}}\\ \vdots\\ v_{{\scriptscriptstyle 1}}^{\prime}{}^{{\scriptscriptstyle n}} \end{bmatrix}=V^{\prime}\left[\boldsymbol{v}_{{\scriptscriptstyle 1}}\right]_{{\scriptscriptstyle V^{\prime}}}\\ \vdots\\ \boldsymbol{v}_{{\scriptscriptstyle n}}= & v_{{\scriptscriptstyle n}}^{\prime}{}^{{\scriptscriptstyle 1}}\boldsymbol{v}_{{\scriptscriptstyle 1}}^{\prime}+\cdots+v_{{\scriptscriptstyle n}}^{\prime}{}^{{\scriptscriptstyle n}}\boldsymbol{v}_{{\scriptscriptstyle n}}^{\prime}=v_{{\scriptscriptstyle n}}^{\prime}{}^{{\scriptscriptstyle 1}}\begin{bmatrix}|\\ \boldsymbol{v}_{{\scriptscriptstyle 1}}^{\prime}\\ | \end{bmatrix}+\cdots+v_{{\scriptscriptstyle n}}^{\prime}{}^{{\scriptscriptstyle n}}\begin{bmatrix}|\\ \boldsymbol{v}_{{\scriptscriptstyle n}}^{\prime}\\ | \end{bmatrix}=\begin{bmatrix}| & & |\\ \boldsymbol{v}_{{\scriptscriptstyle 1}}^{\prime} & \cdots & \boldsymbol{v}_{{\scriptscriptstyle n}}^{\prime}\\ | & & | \end{bmatrix}\begin{bmatrix}v_{{\scriptscriptstyle 1}}^{\prime}{}^{{\scriptscriptstyle n}}\\ \vdots\\ v_{{\scriptscriptstyle n}}^{\prime}{}^{{\scriptscriptstyle n}} \end{bmatrix}=V^{\prime}\left[\boldsymbol{v}_{{\scriptscriptstyle n}}\right]_{{\scriptscriptstyle V^{\prime}}}\\ \Downarrow\\ \begin{bmatrix}| & & |\\ \boldsymbol{v}_{{\scriptscriptstyle 1}} & \cdots & \boldsymbol{v}_{{\scriptscriptstyle n}}\\ | & & | \end{bmatrix}= & \begin{array}{c} v_{{\scriptscriptstyle 1}}^{\prime}{}^{{\scriptscriptstyle 1}}\\ \vdots\\ v_{{\scriptscriptstyle n}}^{\prime}{}^{{\scriptscriptstyle 1}} \end{array}\begin{bmatrix}|\\ \boldsymbol{v}_{{\scriptscriptstyle 1}}^{\prime}\\ | \end{bmatrix}\begin{array}{c} +\\ \\ + \end{array}\begin{array}{c} \cdots\\ \curvearrowright\\ \cdots \end{array}\begin{array}{c} +\\ \\ + \end{array}\begin{array}{c} v_{{\scriptscriptstyle 1}}^{\prime}{}^{{\scriptscriptstyle n}}\\ \vdots\\ v_{{\scriptscriptstyle n}}^{\prime}{}^{{\scriptscriptstyle n}} \end{array}\begin{bmatrix}|\\ \boldsymbol{v}_{{\scriptscriptstyle n}}^{\prime}\\ | \end{bmatrix}\\ = & \begin{bmatrix}| & & |\\ \boldsymbol{v}_{{\scriptscriptstyle 1}}^{\prime} & \cdots & \boldsymbol{v}_{{\scriptscriptstyle n}}^{\prime}\\ | & & | \end{bmatrix}\begin{bmatrix}v_{{\scriptscriptstyle 1}}^{\prime}{}^{{\scriptscriptstyle 1}} & \cdots & v_{{\scriptscriptstyle n}}^{\prime}{}^{{\scriptscriptstyle 1}}\\ \vdots & \ddots & \vdots\\ v_{{\scriptscriptstyle 1}}^{\prime}{}^{{\scriptscriptstyle n}} & \cdots & v_{{\scriptscriptstyle n}}^{\prime}{}^{{\scriptscriptstyle n}} \end{bmatrix}=\begin{bmatrix}| & & |\\ \boldsymbol{v}_{{\scriptscriptstyle 1}}^{\prime} & \cdots & \boldsymbol{v}_{{\scriptscriptstyle n}}^{\prime}\\ | & & | \end{bmatrix}\begin{bmatrix}| & & |\\ \left[\boldsymbol{v}_{{\scriptscriptstyle 1}}\right]_{{\scriptscriptstyle V^{\prime}}} & \cdots & \left[\boldsymbol{v}_{{\scriptscriptstyle n}}\right]_{{\scriptscriptstyle V^{\prime}}}\\ | & & | \end{bmatrix}=V^{\prime}\left[V\right]_{{\scriptscriptstyle V^{\prime}}}\\ V= & V^{\prime}\left[V\right]_{{\scriptscriptstyle V^{\prime}}}\overset{\text{if }V^{\prime}\text{ invertible}}{\Longleftrightarrow}\left[V\right]_{{\scriptscriptstyle V^{\prime}}}=V^{\prime{\scriptscriptstyle -1}}V \end{aligned}$$

---

$$\left[V\right]_{{\scriptscriptstyle V^{\prime}}}=V^{\prime{\scriptscriptstyle -1}}V:\left[V^{\prime}\middle|V\right]\overset{\text{Gauss-Jordan delimination}}{\longrightarrow}\left[I\middle|V^{\prime{\scriptscriptstyle -1}}V\right]=\left[I\middle|\left[V\right]_{{\scriptscriptstyle V^{\prime}}}\right]$$

$$\left[V^{\prime}\right]_{{\scriptscriptstyle V}}=V^{{\scriptscriptstyle -1}}V^{\prime}:\left[V\middle|V^{\prime}\right]\overset{\text{Gauss-Jordan delimination}}{\longrightarrow}\left[I\middle|V^{{\scriptscriptstyle -1}}V^{\prime}\right]=\left[I\middle|\left[V^{\prime}\right]_{{\scriptscriptstyle V}}\right]$$

---

$$\begin{cases} \left[V\right]_{{\scriptscriptstyle V^{\prime}}}=V^{\prime{\scriptscriptstyle -1}}V: & \left[V^{\prime}\middle|V\right]\overset{\text{Gauss-Jordan delimination}}{\longrightarrow}\left[I\middle|V^{\prime{\scriptscriptstyle -1}}V\right]=\left[I\middle|\left[V\right]_{{\scriptscriptstyle V^{\prime}}}\right]\\ \left[V^{\prime}\right]_{{\scriptscriptstyle V}}=V^{{\scriptscriptstyle -1}}V^{\prime}: & \left[V\middle|V^{\prime}\right]\overset{\text{Gauss-Jordan delimination}}{\longrightarrow}\left[I\middle|V^{{\scriptscriptstyle -1}}V^{\prime}\right]=\left[I\middle|\left[V^{\prime}\right]_{{\scriptscriptstyle V}}\right] \end{cases}$$

---

$$\begin{aligned} \boldsymbol{v}= & V\left[\boldsymbol{v}\right]_{{\scriptscriptstyle V}}=V^{\prime}\left[\boldsymbol{v}\right]_{{\scriptscriptstyle V^{\prime}}}\\ = & V\left[\boldsymbol{v}\right]_{{\scriptscriptstyle V}},\wedge V=V^{\prime}\left[V\right]_{{\scriptscriptstyle V^{\prime}}}\\ = & V^{\prime}\left[V\right]_{{\scriptscriptstyle V^{\prime}}}\left[\boldsymbol{v}\right]_{{\scriptscriptstyle V}}\\ V^{\prime}\left[\boldsymbol{v}\right]_{{\scriptscriptstyle V^{\prime}}}= & V^{\prime}\left[V\right]_{{\scriptscriptstyle V^{\prime}}}\left[\boldsymbol{v}\right]_{{\scriptscriptstyle V}}\\ \left[\boldsymbol{v}\right]_{{\scriptscriptstyle V^{\prime}}}= & \left[V\right]_{{\scriptscriptstyle V^{\prime}}}\left[\boldsymbol{v}\right]_{{\scriptscriptstyle V}} \end{aligned}$$

---

$$\left[\boldsymbol{v}\right]_{{\scriptscriptstyle V^{\prime}}}=\left[V\right]_{{\scriptscriptstyle V^{\prime}}}\left[\boldsymbol{v}\right]_{{\scriptscriptstyle V}}$$

---

symmetrically,

$$\left[\boldsymbol{v}\right]_{{\scriptscriptstyle V}}=\left[V^{\prime}\right]_{{\scriptscriptstyle V}}\left[\boldsymbol{v}\right]_{{\scriptscriptstyle V^{\prime}}}$$

---

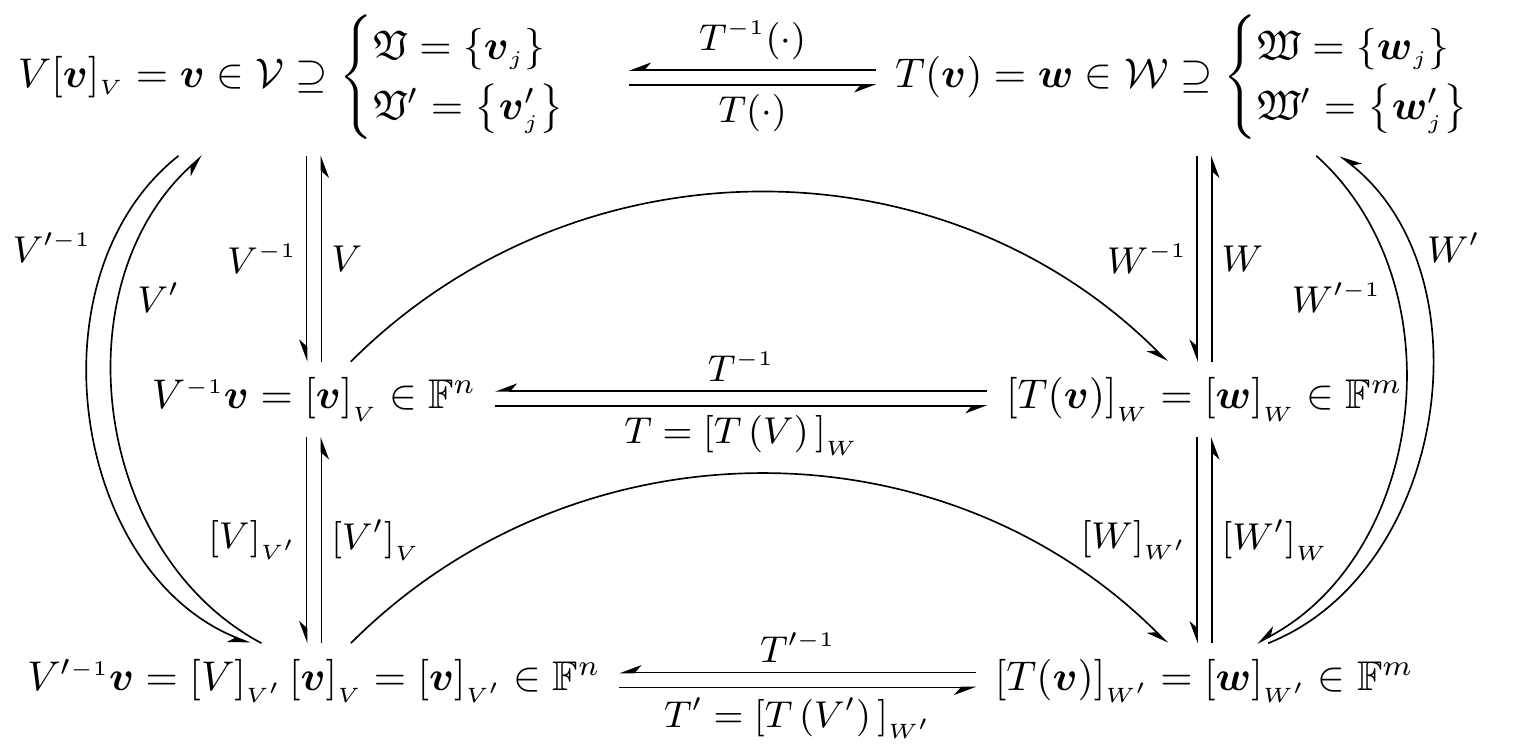
Fig. 30.2: change of coordinate basis under linear transformation

$\left[\boldsymbol{v}\right]_{{\scriptscriptstyle V}}\rightleftharpoons\left[\boldsymbol{v}\right]_{{\scriptscriptstyle V^{\prime}}}$

$$\begin{aligned} \left[\boldsymbol{v}\right]_{{\scriptscriptstyle V}}\overset{\left[V\right]_{{\scriptscriptstyle V^{\prime}}}}{\rightarrow}\left[\boldsymbol{v}\right]_{{\scriptscriptstyle V^{\prime}}}= & \left[V\right]_{{\scriptscriptstyle V^{\prime}}}\left[\boldsymbol{v}\right]_{{\scriptscriptstyle V}}\\ \left[\boldsymbol{v}\right]_{{\scriptscriptstyle V}}\overset{\left[V^{\prime}\right]_{{\scriptscriptstyle V}}}{\leftarrow}\left[\boldsymbol{v}\right]_{{\scriptscriptstyle V^{\prime}}}= & \left[V^{\prime}\right]_{{\scriptscriptstyle V}}^{{\scriptscriptstyle -1}}\left[\boldsymbol{v}\right]_{{\scriptscriptstyle V}}\\ \Downarrow\\ \left[V\right]_{{\scriptscriptstyle V^{\prime}}}= & \left[V^{\prime}\right]_{{\scriptscriptstyle V}}^{{\scriptscriptstyle -1}}\Leftrightarrow\left[V^{\prime}\right]_{{\scriptscriptstyle V}}=\left[V\right]_{{\scriptscriptstyle V^{\prime}}}^{{\scriptscriptstyle -1}} \end{aligned}$$

$\left[\boldsymbol{v}\right]_{{\scriptscriptstyle V}}\rightarrow\left[\boldsymbol{v}\right]_{{\scriptscriptstyle V^{\prime}}}$

$$\begin{aligned} \left[\boldsymbol{v}\right]_{{\scriptscriptstyle V}}\overset{\left[V\right]_{{\scriptscriptstyle V^{\prime}}}}{\rightarrow}\left[\boldsymbol{v}\right]_{{\scriptscriptstyle V^{\prime}}}= & \left[V\right]_{{\scriptscriptstyle V^{\prime}}}\left[\boldsymbol{v}\right]_{{\scriptscriptstyle V}}\\ \left[\boldsymbol{v}\right]_{{\scriptscriptstyle V}}\overset{V}{\rightarrow}\boldsymbol{v}\overset{V^{\prime{\scriptscriptstyle -1}}}{\rightarrow}\left[\boldsymbol{v}\right]_{{\scriptscriptstyle V^{\prime}}}= & V^{\prime{\scriptscriptstyle -1}}V\left[\boldsymbol{v}\right]_{{\scriptscriptstyle V}}\\ \Downarrow\\ \left[V\right]_{{\scriptscriptstyle V^{\prime}}}= & V^{\prime{\scriptscriptstyle -1}}V\overset{\left[V^{\prime}\right]_{{\scriptscriptstyle V}}=\left[V\right]_{{\scriptscriptstyle V^{\prime}}}^{{\scriptscriptstyle -1}}}{\Longleftrightarrow}\left[V^{\prime}\right]_{{\scriptscriptstyle V}}=\left(V^{\prime{\scriptscriptstyle -1}}V\right)^{{\scriptscriptstyle -1}}=V^{{\scriptscriptstyle -1}}V^{\prime} \end{aligned}$$

$\left[\boldsymbol{v}\right]_{{\scriptscriptstyle V^{\prime}}}\rightarrow\left[\boldsymbol{w}\right]_{{\scriptscriptstyle W^{\prime}}}$

$$\begin{aligned} \left[\boldsymbol{v}\right]_{{\scriptscriptstyle V^{\prime}}}\overset{T^{\prime}=\left[T\left(V^{\prime}\right)\right]_{{\scriptscriptstyle W^{\prime}}}}{\rightarrow}\left[\boldsymbol{w}\right]_{{\scriptscriptstyle W^{\prime}}}= & \left[T\left(V^{\prime}\right)\right]_{{\scriptscriptstyle W^{\prime}}}\left[\boldsymbol{v}\right]_{{\scriptscriptstyle V^{\prime}}}\\ \left[\boldsymbol{v}\right]_{{\scriptscriptstyle V^{\prime}}}\overset{\left[V^{\prime}\right]_{{\scriptscriptstyle V}}}{\rightarrow}\left[\boldsymbol{v}\right]_{{\scriptscriptstyle V}}\overset{T=\left[T\left(V\right)\right]_{{\scriptscriptstyle W}}}{\rightarrow}\left[\boldsymbol{w}\right]_{{\scriptscriptstyle W}}\overset{\left[W\right]_{{\scriptscriptstyle W^{\prime}}}}{\rightarrow}\left[\boldsymbol{w}\right]_{{\scriptscriptstyle W^{\prime}}}= & \left[W\right]_{{\scriptscriptstyle W^{\prime}}}\left[T\left(V\right)\right]_{{\scriptscriptstyle W}}\left[V^{\prime}\right]_{{\scriptscriptstyle V}}\left[\boldsymbol{v}\right]_{{\scriptscriptstyle V^{\prime}}}\\ \Downarrow\\ \left[T\left(V^{\prime}\right)\right]_{{\scriptscriptstyle W^{\prime}}}= & \left[W\right]_{{\scriptscriptstyle W^{\prime}}}\left[T\left(V\right)\right]_{{\scriptscriptstyle W}}\left[V^{\prime}\right]_{{\scriptscriptstyle V}}\\ = & W^{\prime{\scriptscriptstyle -1}}W\left[T\left(V\right)\right]_{{\scriptscriptstyle W}}V^{{\scriptscriptstyle -1}}V^{\prime}\\ = & W^{\prime{\scriptscriptstyle -1}}WW^{{\scriptscriptstyle -1}}T\left(V\right)V^{{\scriptscriptstyle -1}}V^{\prime}\\ = & W^{\prime{\scriptscriptstyle -1}}IT\left(V\right)V^{{\scriptscriptstyle -1}}V^{\prime}\\ = & W^{\prime{\scriptscriptstyle -1}}T\left(V\right)V^{{\scriptscriptstyle -1}}V^{\prime} \end{aligned}$$

---

$\left[T\left(V^{\prime}\right)\right]_{{\scriptscriptstyle W^{\prime}}}\rightleftharpoons\left[T\left(V\right)\right]_{{\scriptscriptstyle W}}$

$$\left[T\left(V^{\prime}\right)\right]_{{\scriptscriptstyle W^{\prime}}}=\left[W\right]_{{\scriptscriptstyle W^{\prime}}}\left[T\left(V\right)\right]_{{\scriptscriptstyle W}}\left[V^{\prime}\right]_{{\scriptscriptstyle V}}$$

---

$$\left[T\left(V^{\prime}\right)\right]_{{\scriptscriptstyle W^{\prime}}}=W^{\prime{\scriptscriptstyle -1}}T\left(V\right)V^{{\scriptscriptstyle -1}}V^{\prime}$$

---

$$\begin{aligned} W^{\prime}\left[T\left(V\right)\right]_{{\scriptscriptstyle W^{\prime}}}= & T\left(V\right)\\ \Downarrow\\ \left[T\left(V\right)\right]_{{\scriptscriptstyle W^{\prime}}}= & W^{\prime{\scriptscriptstyle -1}}T\left(V\right) \end{aligned}$$

---

$$\begin{aligned} \left[T\left(V^{\prime}\right)\right]_{{\scriptscriptstyle W^{\prime}}}= & W^{\prime{\scriptscriptstyle -1}}T\left(V\right)V^{{\scriptscriptstyle -1}}V^{\prime}\\ = & \left\{ W^{\prime{\scriptscriptstyle -1}}T\left(V\right)\right\} \left\{ V^{{\scriptscriptstyle -1}}V^{\prime}\right\} \\ = & \left\{ \left[T\left(V\right)\right]_{{\scriptscriptstyle W^{\prime}}}\right\} \left\{ V^{{\scriptscriptstyle -1}}V^{\prime}\right\} \\ = & \left[T\left(V\right)\right]_{{\scriptscriptstyle W^{\prime}}}V^{{\scriptscriptstyle -1}}V^{\prime}\\ , & \begin{cases} \left[T\left(V\right)\right]_{{\scriptscriptstyle W^{\prime}}}=W^{\prime{\scriptscriptstyle -1}}T\left(V\right) & :W^{\prime}\left[T\left(V\right)\right]_{{\scriptscriptstyle W^{\prime}}}=T\left(V\right)\\ V^{{\scriptscriptstyle -1}}V^{\prime} & :\left[V\middle|V^{\prime}\right]\overset{\text{Gauss-Jordan delimination}}{\longrightarrow}\left[I\middle|V^{{\scriptscriptstyle -1}}V^{\prime}\right] \end{cases} \end{aligned}$$

---

$T^{\prime}\rightleftharpoons T$

$$\begin{aligned} \left[T\left(V^{\prime}\right)\right]_{{\scriptscriptstyle W^{\prime}}}= & \left[W\right]_{{\scriptscriptstyle W^{\prime}}}\left[T\left(V\right)\right]_{{\scriptscriptstyle W}}\left[V^{\prime}\right]_{{\scriptscriptstyle V}}\\ T^{\prime}=\left[T\left(V^{\prime}\right)\right]_{{\scriptscriptstyle W^{\prime}}}\Updownarrow & T=\left[T\left(V\right)\right]_{{\scriptscriptstyle W}}\\ T^{\prime}= & \left[W\right]_{{\scriptscriptstyle W^{\prime}}}T\left[V^{\prime}\right]_{{\scriptscriptstyle V}}\\ = & \left[W^{\prime{\scriptscriptstyle -1}}W\right]T\left[V^{{\scriptscriptstyle -1}}V^{\prime}\right]\\ T^{\prime}= & W^{\prime{\scriptscriptstyle -1}}WTV^{{\scriptscriptstyle -1}}V^{\prime} \end{aligned}$$

---

$$T^{\prime}=W^{\prime{\scriptscriptstyle -1}}WTV^{{\scriptscriptstyle -1}}V^{\prime}$$

55.2.3.1 differential polynomial

55.2.3.1.1 Chebyshev polynomial

55.2.3.1.2 Hermite polynomial

55.2.4 singular value decomposition

https://www.youtube.com/watch?v=oPHM-ZWWvlg&list=PLP-JUp2VR1LsFtHT-i_vZ3oNFIAc3t_Ju&index=42

https://www.youtube.com/watch?v=zagHmMPZyoo&list=PLP-JUp2VR1LsFtHT-i_vZ3oNFIAc3t_Ju&index=43

55.3 Chi, Chen-Yu

https://www.youtube.com/playlist?list=PLJWAeYEa8SXBej3kuQMz8vV41VabZUILb