Chapter 24: conic section
conic section 圓錐曲線 / 圓錐截痕
https://en.wikipedia.org/wiki/Conic_section
https://tex.stackexchange.com/questions/222882/drawing-minimal-xy-axis
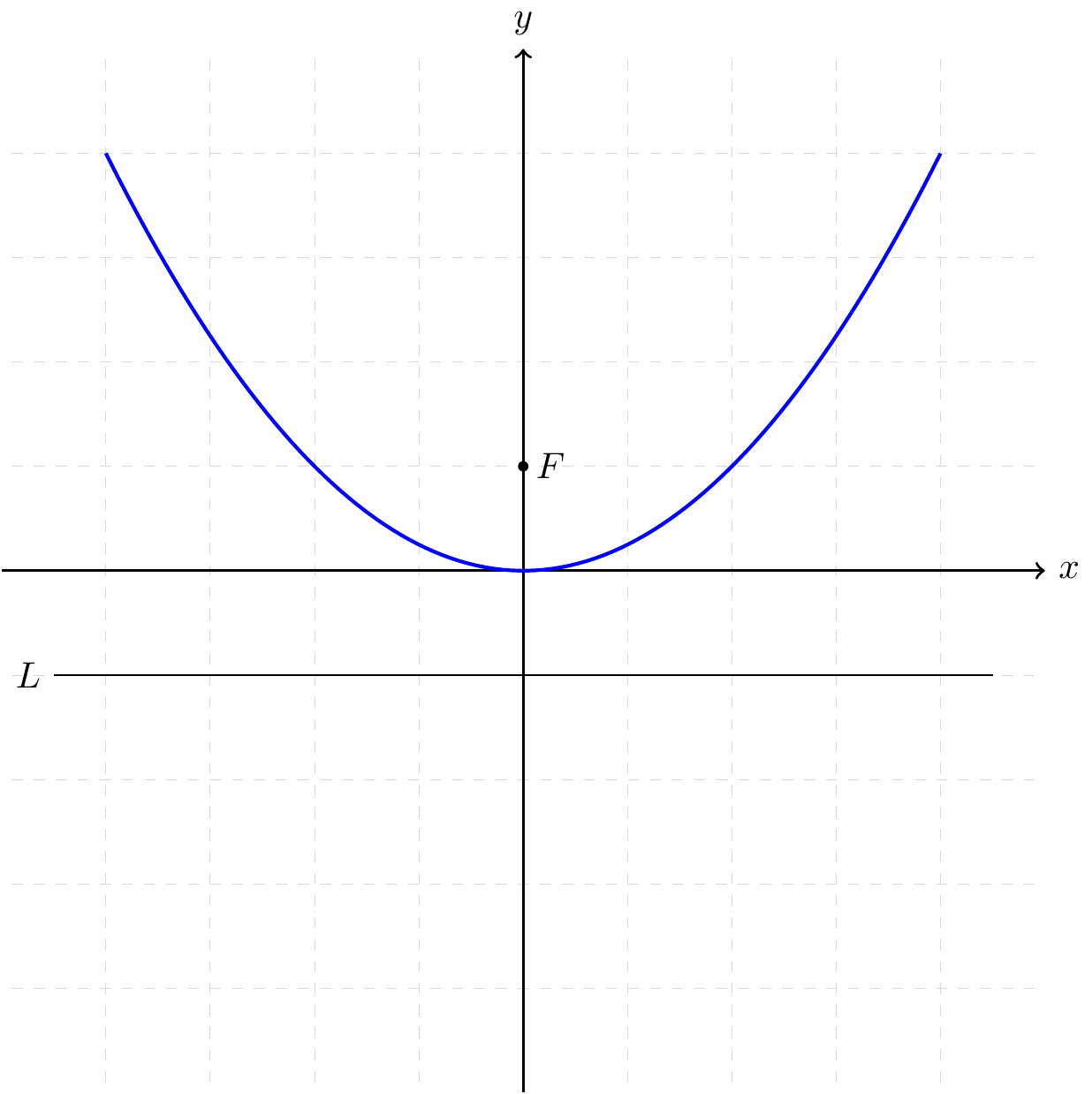
Fig. 24.1: parabola defined by focus, directrix, eccentricity
24.1 Cartesian coordinate: focus, directrix, eccentricity
focus, directrix, eccentricity 焦點, 準線, 離心率
\[ \begin{cases} F=\left(0,y_{{\scriptscriptstyle F}}\right) & F:\text{focus}\\ L=y-y_{{\scriptscriptstyle L}}=0 & L:\text{directrix}\\ \epsilon=\dfrac{\overline{PF}}{d\left(P,L\right)}=\dfrac{\left\Vert \left(x,y\right)-\left(0,y_{{\scriptscriptstyle F}}\right)\right\Vert }{\left\Vert y-y_{{\scriptscriptstyle L}}\right\Vert } & \begin{cases} P=\left(x,y\right)\\ \epsilon:\text{eccentricity} \end{cases} \end{cases} \]
\[ \require{color} \begin{align} 0\le\epsilon=\dfrac{\overline{PF}}{d\left(P,L\right)}=\dfrac{\overline{PF}}{\overline{PP^{\prime}}}= & \dfrac{\left\Vert \left(x,y\right)-\left(0,y_{{\scriptscriptstyle F}}\right)\right\Vert }{\left\Vert \left(x,y\right)-\left(x,y_{{\scriptscriptstyle L}}\right)\right\Vert }=\dfrac{\left\Vert \left(x,y-y_{{\scriptscriptstyle F}}\right)\right\Vert }{\left\Vert \left(0,y-y_{{\scriptscriptstyle L}}\right)\right\Vert } = \dfrac{\sqrt{x^{2}+\left(y-y_{{\scriptscriptstyle F}}\right)^{2}}}{\sqrt{\left(y-y_{{\scriptscriptstyle L}}\right)^{2}}} \tag{24.1}\\ \epsilon^{2}= & \dfrac{x^{2}+\left(y-y_{{\scriptscriptstyle F}}\right)^{2}}{\left(y-y_{{\scriptscriptstyle L}}\right)^{2}}=\dfrac{x^{2}+y^{2}-2y_{{\scriptscriptstyle F}}y+y_{{\scriptscriptstyle F}}^{2}}{y^{2}-2y_{{\scriptscriptstyle L}}y+y_{{\scriptscriptstyle L}}^{2}}\\ 0= & x^{2}+\left(1-\epsilon^{2}\right)y^{2}-2\left(y_{{\scriptscriptstyle F}}-\epsilon^{2}y_{{\scriptscriptstyle L}}\right)y+\left(y_{{\scriptscriptstyle F}}^{2}-\epsilon^{2}y_{{\scriptscriptstyle L}}^{2}\right)\\ \overset{\epsilon\ne1}{=} & x^{2}+\left(1-\epsilon^{2}\right)\left[y^{2}-\dfrac{2\left(y_{{\scriptscriptstyle F}}-\epsilon^{2}y_{{\scriptscriptstyle L}}\right)}{1-\epsilon^{2}}y+\dfrac{y_{{\scriptscriptstyle F}}^{2}-\epsilon^{2}y_{{\scriptscriptstyle L}}^{2}}{1-\epsilon^{2}}\right]\\ = & x^{2}+\left(1-\epsilon^{2}\right)\\ & \left[y^{2}-\dfrac{2\left(y_{{\scriptscriptstyle F}}-\epsilon^{2}y_{{\scriptscriptstyle L}}\right)}{1-\epsilon^{2}}y+\left(\dfrac{y_{{\scriptscriptstyle F}}-\epsilon^{2}y_{{\scriptscriptstyle L}}}{1-\epsilon^{2}}\right)^{2}-\left(\dfrac{y_{{\scriptscriptstyle F}}-\epsilon^{2}y_{{\scriptscriptstyle L}}}{1-\epsilon^{2}}\right)^{2}+\dfrac{y_{{\scriptscriptstyle F}}^{2}-\epsilon^{2}y_{{\scriptscriptstyle L}}^{2}}{1-\epsilon^{2}}\right]\\ = & x^{2}+\left(1-\epsilon^{2}\right)\left[\left(y-\dfrac{y_{{\scriptscriptstyle F}}-\epsilon^{2}y_{{\scriptscriptstyle L}}}{1-\epsilon^{2}}\right)^{2}+\dfrac{\left(y_{{\scriptscriptstyle F}}^{2}-\epsilon^{2}y_{{\scriptscriptstyle L}}^{2}\right)\left(1-\epsilon^{2}\right)-\left(y_{{\scriptscriptstyle F}}-\epsilon^{2}y_{{\scriptscriptstyle L}}\right)^{2}}{\left(1-\epsilon^{2}\right)^{2}}\right]\\ = & x^{2}+\left(1-\epsilon^{2}\right)\left(y-\dfrac{y_{{\scriptscriptstyle F}}-\epsilon^{2}y_{{\scriptscriptstyle L}}}{1-\epsilon^{2}}\right)^{2}+\dfrac{\colorbox{#FFFF66}{$\left(y_{{\scriptscriptstyle F}}^{2}-\epsilon^{2}y_{{\scriptscriptstyle L}}^{2}\right)\left(1-\epsilon^{2}\right)-\left(y_{{\scriptscriptstyle F}}-\epsilon^{2}y_{{\scriptscriptstyle L}}\right)^{2}$}}{1-\epsilon^{2}} \end{align} \]
\[ \require{color} \begin{aligned} & \colorbox{#FFFF66}{$\left(y_{{\scriptscriptstyle F}}^{2}-\epsilon^{2}y_{{\scriptscriptstyle L}}^{2}\right)\left(1-\epsilon^{2}\right)-\left(y_{{\scriptscriptstyle F}}-\epsilon^{2}y_{{\scriptscriptstyle L}}\right)^{2}$}\\ = & \left(1-\epsilon^{2}\right)y_{{\scriptscriptstyle F}}^{2}-\left(\epsilon^{2}-\epsilon^{4}\right)y_{{\scriptscriptstyle L}}^{2}-y_{{\scriptscriptstyle F}}^{2}+2\epsilon^{2}y_{{\scriptscriptstyle F}}y_{{\scriptscriptstyle L}}-\epsilon^{4}y_{{\scriptscriptstyle L}}^{2}\\ = & \left(1-\epsilon^{2}\right)y_{{\scriptscriptstyle F}}^{2}-\left(\epsilon^{2}-\epsilon^{4}\right)y_{{\scriptscriptstyle L}}^{2}-y_{{\scriptscriptstyle F}}^{2}+2\epsilon^{2}y_{{\scriptscriptstyle F}}y_{{\scriptscriptstyle L}}-\epsilon^{4}y_{{\scriptscriptstyle L}}^{2}\\ = & -\epsilon^{2}y_{{\scriptscriptstyle F}}^{2}-\epsilon^{2}y_{{\scriptscriptstyle L}}^{2}+2\epsilon^{2}y_{{\scriptscriptstyle F}}y_{{\scriptscriptstyle L}}=-\colorbox{#FFD1DC}{$\epsilon^{2}\left(y_{{\scriptscriptstyle F}}-y_{{\scriptscriptstyle L}}\right)^{2}$} \end{aligned} \]
\[ \begin{aligned} \dfrac{\colorbox{#FFD1DC}{$\epsilon^{2}\left(y_{{\scriptscriptstyle F}}-y_{{\scriptscriptstyle L}}\right)^{2}$}}{1-\epsilon^{2}}\overset{\epsilon\ne1}{=} & x^{2}+\left(1-\epsilon^{2}\right)\left(y-\dfrac{y_{{\scriptscriptstyle F}}-\epsilon^{2}y_{{\scriptscriptstyle L}}}{1-\epsilon^{2}}\right)^{2}\\ 1\overset{\epsilon\ne0,1}{=} & \begin{cases} \left(\dfrac{x-0}{\dfrac{\epsilon\left(y_{{\scriptscriptstyle F}}-y_{{\scriptscriptstyle L}}\right)}{\sqrt{1-\epsilon^{2}}}}\right)^{2}+\left(\dfrac{y-\dfrac{y_{{\scriptscriptstyle F}}-\epsilon^{2}y_{{\scriptscriptstyle L}}}{1-\epsilon^{2}}}{\dfrac{\epsilon\left(y_{{\scriptscriptstyle F}}-y_{{\scriptscriptstyle L}}\right)}{1-\epsilon^{2}}}\right)^{2} & 1-\epsilon^{2}>0\overset{\epsilon\ge0}{\Rightarrow}0<\epsilon<1\\ -\left(\dfrac{x-0}{\dfrac{\epsilon\left(y_{{\scriptscriptstyle F}}-y_{{\scriptscriptstyle L}}\right)}{\sqrt{\epsilon^{2}-1}}}\right)^{2}+\left(\dfrac{y-\dfrac{y_{{\scriptscriptstyle F}}-\epsilon^{2}y_{{\scriptscriptstyle L}}}{1-\epsilon^{2}}}{\dfrac{\epsilon\left(y_{{\scriptscriptstyle F}}-y_{{\scriptscriptstyle L}}\right)}{1-\epsilon^{2}}}\right)^{2} & 1-\epsilon^{2}<0\overset{\epsilon\ge0}{\Rightarrow}\epsilon>1 \end{cases} \end{aligned} \]
\(\epsilon=0\) or \(\lim\limits _{\left|y_{L}\right|\rightarrow\infty}\epsilon=0\)
\[ r=\overline{PF}=\left\Vert \left(x,y\right)-\left(0,y_{{\scriptscriptstyle F}}\right)\right\Vert =\left\Vert \left(x,y-y_{{\scriptscriptstyle F}}\right)\right\Vert =\sqrt{x^{2}+\left(y-y_{{\scriptscriptstyle F}}\right)^{2}} \]
\[ \epsilon=\dfrac{r}{d\left(P,L\right)}=\dfrac{\overline{PF}}{\overline{PP^{\prime}}}=\dfrac{\left\Vert \left(x,y\right)-\left(0,y_{{\scriptscriptstyle F}}\right)\right\Vert }{\left\Vert \left(x,y\right)-\left(x,y_{{\scriptscriptstyle L}}\right)\right\Vert }=\dfrac{\left\Vert \left(x,y-y_{{\scriptscriptstyle F}}\right)\right\Vert }{\left\Vert \left(0,y-y_{{\scriptscriptstyle L}}\right)\right\Vert }=\dfrac{\sqrt{x^{2}+\left(y-y_{{\scriptscriptstyle F}}\right)^{2}}}{\left|y-y_{{\scriptscriptstyle L}}\right|} \]
\[ \lim_{\left|y_{L}\right|\rightarrow\infty}\epsilon=\lim_{\left|y_{L}\right|\rightarrow\infty}\dfrac{r}{d\left(P,L\right)}=\lim_{\left|y_{L}\right|\rightarrow\infty}\dfrac{\sqrt{x^{2}+\left(y-y_{{\scriptscriptstyle F}}\right)^{2}}}{\left|y-y_{{\scriptscriptstyle L}}\right|}=0 \]
\(\epsilon=1\)
\[ \begin{aligned} 0= & x^{2}+\left(1-\epsilon^{2}\right)y^{2}-2\left(y_{{\scriptscriptstyle F}}-\epsilon^{2}y_{{\scriptscriptstyle L}}\right)y+\left(y_{{\scriptscriptstyle F}}^{2}-\epsilon^{2}y_{{\scriptscriptstyle L}}^{2}\right)\\ \overset{\epsilon=1}{=} & x^{2}+\left(1-1^{2}\right)y^{2}-2\left(y_{{\scriptscriptstyle F}}-1^{2}y_{{\scriptscriptstyle L}}\right)y+\left(y_{{\scriptscriptstyle F}}^{2}-1^{2}y_{{\scriptscriptstyle L}}^{2}\right)\\ = & x^{2}-2\left(y_{{\scriptscriptstyle F}}-y_{{\scriptscriptstyle L}}\right)y+\left(y_{{\scriptscriptstyle F}}^{2}-y_{{\scriptscriptstyle L}}^{2}\right)\\ = & x^{2}-2\left(y_{{\scriptscriptstyle F}}-y_{{\scriptscriptstyle L}}\right)y+\left(y_{{\scriptscriptstyle F}}+y_{{\scriptscriptstyle L}}\right)\left(y_{{\scriptscriptstyle F}}-y_{{\scriptscriptstyle L}}\right)\\ x^{2}= & 2\left(y_{{\scriptscriptstyle F}}-y_{{\scriptscriptstyle L}}\right)\left(y-\dfrac{y_{{\scriptscriptstyle F}}+y_{{\scriptscriptstyle L}}}{2}\right) \end{aligned} \]
Let one curve vertex \(P=V=\left(0,0\right)\) on the curve, and fix the directrix \(L\) or \(y_{{\scriptscriptstyle L}}\),
\(\epsilon\ne1\) \[ \begin{aligned} & 1\overset{P\left(x,y\right)=V\left(0,0\right)}{=}0+\left(\dfrac{0-\dfrac{y_{{\scriptscriptstyle F}}-\epsilon^{2}y_{{\scriptscriptstyle L}}}{1-\epsilon^{2}}}{\dfrac{\epsilon\left(y_{{\scriptscriptstyle F}}-y_{{\scriptscriptstyle L}}\right)}{1-\epsilon^{2}}}\right)^{2}\\ \Rightarrow & y_{{\scriptscriptstyle F}}-\epsilon^{2}y_{{\scriptscriptstyle L}}=\pm\epsilon\left(y_{{\scriptscriptstyle F}}-y_{{\scriptscriptstyle L}}\right)\\ \Rightarrow & \begin{cases} \left(1-\epsilon\right)y_{{\scriptscriptstyle F}}=\epsilon\left(\epsilon-1\right)y_{{\scriptscriptstyle L}} & +\\ \left(1+\epsilon\right)y_{{\scriptscriptstyle F}}=\epsilon\left(\epsilon+1\right)y_{{\scriptscriptstyle L}} & - \end{cases}\\ \Rightarrow & y_{{\scriptscriptstyle F}}=\begin{cases} -\epsilon y_{{\scriptscriptstyle L}} & +\\ \epsilon y_{{\scriptscriptstyle L}} & - \end{cases} \end{aligned} \]
\(\epsilon=1\) \[ \begin{aligned} & x^{2}=2\left(y_{{\scriptscriptstyle F}}-y_{{\scriptscriptstyle L}}\right)\left(y-\dfrac{y_{{\scriptscriptstyle F}}+y_{{\scriptscriptstyle L}}}{2}\right)\\ \overset{P\left(x,y\right)=V\left(0,0\right)}{\Rightarrow} & 0^{2}=2\left(y_{{\scriptscriptstyle F}}-y_{{\scriptscriptstyle L}}\right)\left(0-\dfrac{y_{{\scriptscriptstyle F}}+y_{{\scriptscriptstyle L}}}{2}\right)\\ \Rightarrow & 0=\left(y_{{\scriptscriptstyle F}}-y_{{\scriptscriptstyle L}}\right)\left(y_{{\scriptscriptstyle F}}+y_{{\scriptscriptstyle L}}\right)\\ \Rightarrow & y_{{\scriptscriptstyle F}}=\mp y_{{\scriptscriptstyle L}} \end{aligned} \]
or by definition of eccentricity (24.1)
\[ \begin{aligned} 0\le\epsilon=\dfrac{\overline{PF}}{d\left(P,L\right)}=\dfrac{\overline{PF}}{\overline{PP^{\prime}}}= & \dfrac{\left\Vert \left(x,y\right)-\left(0,y_{{\scriptscriptstyle F}}\right)\right\Vert }{\left\Vert \left(x,y\right)-\left(x,y_{{\scriptscriptstyle L}}\right)\right\Vert }=\dfrac{\left\Vert \left(x,y-y_{{\scriptscriptstyle F}}\right)\right\Vert }{\left\Vert \left(0,y-y_{{\scriptscriptstyle L}}\right)\right\Vert }=\dfrac{\sqrt{x^{2}+\left(y-y_{{\scriptscriptstyle F}}\right)^{2}}}{\sqrt{\left(y-y_{{\scriptscriptstyle L}}\right)^{2}}}\\ & \overset{P\left(x,y\right)=V\left(0,0\right)}{=}\dfrac{\sqrt{0^{2}+\left(0-y_{{\scriptscriptstyle F}}\right)^{2}}}{\sqrt{\left(0-y_{{\scriptscriptstyle L}}\right)^{2}}}=\sqrt{\left(\dfrac{y_{{\scriptscriptstyle F}}}{y_{{\scriptscriptstyle L}}}\right)^{2}}\\ \epsilon^{2}= & \left(\dfrac{y_{{\scriptscriptstyle F}}}{y_{{\scriptscriptstyle L}}}\right)^{2}\Rightarrow y_{{\scriptscriptstyle F}}=\mp\epsilon y_{{\scriptscriptstyle L}} \end{aligned} \]
actually,
\[ y_{{\scriptscriptstyle F}}=-\epsilon y_{{\scriptscriptstyle L}} \]
24.2 two-definition equivalence for ellipse and hyperbola
https://www.geogebra.org/calculator/zkppuxwp
Fig. 17.1: conic sections
\[ \begin{cases} P=\left(x,y\right)\\ F=\left(x_{{\scriptscriptstyle F}},y_{{\scriptscriptstyle F}}\right)=\left(\alpha,\varphi\right) & F^{\prime}=\left(x_{{\scriptscriptstyle F^{\prime}}},y_{{\scriptscriptstyle F^{\prime}}}\right)=\left(\chi,\psi\right)\\ L=A^{\prime}x+B^{\prime}y+C^{\prime}=0 \end{cases} \]
24.2.1 first definition for conic sections including ellipses and hyperbolas
distance from a point to a line[^25^]
\[ 0\le\epsilon=\dfrac{\overline{PF}}{d\left(P,L\right)}=\dfrac{\sqrt{\left(x-x_{{\scriptscriptstyle F}}\right)^{2}+\left(y-y_{{\scriptscriptstyle F}}\right)^{2}}}{\dfrac{\left|A^{\prime}x+B^{\prime}y+C^{\prime}\right|}{\sqrt{A^{\prime}{}^{2}+B^{\prime}{}^{2}}}}=\dfrac{\sqrt{\left(x-\alpha\right)^{2}+\left(y-\varphi\right)^{2}}}{\left|Ax+By+C\right|},\begin{cases} A=\dfrac{A^{\prime}}{\sqrt{A^{\prime}{}^{2}+B^{\prime}{}^{2}}}\\ B=\dfrac{B^{\prime}}{\sqrt{A^{\prime}{}^{2}+B^{\prime}{}^{2}}}\\ C=\dfrac{C^{\prime}}{\sqrt{A^{\prime}{}^{2}+B^{\prime}{}^{2}}} \end{cases} \]
\[ A^{2}+B^{2}=\left(\dfrac{A^{\prime}}{\sqrt{A^{\prime}{}^{2}+B^{\prime}{}^{2}}}\right)^{2}+\left(\dfrac{B^{\prime}}{\sqrt{A^{\prime}{}^{2}+B^{\prime}{}^{2}}}\right)^{2}=1 \]
or allowing \(\epsilon<0\) by squaring the definition
\[ \epsilon^{2}=\dfrac{\left(x-\alpha\right)^{2}+\left(y-\varphi\right)^{2}}{\left(Ax+By+C\right)^{2}}=\dfrac{\left(x-x_{{\scriptscriptstyle F}}\right)^{2}+\left(y-y_{{\scriptscriptstyle F}}\right)^{2}}{\dfrac{\left(A^{\prime}x+B^{\prime}y+C^{\prime}\right)^{2}}{A^{\prime}{}^{2}+B^{\prime}{}^{2}}} \]
\[ \left(x-\alpha\right)^{2}+\left(y-\varphi\right)^{2}=\left[\epsilon\left(Ax+By+C\right)\right]^{2} \]
24.2.2 second definition for ellipses and hyperbolas
\[ \begin{aligned} 2c=\overline{FF^{\prime}}= & \left\Vert \left(x_{{\scriptscriptstyle F}},y_{{\scriptscriptstyle F}}\right)-\left(x_{{\scriptscriptstyle F^{\prime}}},y_{{\scriptscriptstyle F^{\prime}}}\right)\right\Vert =\left\Vert \left(\alpha,\varphi\right)-\left(\chi,\psi\right)\right\Vert \\ = & \sqrt{\left(\alpha-\chi\right)^{2}+\left(\chi-\psi\right)^{2}} \end{aligned} \]
\[ \begin{aligned} D= & \begin{cases} \sqrt{\left(x-x_{{\scriptscriptstyle F}}\right)^{2}+\left(y-y_{{\scriptscriptstyle F}}\right)^{2}}+\sqrt{\left(x-x_{{\scriptscriptstyle F^{\prime}}}\right)^{2}+\left(y-y_{{\scriptscriptstyle F^{\prime}}}\right)^{2}} & \text{ellipse}\\ \sqrt{\left(x-x_{{\scriptscriptstyle F}}\right)^{2}+\left(y-y_{{\scriptscriptstyle F}}\right)^{2}}-\sqrt{\left(x-x_{{\scriptscriptstyle F^{\prime}}}\right)^{2}+\left(y-y_{{\scriptscriptstyle F^{\prime}}}\right)^{2}} & \text{hyperbola} \end{cases}\\ = & \sqrt{\left(x-x_{{\scriptscriptstyle F}}\right)^{2}+\left(y-y_{{\scriptscriptstyle F}}\right)^{2}}\pm\sqrt{\left(x-x_{{\scriptscriptstyle F^{\prime}}}\right)^{2}+\left(y-y_{{\scriptscriptstyle F^{\prime}}}\right)^{2}}\\ = & \sqrt{\left(x-\alpha\right)^{2}+\left(y-\varphi\right)^{2}}\pm\sqrt{\left(x-\chi\right)^{2}+\left(y-\psi\right)^{2}} \end{aligned} \]
\[ \begin{aligned} \left(x-\alpha\right)^{2}+\left(y-\varphi\right)^{2}= & \left(D\mp\sqrt{\left(x-\chi\right)^{2}+\left(y-\psi\right)^{2}}\right)^{2}\\ = & D^{2}\mp2D\sqrt{\left(x-\chi\right)^{2}+\left(y-\psi\right)^{2}}\\ & +\left(x-\chi\right)^{2}+\left(y-\psi\right)^{2} \end{aligned} \]
\[ \begin{aligned} D^{2}= & \left(x-\alpha\right)^{2}+\left(y-\varphi\right)^{2}+\left(x-\chi\right)^{2}+\left(y-\psi\right)^{2}\\ & \pm2\sqrt{\left[\left(x-\alpha\right)^{2}+\left(y-\varphi\right)^{2}\right]\left[\left(x-\chi\right)^{2}+\left(y-\psi\right)^{2}\right]}\\ & \left(x-\alpha\right)^{2}+\left(y-\varphi\right)^{2}+\left(x-\chi\right)^{2}+\left(y-\psi\right)^{2}-D^{2}\\ = & \mp2\sqrt{\left[\left(x-\alpha\right)^{2}+\left(y-\varphi\right)^{2}\right]\left[\left(x-\chi\right)^{2}+\left(y-\psi\right)^{2}\right]}\\ & \left[\left(x-\alpha\right)^{2}+\left(y-\varphi\right)^{2}+\left(x-\chi\right)^{2}+\left(y-\psi\right)^{2}\right]^{2}+D^{4}\\ & -2D^{2}\left[\left(x-\alpha\right)^{2}+\left(y-\varphi\right)^{2}+\left(x-\chi\right)^{2}+\left(y-\psi\right)^{2}\right]\\ = & 4\left[\left(x-\alpha\right)^{2}+\left(y-\varphi\right)^{2}\right]\left[\left(x-\chi\right)^{2}+\left(y-\psi\right)^{2}\right]\\ & \left[\left(x-\alpha\right)^{2}+\left(y-\varphi\right)^{2}\right]^{2}+\left[\left(x-\chi\right)^{2}+\left(y-\psi\right)^{2}\right]^{2}\\ & +2\left[\left(x-\alpha\right)^{2}+\left(y-\varphi\right)^{2}\right]\left[\left(x-\chi\right)^{2}+\left(y-\psi\right)^{2}\right]+D^{4}\\ & -2D^{2}\left[\left(x-\alpha\right)^{2}+\left(y-\varphi\right)^{2}+\left(x-\chi\right)^{2}+\left(y-\psi\right)^{2}\right]\\ = & 4\left[\left(x-\alpha\right)^{2}+\left(y-\varphi\right)^{2}\right]\left[\left(x-\chi\right)^{2}+\left(y-\psi\right)^{2}\right]\\ 0= & \left[\left(x-\alpha\right)^{2}+\left(y-\varphi\right)^{2}\right]^{2}+\left[\left(x-\chi\right)^{2}+\left(y-\psi\right)^{2}\right]^{2}\\ & -2\left[\left(x-\alpha\right)^{2}+\left(y-\varphi\right)^{2}\right]\left[\left(x-\chi\right)^{2}+\left(y-\psi\right)^{2}\right]+D^{4}\\ & -2D^{2}\left[\left(x-\alpha\right)^{2}+\left(y-\varphi\right)^{2}+\left(x-\chi\right)^{2}+\left(y-\psi\right)^{2}\right]\\ 0= & \left\{ \left[\left(x-\alpha\right)^{2}+\left(y-\varphi\right)^{2}\right]-\left[\left(x-\chi\right)^{2}+\left(y-\psi\right)^{2}\right]\right\} ^{2}+D^{4}\\ & -2D^{2}\left\{ \left[\left(x-\alpha\right)^{2}+\left(y-\varphi\right)^{2}\right]+\left[\left(x-\chi\right)^{2}+\left(y-\psi\right)^{2}\right]\right\} \\ 0= & \left\{ \left[\left(x-\chi\right)^{2}+\left(y-\psi\right)^{2}\right]-\left[\left(x-\alpha\right)^{2}+\left(y-\varphi\right)^{2}\right]\right\} ^{2}+D^{4}\\ & -2D^{2}\left\{ \left[\left(x-\chi\right)^{2}+\left(y-\psi\right)^{2}\right]-\left[\left(x-\alpha\right)^{2}+\left(y-\varphi\right)^{2}\right]\right\} \\ & -4D^{2}\left[\left(x-\alpha\right)^{2}+\left(y-\varphi\right)^{2}\right]\\ & \left(2D\right)^{2}\left[\left(x-\alpha\right)^{2}+\left(y-\varphi\right)^{2}\right]\\ = & \left\{ \left[\left(x-\chi\right)^{2}+\left(y-\psi\right)^{2}\right]-\left[\left(x-\alpha\right)^{2}+\left(y-\varphi\right)^{2}\right]-D^{2}\right\} ^{2}\\ = & \left\{ \left[\left(x-\chi\right)^{2}-\left(x-\alpha\right)^{2}\right]+\left[\left(y-\psi\right)^{2}-\left(y-\varphi\right)^{2}\right]-D^{2}\right\} ^{2}\\ = & \left\{ \left(2x-\chi-\alpha\right)\left(\alpha-\chi\right)+\left(2y-\psi-\varphi\right)\left(\varphi-\psi\right)-D^{2}\right\} ^{2}\\ = & \left\{ 2\left(\alpha-\chi\right)x-\left(\alpha^{2}-\chi^{2}\right)+2\left(\varphi-\psi\right)y-\left(\varphi^{2}-\psi^{2}\right)-D^{2}\right\} ^{2}\\ = & \left\{ 2\left(\alpha-\chi\right)x+2\left(\varphi-\psi\right)y-\left[\left(\alpha^{2}-\chi^{2}\right)+\left(\varphi^{2}-\psi^{2}\right)+D^{2}\right]\right\} ^{2}\\ D\ne0\\ & \left(x-\alpha\right)^{2}+\left(y-\varphi\right)^{2}\\ = & \left[\dfrac{\alpha-\chi}{D}x+\dfrac{\varphi-\psi}{D}y-\left(\dfrac{\alpha^{2}-\chi^{2}}{2D}+\dfrac{\varphi^{2}-\psi^{2}}{2D}+\dfrac{D}{2}\right)\right]^{2} \end{aligned} \]
\[ \begin{cases} \left(x-\alpha\right)^{2}+\left(y-\varphi\right)^{2}=\left[\epsilon\left(Ax+By+C\right)\right]^{2}\\ \left(x-\alpha\right)^{2}+\left(y-\varphi\right)^{2}=\left[\dfrac{\alpha-\chi}{D}x+\dfrac{\varphi-\psi}{D}y-\left(\dfrac{\alpha^{2}-\chi^{2}}{2D}+\dfrac{\varphi^{2}-\psi^{2}}{2D}+\dfrac{D}{2}\right)\right]^{2} \end{cases} \]
\[ \left(A,B,C\right)\rightleftarrows\left(\chi,\psi,D\right) \]
\[ \begin{cases} \epsilon A=\pm\dfrac{\alpha-\chi}{D} & \chi\pm\epsilon AD=\alpha\\ \epsilon B=\pm\dfrac{\varphi-\psi}{D} & \psi\pm\epsilon BD=\varphi\\ \epsilon C=\mp\left(\dfrac{\alpha^{2}-\chi^{2}}{2D}+\dfrac{\varphi^{2}-\psi^{2}}{2D}+\dfrac{D}{2}\right) \end{cases} \]
\[ \begin{aligned} 2\epsilon C= & \mp\left(\dfrac{\alpha-\chi}{D}\left(\alpha+\chi\right)+\dfrac{\varphi-\psi}{D}\left(\varphi+\psi\right)+D\right)\\ = & \mp\left(\pm\epsilon A\left(\alpha+\chi\right)\pm\epsilon B\left(\varphi+\psi\right)+D\right)\\ \mp\epsilon\left(A\alpha+B\varphi+2C\right)= & \pm\epsilon A\chi\pm\epsilon B\psi+D \end{aligned} \]
\[ \begin{pmatrix}1 & 0 & \pm\epsilon A\\ 0 & 1 & \pm\epsilon B\\ \pm\epsilon A & \pm\epsilon B & 1 \end{pmatrix}\begin{pmatrix}\chi\\ \psi\\ D \end{pmatrix}=\begin{pmatrix}\alpha\\ \varphi\\ \mp\epsilon\left(A\alpha+B\varphi+2C\right) \end{pmatrix} \]
\[ \begin{pmatrix}1 & 0 & \pm\epsilon A & \alpha\\ 0 & 1 & \pm\epsilon B & \varphi\\ 0 & \pm\epsilon B & 1\mp\epsilon^{2}A^{2} & \mp\epsilon\left(2A\alpha+B\varphi+2C\right) \end{pmatrix} \]
\[ \begin{pmatrix}1 & 0 & \pm\epsilon A & \alpha\\ 0 & 1 & \pm\epsilon B & \varphi\\ 0 & 0 & 1\mp\epsilon^{2}A^{2}\mp\epsilon^{2}B^{2} & \mp\epsilon\left(2A\alpha+2B\varphi+2C\right) \end{pmatrix} \]
\[ \begin{pmatrix}1 & 0 & \pm\epsilon A & \alpha\\ 0 & 1 & \pm\epsilon B & \varphi\\ 0 & 0 & 1 & \dfrac{\mp2\epsilon\left(A\alpha+B\varphi+C\right)}{1\mp\epsilon^{2}\left(A^{2}+B^{2}\right)} \end{pmatrix} \]
\[ A^{2}+B^{2}=\left(\dfrac{A^{\prime}}{\sqrt{A^{\prime}{}^{2}+B^{\prime}{}^{2}}}\right)^{2}+\left(\dfrac{B^{\prime}}{\sqrt{A^{\prime}{}^{2}+B^{\prime}{}^{2}}}\right)^{2}=1 \]
\[ \begin{cases} \chi=\alpha\mp\epsilon AD=\alpha\mp\epsilon\dfrac{A^{\prime}}{\sqrt{A^{\prime}{}^{2}+B^{\prime}{}^{2}}}D\\ \psi=\varphi\mp\epsilon BD=\varphi\mp\epsilon\dfrac{B^{\prime}}{\sqrt{A^{\prime}{}^{2}+B^{\prime}{}^{2}}}D\\ D=\dfrac{\mp2\epsilon\left(A\alpha+B\varphi+C\right)}{1\mp\epsilon^{2}\left(A^{2}+B^{2}\right)}=\dfrac{\mp2\epsilon}{1\mp\epsilon^{2}}\dfrac{A^{\prime}\alpha+B^{\prime}\varphi+C^{\prime}}{\sqrt{A^{\prime}{}^{2}+B^{\prime}{}^{2}}} & A^{2}+B^{2}=1 \end{cases} \]
actually, only one of two solutions is true
\[ \begin{cases} \chi=\alpha-\epsilon AD=\alpha-\epsilon\dfrac{A^{\prime}}{\sqrt{A^{\prime}{}^{2}+B^{\prime}{}^{2}}}D=\alpha-\dfrac{2\epsilon^{2}}{\epsilon^{2}-1}\dfrac{A^{\prime}{}^{2}\alpha+A^{\prime}B^{\prime}\varphi+A^{\prime}C^{\prime}}{A^{\prime}{}^{2}+B^{\prime}{}^{2}}\\ \psi=\varphi-\epsilon BD=\varphi-\epsilon\dfrac{B^{\prime}}{\sqrt{A^{\prime}{}^{2}+B^{\prime}{}^{2}}}D=\varphi-\dfrac{2\epsilon^{2}}{\epsilon^{2}-1}\dfrac{A^{\prime}B^{\prime}\alpha+B^{\prime}{}^{2}\varphi+B^{\prime}C^{\prime}}{A^{\prime}{}^{2}+B^{\prime}{}^{2}}\\ D=\dfrac{-2\epsilon\left(A\alpha+B\varphi+C\right)}{1-\epsilon^{2}\left(A^{2}+B^{2}\right)}=\dfrac{-2\epsilon}{1-\epsilon^{2}}\dfrac{A^{\prime}\alpha+B^{\prime}\varphi+C^{\prime}}{\sqrt{A^{\prime}{}^{2}+B^{\prime}{}^{2}}}=\dfrac{2\epsilon}{\epsilon^{2}-1}\dfrac{A^{\prime}\alpha+B^{\prime}\varphi+C^{\prime}}{\sqrt{A^{\prime}{}^{2}+B^{\prime}{}^{2}}} \end{cases} \]
\[ \begin{cases} \chi=\dfrac{\left(\epsilon^{2}-1\right)\left(A^{\prime}{}^{2}+B^{\prime}{}^{2}\right)\alpha-2\epsilon^{2}\left(A^{\prime}{}^{2}\alpha+A^{\prime}B^{\prime}\varphi+A^{\prime}C^{\prime}\right)}{\left(\epsilon^{2}-1\right)\left(A^{\prime}{}^{2}+B^{\prime}{}^{2}\right)}\\ \psi=\dfrac{\left(\epsilon^{2}-1\right)\left(A^{\prime}{}^{2}+B^{\prime}{}^{2}\right)\varphi-2\epsilon^{2}\left(A^{\prime}B^{\prime}\alpha+B^{\prime}{}^{2}\varphi+B^{\prime}C^{\prime}\right)}{\left(\epsilon^{2}-1\right)\left(A^{\prime}{}^{2}+B^{\prime}{}^{2}\right)}\\ \left|\dfrac{D}{d\left(F,L\right)}\right|=\left|\dfrac{2\epsilon}{1-\epsilon^{2}}\right|\Rightarrow\left(\dfrac{D}{d\left(F,L\right)}\right)^{2}=\left(\dfrac{2\epsilon}{1-\epsilon^{2}}\right)^{2} \end{cases} \]
\[ \begin{aligned} & \left(\epsilon^{2}-1\right)\left(A^{\prime}{}^{2}+B^{\prime}{}^{2}\right)\alpha-2\epsilon^{2}\left(A^{\prime}{}^{2}\alpha+A^{\prime}B^{\prime}\varphi+A^{\prime}C^{\prime}\right)\\ = & \left(-\left(\epsilon^{2}+1\right)A^{\prime}{}^{2}+\left(\epsilon^{2}-1\right)B^{\prime}{}^{2}\right)\alpha-2\epsilon^{2}\left(A^{\prime}B^{\prime}\varphi+A^{\prime}C^{\prime}\right)\\ = & \left(-\left(\epsilon^{2}+1\right)A^{\prime}{}^{2}+\left(\epsilon^{2}-1\right)B^{\prime}{}^{2}\right)\alpha-2\epsilon^{2}\left(A^{\prime}B^{\prime}\varphi+A^{\prime}C^{\prime}\right) \end{aligned} \]
Can the above be more simplified?
\[ \begin{aligned} \overline{FF^{\prime}}^{2}= & \left(\alpha-\chi\right)^{2}+\left(\varphi-\psi\right)^{2}\\ = & \left(\alpha-\left(\alpha-\epsilon AD\right)\right)^{2}+\left(\varphi-\left(\varphi-\epsilon BD\right)\right)^{2}\\ = & \left(\epsilon D\right)^{2}\left(A^{2}+B^{2}\right)\\ = & \left(\epsilon D\right)^{2} \end{aligned} \]
24.2.3 eccentricity and its equivalent representation
\[ \left(\dfrac{c}{a}\right)^{2}=\left(\dfrac{\overline{PF}}{d\left(P,L\right)}\right)^{2}=\epsilon^{2}=\left(\dfrac{\overline{FF^{\prime}}}{D}\right)^{2}=\left(\dfrac{2c}{D}\right)^{2}\Rightarrow D=2a \]
\[ \left(\dfrac{D}{d\left(F,L\right)}\right)^{2}=\left(\dfrac{2\epsilon}{1-\epsilon^{2}}\right)^{2} \]
Fig. 17.2: conic sections: ellipse
Fig. 24.2: conic sections: parabola
Fig. 16.1: conic sections: hyperbola
24.3 Cartesian coordinate: standard form / standard equation
\[ \begin{array}{ccccc} \text{circle} & \left(\dfrac{y-k}{a}\right)^{2}+\left(\dfrac{x-h}{a}\right)^{2} & =1 & & b=a\\ \text{ellipse} & \left(\dfrac{y-k}{b}\right)^{2}+\left(\dfrac{x-h}{a}\right)^{2} & =1 & \text{vertical} & b>a\\ & \left(\dfrac{y-k}{b}\right)^{2}+\left(\dfrac{x-h}{a}\right)^{2} & =1 & \text{horizontal} & a>b\\ \text{parabola} & \left(y-k\right)-4c\left(x-h\right)^{2} & =0 & \text{vertical}\\ & -4c\left(y-k\right)^{2}+\left(x-h\right) & =0 & \text{horizontal}\\ \text{hyperbola} & \left(\dfrac{y-k}{b}\right)^{2}-\left(\dfrac{x-h}{a}\right)^{2} & =1 & \text{vertical} & \dfrac{x-h}{a}=0\Rightarrow\dfrac{y-k}{b}=\pm1\\ & -\left(\dfrac{y-k}{b}\right)^{2}+\left(\dfrac{x-h}{a}\right)^{2} & =1 & \text{horizontal} & \dfrac{y-k}{b}=0\Rightarrow\dfrac{x-h}{a}=\pm1 \end{array} \]
24.4 parametric equation
\[ \begin{array}{cccccccc} \text{circle} & \left(\dfrac{y-k}{a}\right)^{2}+\left(\dfrac{x-h}{a}\right)^{2} & =1 & \begin{pmatrix}x\\ y\\ 1 \end{pmatrix}= & \begin{pmatrix}a & 0 & h\\ 0 & a & k\\ 0 & 0 & 1 \end{pmatrix} & \begin{pmatrix}\cos t\\ \sin t\\ 1 \end{pmatrix} & =\begin{pmatrix}\cos t & 0 & h\\ 0 & \sin t & k\\ 0 & 0 & 1 \end{pmatrix} & \begin{pmatrix}a\\ a\\ 1 \end{pmatrix}\\ \text{ellipse} & \left(\dfrac{y-k}{b}\right)^{2}+\left(\dfrac{x-h}{a}\right)^{2} & =1 & \begin{pmatrix}x\\ y\\ 1 \end{pmatrix}= & \begin{pmatrix}a & 0 & h\\ 0 & b & k\\ 0 & 0 & 1 \end{pmatrix} & \begin{pmatrix}\cos t\\ \sin t\\ 1 \end{pmatrix} & =\begin{pmatrix}\cos t & 0 & h\\ 0 & \sin t & k\\ 0 & 0 & 1 \end{pmatrix} & \begin{pmatrix}a\\ b\\ 1 \end{pmatrix}\\ \text{parabola} & \left(y-k\right)-4c\left(x-h\right)^{2} & =0 & \begin{pmatrix}x\\ y\\ 1 \end{pmatrix}= & \begin{pmatrix}1 & 0 & h\\ 0 & 4c & k\\ 0 & 0 & 1 \end{pmatrix} & \begin{pmatrix}t\\ t^{2}\\ 1 \end{pmatrix} & =\begin{pmatrix}t & 0 & h\\ 0 & t^{2} & k\\ 0 & 0 & 1 \end{pmatrix} & \begin{pmatrix}1\\ 4c\\ 1 \end{pmatrix}\\ & -4c\left(y-k\right)^{2}+\left(x-h\right) & =0 & \begin{pmatrix}x\\ y\\ 1 \end{pmatrix}= & \begin{pmatrix}4c & 0 & h\\ 0 & 1 & k\\ 0 & 0 & 1 \end{pmatrix} & \begin{pmatrix}t^{2}\\ t\\ 1 \end{pmatrix} & =\begin{pmatrix}t^{2} & 0 & h\\ 0 & t & k\\ 0 & 0 & 1 \end{pmatrix} & \begin{pmatrix}4c\\ 1\\ 1 \end{pmatrix}\\ \text{hyperbola} & \left(\dfrac{y-k}{b}\right)^{2}-\left(\dfrac{x-h}{a}\right)^{2} & =1 & \begin{pmatrix}x\\ y\\ 1 \end{pmatrix}= & \begin{pmatrix}a & 0 & h\\ 0 & b & k\\ 0 & 0 & 1 \end{pmatrix} & \begin{pmatrix}\pm\cosh t\\ \sinh t\\ 1 \end{pmatrix} & =\begin{pmatrix}\tan t & 0 & h\\ 0 & \sec t & k\\ 0 & 0 & 1 \end{pmatrix} & \begin{pmatrix}a\\ b\\ 1 \end{pmatrix}\\ & -\left(\dfrac{y-k}{b}\right)^{2}+\left(\dfrac{x-h}{a}\right)^{2} & =1 & \begin{pmatrix}x\\ y\\ 1 \end{pmatrix}= & \begin{pmatrix}a & 0 & h\\ 0 & b & k\\ 0 & 0 & 1 \end{pmatrix} & \begin{pmatrix}\sinh t\\ \pm\cosh t\\ 1 \end{pmatrix} & =\begin{pmatrix}\sec t & 0 & h\\ 0 & \tan t & k\\ 0 & 0 & 1 \end{pmatrix} & \begin{pmatrix}a\\ b\\ 1 \end{pmatrix} \end{array} \]
24.5 polar coordinate
\[ \left(x-\alpha\right)^{2}+\left(y-\varphi\right)^{2}=\left[\epsilon\left(Ax+By+C\right)\right]^{2} \]
\(\begin{cases}x=r\cos\theta\\y=r\sin\theta\end{cases}\)
\[ \left(r\cos\theta-\alpha\right)^{2}+\left(r\sin\theta-\varphi\right)^{2}=\left[\epsilon\left(Ar\cos\theta+Br\sin\theta+C\right)\right]^{2} \]
If \(\begin{cases}F=\left(x_{{\scriptscriptstyle F}},y_{{\scriptscriptstyle F}}\right)=\left(\alpha,\varphi\right)=\left(0,0\right)\\L=Ax+By+C=x+p=0\end{cases}\)
\[ \begin{aligned} \left(r\cos\theta\right)^{2}+\left(r\sin\theta\right)^{2}= & \left[\epsilon\left(r\cos\theta+p\right)\right]^{2}\\ r^{2}=\\ r= & \pm\epsilon\left(r\cos\theta+p\right)\\ = & \pm\left(r\epsilon\cos\theta+\epsilon p\right)\\ r\left(1\mp\epsilon\cos\theta\right)= & \epsilon p\\ r= & \dfrac{\epsilon p}{1\mp\epsilon\cos\theta} \end{aligned} \]
https://www.geogebra.org/calculator/azksjxbq
\(r=\dfrac{\epsilon p}{1-\epsilon\cos\theta}\) will not cross \(L=x+p=0\) on graphs, so maybe it is a more correct solution
\[ r=\dfrac{\epsilon p}{1-\epsilon\cos\theta} \]
Fig. 16.2: polar conic sections: ellipse
Fig. 24.3: polar conic sections: parabola
Fig. 24.4: polar conic sections: hyperbola
24.6 Cartesian coordinate: general form / quadratic equation
https://en.wikipedia.org/wiki/Matrix_representation_of_conic_sections
\[ ax^{2}+bxy+cy^{2}+dx+ey+f=0 \]
\[ \begin{pmatrix}x & y\end{pmatrix}\begin{pmatrix}a & b/2\\ b/2 & c \end{pmatrix}\begin{pmatrix}x\\ y \end{pmatrix}=\begin{pmatrix}x & y\end{pmatrix}\begin{pmatrix}ax+\left(b/2\right)y\\ \left(b/2\right)x+cy \end{pmatrix}=ax^{2}+bxy+cy^{2} \]
\[ \begin{aligned} 0= & \begin{pmatrix}x & y\end{pmatrix}\begin{pmatrix}a & b/2\\ b/2 & c \end{pmatrix}\begin{pmatrix}x\\ y \end{pmatrix}+\begin{pmatrix}d & e\end{pmatrix}\begin{pmatrix}x\\ y \end{pmatrix}+f\\ = & \boldsymbol{x}^{\intercal}A\boldsymbol{x}+\boldsymbol{b}^{\intercal}\boldsymbol{x}+f,\begin{cases} A=\begin{pmatrix}a & b/2\\ b/2 & c \end{pmatrix} & A\text{ real symmetric}\\ \boldsymbol{b}=\begin{pmatrix}d\\ e \end{pmatrix}\\ \boldsymbol{x}=\begin{pmatrix}x\\ y \end{pmatrix} \end{cases} \end{aligned} \]
24.7 homogeneous coordinate
homogeneous coordinate O: HTML, X: PDF becoming web link
X homogeneous coordinate[24.7]
\[ \begin{pmatrix}x & y\end{pmatrix}\begin{pmatrix}a & b/2\\ b/2 & c \end{pmatrix}\begin{pmatrix}x\\ y \end{pmatrix}=\begin{pmatrix}x & y & 1\end{pmatrix}\begin{pmatrix}a & b/2 & ~\\ b/2 & c\\ \\ \end{pmatrix}\begin{pmatrix}x\\ y\\ 1 \end{pmatrix}=\begin{pmatrix}x & y & 1\end{pmatrix}\begin{pmatrix}a & b/2 & 0\\ b/2 & c & 0\\ 0 & 0 & 0 \end{pmatrix}\begin{pmatrix}x\\ y\\ 1 \end{pmatrix} \]
\[ \begin{aligned} \begin{pmatrix}d & e\end{pmatrix}\begin{pmatrix}x\\ y \end{pmatrix}= & \begin{pmatrix}x & y & 1\end{pmatrix}\begin{pmatrix}\alpha & \beta & \gamma\\ \delta & \epsilon & \zeta\\ \eta & \theta & \kappa \end{pmatrix}\begin{pmatrix}x\\ y\\ 1 \end{pmatrix}=\begin{pmatrix}x & y & 1\end{pmatrix}\begin{pmatrix}\alpha x+\beta y+\gamma\\ \delta x+\epsilon y+\zeta\\ \eta x+\theta y+\kappa \end{pmatrix},\begin{cases} \gamma+\eta=d\\ \zeta+\theta=e \end{cases}\\ = & \begin{pmatrix}x & y & 1\end{pmatrix}\begin{pmatrix}0 & 0 & \gamma\\ 0 & 0 & \zeta\\ \eta & \theta & 0 \end{pmatrix}\begin{pmatrix}x\\ y\\ 1 \end{pmatrix}=\begin{pmatrix}x & y & 1\end{pmatrix}\begin{pmatrix}0 & 0 & d/2\\ 0 & 0 & e/2\\ d/2 & e/2 & 0 \end{pmatrix}\begin{pmatrix}x\\ y\\ 1 \end{pmatrix} \end{aligned} \]
\[ \begin{aligned} 0= & ax^{2}+bxy+cy^{2}+dx+ey+f\\ = & \begin{pmatrix}x & y\end{pmatrix}\begin{pmatrix}a & b/2\\ b/2 & c \end{pmatrix}\begin{pmatrix}x\\ y \end{pmatrix}+\begin{pmatrix}d & e\end{pmatrix}\begin{pmatrix}x\\ y \end{pmatrix}+f=\boldsymbol{x}^{\intercal}A\boldsymbol{x}+\boldsymbol{b}^{\intercal}\boldsymbol{x}+f\\ = & \begin{pmatrix}x & y & 1\end{pmatrix}\begin{pmatrix}a & b/2 & d/2\\ b/2 & c & e/2\\ d/2 & e/2 & f \end{pmatrix}\begin{pmatrix}x\\ y\\ 1 \end{pmatrix}=\begin{pmatrix}\boldsymbol{x}^{\intercal} & 1\end{pmatrix}M\begin{pmatrix}\boldsymbol{x}\\ 1 \end{pmatrix},M=\begin{pmatrix}a & b/2 & d/2\\ b/2 & c & e/2\\ d/2 & e/2 & f \end{pmatrix} \end{aligned} \]
\[ \begin{aligned} 0= & ax^{2}+bxy+cy^{2}+dx+ey+f\\ = & \begin{pmatrix}x & y\end{pmatrix}\begin{pmatrix}a & b/2\\ b/2 & c \end{pmatrix}\begin{pmatrix}x\\ y \end{pmatrix}+\begin{pmatrix}d & e\end{pmatrix}\begin{pmatrix}x\\ y \end{pmatrix}+f=\boldsymbol{x}^{\intercal}A\boldsymbol{x}+\boldsymbol{b}^{\intercal}\boldsymbol{x}+f\\ = & \begin{pmatrix}x & y & 1\end{pmatrix}\begin{pmatrix}a & b/2 & d/2\\ b/2 & c & e/2\\ d/2 & e/2 & f \end{pmatrix}\begin{pmatrix}x\\ y\\ 1 \end{pmatrix}=\begin{pmatrix}\boldsymbol{x}^{\intercal} & 1\end{pmatrix}M\begin{pmatrix}\boldsymbol{x}\\ 1 \end{pmatrix},M=\begin{pmatrix}a & b/2 & d/2\\ b/2 & c & e/2\\ d/2 & e/2 & f \end{pmatrix} \end{aligned} \]
https://en.wikipedia.org/wiki/Matrix_representation_of_conic_sections
\[ \begin{aligned} 0=Q= & Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F\\ = & \begin{bmatrix}x & y & 1\end{bmatrix}\begin{bmatrix}A & B/2 & D/2\\ B/2 & C & E/2\\ D/2 & E/2 & F \end{bmatrix}\begin{bmatrix}x\\ y\\ 1 \end{bmatrix}=\boldsymbol{x}_{{\scriptscriptstyle \text{h}}}^{\intercal}A_{{\scriptscriptstyle Q}}\boldsymbol{x}_{{\scriptscriptstyle \text{h}}}\\ = & \begin{bmatrix}x & y\end{bmatrix}\begin{bmatrix}A & B/2\\ B/2 & C \end{bmatrix}\begin{bmatrix}x\\ y \end{bmatrix}+\begin{bmatrix}D & E\end{bmatrix}\begin{bmatrix}x\\ y \end{bmatrix}+F=\boldsymbol{x}^{\intercal}A_{{\scriptscriptstyle Q,33}}\boldsymbol{x}+\boldsymbol{b}^{\intercal}\boldsymbol{x}+F \end{aligned} \]
24.8 TalyorCatAlice: projective geometry
https://www.bilibili.com/video/BV1pK42117UZ
https://www.bilibili.com/video/BV1cx4y1f7w6
https://www.bilibili.com/video/BV1sy421h7aF
https://www.bilibili.com/video/BV1zv421y7iH
https://www.bilibili.com/video/BV1ZH4y1h7vC