Chapter 48: Hilbert space

knitr::opts_chunk$set(fig.pos = "H", out.extra = "")

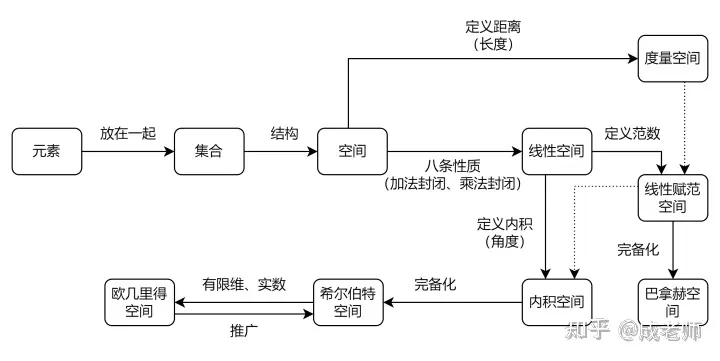
Fig. 30.2: Euclid space construction

¹⁴

48.1 Taylor expansion or Taylor series

https://www.bilibili.com/video/BV15s4y1g7HQ

Lemma 48.1 Newton-Leibniz formula = N-LF, equivalent to first mean value theorem for derivatives / Lagrange mean value theorem = MVTdL / MVTd1

牛頓-萊布尼茨公式 Newton-Leibniz formula = N-LF, equivalent to 第一微分均值定理 / 拉格朗日均值定理 first mean value theorem for derivatives / Lagrange mean value theorem = MVTdL / MVTd1 $\ref{thm:MVTd1}$

\[\begin{equation} \int_{a}^{b}f^{\prime}\left(x\right)\mathrm{d}x=f\left(b\right)-f\left(a\right)\label{eq:N-LF} \end{equation}\]

$\left(\Downarrow\right)$:

$\left(\Uparrow\right)$:

Proof: $\left(\Downarrow\right)$

重疊端點分割 $\left[a,b\right]$ 成 $n$ 部分聯集 $\left(n\in\mathbb{N}\right)$

\[\begin{equation} \left[a,b\right]=\left[x_{0},x_{n}\right]=\left[x_{0},x_{1}\right]\cup\left[x_{0},x_{2}\right]\cup\cdots\cup\left[x_{n-1},x_{n}\right]\label{eq:-72} \end{equation}\]

\[ \begin{aligned} & \begin{cases} \begin{cases} f:\left[a,b\right]\rightarrow\mathbb{R} & \left(0\right)\\ f\text{ continuous on }\left[a,b\right] & \left(1\right)\\ f\text{ differentiable on }\left(a,b\right) & \left(2\right) \end{cases}\overset{\ref{thm:Rolle}}{\Rightarrow}\exists c\in\left(a,b\right)\left\{ f^{\prime}\left(c\right)\left(b-a\right)=f\left(b\right)-f\left(a\right)\right\} & \text{MVTd1 }\ref{thm:MVTd1}\\ \left[a,b\right]=\left[x_{0},x_{n}\right]=\left[x_{0},x_{1}\right]\cup\left[x_{0},x_{2}\right]\cup\cdots\cup\left[x_{n-1},x_{n}\right] & \ref{eq:-72} \end{cases}\\ \Rightarrow & \begin{cases} \left(f:\left[x_{0},x_{n}\right]\rightarrow\mathbb{R}\right)=\left(f:\left[x_{0},x_{1}\right]\cup\left[x_{0},x_{2}\right]\cup\cdots\cup\left[x_{n-1},x_{n}\right]\rightarrow\mathbb{R}\right) & \Leftarrow\left(0\right)\\ f\text{ continuous on }\left[x_{0},x_{1}\right]\cup\left[x_{0},x_{2}\right]\cup\cdots\cup\left[x_{n-1},x_{n}\right] & \Leftarrow\left(1\right)\\ f\text{ differentiable on }\left(x_{0},x_{1}\right]\cup\left[x_{0},x_{2}\right]\cup\cdots\cup\left[x_{n-1},x_{n}\right) & \Leftarrow\left(2\right) \end{cases}\\ \Rightarrow & \begin{cases} f:\left[x_{0},x_{1}\right]\rightarrow\mathbb{R},f:\left[x_{0},x_{2}\right]\rightarrow\mathbb{R},\cdots,f:\left[x_{n-1},x_{n}\right]\rightarrow\mathbb{R} & \Leftarrow\left(0\right)\\ f\text{ continuous on }\left[x_{0},x_{1}\right],\left[x_{0},x_{2}\right],\cdots,\left[x_{n-1},x_{n}\right] & \Leftarrow\left(1\right)\\ f\text{ differentiable on }\left(x_{0},x_{1}\right],\left[x_{0},x_{2}\right],\cdots,\left[x_{n-1},x_{n}\right)\Rightarrow f\text{ differentiable on }\left(x_{0},x_{1}\right),\left(x_{0},x_{2}\right),\cdots,\left(x_{n-1},x_{n}\right) & \Leftarrow\left(2\right) \end{cases}\\ & \overset{\stackrel{\ref{thm:Rolle}}{\ref{thm:MVTd1}}}{\Rightarrow}\begin{cases} \exists c_{1}\in\left(x_{0},x_{1}\right)\left\{ f^{\prime}\left(c_{1}\right)\left(x_{1}-x_{0}\right)=f\left(x_{1}\right)-f\left(x_{0}\right)\right\} \\ \exists c_{2}\in\left(x_{1},x_{2}\right)\left\{ f^{\prime}\left(c_{2}\right)\left(x_{2}-x_{1}\right)=f\left(x_{2}\right)-f\left(x_{1}\right)\right\} \\ \vdots\\ \exists c_{k}\in\left(x_{k-1},x_{k}\right)\left\{ f^{\prime}\left(c_{k}\right)\left(x_{k}-x_{k-1}\right)=f\left(x_{k}\right)-f\left(x_{k-1}\right)\right\} & \forall k\in\mathbb{N}\cap\left[1,n\right]\\ \vdots\\ \exists c_{n}\in\left(x_{n-1},x_{n}\right)\left\{ f^{\prime}\left(c_{n}\right)\left(x_{n}-x_{n-1}\right)=f\left(x_{n}\right)-f\left(x_{n-1}\right)\right\} \end{cases}\\ \Rightarrow & f^{\prime}\left(c_{k}\right)\left(x_{k}-x_{k-1}\right)=f\left(x_{k}\right)-f\left(x_{k-1}\right)\\ \Rightarrow & \sum_{k}f^{\prime}\left(c_{k}\right)\left(x_{k}-x_{k-1}\right)=\sum_{k}f\left(x_{k}\right)-f\left(x_{k-1}\right)\\ \Rightarrow & \sum_{k=1}^{n}f^{\prime}\left(c_{k}\right)\left(x_{k}-x_{k-1}\right)=\sum_{k=1}^{n}f\left(x_{k}\right)-f\left(x_{k-1}\right)\\ & =\left[f\left(x_{1}\right)-f\left(x_{0}\right)\right]+\left[f\left(x_{2}\right)-f\left(x_{1}\right)\right]+\cdots+\left[f\left(x_{n}\right)-f\left(x_{n-1}\right)\right]\\ & =f\left(x_{n}\right)-f\left(x_{0}\right)=f\left(b\right)-f\left(a\right)\\ & \Rightarrow\sum_{k=1}^{n}f^{\prime}\left(c_{k}\right)\left(x_{k}-x_{k-1}\right)=f\left(b\right)-f\left(a\right)\overset{\Delta x_{k}=x_{k}-x_{k-1}}{\Leftrightarrow}\sum_{k=1}^{n}f^{\prime}\left(c_{k}\right)\Delta x_{k}=f\left(b\right)-f\left(a\right)\\ \Rightarrow & \lim_{n\rightarrow\infty}\lim_{\Delta x_{k}=\frac{x_{n}-x_{0}}{n}}\sum_{k=1}^{n}f^{\prime}\left(c_{k}\right)\Delta x_{k}=\lim_{n\rightarrow\infty}\lim_{\Delta x_{k}=\frac{b-a}{n}\rightarrow0}f\left(b\right)-f\left(a\right)=f\left(b\right)-f\left(a\right)\\ \Rightarrow & \int_{a}^{b}f^{\prime}\left(x\right)\mathrm{d}x=\int_{x_{0}}^{x_{n}}f^{\prime}\left(x\right)\mathrm{d}x=f\left(b\right)-f\left(a\right)\\ \Rightarrow & \int_{a}^{b}f^{\prime}\left(x\right)\mathrm{d}x=f\left(b\right)-f\left(a\right) \end{aligned} \]

\[ \int_{a}^{b}f^{\prime}\left(x\right)\mathrm{d}x=f\left(b\right)-f\left(a\right) \]

得到牛頓-萊布尼茨公式 Newton-Leibniz formula = N-LF [eq:N-LF]

\[ \tag*{$\Box$} \]

Proof: $\left(\Uparrow\right)$

\[ \exists c\in\left(a,b\right)\left[f^{\prime}\left(c\right)\left(b-a\right)=f\left(b\right)-f\left(a\right)\right] \]

得到第一微分均值定理 / 拉格朗日均值定理 first mean value theorem for derivatives / Lagrange mean value theorem = MVTdL / MVTd1 [thm:MVTd1]

\[ \tag*{$\Box$} \]

\[ \begin{aligned} \int_{a}^{b}f^{\prime}\left(x\right)\mathrm{d}x= & f\left(b\right)-f\left(a\right)\\ \int_{x_{{\scriptscriptstyle 0}}}^{x}f^{\prime}\left(t\right)\mathrm{d}t= & f\left(x\right)-f\left(x_{{\scriptscriptstyle 0}}\right)\\ f\left(x\right)= & f\left(x_{{\scriptscriptstyle 0}}\right)+\int_{x_{{\scriptscriptstyle 0}}}^{x}f^{\prime}\left(t\right)\mathrm{d}t \end{aligned} \]

\[ f\left(x\right)=f\left(x_{{\scriptscriptstyle 0}}\right)+\int_{x_{{\scriptscriptstyle 0}}}^{x}f^{\prime}\left(t\right)\mathrm{d}t \]

Lemma 48.2 univariable product rule

\[ \mathrm{d}\left(uv\right)=\left(\mathrm{d}u\right)v+u\mathrm{d}v=v\mathrm{d}u+u\mathrm{d}v \]

\[ \frac{\mathrm{d}\left(uv\right)}{\mathrm{d}t}=v\frac{\mathrm{d}u}{\mathrm{d}t}+u\frac{\mathrm{d}v}{\mathrm{d}t} \]

Lemma 48.3 integration by parts

\[\begin{eqnarray} \int\frac{\mathrm{d}\left(uv\right)}{\mathrm{d}t}\thinspace\mathrm{d}t & = & \int v\frac{\mathrm{d}u}{\mathrm{d}t}+u\frac{\mathrm{d}v}{\mathrm{d}t}\mathrm{d}t\nonumber \\ \int\mathrm{d}\left(uv\right)= & & =\int v\frac{\mathrm{d}u}{\mathrm{d}t}\mathrm{d}t+\int u\frac{\mathrm{d}v}{\mathrm{d}t}\mathrm{d}t\nonumber \\ uv= & & =\int v\mathrm{d}u+\int u\mathrm{d}v\nonumber \\ \int u\frac{\mathrm{d}v}{\mathrm{d}t}\mathrm{d}t & = & uv-\int v\frac{\mathrm{d}u}{\mathrm{d}t}\mathrm{d}t\text{ "switching derivatives"}\label{eq:switchingDerivatives}\\ \int u\mathrm{d}v & = & uv-\int v\mathrm{d}u\text{ "switching differentials"}\label{eq:switchingDifferentials} \end{eqnarray}\]

Theorem 18.1 univariable Taylor theorem with the remainder in integral form

\[ f\left(x\right)=\sum\limits _{k=0}^{n}\frac{f^{\left(k\right)}\left(a\right)}{k!}\left(x-a\right)^{k}+\int_{a}^{x}f^{\left(n+1\right)}\left(t\right)\frac{\left(t-x\right)^{n}}{n!}\mathrm{d}t \]

\[ f\left(x\right)=\sum\limits _{k=0}^{n}\frac{f^{\left(k\right)}\left(a\right)}{k!}\left(x-a\right)^{k}+\int_{a}^{x}f^{\left(n+1\right)}\left(t\right)\frac{\left(x-t\right)^{n}}{n!}\mathrm{d}t \]

Proof: relatively weird $(t-x)$

\[\begin{eqnarray} & & f\left(x\right)-f\left(a\right)\\ & \overset{\ref{thm:N-LF}}{=} & \int_{a}^{x}f'\left(t\right)\mathrm{d}t=\int_{a}^{x}f'\left(t\right)\frac{\mathrm{d}\left(t-x\right)}{\mathrm{d}t}\mathrm{d}t\overset{\ref{eq:switchingDerivatives}}{=}\left[f'\left(t\right)\left(t-x\right)\right]_{t=a}^{x}-\int_{a}^{x}\left(t-x\right)\frac{\mathrm{d}f'\left(t\right)}{\mathrm{d}t}\mathrm{d}t\\ & = & \left[-f'\left(a\right)\left(a-x\right)\right]-\int_{a}^{x}f''\left(t\right)\left(t-x\right)\mathrm{d}t=f'\left(a\right)\left(x-a\right)-\int_{a}^{x}f''\left(t\right)\frac{\mathrm{d}\frac{\left(t-x\right)^{2}}{2}}{\mathrm{d}t}\mathrm{d}t\\ & = & f'\left(a\right)\left(x-a\right)-\left(\left[f''\left(t\right)\frac{\left(t-x\right)^{2}}{2}\right]_{t=a}^{x}-\int_{a}^{x}\frac{\left(t-x\right)^{2}}{2}\frac{\mathrm{d}f''\left(t\right)}{\mathrm{d}t}\mathrm{d}t\right)\\ & = & f'\left(a\right)\left(x-a\right)-\left(\left[-f''\left(a\right)\frac{\left(x-a\right)^{2}}{2}\right]-\int_{a}^{x}f'''\left(t\right)\frac{\left(t-x\right)^{2}}{2}\mathrm{d}t\right)\\ & = & f'\left(a\right)\left(x-a\right)+f''\left(a\right)\frac{\left(x-a\right)^{2}}{2}+\int_{a}^{x}f'''\left(t\right)\frac{\left(t-x\right)^{2}}{2}\mathrm{d}t\\ & = & f'\left(a\right)\left(x-a\right)+f''\left(a\right)\frac{\left(x-a\right)^{2}}{2}+\int_{a}^{x}f'''\left(t\right)\frac{\mathrm{d}\frac{\left(t-x\right)^{3}}{2\cdot3}}{\mathrm{d}t}\mathrm{d}t\\ & = & f'\left(a\right)\left(x-a\right)+f''\left(a\right)\frac{\left(x-a\right)^{2}}{2}+\left(\left[f'''\left(t\right)\frac{\left(t-x\right)^{3}}{2\cdot3}\right]_{t=a}^{x}-\int_{a}^{x}\frac{\left(t-x\right)^{3}}{2\cdot3}\frac{\mathrm{d}f'''\left(t\right)}{\mathrm{d}t}\mathrm{d}t\right)\\ & = & f'\left(a\right)\left(x-a\right)+f''\left(a\right)\frac{\left(x-a\right)^{2}}{2}+\left(\left[f'''\left(a\right)\frac{\left(x-a\right)^{3}}{2\cdot3}\right]-\int_{a}^{x}f^{\left(4\right)}\left(t\right)\frac{\left(t-x\right)^{3}}{2\cdot3}\mathrm{d}t\right)\\ & = & f'\left(a\right)\left(x-a\right)+f''\left(a\right)\frac{\left(x-a\right)^{2}}{2}+f'''\left(t\right)\frac{\left(x-a\right)^{3}}{2\cdot3}-\int_{a}^{x}f^{\left(4\right)}\left(t\right)\frac{\left(t-x\right)^{3}}{2\cdot3}\mathrm{d}t\\ & = & f'\left(a\right)\left(x-a\right)+f''\left(a\right)\frac{\left(x-a\right)^{2}}{2}+f'''\left(t\right)\frac{\left(x-a\right)^{3}}{2\cdot3}-\int_{a}^{x}f^{\left(4\right)}\left(t\right)\frac{\mathrm{d}\frac{\left(t-x\right)^{4}}{2\cdot3\cdot4}}{\mathrm{d}t}\mathrm{d}t\\ & = & f'\left(a\right)\left(x-a\right)+f''\left(a\right)\frac{\left(x-a\right)^{2}}{2}+f'''\left(t\right)\frac{\left(x-a\right)^{3}}{2\cdot3}\\ & & -\left(\left[f^{\left(4\right)}\left(t\right)\frac{\left(t-x\right)^{4}}{2\cdot3\cdot4}\right]_{t=a}^{x}-\int_{a}^{x}\frac{\left(t-x\right)^{4}}{2\cdot3\cdot4}\frac{\mathrm{d}f^{\left(4\right)}\left(t\right)}{\mathrm{d}t}\mathrm{d}t\right)\\ & = & f'\left(t\right)\left(x-a\right)+f''\left(a\right)\frac{\left(x-a\right)^{2}}{2}+f'''\left(t\right)\frac{\left(x-a\right)^{3}}{2\cdot3}\\ & & -\left(\left[-f^{\left(4\right)}\left(a\right)\frac{\left(x-a\right)^{4}}{2\cdot3\cdot4}\right]-\int_{a}^{x}f^{\left(5\right)}\left(t\right)\frac{\left(t-x\right)^{4}}{2\cdot3\cdot4}\mathrm{d}t\right)\\ & = & f'\left(t\right)\left(x-a\right)+f''\left(a\right)\frac{\left(x-a\right)^{2}}{2}+f'''\left(a\right)\frac{\left(x-a\right)^{3}}{2\cdot3}+f^{\left(4\right)}\left(a\right)\frac{\left(x-a\right)^{4}}{2\cdot3\cdot4}\\ & \vdots & +\int_{a}^{x}f^{\left(5\right)}\left(t\right)\frac{\left(t-x\right)^{4}}{2\cdot3\cdot4}\mathrm{d}t\\ & = & \sum_{k=1}^{n}\frac{f^{\left(k\right)}\left(a\right)}{k!}\left(x-a\right)^{k}+\int_{a}^{x}f^{\left(n+1\right)}\left(t\right)\frac{\left(t-x\right)^{n}}{n!}\mathrm{d}t\textrm{ remainder in integral form} \end{eqnarray}\]

\[ \tag*{$\Box$} \]

Proof:

\[ \begin{aligned} & f\left(x\right)-f\left(a\right)\\ \overset{\ref{thm:N-LF}}{=} & \int_{a}^{x}f'\left(t\right)\mathrm{d}t=\int_{a}^{x}f'\left(t\right)\frac{\mathrm{d}\left(t-x\right)}{\mathrm{d}t}\mathrm{d}t\overset{\ref{eq:switchingDerivatives}}{=}\left[f'\left(t\right)\left(t-x\right)\right]_{t=a}^{x}-\int_{a}^{x}\left(t-x\right)\frac{\mathrm{d}f'\left(t\right)}{\mathrm{d}t}\mathrm{d}t\\ = & \left[-f'\left(a\right)\left(a-x\right)\right]-\int_{a}^{x}f''\left(t\right)\left(t-x\right)\mathrm{d}t=f'\left(a\right)\left(x-a\right)+\int_{a}^{x}f''\left(t\right)\left(x-t\right)\mathrm{d}t\\ = & f'\left(a\right)\left(x-a\right)-\int_{a}^{x}f''\left(t\right)\left(t-x\right)\mathrm{d}t=\sum\limits _{k=1}^{1}\frac{f^{\left(k\right)}\left(a\right)}{k!}\left(x-a\right)^{k}+\int_{a}^{x}f''\left(t\right)\left(x-t\right)\mathrm{d}t\\ = & f'\left(a\right)\left(x-a\right)-\int_{a}^{x}f''\left(t\right)\frac{\mathrm{d}\frac{\left(t-x\right)^{2}}{2}}{\mathrm{d}t}\mathrm{d}t\\ = & f'\left(a\right)\left(x-a\right)-\left(\left[f''\left(t\right)\frac{\left(t-x\right)^{2}}{2}\right]_{t=a}^{x}-\int_{a}^{x}\frac{\left(t-x\right)^{2}}{2}\frac{\mathrm{d}f''\left(t\right)}{\mathrm{d}t}\mathrm{d}t\right)\\ = & f'\left(a\right)\left(x-a\right)-\left(\left[-f''\left(a\right)\frac{\left(x-a\right)^{2}}{2}\right]-\int_{a}^{x}f'''\left(t\right)\frac{\left(t-x\right)^{2}}{2}\mathrm{d}t\right)\\ = & f'\left(a\right)\left(x-a\right)+f''\left(a\right)\frac{\left(x-a\right)^{2}}{2}+\int_{a}^{x}f'''\left(t\right)\frac{\left(t-x\right)^{2}}{2}\mathrm{d}t\\ = & \sum\limits _{k=1}^{2}\frac{f^{\left(k\right)}\left(a\right)}{k!}\left(x-a\right)^{k}+\int_{a}^{x}f'''\left(t\right)\frac{\left(t-x\right)^{2}}{2}\mathrm{d}t=\sum\limits _{k=1}^{2}\frac{f^{\left(k\right)}\left(a\right)}{k!}\left(x-a\right)^{k}+\int_{a}^{x}f'''\left(t\right)\frac{\left(x-t\right)^{2}}{2!}\mathrm{d}t\\ = & f'\left(a\right)\left(x-a\right)+f''\left(a\right)\frac{\left(x-a\right)^{2}}{2}+\int_{a}^{x}f'''\left(t\right)\frac{\mathrm{d}\frac{\left(t-x\right)^{3}}{2\cdot3}}{\mathrm{d}t}\mathrm{d}t\\ = & f'\left(a\right)\left(x-a\right)+f''\left(a\right)\frac{\left(x-a\right)^{2}}{2}+\left(\left[f'''\left(t\right)\frac{\left(t-x\right)^{3}}{2\cdot3}\right]_{t=a}^{x}-\int_{a}^{x}\frac{\left(t-x\right)^{3}}{2\cdot3}\frac{\mathrm{d}f'''\left(t\right)}{\mathrm{d}t}\mathrm{d}t\right)\\ = & f'\left(a\right)\left(x-a\right)+f''\left(a\right)\frac{\left(x-a\right)^{2}}{2}+\left(\left[f'''\left(a\right)\frac{\left(x-a\right)^{3}}{2\cdot3}\right]-\int_{a}^{x}f^{\left(4\right)}\left(t\right)\frac{\left(t-x\right)^{3}}{2\cdot3}\mathrm{d}t\right)\\ = & f'\left(a\right)\left(x-a\right)+f''\left(a\right)\frac{\left(x-a\right)^{2}}{2}+f'''\left(t\right)\frac{\left(x-a\right)^{3}}{2\cdot3}-\int_{a}^{x}f^{\left(4\right)}\left(t\right)\frac{\left(t-x\right)^{3}}{2\cdot3}\mathrm{d}t\\ = & \sum\limits _{k=1}^{3}\frac{f^{\left(k\right)}\left(a\right)}{k!}\left(x-a\right)^{k}-\int_{a}^{x}f^{\left(4\right)}\left(t\right)\frac{\left(t-x\right)^{3}}{2\cdot3}\mathrm{d}t=\sum\limits _{k=1}^{3}\frac{f^{\left(k\right)}\left(a\right)}{k!}\left(x-a\right)^{k}+\int_{a}^{x}f^{\left(4\right)}\left(t\right)\frac{\left(x-t\right)^{3}}{3!}\mathrm{d}t\\ \overset{\vdots}{=} & \sum_{k=1}^{n}\frac{f^{\left(k\right)}\left(a\right)}{k!}\left(x-a\right)^{k}+\int_{a}^{x}f^{\left(n+1\right)}\left(t\right)\frac{\left(x-t\right)^{n}}{n!}\mathrm{d}t\\ f\left(x\right)-f\left(a\right)= & \sum_{k=1}^{n}\frac{f^{\left(k\right)}\left(a\right)}{k!}\left(x-a\right)^{k}+\int_{a}^{x}f^{\left(n+1\right)}\left(t\right)\frac{\left(x-t\right)^{n}}{n!}\mathrm{d}t\\ f\left(x\right)= & f\left(a\right)+\sum_{k=1}^{n}\frac{f^{\left(k\right)}\left(a\right)}{k!}\left(x-a\right)^{k}+\int_{a}^{x}f^{\left(n+1\right)}\left(t\right)\frac{\left(x-t\right)^{n}}{n!}\mathrm{d}t\\ = & \frac{f^{\left(0\right)}\left(a\right)}{0!}\left(x-a\right)^{0}+\sum_{k=1}^{n}\frac{f^{\left(k\right)}\left(a\right)}{k!}\left(x-a\right)^{k}+\int_{a}^{x}f^{\left(n+1\right)}\left(t\right)\frac{\left(x-t\right)^{n}}{n!}\mathrm{d}t\\ = & \sum_{k=0}^{n}\frac{f^{\left(k\right)}\left(a\right)}{k!}\left(x-a\right)^{k}+\int_{a}^{x}f^{\left(n+1\right)}\left(t\right)\frac{\left(x-t\right)^{n}}{n!}\mathrm{d}t \end{aligned} \]

\[ \tag*{$\Box$} \]

Theorem 26.3 univariable Taylor theorem with the remainder in Lagrange form

\[ f\left(x\right)=\sum_{k=0}^{n}\frac{f^{\left(k\right)}\left(a\right)}{k!}\left(x-a\right)^{k}+\frac{f^{\left(n+1\right)}\left(\xi\right)}{\left(n+1\right)!}\left(x-a\right)^{n+1} \]

Proof:

by 連續函數極值定理 / 最大最小值定理 / 最小最大值定理 continuous function extreme value theorem = CFEVT / extreme value theorem = EVT $\ref{thm:EVT}$ and 連續函數介值定理 / 中間值定理 continuous function intermediate value theorem = CFIVT / intermediate value theorem = IVT $\ref{thm:IVT}$

\[\begin{eqnarray} \textrm{let }f\left(x\right) & = & \sum_{k=0}^{n}\frac{f^{\left(k\right)}\left(a\right)}{k!}\left(x-a\right)^{k}+r_{n}\left(x\right)\\ r_{n}\left(x\right) & = & \int_{a}^{x}f^{\left(n+1\right)}\left(t\right)\frac{\left(t-x\right)^{n}}{n!}\mathrm{d}t\\ \textrm{let }n & \in & \left\{ 2k-1|k\in\mathbb{N}\right\} \\ \textrm{let }f\left(t\right) & \overset{\ref{thm:EVT}}{\in} & \left[m,M\right]\subseteq f\left(\left(a,x\right)\right)\textrm{ when }a<x\\ \int_{a}^{x}m\frac{\left(t-x\right)^{n}}{n!}\mathrm{d}t\le & r_{n}\left(x\right) & \le\int_{a}^{x}M\frac{\left(t-x\right)^{n}}{n!}\mathrm{d}t\\ m\int_{a}^{x}\frac{\left(t-x\right)^{n}}{n!}\mathrm{d}t= & & =M\int_{a}^{x}\frac{\left(t-x\right)^{n}}{n!}\mathrm{d}t\\ m\left[\frac{\left(t-x\right)^{n+1}}{\left(n+1\right)!}\right]_{t=a}^{x}= & & =M\left[\frac{\left(t-x\right)^{n+1}}{\left(n+1\right)!}\right]_{t=a}^{x}\\ m\frac{\left(x-a\right)^{n+1}}{\left(n+1\right)!}= & & =M\frac{\left(x-a\right)^{n+1}}{\left(n+1\right)!}\\ & \Downarrow & \ref{thm:IVT}\\ r_{n}\left(x\right) & \overset{\exists\xi\in\left(a,x\right)}{=} & f^{\left(n+1\right)}\left(\xi\right)\frac{\left(x-a\right)^{n+1}}{\left(n+1\right)!}\\ f\left(x\right) & = & \sum_{k=0}^{n}\frac{f^{\left(k\right)}\left(a\right)}{k!}\left(x-a\right)^{k}+f^{\left(n+1\right)}\left(\xi\right)\frac{\left(x-a\right)^{n+1}}{\left(n+1\right)!}\\ & = & \sum_{k=0}^{n}\frac{f^{\left(k\right)}\left(a\right)}{k!}\left(x-a\right)^{k}+\frac{f^{\left(n+1\right)}\left(\xi\right)}{\left(n+1\right)!}\left(x-a\right)^{n+1} \end{eqnarray}\]

\[ \tag*{$\Box$} \]

Theorem 48.1 univariable Taylor theorem with the remainder in big O form

\[ f\left(a+h\right)=\sum_{k=0}^{n}\frac{f^{\left(k\right)}\left(a\right)}{k!}h^{k}+\mathrm{O}\left(h^{n+1}\right) \]

Proof:

\[\begin{eqnarray} \textrm{if }\left|f^{\left(n+1\right)}\left(t\right)\right| & \le & K\thinspace\forall t\in\left(a,x\right)\\ \left|r_{n}\left(x\right)\right|=\left|\frac{f^{\left(n+1\right)}\left(\xi\right)}{\left(n+1\right)!}\left(x-a\right)^{n+1}\right| & \le & \frac{K}{\left(n+1\right)!}\left|x-a\right|^{n+1}\\ r_{n}\left(x\right) & \in & \mathrm{O}\left(\left(x-a\right)^{n+1}\right)\\ \textrm{let }R_{n}\left(h\right) & = & r_{n}\left(a+h\right)\\ R_{n}\left(h\right) & \in & \mathrm{O}\left(h^{n+1}\right)\\ f\left(a+h\right) & = & \sum_{k=0}^{n}\frac{f^{\left(k\right)}\left(a\right)}{k!}h^{k}+\frac{f^{\left(n+1\right)}\left(\xi\right)}{\left(n+1\right)!}h^{n+1}\\ & = & \sum_{k=0}^{n}\frac{f^{\left(k\right)}\left(a\right)}{k!}h^{k}+\mathrm{O}\left(h^{n+1}\right) \end{eqnarray}\]

\[ \tag*{$\Box$} \]

\[ f\left(x\right)=\sum\limits _{k=0}^{n}\frac{f^{\left(k\right)}\left(a\right)}{k!}\left(x-a\right)^{k}+\int_{a}^{x}f^{\left(n+1\right)}\left(t\right)\frac{\left(x-t\right)^{n}}{n!}\mathrm{d}t \]

$f\left(x\right)=\sin\left(x\right)$

\[ \sin\left(x\right)=\sum\limits _{k=0}^{n}\frac{\sin^{\left(k\right)}\left(a\right)}{k!}\left(x-a\right)^{k}+\int_{a}^{x}\sin^{\left(n+1\right)}\left(t\right)\frac{\left(x-t\right)^{n}}{n!}\mathrm{d}t \]

$a=0$

\[ \sin\left(x\right)=\sum\limits _{k=0}^{n}\frac{\sin^{\left(k\right)}\left(0\right)}{k!}\left(x-0\right)^{k}+\int_{0}^{x}\sin^{\left(n+1\right)}\left(t\right)\frac{\left(x-t\right)^{n}}{n!}\mathrm{d}t \]

\[ \begin{aligned} \sin\left(x\right)= & \sum\limits _{k=0}^{n}\frac{\sin^{\left(k\right)}\left(0\right)}{k!}\left(x-0\right)^{k}+\int_{0}^{x}\sin^{\left(n+1\right)}\left(t\right)\frac{\left(x-t\right)^{n}}{n!}\mathrm{d}t\\ = & \sum\limits _{k=0}^{n}\frac{\sin^{\left(k\right)}\left(0\right)}{k!}x^{k}+\int_{0}^{x}\sin^{\left(n+1\right)}\left(t\right)\frac{\left(x-t\right)^{n}}{n!}\mathrm{d}t\\ = & \frac{\sin^{\left(0\right)}\left(0\right)}{0!}x^{0}+\frac{\sin^{\left(1\right)}\left(0\right)}{1!}x^{1}+\frac{\sin^{\left(2\right)}\left(0\right)}{2!}x^{2}+\frac{\sin^{\left(3\right)}\left(0\right)}{3!}x^{3}\\ & +\int_{0}^{x}\sin^{\left(3+1\right)}\left(t\right)\frac{\left(x-t\right)^{3}}{3!}\mathrm{d}t\\ = & \frac{0}{0!}x^{0}+\frac{\cos\left(0\right)}{1!}x^{1}+\frac{-\sin\left(0\right)}{2!}x^{2}+\frac{-\cos\left(0\right)}{3!}x^{3}\\ & +\int_{0}^{x}\sin^{\left(4\right)}\left(t\right)\frac{\left(x-t\right)^{3}}{3!}\mathrm{d}t\\ = & 0+\frac{1}{1}x+0-\frac{1}{6}x^{3}+\int_{0}^{x}\sin\left(t\right)\frac{\left(x-t\right)^{3}}{6}\mathrm{d}t\\ = & x-\frac{1}{6}x^{3}+\frac{1}{6}\int_{0}^{x}\left(x-t\right)^{3}\sin\left(t\right)\mathrm{d}t\\ \sin\left(x\right)= & x-\frac{1}{6}x^{3}+\frac{1}{6}\int_{0}^{x}\left(x-t\right)^{3}\sin\left(t\right)\mathrm{d}t \end{aligned} \]

\[ \begin{aligned} \sin\left(x\right)= & \sum\limits _{k=0}^{n}\frac{\sin^{\left(k\right)}\left(0\right)}{k!}\left(x-0\right)^{k}+\int_{0}^{x}\sin^{\left(n+1\right)}\left(t\right)\frac{\left(x-t\right)^{n}}{n!}\mathrm{d}t\\ = & \sum\limits _{k=0}^{n}\frac{\sin^{\left(k\right)}\left(0\right)}{k!}x^{k}+\int_{0}^{x}\sin^{\left(n+1\right)}\left(t\right)\frac{\left(x-t\right)^{n}}{n!}\mathrm{d}t\\ = & \frac{\sin^{\left(0\right)}\left(0\right)}{0!}x^{0}+\frac{\sin^{\left(1\right)}\left(0\right)}{1!}x^{1}+\frac{\sin^{\left(2\right)}\left(0\right)}{2!}x^{2}+\frac{\sin^{\left(3\right)}\left(0\right)}{3!}x^{3}+\frac{\sin^{\left(4\right)}\left(0\right)}{4!}x^{4}\\ & +\int_{0}^{x}\sin^{\left(4+1\right)}\left(t\right)\frac{\left(x-t\right)^{4}}{4!}\mathrm{d}t\\ = & \frac{0}{0!}x^{0}+\frac{\cos\left(0\right)}{1!}x^{1}+\frac{-\sin\left(0\right)}{2!}x^{2}+\frac{-\cos\left(0\right)}{3!}x^{3}+\frac{\sin\left(0\right)}{4!}x^{4}\\ & +\int_{0}^{x}\sin^{\left(5\right)}\left(t\right)\frac{\left(x-t\right)^{4}}{4!}\mathrm{d}t\\ = & 0+\frac{1}{1}x+0-\frac{1}{6}x^{3}+0+\int_{0}^{x}\cos\left(t\right)\frac{\left(x-t\right)^{4}}{24}\mathrm{d}t\\ = & x-\frac{1}{6}x^{3}+\frac{1}{24}\int_{0}^{x}\left(x-t\right)^{4}\cos\left(t\right)\mathrm{d}t\\ \sin\left(x\right)= & x-\frac{1}{6}x^{3}+\frac{1}{24}\int_{0}^{x}\left(x-t\right)^{4}\cos\left(t\right)\mathrm{d}t \end{aligned} \]

\[ \begin{aligned} \sin\left(x\right)= & x-\frac{1}{6}x^{3}+\frac{1}{6}\int_{0}^{x}\left(x-t\right)^{3}\sin\left(t\right)\mathrm{d}t\\ = & x-\frac{1}{6}x^{3}+\frac{1}{24}\int_{0}^{x}\left(x-t\right)^{4}\cos\left(t\right)\mathrm{d}t\\ \Downarrow\\ \frac{1}{6}\int_{0}^{x}\left(x-t\right)^{3}\sin\left(t\right)\mathrm{d}t= & \frac{1}{24}\int_{0}^{x}\left(x-t\right)^{4}\cos\left(t\right)\mathrm{d}t\\ \Downarrow\\ \int_{0}^{x}\left(x-t\right)^{4}\cos\left(t\right)\mathrm{d}t= & 4\int_{0}^{x}\left(x-t\right)^{3}\sin\left(t\right)\mathrm{d}t \end{aligned} \]

\[ f\left(x\right)=\sum\limits _{k=0}^{n}\frac{f^{\left(k\right)}\left(a\right)}{k!}\left(x-a\right)^{k}+\int_{a}^{x}f^{\left(n+1\right)}\left(t\right)\frac{\left(x-t\right)^{n}}{n!}\mathrm{d}t \]

$f\left(x\right)=\mathrm{e}^{x}=\exp\left(x\right)$

\[ \mathrm{e}^{x}=\sum\limits _{k=0}^{n}\frac{\exp^{\left(k\right)}\left(a\right)}{k!}\left(x-a\right)^{k}+\int_{a}^{x}\exp^{\left(n+1\right)}\left(t\right)\frac{\left(x-t\right)^{n}}{n!}\mathrm{d}t \]

$a=0$

\[ \mathrm{e}^{x}=\sum\limits _{k=0}^{n}\frac{\exp^{\left(k\right)}\left(0\right)}{k!}\left(x-0\right)^{k}+\int_{0}^{x}\exp^{\left(n+1\right)}\left(t\right)\frac{\left(x-t\right)^{n}}{n!}\mathrm{d}t \]

\[ \begin{aligned} \mathrm{e}^{x}= & \sum\limits _{k=0}^{n}\frac{\exp^{\left(k\right)}\left(0\right)}{k!}\left(x-0\right)^{k}+\int_{0}^{x}\exp^{\left(n+1\right)}\left(t\right)\frac{\left(x-t\right)^{n}}{n!}\mathrm{d}t\\ = & \sum\limits _{k=0}^{n}\frac{\exp^{\left(k\right)}\left(0\right)}{k!}x^{k}+\int_{0}^{x}\exp^{\left(n+1\right)}\left(t\right)\frac{\left(x-t\right)^{n}}{n!}\mathrm{d}t\\ = & \sum\limits _{k=0}^{n}\frac{\exp\left(0\right)}{k!}x^{k}+\int_{0}^{x}\exp\left(t\right)\frac{\left(x-t\right)^{n}}{n!}\mathrm{d}t\\ = & \sum\limits _{k=0}^{n}\frac{\mathrm{e}^{0}}{k!}x^{k}+\int_{0}^{x}\mathrm{e}^{t}\frac{\left(x-t\right)^{n}}{n!}\mathrm{d}t=\sum\limits _{k=0}^{n}\frac{1}{k!}x^{k}+\int_{0}^{x}\mathrm{e}^{t}\frac{\left(x-t\right)^{n}}{n!}\mathrm{d}t\\ = & \sum\limits _{k=0}^{n}\frac{x^{k}}{k!}+\frac{1}{n!}\int_{0}^{x}\left(x-t\right)^{n}\mathrm{e}^{t}\mathrm{d}t\\ \mathrm{e}^{x}= & \sum\limits _{k=0}^{n}\frac{x^{k}}{k!}+\frac{1}{n!}\int_{0}^{x}\left(x-t\right)^{n}\mathrm{e}^{t}\mathrm{d}t \end{aligned} \]

\[ \mathrm{e}^{x}=\sum\limits _{k=0}^{n}\frac{x^{k}}{k!}+\frac{1}{n!}\int_{0}^{x}\left(x-t\right)^{n}\mathrm{e}^{t}\mathrm{d}t \]

$\lim\limits _{n\rightarrow\infty}\dfrac{1+n+\dfrac{n^{2}}{2}+\cdots+\dfrac{n^{n}}{n!}}{\mathrm{e}^{n}}$

\[ \begin{aligned} & \lim\limits _{n\rightarrow\infty}\dfrac{1+n+\dfrac{n^{2}}{2}+\cdots+\dfrac{n^{n}}{n!}}{\mathrm{e}^{n}},\wedge\mathrm{e}^{x}=\sum\limits _{k=0}^{n}\frac{x^{k}}{k!}+\frac{1}{n!}\int_{0}^{x}\left(x-t\right)^{n}\mathrm{e}^{t}\mathrm{d}t\\ = & \lim\limits _{n\rightarrow\infty}\dfrac{\sum\limits _{k=0}^{n}\frac{n^{k}}{k!}}{\mathrm{e}^{n}},\wedge\mathrm{e}^{n}=\sum\limits _{k=0}^{n}\frac{n^{k}}{k!}+\frac{1}{n!}\int_{0}^{n}\left(n-t\right)^{n}\mathrm{e}^{t}\mathrm{d}t\Rightarrow\sum\limits _{k=0}^{n}\frac{n^{k}}{k!}=\mathrm{e}^{n}-\frac{1}{n!}\int_{0}^{n}\left(n-t\right)^{n}\mathrm{e}^{t}\mathrm{d}t\\ = & \lim\limits _{n\rightarrow\infty}\dfrac{\mathrm{e}^{n}-\frac{1}{n!}\int_{0}^{n}\left(n-t\right)^{n}\mathrm{e}^{t}\mathrm{d}t}{\mathrm{e}^{n}}=\lim\limits _{n\rightarrow\infty}\left[1-\frac{1}{n!}\int_{0}^{n}\left(n-t\right)^{n}\mathrm{e}^{t-n}\mathrm{d}t\right],\text{ if }\lim\limits _{n\rightarrow\infty}\frac{1}{n!}\int_{0}^{n}\left(t-n\right)^{n}\mathrm{e}^{t-n}\mathrm{d}t\in\mathbb{R}\\ = & \lim\limits _{n\rightarrow\infty}1-\lim\limits _{n\rightarrow\infty}\frac{1}{n!}\int_{0}^{n}\left(n-t\right)^{n}\mathrm{e}^{t-n}\mathrm{d}t=1-\lim\limits _{n\rightarrow\infty}\frac{1}{n!}\int_{0}^{n}\left(n-t\right)^{n}\mathrm{e}^{t-n}\mathrm{d}t \end{aligned} \]

$\lim\limits _{n\rightarrow\infty}\frac{1}{n!}\int_{0}^{n}\left(n-t\right)^{n}\mathrm{e}^{t-n}\mathrm{d}t$

\[ \begin{aligned} & \lim\limits _{n\rightarrow\infty}\frac{1}{n!}\int_{0}^{n}\left(n-t\right)^{n}\mathrm{e}^{t-n}\mathrm{d}t,x=n-t\\ = & \lim\limits _{n\rightarrow\infty}\frac{1}{n!}\int_{t=0}^{t=n}\left(n-t\right)^{n}\mathrm{e}^{t-n}\mathrm{d}t,t=n-x\\ = & \lim\limits _{n\rightarrow\infty}\frac{1}{n!}\int_{n-x=0}^{n-x=n}\left(n-\left(n-x\right)\right)^{n}\mathrm{e}^{\left(n-x\right)-n}\mathrm{d}\left(n-x\right)\\ = & \lim\limits _{n\rightarrow\infty}\frac{1}{n!}\left(-\int_{x=n}^{x=0}x^{n}\mathrm{e}^{-x}\mathrm{d}x\right)=\lim\limits _{n\rightarrow\infty}\frac{1}{n!}\left(\int_{x=0}^{x=n}x^{n}\mathrm{e}^{-x}\mathrm{d}x\right)\\ = & \lim\limits _{n\rightarrow\infty}\frac{1}{n!}\int_{0}^{n}x^{n}\mathrm{e}^{-x}\mathrm{d}x \end{aligned} \]

$\int x^{n}\mathrm{e}^{-x}\mathrm{d}x$

difficult process

\[ \begin{aligned} \int x^{n}\mathrm{e}^{-x}\mathrm{d}x= & -\int x^{n}\mathrm{d}\mathrm{e}^{-x}\\ = & -\left[x^{n}\mathrm{e}^{-x}-\int\mathrm{e}^{-x}\mathrm{d}x^{n}\right]\\ = & -\left[x^{n}\mathrm{e}^{-x}-\int\mathrm{e}^{-x}nx^{n-1}\mathrm{d}x\right]\\ = & -x^{n}\mathrm{e}^{-x}+n\int x^{n-1}\mathrm{e}^{-x}\mathrm{d}x \end{aligned} \]

\[ \int x^{n}\mathrm{e}^{-x}\mathrm{d}x=-x^{n}\mathrm{e}^{-x}+n\int x^{n-1}\mathrm{e}^{-x}\mathrm{d}x \]

\[ \begin{aligned} \int_{0}^{n}x^{n}\mathrm{e}^{-x}\mathrm{d}x= & \left[-x^{n}\mathrm{e}^{-x}\right]_{x=0}^{n}+n\int_{0}^{n}x^{n-1}\mathrm{e}^{-x}\mathrm{d}x\\ = & \left[-n^{n}\mathrm{e}^{-n}-\left(-0^{n}\mathrm{e}^{-0}\right)\right]+n\int_{0}^{n}x^{n-1}\mathrm{e}^{-x}\mathrm{d}x\\ = & -n^{n}\mathrm{e}^{-n}+n\int_{0}^{n}x^{n-1}\mathrm{e}^{-x}\mathrm{d}x \end{aligned} \]

\[ \int_{0}^{n}x^{n}\mathrm{e}^{-x}\mathrm{d}x=-n^{n}\mathrm{e}^{-n}+n\int_{0}^{n}x^{n-1}\mathrm{e}^{-x}\mathrm{d}x \]

more formal process with gamma function

https://www.wolframalpha.com/input?i2d=true&i=Divide%5BIntegrate%5BPower%5Bx%2Cn%5DPower%5Be%2C-x%5D%2C%7Bx%2C0%2Cn%7D%5D%2Cn%21%5D

https://www.wolframalpha.com/input?i2d=true&i=Limit%5BDivide%5BIntegrate%5BPower%5Bx%2Cn%5DPower%5Be%2C-x%5D%2C%7Bx%2C0%2Cn%7D%5D%2Cn%21%5D%2Cn-%3E%E2%88%9E%5D

\[ \text{to be proved} \]

https://www.bilibili.com/video/BV1du411a7qB

48.1.1 Elliot Schneider: Taylor series

https://www.youtube.com/watch?v=HQsZG8Yxb7w

https://www.youtube.com/watch?v=HQsZG8Yxb7w&t=12m25s

\[ f\left(x\right)=\sum\limits _{k=0}^{n}\frac{f^{\left(k\right)}\left(x_{{\scriptscriptstyle 0}}\right)}{k!}\left(x-x_{{\scriptscriptstyle 0}}\right)^{k}+\frac{f^{\left(n+1\right)}\left(\xi\right)}{\left(n+1\right)!}\left(x-x_{{\scriptscriptstyle 0}}\right)^{n+1} \]

\[ f\left(x_{{\scriptscriptstyle 0}}+\epsilon\right)=\sum\limits _{k=0}^{n}\frac{f^{\left(k\right)}\left(x_{{\scriptscriptstyle 0}}\right)}{k!}\epsilon^{k}+\mathrm{O}\left(\epsilon^{n+1}\right),\epsilon=x-x_{{\scriptscriptstyle 0}} \]

\[ f\left(x+\epsilon\right)=\sum\limits _{n=0}^{\infty}\frac{f^{\left(n\right)}\left(x\right)}{n!}\epsilon^{n} \]

\[ \begin{aligned} f\left(x+\epsilon\right)= & \sum\limits _{n=0}^{\infty}\frac{f^{\left(n\right)}\left(x\right)}{n!}\epsilon^{n}=\sum\limits _{n=0}^{\infty}\frac{\dfrac{\mathrm{d}^{n}}{\mathrm{d}x^{n}}f\left(x\right)}{n!}\epsilon^{n}=\sum\limits _{n=0}^{\infty}\frac{\left(\dfrac{\mathrm{d}}{\mathrm{d}x}\right)^{n}f\left(x\right)}{n!}\epsilon^{n}\\ = & \sum\limits _{n=0}^{\infty}\frac{\left(\epsilon\dfrac{\mathrm{d}}{\mathrm{d}x}\right)^{n}f\left(x\right)}{n!}=\left(\sum\limits _{n=0}^{\infty}\frac{\left(\epsilon\dfrac{\mathrm{d}}{\mathrm{d}x}\right)^{n}}{n!}\right)f\left(x\right)=\mathrm{e}^{{\scriptscriptstyle \epsilon\frac{\mathrm{d}}{\mathrm{d}x}}}f\left(x\right) \end{aligned} \]

univariable Taylor operator

\[ f\left(x+\epsilon\right)=\mathrm{e}^{{\scriptscriptstyle \epsilon\frac{\mathrm{d}}{\mathrm{d}x}}}f\left(x\right) \]

\[ \mathrm{e}^{{\scriptscriptstyle \epsilon\frac{\mathrm{d}}{\mathrm{d}x}}}=\sum\limits _{n=0}^{\infty}\frac{\left(\epsilon\dfrac{\mathrm{d}}{\mathrm{d}x}\right)^{n}}{n!}=1+\epsilon\dfrac{\mathrm{d}}{\mathrm{d}x}+\dfrac{1}{2}\epsilon^{2}\dfrac{\mathrm{d}^{2}}{\mathrm{d}x^{2}}+\cdots \]

$f\left(x\right)=mx+b$,

\[ \begin{aligned} \mathrm{e}^{{\scriptscriptstyle \epsilon\frac{\mathrm{d}}{\mathrm{d}x}}}f\left(x\right)= & \left(1+\epsilon\dfrac{\mathrm{d}}{\mathrm{d}x}+\dfrac{1}{2}\epsilon^{2}\dfrac{\mathrm{d}^{2}}{\mathrm{d}x^{2}}+\cdots\right)\left(mx+b\right)\\ = & 1\left(mx+b\right)+\epsilon\dfrac{\mathrm{d}}{\mathrm{d}x}\left(mx+b\right)+\dfrac{1}{2}\epsilon^{2}\dfrac{\mathrm{d}^{2}}{\mathrm{d}x^{2}}\left(mx+b\right)+\cdots\\ = & \left(mx+b\right)+\left(\epsilon m\right)+\left(\dfrac{1}{2}\epsilon^{2}0\right)+\left(0+0+\cdots\right)\\ = & \left(mx+b\right)+\left(\epsilon m\right)+\left(0+0+\cdots\right)\\ = & \left(mx+b\right)+\left(\epsilon m\right)+0\\ = & mx+b+m\epsilon=m\left(x+\epsilon\right)+b=f\left(x+\epsilon\right) \end{aligned} \]

https://www.youtube.com/watch?v=HQsZG8Yxb7w&t=15m34s

multivariable …

\[ \begin{aligned} f\left(x+\epsilon\right)= & \mathrm{e}^{{\scriptscriptstyle \epsilon\frac{\mathrm{d}}{\mathrm{d}x}}}f\left(x\right)\\ f\left(x+\epsilon_{{\scriptscriptstyle x}},y+\epsilon_{{\scriptscriptstyle y}},z+\epsilon_{{\scriptscriptstyle z}}\right)= & f\left(x,y+\epsilon_{{\scriptscriptstyle y}},z+\epsilon_{{\scriptscriptstyle z}}\right)\\ + & \epsilon\dfrac{\partial}{\partial x}f\left(x,y+\epsilon_{{\scriptscriptstyle y}},z+\epsilon_{{\scriptscriptstyle z}}\right)\\ + & \dfrac{1}{2}\epsilon^{2}\dfrac{\partial^{2}}{\partial x^{2}}f\left(x,y+\epsilon_{{\scriptscriptstyle y}},z+\epsilon_{{\scriptscriptstyle z}}\right)\\ + & \cdots \end{aligned} \]

\[ \begin{aligned} f\left(x+\epsilon\right)= & \mathrm{e}^{{\scriptscriptstyle \epsilon\frac{\mathrm{d}}{\mathrm{d}x}}}f\left(x\right)\\ f\left(x+\epsilon_{{\scriptscriptstyle x}},y+\epsilon_{{\scriptscriptstyle y}},z+\epsilon_{{\scriptscriptstyle z}}\right)=f\left(\boldsymbol{r}+\boldsymbol{\epsilon}\right)= & \mathrm{e}^{{\scriptscriptstyle \boldsymbol{\epsilon}\cdot\boldsymbol{\nabla}}}f\left(\boldsymbol{r}\right),\begin{cases} \boldsymbol{r}=\left(x,y,z\right)\\ \boldsymbol{\epsilon}=\left(\epsilon_{{\scriptscriptstyle x}},\epsilon_{{\scriptscriptstyle y}},\epsilon_{{\scriptscriptstyle z}}\right)\\ \boldsymbol{\nabla}=\left(\dfrac{\partial}{\partial x},\dfrac{\partial}{\partial y},\dfrac{\partial}{\partial z}\right) \end{cases} \end{aligned} \]

\[ \boldsymbol{\epsilon}\cdot\boldsymbol{\nabla}=\left(\epsilon_{{\scriptscriptstyle x}},\epsilon_{{\scriptscriptstyle y}},\epsilon_{{\scriptscriptstyle z}}\right)\cdot\left(\dfrac{\partial}{\partial x},\dfrac{\partial}{\partial y},\dfrac{\partial}{\partial z}\right)=\epsilon_{{\scriptscriptstyle x}}\dfrac{\partial}{\partial x}+\epsilon_{{\scriptscriptstyle y}}\dfrac{\partial}{\partial y}+\epsilon_{{\scriptscriptstyle z}}\dfrac{\partial}{\partial z} \]

multivariable Taylor operator

\[ f\left(\boldsymbol{r}+\boldsymbol{\epsilon}\right)=\mathrm{e}^{{\scriptscriptstyle \boldsymbol{\epsilon}\cdot\boldsymbol{\nabla}}}f\left(\boldsymbol{r}\right) \]

https://www.youtube.com/watch?v=HQsZG8Yxb7w&t=17m36s

physics

48.1.1.1 making complicated equastion simple

linearize

simple pendulum

sin(x) to x linearization

potential energy

\[ f\left(x_{{\scriptscriptstyle 0}}+\epsilon\right)=\sum\limits _{k=0}^{n}\frac{f^{\left(k\right)}\left(x_{{\scriptscriptstyle 0}}\right)}{k!}\epsilon^{k}+\mathrm{O}\left(\epsilon^{n+1}\right) \]

\[ U\left(x_{{\scriptscriptstyle 0}}+\epsilon\right)=\sum\limits _{k=0}^{n}\frac{U^{\left(k\right)}\left(x_{{\scriptscriptstyle 0}}\right)}{k!}\epsilon^{k}+\mathrm{O}\left(\epsilon^{n+1}\right)=U\left(x_{{\scriptscriptstyle 0}}\right)+U^{\prime}\left(x_{{\scriptscriptstyle 0}}\right)x+\dfrac{1}{2}U^{\prime\prime}\left(x_{{\scriptscriptstyle 0}}\right)x^{2}+\cdots \]

\[ F=\dfrac{-\mathrm{d}U}{\mathrm{d}x}=-U^{\prime}\left(x_{{\scriptscriptstyle 0}}\right)-U^{\prime\prime}\left(x_{{\scriptscriptstyle 0}}\right)x-\cdots\overset{\text{if }U^{\prime}\left(x_{{\scriptscriptstyle 0}}\right)=0}{=}-U^{\prime\prime}\left(x_{{\scriptscriptstyle 0}}\right)x=-kx,k=U^{\prime\prime}\left(x_{{\scriptscriptstyle 0}}\right) \]

48.1.1.2 non-relativistic limit

https://www.youtube.com/watch?v=HQsZG8Yxb7w&t=22m32s

\[ \begin{aligned} E= & \sqrt{\left(mc^{2}\right)^{2}+\left(pc\right)^{2}}=\sqrt{m^{2}c^{4}+p^{2}c^{2}}\\ = & mc^{2}\sqrt{1+\left(\dfrac{pc}{mc^{2}}\right)^{2}}=mc^{2}\sqrt{1+\left(\dfrac{p}{mc}\right)^{2}}=mc^{2}\left(1+\left(\dfrac{p}{mc}\right)^{2}\right)^{\frac{1}{2}}\\ = & mc^{2}\left[\dfrac{1}{0!}+\dfrac{1}{1!}\left(\dfrac{1}{2}\right)\left(\left(\dfrac{p}{mc}\right)^{2}\right)^{1}+\dfrac{1}{2!}\left(\dfrac{1}{2}\right)\left(\dfrac{1}{2}-1\right)\left(\left(\dfrac{p}{mc}\right)^{2}\right)^{2}+\cdots\right]\\ = & mc^{2}\left[1+\dfrac{1}{2}\left(\dfrac{p}{mc}\right)^{2}-\dfrac{1}{8}\left(\dfrac{p}{mc}\right)^{4}+\cdots\right]=mc^{2}\left[1+\dfrac{1}{2}\dfrac{p^{2}}{m^{2}c^{2}}-\dfrac{1}{8}\dfrac{p^{4}}{m^{4}c^{4}}+\cdots\right]\\ = & mc^{2}+\dfrac{1}{2}\dfrac{p^{2}}{m}-\dfrac{1}{8}\dfrac{p^{4}}{m^{3}c^{2}}+\cdots=mc^{2}+\dfrac{p^{2}}{2m}-\dfrac{p^{4}}{8m^{3}c^{2}}+\cdots\\ = & E_{{\scriptscriptstyle 0}}+\dfrac{p^{2}}{2m}-\dfrac{p^{4}}{8m^{3}c^{2}}+\cdots,\begin{cases} E_{{\scriptscriptstyle 0}}=mc^{2}\\ \dfrac{p^{2}}{2m}=\dfrac{\left(mv\right)^{2}}{2m}=\dfrac{mv^{2}}{2}=\dfrac{1}{2}mv^{2} \end{cases} \end{aligned} \]

sluppy here $p=\gamma mv$

https://www.youtube.com/watch?v=HQsZG8Yxb7w&t=24m50s

leading relativistic correction

\[ -\dfrac{p^{4}}{8m^{3}c^{2}} \]

binding energy of hydrogen atom

https://www.youtube.com/watch?v=HQsZG8Yxb7w&t=25m40s

fine-structure constant

48.1.1.3 quantum momentum operator

https://www.youtube.com/watch?v=HQsZG8Yxb7w&t=29m13s

48.2 Dirac delta function

https://www.bilibili.com/video/BV1qu411578c

Dirac function = Dirac delta function

https://tikz.net/delta_function/

https://tikz.dev/tikz-arrows

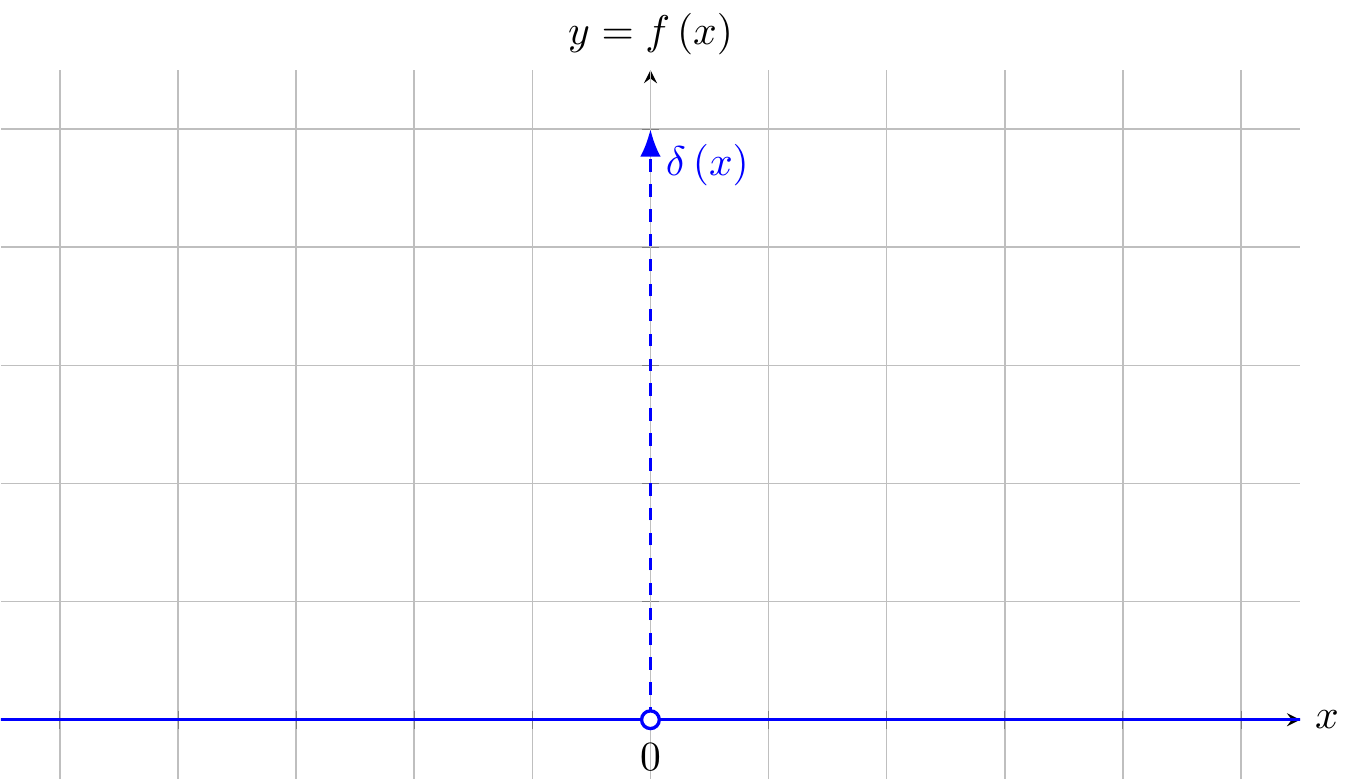
Fig. 24.4: Dirac function = Dirac delta function

\[ \delta\left(x\right)=\begin{cases} 0 & x\ne0\\ \infty & x=0 \end{cases},\int_{-\infty}^{\infty}\delta\left(x\right)\mathrm{d}x=1 \]

\[ \mathrm{supp}\left(f\right)=\left\{ x\middle|\begin{cases} x\in\mathcal{D}\\ f\left(x\right)\ne0 \end{cases}\right\} \]

\[ \mathrm{supp}\left(\delta\right)=\left\{ x\middle|\begin{cases} x\in\mathcal{D}=\mathbb{R}\\ \delta\left(x\right)\ne0 \end{cases}\right\} =\left\{ 0\right\} \]

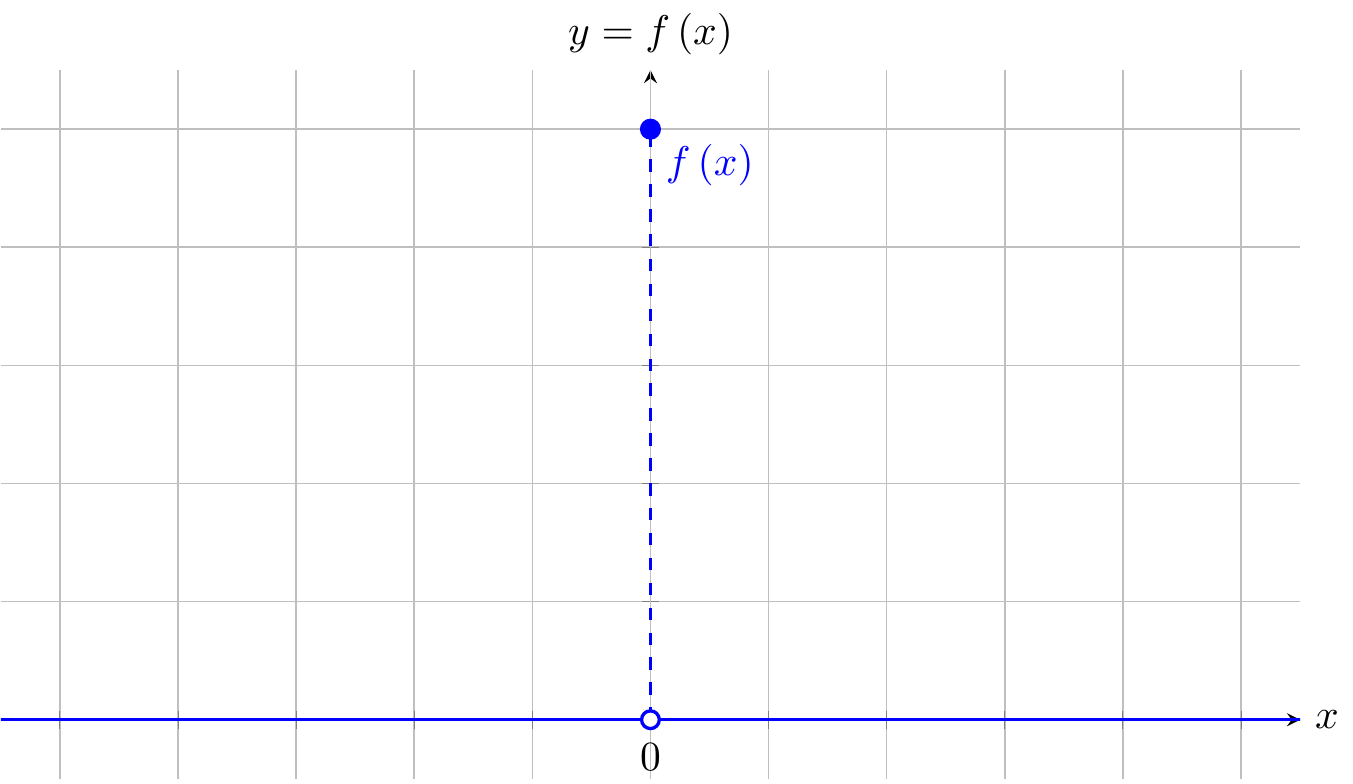
$f(x)=1 \text{ if } x=0 \text{ else } 0$

Fig. 48.1: $f(x)=1 \text{ if } x=0 \text{ else } 0$

\[ f\left(x\right)=\begin{cases} 0 & x\ne0\\ 1 & x=0 \end{cases} \]

https://tex.stackexchange.com/questions/45275/tikz-get-values-for-predefined-dash-patterns

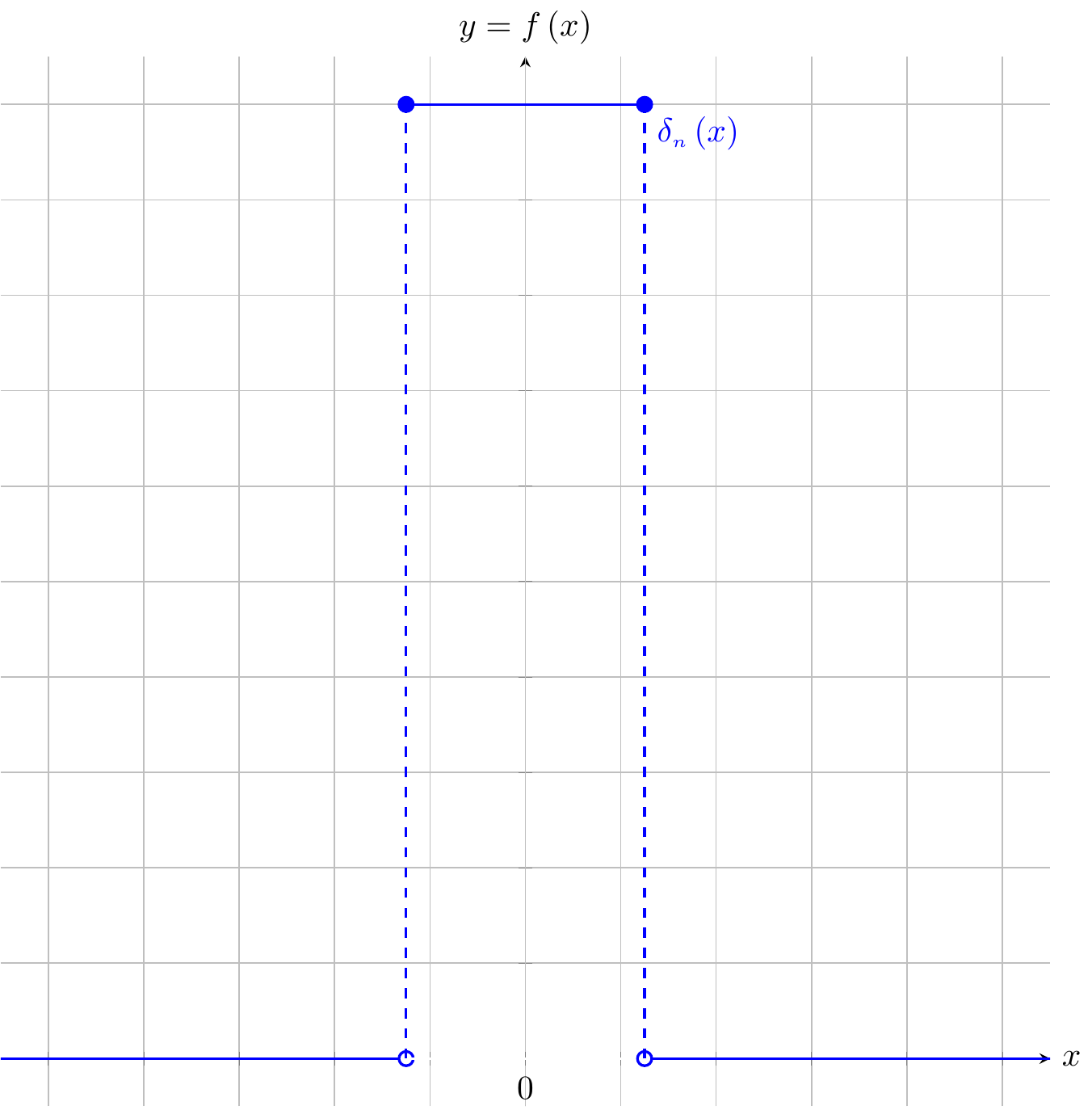
$\delta_{{\scriptscriptstyle n}}\left(x\right)$

Fig. 48.2: $\delta_{{\scriptscriptstyle n}}\left(x\right)$

\[ \delta_{{\scriptscriptstyle n}}\left(x\right)=\begin{cases} 0 & \left|x\right|>\dfrac{1}{2n}\\ n & \left|x\right|\le\dfrac{1}{2n} \end{cases},\forall n\in\mathbb{N} \]

\[ \delta\left(x\right)=\left\{ \delta_{{\scriptscriptstyle n}}\left(x\right)\middle|n\in\mathbb{N}\right\} =\left\{ \delta_{{\scriptscriptstyle 1}}\left(x\right),\delta_{{\scriptscriptstyle 2}}\left(x\right),\cdots\right\} =\lim\limits _{n\rightarrow\infty}\delta_{{\scriptscriptstyle n}}\left(x\right) \]

\[ \delta_{{\scriptscriptstyle n}}\left(x\right)=\begin{cases} 0 & \left|x\right|>\dfrac{1}{2n}\Leftrightarrow\begin{cases} x>\dfrac{1}{2n}\\ x<\dfrac{-1}{2n} \end{cases}\\ n & \left|x\right|\le\dfrac{1}{2n}\Leftrightarrow\dfrac{-1}{2n}\le x\le\dfrac{1}{2n}\Leftrightarrow x\in\left[\dfrac{-1}{2n},\dfrac{1}{2n}\right] \end{cases},\forall n\in\mathbb{N} \]

\[ \int_{-\infty}^{\infty}\delta_{{\scriptscriptstyle n}}\left(x\right)\mathrm{d}x=\int_{-\frac{1}{2n}}^{\frac{1}{2n}}n\mathrm{d}x=n\int_{-\frac{1}{2n}}^{\frac{1}{2n}}\mathrm{d}x=n\left[x\right]_{\frac{-1}{2n}}^{\frac{1}{2n}}=n\left[\frac{1}{2n}-\frac{-1}{2n}\right]=n\cdot\dfrac{1}{n}=1 \]

\[ \begin{aligned} \int_{-\infty}^{\infty}\delta\left(x\right)f\left(x\right)\mathrm{d}x= & \lim\limits _{n\rightarrow\infty}\int_{-\infty}^{\infty}\delta_{{\scriptscriptstyle n}}\left(x\right)f\left(x\right)\mathrm{d}x\\ = & \lim\limits _{n\rightarrow\infty}\int_{-\frac{1}{2n}}^{\frac{1}{2n}}\delta_{{\scriptscriptstyle n}}\left(x\right)f\left(x\right)\mathrm{d}x\\ = & \lim\limits _{n\rightarrow\infty}\int_{-\frac{1}{2n}}^{\frac{1}{2n}}nf\left(x\right)\mathrm{d}x,\begin{cases} f\left(x\right)\in\left[m,M\right]\subseteq f\left(\left[\dfrac{-1}{2n},\dfrac{1}{2n}\right]\right)\\ \Downarrow\\ m\le f\left(x\right)\le M \end{cases}\\ \int_{-\frac{1}{2n}}^{\frac{1}{2n}}nm\mathrm{d}x\le & \int_{-\frac{1}{2n}}^{\frac{1}{2n}}nf\left(x\right)\mathrm{d}x\le\int_{-\frac{1}{2n}}^{\frac{1}{2n}}nM\mathrm{d}x\\ m=m\cdot1=m\int_{-\frac{1}{2n}}^{\frac{1}{2n}}n\mathrm{d}x\le & \int_{-\frac{1}{2n}}^{\frac{1}{2n}}nf\left(x\right)\mathrm{d}x\le M\int_{-\frac{1}{2n}}^{\frac{1}{2n}}n\mathrm{d}x=M\cdot1=M\\ \Downarrow & \ref{thm:IVT}\\ \int_{-\frac{1}{2n}}^{\frac{1}{2n}}nf\left(x\right)\mathrm{d}x\overset{\exists\xi_{{\scriptscriptstyle n}}\in\left(\frac{-1}{2n},\frac{1}{2n}\right)}{=} & f\left(\xi_{{\scriptscriptstyle n}}\right)\int_{-\frac{1}{2n}}^{\frac{1}{2n}}n\mathrm{d}x=f\left(\xi_{{\scriptscriptstyle n}}\right)\cdot1=f\left(\xi_{{\scriptscriptstyle n}}\right)\\ \int_{-\infty}^{\infty}\delta\left(x\right)f\left(x\right)\mathrm{d}x=\lim\limits _{n\rightarrow\infty}\int_{-\frac{1}{2n}}^{\frac{1}{2n}}nf\left(x\right)\mathrm{d}x= & \lim\limits _{n\rightarrow\infty}f\left(\xi_{{\scriptscriptstyle n}}\right),\xi_{{\scriptscriptstyle n}}\in\left(\frac{-1}{2n},\frac{1}{2n}\right)\\ = & f\left(0\right)\\ \int_{-\infty}^{\infty}\delta\left(x\right)f\left(x\right)\mathrm{d}x= & f\left(0\right) \end{aligned} \]

\[ \int_{-\infty}^{\infty}\delta\left(x\right)f\left(x\right)\mathrm{d}x=f\left(0\right) \]

$\int_{-\infty}^{\infty}\delta\left(x\right)f\left(x\right)\mathrm{d}x=f\left(0\right)$

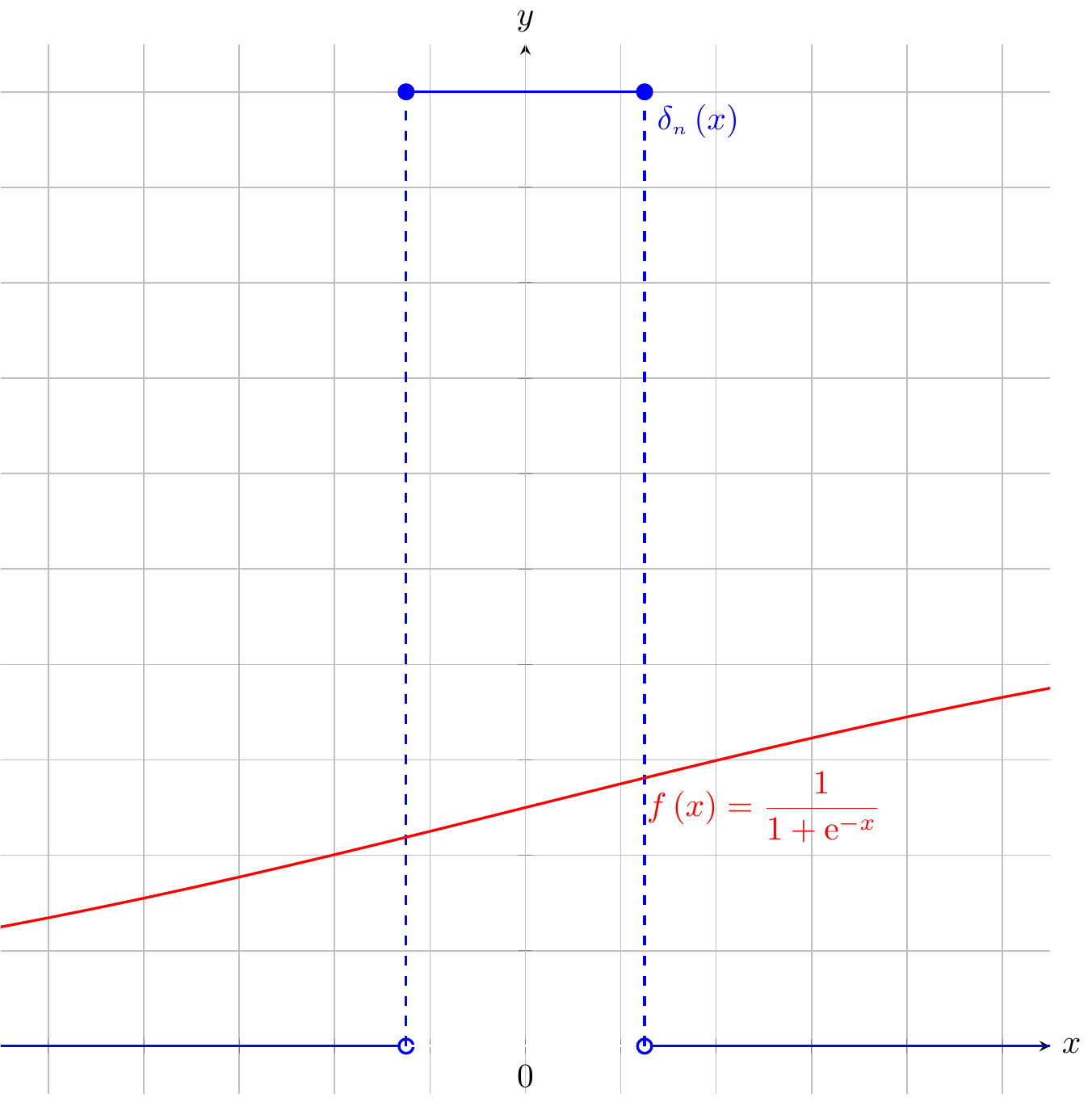
Fig. 48.3: $\int_{-\infty}^{\infty}\delta\left(x\right)f\left(x\right)\mathrm{d}x=f\left(0\right)$

\[ \begin{aligned} \int_{-\infty}^{\infty}\delta\left(x\right)f\left(x\right)\mathrm{d}x= & \lim\limits _{n\rightarrow\infty}\int_{-\frac{1}{2n}}^{\frac{1}{2n}}\delta_{{\scriptscriptstyle n}}\left(x\right)f\left(x\right)\mathrm{d}x\\ = & \lim\limits _{n\rightarrow\infty}\int_{-\frac{1}{2n}}^{\frac{1}{2n}}nf\left(x\right)\mathrm{d}x\\ = & \lim\limits _{n\rightarrow\infty}f\left(\xi_{{\scriptscriptstyle n}}\right),\xi_{{\scriptscriptstyle n}}\in\left(\frac{-1}{2n},\frac{1}{2n}\right) \end{aligned} \]

\[ \int_{-\infty}^{\infty}\delta\left(x\right)f\left(x\right)\mathrm{d}x=f\left(0\right) \]

\[ \int_{-\infty}^{\infty}\delta\left(x-0\right)f\left(x\right)\mathrm{d}x=f\left(0\right) \]

\[ \int_{-\infty}^{\infty}\delta\left(x\right)f\left(x\right)\mathrm{d}x=f\left(0\right) \]

\[ \int_{-\infty}^{\infty}\delta\left(x-0\right)f\left(x\right)\mathrm{d}x=f\left(0\right) \]

https://math.stackexchange.com/questions/73010/proof-of-dirac-deltas-sifting-property

https://www.youtube.com/watch?v=2QaRZ7u-BgM

SIFTing property

SIFT = scale-invariant feature transform

https://en.wikipedia.org/wiki/Scale-invariant_feature_transform

Proof:

Similarly to:

$f\left(x\right)\in\left[m,M\right]\subseteq f\left(\left[x_{{\scriptscriptstyle 0}}-\frac{1}{2n},x_{{\scriptscriptstyle 0}}+\frac{1}{2n}\right]\right)$,

\[ \begin{aligned} \int_{-\infty}^{\infty}\delta\left(x-x_{{\scriptscriptstyle 0}}\right)f\left(x\right)\mathrm{d}x= & \lim\limits _{n\rightarrow\infty}\int_{-\infty}^{\infty}\delta_{{\scriptscriptstyle n}}\left(x-x_{{\scriptscriptstyle 0}}\right)f\left(x\right)\mathrm{d}x\\ =\lim\limits _{n\rightarrow\infty}\Biggl[\int_{-\infty}^{x_{{\scriptscriptstyle 0}}-\frac{1}{2n}}\delta_{{\scriptscriptstyle n}}\left(x-x_{{\scriptscriptstyle 0}}\right)f\left(x\right)\mathrm{d}x+ & \int_{x_{{\scriptscriptstyle 0}}-\frac{1}{2n}}^{x_{{\scriptscriptstyle 0}}+\frac{1}{2n}}\delta_{{\scriptscriptstyle n}}\left(x-x_{{\scriptscriptstyle 0}}\right)f\left(x\right)\mathrm{d}x+\lim\limits _{n\rightarrow\infty}\int_{x_{{\scriptscriptstyle 0}}+\frac{1}{2n}}^{\infty}\delta_{{\scriptscriptstyle n}}\left(x-x_{{\scriptscriptstyle 0}}\right)f\left(x\right)\mathrm{d}x\Biggr]\\ =\lim\limits _{n\rightarrow\infty}\Biggl[\int_{-\infty}^{x_{{\scriptscriptstyle 0}}-\frac{1}{2n}}0f\left(x\right)\mathrm{d}x+ & \int_{x_{{\scriptscriptstyle 0}}-\frac{1}{2n}}^{x_{{\scriptscriptstyle 0}}+\frac{1}{2n}}nf\left(x\right)\mathrm{d}x+\lim\limits _{n\rightarrow\infty}\int_{x_{{\scriptscriptstyle 0}}+\frac{1}{2n}}^{\infty}0f\left(x\right)\mathrm{d}x\Biggr]\\ = & \lim\limits _{n\rightarrow\infty}\int_{x_{{\scriptscriptstyle 0}}-\frac{1}{2n}}^{x_{{\scriptscriptstyle 0}}+\frac{1}{2n}}nf\left(x\right)\mathrm{d}x,\begin{cases} f\left(x\right)\in\left[m,M\right]\subseteq f\left(\left[x_{{\scriptscriptstyle 0}}-\frac{1}{2n},x_{{\scriptscriptstyle 0}}+\frac{1}{2n}\right]\right)\\ \Downarrow\\ m\le f\left(x\right)\le M \end{cases}\\ \int_{x_{{\scriptscriptstyle 0}}-\frac{1}{2n}}^{x_{{\scriptscriptstyle 0}}+\frac{1}{2n}}nm\mathrm{d}x\le & \int_{x_{{\scriptscriptstyle 0}}-\frac{1}{2n}}^{x_{{\scriptscriptstyle 0}}+\frac{1}{2n}}nf\left(x\right)\mathrm{d}x\le\int_{x_{{\scriptscriptstyle 0}}-\frac{1}{2n}}^{x_{{\scriptscriptstyle 0}}+\frac{1}{2n}}nM\mathrm{d}x\\ m=m\cdot1=m\int_{x_{{\scriptscriptstyle 0}}-\frac{1}{2n}}^{x_{{\scriptscriptstyle 0}}+\frac{1}{2n}}n\mathrm{d}x\le & \int_{x_{{\scriptscriptstyle 0}}-\frac{1}{2n}}^{x_{{\scriptscriptstyle 0}}+\frac{1}{2n}}nf\left(x\right)\mathrm{d}x\le M\int_{x_{{\scriptscriptstyle 0}}-\frac{1}{2n}}^{x_{{\scriptscriptstyle 0}}+\frac{1}{2n}}n\mathrm{d}x=M\cdot1=M\\ \Downarrow & \ref{thm:IVT}\\ \int_{x_{{\scriptscriptstyle 0}}-\frac{1}{2n}}^{x_{{\scriptscriptstyle 0}}+\frac{1}{2n}}nf\left(x\right)\mathrm{d}x\overset{\exists\xi_{{\scriptscriptstyle n}}\in\left(x_{{\scriptscriptstyle 0}}-\frac{1}{2n},x_{{\scriptscriptstyle 0}}+\frac{1}{2n}\right)}{=} & f\left(\xi_{{\scriptscriptstyle n}}\right)\int_{x_{{\scriptscriptstyle 0}}-\frac{1}{2n}}^{x_{{\scriptscriptstyle 0}}+\frac{1}{2n}}n\mathrm{d}x=f\left(\xi_{{\scriptscriptstyle n}}\right)\cdot1=f\left(\xi_{{\scriptscriptstyle n}}\right)\\ \int_{-\infty}^{\infty}\delta\left(x\right)f\left(x\right)\mathrm{d}x=\lim\limits _{n\rightarrow\infty}\int_{x_{{\scriptscriptstyle 0}}-\frac{1}{2n}}^{x_{{\scriptscriptstyle 0}}+\frac{1}{2n}}nf\left(x\right)\mathrm{d}x= & \lim\limits _{n\rightarrow\infty}f\left(\xi_{{\scriptscriptstyle n}}\right),\xi_{{\scriptscriptstyle n}}\in\left(x_{{\scriptscriptstyle 0}}-\frac{1}{2n},x_{{\scriptscriptstyle 0}}+\frac{1}{2n}\right)\\ = & f\left(x_{{\scriptscriptstyle 0}}\right)\\ \int_{-\infty}^{\infty}\delta\left(x-x_{{\scriptscriptstyle 0}}\right)f\left(x\right)\mathrm{d}x= & f\left(x_{{\scriptscriptstyle 0}}\right) \end{aligned} \]

\[ \int_{-\infty}^{\infty}\delta\left(x-x_{{\scriptscriptstyle 0}}\right)f\left(x\right)\mathrm{d}x=f\left(x_{{\scriptscriptstyle 0}}\right) \]

\[ \tag*{$\Box$} \]

\[ \int_{-\infty}^{\infty}\delta\left(x-x_{{\scriptscriptstyle 0}}\right)f\left(x\right)\mathrm{d}x=f\left(x_{{\scriptscriptstyle 0}}\right) \]

\[ \int_{-\infty}^{\infty}\delta\left(x-x^{\prime}\right)f\left(x\right)\mathrm{d}x=f\left(x^{\prime}\right) \]

https://www.youtube.com/watch?v=nDa3cqFk80o

\[ \begin{aligned} & \left\{ \left\{ f_{{\scriptscriptstyle n}}\left(x\right)\middle|n\in\mathbb{N}\right\} \middle|\begin{cases} f_{{\scriptscriptstyle n}}:\mathbb{R}\rightarrow\mathbb{R}\\ \int_{-\infty}^{\infty}f_{{\scriptscriptstyle n}}\left(x\right)\mathrm{d}x=1 \end{cases}\right\} \\ =\Biggl\{ & \left\{ \dfrac{n}{2}\mathrm{e}^{-n\left|x\right|}\middle|n\in\mathbb{N}\right\} ,\\ & \left\{ \dfrac{1}{\pi}\dfrac{n}{n^{2}x^{2}+1}\middle|n\in\mathbb{N}\right\} ,\\ & \left\{ \dfrac{n}{\sqrt{\pi}}\mathrm{e}^{-n^{2}x^{2}}\middle|n\in\mathbb{N}\right\} ,\\ & \left\{ \dfrac{1}{\pi}\dfrac{\sin\left(nx\right)}{x}\middle|n\in\mathbb{N}\right\} ,\cdots\Biggr\} \end{aligned} \]

\[ \left\{ \delta\left(x\right)\middle|\begin{cases} \delta:\mathbb{R}\rightarrow\mathbb{R}\\ \int_{-\infty}^{\infty}\delta\left(x\right)\cdot1\mathrm{d}x=1 \end{cases}\right\} \]

\[ \left\{ \delta\left(x\right)\middle|\begin{cases} \delta:\mathbb{R}\rightarrow\mathbb{R}\\ \int_{-\infty}^{\infty}\delta\left(x-0\right)\cdot f\left(x\right)\mathrm{d}x=f\left(0\right) \end{cases}\right\} \]

In measure theory, we can define the distance of two functions by

\[ d\left(f,g\right)=\sqrt{\int_{-\infty}^{\infty}\left[f\left(x\right)-g\left(x\right)\right]^{2}\mathrm{d}x} \]

for real distance of two square delta function approximations,

\[ \begin{aligned} d\left(\delta_{{\scriptscriptstyle m}},\delta_{{\scriptscriptstyle n}}\right)= & \sqrt{\int_{-\infty}^{\infty}\left[\delta_{{\scriptscriptstyle m}}\left(x\right)-\delta_{{\scriptscriptstyle n}}\left(x\right)\right]^{2}\mathrm{d}x}\\ = & \sqrt{\int_{-\infty}^{\infty}\left[\delta_{{\scriptscriptstyle m}}\left(x\right)\right]^{2}-2\delta_{{\scriptscriptstyle m}}\left(x\right)\delta_{{\scriptscriptstyle n}}\left(x\right)+\left[\delta_{{\scriptscriptstyle n}}\left(x\right)\right]^{2}\mathrm{d}x}\\ = & \sqrt{\int_{-\infty}^{\infty}\left[\delta_{{\scriptscriptstyle m}}\left(x\right)\right]^{2}\mathrm{d}x-2\int_{-\infty}^{\infty}\delta_{{\scriptscriptstyle m}}\left(x\right)\delta_{{\scriptscriptstyle n}}\left(x\right)\mathrm{d}x+\int_{-\infty}^{\infty}\left[\delta_{{\scriptscriptstyle n}}\left(x\right)\right]^{2}\mathrm{d}x}\\ = & \sqrt{\int_{-\infty}^{\infty}\delta_{{\scriptscriptstyle m}}\left(x\right)\delta_{{\scriptscriptstyle m}}\left(x\right)\mathrm{d}x-2\int_{-\infty}^{\infty}\delta_{{\scriptscriptstyle m}}\left(x\right)\delta_{{\scriptscriptstyle n}}\left(x\right)\mathrm{d}x+\int_{-\infty}^{\infty}\delta_{{\scriptscriptstyle n}}\left(x\right)\delta_{{\scriptscriptstyle n}}\left(x\right)\mathrm{d}x}\\ = & \sqrt{\delta_{{\scriptscriptstyle m}}\left(\xi_{{\scriptscriptstyle m}}\right)-2\int_{-\infty}^{\infty}\delta_{{\scriptscriptstyle m}}\left(x\right)\delta_{{\scriptscriptstyle n}}\left(x\right)\mathrm{d}x+\delta_{{\scriptscriptstyle n}}\left(\xi_{{\scriptscriptstyle n}}\right)},\begin{cases} \xi_{{\scriptscriptstyle m}}\in\left(\frac{-1}{2m},\frac{1}{2m}\right)\\ \xi_{{\scriptscriptstyle n}}\in\left(\frac{-1}{2n},\frac{1}{2n}\right) \end{cases}\\ = & \sqrt{m-2\int_{-\infty}^{\infty}\delta_{{\scriptscriptstyle m}}\left(x\right)\delta_{{\scriptscriptstyle n}}\left(x\right)\mathrm{d}x+n},\text{ if }m>n\\ = & \sqrt{m-2\delta_{{\scriptscriptstyle n}}\left(\xi_{{\scriptscriptstyle n}}\right)+n},\xi_{{\scriptscriptstyle n}}\in\left(\frac{-1}{2n},\frac{1}{2n}\right)\\ = & \sqrt{m-2n+n}=\sqrt{m-n}\in\mathbb{R}\\ d\left(\delta_{{\scriptscriptstyle m}},\delta_{{\scriptscriptstyle n}}\right)\overset{m>n}{=} & \sqrt{m-n}\in\mathbb{R} \end{aligned} \]

\[ \left\langle d\left(\delta_{{\scriptscriptstyle m}},\delta_{{\scriptscriptstyle n}}\right)\right\rangle _{{\scriptscriptstyle n\in\mathbb{N}}}=\left\langle \sqrt{m-n}\right\rangle _{{\scriptscriptstyle n\in\mathbb{N}}}\text{ is not a Cauchy series, not even mentioned convergence} \]

Def: 48.2

48.2.1 complex delta function

\[ \delta\left(k\right)=\frac{1}{2\pi}\int_{-\infty}^{\infty}\mathrm{e}^{\mathrm{i}kx}\mathrm{d}x \]

\[ \begin{aligned} & \int_{-\infty}^{\infty}\left(\frac{1}{2\pi}\int_{-\infty}^{\infty}\mathrm{e}^{\mathrm{i}kx}\mathrm{d}x\right)f\left(k,x\right)\mathrm{d}k\\ = & \lim\limits _{k^{\prime}\rightarrow0}\left[\int_{-\infty}^{k^{\prime-}}\left(\frac{1}{2\pi}\int_{-\infty}^{\infty}\mathrm{e}^{\mathrm{i}kx}\mathrm{d}x\right)f\left(k,x\right)\mathrm{d}k+\int_{k^{\prime-}}^{k^{\prime+}}\left(\frac{1}{2\pi}\int_{-\infty}^{\infty}\mathrm{e}^{\mathrm{i}kx}\mathrm{d}x\right)f\left(k,x\right)\mathrm{d}k+\int_{k^{\prime+}}^{\infty}\left(\frac{1}{2\pi}\int_{-\infty}^{\infty}\mathrm{e}^{\mathrm{i}kx}\mathrm{d}x\right)f\left(k,x\right)\mathrm{d}k\right]\\ \approx & \lim\limits _{k^{\prime}\rightarrow0}\left[\int_{-\infty}^{0}\left(\frac{1}{2\pi}\int_{-\infty}^{\infty}\mathrm{e}^{\mathrm{i}kx}\mathrm{d}x\right)f\left(k,x\right)\mathrm{d}k+\int_{k^{\prime-}}^{k^{\prime+}}\left(\frac{1}{2\pi}\int_{-\infty}^{\infty}\mathrm{e}^{\mathrm{i}0x}\mathrm{d}x\right)f\left(0,x\right)\mathrm{d}k+\int_{0}^{\infty}\left(\frac{1}{2\pi}\int_{-\infty}^{\infty}\mathrm{e}^{\mathrm{i}kx}\mathrm{d}x\right)f\left(k,x\right)\mathrm{d}k\right]\\ \approx & \lim\limits _{k^{\prime}\rightarrow0}\left[\int_{-\infty}^{0}\left(\frac{1}{2\pi}\int_{-\infty}^{\infty}\mathrm{e}^{\mathrm{i}kx}\mathrm{d}x\right)f\left(k,x\right)\mathrm{d}k+\int_{k^{\prime-}}^{k^{\prime+}}\left(\frac{1}{2\pi}\int_{-\infty}^{\infty}1\mathrm{d}x\right)f\left(0,x\right)\mathrm{d}k+\int_{0}^{\infty}\left(\frac{1}{2\pi}\int_{-\infty}^{\infty}\mathrm{e}^{\mathrm{i}kx}\mathrm{d}x\right)f\left(k,x\right)\mathrm{d}k\right]\\ \approx & \lim\limits _{k^{\prime}\rightarrow0}\left[-\int_{0}^{\infty}\left(\frac{1}{2\pi}\int_{-\infty}^{\infty}\mathrm{e}^{-\mathrm{i}kx}\mathrm{d}x\right)f\left(k,x\right)\mathrm{d}k+\int_{k^{\prime-}}^{k^{\prime+}}\left(\frac{1}{2\pi}\int_{-\infty}^{\infty}1\mathrm{d}x\right)f\left(0,x\right)\mathrm{d}k+\int_{0}^{\infty}\left(\frac{1}{2\pi}\int_{-\infty}^{\infty}\mathrm{e}^{\mathrm{i}kx}\mathrm{d}x\right)f\left(k,x\right)\mathrm{d}k\right]\\ \approx & \lim\limits _{k^{\prime}\rightarrow0}\left[-\int_{0}^{\infty}\left(\frac{1}{2\pi}\int_{-\infty}^{\infty}\mathrm{e}^{-\mathrm{i}kx}\mathrm{d}x\right)f\left(x\right)\mathrm{d}k+\int_{k^{\prime-}}^{k^{\prime+}}\left(\frac{1}{2\pi}\infty\right)f\left(0,x\right)\mathrm{d}k+\int_{0}^{\infty}\left(\frac{1}{2\pi}\int_{-\infty}^{\infty}\mathrm{e}^{\mathrm{i}kx}\mathrm{d}x\right)f\left(k,x\right)\mathrm{d}k\right]\\ \approx & \lim\limits _{k^{\prime}\rightarrow0}\left[\int_{k^{\prime-}}^{k^{\prime+}}\dfrac{1}{\mathrm{d}k}f\left(0,x\right)\mathrm{d}k+\int_{0}^{\infty}\left(\frac{1}{2\pi}\int_{-\infty}^{\infty}\mathrm{e}^{\mathrm{i}kx}-\mathrm{e}^{-\mathrm{i}kx}\mathrm{d}x\right)f\left(k,x\right)\mathrm{d}k\right]\\ \approx & \lim\limits _{k^{\prime}\rightarrow0}\left[f\left(0,x\right)+\int_{0}^{\infty}\left(\frac{1}{2\pi}0\right)f\left(k,x\right)\mathrm{d}k\right]\approx f\left(0,x\right)\\ & f\left(0,x\right)=\int_{-\infty}^{\infty}\left(\frac{1}{2\pi}\int_{-\infty}^{\infty}\mathrm{e}^{\mathrm{i}kx}\mathrm{d}x\right)f\left(k,x\right)\mathrm{d}k=\int_{-\infty}^{\infty}\delta\left(k\right)f\left(k,x\right)\mathrm{d}k=\int_{-\infty}^{\infty}\delta\left(k-0\right)f\left(k,x\right)\mathrm{d}k \end{aligned} \]

https://tex.stackexchange.com/questions/150138/how-can-i-create-a-polar-plot-on-a-cartesian-grid

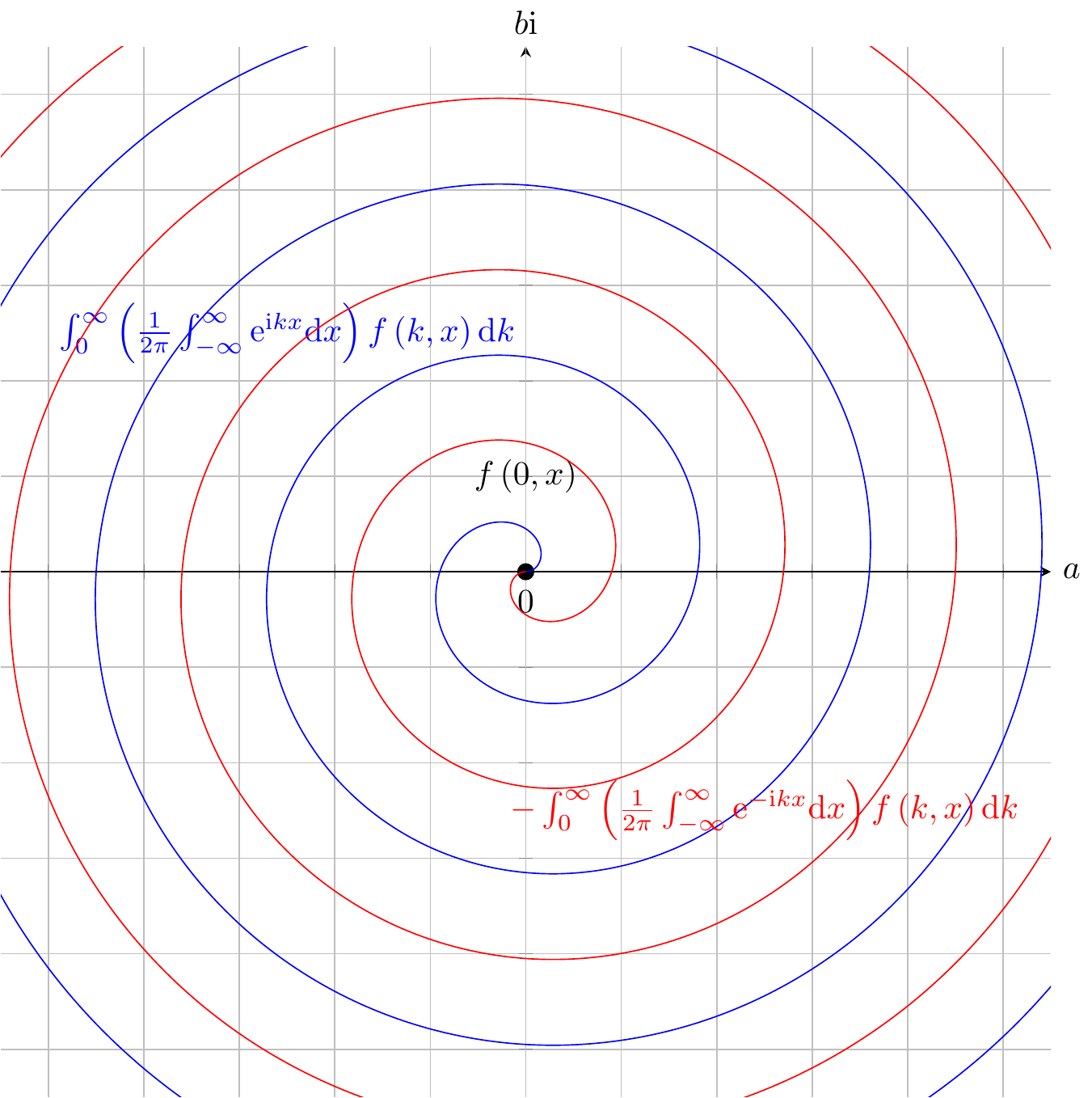
$\int_{-\infty}^{\infty}\left(\frac{1}{2\pi}\int_{-\infty}^{\infty}\mathrm{e}^{\mathrm{i}kx}\mathrm{d}x\right)f\left(k,x\right)\mathrm{d}k$

Fig. 48.4: $\int_{-\infty}^{\infty}\left(\frac{1}{2\pi}\int_{-\infty}^{\infty}\mathrm{e}^{\mathrm{i}kx}\mathrm{d}x\right)f\left(k,x\right)\mathrm{d}k$

\[ \begin{aligned} f\left(0,x\right)= & \int_{-\infty}^{\infty}\left(\frac{1}{2\pi}\int_{-\infty}^{\infty}\mathrm{e}^{\mathrm{i}kx}\mathrm{d}x\right)f\left(k,x\right)\mathrm{d}k\\ = & \int_{-\infty}^{\infty}\delta\left(k-0\right)f\left(k,x\right)\mathrm{d}k \end{aligned} \]

¹³ p.18~20

\[ \delta\left(x\right)=\begin{cases} 0 & x\ne0\\ \int_{-\infty}^{\infty}\delta\left(x\right)\mathrm{d}x=1 \end{cases} \]

According the SIFTing property above,

\[ \int_{-\infty}^{\infty}\delta\left(x-x^{\prime}\right)f\left(x\right)\mathrm{d}x=f\left(x^{\prime}\right) \]

And according to Fourier transform and inverse transform, Fourier analysis^[53] with $2\pi$ in the powers,

\[ f\left(x\right)=\int_{-\infty}^{\infty}\mathrm{e}^{2\pi\mathrm{i}xk}\left(\int_{-\infty}^{\infty}\mathrm{e}^{-2\pi\mathrm{i}kx^{\prime}}f\left(x^{\prime}\right)\mathrm{d}x^{\prime}\right)\mathrm{d}k \]

\[ \begin{aligned} f\left(x\right)= & \int_{-\infty}^{\infty}\mathrm{e}^{2\pi\mathrm{i}xk}\left(\int_{-\infty}^{\infty}\mathrm{e}^{-2\pi\mathrm{i}kx^{\prime}}f\left(x^{\prime}\right)\mathrm{d}x^{\prime}\right)\mathrm{d}k\\ = & \int_{-\infty}^{\infty}\mathrm{e}^{2\pi\mathrm{i}xk}f\left(x^{\prime}\right)\mathrm{d}x^{\prime}\left(\int_{-\infty}^{\infty}\mathrm{e}^{-2\pi\mathrm{i}kx^{\prime}}\right)\mathrm{d}k\\ = & \int_{-\infty}^{\infty}f\left(x^{\prime}\right)\mathrm{d}x^{\prime}\left(\int_{-\infty}^{\infty}\mathrm{e}^{2\pi\mathrm{i}xk}\mathrm{e}^{-2\pi\mathrm{i}kx^{\prime}}\right)\mathrm{d}k\\ = & \int_{-\infty}^{\infty}f\left(x^{\prime}\right)\mathrm{d}x^{\prime}\left(\int_{-\infty}^{\infty}\mathrm{e}^{2\pi\mathrm{i}k\left(x-x^{\prime}\right)}\right)\mathrm{d}k\\ = & \int_{-\infty}^{\infty}\left(\int_{-\infty}^{\infty}\mathrm{e}^{2\pi\mathrm{i}k\left(x-x^{\prime}\right)}\right)f\left(x^{\prime}\right)\mathrm{d}x^{\prime}\mathrm{d}k\\ \overset{\text{Fubini}}{=} & \int_{-\infty}^{\infty}\left(\int_{-\infty}^{\infty}\mathrm{e}^{2\pi\mathrm{i}k\left(x-x^{\prime}\right)}\right)f\left(x^{\prime}\right)\mathrm{d}k\mathrm{d}x^{\prime}\\ = & \int_{-\infty}^{\infty}\left(\int_{-\infty}^{\infty}\mathrm{e}^{2\pi\mathrm{i}k\left(x-x^{\prime}\right)}\mathrm{d}k\right)f\left(x^{\prime}\right)\mathrm{d}x^{\prime}\\ f\left(x\right)= & \int_{-\infty}^{\infty}\left(\int_{-\infty}^{\infty}\mathrm{e}^{2\pi\mathrm{i}k\left(x-x^{\prime}\right)}\mathrm{d}k\right)f\left(x^{\prime}\right)\mathrm{d}x^{\prime} \end{aligned} \]

comparing with SIFTing definition of Dirac delta function,

\[ \int_{-\infty}^{\infty}\delta\left(x-x^{\prime}\right)f\left(x\right)\mathrm{d}x=f\left(x^{\prime}\right) \]

thus

\[ \int_{-\infty}^{\infty}\mathrm{e}^{2\pi\mathrm{i}k\left(x-x^{\prime}\right)}\mathrm{d}k=\delta\left(x-x^{\prime}\right) \]

i.e.

\[ \delta\left(x-x^{\prime}\right)=\int_{-\infty}^{\infty}\mathrm{e}^{2\pi\mathrm{i}k\left(x-x^{\prime}\right)}\mathrm{d}k \]

\[ \begin{aligned} f\left(x\right)= & \int_{-\infty}^{\infty}\left(\int_{-\infty}^{\infty}\mathrm{e}^{2\pi\mathrm{i}k\left(x-x^{\prime}\right)}\mathrm{d}k\right)f\left(x^{\prime}\right)\mathrm{d}x^{\prime}\\ = & \int_{-\infty}^{\infty}\delta\left(x-x^{\prime}\right)f\left(x^{\prime}\right)\mathrm{d}x^{\prime},\begin{cases} k^{\prime}=2\pi k & \Leftrightarrow k=\dfrac{k^{\prime}}{2\pi}\\ x-x^{\prime}=\varepsilon & \Leftrightarrow x^{\prime}=x-\varepsilon \end{cases}\\ = & \int_{-\infty}^{\infty}\left(\dfrac{1}{2\pi}\int_{-\infty}^{\infty}\mathrm{e}^{\mathrm{i}\varepsilon k^{\prime}}\mathrm{d}k^{\prime}\right)f\left(x^{\prime}\right)\mathrm{d}x^{\prime}=\int_{-\infty}^{\infty}\lim\limits _{K\rightarrow\infty}\left(\dfrac{1}{2\pi}\int_{-K}^{K}\mathrm{e}^{\mathrm{i}\varepsilon k^{\prime}}\mathrm{d}k^{\prime}\right)f\left(x^{\prime}\right)\mathrm{d}x^{\prime},K>0\\ = & \int_{-\infty}^{\infty}\lim\limits _{K\rightarrow\infty}\left(\dfrac{1}{2\pi}\left[\dfrac{\mathrm{e}^{\mathrm{i}\varepsilon k^{\prime}}}{\mathrm{i}\varepsilon}\right]_{{\scriptscriptstyle k^{\prime}=-K}}^{{\scriptscriptstyle K}}\right)f\left(x^{\prime}\right)\mathrm{d}x^{\prime}=\int_{-\infty}^{\infty}\lim\limits _{K\rightarrow\infty}\left(\dfrac{1}{2\pi}\left[\dfrac{\mathrm{e}^{\mathrm{i}\varepsilon K}-\mathrm{e}^{\mathrm{i}\varepsilon\left(-K\right)}}{\mathrm{i}\varepsilon}\right]\right)f\left(x^{\prime}\right)\mathrm{d}x^{\prime}\\ = & \int_{-\infty}^{\infty}\lim\limits _{K\rightarrow\infty}\left(\dfrac{1}{\pi\varepsilon}\left[\dfrac{\mathrm{e}^{\mathrm{i}\varepsilon K}-\mathrm{e}^{-\mathrm{i}\varepsilon K}}{2\mathrm{i}}\right]\right)f\left(x^{\prime}\right)\mathrm{d}x^{\prime}=\int_{-\infty}^{\infty}\lim\limits _{K\rightarrow\infty}\left(\dfrac{1}{\pi\varepsilon}\left[\sin\left(\varepsilon K\right)\right]\right)f\left(x^{\prime}\right)\mathrm{d}x^{\prime}\\ = & \int_{-\infty}^{\infty}\lim\limits _{K\rightarrow\infty}\left(\dfrac{1}{\pi}\dfrac{\sin\left(\varepsilon K\right)}{\varepsilon}\right)f\left(x^{\prime}\right)\mathrm{d}x^{\prime}=\int_{-\infty}^{\infty}\lim\limits _{K\rightarrow\infty}\left(\dfrac{1}{\pi}\dfrac{\sin\left(K\varepsilon\right)}{\varepsilon}\right)f\left(x^{\prime}\right)\mathrm{d}x^{\prime},\begin{cases} x^{\prime}-x=-\varepsilon & \Leftrightarrow\varepsilon=x-x^{\prime}\\ & \Downarrow x=0\\ x^{\prime}=-\varepsilon & \Leftrightarrow\varepsilon=-x^{\prime}\\ Kx^{\prime}=u & \Leftrightarrow x^{\prime}=\dfrac{u}{K} \end{cases}\\ \overset{x=0}{=} & \int_{-\infty}^{\infty}\lim\limits _{K\rightarrow\infty}\left(\dfrac{1}{\pi}\dfrac{\sin\left(K\left[-x^{\prime}\right]\right)}{-x^{\prime}}\right)f\left(x^{\prime}\right)\mathrm{d}x^{\prime}=\int_{-\infty}^{\infty}\lim\limits _{K\rightarrow\infty}\left(\dfrac{1}{\pi}\dfrac{-\sin\left(Kx^{\prime}\right)}{-x^{\prime}}\right)f\left(x^{\prime}\right)\mathrm{d}x^{\prime}\\ = & \int_{x^{\prime}=-\infty}^{x^{\prime}=\infty}\lim\limits _{K\rightarrow\infty}\left(\dfrac{1}{\pi}\dfrac{\sin\left(Kx^{\prime}\right)}{x^{\prime}}\right)f\left(x^{\prime}\right)\mathrm{d}x^{\prime},\begin{cases} x^{\prime}=-\varepsilon & \Leftrightarrow\varepsilon=-x^{\prime}\\ Kx^{\prime}=u & \Leftrightarrow x^{\prime}=\dfrac{u}{K},\wedge K>0 \end{cases}\\ = & \int_{\dfrac{u}{K}=-\infty}^{\dfrac{u}{K}=\infty}\lim\limits _{K\rightarrow\infty}\left(\dfrac{1}{\pi}\dfrac{\sin\left(u\right)}{\dfrac{u}{K}}\right)f\left(\dfrac{u}{K}\right)\mathrm{d}\dfrac{u}{K}=\int_{u=-\infty}^{u=\infty}\lim\limits _{K\rightarrow\infty}\left(\dfrac{K}{\pi}\dfrac{\sin\left(u\right)}{u}\right)f\left(\dfrac{u}{K}\right)\dfrac{1}{K}\mathrm{d}u\\ = & \int_{-\infty}^{\infty}\lim\limits _{K\rightarrow\infty}\left(\dfrac{K}{\pi}\dfrac{\sin\left(u\right)}{u}\right)f\left(\dfrac{u}{K}\right)\dfrac{1}{K}\mathrm{d}u=\int_{-\infty}^{\infty}\lim\limits _{K\rightarrow\infty}\left(\dfrac{1}{\pi}\dfrac{\sin\left(u\right)}{u}\right)f\left(\dfrac{u}{K}\right)\mathrm{d}u\\ = & \dfrac{1}{\pi}\lim\limits _{K\rightarrow\infty}\int_{-\infty}^{\infty}\dfrac{\sin\left(u\right)}{u}f\left(\dfrac{u}{K}\right)\mathrm{d}u\overset{\text{MVT}}{=}\dfrac{1}{\pi}\lim\limits _{K\rightarrow\infty}f\left(\dfrac{\xi}{K}\right)\int_{-\infty}^{\infty}\dfrac{\sin\left(u\right)}{u}\mathrm{d}u,\exists\xi\in\left(-\epsilon,+\epsilon\right),\epsilon\in\mathbb{R}_{{\scriptscriptstyle >0}}\\ = & \dfrac{1}{\pi}f\left(0\right)\int_{-\infty}^{\infty}\dfrac{\sin\left(u\right)}{u}\mathrm{d}u\overset{\text{Feynman method or residue method}}{=}\dfrac{1}{\pi}f\left(0\right)\pi=f\left(0\right)=\left[f\left(x\right)\right]_{{\scriptscriptstyle x=0}} \end{aligned} \]

$\int_{-\infty}^{\infty}\dfrac{\sin\left(u\right)}{u}\mathrm{d}u=\pi$ see Feynman method of integration / integral technique^[47.2]

According to Fourier transform and inverse transform, Fourier analysis^[53] without $2\pi$ in the powers,

\[ f\left(t\right)=\frac{1}{2\pi}\int_{-\infty}^{\infty}\mathrm{e}^{\mathrm{i}t\cdot\omega}\left(\int_{-\infty}^{\infty}\mathrm{e}^{-\mathrm{i}\omega\cdot s}f\left(s\right)\mathrm{d}s\right)\mathrm{d}\omega \]

\[ f\left(x\right)=\frac{1}{2\pi}\int_{-\infty}^{\infty}\mathrm{e}^{\mathrm{i}xk}\left(\int_{-\infty}^{\infty}\mathrm{e}^{-\mathrm{i}kx^{\prime}}f\left(x^{\prime}\right)\mathrm{d}x^{\prime}\right)\mathrm{d}k \]

\[ f\left(t\right)=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}\mathrm{e}^{\mathrm{i}t\cdot\omega}\left(\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}\mathrm{e}^{-\mathrm{i}\imath\omega\cdot s}f\left(s\right)\mathrm{d}s\right)\mathrm{d}\omega \]

\[ f\left(t\right)=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}\mathrm{e}^{\mathrm{i}xk}\left(\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}\mathrm{e}^{-\mathrm{i}kx^{\prime}}f\left(x^{\prime}\right)\mathrm{d}x^{\prime}\right)\mathrm{d}k \]

complex function if analytic always with better properties than real function

\[ \begin{aligned} & \left\{ \left\{ \delta\left(k\right)\middle|k\in\mathbb{R}\right\} \middle|\begin{cases} \delta:\mathbb{R}\rightarrow\mathbb{C}\\ \int_{-\infty}^{\infty}\delta\left(k-0\right)f\left(k,x\right)\mathrm{d}k=f\left(0,x\right) \end{cases}\right\} \\ = & \left\{ \left\{ K\int_{-\infty}^{\infty}\mathrm{e}^{\mathrm{i}kx}\left(\cdot\right)\mathrm{d}k\middle|k\in\mathbb{R}\right\} ,\cdots\right\} \end{aligned} \]

\[ \delta\left(k\right)=\frac{1}{2\pi}\int_{-\infty}^{\infty}\mathrm{e}^{\mathrm{i}kx}\left(\cdot\right)\mathrm{d}x \]

\[ \delta\left(x\right)=\frac{1}{2\pi}\int_{-\infty}^{\infty}\mathrm{e}^{\mathrm{i}kx}\left(\cdot\right)\mathrm{d}k \]

\[ \delta\left(x^{\prime}\right)=\frac{1}{2\pi}\int_{-\infty}^{\infty}\mathrm{e}^{\mathrm{i}kx^{\prime}}\left(\cdot\right)\mathrm{d}k \]

$\psi\left(x\right)=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}\mathrm{e}^{\mathrm{i}kx}\psi\left(k\right)\mathrm{d}k$

\[ \psi\left(k\right)=\dfrac{1}{\sqrt{2\pi}}\int\mathrm{e}^{-\mathrm{i}kx}\psi\left(x\right)\mathrm{d}x \]

\[ \begin{aligned} & \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}\mathrm{e}^{\mathrm{i}kx}\psi\left(k\right)\mathrm{d}k\\ = & \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}\mathrm{e}^{\mathrm{i}kx}\left(\dfrac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}\mathrm{e}^{-\mathrm{i}kx^{\prime}}\psi\left(x^{\prime}\right)\mathrm{d}x^{\prime}\right)\mathrm{d}k\\ = & \frac{1}{2\pi}\int_{-\infty}^{\infty}\left(\int_{-\infty}^{\infty}\mathrm{e}^{\mathrm{i}kx}\mathrm{e}^{-\mathrm{i}kx^{\prime}}\psi\left(x^{\prime}\right)\mathrm{d}x^{\prime}\right)\mathrm{d}k\\ \overset{\text{Fubini}}{=} & \frac{1}{2\pi}\int_{-\infty}^{\infty}\left(\int_{-\infty}^{\infty}\mathrm{e}^{\mathrm{i}k\left(x-x^{\prime}\right)}\psi\left(x^{\prime}\right)\mathrm{d}k\right)\mathrm{d}x^{\prime}\\ = & \int_{-\infty}^{\infty}\left(\frac{1}{2\pi}\int_{-\infty}^{\infty}\mathrm{e}^{\mathrm{i}k\left(x-x^{\prime}\right)}\psi\left(x^{\prime}\right)\mathrm{d}k\right)\mathrm{d}x^{\prime}\\ = & \int_{-\infty}^{\infty}\psi\left(x^{\prime}\right)\left(\frac{1}{2\pi}\int_{-\infty}^{\infty}\mathrm{e}^{\mathrm{i}k\left(x-x^{\prime}\right)}\mathrm{d}k\right)\mathrm{d}x^{\prime}\\ = & \int_{-\infty}^{\infty}\psi\left(x^{\prime}\right)\delta\left(x-x^{\prime}\right)\mathrm{d}x^{\prime}=\int_{-\infty}^{\infty}\delta\left(x-x^{\prime}\right)\psi\left(x^{\prime}\right)\mathrm{d}x^{\prime}=\psi\left(x\right) \end{aligned} \]

\[ \psi\left(x\right)=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}\mathrm{e}^{\mathrm{i}kx}\psi\left(k\right)\mathrm{d}k \]

$\int_{-\infty}^{\infty}\left|\psi\left(k\right)\right|^{2}\mathrm{d}k=\int_{-\infty}^{\infty}\left|\psi\left(x\right)\right|^{2}\mathrm{d}x$

\[ \begin{cases} \psi\left(x\right)=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}\mathrm{e}^{\mathrm{i}kx}\psi\left(k\right)\mathrm{d}k\\ \psi\left(k\right)=\dfrac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}\mathrm{e}^{-\mathrm{i}kx}\psi\left(x\right)\mathrm{d}x \end{cases} \]

\[ \begin{aligned} \psi^{*}\left(k\right)=\overline{\psi}\left(k\right)= & \overline{\dfrac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}\mathrm{e}^{-\mathrm{i}kx}\psi\left(x\right)\mathrm{d}x}\\ = & \dfrac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}\overline{\mathrm{e}^{-\mathrm{i}kx}\psi\left(x\right)}\mathrm{d}x\\ = & \dfrac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}\overline{\mathrm{e}^{-\mathrm{i}kx}}\overline{\psi\left(x\right)}\mathrm{d}x\\ = & \dfrac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}\mathrm{e}^{\mathrm{i}kx}\psi^{*}\left(x\right)\mathrm{d}x \end{aligned} \]

\[ \begin{aligned} & \int_{-\infty}^{\infty}\left|\psi\left(k\right)\right|^{2}\mathrm{d}k=\int_{-\infty}^{\infty}\psi^{*}\left(k\right)\psi\left(k\right)\mathrm{d}k\\ = & \int_{-\infty}^{\infty}\left(\dfrac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}\mathrm{e}^{\mathrm{i}kx}\psi^{*}\left(x\right)\mathrm{d}x\right)\left(\dfrac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}\mathrm{e}^{-\mathrm{i}kx^{\prime}}\psi\left(x^{\prime}\right)\mathrm{d}x^{\prime}\right)\mathrm{d}k\\ = & \frac{1}{2\pi}\int_{-\infty}^{\infty}\left(\int_{-\infty}^{\infty}\mathrm{e}^{\mathrm{i}kx}\psi^{*}\left(x\right)\mathrm{d}x\right)\left(\int_{-\infty}^{\infty}\mathrm{e}^{-\mathrm{i}kx^{\prime}}\psi\left(x^{\prime}\right)\mathrm{d}x^{\prime}\right)\mathrm{d}k\\ = & \frac{1}{2\pi}\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\psi^{*}\left(x\right)\int_{-\infty}^{\infty}\mathrm{e}^{\mathrm{i}kx}\mathrm{e}^{-\mathrm{i}kx^{\prime}}\psi\left(x^{\prime}\right)\mathrm{d}x^{\prime}\mathrm{d}x\mathrm{d}k\\ = & \frac{1}{2\pi}\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\psi^{*}\left(x\right)\int_{-\infty}^{\infty}\mathrm{e}^{\mathrm{i}k\left(x-x^{\prime}\right)}\psi\left(x^{\prime}\right)\mathrm{d}x^{\prime}\mathrm{d}x\mathrm{d}k\\ = & \int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\psi^{*}\left(x\right)\frac{1}{2\pi}\int_{-\infty}^{\infty}\mathrm{e}^{\mathrm{i}k\left(x-x^{\prime}\right)}\psi\left(x^{\prime}\right)\mathrm{d}x^{\prime}\mathrm{d}x\mathrm{d}k\\ \overset{\text{Fubini}}{=} & \int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\psi^{*}\left(x\right)\frac{1}{2\pi}\int_{-\infty}^{\infty}\mathrm{e}^{\mathrm{i}k\left(x-x^{\prime}\right)}\psi\left(x^{\prime}\right)\mathrm{d}k\mathrm{d}x^{\prime}\mathrm{d}x\\ = & \int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\psi^{*}\left(x\right)\psi\left(x^{\prime}\right)\frac{1}{2\pi}\int_{-\infty}^{\infty}\mathrm{e}^{\mathrm{i}k\left(x-x^{\prime}\right)}\mathrm{d}k\mathrm{d}x^{\prime}\mathrm{d}x\\ = & \int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\psi^{*}\left(x\right)\psi\left(x^{\prime}\right)\delta\left(x-x^{\prime}\right)\mathrm{d}x^{\prime}\mathrm{d}x\\ = & \int_{-\infty}^{\infty}\psi^{*}\left(x\right)\int_{-\infty}^{\infty}\psi\left(x^{\prime}\right)\delta\left(x-x^{\prime}\right)\mathrm{d}x^{\prime}\mathrm{d}x\\ = & \int_{-\infty}^{\infty}\psi^{*}\left(x\right)\psi\left(x\right)\mathrm{d}x=\int_{-\infty}^{\infty}\left|\psi\left(x\right)\right|^{2}\mathrm{d}x \end{aligned} \]

\[ \int_{-\infty}^{\infty}\left|\psi\left(k\right)\right|^{2}\mathrm{d}k=\int_{-\infty}^{\infty}\left|\psi\left(x\right)\right|^{2}\mathrm{d}x \]

convolution

$\psi\left(x\right)=\int_{-\infty}^{\infty}\psi_{{\scriptscriptstyle 1}}\left(y\right)\psi_{{\scriptscriptstyle 2}}\left(x-y\right)\mathrm{d}y\Rightarrow\psi\left(k\right)=\sqrt{2\pi}\psi_{{\scriptscriptstyle 1}}\left(k\right)\psi_{{\scriptscriptstyle 2}}\left(k\right)$

\[ \psi\left(x\right)=\int_{-\infty}^{\infty}\psi_{{\scriptscriptstyle 1}}\left(y\right)\psi_{{\scriptscriptstyle 2}}\left(x-y\right)\mathrm{d}y \]

\[ \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}\mathrm{e}^{\mathrm{i}k_{{\scriptscriptstyle 1}}y}\psi_{{\scriptscriptstyle 1}}\left(k_{{\scriptscriptstyle 1}}\right)\mathrm{d}k_{{\scriptscriptstyle 1}} \]

\[ \psi_{{\scriptscriptstyle 2}}\left(x-y\right)=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}\mathrm{e}^{\mathrm{i}k_{{\scriptscriptstyle 2}}\left(x-y\right)}\psi_{{\scriptscriptstyle 2}}\left(k_{{\scriptscriptstyle 2}}\right)\mathrm{d}k_{{\scriptscriptstyle 2}} \]

\[ \begin{cases} \psi\left(x\right)= & \int_{-\infty}^{\infty}\psi_{{\scriptscriptstyle 1}}\left(y\right)\psi_{{\scriptscriptstyle 2}}\left(x-y\right)\mathrm{d}y\\ \psi_{{\scriptscriptstyle 1}}\left(y\right)= & \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}\mathrm{e}^{\mathrm{i}k_{{\scriptscriptstyle 1}}y}\psi_{{\scriptscriptstyle 1}}\left(k_{{\scriptscriptstyle 1}}\right)\mathrm{d}k_{{\scriptscriptstyle 1}}\\ \psi_{{\scriptscriptstyle 2}}\left(x-y\right)= & \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}\mathrm{e}^{\mathrm{i}k_{{\scriptscriptstyle 2}}\left(x-y\right)}\psi_{{\scriptscriptstyle 2}}\left(k_{{\scriptscriptstyle 2}}\right)\mathrm{d}k_{{\scriptscriptstyle 2}} \end{cases} \]

\[ \begin{aligned} & \psi\left(k\right)=\dfrac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}\mathrm{e}^{-\mathrm{i}kx}\psi\left(x\right)\mathrm{d}x=\dfrac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}\mathrm{e}^{-\mathrm{i}kx}\int_{-\infty}^{\infty}\psi_{{\scriptscriptstyle 1}}\left(y\right)\psi_{{\scriptscriptstyle 2}}\left(x-y\right)\mathrm{d}y\mathrm{d}x\\ = & \dfrac{1}{\left(\sqrt{2\pi}\right)^{3}}\int_{-\infty}^{\infty}\mathrm{e}^{-\mathrm{i}kx}\int_{-\infty}^{\infty}\left(\int_{-\infty}^{\infty}\mathrm{e}^{\mathrm{i}k_{{\scriptscriptstyle 1}}y}\psi_{{\scriptscriptstyle 1}}\left(k_{{\scriptscriptstyle 1}}\right)\mathrm{d}k_{{\scriptscriptstyle 1}}\right)\left(\int_{-\infty}^{\infty}\mathrm{e}^{\mathrm{i}k_{{\scriptscriptstyle 2}}\left(x-y\right)}\psi_{{\scriptscriptstyle 2}}\left(k_{{\scriptscriptstyle 2}}\right)\mathrm{d}k_{{\scriptscriptstyle 2}}\right)\mathrm{d}y\mathrm{d}x\\ = & \dfrac{1}{\left(\sqrt{2\pi}\right)^{3}}\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\mathrm{e}^{\mathrm{i}k_{{\scriptscriptstyle 1}}y}\mathrm{e}^{-\mathrm{i}k_{{\scriptscriptstyle 2}}y}\psi_{{\scriptscriptstyle 1}}\left(k_{{\scriptscriptstyle 1}}\right)\mathrm{e}^{-\mathrm{i}kx}\mathrm{e}^{\mathrm{i}k_{{\scriptscriptstyle 2}}x}\psi_{{\scriptscriptstyle 2}}\left(k_{{\scriptscriptstyle 2}}\right)\mathrm{d}k_{{\scriptscriptstyle 1}}\mathrm{d}k_{{\scriptscriptstyle 2}}\mathrm{d}y\mathrm{d}x\\ = & \dfrac{1}{\left(\sqrt{2\pi}\right)^{3}}\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\mathrm{e}^{\mathrm{i}\left(k_{{\scriptscriptstyle 1}}-k_{{\scriptscriptstyle 2}}\right)y}\psi_{{\scriptscriptstyle 1}}\left(k_{{\scriptscriptstyle 1}}\right)\mathrm{e}^{\mathrm{i}\left(k_{{\scriptscriptstyle 2}}-k\right)x}\psi_{{\scriptscriptstyle 2}}\left(k_{{\scriptscriptstyle 2}}\right)\mathrm{d}k_{{\scriptscriptstyle 1}}\mathrm{d}k_{{\scriptscriptstyle 2}}\mathrm{d}y\mathrm{d}x\\ \overset{\text{Fubini}}{=} & \dfrac{1}{\left(\sqrt{2\pi}\right)^{3}}\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\mathrm{e}^{\mathrm{i}\left(k_{{\scriptscriptstyle 1}}-k_{{\scriptscriptstyle 2}}\right)y}\psi_{{\scriptscriptstyle 1}}\left(k_{{\scriptscriptstyle 1}}\right)\mathrm{e}^{\mathrm{i}\left(k_{{\scriptscriptstyle 2}}-k\right)x}\psi_{{\scriptscriptstyle 2}}\left(k_{{\scriptscriptstyle 2}}\right)\mathrm{d}y\mathrm{d}x\mathrm{d}k_{{\scriptscriptstyle 1}}\mathrm{d}k_{{\scriptscriptstyle 2}}\\ = & \dfrac{1}{\left(\sqrt{2\pi}\right)^{3}}\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\left(\int_{-\infty}^{\infty}\mathrm{e}^{\mathrm{i}\left(k_{{\scriptscriptstyle 1}}-k_{{\scriptscriptstyle 2}}\right)y}\psi_{{\scriptscriptstyle 1}}\left(k_{{\scriptscriptstyle 1}}\right)\mathrm{d}y\right)\left(\int_{-\infty}^{\infty}\mathrm{e}^{\mathrm{i}\left(k_{{\scriptscriptstyle 2}}-k\right)x}\psi_{{\scriptscriptstyle 2}}\left(k_{{\scriptscriptstyle 2}}\right)\mathrm{d}x\right)\mathrm{d}k_{{\scriptscriptstyle 1}}\mathrm{d}k_{{\scriptscriptstyle 2}} \end{aligned} \]

\[ \begin{aligned} & \dfrac{1}{\left(\sqrt{2\pi}\right)^{3}}\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\left(\int_{-\infty}^{\infty}\mathrm{e}^{\mathrm{i}\left(k_{{\scriptscriptstyle 1}}-k_{{\scriptscriptstyle 2}}\right)y}\psi_{{\scriptscriptstyle 1}}\left(k_{{\scriptscriptstyle 1}}\right)\mathrm{d}y\right)\left(\int_{-\infty}^{\infty}\mathrm{e}^{\mathrm{i}\left(k_{{\scriptscriptstyle 2}}-k\right)x}\psi_{{\scriptscriptstyle 2}}\left(k_{{\scriptscriptstyle 2}}\right)\mathrm{d}x\right)\mathrm{d}k_{{\scriptscriptstyle 1}}\mathrm{d}k_{{\scriptscriptstyle 2}}\\ = & \sqrt{2\pi}\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\left[\frac{1}{2\pi}\int_{-\infty}^{\infty}\mathrm{e}^{\mathrm{i}\left(k_{{\scriptscriptstyle 1}}-k_{{\scriptscriptstyle 2}}\right)y}\psi_{{\scriptscriptstyle 1}}\left(k_{{\scriptscriptstyle 1}}\right)\mathrm{d}y\right]\left[\frac{1}{2\pi}\int_{-\infty}^{\infty}\mathrm{e}^{\mathrm{i}\left(k_{{\scriptscriptstyle 2}}-k\right)x}\psi_{{\scriptscriptstyle 2}}\left(k_{{\scriptscriptstyle 2}}\right)\mathrm{d}x\right]\mathrm{d}k_{{\scriptscriptstyle 1}}\mathrm{d}k_{{\scriptscriptstyle 2}}\\ = & \sqrt{2\pi}\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\left[\psi_{{\scriptscriptstyle 1}}\left(k_{{\scriptscriptstyle 1}}\right)\frac{1}{2\pi}\int_{-\infty}^{\infty}\mathrm{e}^{\mathrm{i}\left(k_{{\scriptscriptstyle 1}}-k_{{\scriptscriptstyle 2}}\right)y}\mathrm{d}y\right]\left[\psi_{{\scriptscriptstyle 2}}\left(k_{{\scriptscriptstyle 2}}\right)\frac{1}{2\pi}\int_{-\infty}^{\infty}\mathrm{e}^{\mathrm{i}\left(k_{{\scriptscriptstyle 2}}-k\right)x}\mathrm{d}x\right]\mathrm{d}k_{{\scriptscriptstyle 1}}\mathrm{d}k_{{\scriptscriptstyle 2}}\\ = & \sqrt{2\pi}\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\left[\psi_{{\scriptscriptstyle 1}}\left(k_{{\scriptscriptstyle 1}}\right)\delta\left(k_{{\scriptscriptstyle 1}}-k_{{\scriptscriptstyle 2}}\right)\right]\left[\psi_{{\scriptscriptstyle 2}}\left(k_{{\scriptscriptstyle 2}}\right)\delta\left(k_{{\scriptscriptstyle 2}}-k\right)\right]\mathrm{d}k_{{\scriptscriptstyle 1}}\mathrm{d}k_{{\scriptscriptstyle 2}}\\ \overset{\text{Fubini}}{=} & \sqrt{2\pi}\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\left[\psi_{{\scriptscriptstyle 1}}\left(k_{{\scriptscriptstyle 1}}\right)\delta\left(k_{{\scriptscriptstyle 1}}-k_{{\scriptscriptstyle 2}}\right)\right]\left[\psi_{{\scriptscriptstyle 2}}\left(k_{{\scriptscriptstyle 2}}\right)\delta\left(k_{{\scriptscriptstyle 2}}-k\right)\right]\mathrm{d}k_{{\scriptscriptstyle 2}}\mathrm{d}k_{{\scriptscriptstyle 1}}\\ = & \sqrt{2\pi}\int_{-\infty}^{\infty}\left[\psi_{{\scriptscriptstyle 1}}\left(k_{{\scriptscriptstyle 1}}\right)\right]\left[\int_{-\infty}^{\infty}\delta\left(k_{{\scriptscriptstyle 1}}-k_{{\scriptscriptstyle 2}}\right)\psi_{{\scriptscriptstyle 2}}\left(k_{{\scriptscriptstyle 2}}\right)\delta\left(k_{{\scriptscriptstyle 2}}-k\right)\mathrm{d}k_{{\scriptscriptstyle 2}}\right]\mathrm{d}k_{{\scriptscriptstyle 1}}\\ = & \sqrt{2\pi}\int_{-\infty}^{\infty}\left[\psi_{{\scriptscriptstyle 1}}\left(k_{{\scriptscriptstyle 1}}\right)\right]\left[\delta\left(k_{{\scriptscriptstyle 1}}-k\right)\psi_{{\scriptscriptstyle 2}}\left(k\right)\right]\mathrm{d}k_{{\scriptscriptstyle 1}}=\sqrt{2\pi}\psi_{{\scriptscriptstyle 2}}\left(k\right)\int_{-\infty}^{\infty}\psi_{{\scriptscriptstyle 1}}\left(k_{{\scriptscriptstyle 1}}\right)\delta\left(k_{{\scriptscriptstyle 1}}-k\right)\mathrm{d}k_{{\scriptscriptstyle 1}}\\ = & \sqrt{2\pi}\psi_{{\scriptscriptstyle 2}}\left(k\right)\psi_{{\scriptscriptstyle 1}}\left(k\right)=\sqrt{2\pi}\psi_{{\scriptscriptstyle 1}}\left(k\right)\psi_{{\scriptscriptstyle 2}}\left(k\right) \end{aligned} \]

\[ \begin{array}{c} \begin{cases} \psi\left(x\right)= & \int_{-\infty}^{\infty}\psi_{{\scriptscriptstyle 1}}\left(y\right)\psi_{{\scriptscriptstyle 2}}\left(x-y\right)\mathrm{d}y\\ \psi_{{\scriptscriptstyle 1}}\left(y\right)= & \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}\mathrm{e}^{\mathrm{i}k_{{\scriptscriptstyle 1}}y}\psi_{{\scriptscriptstyle 1}}\left(k_{{\scriptscriptstyle 1}}\right)\mathrm{d}k_{{\scriptscriptstyle 1}}\\ \psi_{{\scriptscriptstyle 2}}\left(x-y\right)= & \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}\mathrm{e}^{\mathrm{i}k_{{\scriptscriptstyle 2}}\left(x-y\right)}\psi_{{\scriptscriptstyle 2}}\left(k_{{\scriptscriptstyle 2}}\right)\mathrm{d}k_{{\scriptscriptstyle 2}} \end{cases}\\ \Downarrow\\ \psi\left(k\right)=\sqrt{2\pi}\psi_{{\scriptscriptstyle 1}}\left(k\right)\psi_{{\scriptscriptstyle 2}}\left(k\right) \end{array} \]

48.2.2 3D delta function

https://www.youtube.com/watch?v=Y8y965ZAmQE

\[ \delta\left(\boldsymbol{r}-\boldsymbol{r}^{\prime}\right)=\delta\left(x-x^{\prime}\right)\delta\left(y-y^{\prime}\right)\delta\left(z-z^{\prime}\right) \]

Poisson equation

Feynman method of differentiation / derivative technique^[47.1]

\[ \begin{aligned} \Delta\left(\dfrac{1}{r}\right)= & \boldsymbol{\nabla}^{2}\left(\dfrac{1}{\sqrt{\boldsymbol{r}^{2}}}\right)=\boldsymbol{\nabla}\cdot\boldsymbol{\nabla}\left(\dfrac{1}{\sqrt{\boldsymbol{r}\cdot\boldsymbol{r}}}\right)=\boldsymbol{\nabla}\cdot\left(\dfrac{\partial}{\partial x},\dfrac{\partial}{\partial y},\dfrac{\partial}{\partial z}\right)\left(\dfrac{1}{\sqrt{x^{2}+y^{2}+z^{2}}}\right)\\ = & \boldsymbol{\nabla}\cdot\left(\dfrac{-x}{\left(x^{2}+y^{2}+z^{2}\right)^{\frac{3}{2}}},\dfrac{-y}{\left(x^{2}+y^{2}+z^{2}\right)^{\frac{3}{2}}},\dfrac{-z}{\left(x^{2}+y^{2}+z^{2}\right)^{\frac{3}{2}}}\right)=\boldsymbol{\nabla}\cdot\dfrac{-\boldsymbol{r}}{r^{3}}\\ = & \left(\dfrac{\partial}{\partial x},\dfrac{\partial}{\partial y},\dfrac{\partial}{\partial z}\right)\cdot\left(\dfrac{-x}{\left(x^{2}+y^{2}+z^{2}\right)^{\frac{3}{2}}},\dfrac{-y}{\left(x^{2}+y^{2}+z^{2}\right)^{\frac{3}{2}}},\dfrac{-z}{\left(x^{2}+y^{2}+z^{2}\right)^{\frac{3}{2}}}\right)\\ = & \dfrac{\partial}{\partial x}\dfrac{-x}{\left(x^{2}+y^{2}+z^{2}\right)^{\frac{3}{2}}}+\dfrac{\partial}{\partial y}\dfrac{-y}{\left(x^{2}+y^{2}+z^{2}\right)^{\frac{3}{2}}}+\dfrac{\partial}{\partial z}\dfrac{-z}{\left(x^{2}+y^{2}+z^{2}\right)^{\frac{3}{2}}}\\ = & \dfrac{+2x^{2}-y^{2}-z^{2}}{\left(x^{2}+y^{2}+z^{2}\right)^{\frac{5}{2}}}+\dfrac{-x^{2}+2y^{2}-z^{2}}{\left(x^{2}+y^{2}+z^{2}\right)^{\frac{5}{2}}}+\dfrac{-x^{2}-y^{2}+2z^{2}}{\left(x^{2}+y^{2}+z^{2}\right)^{\frac{5}{2}}}=0 \end{aligned} \]

$\Delta\left(\dfrac{1}{r}\right)=-4\pi\delta\left(\boldsymbol{r}\right)$

https://math.stackexchange.com/questions/3774483/derivatives-of-frac1r-and-dirac-delta-function

\[ \begin{aligned} \Delta\dfrac{1}{r\left(\epsilon\right)}= & \boldsymbol{\nabla}^{2}\dfrac{1}{\sqrt{\boldsymbol{r}^{2}+\epsilon^{2}}}=\boldsymbol{\nabla}\cdot\boldsymbol{\nabla}\dfrac{1}{\sqrt{x^{2}+y^{2}+z^{2}+\epsilon^{2}}}\\ = & \boldsymbol{\nabla}\cdot\left(\dfrac{\partial}{\partial x},\dfrac{\partial}{\partial y},\dfrac{\partial}{\partial z}\right)\left(\dfrac{1}{\sqrt{x^{2}+y^{2}+z^{2}+\epsilon^{2}}}\right)\\ = & \boldsymbol{\nabla}\cdot\left(\dfrac{-x}{\left(x^{2}+y^{2}+z^{2}+\epsilon^{2}\right)^{\frac{3}{2}}},\dfrac{-y}{\left(x^{2}+y^{2}+z^{2}+\epsilon^{2}\right)^{\frac{3}{2}}},\dfrac{-z}{\left(x^{2}+y^{2}+z^{2}+\epsilon^{2}\right)^{\frac{3}{2}}}\right)\\ = & \dfrac{\partial}{\partial x}\dfrac{-x}{\left(x^{2}+y^{2}+z^{2}+\epsilon^{2}\right)^{\frac{3}{2}}}+\dfrac{\partial}{\partial y}\dfrac{-y}{\left(x^{2}+y^{2}+z^{2}+\epsilon^{2}\right)^{\frac{3}{2}}}+\dfrac{\partial}{\partial z}\dfrac{-z}{\left(x^{2}+y^{2}+z^{2}+\epsilon^{2}\right)^{\frac{3}{2}}}\\ = & \dfrac{+2x^{2}-y^{2}-z^{2}-\epsilon^{2}}{\left(x^{2}+y^{2}+z^{2}+\epsilon^{2}\right)^{\frac{5}{2}}}+\dfrac{-x^{2}+2y^{2}-z^{2}-\epsilon^{2}}{\left(x^{2}+y^{2}+z^{2}+\epsilon^{2}\right)^{\frac{5}{2}}}+\dfrac{-x^{2}-y^{2}+2z^{2}-\epsilon^{2}}{\left(x^{2}+y^{2}+z^{2}+\epsilon^{2}\right)^{\frac{5}{2}}}\\ = & \dfrac{-3\epsilon^{2}}{\left(x^{2}+y^{2}+z^{2}+\epsilon^{2}\right)^{\frac{5}{2}}}=\dfrac{-3\epsilon^{2}}{\left(\boldsymbol{r}^{2}+\epsilon^{2}\right)^{\frac{5}{2}}} \end{aligned} \]

\[ \Delta\left(\dfrac{1}{r}\right)=\boldsymbol{\nabla}^{2}\left(\dfrac{1}{r}\right)=\boldsymbol{\nabla}^{2}\dfrac{1}{\left|\boldsymbol{r}\right|}=\boldsymbol{\nabla}^{2}\dfrac{1}{\left|\boldsymbol{r}-\boldsymbol{0}\right|}=\Delta\dfrac{1}{\left|\boldsymbol{r}-\boldsymbol{0}\right|}=\Delta\left(\boldsymbol{r}-\boldsymbol{0}\right)=\Delta\left(\boldsymbol{r}\right) \]

\[ \Delta\dfrac{1}{r\left(\epsilon\right)}=\Delta_{\epsilon}\left(r\right)=\Delta_{\epsilon}\left(\boldsymbol{r}\right)=\Delta_{\epsilon}\left(\boldsymbol{r}-\boldsymbol{0}\right) \]

\[ \lim\limits _{\epsilon\rightarrow0}\Delta_{\epsilon}\left(\boldsymbol{r}\right)=\lim\limits _{\epsilon\rightarrow0}\Delta\dfrac{1}{r\left(\epsilon\right)}=\Delta\left(\dfrac{1}{r}\right)=\Delta\left(\boldsymbol{r}\right) \]

\[ K_{{\scriptscriptstyle 3}}\int_{\mathbb{R}^{3}}f\left(\boldsymbol{r}\right)\Delta\left(\boldsymbol{r}\right)\mathrm{d}\boldsymbol{r}=\lim\limits _{\epsilon\rightarrow0}K_{{\scriptscriptstyle 3}}\int_{\mathbb{R}^{3}}f\left(\boldsymbol{r}\right)\Delta_{\epsilon}\left(\boldsymbol{r}\right)\mathrm{d}\boldsymbol{r}=\lim\limits _{\epsilon\rightarrow0}K_{{\scriptscriptstyle 3}}\int_{\mathbb{R}^{3}}f\left(\boldsymbol{r}\right)\Delta_{\epsilon}\left(\boldsymbol{r}-\boldsymbol{0}\right)\mathrm{d}\boldsymbol{r}=f\left(\boldsymbol{0}\right) \]

\[ K_{{\scriptscriptstyle 1}}\int_{\mathbb{R}^{1}}f\left(x\right)\delta\left(x\right)\mathrm{d}x=\lim\limits _{n\rightarrow\infty}K_{{\scriptscriptstyle 1}}\int_{\mathbb{R}^{1}}f\left(x\right)\delta_{{\scriptscriptstyle n}}\left(x\right)\mathrm{d}x=K_{{\scriptscriptstyle 1}}\int_{\mathbb{R}^{1}}f\left(x\right)\delta_{{\scriptscriptstyle n}}\left(x-0\right)\mathrm{d}x=f\left(0\right) \]

\[ \begin{aligned} & \int_{\mathbb{R}^{3}}f\left(\boldsymbol{r}\right)\Delta_{\epsilon}\left(\boldsymbol{r}\right)\mathrm{d}\boldsymbol{r}=\int_{\mathbb{R}^{3}}f\left(\boldsymbol{r}\right)\dfrac{-3\epsilon^{2}}{\left(\boldsymbol{r}^{2}+\epsilon^{2}\right)^{\frac{5}{2}}}\mathrm{d}\boldsymbol{r},\begin{cases} \boldsymbol{r}=r\boldsymbol{n}_{\mathbb{{\scriptscriptstyle S}}}\\ \boldsymbol{n}_{\mathbb{{\scriptscriptstyle S}}}=\begin{pmatrix}\sin\phi\cos\theta\\ \sin\phi\sin\theta\\ \cos\phi \end{pmatrix} \end{cases}\\ = & \int_{0}^{\infty}\int_{\mathbb{S}^{2}}f\left(r\boldsymbol{n}_{\mathbb{{\scriptscriptstyle S}}}\right)\dfrac{-3\epsilon^{2}}{\left(r^{2}+\epsilon^{2}\right)^{\frac{5}{2}}}r^{2}\sigma\left(\mathrm{d}\boldsymbol{n}_{{\scriptscriptstyle S}}\right)\mathrm{d}r,\begin{cases} \mathbb{S}^{2}=\text{unit sphere centered at the origin}\\ \sigma\left(\mathrm{d}\boldsymbol{n}_{{\scriptscriptstyle S}}\right)\text{ is the surface measure of }\mathbb{S}^{2}\\ r^{2}\sigma\left(\mathrm{d}\boldsymbol{n}_{{\scriptscriptstyle S}}\right)=r^{2}\sin\phi\mathrm{d}\phi\mathrm{d}\theta\\ r=\epsilon s \end{cases}\\ = & \int_{0}^{\infty}\int_{\mathbb{S}^{2}}f\left(\epsilon s\boldsymbol{n}_{\mathbb{{\scriptscriptstyle S}}}\right)\dfrac{-3\epsilon^{2}}{\left(\left(\epsilon s\right)^{2}+\epsilon^{2}\right)^{\frac{5}{2}}}\left(\epsilon s\right)^{2}\sigma\left(\mathrm{d}\boldsymbol{n}_{{\scriptscriptstyle S}}\right)\mathrm{d}\epsilon s\\ = & \int_{0}^{\infty}\int_{\mathbb{S}^{2}}f\left(\epsilon s\boldsymbol{n}_{\mathbb{{\scriptscriptstyle S}}}\right)\dfrac{-3\epsilon^{5}}{\epsilon^{5}\left(s^{2}+1\right)^{\frac{5}{2}}}s^{2}\sigma\left(\mathrm{d}\boldsymbol{n}_{{\scriptscriptstyle S}}\right)\mathrm{d}s=-\int_{0}^{\infty}\int_{\mathbb{S}^{2}}f\left(\epsilon s\boldsymbol{n}_{\mathbb{{\scriptscriptstyle S}}}\right)\dfrac{3s^{2}}{\left(s^{2}+1\right)^{\frac{5}{2}}}\sigma\left(\mathrm{d}\boldsymbol{n}_{\mathbb{{\scriptscriptstyle S}}}\right)\mathrm{d}s\\ = & -\int_{0}^{\infty}\int_{0}^{2\pi}\int_{0}^{2\pi}f\left(\epsilon s\boldsymbol{n}_{\mathbb{{\scriptscriptstyle S}}}\right)\dfrac{3s^{2}}{\left(s^{2}+1\right)^{\frac{5}{2}}}\sin\phi\mathrm{d}\phi\mathrm{d}\theta\mathrm{d}s=-\int_{0}^{\infty}4\pi f\left(\epsilon s\boldsymbol{n}_{\mathbb{{\scriptscriptstyle S}}}\right)\dfrac{3s^{2}}{\left(s^{2}+1\right)^{\frac{5}{2}}}\mathrm{d}s \end{aligned} \] \[ \begin{aligned} & \lim\limits _{\epsilon\rightarrow0}\int_{\mathbb{R}^{3}}f\left(\boldsymbol{r}\right)\Delta_{\epsilon}\left(\boldsymbol{r}\right)\mathrm{d}\boldsymbol{r}\\ = & \lim\limits _{\epsilon\rightarrow0}\left[-\int_{0}^{\infty}4\pi f\left(\epsilon s\boldsymbol{n}_{\mathbb{{\scriptscriptstyle S}}}\right)\dfrac{3s^{2}}{\left(s^{2}+1\right)^{\frac{5}{2}}}\mathrm{d}s\right]\\ = & -4\pi f\left(\boldsymbol{0}\right)\int_{0}^{\infty}\dfrac{3s^{2}}{\left(s^{2}+1\right)^{\frac{5}{2}}}\mathrm{d}s \end{aligned} \]

https://www.integral-calculator.com/

\[ \begin{aligned} & \int\dfrac{3s^{2}}{\left(s^{2}+1\right)^{\frac{5}{2}}}\mathrm{d}s,s=\tan u\\ = & \int\dfrac{3\tan^{2}u}{\left(\tan^{2}u+1\right)^{\frac{5}{2}}}\mathrm{d}\tan u=\int\dfrac{3\tan^{2}u}{\left(\tan^{2}u+1\right)^{\frac{5}{2}}}\sec^{2}u\mathrm{d}u\\ = & \int\dfrac{3\tan^{2}u}{\left(\sec^{2}u\right)^{\frac{5}{2}}}\sec^{2}u\mathrm{d}u=\int\dfrac{3\tan^{2}u}{\sec^{5}u}\sec^{2}u\mathrm{d}u=\int\dfrac{3\tan^{2}u}{\sec^{3}u}\mathrm{d}u\\ = & \int\dfrac{3\left(\frac{\sin u}{\cos u}\right)^{2}}{\left(\frac{1}{\cos u}\right)^{3}}\mathrm{d}u=3\int\sin^{2}u\cos u\mathrm{d}u=3\int\sin^{2}u\mathrm{d}\sin u=3\dfrac{\sin^{3}u}{3}+C\\ = & \sin^{3}u+C=\left(\frac{s}{\sqrt{s^{2}+1}}\right)^{3}+C=\dfrac{s^{3}}{\left(s^{2}+1\right)^{\frac{3}{2}}}+C\overset{s>0}{=}\dfrac{1}{\left(1+s^{-2}\right)^{\frac{3}{2}}}+C \end{aligned} \]

\[ \int_{0}^{\infty}\dfrac{3s^{2}}{\left(s^{2}+1\right)^{\frac{5}{2}}}\mathrm{d}s=\left[\dfrac{s^{3}}{\left(s^{2}+1\right)^{\frac{3}{2}}}\right]_{0}^{\infty}=\left[\dfrac{1}{\left(1+s^{-2}\right)^{\frac{3}{2}}}\right]_{s=\infty}-\left[\dfrac{s^{3}}{\left(s^{2}+1\right)^{\frac{3}{2}}}\right]_{s=0}=1-0=1 \]

\[ \begin{aligned} & \lim\limits _{\epsilon\rightarrow0}\int_{\mathbb{R}^{3}}f\left(\boldsymbol{r}\right)\Delta_{\epsilon}\left(\boldsymbol{r}\right)\mathrm{d}\boldsymbol{r}\\ = & \lim\limits _{\epsilon\rightarrow0}\left[-\int_{0}^{\infty}4\pi f\left(\epsilon s\boldsymbol{n}_{\mathbb{{\scriptscriptstyle S}}}\right)\dfrac{3s^{2}}{\left(s^{2}+1\right)^{\frac{5}{2}}}\mathrm{d}s\right]\\ = & -4\pi f\left(\boldsymbol{0}\right)\int_{0}^{\infty}\dfrac{3s^{2}}{\left(s^{2}+1\right)^{\frac{5}{2}}}\mathrm{d}s=-4\pi f\left(\boldsymbol{0}\right)1=-4\pi f\left(\boldsymbol{0}\right) \end{aligned} \]

\[ \int_{\mathbb{R}^{3}}f\left(\boldsymbol{r}\right)\Delta\left(\boldsymbol{r}\right)\mathrm{d}\boldsymbol{r}=\lim\limits _{\epsilon\rightarrow0}\int_{\mathbb{R}^{3}}f\left(\boldsymbol{r}\right)\Delta_{\epsilon}\left(\boldsymbol{r}\right)\mathrm{d}\boldsymbol{r}=-4\pi f\left(\boldsymbol{0}\right)=-4\pi\int_{\mathbb{R}^{3}}f\left(\boldsymbol{r}\right)\delta\left(\boldsymbol{r}\right)\mathrm{d}\boldsymbol{r} \]

\[ \Delta\left(\dfrac{1}{r}\right)=\Delta\left(\boldsymbol{r}\right)=-4\pi\delta\left(\boldsymbol{r}\right) \]

Big Delta reciprocal r is minus 4 pi delta r.

\[ \tag*{$\Box$} \]

\[ \Delta\left(\dfrac{1}{r}\right)=-4\pi\delta\left(\boldsymbol{r}\right) \]

Poisson equation rigorous proof by general function and Green theorem

https://zhuanlan.zhihu.com/p/154094937

Fig. 16.3: Poisson equation rigorous proof by general function and Green theorem

https://math.stackexchange.com/questions/368155/where-does-the-relation-nabla21-r-4-pi-delta3-bf-r-between-laplacian

[37.1.3]

\[ \begin{aligned} & \left\{ \left\{ \delta\left(\boldsymbol{k}\right)\middle|\boldsymbol{k}\in\mathbb{R}^{3}\right\} \middle|\begin{cases} \delta:\mathbb{R}^{3}\rightarrow\mathbb{H}\\ \int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\delta\left(\boldsymbol{k}-\boldsymbol{0}\right)f\left(\boldsymbol{k},\boldsymbol{r}\right)\mathrm{d}^{3}\boldsymbol{r}=f\left(\boldsymbol{0},\boldsymbol{r}\right) \end{cases}\right\} \\ = & \left\{ \left\{ K\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\mathrm{e}^{\mathrm{i}\boldsymbol{k}\cdot\boldsymbol{r}}\left(\cdot\right)\mathrm{d}^{3}\boldsymbol{k}\middle|\boldsymbol{k}\in\mathbb{R}^{3}\right\} ,\cdots\right\} \end{aligned} \]

Columb law

\[ F_{\text{e}}=k\dfrac{Qq}{r^{2}} \] \[ \boldsymbol{F}_{\text{e}}=k\dfrac{Qq}{r^{2}}\hat{\boldsymbol{r}} \]

electric field from point electric charge

\[ \begin{aligned} \boldsymbol{E}\left(\boldsymbol{r}\right)=\boldsymbol{E}\left(r\right)=\boldsymbol{E}=&k\dfrac{q}{r^{2}}\hat{\boldsymbol{r}}=k_{\text{e}}\dfrac{q}{\left|\boldsymbol{r}\right|^{2}}\dfrac{\boldsymbol{r}}{\left|\boldsymbol{r}\right|}=k_{\text{e}}q\dfrac{\boldsymbol{r}}{\left|\boldsymbol{r}\right|^{3}}=k_{\text{e}}q\dfrac{\boldsymbol{r}}{\left(\boldsymbol{r}^{2}\right)^{\frac{3}{2}}}\\=&k_{\text{e}}q\dfrac{\boldsymbol{r}}{\left(\boldsymbol{r}^{2}\right)^{\frac{3}{2}}}=k_{\text{e}}q\left(-\boldsymbol{\nabla}\frac{1}{\sqrt{\boldsymbol{r}\cdot\boldsymbol{r}}}\right)=-k_{\text{e}}q\boldsymbol{\nabla}\dfrac{1}{\left\Vert \boldsymbol{r}\right\Vert } \end{aligned} \]

\[ \boldsymbol{E}\left(\boldsymbol{r}\right)=-k_{\text{e}}q\boldsymbol{\nabla}\dfrac{1}{\left\Vert \boldsymbol{r}\right\Vert } \]

electric field from tiny point electric charge

\[ \begin{aligned} \mathrm{d}\boldsymbol{E}\left(\boldsymbol{r}\right)=\mathrm{d}\boldsymbol{E}\left(r\right)=\mathrm{d}\boldsymbol{E}= & k\dfrac{\mathrm{d}q}{r^{2}}\hat{\boldsymbol{r}}=k\dfrac{\mathrm{d}q\left(r\right)}{r^{2}}\hat{\boldsymbol{r}}=k_{\text{e}}\mathrm{d}q\left(\boldsymbol{r}\right)\dfrac{\boldsymbol{r}}{\left(\boldsymbol{r}^{2}\right)^{\frac{3}{2}}}\\ = & k_{\text{e}}\mathrm{d}q\left(\boldsymbol{r}\right)\dfrac{\boldsymbol{r}}{\left(\boldsymbol{r}^{2}\right)^{\frac{3}{2}}}=k_{\text{e}}\mathrm{d}q\left(\boldsymbol{r}\right)\boldsymbol{\nabla}\dfrac{1}{\left\Vert \boldsymbol{r}\right\Vert } \end{aligned} \]

\[ \mathrm{d}\boldsymbol{E}\left(\boldsymbol{r}\right)=-k_{\text{e}}\mathrm{d}q\left(\boldsymbol{r}\right)\boldsymbol{\nabla}\dfrac{1}{\left\Vert \boldsymbol{r}\right\Vert } \]

\[ \mathrm{d}q=\rho\mathrm{d}V\Leftrightarrow\rho=\dfrac{\mathrm{d}q}{\mathrm{d}V} \]

\[ \mathrm{d}q\left(\boldsymbol{r}\right)=\rho\left(\boldsymbol{r}\right)\mathrm{d}V\Leftrightarrow\rho\left(\boldsymbol{r}\right)=\dfrac{\mathrm{d}q\left(\boldsymbol{r}\right)}{\mathrm{d}V} \]

\[ q=\int_{q}\mathrm{d}q\left(\boldsymbol{r}\right)=\int_{V}\rho\left(\boldsymbol{r}\right)\mathrm{d}V=\iiint_{V}\rho\left(\boldsymbol{r}\right)\mathrm{d}^{3}\boldsymbol{r} \]

\[ \begin{aligned} \boldsymbol{E}= & \iiint_{V}\boldsymbol{E}\left(\boldsymbol{r}\right)\mathrm{d}^{3}\boldsymbol{r}=\iiint_{V}\left(-k_{\text{e}}\rho\left(\boldsymbol{r}\right)\boldsymbol{\nabla}\dfrac{1}{\left\Vert \boldsymbol{r}\right\Vert }\right)\mathrm{d}^{3}\boldsymbol{r}\\ = & -k_{\text{e}}\iiint_{V}\left(\rho\left(\boldsymbol{r}\right)\boldsymbol{\nabla}\dfrac{1}{\left\Vert \boldsymbol{r}\right\Vert }\right)\mathrm{d}^{3}\boldsymbol{r}\\ = & -k_{\text{e}}\iiint_{V}\left(\rho\left(\boldsymbol{r}\right)\boldsymbol{\nabla}\dfrac{1}{\left\Vert \boldsymbol{r}-\boldsymbol{0}\right\Vert }\right)\mathrm{d}^{3}\boldsymbol{r}=\boldsymbol{E}\left(\boldsymbol{0}\right) \end{aligned} \]

\[ \begin{aligned} \Downarrow & \begin{cases} Q\text{ at }\boldsymbol{r}\\ \mathrm{d}q\text{ or }\rho\text{ at }\boldsymbol{r}^{\prime},\text{ totally }V \end{cases}\\ \boldsymbol{E}\left(\boldsymbol{r}\right)= & \iiint_{V}\left(-k_{\text{e}}\rho\left(\boldsymbol{r}^{\prime}\right)\boldsymbol{\nabla}\dfrac{1}{\left\Vert \boldsymbol{r}-\boldsymbol{r}^{\prime}\right\Vert }\right)\mathrm{d}^{3}\boldsymbol{r}^{\prime}=\iiint_{V}\left(-k_{\text{e}}\rho\left(\boldsymbol{r}^{\prime}\right)\boldsymbol{\nabla}_{{\scriptscriptstyle \boldsymbol{r}}}\dfrac{1}{\left\Vert \boldsymbol{r}-\boldsymbol{r}^{\prime}\right\Vert }\right)\mathrm{d}^{3}\boldsymbol{r}^{\prime}\\ \boldsymbol{\nabla}_{{\scriptscriptstyle \boldsymbol{r}}}\cdot\boldsymbol{E}\left(\boldsymbol{r}\right)= & \boldsymbol{\nabla}_{{\scriptscriptstyle \boldsymbol{r}}}\cdot\iiint_{V}\left(-k_{\text{e}}\rho\left(\boldsymbol{r}^{\prime}\right)\boldsymbol{\nabla}_{{\scriptscriptstyle \boldsymbol{r}}}\dfrac{1}{\left\Vert \boldsymbol{r}-\boldsymbol{r}^{\prime}\right\Vert }\right)\mathrm{d}^{3}\boldsymbol{r}^{\prime}=\iiint_{V}\left(-k_{\text{e}}\rho\left(\boldsymbol{r}^{\prime}\right)\boldsymbol{\nabla}_{{\scriptscriptstyle \boldsymbol{r}}}\cdot\boldsymbol{\nabla}_{{\scriptscriptstyle \boldsymbol{r}}}\dfrac{1}{\left\Vert \boldsymbol{r}-\boldsymbol{r}^{\prime}\right\Vert }\right)\mathrm{d}^{3}\boldsymbol{r}^{\prime}\\ = & \iiint_{V}\left(-k_{\text{e}}\rho\left(\boldsymbol{r}^{\prime}\right)\boldsymbol{\nabla}_{{\scriptscriptstyle \boldsymbol{r}}}^{2}\dfrac{1}{\left\Vert \boldsymbol{r}-\boldsymbol{r}^{\prime}\right\Vert }\right)\mathrm{d}^{3}\boldsymbol{r}^{\prime}=\iiint_{V}\left(-k_{\text{e}}\rho\left(\boldsymbol{r}^{\prime}\right)\Delta_{{\scriptscriptstyle \boldsymbol{r}}}\dfrac{1}{\left\Vert \boldsymbol{r}-\boldsymbol{r}^{\prime}\right\Vert }\right)\mathrm{d}^{3}\boldsymbol{r}^{\prime}\\ = & \iiint_{V}f\left(\boldsymbol{r}^{\prime}\right)\Delta\left(\boldsymbol{r}-\boldsymbol{r}^{\prime}\right)\mathrm{d}^{3}\boldsymbol{r}^{\prime},f\left(\boldsymbol{r}^{\prime}\right)=-k_{\text{e}}\rho\left(\boldsymbol{r}^{\prime}\right)\\ = & \iiint_{V}f\left(\boldsymbol{r}^{\prime}\right)\delta\left(\boldsymbol{r}-\boldsymbol{r}^{\prime}\right)\mathrm{d}^{3}\boldsymbol{r}^{\prime},f\left(\boldsymbol{r}^{\prime}\right)=-k_{\text{e}}\rho\left(\boldsymbol{r}^{\prime}\right)\\ = & -4\pi f\left(\boldsymbol{r}^{\prime}=\boldsymbol{r}\right)=-4\pi\left[-k_{\text{e}}\rho\left(\boldsymbol{r}^{\prime}=\boldsymbol{r}\right)\right]\\ = & -4\pi f\left(\boldsymbol{r}\right)=-4\pi\left[-k_{\text{e}}\rho\left(\boldsymbol{r}\right)\right]=4\pi k_{\text{e}}\rho\left(\boldsymbol{r}\right)\\ \boldsymbol{\nabla}\cdot\boldsymbol{E}\left(\boldsymbol{r}\right)= & 4\pi k_{\text{e}}\rho\left(\boldsymbol{r}\right) \end{aligned} \]

\[ \boldsymbol{\nabla}\cdot\boldsymbol{E}\left(\boldsymbol{r}\right)=4\pi k_{\text{e}}\rho\left(\boldsymbol{r}\right) \]

gravity

https://zhuanlan.zhihu.com/p/695160620

https://www.bilibili.com/video/BV1qu411578c/?t=7m26s

https://en.wikipedia.org/wiki/Helmholtz_equation

Helmholtz equation

\[ \left(\Delta+k^{2}\right)\dfrac{\mathrm{e}^{\pm\mathrm{i}\boldsymbol{k}\cdot\boldsymbol{r}}}{r}=-4\pi\delta\left(\boldsymbol{r}\right) \]

\[ \left(\boldsymbol{\nabla}_{{\scriptscriptstyle \boldsymbol{r}}}^{2}+\boldsymbol{k}^{2}\right)\dfrac{\mathrm{e}^{\pm\mathrm{i}\boldsymbol{k}\cdot\boldsymbol{r}}}{\left\Vert \boldsymbol{r}\right\Vert }=-4\pi\delta\left(\boldsymbol{r}\right) \]

48.2.3 quantum state

https://www.bilibili.com/video/BV1qu411578c/?t=7m45s

https://www.bilibili.com/video/BV1xu4y1S7W2

48.2.4 rigorous definition of delta function

\[ \int_{-\infty}^{\infty}\delta\left(x-0\right)\cdot f\left(x\right)\mathrm{d}x=f\left(0\right) \]

\[ \int\delta\left(x\right)f\left(x\right)\mathrm{d}x=f\left(0\right) \]

\[ \int\delta\left(x\right)\left(\cdot\right)\mathrm{d}x:f\left(x\right)\rightarrow f\left(0\right) \]

\[ f\left(x\right)\overset{\int\delta\left(x\right)\left(\cdot\right)\mathrm{d}x}{\rightarrow}f\left(0\right) \]

\[ f\text{ must be with good properties} \]

\[ \text{continuous linear functional}\begin{cases} \text{function-like} & \eta_{{\scriptscriptstyle \varphi}}\left(f\right)=\int\varphi\left(x\right)f\left(x\right)\mathrm{d}x\\ \text{non-function-like},\text{ e.g.} & \delta_{{\scriptscriptstyle x^{\prime}}}\left(f\right)=f\left(x^{\prime}\right) \end{cases} \]

general function with “formally” integral notation

\[ \delta_{{\scriptscriptstyle x^{\prime}}}\left(f\right)=\int\delta\left(x-x^{\prime}\right)f\left(x\right)\mathrm{d}x=f\left(x^{\prime}\right) \]

https://www.bilibili.com/video/BV1qu411578c/?t=11m36s

Quantum mechanics is founded on Hilbert space; Hoever, Dirac delta function is not a linear functional on Hilbert space.?

One of the reason is that we cannot find 1-1 of Dirac delta function, but many-to-one or one-to-many functions.

量子力學本不需 Dirac delta function, 其卻仍大行其道, 實廣義函數為其負重前行.

狄拉克函數不是希爾伯特空間的線性泛函. Dirac delta function is not a linear functional on Hilbert space.

狄拉克括號卻是希爾伯特空間的向量表示. Dirac bra-ket brackets are vector representation on Hilbert space.

48.3 Fourier expansion or Fourier series

vector space definition^[43.2]

Fig: 43.1

linear space of function^[46.1]

https://www.bilibili.com/video/BV1PX4y167RS

https://www.bilibili.com/video/BV1m24y1A74K

https://www.bilibili.com/video/BV1m24y1A74K/?=3m2s

48.3.1 Taylor vs. Fourier

\[ f\left(x\right)=x_{{\scriptscriptstyle 0}}x^{0}+x_{{\scriptscriptstyle 1}}x^{1}+x_{{\scriptscriptstyle 2}}x^{2}+\cdots=\sum\limits _{k=0}^{\infty}x_{{\scriptscriptstyle k}}x^{k},x_{{\scriptscriptstyle k}}=\dfrac{f^{\left(k\right)}\left(0\right)}{k!} \]

\[ f\left(r\right)=r_{{\scriptscriptstyle 0}}r^{0}+r_{{\scriptscriptstyle 1}}r^{1}+r_{{\scriptscriptstyle 2}}r^{2}+\cdots=\sum\limits _{k=0}^{\infty}r_{{\scriptscriptstyle k}}r^{k},r_{{\scriptscriptstyle k}}=\dfrac{f^{\left(k\right)}\left(0\right)}{k!} \]

\[ f\left(\theta\right)=a_{{\scriptscriptstyle 0}}\cos\left(0\theta\right)+a_{{\scriptscriptstyle 1}}\cos\left(1\theta\right)+a_{{\scriptscriptstyle 2}}\cos\left(2\theta\right)+\cdots=\sum\limits _{k=0}^{\infty}a_{{\scriptscriptstyle k}}\cos\left(k\theta\right) \]

\[ a_{{\scriptscriptstyle k}}=\int_{-\infty}^{\infty}\cos\left(k\theta\right)f\left(\theta\right)\mathrm{d}\theta \]

\[ \begin{aligned} & f\left(\theta\right)=a_{{\scriptscriptstyle 0}}\cos\left(0\theta\right)+a_{{\scriptscriptstyle 1}}\cos\left(1\theta\right)+a_{{\scriptscriptstyle 2}}\cos\left(2\theta\right)+\cdots=\sum\limits _{k=0}^{\infty}a_{{\scriptscriptstyle k}}\cos\left(k\theta\right)\\ = & a_{{\scriptscriptstyle 0}}\Re\left[\mathrm{e}^{\mathrm{i}0\theta}\right]+a_{{\scriptscriptstyle 1}}\Re\left[\mathrm{e}^{\mathrm{i}1\theta}\right]+a_{{\scriptscriptstyle 2}}\Re\left[\mathrm{e}^{\mathrm{i}2\theta}\right]+\cdots=\sum\limits _{k=0}^{\infty}a_{{\scriptscriptstyle k}}\Re\left[\mathrm{e}^{\mathrm{i}k\theta}\right]=\sum\limits _{k=0}^{\infty}a_{{\scriptscriptstyle k}}\Re\left[\left(\mathrm{e}^{\mathrm{i}\theta}\right)^{k}\right]\\ = & \Re\left[a_{{\scriptscriptstyle 0}}\mathrm{e}^{\mathrm{i}0\theta}+a_{{\scriptscriptstyle 1}}\mathrm{e}^{\mathrm{i}1\theta}+a_{{\scriptscriptstyle 2}}\mathrm{e}^{\mathrm{i}2\theta}+\cdots\right]=\Re\left[\sum\limits _{k=0}^{\infty}a_{{\scriptscriptstyle k}}\mathrm{e}^{\mathrm{i}k\theta}\right]=\Re\left[\sum\limits _{k=0}^{\infty}a_{{\scriptscriptstyle k}}\left(\mathrm{e}^{\mathrm{i}\theta}\right)^{k}\right] \end{aligned} \]

\[ f\left(x\right)=x_{{\scriptscriptstyle 0}}x^{0}+x_{{\scriptscriptstyle 1}}x^{1}+x_{{\scriptscriptstyle 2}}x^{2}+\cdots=\sum\limits _{k=0}^{\infty}x_{{\scriptscriptstyle k}}x^{k} \]

\[ f\left(z\right)=z_{{\scriptscriptstyle 0}}z^{0}+z_{{\scriptscriptstyle 1}}z^{1}+z_{{\scriptscriptstyle 2}}z^{2}+\cdots=\sum\limits _{k=0}^{\infty}z_{{\scriptscriptstyle k}}z^{k} \]

\[ z=r\mathrm{e}^{\mathrm{i}\theta} \]

\[ \begin{aligned} f\left(z\right)= & z_{{\scriptscriptstyle 0}}z^{0}+z_{{\scriptscriptstyle 1}}z^{1}+z_{{\scriptscriptstyle 2}}z^{2}+\cdots=\sum\limits _{k=0}^{\infty}z_{{\scriptscriptstyle k}}z^{k}\\ f\left(r\mathrm{e}^{\mathrm{i}\theta}\right)= & z_{{\scriptscriptstyle 0}}\left(r\mathrm{e}^{\mathrm{i}\theta}\right)^{0}+z_{{\scriptscriptstyle 1}}\left(r\mathrm{e}^{\mathrm{i}\theta}\right)^{1}+z_{{\scriptscriptstyle 2}}\left(r\mathrm{e}^{\mathrm{i}\theta}\right)^{2}+\cdots=\sum\limits _{k=0}^{\infty}z_{{\scriptscriptstyle k}}\left(r\mathrm{e}^{\mathrm{i}\theta}\right)^{k}\\ =f\left(r\right)= & z_{{\scriptscriptstyle 0}}\left(\mathrm{e}^{\mathrm{i}\theta}\right)^{0}r^{0}+z_{{\scriptscriptstyle 1}}\left(\mathrm{e}^{\mathrm{i}\theta}\right)^{1}r^{1}+z_{{\scriptscriptstyle 2}}\left(\mathrm{e}^{\mathrm{i}\theta}\right)^{2}r^{2}+\cdots=\sum\limits _{k=0}^{\infty}z_{{\scriptscriptstyle k}}\left(\mathrm{e}^{\mathrm{i}\theta}\right)^{k}r^{k}\\ = & r_{{\scriptscriptstyle 0}}r^{0}+r_{{\scriptscriptstyle 1}}r^{1}+r_{{\scriptscriptstyle 2}}r^{2}+\cdots=\sum\limits _{k=0}^{\infty}r_{{\scriptscriptstyle k}}r^{k},r_{{\scriptscriptstyle k}}=z_{{\scriptscriptstyle k}}\left(\mathrm{e}^{\mathrm{i}\theta}\right)^{k}\\ =f\left(\mathrm{e}^{\mathrm{i}\theta}\right)= & z_{{\scriptscriptstyle 0}}r^{0}\left(\mathrm{e}^{\mathrm{i}\theta}\right)^{0}+z_{{\scriptscriptstyle 1}}r^{1}\left(\mathrm{e}^{\mathrm{i}\theta}\right)^{1}+z_{{\scriptscriptstyle 2}}r^{2}\left(\mathrm{e}^{\mathrm{i}\theta}\right)^{2}+\cdots=\sum\limits _{k=0}^{\infty}z_{{\scriptscriptstyle k}}r^{k}\left(\mathrm{e}^{\mathrm{i}\theta}\right)^{k}\\ = & \left(\mathrm{e}^{\mathrm{i}\theta}\right)_{{\scriptscriptstyle 0}}\left(\mathrm{e}^{\mathrm{i}\theta}\right)^{0}+\left(\mathrm{e}^{\mathrm{i}\theta}\right)_{{\scriptscriptstyle 1}}\left(\mathrm{e}^{\mathrm{i}\theta}\right)^{1}+\left(\mathrm{e}^{\mathrm{i}\theta}\right)_{{\scriptscriptstyle 2}}\left(\mathrm{e}^{\mathrm{i}\theta}\right)^{2}+\cdots=\sum\limits _{k=0}^{\infty}\left(\mathrm{e}^{\mathrm{i}\theta}\right)_{{\scriptscriptstyle k}}\left(\mathrm{e}^{\mathrm{i}\theta}\right)^{k}\\ & ,\left(\mathrm{e}^{\mathrm{i}\theta}\right)_{{\scriptscriptstyle k}}=z_{{\scriptscriptstyle k}}r^{k} \end{aligned} \]

https://www.bilibili.com/video/BV1nV411F7es

48.4 Hilbert space construction

https://www.zhihu.com/question/19967778/answer/2572975608

https://www.bilibili.com/video/BV1cV411T7hb

Definition 48.1 sequence limit

\[ \lim_{n\rightarrow\infty}a_{n}=a\Leftrightarrow\forall\epsilon>0,\exists N\in\mathbb{N},\forall n\in\mathbb{N}\left(n>N\Rightarrow\left|a_{n}-a\right|<\epsilon\right) \]

\[ x_{{\scriptscriptstyle 1}},x_{{\scriptscriptstyle 2}},\cdots,x_{{\scriptscriptstyle n}},x_{{\scriptscriptstyle n+1}},\cdots \]

to find convergence
- monotone convergence theorem
- split into known sequence
- fraction: Stolz theorem
- sequence itself
  - ratio $\dfrac{x_{{\scriptscriptstyle m}}}{x_{{\scriptscriptstyle n}}}$, but not good for some terms being zero
  - difference $x_{{\scriptscriptstyle m}}-x_{{\scriptscriptstyle n}}$

Theorem 18.4 Cauchy convergence theorem

\[ \begin{array}{c} \left\{ x_{{\scriptscriptstyle n}}\right\} _{{\scriptscriptstyle n\in\mathbb{N}}}\text{ is convergent}\\ \Updownarrow\\ \forall\epsilon>0,\exists N\in\mathbb{N},\forall m,n\in\mathbb{N}\left(m,n>N\Rightarrow\left|x_{{\scriptscriptstyle m}}-x_{{\scriptscriptstyle n}}\right|<\epsilon\right)\Leftrightarrow\left\{ x_{{\scriptscriptstyle n}}\right\} _{{\scriptscriptstyle n\in\mathbb{N}}}\text{ is a Cauchy sequence} \end{array} \]

Definition 48.2 Cauchy sequence

\[ \begin{array}{c} \left\{ x_{{\scriptscriptstyle n}}\right\} _{{\scriptscriptstyle n\in\mathbb{N}}}\text{ is a Cauchy sequence}\\ \Updownarrow\\ \forall\epsilon>0,\exists N\in\mathbb{N},\forall m,n\in\mathbb{N}\left(m,n>N\Rightarrow\left|x_{{\scriptscriptstyle m}}-x_{{\scriptscriptstyle n}}\right|<\epsilon\right) \end{array} \]

\[ \text{convergence}\begin{cases} \left|x_{{\scriptscriptstyle n}}-x\right|<\epsilon & \text{convergent sequence}\\ \left|x_{{\scriptscriptstyle m}}-x_{{\scriptscriptstyle n}}\right|<\epsilon & \text{Cauchy sequence} \end{cases} \]

\[ \text{convergence}\begin{cases} \left|x_{{\scriptscriptstyle n}}-x\right|<\epsilon & \text{convergent sequence}\\ \Downarrow\text{easy proof} & \Uparrow\text{hard proof, weak condition needs all real number as supporting base}\\ \left|x_{{\scriptscriptstyle m}}-x_{{\scriptscriptstyle n}}\right|<\epsilon & \text{Cauchy sequence} \end{cases} \]

\[ \text{convergence}\begin{cases} \left|x_{{\scriptscriptstyle n}}-x\right|<\epsilon & \text{convergent sequence}\\ \Downarrow & \Uparrow x_{{\scriptscriptstyle n}},x_{{\scriptscriptstyle m}},x\in\mathbb{R}\text{ with real completeness}\\ \left|x_{{\scriptscriptstyle m}}-x_{{\scriptscriptstyle n}}\right|<\epsilon & \text{Cauchy sequence} \end{cases} \]

48.4.1 inner product space

vector space definition^[43.2]

Fig: 43.1

Fig. 48.5: inner product space construction

\[ \left\langle \cdot\middle|\cdot\right\rangle :\begin{cases} \left\langle f\middle|g+h\right\rangle =\left\langle f\middle|g\right\rangle +\left\langle f\middle|h\right\rangle \\ \left\langle f\middle|cg\right\rangle =c\left\langle f\middle|g\right\rangle \\ \left\langle f\middle|g\right\rangle =\overline{\left\langle g\middle|f\right\rangle }=\left\langle g\middle|f\right\rangle ^{*}\\ \left\langle f\middle|f\right\rangle \underset{f=0\Leftrightarrow\left\langle f\middle|f\right\rangle =0}{\ge}0 \end{cases} \]

definition of distance

Definition 48.3 distance

\[ d\left(f,g\right)=d\left\langle f\middle|g\right\rangle =\sqrt{\left\langle f-g\middle|f-g\right\rangle } \]

For real number,

\[ \begin{array}{c} \begin{cases} d\left(f,g\right)=d\left\langle f\middle|g\right\rangle =\sqrt{\left\langle f-g\middle|f-g\right\rangle }\\ f,g\in\mathbb{R}\\ \left\langle f\middle|g\right\rangle =fg=f\cdot g \end{cases}\\ \Downarrow\\ d\left\langle f\middle|g\right\rangle =\sqrt{\left(f-g\right)^{2}}=\left|f-g\right| \end{array} \]

For $n$-dimensional vector

\[ \begin{array}{c} \begin{cases} d\left(f,g\right)=d\left\langle f\middle|g\right\rangle =\sqrt{\left\langle f-g\middle|f-g\right\rangle }\\ f,g\in F^{n}\\ \left\langle f\middle|g\right\rangle =\sum\limits _{k=1}^{n}f_{{\scriptscriptstyle k}}g_{{\scriptscriptstyle k}} \end{cases}\\ \Downarrow\\ d\left\langle f\middle|g\right\rangle =\sqrt{\sum\limits _{k=1}^{n}\left(f_{{\scriptscriptstyle k}}-g_{{\scriptscriptstyle k}}\right)^{2}} \end{array} \]

For continuous complex function on $\left[a,b\right]$,

\[ \begin{array}{c} \begin{cases} d\left(f,g\right)=d\left\langle f\middle|g\right\rangle =\sqrt{\left\langle f-g\middle|f-g\right\rangle }\\ f,g\in C_{\mathbb{{\scriptscriptstyle C}}}\left(\left[a,b\right]\right) & \text{continuous complex function}\\ \left\langle f\middle|g\right\rangle =\int_{a}^{b}\overline{f\left(x\right)}g\left(x\right)\mathrm{d}x \end{cases}\\ \Downarrow\\ d\left\langle f\middle|g\right\rangle =\sqrt{\int_{a}^{b}\overline{\left[f-g\right]\left(x\right)}\left[f-g\right]\left(x\right)\mathrm{d}x}=\sqrt{\int_{a}^{b}\left|\left[f-g\right]\left(x\right)\right|^{2}\mathrm{d}x} \end{array} \]

For real number sequence,

For complex function sequence,

\[ \text{function convergence}\begin{cases} d\left\langle f_{{\scriptscriptstyle n}}\middle|f\right\rangle <\epsilon & \text{convergent function sequence}\\ d\left\langle f_{{\scriptscriptstyle m}}\middle|f_{{\scriptscriptstyle n}}\right\rangle <\epsilon & \text{Cauchy function sequence} \end{cases} \]

\[ \text{function convergence}\begin{cases} d\left\langle f_{{\scriptscriptstyle n}}\middle|f\right\rangle <\epsilon & \text{convergent function sequence}\\ \Downarrow & \not\Uparrow\text{ not always continuous}\\ d\left\langle f_{{\scriptscriptstyle m}}\middle|f_{{\scriptscriptstyle n}}\right\rangle <\epsilon & \text{Cauchy function sequence} \end{cases} \]

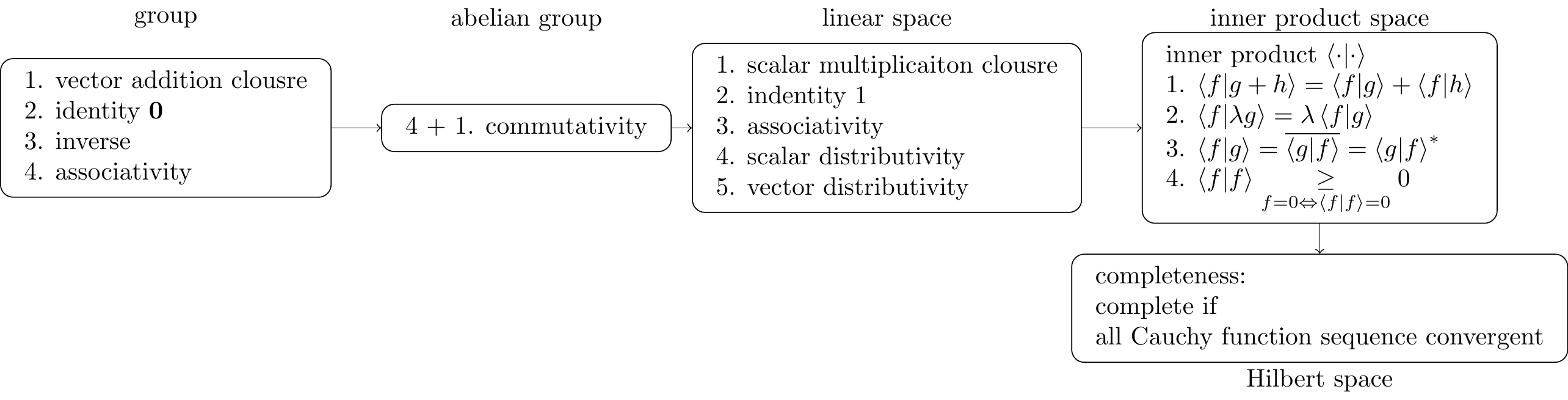
Fig. 48.6: Hilbert space construction

https://www.zhihu.com/question/19967778/answer/2572975608

Fig. 48.7: metric vs. inner product

Fig. 16.5: Euclid space construction

https://zhuanlan.zhihu.com/p/85867887

48.4.2 Riesz representation theorem

https://zhuanlan.zhihu.com/p/308879557

48.5 Dirac bracket

https://www.bilibili.com/video/BV1GN411m7A9

reciprocal space^[43.4.1]

double dual concept^[43.4.1.2]

\[ \begin{array}{cccccccccc} & & & V & =\{ & \boldsymbol{e}_{{\scriptscriptstyle 1}} & \boldsymbol{e}_{{\scriptscriptstyle 2}} & \boldsymbol{e}_{{\scriptscriptstyle 3}} & \boldsymbol{v} & \cdots\}\\ & \boldsymbol{e}^{{\scriptscriptstyle 1}} & : & \downarrow & & \downarrow & \downarrow & \downarrow & \downarrow\\ V^{*}=\{ & \boldsymbol{e}^{{\scriptscriptstyle 2}} & \} & F & \supseteq\{ & 1 & 0 & 0 & v_{{\scriptscriptstyle 1}} & \cdots\}\\ & \boldsymbol{e}^{{\scriptscriptstyle 3}} & & V & =\{ & \boldsymbol{e}_{{\scriptscriptstyle 1}} & \boldsymbol{e}_{{\scriptscriptstyle 2}} & \boldsymbol{e}_{{\scriptscriptstyle 3}} & \boldsymbol{v} & \cdots\}\\ & \boldsymbol{v}^{*} & : & \downarrow & & \downarrow & \downarrow & \downarrow & \downarrow\\ & \vdots & & F & \supseteq\{ & v^{*{\scriptscriptstyle 1}} & v^{*{\scriptscriptstyle 2}} & v^{*{\scriptscriptstyle 3}} & v^{*{\scriptscriptstyle i}}v_{{\scriptscriptstyle i}} & \cdots\} \end{array} \]

\[ \begin{array}{cccccccccc} & & & V^{*} & =\{ & \boldsymbol{e}^{{\scriptscriptstyle 1}} & \boldsymbol{e}^{{\scriptscriptstyle 2}} & \boldsymbol{e}^{{\scriptscriptstyle 3}} & \boldsymbol{\omega} & \cdots\}\\ & \boldsymbol{e}^{{\scriptscriptstyle 1}*} & : & \downarrow & & \downarrow & \downarrow & \downarrow & \downarrow\\ V^{**}=\{ & \boldsymbol{e}^{{\scriptscriptstyle 2}*} & \} & F & \supseteq\{ & 1 & 0 & 0 & \omega^{{\scriptscriptstyle 1}} & \cdots\}\\ & \boldsymbol{e}^{{\scriptscriptstyle 3}*} & & V^{*} & =\{ & \boldsymbol{e}^{{\scriptscriptstyle 1}} & \boldsymbol{e}^{{\scriptscriptstyle 2}} & \boldsymbol{e}^{{\scriptscriptstyle 3}} & \boldsymbol{\omega} & \cdots\}\\ & \boldsymbol{\omega}^{*} & : & \downarrow & & \downarrow & \downarrow & \downarrow & \downarrow\\ & \vdots & & F & \supseteq\{ & \omega^{{\scriptscriptstyle 1}*} & \omega^{{\scriptscriptstyle 2}*} & \omega^{{\scriptscriptstyle 3}*} & \omega^{{\scriptscriptstyle \mu}*}\omega^{{\scriptscriptstyle \mu}} & \cdots\}\\ & & & V^{*} & =\{ & \boldsymbol{e}^{{\scriptscriptstyle 1}} & \boldsymbol{e}^{{\scriptscriptstyle 2}} & \boldsymbol{e}^{{\scriptscriptstyle 3}} & \boldsymbol{v}^{*} & \cdots\}\\ & \boldsymbol{e}_{{\scriptscriptstyle 1}} & : & \downarrow & & \downarrow & \downarrow & \downarrow & \downarrow\\ \cong V=\{ & \boldsymbol{e}_{{\scriptscriptstyle 2}} & \} & F & \supseteq\{ & 1 & 0 & 0 & v^{*{\scriptscriptstyle 1}} & \cdots\}\\ & \boldsymbol{e}_{{\scriptscriptstyle 3}} & & V^{*} & =\{ & \boldsymbol{e}^{{\scriptscriptstyle 1}} & \boldsymbol{e}^{{\scriptscriptstyle 2}} & \boldsymbol{e}^{{\scriptscriptstyle 3}} & \boldsymbol{v}^{*} & \cdots\}\\ & \boldsymbol{v} & : & \downarrow & & \downarrow & \downarrow & \downarrow & \downarrow\\ & \vdots & & F & \supseteq\{ & v_{{\scriptscriptstyle 1}} & v_{{\scriptscriptstyle 2}} & v_{{\scriptscriptstyle 3}} & v_{{\scriptscriptstyle \mu}}v^{*{\scriptscriptstyle \mu}} & \cdots\} \end{array} \]

dual space of span of partials^[44.2]

coefficient of linear combination for vector space and dual space^[44.4]

inner product space^[48.4.1]

\[ \begin{array}{c} \begin{cases} d\left(f,g\right)=d\left\langle f\middle|g\right\rangle =\sqrt{\left\langle f-g\middle|f-g\right\rangle }\\ f,g\in C_{\mathbb{{\scriptscriptstyle C}}}\left(\left[a,b\right]\right) & \text{continuous complex function}\\ \left(f,g\right)=\left\langle f\middle|g\right\rangle =\int_{a}^{b}\overline{f\left(x\right)}g\left(x\right)\mathrm{d}x=\int_{a}^{b}f^{*}\left(x\right)g\left(x\right)\mathrm{d}x \end{cases}\\ \Downarrow\\ d\left\langle f\middle|g\right\rangle =\sqrt{\int_{a}^{b}\overline{\left[f-g\right]\left(x\right)}\left[f-g\right]\left(x\right)\mathrm{d}x}=\sqrt{\int_{a}^{b}\left|\left[f-g\right]\left(x\right)\right|^{2}\mathrm{d}x} \end{array} \]

\[ v^{*}\left(f\right)=\eta_{{\scriptscriptstyle f}}\left(\cdot\right)=\left(f,\cdot\right)=\left\langle f\middle|\cdot\right\rangle =\int_{a}^{b}\overline{f\left(x\right)}\left(\cdot\right)\mathrm{d}x=\int_{a}^{b}f^{*}\left(x\right)\left(\cdot\right)\mathrm{d}x \]

\[ \eta_{{\scriptscriptstyle f}}\left(g\right)=\left(f,g\right)=\left\langle f\middle|g\right\rangle =\int_{a}^{b}\overline{f\left(x\right)}g\left(x\right)\mathrm{d}x=\int_{a}^{b}f^{*}\left(x\right)g\left(x\right)\mathrm{d}x \]

https://en.wikipedia.org/wiki/Antilinear_map

\[ \begin{cases} v^{*}\left(f+g\right)=v^{*}\left(f\right)+v^{*}\left(g\right) & \text{addivity}=\text{superposition}\\ v^{*}\left(\lambda f\right)=\lambda^{*}v^{*}\left(f\right)=\overline{\lambda}v^{*}\left(f\right) & \text{conjugate homogeneity}=\text{complex conjugate} \end{cases} \]

\[ \begin{aligned} & \begin{cases} v^{*}\left(f+g\right)=v^{*}\left(f\right)+v^{*}\left(g\right) & \text{addivity}=\text{superposition}\\ v^{*}\left(\lambda f\right)=\lambda^{*}v^{*}\left(f\right)=\overline{\lambda}v^{*}\left(f\right) & \text{conjugate homogeneity}=\text{complex conjugate} \end{cases}\\ \Leftrightarrow & \begin{cases} v^{*}\left(f+g\right)=\lambda^{*}v^{*}\left(f\right)+v^{*}\left(g\right)=\overline{\lambda}v^{*}\left(f\right)+v^{*}\left(g\right) & \text{antilinearity}\end{cases} \end{aligned} \]

\[ \begin{array}{cccccccccc} & & & V & =\{ & \hat{f}_{{\scriptscriptstyle 1}} & \hat{f}_{{\scriptscriptstyle 2}} & \hat{f}_{{\scriptscriptstyle 3}} & f & \cdots\}\\ & \hat{f}^{{\scriptscriptstyle 1}}=\left(\hat{f}_{{\scriptscriptstyle 1}},\cdot\right) & : & \downarrow & & \downarrow & \downarrow & \downarrow & \downarrow\\ V^{*}=\{ & \hat{f}^{{\scriptscriptstyle 2}}=\left(\hat{f}_{{\scriptscriptstyle 2}},\cdot\right) & \} & F & \supseteq\{ & \left(\hat{f}_{{\scriptscriptstyle 1}},\hat{f}_{{\scriptscriptstyle 1}}\right)=1 & \left(\hat{f}_{{\scriptscriptstyle 1}},\hat{f}_{{\scriptscriptstyle 2}}\right)=0 & \left(\hat{f}_{{\scriptscriptstyle 1}},\hat{f}_{{\scriptscriptstyle 3}}\right)=0 & \left(\hat{f}_{{\scriptscriptstyle 1}},f\right) & \cdots\}\\ & \hat{f}^{{\scriptscriptstyle 3}}=\left(\hat{f}_{{\scriptscriptstyle 3}},\cdot\right) & & V & =\{ & \hat{f}_{{\scriptscriptstyle 1}} & \hat{f}_{{\scriptscriptstyle 2}} & \hat{f}_{{\scriptscriptstyle 3}} & f & \cdots\}\\ & f^{*}=\left(f,\cdot\right) & : & \downarrow & & \downarrow & \downarrow & \downarrow & \downarrow\\ & \vdots & & F & \supseteq\{ & \left(f,\hat{f}_{{\scriptscriptstyle 1}}\right) & \left(f,\hat{f}_{{\scriptscriptstyle 2}}\right) & \left(f,\hat{f}_{{\scriptscriptstyle 3}}\right) & \left(f,f\right) & \cdots\} \end{array} \]

\[ \begin{array}{cccccccccc} & & & V & =\{ & \hat{f}_{{\scriptscriptstyle 1}} & \hat{f}_{{\scriptscriptstyle 2}} & \hat{f}_{{\scriptscriptstyle 3}} & f & \cdots\}\\ & \hat{f}^{{\scriptscriptstyle 1}}=\left\langle \hat{f}_{{\scriptscriptstyle 1}}\middle|\cdot\right\rangle & : & \downarrow & & \downarrow & \downarrow & \downarrow & \downarrow\\ V^{*}=\{ & \hat{f}^{{\scriptscriptstyle 2}}=\left\langle \hat{f}_{{\scriptscriptstyle 2}}\middle|\cdot\right\rangle & \} & F & \supseteq\{ & \left\langle \hat{f}_{{\scriptscriptstyle 1}}\middle|\hat{f}_{{\scriptscriptstyle 1}}\right\rangle =1 & \left\langle \hat{f}_{{\scriptscriptstyle 1}}\middle|\hat{f}_{{\scriptscriptstyle 2}}\right\rangle =0 & \left\langle \hat{f}_{{\scriptscriptstyle 1}}\middle|\hat{f}_{{\scriptscriptstyle 3}}\right\rangle =0 & \left\langle \hat{f}_{{\scriptscriptstyle 1}}\middle|f\right\rangle & \cdots\}\\ & \hat{f}^{{\scriptscriptstyle 3}}=\left\langle \hat{f}_{{\scriptscriptstyle 3}}\middle|\cdot\right\rangle & & V & =\{ & \hat{f}_{{\scriptscriptstyle 1}} & \hat{f}_{{\scriptscriptstyle 2}} & \hat{f}_{{\scriptscriptstyle 3}} & f & \cdots\}\\ & f^{*}=\left\langle f\middle|\cdot\right\rangle & : & \downarrow & & \downarrow & \downarrow & \downarrow & \downarrow\\ & \vdots & & F & \supseteq\{ & \left\langle f\middle|\hat{f}_{{\scriptscriptstyle 1}}\right\rangle & \left\langle f\middle|\hat{f}_{{\scriptscriptstyle 2}}\right\rangle & \left\langle f\middle|\hat{f}_{{\scriptscriptstyle 3}}\right\rangle & \left\langle f\middle|f\right\rangle & \cdots\} \end{array} \]

row vector is dual vector of column vector

\[ f=\begin{pmatrix}a\\ b \end{pmatrix}\rightarrow v^{*}\left(f\right)=\eta_{{\scriptscriptstyle f}}=\begin{pmatrix}a^{*} & b^{*}\end{pmatrix}=\begin{pmatrix}\overline{a} & \overline{b}\end{pmatrix}=\overline{\begin{pmatrix}a\\ b \end{pmatrix}}^{\intercal}=\overline{\begin{pmatrix}a\\ b \end{pmatrix}^{\intercal}}=\begin{pmatrix}a\\ b \end{pmatrix}^{\dagger} \]

\[ \eta_{{\scriptscriptstyle f}}\cdot f=\begin{pmatrix}a^{*} & b^{*}\end{pmatrix}\begin{pmatrix}a\\ b \end{pmatrix}=a^{*}a+b^{*}b \]

https://www.bilibili.com/video/BV1GN411m7A9/?t=2m40s

https://en.wikipedia.org/wiki/Riesz_representation_theorem

Theorem 18.6 Riesz representation theorem

\[ \text{to be proved} \]

https://www.bilibili.com/video/BV1GN411m7A9/?t=6m20s

\[ \text{Hilbert space }V\begin{cases} B=\left\{ \hat{f}_{{\scriptscriptstyle i}}\right\} _{i\in I}=\left\{ \cdots,\hat{f}_{{\scriptscriptstyle i}},\cdots\right\} \\ \begin{cases} \sum\limits _{i}c_{{\scriptscriptstyle i}}\hat{f}_{{\scriptscriptstyle i}}=0\Rightarrow c_{{\scriptscriptstyle i}}=0 & \text{bases are linear independent}\\ f=\sum\limits _{i}c_{{\scriptscriptstyle i}}\hat{f}_{{\scriptscriptstyle i}},c_{{\scriptscriptstyle i}}\in\mathbb{C} & \text{expansion over bases} \end{cases}\\ \begin{cases} \left(\hat{f}_{{\scriptscriptstyle i}},\hat{f}_{{\scriptscriptstyle j}}\right)=\left\langle \hat{f}_{{\scriptscriptstyle i}}\middle|\hat{f}_{{\scriptscriptstyle j}}\right\rangle =\delta_{{\scriptscriptstyle ij}}\\ \text{completeness}:\forall\hat{f}_{{\scriptscriptstyle i}}\in B,\not\exists f\in V-B\left[\left(\hat{f}_{{\scriptscriptstyle i}},f\right)=\left\langle \hat{f}_{{\scriptscriptstyle i}}\middle|f\right\rangle =0\right] \end{cases} \end{cases} \]

\[ f=\sum\limits _{i}\left(\hat{f}_{{\scriptscriptstyle i}}\cdot f\right)\hat{f}_{{\scriptscriptstyle i}}=\sum\limits _{i}\left(\hat{f}_{{\scriptscriptstyle i}},\hat{f}_{{\scriptscriptstyle j}}\right)\hat{f}_{{\scriptscriptstyle i}}=\sum\limits _{i}\left\langle \hat{f}_{{\scriptscriptstyle i}}\middle|\hat{f}_{{\scriptscriptstyle j}}\right\rangle \hat{f}_{{\scriptscriptstyle i}} \]

https://www.bilibili.com/video/BV1GN411m7A9/?t=7m55s

48.5.1 Dirac bracket symmetry

\[ f=\sum\limits _{i}\left(\hat{f}_{{\scriptscriptstyle i}},f\right)\hat{f}_{{\scriptscriptstyle i}}=\sum\limits _{i}\hat{f}_{{\scriptscriptstyle i}}\left(\hat{f}_{{\scriptscriptstyle i}},f\right) \]

\[ \begin{aligned} f^{*}=\left(f,\cdot\right)= & \left(\sum\limits _{i}\left(\hat{f}_{{\scriptscriptstyle i}},f\right)\hat{f}_{{\scriptscriptstyle i}},\cdot\right)=\left(\sum\limits _{i}\hat{f}_{{\scriptscriptstyle i}}\left(\hat{f}_{{\scriptscriptstyle i}},f\right),\cdot\right)\\ \overset{\text{antilinearity}}{=} & \overline{\sum\limits _{i}\left(\hat{f}_{{\scriptscriptstyle i}},f\right)}\left(\hat{f}_{{\scriptscriptstyle i}},\cdot\right)=\sum\limits _{i}\overline{\left(\hat{f}_{{\scriptscriptstyle i}},f\right)}\left(\hat{f}_{{\scriptscriptstyle i}},\cdot\right)\\ = & \sum\limits _{i}\left(f,\hat{f}_{{\scriptscriptstyle i}}\right)\left(\hat{f}_{{\scriptscriptstyle i}},\cdot\right)\\ \overset{\text{Dirac bracket}}{\rightarrow} & \sum\limits _{i}\left\langle f\middle|\hat{f}_{{\scriptscriptstyle i}}\right\rangle \left\langle \hat{f}_{{\scriptscriptstyle i}}\right|=\left\langle f\right|\\ \Updownarrow\\ f= & \sum\limits _{i}\hat{f}_{{\scriptscriptstyle i}}\left(\hat{f}_{{\scriptscriptstyle i}},f\right)\\ \overset{\text{Dirac bracket}}{\rightarrow} & \sum\limits _{i}\left|\hat{f}_{{\scriptscriptstyle i}}\right\rangle \left\langle \hat{f}_{{\scriptscriptstyle i}}\middle|f\right\rangle =\left|f\right\rangle \end{aligned} \]

\[ \begin{cases} \left|f\right\rangle =\sum\limits _{i}\left|\hat{f}_{{\scriptscriptstyle i}}\right\rangle \left\langle \hat{f}_{{\scriptscriptstyle i}}\middle|f\right\rangle =\sum\limits _{i}\left\langle \hat{f}_{{\scriptscriptstyle i}}\middle|f\right\rangle \left|\hat{f}_{{\scriptscriptstyle i}}\right\rangle \\ \left\langle f\right|=\sum\limits _{i}\left\langle f\middle|\hat{f}_{{\scriptscriptstyle i}}\right\rangle \left\langle \hat{f}_{{\scriptscriptstyle i}}\right|\\ \left\langle \hat{f}_{{\scriptscriptstyle i}}\middle|\hat{f}_{{\scriptscriptstyle j}}\right\rangle =\delta_{{\scriptscriptstyle ij}} \end{cases} \]

\[ \begin{array}{cccccccccc} & & & V & =\{ & \left|\hat{f}_{{\scriptscriptstyle 1}}\right\rangle & \left|\hat{f}_{{\scriptscriptstyle 2}}\right\rangle & \left|\hat{f}_{{\scriptscriptstyle 3}}\right\rangle & \left|f\right\rangle & \cdots\}\\ & \left\langle \hat{f}_{{\scriptscriptstyle 1}}\right| & : & \downarrow & & \downarrow & \downarrow & \downarrow & \downarrow\\ V^{*}=\{ & \left\langle \hat{f}_{{\scriptscriptstyle 2}}\right| & \} & F & \supseteq\{ & \left\langle \hat{f}_{{\scriptscriptstyle 1}}\middle|\hat{f}_{{\scriptscriptstyle 1}}\right\rangle =1 & \left\langle \hat{f}_{{\scriptscriptstyle 1}}\middle|\hat{f}_{{\scriptscriptstyle 2}}\right\rangle =0 & \left\langle \hat{f}_{{\scriptscriptstyle 1}}\middle|\hat{f}_{{\scriptscriptstyle 3}}\right\rangle =0 & \left\langle \hat{f}_{{\scriptscriptstyle 1}}\middle|f\right\rangle & \cdots\}\\ & \left\langle \hat{f}_{{\scriptscriptstyle 3}}\right| & & V & =\{ & \left|\hat{f}_{{\scriptscriptstyle 1}}\right\rangle & \left|\hat{f}_{{\scriptscriptstyle 2}}\right\rangle & \left|\hat{f}_{{\scriptscriptstyle 3}}\right\rangle & \left|f\right\rangle & \cdots\}\\ & \left\langle f\right| & : & \downarrow & & \downarrow & \downarrow & \downarrow & \downarrow\\ & \vdots & & F & \supseteq\{ & \left\langle f\middle|\hat{f}_{{\scriptscriptstyle 1}}\right\rangle & \left\langle f\middle|\hat{f}_{{\scriptscriptstyle 2}}\right\rangle & \left\langle f\middle|\hat{f}_{{\scriptscriptstyle 3}}\right\rangle & \left\langle f\middle|f\right\rangle & \cdots\} \end{array} \]

\[ \begin{cases} \left(c\psi,\cdot\right)\rightarrow\left\langle c\psi\right|=c^{*}\left\langle \psi\right| & c\psi\rightarrow\left|c\psi\right\rangle =c\left|\psi\right\rangle \\ \left\langle \psi\right|\leftrightarrow\left|\psi\right\rangle \\ \left\langle \psi|\phi\right\rangle =\overline{\left\langle \phi|\psi\right\rangle } & \left\langle \phi|\psi\right\rangle =\overline{\left\langle \psi|\phi\right\rangle }\\ \left\langle c\psi|\phi\right\rangle =c^{*}\left\langle \psi|\phi\right\rangle & \left\langle \phi|c\psi\right\rangle =c\left\langle \phi|\psi\right\rangle \end{cases} \]

$\left|f\right\rangle \left\langle g\right|=?$

\[ \begin{array}{c} \left|f\right\rangle \left\langle g\right|\left|h\right\rangle =\left|f\right\rangle \left\langle g\middle|h\right\rangle =\left\langle g\middle|h\right\rangle \left|f\right\rangle \\ \Downarrow\\ \left|h\right\rangle \overset{\left|f\right\rangle \left\langle g\right|}{\rightarrow}\left|f\right\rangle \left\langle g\right|\left|h\right\rangle =\left\langle g\middle|h\right\rangle \left|f\right\rangle \end{array} \]

\[ \begin{array}{c} \left\langle h\right|\left|f\right\rangle \left\langle g\right|=\left\langle h\middle|f\right\rangle \left\langle g\right|\\ \Downarrow\\ \left\langle h\right|\overset{\left|f\right\rangle \left\langle g\right|}{\rightarrow}\left\langle h\right|\left|f\right\rangle \left\langle g\right|=\left\langle h\middle|f\right\rangle \left\langle g\right| \end{array} \]

\[ \left|f\right\rangle \left\langle g\right|\text{ is a linear transform or rank-}2\text{ tensor} \]

\[ \begin{aligned} \left|f\right\rangle = & \sum\limits _{i}\left|\hat{f}_{{\scriptscriptstyle i}}\right\rangle \left\langle \hat{f}_{{\scriptscriptstyle i}}\middle|f\right\rangle \\ = & \sum\limits _{i}\left|\hat{f}_{{\scriptscriptstyle i}}\right\rangle \left\langle \hat{f}_{{\scriptscriptstyle i}}\right|\left|f\right\rangle \\ = & \left(\sum\limits _{i}\left|\hat{f}_{{\scriptscriptstyle i}}\right\rangle \left\langle \hat{f}_{{\scriptscriptstyle i}}\right|\right)\left|f\right\rangle =1\left|f\right\rangle =\left|f\right\rangle \\ 1= & \sum\limits _{i}\left|\hat{f}_{{\scriptscriptstyle i}}\right\rangle \left\langle \hat{f}_{{\scriptscriptstyle i}}\right|\\ \sum\limits _{i}\left|\hat{f}_{{\scriptscriptstyle i}}\right\rangle \left\langle \hat{f}_{{\scriptscriptstyle i}}\right|= & 1 \end{aligned} \]

\[ \sum\limits _{i}\left|\hat{f}_{{\scriptscriptstyle i}}\right\rangle \left\langle \hat{f}_{{\scriptscriptstyle i}}\right|=1 \]

the above is completeness relationship.

\[ \begin{cases} \left|f\right\rangle =1\left|f\right\rangle =\left(\sum\limits _{i}\left|\hat{f}_{{\scriptscriptstyle i}}\right\rangle \left\langle \hat{f}_{{\scriptscriptstyle i}}\right|\right)\left|f\right\rangle =\sum\limits _{i}\left|\hat{f}_{{\scriptscriptstyle i}}\right\rangle \left\langle \hat{f}_{{\scriptscriptstyle i}}\middle|f\right\rangle \\ \left\langle f\right|=\left\langle f\right|1=\left\langle f\right|\left(\sum\limits _{i}\left|\hat{f}_{{\scriptscriptstyle i}}\right\rangle \left\langle \hat{f}_{{\scriptscriptstyle i}}\right|\right)=\sum\limits _{i}\left\langle f\middle|\hat{f}_{{\scriptscriptstyle i}}\right\rangle \left\langle \hat{f}_{{\scriptscriptstyle i}}\right| \end{cases} \]

The sculpture is already complete within the marble block, before I start my work. It is already there, I just have to chisel away the superfluous material. Michelangelo

https://www.goodreads.com/quotes/1191114-the-sculpture-is-already-complete-within-the-marble-block-before

https://www.bilibili.com/video/BV1y84y1U7Ps