2.3 定積分の性質
ここでは,定積分のいくつかの性質について紹介する.
2.3.1 偶関数・奇関数
Theorem 2.3 (偶関数・奇関数の定積分) 関数\(f(x)\)が偶関数とする.すなわち,\(f(x) = f(-x)\)が成り立つとする.このとき, \[\begin{align} \int_{-a}^a f(x) dx = 2 \int_0^a f(x)dx \end{align}\] が成り立つ.
また,関数\(g(x)\)が奇関数,すなわち\(f(x) = -g(-x)\)が成り立つ時,
\[\begin{align} \int_{-a}^a g(x) dx = 0 \end{align}\]
が成り立つ.
偶関数とは,\(y\)軸に対して対称であるような関数で,奇関数は原点対称となるような関数である. これらは実際に可視化するとよりわかりやすい. ここでは,偶関数の例として\(x^2\)をみてみよう.なお,\(x^3 - 2x\)は奇関数であり(x^3と2xがそれぞれ奇関数であり,その和も奇関数となる), 図2.1がそのまま例となっている・
Figure 2.2: 偶関数の面積
図2.2は\(x^2\)の\([-2,2]\)でのグラフだが,\(y\)軸について対称であり,面積についても,\([-2,0]\)と\([0,2]\)が同じであることが視覚的にもわかるだろう. つまり,\([-2,2]\)の面積と\([0,2]\)の面積を2倍にしたものが一致するであろう,というのが定理の意味するところである. 逆に,奇関数は正負が逆転するため足し上げると0になる,ということである.
Theorem 2.4 (二つの関数で囲まれた領域の面積) 関数\(f,g\)に対して,区間\(I=[a,b]\)上で\(f(x) \geq g(x)\)が成り立つ時,
\[\begin{align} \int_a^b f(x) - g(x) dx \end{align}\]
は\(x=a, x=b, f(x), g(x)\)で囲まれた部分の面積を表す.
図2.3は,\(f(x) = e^x, g(x) = 2\sin(5x)\)とした時の,\([1,3]\)における面積を可視化したものである.見ての通りTheorem2.4の仮定を満たしており,面積をそのように求めることができる.
Figure 2.3: 二つの関数に囲まれた領域の面積
Theorem 2.1 (定積分の性質) 定積分について,次の3つの性質が成り立つ.
- 関数\(f(x)\)に対して,
\[\begin{align} \int_a^b f(x) dx + \int_b^c f(x) dx = \int_a^c f(x) dx \end{align}\]
が成り立つ.また,\(\int_a^a f(x) dx = 0\)より,\(\int_a^b f(x) dx = - \int_b^a f(x) dx\)となる.
- 関数\(f(x)\)に対して, \[\begin{align} \left| \int_a^b f(x) dx \right| \leq \int_a^b |f(x)| dx \end{align}\]
が成り立つ.
- 関数\(f(x)\)が区間\(I=[a,b]\)上で\(f(x) \geq 0\)とする.このとき
\[\begin{align} \int_a^b f(x) dx \geq 0 \end{align}\]
が成り立つ.もし関数\(f(x)\)が連続関数であれば,等号成立は\({}^{\forall}x \in I, f(x) = 0\)のときのみである.
また,関数\(f(x), g(x)\)が区間\(I\)上で\(f(x) \geq g(x)\)とすると,
\[\begin{align} \int_a^b f(x) dx \geq \int_a^b g(x) dx \end{align}\]
が成り立つ.\(f,g\)がともに連続関数の場合,等号成立は\({}^{\forall}x \in I, f(x) = g(x)\)のときのみである.
それぞれの証明は(椎名・姫野・保科 2019)を参照のこと.
Theorem 2.5 (リーマン和) 関数\(f(x)\)についての定積分\(\int_a^b f(x) dx\)は \[\begin{align} \int_a^b f(x) dx = \lim_{n \rightarrow \infty} \sum_{i=1}^{n} {b-a \over n} f \left( a + (b-a){i \over n} \right) \end{align}\] としても計算される.これをリーマン和とも呼ぶ.
Figure 2.4: n=10の場合のリーマン和
図2.4は\(f(x) = x^3 - 2x + 3\)の関数をリーマン和の考え方に従って\(n=10\)とした時の面積の近似である. このように,我々が求めやすい長方形を使って細かく分割して面積を足し上げると言うのが基本的な考え方である.
次に,この分割数\(n\)を大きくしていった時に,面積の近似がどの程度になるのかを可視化してみよう.
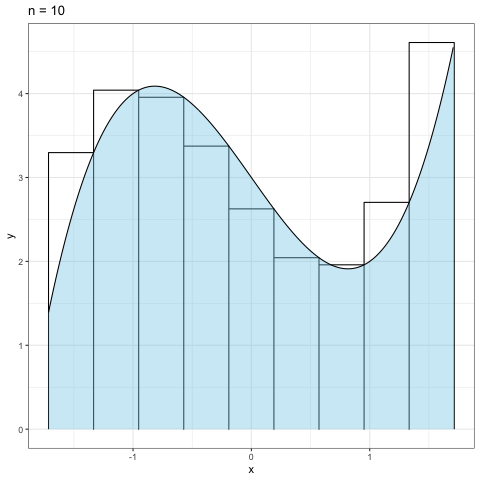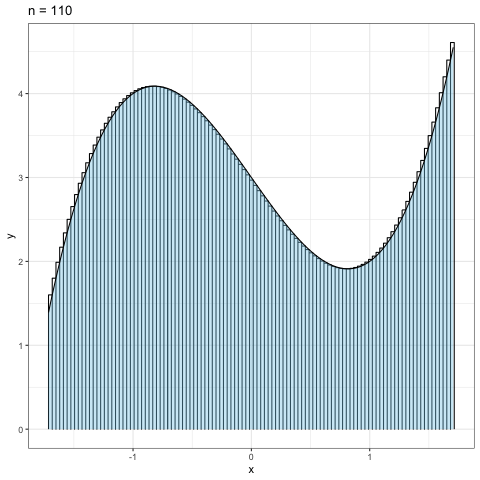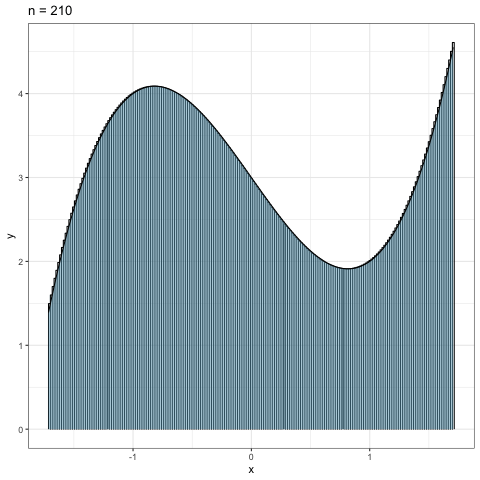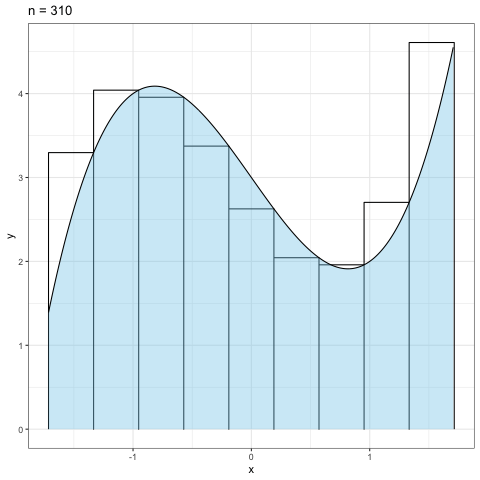
Figure 2.5: リーマン和のnを大きくしていった場合
図2.5は分割数の\(n\)を\(10\)から\(300\)まで10刻みで増やしていった時の 近似具合を見たものである.当然だが,分割数が大きくなればなるほど近似精度が高まっていくことが見て取れるだろう.
Exercise 2.3 (定積分2) hoge