2.6 広義積分

次の図2.6のように，ある点だけ（ここでは$x=0$）で定義されていない 関数について，その点を含む区間で積分を考えたい場合がある． このような時に広義積分が役に立つ．

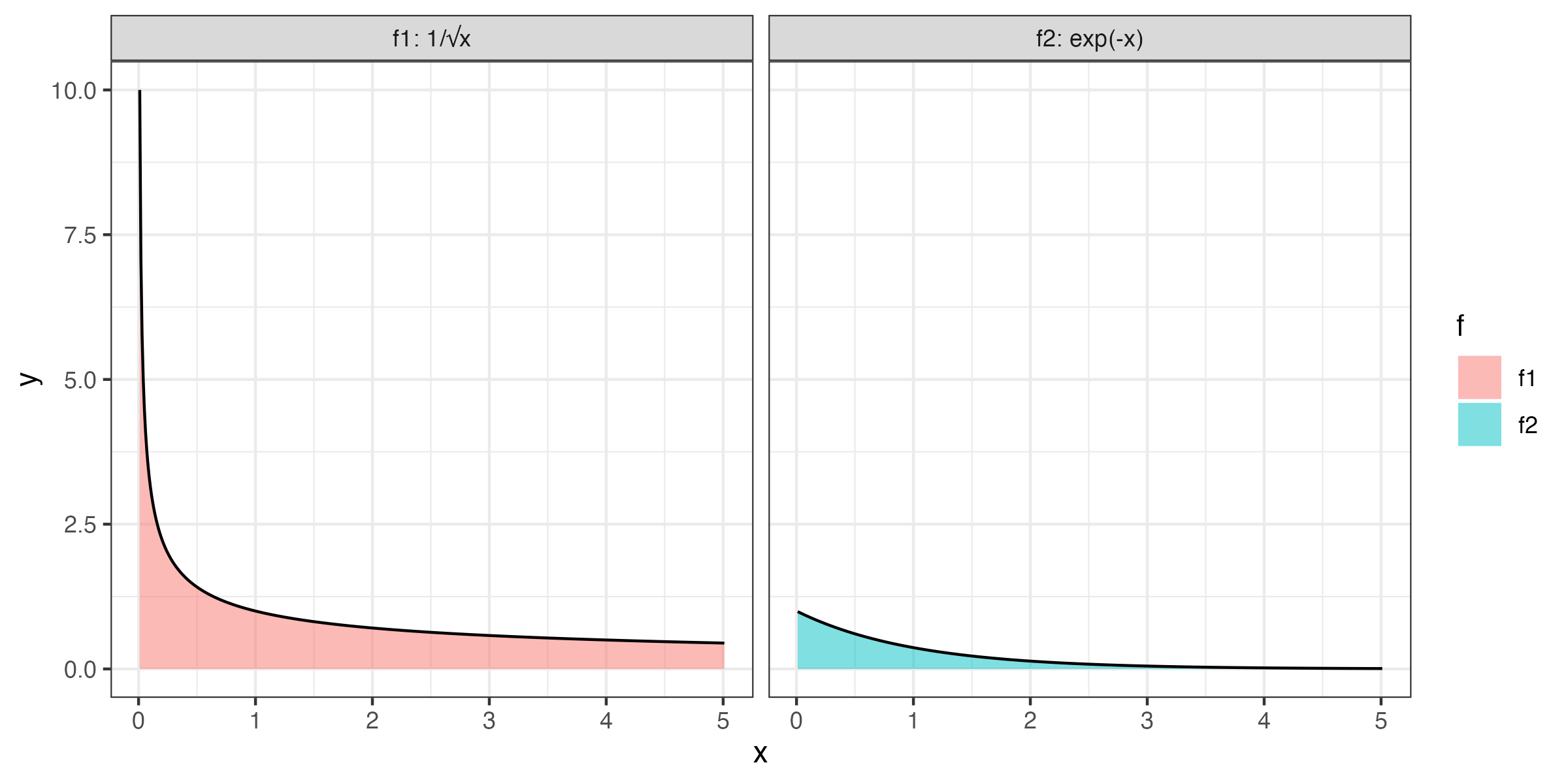
Figure 2.6: 広義積分の例

例えば，このよう場合，$f(x) = 1/\sqrt{x}$では$x=0$で有限な値を取らないし，$f(x) = \exp(-x)$では$x \rightarrow \infty$での定積分を計算する際は区間幅が無限大となってしまう．

Definition 2.3 (広義積分) 関数$f$の区間$I = (a,b]$上での定積分を考える．ただし，$f(x)$は$x=a$で定義されていないとする．ここで， $$\begin{align} \lim_{x \rightarrow a} \int_x^b f(t)dt \end{align}$$ が存在する時，この極限を$f(x)$の$x=a$から$x=b$での広義積分と呼び， 通常の定積分と同様に$\int_a^b f(x) dx$と表す．また，関数$f$の区間$I=[a, \infty)$上での定積分については， $$\begin{align} \lim_{x \rightarrow \infty} \int_a^x f(t) dt \end{align}$$

が存在する時，この極限を$f(x)$の$x=a$から$x=\infty$での広義積分といい，$\int_a^\infty f(x) dx$と表す．

一つ広義積分の例を見てみよう．

Example 2.1 (広義積分の例) $$\begin{align} \int_0^2 {1 \over \sqrt{x}} dx &= \int_0^2 x^{-1/2} dx \\ &= \left[ 2 x^{1 \over 2} \right]_0^2 \\ &= 2\sqrt{2} \end{align}$$

ここで見たように実用上は，通常の定積分と同じように計算を進めれば良いが， その過程で広義積分となっているかどうかについてはしっかりと把握しているべきである．

Exercise 2.5 (広義積分) 次の関数を広義積分せよ． $$\begin{align} \int_0^\infty e^{-x} dx \end{align}$$