Some Diagnostics for MCMC
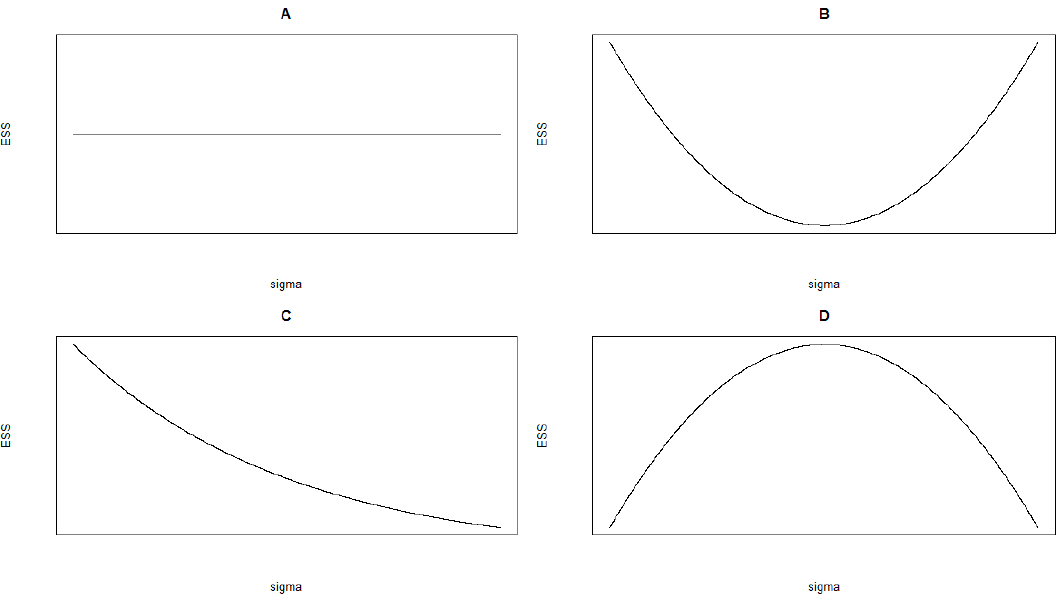
- Consider a Metropolis algorithm where given current state \(x\), the proposed state is generated from a \(N(x, \sigma)\) distribution. Suppose you run the algorithm for many different values of \(\sigma\) and compute the effective sample size (ESS) for each. All other thing being equal, which one of the following plots best depicts the relationship between \(\sigma\) and ESS? Choose one and briefly explain your reasoning.
- The following are trace plots from three different MCMC algorithms for simulating values from a N(0, 1) posterior distribution. That is, the target distribution is the N(0, 1) distribution. Each algorithm has been run for 10000 steps after a warm up (burn in) period of 1000 steps. Note: all plots are on the same scale; pay attention to the scale. Use the plots to answer the following questions. For each prompt choose a plot and explain your reasoning.
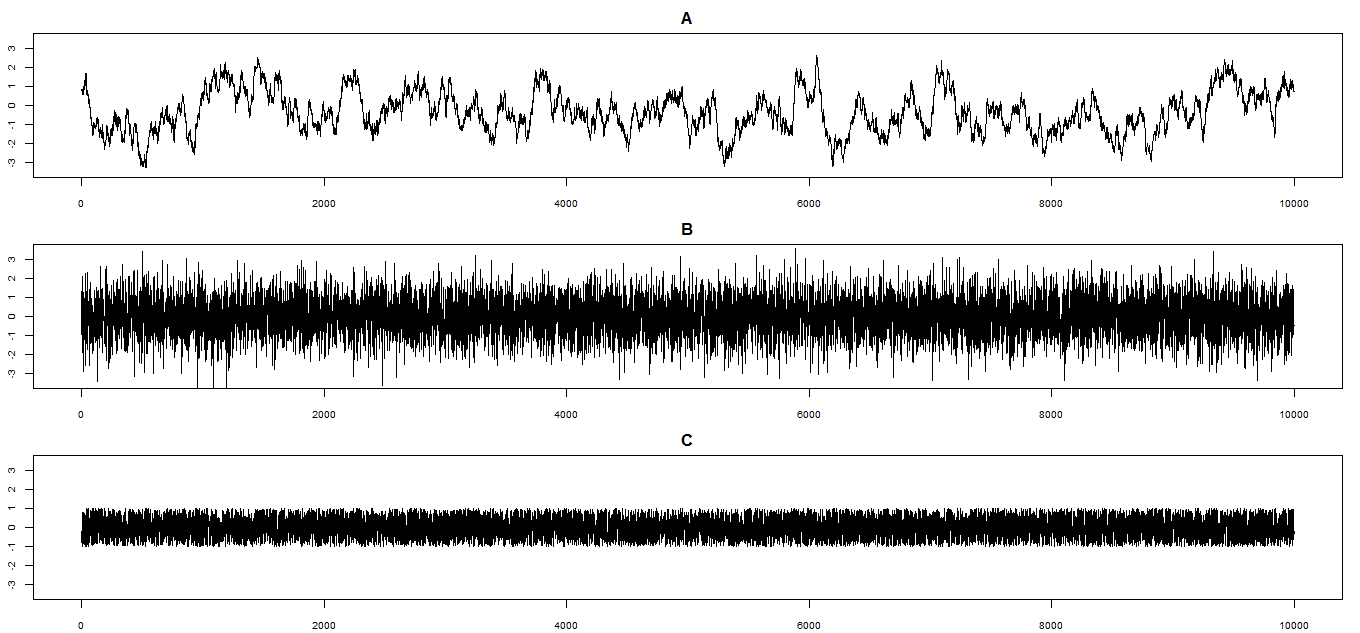
- Which plot corresponds to the smallest effective sample size?
- Which plot corresponds to the most UNrepresentative sample?
- Which plot corresponds to the algorithm that best achieves its goal?
- You use a Metropolis-Hastings algorithm to simulate from the probability distribution
\[\begin{align*} x & & 1 & & 2 & & 3\\ \pi(x) & & 0.2 & & 0.3 & & 0.5 \end{align*}\]
Suppose that for each of the following three proposal chains, a Metropolis-Hastings algorithm is used to run an MC.
\[ \mathbf{Q_1} = \begin{bmatrix} 0 & 1 & 0\\ 0.5 & 0.3 & 0.2\\ 0.6 & 0.4 & 0 \end{bmatrix} \]
\[ \mathbf{Q_2} = \begin{bmatrix} 0.1 & 0.4 & 0.5\\ 0.2 & 0.3 & 0.5\\ 0.1 & 0.3 & 0.6 \end{bmatrix} \]
\[ \mathbf{Q_3} = \begin{bmatrix} 0.7 & 0.3 & 0\\ 0 & 0.9 & 0.1\\ 0 & 0.2 & 0.8 \end{bmatrix} \]
All other things being equal, for which of the three cases would the effective sample size (ESS) be smallest? Explain your reasoning.
All other things being equal, for which of the three cases would the shortest “warm up” (“burn in”) period be required? Explain your reasoning.